Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intercalation-dependent elastic properties of transition metal dichalcogenides†
Conor Jason
Price
 * and
Steven Paul
Hepplestone
* and
Steven Paul
Hepplestone
 *
*
Department of Physics, University of Exeter, Stocker Road, Exeter, EX4 4QL, UK. E-mail: cjp225@exeter.ac.uk; S.P.Hepplestone@exeter.ac.uk
First published on 30th August 2023
Abstract
We present a first-principles study into the elastic behaviour of layered TMDCs and their lithium- or magnesium-intercalated structures. Assessment of the elastic matrices allow us to evaluate key properties such as the bulk, shear, and Young's moduli. These show a general increase with the addition of an intercalant species, though TMDCs composed of later Group transition metals break this trend. We also assess elastic ratios which describe the ductility of a material, allowing us to conclude that the pristine materials are brittle, but become more ductile with the addition of lithium or magnesium. The anisotropy of these materials is also assessed using a combination of the universal anisotropy metric and a direct calculation of the angular dependence of the Young's modulus. The pristine van der Waals materials demonstrate a high degree of anisotropy due to their relatively weak interactions across the vdW spacing, but the introduction of an ion within the vdW region reduced this anisotropy. Finally, we have also explored the elastic properties of intermediate intercalant concentrations for selected systems, where we conclude that different intercalant configurations or the use of multivalent intercalant species can cause significant deviations from commonly-used linear extrapolations.
1. Introduction
Layered van der Waals (vdW) materials have been the subject of intense study over the past few decades due to the wide range of electronic, optical, and chemical properties they can exhibit. This is further enhanced by the ability to tune these properties through layer control and defect engineering, resulting in them being utilised across a wide range of applications. Besides the optical and electronic properties that are typically of direct practical interest, other fundamental properties such as the mechanical behaviour are also important for all industrial applications. However, very few investigations have been carried out to explore such mechanical behaviour. Nevertheless, due to the presence of a vdW gap, the mechanical properties of layered materials are highly anisotropic,1 making them interesting candidates for thermoelectric,2,3 superconducting,4,5 and piezoelectric6–8 applications.One application in which the layered vdW materials have found particular success is as intercalation electrodes. Conventional materials experience stresses arising from the intercalation of ions into their structure due to phase changes,9–11 ionic diffusion,12 and volumetric expansion.13 These lead to material ‘fracturing’, ultimately resulting in structural degradation and device failure. However, the intrinsic interlayer spacings within vdW materials allow for easy storage and transport of ions during cell cycling,14,15 resulting in relatively low volumetric expansions.16 As such, many vdW materials, such as the NMC variants,17–19 graphite,20–22 and MXenes,23 have each been the subject of many studies in recent years. The transition metal dichalcogenides (TMDCs), a broad family of such vdW materials, have also been the subject of many investigations with recent works highlighting their voltages, thermodynamic stability, and ideal expansion.24,25 Unfortunately, despite their ideal layered nature, vdW materials are not totally immune from the intercalant-related stresses, and can suffer from limited lifetimes because of this.
Several models based on solid-state diffusion and continuum mechanics have been developed to investigate stresses in electrodes associated with ionic diffusion,26–32 and have been applied to graphite. However, these rely on quantities describing the mechanical and elastic behaviour of the material, such as the Young's modulus, Poisson ratio, or elements of the elastic tensor. Though the elastic properties of several materials have been explored using experimental and theoretical methods, many quantities are typically absent from literature as experimental investigations into these mechanical properties are difficult to perform. Consequently, such investigations of intercalated materials are often restricted to the limits of intercalation: For example, the elastic properties of lithium-intercalated graphite have been explored using ultrasonic resonance and neutron scattering techniques,33–36 and though data is available for the pure graphite and Li6C compositions, little is known about the elastic properties for intermediate concentrations. Even recent techniques such as nanoindentation limit studies of vdW materials to samples of a few layers,37–43 raising issues of resolving vdW adhesion to substrate materials.44 Further, reported elastic properties of bulk TMDC samples are typically dominated by defects at grain boundaries and existing cracks, which have been studies using molecular dynamics simulations,45–47 but are not intrinsic to the material.43
In the absence of such experimental data, then, approximations and assumptions must be made. For unintercalated materials, extrapolation from the elastic properties of chemically or structurally related materials has been suggested,48,49 though this requires an in-depth investigation of at least one related structure and calibrations for non-linear properties are needed. For the evolution of elastic properties with increased intercalant concentration, on the other hand, one approach is to assume the elastic moduli and components of the elasticity tensor are independent of intercalant concentration, whereas another is to assume a linear trend between the initial and final charge states.50,51 Clearly, an investigation into the fundamental elastic behaviour of these materials is required: Not only will this further our understanding of the elastic properties of layered materials and how these change with the loss of the vdW spacing, but will also provide necessary quantities for continuum models.
In this article, we report on a theoretical modelling of the mechanical properties of TMDC layers, with a focus on their properties for use as electrode materials in lithium and magnesium ion cells. From the calculated elastic tensor we derive many key elastic quantities, including the bulk and shear moduli, and commonly-considered elastic ratios. We also comment on the elastic anisotropy using this universal anisotropy metric and the angular Young's modulus. Finally, we investigate how these properties vary with intercalant concentration. Further details and discussions that go towards supporting the work presented in this article are presented in the ESI.†
2 Methods
2.1 First-principles methods
In this work, first principles techniques based on density functional theory were used to determine the elastic properties of layered MX2 materials, as well as their lithium- and magnesium-intercalated structures. These calculations were performed using the Vienna ab initio simulation package (VASP).52–55 The valence electrons included for each species, along with further calculation details, are indicated in ESI† Section SI.A. The projector augmented wave method56 was used to describe the interaction between core and valence electrons, and a plane-wave basis set was used with an energy cutoff of 700 eV. van der Waals interactions have been addressed using the zero damping DFT-D3 method.57This study focuses on 1T-phase TMDCs, as many of the TMDCs exhibit the 1T-phase58–61 and previous work has highlighted the preference for the T-phase structure with intercalation.25 Individual TMDC sheets are held together by covalent M–X bonds with p–d hybridisation,62 whilst the sheets are coupled to each other by weak van der Waals forces.63 Intercalant ions were introduced into the vdW spacing, choosing the octahedrally-coordinated site above the metal atom of the host structure as this has been shown in a previous work to be the lowest in energy.25 The modelled structure are illustrated in Fig. 1. Initial structural relaxations (allowing for both ionic and unit cell optimisation) to determine the geometry were completed using the Perdew–Burke–Ernzerhof (PBE)64 functional form of the generalised gradient approximation (GGA). These were converged to a force tolerance of 0.0001 eV Å−1 per atom, electronic self-consistency was considered to an accuracy of 10−8 eV, using a Monkhorst–Pack65k-point grids of 12 × 12 × 12.
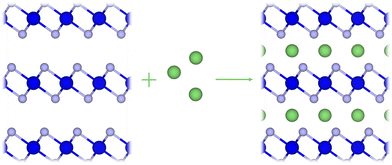 | ||
| Fig. 1 An illustration of the layered TMDC structure (blue) considered in this work, and where the intercalant ions (green) are located within the vdW gap. | ||
As transition metal compounds allow for the possibility of unpaired electrons in d and f orbitals, all calculations have been performed allowing for optimisation of collinear spin-polarization without specifying any initial spin configuration. Spin–orbit effects have not been considered, and previous works have shown that calculations including spin–orbit effects may not yield significantly different elastic properties compared to simpler calculations.66,67 Further discussion is presented in ESI† Section SI.A.
Due to the small changes in energy that can be involved, the elements of the elastic tensor can be sensitive to the sampling of reciprocal space.51 For the primitive unit cells considered, Monkhorst–Pack k-point grids of 18 × 18 × 18 were used, and for the 2 × 2 × 2 supercells comparable grids of 9 × 9 × 9. We assess the convergence of the used k-point grids in ESI† Section SI.B, and provide a discussion on the use of hybrid functionals or +U corrections, which have not been used in this work.
It is important to make comparison with experiment to offer an indication of the error associated with theoretical modelling of a material. Unfortunately, investigations into the elastic/mechanical properties of materials (including the TMDCs) are limited as they can be difficult to perform. In place of such direct comparisons of our work with experiment, we have provided a brief discussion in ESI† Section SI.A comparing different first principles methods with experiment for several different materials, where we find that predicted values typically lie within ∼10% of those obtained experimentally. This agrees with the typical errors previous works have associated with calculation of elastic properties using such methods.68 We also present a small study in ESI† Section SI.B† into graphite and LiCoO2, materials that are very similar to the TMDC considered in this work and have several studies available within the literature. Again, we find that calculated values lie within ∼10% of those obtained experimentally. We also make comparison to available works on the Materials Project69,70 in ESI† Section SII.B.1.
As mentioned above, this work focuses on the T-phase TMDC structure. In ESI† Section SI.C, we compare the energetic difference between the T-phase and the common alternative H-phase, where we conclude that the H-phase is relevant only for pristine Group VI TMDCs, lithium-intercalated Group V TMDCs, and magnesium-intercalated Group IV TMDCs. However, as the energy differences between the two phases remain relatively small, the T-phase is determined to be of the most interest due to the preference of the wider TMDC family to exhibit it, the relevance of the T-phase even for those TMDCs which adopt the H-phase, and for a consistent comparison.
We have also included in ESI† Section SI.C a discussion on the stability of TMDCs with intercalation, using both a simple formation energy and a metric used to describe the stability of TMDCs against conversion into Li2X or MgX. Using the formation energy, we find that it is energetically favourable for all TMDCs (with one exception) to be intercalated. Though the intercalation of an arbitrary species into the vdW gap must overcome the endothermic expansion of layers, Group I and II species offer a significant electron donation to the host TMDC (in particular, to the X species). In our previous work,25 we identified a large charge transfer of 0.86 electrons from lithium and 1.63 electrons from magnesium. The larger charge donation allows for bonding of a more ionic nature between an intercalant with a large positive charge (Li or Mg) and the chalcogen with a very negative charge, in place of the weak vdW bonding across the gap. Further, the octahedral voids that the intercalant species occupy are large enough to accommodate the ions,14 and similarity between the intercalant ion and the transition metal of the host TMDC means that little separation of the TMDC layers is required. We showed in our previous work that the vertical separation between the X species on opposite sides of the vdW spacing changes from ∼2 Å to ∼3 Å in the most extreme case. Conversely, the accommodation of multiple atoms (such as N2 or NO271,72) per site within the layer results in a larger separation (from ∼3 Å to ∼6 Å). Finally, we also show in ESI† Section SI.C that many TMDCs are found to be stable against conversion reactions. In general, the intercalation of a TMDC with magnesium is energetically more costly than intercalation with lithium.
2.2 Methods for evaluation of elastic properties
 | (1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 and point group
m1 and point group ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/m), with the exception of LiCrS2, further details of which are presented in the ESI† Section SII.B. This space group number was found to be the most prevalent in a recent study of vdW layered structures, and was also frequently observed for the related ionic structures.1 For such trigonal crystal systems, the elastic matrix has the form,
2/m), with the exception of LiCrS2, further details of which are presented in the ESI† Section SII.B. This space group number was found to be the most prevalent in a recent study of vdW layered structures, and was also frequently observed for the related ionic structures.1 For such trigonal crystal systems, the elastic matrix has the form, | (2) |
 . The above matrix takes the form of a hexagonal crystal system when the element c14 is equal to zero.79 We have evaluated the elastic matrix for the considered materials, as this is the fundamental object for the following discussions. All of the elements are presented in ESI† Section SII.B for each of the materials considered.
. The above matrix takes the form of a hexagonal crystal system when the element c14 is equal to zero.79 We have evaluated the elastic matrix for the considered materials, as this is the fundamental object for the following discussions. All of the elements are presented in ESI† Section SII.B for each of the materials considered.
Previous works have assessed the thermodynamic stability of the intercalated TMDCs,25 finding most to be stable with the inclusion of lithium or small amounts of magnesium, though they were found to be susceptible to conversion reactions for high concentrations of magnesium (see ESI† Section SI.C). Whilst the mechanical stability of a material is usually evaluated by identifying the presence of any imaginary (ω2 < 0) phonon modes, calculation of full phonon dispersions are not conducive to broad high throughput investigations. However, as these instabilities occur for long wavelength modes (q → 0), we can instead utilise the Born stability criteria to assess stability from the elastic tensor.1,80 This is because the elastic tensor is derived from the linear approximation of the stress–strain relationship, and so the components are related to the dispersion curves for low energy acoustic phonons.1 The elastic stability conditions have been outlined elsewhere for different crystal systems,79 which for trigonal crystals are,
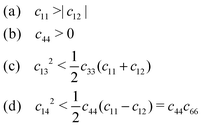 | (3) |
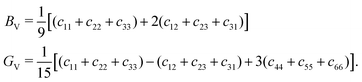 | (4) |
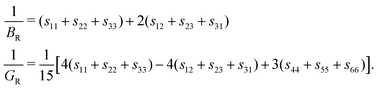 | (5) |
 | (6) |
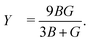 | (7) |
 | (8) |
 | (9) |
The anisotropic Young's modulus of a general crystal class can be calculated from the compliance tensor,90 starting from,
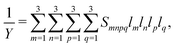 | (10) |
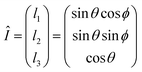 | (11) |
 | (12) |
3 Results
3.1 Single crystal bulk modulus
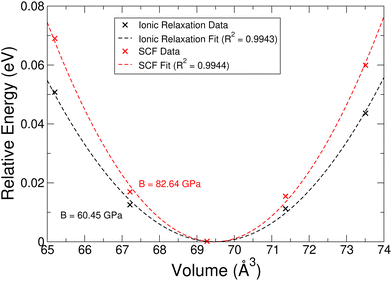
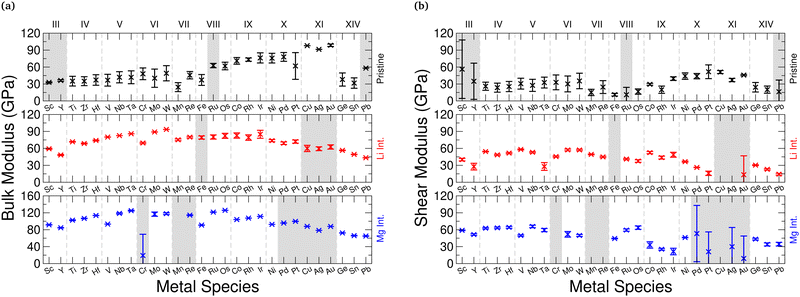
The single-crystal bulk modulus can be obtained using eqn (1), and we present the results of this in Fig. 3 for the pristine and intercalated systems. For the pristine structures, we see a gradual increase in the bulk modulus as the Group of the metal composing the host TMDC increases. Using the TMDC sulfides as an example to highlight this, there is an increase from 36.86 GPa (ScS2) to 103.92 GPa (AuS2). Though there is a general linear trend between these points, the central transition metal Groups VII and VIII drop below this. A closer look at the magnetic configuration of these materials, however, reveals a change in the spin state for different strains. Being able to utilise this spin degree of freedom allows for further energy minimisation in these materials and so they can achieve a lower bulk modulus, and also highlights the potential to utilise these materials for their magnetoelastic properties.With intercalation, we notice a general increase in the bulk modulus. For example, with lithium intercalation, the bulk modulus of TiS2 increases from 43.24 GPa to 72.60 GPa in LiTiS2, and for magnesium intercalation it increases to 101.72 GPa. This increase in the bulk modulus is observed for most materials, specifically for those composed of transition metals in Groups III to VIII. This can be understood by an increase in the bonding strength between TMDC layers, facilitated by the introduction of the ionic intercalants, and the consequent formation of ionic bonds between the intercalant and the TMDC layers.1,14 We note a surprising change in this trend for later transition metals: for Group IX compounds, the bulk modulus of the magnesium-intercalated structure remains the largest. However, the values for the pristine and lithium-intercalated compounds are near equal, with relatively small (∼10 GPa) differences between them, and there are some cases where the lithium-intercalated bulk modulus is smaller than that of the pristine material, such as with CoSe2 (B = 67.58 GPa) and LiCoSe2 (B = 72.31 GPa). For Group X compounds, this evolves to the bulk modulus of magnesium-intercalated compounds being comparable with the pristine compounds, and for Group XI materials the bulk modulus of the pristine structures is higher than that of the corresponding intercalated compounds. With few exceptions, we also identify a reduction in the bulk modulus with increased mass of the chalcogen, in line with increased formation energy92 and hence weaker bonding.
Changing the chalcogen species results in comparable changes to those arising from a change in the transition metal. We note a general decrease in the bulk modulus as the atomic number of the chalcogen is increased. For example, the pristine TiX2 materials offer a bulk modulus of 43.24 GPa (sulfide), 37.42 GPa (selenide), and 32.17 GPa (telluride). As the atomic number of the chalcogen is increased, the formation energy of TMDC layers similarly increases,92 highlighting TMDC formation is less favourable. This reduction in favourability is an indication of a weakened bonding. It has also previously been shown that there is a reduction in the (2D) Young's modulus with increased formation energy,73 hence we can conclude that the reduction in the bulk modulus as the chalcogen is changed S → Se → Te can be attributed to a weakening of the TMDC bonding. Likewise, there is a change in the bulk modulus with change in chalcogen species. For example, the LiTiX2 materials the bulk modulus is 72.60 GPa (sulfide), 54.85 GPa (selenide), and 40.97 GPa (telluride), and for the MgTiX2 compounds it is 101.72 GPa (sulfide), 78.07 GPa (selenide), and 42.72 GPa (telluride). We see a similar increase in the formation energy for the intercalated TMDC structures (see ESI† Section SI.C), and so the above discussion using the weakened bonding to explain this reduction holds. Further details of the single crystal bulk modulus are presented in ESI† Section SII.A.
3.2 Elastic stability
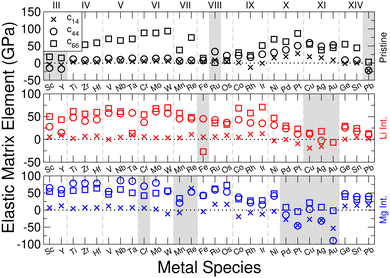
Evaluating the above elastic stability conditions for each of the materials presented, we find that of the 252 materials considered, 204 are elastically stable. In the following presentation of results, regardless of which criteria are violated, we also include data for the elastically unstable materials, but shade their data ranges to identify them. For the pristine materials, we find that twelve materials break the elastic stability equations outlined in eqn (3). We find that all twelve break condition (d), and of these eight break condition (b). Three materials break condition (a), and one breaks condition (c). For lithium-intercalated TMDCs, there are ten materials which break the stability conditions: five break condition (a), four break condition (b), three break condition (c), and eight break condition (d). For magnesium-intercalated TMDCs, twenty six materials which break the stability conditions: eight break condition (a), fifteen break condition (b), five break condition (c), and twenty three break condition (d). We note that conditions (b) and (d) are most commonly broken by materials that are not elastically stable. These conditions can both be related to the element c44, and so we conclude that the largest source of instability arise from the response to shear deformations. This is to be expected due to the relatively weak interactions across the vdW spacing in the pristine structures, and the dramatic change in this interaction with the addition of an intercalant. For the sulfide materials, we present in Fig. 4 the elements of the elastic matrix, c14, c44, and c66, which are present in the stability conditions. It is now clear to see the cases which typically lead to elastic instability in these materials: negative values of either the element c44 (as with ScS2, YS2, and PbS2) or the element c66 (as with LiFeS2). These would both result in negative quantities on the right hand side of stability condition (d).Materials composed of the central Mn, Re, and Fe metals frequently break the stability conditions. These materials have magnetic moments that deserve close attention. Although we have allowed for different (collinear) spin configurations in the following presentation of results, a more careful consideration of their spin configurations might remove the elastic instabilities shown here. With the introduction of an intercalant, we find that many late-transition metal TMDCs lose their elastic stability. However, we do identify some materials, such as ScS2 and YS2, where the introduction of an intercalant results in an elastically stable compound. Finally, we find that twenty two selenide materials break stability conditions, which is more than the sulfide (fifteen) or telluride (eleven) materials. However, overall the same trends (in terms of which conditions are broken most frequently) are seen across TMDCs composed of different chalcogen atoms, further details of which are presented in ESI† Section SII.C.
3.3 Polycrystalline properties
We note some exceptions to the upward trend exhibited by the pristine materials, and point out the drop in bulk modulus for the Group VII and Group VIII sulfides. For TMDCs composed of these transition metals we see that the magnetic state changes by as much as 0.2μB per unit cell across the unique distortions made. This spin degree of freedom is not utilised in the other TMDCs, and allows for further energy minimisation (and hence a lower bulk modulus). This is in line with results presented elsewhere,93 where magnetic materials with larger magnetic moments typically showed a lower bulk modulus than those with a zero magnetic moment. We also notice a drop for the Group XIV metals, where we have determined a value of 37.98 GPa for GeS2, though these are post-transition metal materials, and the difference in behaviour from main-block transition metals is not surprising. Beyond these exceptions, however, the general upwards trend is evident in Fig. 5a for the sulfides.
For the selenide and telluride materials, the bulk modulus follows the same trends as those shown by the sulfides. However, we do note a general reduction in the bulk modulus. For example, the Voigt–Reuss–Hill values for TiX2 compounds decreases from 35.07 GPa (sulfide), to 28.95 GPa (selenide), to 22.60 GPa (telluride). For the lithium-intercalated LiTiX2 structures this reduction is again seen, decreasing from 71.64 GPa (sulfide), to 57.23 GPa (selenide), to 40.27 GPa (telluride), as well as for the magnesium-intercalated MgTiX2 structures, with values of 102.47 GPa (sulfide), 80.41 GPa (selenide), and 39.88 GPa (telluride). This is in line with what was seen for the single-crystal bulk modulus discussed above, which was rationalised with the reduction in TMDC bonding strength. Further details are presented in ESI† Section SII.D.
Using the different schemes (Voigt, Reuss, VRH) we can obtain different estimates for the elastic moduli. For the pristine systems, there is a large spread between the Voigt and Reuss values of bulk modulus. We find that these values are closer for the materials composed of larger chalcogen species: using the WX2 materials as an example, the difference between the bulk modulus using the Voigt and Reuss schemes are 26.94 GPa, 17.24 GPa, and 5.03 GPa for the WS2, WSe2, and WTe2 materials, respectively. Once intercalated, this difference between the Voigt and Reuss values is decreased (for example, to 0.04 GPa for LiWS2 and to 2.09 GPa for MgWS2).
In Fig. 5b we show the polycrystalline shear modulus for the sulfide materials. For the pristine materials (black) the shear modulus shows a general increase with increasing Group number, from 23.56 GPa (ZrS2) to 51.69 (PtS2) for the sulfides in the VRH scheme. Again, the central transition metals (Groups VII to IX) fall below this trend by utilising their spin state during deformation. There is then a further, but small, reduction for the Group XI materials. Finally, the Group XIV materials shown the lowest values of shear modulus, for example with values of 20.00 GPa, 16.94 GPa, and 7.54 GPa for SnS2, SnSe2, and SnTe2, respectively. We present the equivalent selenide and telluride shear modulus data in the ESI† Section SII.D. However, for the pristine materials, we note a less dramatic change as the chalcogen species is changed. Using the TiX2 materials to highlight this, the Voigt–Reuss–Hill values of shear modulus are 26.03 GPa (sulfide), to 20.36 GPa (selenide), to 20.95 GPa (telluride). The similarity in these values is likely due to the weak vdW interaction coupling different MX2 layers.
We also identify a spread in the shear moduli using the different (Voigt, Reuss, VRH) schemes, larger than the spread that was present for the bulk modulus. Whilst this spread is typically reduced with the inclusion of an intercalant, many materials, such as the magnesium-intercalated Group XI materials, have a greater spread than their pristine counterparts. However, we explain this through consideration of the elastic stability: From eqn (4) and (5) we can see that the polycrystalline bulk modulus does not depend on the c44 element of the elastic tensor (which we determined above to be the cause of the elastic instability present in these materials). As such, it would be expected that the values of bulk modulus be relatively well behaved regardless of the elastic stability. However, the dependence of the polycrystalline shear modulus on the c44 element results in the anomalous values of the shear modulus. We highlight this with the magnesium-intercalated compounds: whilst equivalent materials that are elastically stable show very little variation in shear modulus between the different schemes, elastic instability leads to dramatic differences. The Group XI TMDCs (CuX2, AgX2, AuX2), for example, show differences in excess of 100 GPa and some unphysical negative values when intercalated with magnesium.
The spread in bulk and shear moduli will propagate into the elastic properties that are determined from B and G, as can be seen from eqn (7) and (8). In the following, we present only the results of the VRH scheme for clarity and brevity, but the Voigt and Reuss results are presented graphically and numerically in ESI† Section II.D.
With changing chalcogen species, we find that TMDC composed of chalcogens with higher atomic number show a general reduction in the polycrystalline Young's modulus. Using the ZrX2 materials to highlight this, the Young's modulus (using the Voigt–Reuss–Hill scheme) reduces from 57.73 GPa (ZrS2), to 51.82 GPa (ZrSe2), to 44.17 GPa (ZrTe2). Above, we discussed how the increase in formation energy with S → Se → Te92 is an indication of a weakened bonding, and that an increased formation energy has led to a corresponding decrease to the (2D) Young's modulus for similarly layered structures.73 In fact, it has previously been reported that a reduction in the charge transfer between the metal and chalcogen atoms leads to a reduction in the (2D) Young's modulus of ultra-thin TMDCs.43 We do stress, however, that due to the sensitivity of the Young's modulus on the bulk and shear values through eqn (7) and the choice of scheme used to calculate them, there are several examples of TMDCs which break this trend, though not by much. Further details of the values obtained using the different schemes and equivalent data for the selenide and telluride materials are presented in ESI† Section II.D.
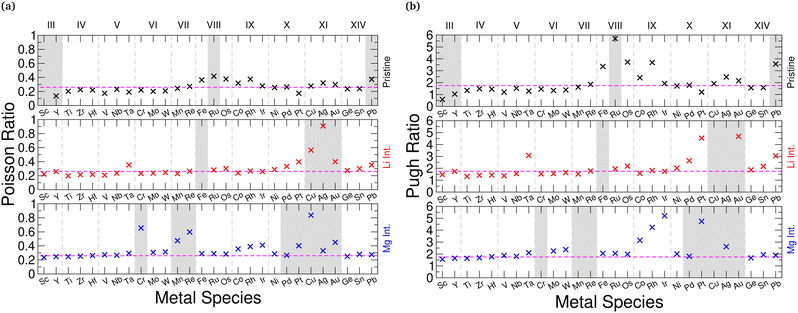
We find that for the unintercalated structures, the materials composed of Group III–VI transition metals show Poisson and Pugh ratios that lie below the respective limits, indicating they are brittle in nature. With lithium intercalation, each group displays a slightly different response: Group III show an increase in the elastic ratios, however their pristine structures are elastically unstable and so a direct comparison with the intercalated structures is not appropriate. The Group IV sulfides show a stiffening (reduction in Poisson and Pugh ratios), the selenides retain a similar stiffness/ductility, and the tellurides show an increased ductility (increase in Poisson and Pugh ratios). The Group V materials become more ductile, and the Group VI materials experience little change to their ductility. With magnesium intercalation, we see a universal increase in the material ratios, though, with each of these early-Group TMDCs showing an increased ductility. For materials composed of later transition metals, most exhibit a higher ductility and lie above the Poisson and Pugh criteria. For both lithium and magnesium intercalation, Group VII to IX materials show a shift towards the brittle/ductile limit, but the Group X and XI materials show increase Poisson and Pugh ratios. We do highlight, however, that the intercalated Group XI TMDCs are not elastically stable. Compared to the changes that arise with choice of transition metal, we notice very little difference arising with choice of chalcogen, with most changes being within 0.05 (Poisson ratio) and 0.2 (Pugh ratio) of each other.
3.4 Elastic anisotropy
With intercalation, there is then a dramatic reduction in the elastic anisotropy of the TMDCs: Fig. 9a shows that almost all of the intercalated systems possess anisotropy indices less than unity, with very few exceeding even 2, and this extends to the selenide and telluride materials. This follows other works which have compared the anisotropy between vdW and ionic materials.1 It is not surprising that the anisotropy of these layered materials is reduced with intercalation: the presence of the van der Waals gap results in a large difference between the in-plane and out-of-plane bonding, and hence the restoring forces to any elastic deformation. The inclusion of an intercalant removes this van der Waals gap and introduces a large positive charge between the negatively charged chalcogen species,25 and so a significant change in the elastic properties is to be expected. However, as the two intercalants considered in this work are metals and possess positive charges once intercalated, they are qualitatively very similar to the metals constituting the host structure, and so the out-of-plane bonding becomes comparable to the in-plane bonding, demonstrating a similar elastic response.
Using the ratios of the Voigt and Reuss values of bulk and shear moduli we can construct an elastic anisotropy diagram (EAD), which is presented in Fig. 9b. The advantages of such a diagram have previously been described elsewhere,89 but we briefly outline them here: we see from Fig. 9b that the 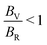 and
and  regions are inadmissible, and the included lines of constant anisotropy (which have a slope of −5) highlight that changes in
regions are inadmissible, and the included lines of constant anisotropy (which have a slope of −5) highlight that changes in 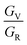 have a greater influence on crystal elasticity than an equivalent change in
have a greater influence on crystal elasticity than an equivalent change in  . Cubic crystals have been shown to cluster along the line given by
. Cubic crystals have been shown to cluster along the line given by  , and so other materials that lay along this line are elastically similar to cubic crystals, despite their trigonal symmetry. As locally isotropic materials appear closer to the
, and so other materials that lay along this line are elastically similar to cubic crystals, despite their trigonal symmetry. As locally isotropic materials appear closer to the  point than those that are not locally isotropic, we see that the main effect of intercalation is to reduce the anisotropy of the TMDC family, as was shown with Fig. 9a. Many of the pristine TMDCs are scattered across the EAD away from the
point than those that are not locally isotropic, we see that the main effect of intercalation is to reduce the anisotropy of the TMDC family, as was shown with Fig. 9a. Many of the pristine TMDCs are scattered across the EAD away from the  point, but after intercalation there is a significant shift of all points towards
point, but after intercalation there is a significant shift of all points towards  .
.
Similar figures for other TMDCs are presented in Section SII.E (ESI†), where we find a very similar evolution of the Young's modulus with intercalation. In particular, we have included equivalent data for TiSe2 and its intercalated structures for comparison with TiS2 shown in Fig. 10. Aside from a global reduction of about 40 GPa due to the reduced bonding of the selenide TMDC compared to the sulfide equivalents, as was discussed above, the general shape shown in Fig. 10 is reproduced. Specifically when intercalated with lithium, we see the increase in the Young's modulus out-of-plane, resulting in a more isotropic Young's modulus similar to what is shown in Fig. 10b. When intercalated with magnesium, we see the extremes in Young's modulus along the Ti–Se bonds, and the comparable Young's modulus in-plane and out-of-plane (coloured blue), similar to what is shown in Fig. 10c.
A broader investigation of the Young's modulus can be achieved by comparing the relative variation of the Young's modulus over a large, evenly-distributed set of angles with the universal anisotropy. We present this in Fig. 10d, where, by fitting with guidelines given in the figure, we find that these slopes are close to the Estd/Eavg ∝ (AU)0.5 determined elsewhere.1 Similarly, we present the ratio of out-of-plane and in-plane Young's modulus against the anisotropy metric. The pristine structures (black) show the largest deviation from the constant YOut/YIn = 1 line of equivalence, in most cases dropping below it due to the significant difference between the weak out-of-plane vdW bonding to the strong in-plane covalent bonding. With the addition of lithium (red), there is a general movement of these materials upwards, towards the YOut/YIn = 1 line, and hence show a reduction in the anisotropy. However, they again fall below the constant line, indicating that the in-plane bonding is much stronger than out-of-plane. Finally, for magnesium intercalation (blue) we see a further shift upwards and a reduction in the anisotropy. Many of the magnesium-intercalated compounds fall on the line of equivalence, showing that the magnesium intercalant facilitates bonding between layers that is similar in strength to those in-plane. In fact, many of the magnesium-intercalated structures (as well as some lithium-intercalated) demonstrate bonding out-of-plane that is stronger than bonding in-plane. For large AU, there is little trend YOut/YIn, as has been shown in a broader study of layered materials.1
3.5 Dependence on intercalant concentration
So far, we have only considered the limiting cases of pristine bulk TMDCs and their fully intercalated LiMX2 and MgMX2 forms. However, it is possible to intercalate these materials by intermediate amounts through control of precursor or by limiting the discharge voltage in a half-cell arrangement. The elastic properties of similarly layered materials graphite and LiCoO2 have been shown to be linearly dependent on the concentration of an intercalant species,50,51 which suggests the possibility of tuning the elastic properties of the TMDCs by controlling the level to which they are intercalated. Due to the larger cell sizes required for a finer sampling of intercalant concentration, and hence larger computational cost, we have investigated TiS2 and ZrS2 and their intercalated forms for closer study.We present the single-crystal bulk modulus for lithium- and magnesium-intercalated TiS2 in Fig. 11a, and the equivalent ZrS2 structures in Fig. 11b. For visual aid, we have included the linear trend suggested previously with dashed lines. With increased lithium intercalation we find the single-crystal bulk modulus falls slightly below the linear, with the largest deviation being at the Li0.5 TiS2 and Li0.5 ZrS2 compositions. As we show for Li0.5 ZrS2 in Fig. 11b, the smallest values arise from intercalation into a single vdW spacing (labelled abcd) as such intercalant arrangement retains an uninterrupted, weakly-bonded vdW region. The largest bulk modulus is then achieved with a uniform distribution of lithium across the vdW layers (labelled adfg), hence coupling each of the TMDC layers with an intercalant.
For magnesium intercalation, we identify a more significant deviation from the linear trend than was seen for lithium intercalation. The intercalant configurations which display the lowest bulk modulus are again those where a single vdW spacing is filled (as has been indicated by labels a, ab, abc, and abcd in Fig. 11a) and more equal filling between the layers results in higher values of bulk modulus. However, comparing the energies for these different configurations show that the filling of a single layer is the least energetically favourable, and more homogeneous filling is preferred. As such, we would still expect the bulk modulus to vary roughly linearly between the start and end of intercalation in an experimental investigation, for both lithium- and magnesium-intercalated materials. Regardless, this does indicate the importance of considering intermediate intercalant concentrations, as there can be a wide range in elastic properties between different intercalant arrangements for a given concentration, and hence significant deviations from the linear trend that is often assumed.
4 Conclusion
In this work, we have presented a first-principles study into the elastic behaviour of layered TMDCs and their intercalated structures. We have determined the elastic matrices, allowing us to evaluate key properties including the bulk, shear, and Young's moduli, and show that there is a general increase in these quantities with intercalation. Commonly used elastic ratios which describe the ductility of a material have also been calculated, allowing us to conclude that the pristine materials are brittle, but become more ductile with the addition of lithium or magnesium. The anisotropy of these materials was also assessed using a combination of the universal anisotropy metric and a direct calculation of the angular dependence of the Young's modulus. These showed that the pristine van der Waals materials possess a high degree of anisotropy, which is to be expected given the relatively weak interactions across the vdW spacing in the pristine structures. However, this anisotropy is reduced with the introduction of a positively charged intercalant. Finally, for selected systems we have also explored intermediate intercalant concentrations, and conclude that, whilst linear extrapolation of elastic properties between the limits of intercalation may be suitable in some situations, different intercalant configurations or the use of multivalent intercalant species can cause significant deviations from this.This work builds upon previous studies which have investigated the energetic and electronic properties of intercalated TMDCs. The elastic properties of materials are important for all industrial applications, and are particularly important for modelling electrodes beyond the atomic scale. The work presented here therefore allows for further investigation into the layered TMDCs as electrode materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge financial support from the EPSRC (United Kingdom), (grant no. EP/L015331/1) and the Materials Chemistry Consortium, (EP/L000202, EP/R029431, EP/X035859). The authors acknowledge the use of the University of Exeter HPC facility. This work used the Isambard 2 UK National Tier-2 HPC Service (https://gw4.ac.uk/isambard/) operated by GW4 and the UK Met Office, and funded by EPSRC (EP/T022078/1). We wish to acknowledge the use of the EPSRC funded Physical Sciences Data-science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1.Notes and references
- R. W. McKinney, P. Gorai, S. Manna, E. Toberer and V. Stevanović, J. Mater. Chem. A, 2018, 6, 15828 RSC , arXiv:1805.10489.
- S. K. Saha and G. Dutta, Phys. Rev. B, 2016, 94, 125209 CrossRef.
- M. Güler, Ş. Uğur, G. Uğur and E. Güler, Int. J. Quantum Chem., 2023, 123, 1 CrossRef.
- G. Logvenov, A. Gozar and I. Bozovic, Science, 2009, 326, 699 CrossRef CAS PubMed.
- C. Scheuerlein, B. Fedelich, P. Alknes, G. Arnau and R. Bjoerstad, IEEE Trans. Appl. Supercond., 2015, 25, 1–15 Search PubMed.
- K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871 CrossRef CAS.
- J. Zhang, C. Wang and C. Bowen, Nanoscale, 2014, 6, 13314 RSC.
- L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214103 CrossRef.
- Y. Liu, N. S. Hudak, D. L. Huber, S. J. Limmer, J. P. Sullivan and J. Y. Huang, Nano Lett., 2011, 11, 4188 CrossRef CAS PubMed.
- Q. Li, P. Wang, Q. Feng, M. Mao, J. Liu, S. X. Mao and H. Wang, Chem. Mater., 2014, 26, 4102 CrossRef CAS.
- Q. Li, P. Wang, Q. Feng, M. Mao, J. Liu, S. X. Mao and H. Wang, Chem. Mater., 2014, 26, 4102 CrossRef CAS.
- S. Prussin, J. Appl. Phys., 1961, 32, 1876 CrossRef CAS.
- L. Y. Beaulieu, K. W. Eberman, R. L. Turner, L. J. Krause and J. R. Dahn, Electrochem. Solid-State Lett., 2001, 4, A137 CrossRef CAS.
- M. S. Whittingham, J. Electrochem. Soc., 1976, 123, 315 CrossRef CAS.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Solid State Ionics, 1981, 3–4, 171 CrossRef CAS.
- Y. Sun, N. Liu and Y. Cui, Nat. Energy, 2016, 1, 1 Search PubMed.
- Y. Wei, J. Zheng, S. Cui, X. Song, Y. Su, W. Deng, Z. Wu, X. Wang, W. Wang, M. Rao, Y. Lin, C. Wang, K. Amine and F. Pan, J. Am. Chem. Soc., 2015, 137, 8364 CrossRef CAS PubMed.
- J. Kasnatscheew, S. Röser, M. Börner and M. Winter, ACS Appl. Energy Mater., 2019, 2, 7733 CrossRef CAS.
- N. D. Phillip, A. S. Westover, C. Daniel and G. M. Veith, ACS Appl. Energy Mater., 2020, 3, 1768 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nanoscience and Technology: A Collection of Reviews from Nature Journals, Macmillan Publishers Ltd, UK, 2009, pp. 11–19, arXiv:0702595 Search PubMed.
- G. Wang, X. Shen, J. Yao and J. Park, Carbon, 2009, 47, 2049 CrossRef CAS.
- Q. D. Chen, S. F. Yuan, J. H. Dai and Y. Song, Phys. Chem. Chem. Phys., 2021, 23, 1038 RSC.
- C. J. Price, J. Pitfield, E. A. D. Baker and S. P. Hepplestone, Phys. Chem. Chem. Phys., 2023, 25, 2167 RSC.
- C. J. Price, E. A. D. Baker and S. P. Hepplestone, J. Mater. Chem. A, 2023, 11, 12354 RSC.
- J. Christensen and J. Newman, J. Electrochem. Soc., 2006, 153, A1019 CrossRef CAS.
- J. Christensen and J. Newman, J. Solid State Electrochem., 2006, 10, 293 CrossRef CAS.
- X. Zhang, W. Shyy and A. Marie Sastry, J. Electrochem. Soc., 2007, 154, A910 CrossRef CAS.
- Y.-T. Cheng and M. W. Verbrugge, J. Appl. Phys., 2008, 104, 083521 CrossRef.
- S. Renganathan, G. Sikha, S. Santhanagopalan and R. E. White, J. Electrochem. Soc., 2010, 157, A155 CrossRef CAS.
- I. Ryu, J. W. Choi, Y. Cui and W. D. Nix, J. Mech. Phys. Solids, 2011, 59, 1717 CrossRef CAS.
- F. Hao, X. Gao and D. Fang, J. Appl. Phys., 2012, 112, 103507 CrossRef.
- E. J. Seldin and C. W. Nezbeda, J. Appl. Phys., 1970, 41, 3389 CrossRef CAS.
- H. Zabel, A. Magerl and J. J. Rush, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 3930 CrossRef CAS.
- P. Zhou and J. E. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 12643 CrossRef CAS PubMed.
- W. Kamitakahara, J. Phys. Chem. Solids, 1996, 57, 671 CrossRef CAS.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385 CrossRef CAS PubMed.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703 CrossRef CAS PubMed.
- A. Castellanos-Gomez, M. Poot, G. A. Steele, H. S. J. van der Zant, N. Agraït and G. Rubio-Bollinger, Adv. Mater., 2012, 24, 772 CrossRef CAS PubMed.
- K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Nano Lett., 2014, 14, 5097 CrossRef CAS PubMed.
- R. Zhang, V. Koutsos and R. Cheung, Appl. Phys. Lett., 2016, 108, 042104 CrossRef.
- Y. Sun, J. Pan, Z. Zhang, K. Zhang, J. Liang, W. Wang, Z. Yuan, Y. Hao, B. Wang, J. Wang, Y. Wu, J. Zheng, L. Jiao, S. Zhou, K. Liu, C. Cheng, W. Duan, Y. Xu, Q. Yan and K. Liu, Nano Lett., 2019, 19, 761 CrossRef CAS PubMed.
- A. Sheraz, N. Mehmood, M. M. Çiçek, İ. Ergün, H. R. Rasouli, E. Durgun and T. S. Kasırga, Nanoscale Adv., 2021, 3, 3894 RSC.
- D. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, K. M. Liechti, N. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Yakobson, T. Zhang, Y.-W. Zhang, Y. Zhou and Y. Zhu, Extreme Mech. Lett., 2017, 13, 42 CrossRef , arXiv:1611.01555.
- W. Ding, D. Han, J. Zhang and X. Wang, Mater. Res. Express, 2019, 6, 085071 CrossRef CAS.
- Z. Islam and A. Haque, J. Phys. Chem. Solids, 2021, 148, 109669 CrossRef CAS.
- N. Sakib, S. Paul, N. Nayir, A. C. T. van Duin, S. Neshani and K. Momeni, Phys. Chem. Chem. Phys., 2022, 24, 27241 RSC.
- P. Hess, RSC Adv., 2017, 7, 29786 RSC.
- P. Hess, Phys. Chem. Chem. Phys., 2018, 20, 7604 RSC.
- Y. Qi, H. Guo, L. G. Hector and A. Timmons, J. Electrochem. Soc., 2010, 157, A558 CrossRef CAS.
- Y. Qi, L. G. Hector, C. James and K. J. Kim, J. Electrochem. Soc., 2014, 161, F3010 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Whittingham, Prog. Solid State Chem., 1978, 12, 41 CrossRef CAS.
- M. Kamaratos, D. Vlachos, C. A. Papageorgopoulos, A. Schellenberger, W. Jaegermann and C. Pettenkofer, J. Phys.: Condens. Matter, 2002, 14, 8979 CrossRef CAS.
- H. Katzke, P. Tolédano and W. Depmeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1 CrossRef.
- J. Ribeiro-Soares, R. M. Almeida, E. B. Barros, P. T. Araujo, M. S. Dresselhaus, L. G. Cançado and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115438 CrossRef , arXiv:1407.1226.
- C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983 CrossRef CAS.
- A. V. Kolobov and J. Tominaga, Two-Dimensional Transition-Metal Dichalcogenides, Springer International Publishing, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. Bera, A. Betal and S. Sahu, J. Alloys Compd., 2021, 872, 159704 CrossRef CAS.
- L. Liu, J. Cao, W. Guo and C. Wang, Chin. Phys. B, 2022, 31, 016105 CrossRef.
- K. Lejaeghere, V. Van Speybroeck, G. Van Oost and S. Cottenier, Crit. Rev. Solid State Mater. Sci., 2014, 39, 1 CrossRef CAS , arXiv:1204.2733.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- M. de Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. Krishna Ande, S. van der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Scientific Data, 2015, 2, 150009 CrossRef CAS PubMed.
- V. M. Bermudez, J. Phys. Chem. C, 2020, 124, 15275 CrossRef CAS.
- M. J. Szary, Appl. Surf. Sci., 2023, 611, 155514 CrossRef CAS.
- X.-F. Liu, Z.-J. Luo, X. Zhou, J.-M. Wei, Y. Wang, X. Guo, B. Lv and Z. Ding, Chin. Phys. B, 2019, 28, 086105 CrossRef CAS.
- T. Soma, J. Phys. C-Solid State Phys., 1978, 11, 2669 CrossRef CAS.
- A. Mentefa, F. Z. Boufadi, M. Ameri, F. Gaid, L. Bellagoun, A. A. Odeh and Y. Al-Douri, J. Supercond. Novel Magn., 2021, 34, 269 CrossRef CAS.
- N. T. Taylor, F. H. Davies and S. P. Hepplestone, Mater. Res. Express, 2017, 4, 125904 CrossRef.
- N. Bock, E. Holmström, T. B. Peery, R. Lizárraga, E. D.Chisolm, G. De Lorenzi-Venneri and D. C. Wallace, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144101 CrossRef.
- M. Ezzeldien, S. Al-Qaisi, Z. A. Alrowaili, M. Alzaid, E. Maskar, A. Es-Smairi, T. V. Vu and D. P. Rai, Sci. Rep., 2021, 11, 20622 CrossRef CAS PubMed.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- G. Grimvall, B. Magyari-Köpe, V. Ozolinš and K. A. Persson, Rev. Mod. Phys., 2012, 84, 945 CrossRef CAS.
- Z.-j Wu, E.-j Zhao, H.-p Xiang, X.-f Hao, X.-j Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- M. Woodcox, J. Young and M. Smeu, Phys. Rev. B, 2019, 100, 104105 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909 CrossRef CAS.
- S. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823 CrossRef CAS.
- L. Zhu, L. Li, T. Cheng and D. Xu, J. Mater. Chem. A, 2015, 3, 5449 RSC.
- M. Woodcox, R. Shepard and M. Smeu, J. Power Sources, 2021, 516, 230620 CrossRef CAS.
- C.-B. Zhang, W.-D. Li, P. Zhang and B.-T. Wang, Chin. Phys. B, 2021, 30, 056202 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 3 CrossRef PubMed.
- Y. Ding and B. Xiao, Comput. Mater. Sci., 2014, 82, 202 CrossRef CAS.
- V. A. Gorodtsov and D. S. Lisovenko, Crystals, 2021, 11, 863 CrossRef CAS.
- F. A. Rasmussen and K. S. Thygesen, J. Phys. Chem. C, 2015, 119, 13169 CrossRef CAS , arXiv:1506.02841.
- K. Choudhary, G. Cheon, E. Reed and F. Tavazza, Phys. Rev. B, 2018, 98, 014107 CrossRef CAS PubMed.
- H. Niu, X. Q. Chen, P. Liu, W. Xing, X. Cheng, D. Li and Y. Li, Sci. Rep., 2012, 2, 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc02106h |
| This journal is © The Royal Society of Chemistry 2023 |