Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photoluminescence spectroscopy of dibenzopentacene single-crystals: multiple emissive states across temperature, time, and magnetic field in a pursuit of exothermic singlet fission†
Marco
Rosenkranz
,
Lukas
Graf
 ,
Bernd
Büchner
,
Martin
Knupfer
and
Alexey A.
Popov
,
Bernd
Büchner
,
Martin
Knupfer
and
Alexey A.
Popov
 *
*
Leibniz Institute for Solid State and Materials Research (Leibniz-IFW Dresden), 01069 Dresden, Germany. E-mail: a.popov@ifw-dresden.de
First published on 22nd August 2023
Abstract
Dibenzopentacene is a close analogue of pentacene, but it has attracted much less attention than its acene cousin, and its solid-state photophysics remains nearly unknown. In this work we present the first study of dibenzopentacene single crystals using photoluminescence spectroscopy, combining steady-state and time-resolved measurements at different temperatures and in different magnetic fields. A complex evolution of excitation was found between 5 and 300 K, with in total five co-existing and interconverting emissive states. Free excitons dominate the PL spectra below 20 K, but then convert to self-trapped excitons (STEs) at higher temperatures. The interconversion between free exciton and STE states has been found to be thermally activated, and the barriers were determined from the temperature dependence of emission lifetimes. A 20-fold decrease of the PL intensity between 120 K and room temperature is ascribed to the singlet fission, which is confirmed by magneto-PL measurements. However, the large driving force expected for exothermic singlet fission in dibenzopentacene appears to be not fully consistent with its overall photoluminescence behavior, especially at low temperatures. This work highlights that the relationship between photoluminescence and singlet fission for systems with a large energy difference between S1 and T1 + T1, in which the reversibility of SF is hard to expect, is still not well understood.
Introduction
A delocalized π-system of small-molecular organic semiconductors not only determines their intramolecular energy states, but also leads to a considerable intermolecular overlap. Although comparably weak, these intermolecular interactions add a new dimension to the electronic structure of organic semiconductors and create a plethora of electronic properties, sensitive to subtle variations of molecular arrangements in solids and therefore tunable by crystal engineering.1,2 Organic semiconductors thus provide an inexhaustible playground at the crossroad of the electron transfer, electron transport and photoexcitation, which already resulted in several wide-spread applications and is the prospective background for more to come.3,4An electronic excitation upon photon absorption is one of the most fundamental properties of these materials. For an organic molecule isolated from the neighbors in solution or inert matrix, a photoexcitation is usually followed by the fluorescence from the singlet excited state (S1) or intersystem crossing to triplet state (T1) with subsequent phosphorescence. The radiative processes compete with non-radiative deactivation, in which excess electronic energy is dissipated to vibrational degrees of freedom. In the solid state, possible photoexcitation pathways are expanded by exciton self-trapping, inter-exciton interactions, including multiexcitonic states, and exciton diffusion, all made possible by intermolecular interactions.5,6 Although these processes have been studied for many decades, their new aspects still continue to appear. Singlet fission (SF) is one such process, for which dramatic progress in the understanding of the underlying mechanisms has been achieved during the last decade.7–14 In SF, a singlet exciton (S1) initially produced by a photoexcitation then transforms into two triplet excitons (T1 + T1), and a revival of interest in SF is in part caused by a carrier multiplication (two excitons for one absorbed photon), which is of high interest for photovoltaic applications.7,15–19
SF materials require the S1 energy to be close to or higher than the doubled triplet exciton energy 2 × T1. This requirement can be realized in many organic molecules,20–23 but the lion's share of SF studies is still dedicated to only a few systems, such as tetracene, pentacene, and their derivatives, which were drosophila flies in SF research for decades.24–26 An increase of the lengths in acenes quickly leads to a fast decrease of the S1 and T1 energies and makes SF more exothermic, but also reduces their stability. There have been several studies of SF in hexacene,27–31 but we are not aware of any SF reports in heptacene. Branching of the PAH core has a less obvious effect on the S1 and T1 energies and can give both more or less stable π-systems depending on the position of additional rings. Singlet fission studies were reported for two PAH derivatives with the pentacene core variously fused with benzene rings, heptazethrene32 and tetrabenzopentacene.33 Pentacene is known for its mildly exothermic SF,24 a slightly exothermic SF was also found in heptazethrene,32 but tetrabenzopentacene appeared more similar to tetracene with mildly endothermic SF.33 1,2;8,9-dibenzopentacene (DBP hereafter, Fig. 1a), which also has a pentacene core with two fused benzenes, but in a different position than in heptazethrene, managed to avoid attention despite its availability as an unsubstituted PAH and enhanced photo and air stability in comparison to pentacene.
Recently we succeeded in the single-crystal growth of DBP, its optical characterization, and the study of exciton band structure by electron energy loss spectroscopy (EELS).34 Preliminary attempts of photoluminescence (PL) measurements of DBP crystals showed strong variation with temperature, which pointed towards SF and required a deeper study of this phenomenon. In parallel, Manna et al. reported a room-temperature photophysics study of polycrystalline DBP film by time-resolved-PL and transient photoabsorption, which provided the first evidence of SF in solid DBP.35 To obtain a deeper understanding of photoexcitation dynamics in DBP and its possible relationship with singlet fission, in this work we performed a comprehensive study of the photoluminescence of its single-crystals combining temperature dependence, magnetic field dependence, steady-state and time resolved measurements.
Experimental details
The growth of DBP single crystals by vapor transport and DBP crystal structure analysis were described in ref. 34. The as-grown crystals had a smooth surface and were used in further measurements without cutting. Photoluminescence measurements of DBP crystals were performed using a home-made microscope and photoexcitation with Omicron PhoxX diode lasers at 405 and 488 nm. The laser power was kept below 5 mW mm−2 at the crystal surface, which was found to be sufficiently low to avoid photodegradation of the sample during the whole duration of the experiments. CW-PL spectra were recorded using a Kymera 328i spectrograph (Andor) and Newton 920 CCD camera (Andor) for detection in the visible range (the useful range to 950 nm in our setup) calibrated versus an Avalight-Hal lamp (Avantes) for sensitivity correction over the wavelength of the optical pathway and detector, and with an AvaLight-Cal Ar lamp (Avantes) for wavelengths. Additional measurements in the NIR range (λ = 900–1700 nm) were performed with an Andor iDus 1.7 μm InGaAs camera. PL polarization was measured by inserting a rotatable U-AN360 analyzer (Olympus) in the detector path.Variable-temperature measurements were performed with an Oxford Instruments MO2 magnetooptical cryostat equipped with a superconducting magnet. Crystals of DBP were glued to the copper holder of the cryostat with STYCAST 2850FT epoxy to ensure good thermal contact. The temperature in the cryostat was varied in the 5–300 K range, and the magnetic field was ramped up to 4 Tesla. In the studies of magnetic field dependence, the spectra were typically acquired at each 10 mT during the field sweeps up to 4 T with the rate of 100 mT min−1, and the typical acquisition time for a single spectrum was 1 s. Additional field-dependence measurements at room temperature were performed using the optical EPR cavity ER 4104OR (Bruker Germany) and an electromagnet of the Bruker EPR spectrometer system. The crystal was placed in a thin flat EPR cell, which was rotated around the main cell axis inside the cavity, allowing us to change the angle between the field direction and ac plane of the crystal. The excitation laser and emitted light were transferred to/from the sample through the aperture in the EPR cavity using a Y-shaped lightguide.
Luminescence lifetimes were measured using the time-correlated single-photon counting (TCSPC) method. A 405 nm Omicron QuixX diode laser provided a pulse-width of <100 ps. The emitted light from the sample was passed through a single-grating scanning monochromator Sciencetech 9030 to the photomultiplier PMA 192 (PicoQuant) and acquired by a TCSPC system based on the TimeHarp 260 counter/timer (PicoQuant). Time-resolved spectra were obtained by stepping the monochromator in 10 nm steps with the 16 nm bandwidth. In temperature-dependent PL decay studies at selected wavelengths, the monochromator bandwidth was set to 16 nm. The setup allows lifetime measurements down to 0.3–0.4 ns, whereas multiexponential analysis becomes complicated below 1–2 ns.
Results and discussion
Molecular and crystal structure of DBP
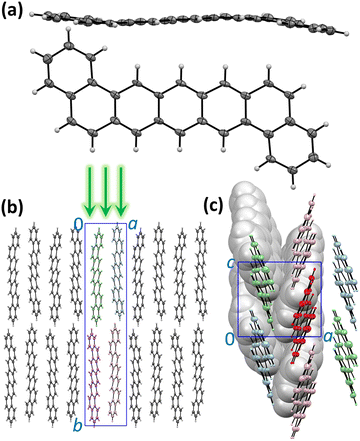
The molecular and crystal structure of DBP is described in Fig. 1. Although the isolated molecule should be planar, it shows a noticeable distortion from planarity in the crystal (Fig. 1a).34 The unit cell contains four symmetry-equivalent DBP molecules (space group P21212, Fig. 1b). The molecules are packed in layers parallel to the ac plane with a herringbone arrangement in each layer so that each DBP molecule has 6 close neighbors and three types of DBP⋯DBP intermolecular contacts in the layer (Fig. 1c). This kind of intermolecular arrangement is typical for many organic semiconductors, such as the closely-related pentacene. The layers are stacked along the b axis, which is also parallel to the long axis of the molecule. The crystals grow as thin flat plates parallel to the ac plane. In the photoluminescence (PL) measurements described below, DBP crystals were lying flat on the holder and studied with a microscope in back-scattering geometry so that the excitation beam and collected light were oriented along the b direction perpendicular to the ac plane (Fig. 1b). The crystal structure shown in Fig. 1 was determined at 100 K.34 Electron diffraction measurements at different temperatures between 20 and 300 K did not show noticeable changes in diffraction pattern (Fig. S1, ESI†), and we conclude that the crystal structure remains the same in the whole temperature range studied in this work and DBP did not undergo a phase transition.Absorption and emission spectra, general remarks
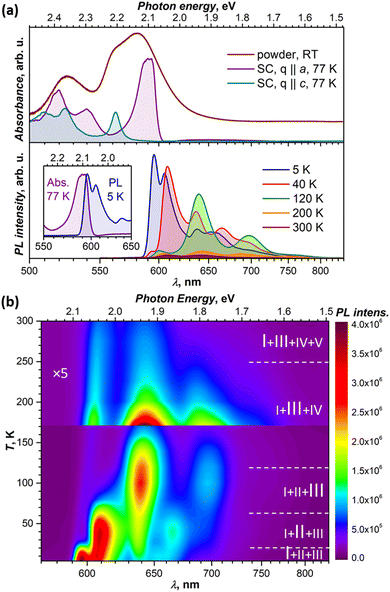
In toluene, dichlorobenzene or tetrahydrofuran solution, the lowest-energy absorption of DBP assigned to S0 → S1 excitation occurs at around 2.34 eV and is followed by 2–3 vibrational replica at 0.15–0.18 eV.34–36 Very similar absorption spectra with S0 → S1 transition at 2.34 eV were also obtained for DBP diluted in a polystyrene matrix in ref. 36 and in this work (Fig. S2, ESI†). In crystalline DBP, intermolecular interactions shift the S0 – S1 excitation to lower energy by 0.25 eV.34 Furthermore, the DBP single crystal shows strongly polarized absorption with well-resolved Davydov splitting (Fig. 2a). The more intense Davydov component with the maximum at 2.09 eV is polarized parallel to the a direction, whereas the second Davydov component is shifted to higher energy by 0.11 eV and polarized parallel to c. The powder absorption spectrum in the energy range of the S0 → S1 transition measured at room temperature is considerably broadened but does not exhibit new transitions which might be ascribed to polarization parallel to b (Fig. 2a).Fluorescence studies of DBP in solution were reported by Canuel et al.,37 Tovstopyat et al.36 and Manna et al.35 The S1 → S0 emission has the main peak at 2.33–2.38 eV and quantum yield of 30–50% (the values depend on the solvent polarity). The PL spectra of DBP diluted in polystyrene (Fig. S2, ESI†) are similar to those in solutions and have a 0–0 peak of the S1 → S0 transition at 2.33 eV followed by two vibronic peaks with a vibrational increment of 0.18 eV, which is typical for polyaromatic compounds and correspond to C–C stretching modes of the aromatic core. In the polycrystalline film, studied at room temperature in ref. 35, the emission peak shifted to lower energy by 0.28 eV, while the quantum yield decreased by two orders of magnitude in comparison to isolated molecules in solutions.
Our PL measurements of DBP single crystals revealed that both PL intensity and the spectral shape are strongly temperature dependent. Fig. 2a compares the spectra measured at several representative temperatures, while complete temperature evolution between 5 K and 300 K is plotted in Fig. 2b. Upon cooling, the PL intensity increases dramatically, while the spectra undergo several stepwise changes, indicating that photoluminescence of the DBP single-crystal is a complex process with interconversion and co-existence of several emissive states. At the same time, the PL spectra for DBP diluted in polystyrene showed only minor variations in the whole 5–300 K range (Fig. S2, ESI†). Thus, changes in the PL spectra of single crystal are caused by intermolecular interactions and delocalization of excitations in the solid state. Detailed analysis of these phenomena is presented in the next section.
The measurements of several DBP crystals from the same growth batch showed some variations in the positions of the PL peaks and in the ratio of emissive states. Thicker crystals tend to have PL peaks at longer wavelengths than the thinner ones, with variations up to 5–7 nm. The strongest differences in the relative intensities were observed for the lowest-energy peak at 5 K and for the ratio of emission peaks at room temperature. The former is likely the effect of reabsorption since emission and absorption spectra overlap considerably as can be seen in Fig. 2a. Notwithstanding this variability, the overall spectral patterns and their temperature dependencies remained unaltered.
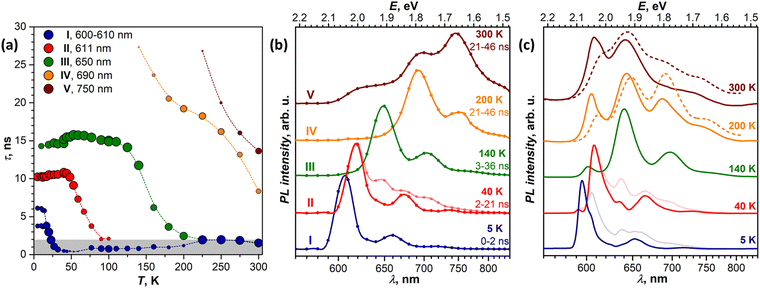
Variable-temperature PL measurements
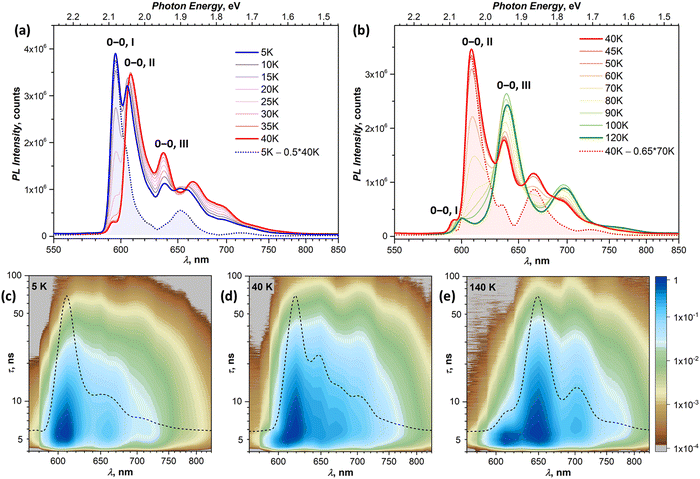
In this section, we focus on variable-temperature PL measurements of DBP single-crystal. To help in identifying overlapping spectral features of different emissive states, CW spectroscopy was augmented with time-resolved (TR) measurements. First, we measured TR-(τ, λ) maps at selected temperatures. These maps, together with the CW spectra, allowed preliminary identification of the number of emissive states and their main wavelengths. Then, the temperature dependence of τ was measured at chosen wavelengths with smaller temperature steps, which were varied depending on the observed PL kinetics, and decay curves were fitted with 2–3 exponential decays (Table S1, ESI†). The details of CW and TR spectra in separate temperature intervals are presented in Fig. 3 (5–120 K) and Fig. 4 (120–300 K), while Fig. 5 summarizes the temperature evolution of PL lifetimes and compares the CW and TR spectra of the identified emissive states. Further details on the temperature dependence of PL and time-resolved data are given in Fig. S3–S7 (ESI†).Analysis of the PL decay curves at 5–10 K revealed the presence of three emissive states with decay times (τ) τI = 4–6 ns with the largest contribution at 600 nm (state I), τII ≈ 10 ns at 610 nm (state II), and τIII ≈ 14–15 ns at 650 nm (state III) (Fig. 5a). The rise time of state II is slightly longer than for the state I as the signal at 610 nm reaches the maximum at 0.1 ns later than the signal at 600 nm (Fig. S5, ESI†). As state I has a high relative intensity and the shortest lifetime among the three, it has an enhanced contribution to the overall PL at short times after a laser pulse (Fig. S4a, ESI†). Thus, integration of the TR spectral data obtained at 5 K in the first 2 ns gives the spectrum in Fig. 5b, which is virtually free from other components and is nearly identical to the result of CW spectra subtraction shown in Fig. 3a.
The fast drop of the intensity of state I with temperature in the CW spectra is accompanied by a decrease of τI to sub-ns values at T > 30 K, reducing to 0.4 ns at 40 K (Fig. 5a). Concomitant increase of the intensity of states II and III indicates that state I interconverts into II/III, while the shape of the temperature dependence of τI in Arrhenius coordinates points to the thermally activated mechanism (Fig. S7a, ESI†). Fitting the linear part gives the activation barrier of 6.5 meV (52 cm−1).
In the TR spectra at 40 K, the contribution of state I is detectable only during the first 2 ns (Fig. S4b, ESI†). Lifetimes of II and III are not different enough to resolve the spectrum of state II in the short time domain. However, the contribution of III increases visibly at longer times, which allows us to obtain the spectrum of II by subtracting 26–146 ns data from 2–21 ns. The resulting TR spectrum of state II with the intense 0–0 peak and two vibrational features of decreasing intensity matches well with the CW spectrum. Above 50 K, the lifetime and PL intensity of state II decrease quickly, and its spectral features cannot be identified in the spectra above 120 K. It is hard to distinguish whether it completely vanishes or merges with state I, which gradually decreases its energy (Fig. S3b, ESI†). Either way, based on the temperature dependence of τII and integral PL intensity (Fig. S7b, ESI†), the quenching of state II can be described as a thermally activated conversion into state III with the barrier of 16 meV (128 cm−1).
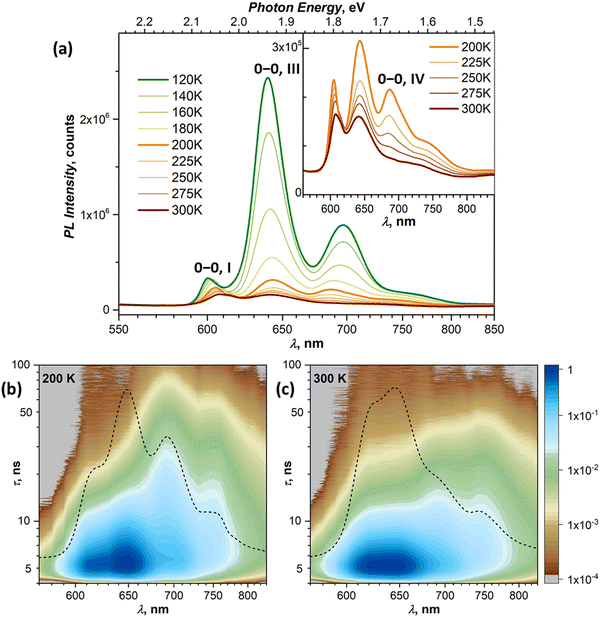
At 120–140 K, state III contributes ca 95% of the total PL intensity, the only other visible contributor in the CW spectra being state I. The latter has a much shorter lifetime of ∼1 ns, and a clean TR spectrum of state III can be obtained by discarding the first nanoseconds after the pulse and integrating between 3 and 36 ns (Fig. 5b). However, analysis of long-time 2D-TR data (>40 ns) shows the presence of yet another emissive state with PL maximum near 690 nm (Fig. 3e and Fig. S4c, ESI†). It is close to the first vibronic transition of state III and cannot be resolved in the CW spectra at 120 K, but becomes more visible at higher temperatures.
Simultaneously with the drop of the PL intensity of state III, its lifetime shortens from 15 ns at 120 K to 2.5 ns at 200 K. At the same time, the lifetime of state I measured at 610 nm increases to 1.5–2 ns. However, the 2D-TR map measured at 200 K reveals the components with much longer lifetimes near 690 and 750 nm (Fig. 4c). Integration over time shows that states I and III become insignificant by 16 ns after the pulse (Fig. S4d, ESI†), and a well-defined spectrum of the emissive state IV can be obtained by integration over the 21–46 ns period (Fig. 5b). In addition to the 0–0 transition at 687 nm (1.81 eV), state IV also has a broadened vibronic peak at 750 nm (ΔEvib ≈ 0.16 eV). The lifetime of state IV at 200 K is 19 ns. We can also follow the presence of this long-living state down to at least 140 K (τIV ≈ 27 ns), but determination of its lifetime becomes increasingly less reliable at lower temperatures due to an overlap with much brighter state III.
The quenching of state III between 140 and 200 K can be described as a thermally-activated process with the barrier of 63 meV (509 cm−1). However, it is not a conversion into another bright state, as happened with states I and II. Thus, either it can be a conversion into state IV, in which the main decay channel is not radiative, or state IV is not involved in this process, and a new non-radiative channel is open for state III itself.
It is worth noting that by reaching room temperature, thermal energy becomes high enough in comparison to the energy difference and thermal barriers between states I–III, which enables thermal repopulation of higher-energy emissive states. Essentially, one can imagine a nearly free motion of the exciton on the section of the potential energy surface encompassing these states. This can explain why apparent lifetimes of state I and III become equal within experimental uncertainty. A similar argument can be applied to explain why state II “disappears” at ∼120 K. As the barrier between states I and II becomes low in comparison to thermal energy, these two states can merge. The gradual shift of the state I 0–0 transition to a lower energy with temperature may be a part of this process.
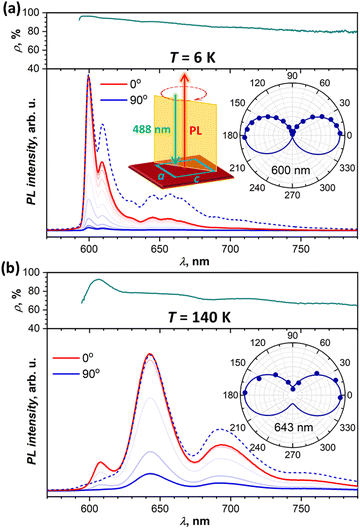
Polarization dependence
To obtain more information on the nature of the emissive states from their polarization, we performed angular-dependent measurements at selected temperatures for two different crystals. Both exhibited comparable patterns, and Fig. 6 shows two exemplary dependencies, while more data can be found in the ESI† (Fig. S9). At all temperatures and all wavelengths, emission is polarized along the a crystallographic axis. This corresponds to the polarization of the lowest-energy Davydov component in the absorption spectra (Fig. 2a). The absence of c-polarized emission excludes the assignment of any of the emissive states to the second Davydov component.At the same time, we found that PL polarization varies noticeably along the spectrum and with temperature. Fig. 6a shows angular dependence of the PL spectra measured at 6 K. The PL intensity is reduced drastically when measured for polarization along c (90°), but scaling the c-polarized spectrum to match the intensity of the a-polarized one (0°) shows that state I has more pronounced polarization than states II and III. The polarization ratio, ρ = (I0 − I90)/(I0 + I90), is near 96%, 94%, and 90% for the 0–0 transitions of states I, II, and III, respectively. Furthermore, ρ tends to decrease gradually with the increase of the wavelength. Note that we calibrated our spectrometer with unpolarized light to ensure that this wavelength dependence is not caused by the polarization-dependent sensitivity of the gratings, CCD camera, and other optical components. the polarization ratio also decreases with temperature growth. For instance, at 140 K (Fig. 6b), the ρ value of state III is reduced to 78%, however state I still preserves its enhanced polarization with ρI = 93%. At room temperature, polarization is reduced further with ρI = 82%, ρIII = 72%, and ρ = 60–65% for states IV and V at longer wavelengths.
Magnetic field dependence of PL
Singlet fission (SF) occurs in the DBP film at room temperature35 and is a plausible reason for a decrease of PL with temperature that we observe in the DBP single crystal. In a currently accepted model of SF,38,39 it is described as a multistep process, starting with a conversion of a singlet-exciton complex (S1S0) into a strongly-bound (correlated) triplet pair 1(T1T1), which then undergoes a transformation into a weakly-bound triplet-pair (T1⋯T1), eventually followed by dissociation of the latter into free triplets:| (S1S0) ⇄ 1(T1T1) ⇄ (T1⋯T1) ⇄ T1 + T1 |
Since Merrifield et al. discovered and provided the first explanation for the magnetic field influence on the delayed fluorescence in anthracene,40,41 characteristic variation of PL intensity with the magnetic field is recognized as an important feature of triplet-triplet annihilation and SF.42,43 Merrifield's theory described the weak interaction limit, in which a population of the emissive S1S0 state, and with it the PL intensity, changes when singlet contributions in individual (T1⋯T1) spin states vary with the magnetic field. Typically, when the magnetic field is ramped from zero, the PL intensity of SF materials first decreases to a certain minimum in a small field of μ0H < 0.05 T, then reverses the trend and increases until μ0H = 0.2–0.3 T, after which it stabilizes at a plateau. The exact values depend on kinetic parameters and spin–spin interaction strengths in triplet pairs.33 Spin state compositions of strongly correlated pairs are not affected by a small magnetic field, but can become visible in a high field (>1 T) when the 1(T1T1) energy level crosses 3(T1T1) or 5(T1T1) as a result of the Zeeman effect.44–46 PL intensity as a function of the magnetic field has negative peaks at such crossing points.
Both weak and strong interaction regimes imply that the emissive state, either (S1S0) or sometimes 1(T1T1), is in some kind of a dynamic equilibrium with 1(T1T1) and (T1⋯T1).42,47 This condition appears to be fulfilled for tetracene,48 rubrene,47 tetrabenzopentacene,33 anthradithiophene,49 or diphenyl-hexatriene,45,50–52 but becomes less obvious for compounds with exothermic SF. We are not aware of any magneto-PL studies of hexacene, the compound which has strongly exothermic SF similar to DBP, although the magnetic field effect was reported for the photocurrent of a photovoltaic cell based on the hexacene derivative.31 Even for the archetypical pentacene, despite numerous studies of its SF, magneto-PL measurements are not described in the literature.
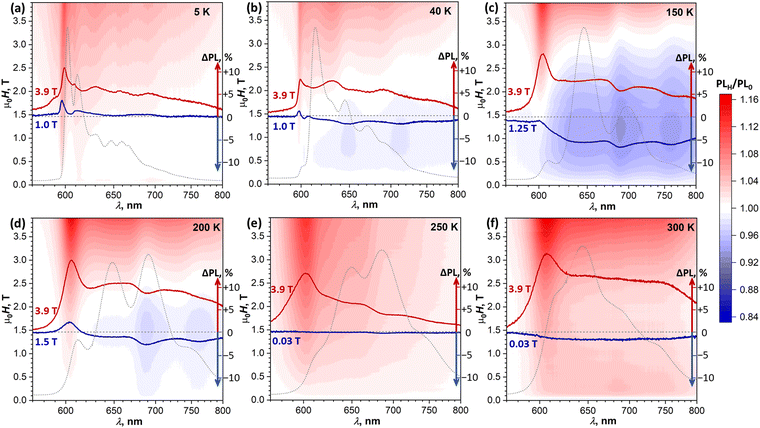
To determine if the magnetic field has an influence on the PL of DBP and identify possible SF signatures, we measured PL spectra during magnetic field sweeps at selected temperatures. The ratio of the PL intensity in a certain field μ0H to the intensity in zero field, PLH/PL0, was calculated at each wavelength and is presented in Fig. 7 in the form of (λ, μ0H) maps. Besides, for each temperature, Fig. 7 shows two PLH/PL0 traces, one at μ0H = 3.9 T, where the PLH/PL0 values are the highest, and one at the field with the most pronounced negative effect on the PL intensity. Further magneto-PL data, including PLH/PL0 traces at different fields and temperatures and field dependencies of PL intensity are shown in Fig. S10–S13 (ESI†).
At 5 K, the PL map shows a gradual increase of the 600 nm peak through the whole studied field range of 0–3.9 T. A similar increase of this peak was found at all other temperatures. Even when state I has low intensity in the PL spectra (40–250 K), it still gives the most pronounced positive PLH/PL0 feature at a high field. At 40 K, a new phenomenon can be identified – a negative field effect (PLH/PL0 < 1) is well seen between 0.5 and 1.5 T at 645 and 710 nm, approximately matching the main PL bands of state III. At 1 T, when this effect is most pronounced, PLH is decreased by almost 2% relative to the zero field. A more careful analysis of the intensity evolution with the magnetic field shows that the PLH/PL0 features at 645 and 710 nm first increase slightly in a small field of 0.05–0.1 T, and then change to more pronounced negative peaks at higher field (Fig. S10b and S11, ESI†). This kind of field dependence, which is opposite to the typical SF field-dependence, may point to a certain contribution of a triplet–triplet annihilation to the formation of state III.
A negative field effect is also observed at 150–200 K, but this time at 690 and 760 nm, which corresponds to state IV. Note that at 150 K this state is still not clearly seen in the CW PL spectrum, but its signatures in the PLH/PL0 spectra are well developed. Negative peaks in the PLH/PL0 curves are superimposed over a featureless background, especially strong at 150 K, which obscures the field dependence of these negative peaks in (λ, μ0H) maps. Analysis of their height below the background reveals that they are developed quickly within the first 0.15 T, and then exhibit a slow but steady growth at higher fields (Fig. S12b, ESI†). At 3.9 T, when the overall PLH/PL0 is >1, the negative peak at 690 nm is still clearly seen both at 150 and 200 K.
At 250 K, the system starts to demonstrate a new regime of field dependence. The PL first decreases slightly in a small field of ∼0.03 T, and then tends to grow in a higher field. PLH/PL0 curves are almost featureless below 1 T, except for the aforementioned positive peak at 605 nm observed at all temperatures. Above 1 T, the negative peak at 690 nm develops. Thus, at 250 K PLH/PL0 reveals the first signatures of SF in the form expected for the presence of weakly-coupled (T1⋯T1) pairs, while still showing some negative field effect at 690 nm, similar to that at 150–200 K.
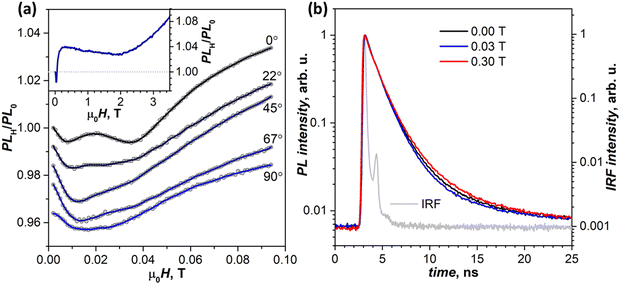
By 300 K, the transition to the new regime is complete. The negative peak at 690 nm is absent in the whole 0–4 T range, while the (T1⋯T1)-specific PLH/PL0 behavior with a negative dip of −1.5% at 0.02 T followed by a growth to +4% at 0.2 T becomes much more pronounced than at 250 K (Fig. 8a, inset). The fact that this classical SF magneto-PL effect is not state specific is quite noteworthy, considering the coexistence of 4 emissive states at room temperature. The low-field variation of PL at 300 K was studied then in the EPR spectrometer, which allowed rotating the crystal and thus changing the angle between the magnetic field and ac plane. Fig. 8a shows that not only the dip at 0.02–0.04 T is reproduced well in these measurements, but also an angular dependence of its shape can be clearly seen.41,48
To determine if changes in the PL intensity in the magnetic field are associated with variations of emission lifetimes, PL decays were measured with particular focus on the wavelengths and fields corresponding to pronounced features in (λ, μ0H) maps. No quantum beating53,54 in decay curves was observed in the zero field or any other field we applied. These measurements also did not reveal any discernable difference in normalized decay curves below room temperature, and only at 300 K a certain dependence of the decay shape on the magnetic field is visible (Fig. 8b). At 0.03 T, the PL decay is slightly faster than in the zero field in line with the decrease of PLH/PL0, while at 0.3 T and higher fields the PL decay is slower, again in line with the increased PLH/PL0 (see Table S1a for fitted times and weights, ESI†).
To summarize, magneto-PL measurements of DBP single-crystal demonstrate:
(1) Classical Merrifield's signatures of singlet fission at 250–300 K, not state-specific;
(2) State-specific negative effect at 645/710 nm (state III) at 40 K, and 690/760 nm (state IV) at 150–250 K;
(3) Positive field effect in large fields at all wavelengths and all temperatures, and a pronounced positive effect at 600–605 nm (state I). Given the enhanced polarization of emission at 600–605 nm, we cannot exclude that this effect may be caused by the Faraday rotation.55
None of these phenomena resemble the modulation of PL expected at the level crossing of 1,3,5(T1T1) spin states.45 The areas of negative field effect in (λ, μ0H) maps shift to higher field with higher temperature, while the level crossing should not be temperature dependent. Note that the magnetic field range available to us should be sufficient to reach the 1(T1T1)–3(T1T1) crossing (μ0H = 2J) and the first of the two 1(T1T1)–5(T1T1) crossings (μ0H = 3J), but is maybe not high enough to reach the second 1(T1T1)–5(T1T1) crossings at μ0H = 6J, where J is the exchange coupling between triplets in the (T1T1) pair.44,45,56 Observation of the negative magnetic field effect specific for state IV is quite interesting as it implies a particular connection of this state to triplets, although the exact nature of this connection is not clear at this moment. Note that conventional intersystem crossing between S1 and T1 can also exhibit magnetic field dependence.
Discussion
The richness of the PL spectra of DBP single crystals and their variation with temperature are quite remarkable but not completely uncommon for small-molecule organic semiconductors.57 From a bird's-eye view of the photoexcitation evolution in such systems, we can distinguish at least three types of emission-generating phenomena, which are relevant for this work:(1) The most fundamental one is a free exciton, S1. The current consensus is that it can be described as a Frenkel exciton with an admixture of a charge-transfer excitation (Fig. 9, inset),58,59 which implies a considerable S1–S0 interaction and can be thus designated as S1S0. The weight of the charge transfer can be correlated with the Davydov splitting in the absorption spectra, whereas the 0–0 emission peak of a free exciton matches the lowest-energy Davydov component with a small Stokes shift. A spatial extent of the free exciton can vary from tens of molecules at helium temperatures60,61 to a fairly localized state at high temperatures and can be assessed for by the dispersion of the exciton band.62 The radiative relaxation rate of a free exciton in the solid state is close to that of isolated molecules (e.g. measured in dilute solutions), but can be accelerated by delocalization at low-temperature and lead to a superradiance, a marked increase of emission intensity particularly for the 0–0 peak.60,61
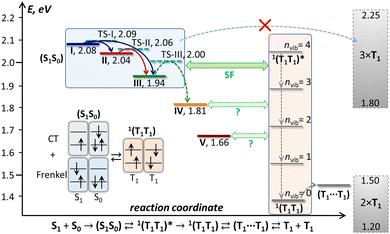 | ||
| Fig. 9 Schematic energy diagram of the excited states in DBP single crystal. Emissive states I–V found in PL measurements are shown in colors corresponding to the spectra in Fig. 5, and the transition state levels (TS-I, TS-II, TS-III) are shown as dashed cyan lines. The triplet state energy of DBP is not well known; a conservative estimation places it between 0.60 and 0.75 eV, hence 2 × T1 and 3 × T1 levels are depicted as rectangles spanning possible energy ranges, and 1(T1T1) and (T1⋯T1) levels are shown at arbitrary energies within the 2 × T1 range, while vibrational levels of 1(T1T1) are plotted equidistantly with Evib = 160 meV. Also shown is a schematic description of a singlet exciton complex (S1S0) as a mixture of Frenkel and charge-transfer excitations and its conversion into a singlet 1(T1T1) pair. | ||
(2) Different intermolecular interactions between excited molecules (S1) with those in the ground state (S0) can produce energy minima in the excited-state potential energy surface, which have no counterparts in the ground-state surface. Radiative relaxation from these transient S1S0 minima produces fluorescence shifted to the red from the free exciton emission and often characterized by prolonged emission lifetimes.49,63–71 This phenomenon is described as a self-trapped exciton (STE) or an excimer. The term excimer is usually invoked for a broad and non-structured emission, whereas more structured emission is ascribed to self-trapped excitons.
(3) Singlet fission (SF) also has a strong influence on the luminescence. On the one hand, it is a non-radiative relaxation process, which can dramatically reduce the PL intensity when its rate is fast. On the other hand, there is an increasing number of reports that a coupled triplet pair 1(T1T1), a key intermediate on the pathway from S1S0 to T1 + T1, can itself be emissive,32,33,49,72–76 although this possibility is debated in some other works.67,77 Fluorescence of 1(T1T1) is forbidden by symmetry, but it can borrow intensity from the S1 → S0 transition by the Herzberg–Teller mechanism, which results in an emission profile with a reduced intensity of the 0–0 peak11 and a comparably long radiative lifetime. The 1(T1T1) emission competes with the triplet exciton diffusion, which first yields a weakly-coupled pair (T1⋯T1) and eventually free triplets T1 + T1. The triplet diffusion is a thermally-activated process, and a temperature dependence of its rate is therefore a crucial factor for SF.49,74,75,78 At low temperature, when diffusion is very slow, the 1(T1T1) state can live long enough to relax radiatively or re-fuse back to S1S0. At temperatures above 150–200 K, the triplet diffusion becomes fast and outperforms radiative processes, thus suppressing PL. In this regime, the Merrifield-type magnetic field effect and quantum beating, both betraying the presence of weakly-coupled (T1⋯T1) pairs, can become visible in PL.53,54,74,79 Note that the reverse process, triplet fusion (triplet–triplet annihilation), proceeds through formation of (T1⋯T1) and then 1(T1T1) pairs from free triplets, and can also lead to magnetic field effects, 1(T1T1) emission, and delayed S1 fluorescence with long lifetimes.49
In systems where all these phenomena take place, PL is strongly temperature dependent. At helium temperatures, emission is usually dominated by a free exciton, sometimes amplified by a superradiance. The temperature increase facilitates transition to STE/excimer states, which can then compete with singlet fission. In fact, STE emission is hard to distinguish from 1(T1T1) emission, and the role of STE states in singlet fission is still debated. In different systems, formation of STE was discussed as an intermediate on the pathway to 1(T1T1),80,81 as a parallel route competing with singlet fission,68,82,83 or as a trap hindering singlet fission.67,69,84–87 Either way, singlet fission usually becomes the main relaxation process at room temperature, while PL intensity decreases to only a small fraction of that observed at helium temperature.
Complete interpretation of the photoexcitation mechanism in DBP crystals will require a multitechnique study involving transient absorption and time-resolved EPR spectroscopy, as well as time-resolved PL with much higher time resolution than available to us, and thus inevitably goes beyond the scope of this work. Yet, an analysis of the VT-PL data along the guidelines outlined above allows us to make the first approach to this problem.
Free and self-trapped excitons
PL of DBP crystal below 120 K can be explained by assuming that state I is a free exciton while states II and III are two kinds of a self-trapped exciton.The strongest PL intensity of state I with a narrow 0–0 peak below 10 K is in line with the enhanced intensity of the free exciton emission in other organic semiconductors at helium temperatures. At 5–10 K, the PL decay of state I at 600 nm is described by two lifetimes, 3.8 and 6.1 ns with equal weights, which are close to the fluorescence lifetime of 5.2–7.4 ns determined for isolated DBP molecules in different solvents35–37 or 4.1–4.7 ns measured in polystyrene matrix in this work. The superradiance effect, if present, is not very pronounced as we do not observe a decrease of the lifetime upon cooling (Fig. 5a). Note that the degree of exciton delocalization can be assessed from the exciton band dispersion measured by EELS at 20 K, which shows that the value of DBP, 70 meV,34 is between that in pentacene-SC (110 meV)88 and in tetracene-SC (55 meV for the lowest Davydov component).89 Nonetheless, unlike in DBP and pentacene, the superradiance effect in tetracene PL is well documented.60,61 Thus, there appears to be no direct correlation between the exciton bandwidth and superradiance.
Low-temperature lifetimes of states II and III, 9.9–10.1 and 14.5–15.8 ns, are longer than for isolated DBP molecules, which is typical for self-trapped excitons. A comparable population of states I–III is present at 5 K, below the temperature at which interconversion between these states takes place. This means that internal conversion after photoexcitation populates all three states at once. The initial populations at 5–10 K are non-equilibrium, but remain frozen until thermal energy allows the barriers between these states to be overcome. At 15–40 K, the free exciton leaves its apparently rather shallow minimum (the escape barrier is only 52 cm−1) and equally populates both STE states. Then, at 50–120 K, the higher-energy STE (state II) converts into the lower-energy STE (state III) over the barrier of 118 cm−1. These barriers are in the energy range of low-frequency modes of the DBP crystal corresponding to intermolecular vibrations mixed with non-planar deformations of DBP molecules. The Raman spectrum of DBP crystal in this range is quite rich and includes a stand-alone mode at 60 cm−1 and a group of peaks at 107, 127, 137, and 152 cm−1 (see ref. 34 and Fig. S8, ESI†). When the thermal energy becomes comparable to barriers between STE and free exciton states, populations of the high-energy state can become significant as a result of thermal equilibrium, which leads to equalization of lifetimes at higher temperatures.
The fact that there is more than one STE state should not be surprising. For instance, α-PTCDA (3,4,9,10-perylene-tetracarboxylic-dianhydride) showed two STE and one excimer states in addition to a free exciton,63,90 while pyrene and perylene are well known for having several emissive states of STE nature.71,91 STE is characterized by a certain displacement along the intermolecular vibrational coordinate leading to an enhanced interaction between the excited molecule and a neighboring molecule remaining in the ground electronic state. As each DBP molecule has three pairs of close neighbors in the crystal (Fig. 1c), this simplified dimer-like description of STE already implies a possibility of three (S1S0)STE pair states. Structural deformation in the STE states also implies a loosening of symmetry selection rules and thus explains the lower polarization degree of STE emission in comparison to the free exciton emission (Fig. 6), which proceeds under rigorous crystallographic symmetry. Advanced computational studies such as those performed for tetracene,56,92 pentacene,93,94 or hexacene,28 will be required to disclose structural details and energetics of different S1S0 pair states, but they exceed the scope of this work.
Exothermic singlet fission in DBP
Interpretation of the PL evolution above 120 K is more ambiguous. On the first sight, the changes between 120 and 200 K can be described as the next step on the energy ladder, in which state III transforms to state IV over the barrier of 509 cm−1/63 meV (Fig. 9). State IV can be another STE with more pronounced intermolecular displacement and enhanced S1–S0 interaction. The long lifetime of state IV (Fig. 5) is in line with the STE conjecture. The size of the barrier corresponds to the internal vibrations of DBP, suggesting that the intramolecular deformation in this STE should be more pronounced in comparison to state II and III. What makes this interpretation insufficient is the considerable weakening of PL above 120 K.A strong decrease of the PL intensity during heating implies a thermally-activated non-radiative process, which does not produce a new emissive state. Given the clear signatures of singlet fission in DBP crystal from magneto-PL measurements and considering the mechanism of SF in other organic compounds, this thermally-activated process might be a dissociation of triplet 1(T1T1) pairs and/or a diffusion (hopping) of already dissociated free triplet excitons. The thermal barrier of 63 meV is in the energy range of a triplet pair binding energy (20–200 meV).11 When temperature increases, SF becomes the main relaxation mechanism, while the lifetimes of all emissive states decrease accordingly. Indeed, the recent room-temperature PL and transient absorption study of DBP polycrystalline film by Manna et al. revealed a fast decay of the S1 state into the 1(T1T1) pair with the time constant of 5–7 ps, followed by formation of free triplets on a time scale of 135 ps with the triplet yield of 196%.35 The PL spectrum in ref. 35 has the main peak at 600 nm and corresponds well to the free exciton emission in single crystals. Different to ref. 35, the room temperature S1 lifetime in our work is still about 1 ns, but our time resolution does not allow detection of a fast process with a time constant of a few ps. Ref. 35 also reported a minor PL component with a lifetime of 8–11 ns and 0.3 eV lower energy, which matches the parameters of our state IV. State IV in this scheme appears to be a trap, which is populated in parallel to SF. Furthermore, given the temperature range of its rise and decay as well as specific magnetic field effect, state IV might be even considered to be the 1(T1T1) pair. However, the energy of state IV is too high and its lifetime is too long at room temperature, hence the interpretation of state IV as STE appears more plausible.
The energy difference between the correlated triplet pair 1(T1T1) and the free exciton is a crucial parameter of SF. Unfortunately, nothing is known about the 1(T1T1) energy in DBP. The 1(T1T1) energy is usually close to that of two separated triplet excitons, 2 × T1, but the T1 energy for DBP is also not known precisely. An upper bound of 0.8 eV in solution was given by a triplet sensitization study in ref. 35, while TD-DFT calculations in the same work gave the value of 0.64 eV for an isolated molecule. In the solid state, T1 energy is likely to be lower than for an isolated molecule by ∼0.05 eV. If we assume the range of 0.60–0.75 eV as a conservative estimation of the T1 energy in crystalline DBP, the 2 × T1 energy is expected to be 1.2–1.5 eV (Fig. 9). Thus, SF in crystalline DBP is highly exothermic with −ΔESF = −{2E(T1) − E(S1S0)} > 0.5 eV. For the vast majority of molecular SF materials, either endothermic or exothermic, |ΔESF| < 0.2 eV, and only hexacene has a comparably large −ΔESF of 0.5–0.6 eV.29,30 In fact, for both DBP and hexacene, the singlet exciton energy is already close to 3 × T1.
Although SF in hexacene is not yet studied as thoroughly as in pentacene and tetracene, the corpus of publications27–31,95–98 grows steadily and forms useful reference points for DBP. Busby et al. analyzed if SF in hexacene can proceed with the formation of three triplet excitons from one singlet.30 Their modelling showed that the probability of this process is very low but can become considerable if the charge-transfer contribution to the singlet exciton is increased. An indirect measure of the charge-transfer contribution is the Davydov splitting,58 which amounts to 0.15–0.18 eV in hexacene28,30,99 and 0.11 eV in DBP (Fig. 2a).34 Thus, formation of three triplets from one singlet exciton in DBP appears less probable than in hexacene and will not be considered further. Busby et al. also showed that the large exothermicity has a negative influence on the SF kinetics because the driving force is considerably larger than phonon energies.30 This requires a multiphonon relaxation and leads to a slower SF rate in hexacene (τSF = 0.5 ps at room temperature)30,31 than in pentacene (τSF ≈ 0.1 ps),24 which also has exothermic SF but with the driving force within the one-phonon energy range. Time-resolved two-photon photoemission (TR-2PPE) study of hexacene by Monahan et al.29 revealed that the formation of 1(T1T1) from S1 proceeds via two parallel mechanisms: coherent, which is faster than 50 fs, and incoherent with the time constant of 180 fs. 1(T1T1) then decays to independent triplets on time scales of 270 fs and 700 fs for two crystallographic directions. Similarly fast and anisotropic 1(T1T1) dissociation was reported by Sun et al.28 Variable-temperature transient-absorption study by Qian et al. showed that the rates of 1(T1T1) formation and dissociation in hexacene are both temperature independent in the 77–300 K range.27 Thus, there appears to be no thermally-activated triplet migration, which the authors explained by the large SF driving force. To summarize, both (S1S0) → 1(T1T1) and 1(T1T1) → T1 + T1 steps in hexacene are temperature-independent and occur on sub-ps timescale at all studied temperatures above 77 K. None of these studies reported PL of solid hexacene, but kinetic parameters of its singlet fission suggest that the radiative decay of S1 should be negligible.
Comparing SF in hexacene to what is known so far about DBP, we conclude that while the rate of the (S1S0) → 1(T1T1) transition is similarly affected by the large ΔESF value in DBP35 and in hexacene,30 the overall mechanism is considerably different. In fact, it is hard to reconcile our VT-PL results with the notion of strongly exothermic SF proceeding on a picosecond timescale. The bright emission from states I–III below 120 K indicates that SF does not occur or at least not very efficiently at that temperature. Consider the evolution of photoexcitation below 120 K, when the main radiative relaxation occurs on a timescale of 5–15 ns. The parallel formation of 1(T1T1) on a timescale of a few ps should have quenched the PL, unless 1(T1T1) has a long lifetime allowing it to repopulate the emissive states. However, the large ΔESF in DBP implies that the triplet pair is first formed in the highly vibrationally-excited state denoted as 1(T1T1)* in Fig. 9. Once vibrational relaxation of 1(T1T1)* starts by emitting phonons into the lattice, emissive states I–III cannot be repopulated anymore because of the large energy difference with 1(T1T1). Bright emission of DBP with ns lifetime would then only be possible if vibrational relaxation of 1(T1T1)* were also nanosecond-long, which is very unlikely, although not completely unimaginable. Phonon relaxation in low-temperature molecular crystals usually occurs on a timescale of 1–10 ps, however in some cases it can extend to the 100 ps–1 ns range and be delayed by phonon bottlenecks.100–103 Whether vibrational relaxation of 1(T1T1)* is fast or slow, the 1(T1T1) state formed as a result should have a long lifetime at low temperatures, when triplet diffusion is negligible. 1(T1T1) emission can be then expected in the near-infrared, at λ > 830 nm (1.5 eV). We performed NIR-PL measurements at different temperatures but did not detect any discernable NIR-PL features except for a tail of the visible-range emission (Fig. S14, ESI†). Thus, either 1(T1T1) of DBP is not emissive and decays only non-radiatively, or it is not formed at all at low T. Note that the T1 phosphorescence of DBP was not found either, but this may be caused by the limited NIR detection range of our spectrometer (λ < 1650 nm).
Another way how strong PL below 120 K might be compatible with the fast exothermic singlet fission is if (S1S0) → 1(T1T1)* occurs efficiently only in a special favorable arrangement of S1 and S0 molecules, i.e. via a certain (S1S0)STE intermediate, which is not accessible at low temperature. Then the barrier of 63 meV determined from the temperature dependence of τIII could correspond to the conversion of state III into this STE-intermediate. Neither state IV nor state V can be such an intermediate because their lifetimes are too long, whereas the fast transformation of the STE-intermediate into triplets should strongly shorten its lifetime and presumably make it dark in PL. In fact, the role and nature of the IV and V states is not very clear from this study. They may be STEs with deeper energy, and V might also be an excimer state (note that we cannot clearly establish its vibronic structure). But their formation with a delay of 1–1.5 ns (Fig. S5, ESI†) indicates that they may be formed as a result of some follow-up process, for which a triplet fusion would be a plausible candidate. The lower energy makes them more accessible for the reversed-SF process than for free exciton or states II and III. Besides, as states IV and V have long lifetimes and seem to be decoupled from the kinetics of states I–III, they can also correspond to defects in the crystals, particularly surface traps.
The large ΔESF value in DBP also makes interpretation of the magnetic field effect on PL problematic, if we recall that Merrifield theory implies a dynamic equilibrium between (S1S0) and (T1⋯T1). The energy difference between (S1S0) and two triplets in DBP is just too large in comparison to thermal energy even at 300 K, and SF should be irreversible.
To conclude, DBP presents an interesting case of the complex photoexcitation evolution, which on the other hand seems to be in line with the behavior of small molecule organic semiconductors, but on the hand is hard to fit into the behavior expected from the SF system with a large driving force.
Conclusions
Recent development of the single-crystal growth of dibenzopentacene opened the possibility to study the fundamental electronic properties of this close relative of pentacene in the well-defined structural environment.34 In this work, we presented the first study of the photoluminescence of dibenzopentacene single-crystals. Variable-temperature measurements in the 5–300 K range revealed the presence of at least five emissive states. The free exciton emission dominates the spectra below 20 K, but gives way to states with progressively lower energy when the temperature increases, which is interpreted as the population of self-trapped excitons with different degrees of intermolecular reorganization. The combination of steady-state and time-resolved measurements allowed us to identify spectroscopic patterns of each state, and the temperature dependence of emission lifetimes was utilized to determine thermal barriers of interconversion. The fast drop of the emission intensity upon rising temperature above 120 K points to the setting in of a singlet fission. The latter is further confirmed by the modulation of the PL intensity in the magnetic field, consistent with the Merrifield formulation of the magnetic field effect for systems with equilibrium between singlet excitons and triplet pairs. The large energy difference between singlet states and triplet pairs implies that the singlet fission in dibenzopentacene is strongly exothermic. However, this large exothermicity is not fully consistent with the temperature and magnetic field dependence of the photoluminescence, which may be a general problem for materials with exothermic single fission. In particular, it is not clear how vibrational relaxation of hot triplet pairs competes with re-fusion into singlets, dissociation into triplets, or deactivation. These puzzles cannot be solved using only photoluminescence data and will require an input from other techniques to track dark and triplet states and fast processes at different temperatures. We hope that our results will motivate such studies of dibenzopentacene in the near future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Fupin Liu for help with analysis of the crystal structure of DBP and Frank Ziegs for help with some PL measurements. Financial support was provided by Deutsche Forschungsgemeinschaft (grants PO 1602/6-1 and PO 1602/11-1 to A. A. P.).References
- A. Köhler and H. Bässler, Electronic Processes in Organic Semiconductors, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2015 Search PubMed.
- Physics of Organic Semiconductors, ed. W. Brütting and C. Adachi, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2012 Search PubMed.
- O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412 CrossRef CAS PubMed.
- S. R. Forrest, Organic Electronics: Foundations to Applications, Oxford University Press, 2020 Search PubMed.
- O. P. Dimitriev, Chem. Rev., 2022, 122, 8487–8593 CrossRef CAS PubMed.
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741–2804 RSC.
- K. Bera, S. Y. Kwang and R. R. Frontiera, J. Phys. Chem. C, 2020, 124, 25163–25174 CrossRef CAS.
- W. Kim and A. J. Musser, Adv. Phys. X, 2021, 6, 1918022 Search PubMed.
- S. N. Sanders, A. B. Pun, K. R. Parenti, E. Kumarasamy, L. M. Yablon, M. Y. Sfeir and L. M. Campos, Chem, 2019, 5, 1988–2005 CAS.
- A. J. Musser and J. Clark, Annu. Rev. Phys. Chem., 2019, 70, 323–351 CrossRef CAS PubMed.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- T. Zhu and L. Huang, J. Phys. Chem. Lett., 2018, 9, 6502–6510 CrossRef CAS PubMed.
- N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618 CrossRef CAS PubMed.
- A. J. Baldacchino, M. I. Collins, M. P. Nielsen, T. W. Schmidt, D. R. McCamey and M. J. Y. Tayebjee, Chem. Phys. Rev., 2022, 3, 021304 CrossRef CAS.
- T. Wang, B.-Y. Zhang and H.-L. Zhang, Macromol. Rapid Commun., 2022, 43, 2200326 CrossRef CAS PubMed.
- A. J. Carrod, V. Gray and K. Börjesson, Energy Environ. Sci., 2022, 15, 4982–5016 RSC.
- R. J. Hudson, A. N. Stuart, D. M. Huang and T. W. Kee, J. Phys. Chem. C, 2022, 126, 5369–5377 CrossRef CAS.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- T. Ullrich, D. Munz and D. M. Guldi, Chem. Soc. Rev., 2021, 50, 3485–3518 RSC.
- J. Li, H. Cao, Z. Zhang, S. Liu and Y. Xia, Photonics, 2022, 9, 689 CrossRef CAS.
- M. W. B. Wilson, A. Rao, B. Ehrler and R. H. Friend, Acc. Chem. Res., 2013, 46, 1330–1338 CrossRef CAS PubMed.
- J. J. Burdett and C. J. Bardeen, Acc. Chem. Res., 2013, 46, 1312–1320 CrossRef CAS PubMed.
- W.-L. Chan, T. C. Berkelbach, M. R. Provorse, N. R. Monahan, J. R. Tritsch, M. S. Hybertsen, D. R. Reichman, J. Gao and X. Y. Zhu, Acc. Chem. Res., 2013, 46, 1321–1329 CrossRef CAS PubMed.
- Y. Qian, Z.-C. Huang-Fu, T. Zhang, X. Li, A. R. Harutyunyan, G. Chen, H. Chen and Y. Rao, J. Phys. Chem. C, 2022, 126, 8377–8383 CrossRef CAS.
- D. Sun, G.-H. Deng, B. Xu, E. Xu, X. Li, Y. Wu, Y. Qian, Y. Zhong, C. Nuckolls, A. R. Harutyunyan, H.-L. Dai, G. Chen, H. Chen and Y. Rao, iScience, 2019, 19, 1079–1089 CrossRef CAS PubMed.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X. Y. Zhu, Nat. Chem., 2017, 9, 341–346 CrossRef CAS PubMed.
- E. Busby, T. C. Berkelbach, B. Kumar, A. Chernikov, Y. Zhong, H. Hlaing, X. Y. Zhu, T. F. Heinz, M. S. Hybertsen, M. Y. Sfeir, D. R. Reichman, C. Nuckolls and O. Yaffe, J. Am. Chem. Soc., 2014, 136, 10654–10660 CrossRef CAS PubMed.
- J. Lee, M. J. Bruzek, N. J. Thompson, M. Y. Sfeir, J. E. Anthony and M. A. Baldo, Adv. Mater., 2013, 25, 1445–1448 CrossRef CAS PubMed.
- S. Lukman, J. M. Richter, L. Yang, P. Hu, J. Wu, N. C. Greenham and A. J. Musser, J. Am. Chem. Soc., 2017, 139, 18376–18385 CrossRef CAS PubMed.
- P. J. Budden, L. R. Weiss, M. Müller, N. A. Panjwani, S. Dowland, J. R. Allardice, M. Ganschow, J. Freudenberg, J. Behrends, U. H. F. Bunz and R. H. Friend, Nat. Commun., 2021, 12, 1527 CrossRef CAS PubMed.
- L. Graf, F. Liu, M. Naumann, F. Roth, B. Debnath, B. Büchner, Y. Krupskaya, A. A. Popov and M. Knupfer, ACS Omega, 2022, 7, 21183–21191 CrossRef CAS PubMed.
- B. Manna, A. Nandi and R. Ghosh, J. Phys. Chem. C, 2022, 126, 12082–12090 CrossRef CAS.
- A. Tovstopyat, E. Zojer and G. Leising, J. Appl. Spectrosc., 2016, 83, 20–26 CrossRef CAS.
- C. Canuel, S. Badre, H. Groenzin, M. Berheide and O. C. Mullins, Appl. Spectrosc., 2003, 57, 538–544 CrossRef CAS.
- R. D. Pensack, E. E. Ostroumov, A. J. Tilley, S. Mazza, C. Grieco, K. J. Thorley, J. B. Asbury, D. S. Seferos, J. E. Anthony and G. D. Scholes, J. Phys. Chem. Lett., 2016, 7, 2370–2375 CrossRef CAS PubMed.
- G. D. Scholes, J. Phys. Chem. A, 2015, 119, 12699–12705 CrossRef CAS PubMed.
- R. E. Merrifield, Pure Appl. Chem., 1971, 27, 481–498 CrossRef CAS.
- R. C. Johnson and R. E. Merrifield, Phys. Rev. B: Solid State, 1970, 1, 896–902 CrossRef.
- J. J. Burdett, G. B. Piland and C. J. Bardeen, Chem. Phys. Lett., 2013, 585, 1–10 CrossRef CAS.
- R. Xu, C. Zhang and M. Xiao, Trends Chem., 2022, 4, 528–539 CrossRef CAS.
- T. Yago, K. Ishikawa, R. Katoh and M. Wakasa, J. Phys. Chem. C, 2016, 120, 27858–27870 CrossRef CAS.
- M. Wakasa, M. Kaise, T. Yago, R. Katoh, Y. Wakikawa and T. Ikoma, J. Phys. Chem. C, 2015, 119, 25840–25844 CrossRef CAS.
- S. L. Bayliss, L. R. Weiss, A. Rao, R. H. Friend, A. D. Chepelianskii and N. C. Greenham, Phys. Rev. B, 2016, 94, 045204 CrossRef.
- G. B. Piland, J. J. Burdett, D. Kurunthu and C. J. Bardeen, J. Phys. Chem. C, 2013, 117, 1224–1236 CrossRef CAS.
- H. Bouchriha, V. Ern, J. L. Fave, C. Guthmann and M. Schott, J. Phys. France, 1978, 39, 257–271 CrossRef CAS.
- D. G. Bossanyi, M. Matthiesen, S. Wang, J. A. Smith, R. C. Kilbride, J. D. Shipp, D. Chekulaev, E. Holland, J. E. Anthony, J. Zaumseil, A. J. Musser and J. Clark, Nat. Chem., 2021, 13, 163–171 CrossRef CAS.
- M. Wakasa, T. Yago, Y. Sonoda and R. Katoh, Commun. Chem., 2018, 1, 9 CrossRef.
- C. Shen, S. Yan, X. Chen, L. Niu and Y. Zhang, Org. Electron., 2019, 67, 194–199 CrossRef CAS.
- Y. Sonoda, R. Katoh, N. Tohnai, T. Yago and M. Wakasa, J. Phys. Chem. C, 2022, 126, 8742–8751 CrossRef CAS.
- J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597–8607 CrossRef CAS PubMed.
- R. Wang, C. Zhang, B. Zhang, Y. Liu, X. Wang and M. Xiao, Nat. Commun., 2015, 6, 8602 CrossRef CAS.
- Z. Nelson, L. Delage-Laurin and T. M. Swager, J. Am. Chem. Soc., 2022, 144, 11912–11926 CrossRef CAS PubMed.
- S. L. Bayliss, L. R. Weiss, A. Mitioglu, K. Galkowski, Z. Yang, K. Yunusova, A. Surrente, K. J. Thorley, J. Behrends, R. Bittl, J. E. Anthony, A. Rao, R. H. Friend, P. Plochocka, P. C. M. Christianen, N. C. Greenham and A. D. Chepelianskii, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5077–5082 CrossRef CAS.
- J. Gierschner, J. Shi, B. Milián-Medina, D. Roca-Sanjuán, S. Varghese and S. Park, Adv. Opt. Mater., 2021, 9, 2002251 CrossRef CAS.
- H. Yamagata, J. Norton, E. Hontz, Y. Olivier, D. Beljonne, J. L. Brédas, R. J. Silbey and F. C. Spano, J. Chem. Phys., 2011, 134, 204703 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS.
- A. Camposeo, M. Polo, S. Tavazzi, L. Silvestri, P. Spearman, R. Cingolani and D. Pisignano, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 033306 CrossRef.
- S.-H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef.
- L. Graf, A. Kusber, B. Büchner and M. Knupfer, Phys. Rev. B, 2022, 106, 165429 CrossRef CAS.
- A. Y. Kobitski, R. Scholz, D. R. T. Zahn and H. P. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 155201 CrossRef.
- R. He, X. Chi, A. Pinczuk, D. V. Lang and A. P. Ramirez, Appl. Phys. Lett., 2005, 87, 211117 CrossRef.
- B. Gieseking, T. Schmeiler, B. Müller, C. Deibel, B. Engels, V. Dyakonov and J. Pflaum, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205305 CrossRef.
- R. D. Pensack, R. J. Ashmore, A. L. Paoletta and G. D. Scholes, J. Phys. Chem. C, 2018, 122, 21004–21017 CrossRef CAS.
- C. D. Cruz, E. L. Chronister and C. J. Bardeen, J. Chem. Phys., 2020, 153, 234504 CrossRef CAS PubMed.
- G. Mayonado, K. T. Vogt, J. D. B. Van Schenck, L. Zhu, G. Fregoso, J. Anthony, O. Ostroverkhova and M. W. Graham, J. Phys. Chem. C, 2022, 126, 4433–4445 CrossRef CAS.
- L. Ma, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 201203 CrossRef.
- F. Anger, J. O. Ossó, U. Heinemeyer, K. Broch, R. Scholz, A. Gerlach and F. Schreiber, J. Chem. Phys., 2012, 136, 054701 CrossRef CAS PubMed.
- A. Matsui, J. Opt. Soc. Am. B, 1990, 7, 1615–1629 CrossRef CAS.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797–14805 RSC.
- H. L. Stern, A. J. Musser, S. Gelinas, P. Parkinson, L. M. Herz, M. J. Bruzek, J. Anthony, R. H. Friend and B. J. Walker, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7656–7661 CrossRef CAS PubMed.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205–1212 CrossRef CAS PubMed.
- A. Thampi, H. L. Stern, A. Cheminal, M. J. Y. Tayebjee, A. J. Petty, II, J. E. Anthony and A. Rao, J. Am. Chem. Soc., 2018, 140, 4613–4622 CrossRef CAS PubMed.
- R. D. Pensack, A. J. Tilley, C. Grieco, G. E. Purdum, E. E. Ostroumov, D. B. Granger, D. G. Oblinsky, J. C. Dean, G. S. Doucette, J. B. Asbury, Y.-L. Loo, D. S. Seferos, J. E. Anthony and G. D. Scholes, Chem. Sci., 2018, 9, 6240–6259 RSC.
- T. S. Lee, Y. L. Lin, H. Kim, B. P. Rand and G. D. Scholes, Can. J. Chem., 2019, 97, 465–473 CrossRef CAS.
- E. A. Wolf, D. M. Finton, V. Zoutenbier and I. Biaggio, Appl. Phys. Lett., 2018, 112, 083301 CrossRef.
- C. M. Mauck, P. E. Hartnett, E. A. Margulies, L. Ma, C. E. Miller, G. C. Schatz, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2016, 138, 11749–11761 CrossRef CAS PubMed.
- C. Ye, V. Gray, J. Mårtensson and K. Börjesson, J. Am. Chem. Soc., 2019, 141, 9578–9584 CrossRef CAS PubMed.
- Y. Huang, I. A. Buyanova, C. Phansa, M. E. Sandoval-Salinas, D. Casanova, W. K. Myers, N. C. Greenham, A. Rao, W. M. Chen and Y. Puttisong, Cell Rep. Phys. Sci., 2021, 2, 100339 CrossRef CAS.
- J. Hausch, A. J. Berges, C. Zeiser, T. Rammler, A. Morlok, J. Bredehöft, S. Hammer, J. Pflaum, C. J. Bardeen and K. Broch, J. Phys. Chem. C, 2022, 126, 6686–6693 CrossRef CAS.
- C. B. Dover, J. K. Gallaher, L. Frazer, P. C. Tapping, A. J. Petty, M. J. Crossley, J. E. Anthony, T. W. Kee and T. W. Schmidt, Nat. Chem., 2018, 10, 305–310 CrossRef CAS PubMed.
- Z. Zhang, W. Ni, L. Ma, L. Sun and G. G. Gurzadyan, J. Phys. Chem. C, 2022, 126, 396–403 CrossRef CAS.
- M. L. Williams, I. Schlesinger, C. E. Ramirez, R. M. Jacobberger, P. J. Brown, R. M. Young and M. R. Wasielewski, J. Phys. Chem. C, 2022, 126, 10287–10297 CrossRef CAS.
- X. Fei, S. Zhang, D. Zhai, Z. Wang, J.-L. Lin, Q. Xiao, C.-L. Sun, W. Deng, C. Zhang, W. Hu and H.-L. Zhang, Chem. Sci., 2022, 13, 9914–9920 RSC.
- F. Roth, R. Schuster, A. König, M. Knupfer and H. Berger, J. Chem. Phys., 2012, 136, 204708 CrossRef PubMed.
- F. Roth, M. Nohr, S. Hampel and M. Knupfer, Europhys. Lett., 2015, 112, 37004 CrossRef.
- R. Scholz, A. Y. Kobitski, I. Vragović, H. P. Wagner and D. R. T. Zahn, Org. Electron., 2004, 5, 99–105 CrossRef CAS.
- E. Von Freydorf, J. Kinder and M. E. Michel-Beyerle, Chem. Phys., 1978, 27, 199–209 CrossRef CAS.
- L. E. Aguilar Suarez, C. de Graaf and S. Faraji, Phys. Chem. Chem. Phys., 2021, 23, 14164–14177 RSC.
- T. Nagami, H. Miyamoto, R. Sakai and M. Nakano, J. Phys. Chem. C, 2021, 125, 2264–2275 CrossRef CAS.
- G.-H. Deng, Y. Qian, X. Li, T. Zhang, W. Jiang, A. R. Harutyunyan, G. Chen, H. Chen and Y. Rao, J. Phys. Chem. Lett., 2021, 12, 3142–3150 CrossRef CAS PubMed.
- G.-H. Deng, Q. Wei, J. Han, Y. Qian, J. Luo, A. R. Harutyunyan, G. Chen, H. Bian, H. Chen and Y. Rao, J. Chem. Phys., 2019, 151, 054703 CrossRef.
- J. Han, Q. Xie, J. Luo, G.-H. Deng, Y. Qian, D. Sun, A. R. Harutyunyan, G. Chen and Y. Rao, J. Phys. Chem. Lett., 2020, 11, 1261–1267 CrossRef CAS PubMed.
- S. N. Sanders, E. Kumarasamy, K. J. Fallon, M. Y. Sfeir and L. M. Campos, Chem. Sci., 2020, 11, 1079–1084 RSC.
- S. Nakamura, H. Sakai, M. Fuki, Y. Kobori, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. Lett., 2021, 12, 6457–6463 CrossRef CAS PubMed.
- A. Chernikov, O. Yaffe, B. Kumar, Y. Zhong, C. Nuckolls and T. F. Heinz, J. Phys. Chem. Lett., 2014, 5, 3632–3635 CrossRef CAS PubMed.
- S. Califano and V. Schettino, Int. Rev. Phys. Chem., 1988, 7, 19–57 Search PubMed.
- C. L. Schosser and D. D. Dlott, J. Chem. Phys., 1984, 80, 1394–1406 CrossRef CAS.
- W. H. Hesselink and D. A. Wiersma, J. Chem. Phys., 1981, 74, 886–889 CrossRef CAS.
- D. D. Dlott, in Laser Spectroscopy of Solids II, ed. W. M. Yen, Springer, Berlin, Heidelberg, 1989, pp. 167–200 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01548c |
| This journal is © The Royal Society of Chemistry 2023 |