Open Access Article
Open Access ArticleOptical markers of magnetic phase transition in CrSBr†
W. M.
Linhart
 *a,
M.
Rybak
a,
M.
Birowska
b,
P.
Scharoch
a,
K.
Mosina
c,
V.
Mazanek
c,
D.
Kaczorowski
d,
Z.
Sofer
*a,
M.
Rybak
a,
M.
Birowska
b,
P.
Scharoch
a,
K.
Mosina
c,
V.
Mazanek
c,
D.
Kaczorowski
d,
Z.
Sofer
 c and
R.
Kudrawiec
a
c and
R.
Kudrawiec
a
aDepartment of Semiconductor Materials Engineering, Faculty of Fundamental Problems of Technology, Wrocław University of Science and Technology, Wybrzee Wyspianńskiego 27, 50-370 Wrocław, Poland. E-mail: wojciech.linhart@pwr.edu.pl
bInstitute of Theoretical Physics, Faculty of Physics, University of Warsaw, Pasteura 5, 02-093 Warsaw, Poland
cDepartment of Inorganic Chemistry, University of Chemistry and Technology Prague, Technická 5, 166 28 Prague 6, Czech Republic
dInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, ul. Okólna 2, 50-422 Wrocław, Poland
First published on 30th May 2023
Abstract
Here, we investigate the role of the interlayer magnetic ordering of CrSBr in the framework of ab initio calculations and by using optical spectroscopy techniques. These combined studies allow us to unambiguously determine the nature of the optical transitions. In particular, photoreflectance measurements, sensitive to the direct transitions, have been carried out for the first time. We have demonstrated that optically induced band-to-band transitions visible in optical measurement are remarkably well assigned to the band structure by the momentum matrix elements and energy differences for the magnetic ground state (A-AFM). In addition, our study reveals significant differences in electronic properties for two different interlayer magnetic phases. When the magnetic ordering of A-AFM to FM is changed, the crucial modification of the band structure reflected in the direct-to-indirect band gap transition and the significant splitting of the conduction bands along the Γ–Z direction are obtained. In addition, Raman measurements demonstrate a splitting between the in-plane modes B22g/B23g, which is temperature dependent and can be assigned to different interlayer magnetic states, corroborated by the DFT+U study. Moreover, the B22g mode has not been experimentally observed before. Finally, our results point out the origin of interlayer magnetism, which can be attributed to electronic rather than structural properties. Our results reveal a new approach for tuning the optical and electronic properties of van der Waals magnets by controlling the interlayer magnetic ordering in adjacent layers.
1 Introduction
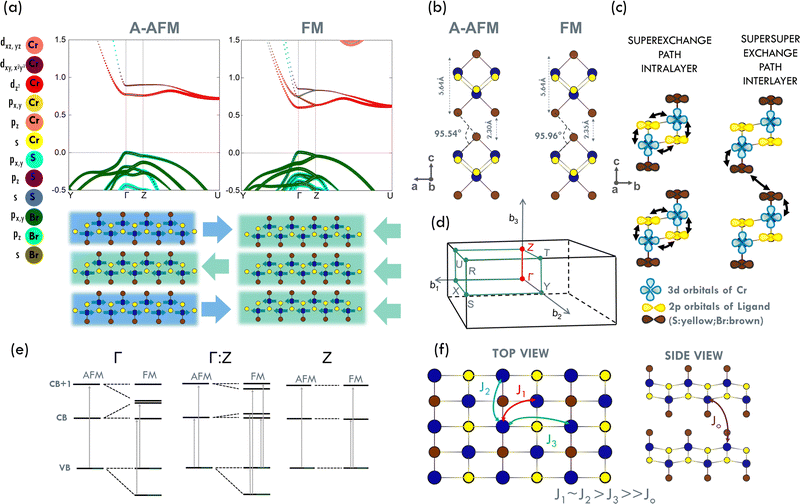
Two-dimensional (2D) magnetic semiconductors give the opportunity to take advantage of the electron charge and the electron spin at the same time, which gives the possibility of broadening modern semiconductor technology and spintronic devices1 and can greatly expand the applications of ferromagnets (FM) in other devices such as transformers, electromagnets, high-density storage, and magnetic random access memory.2 Cr2GE2Te6 and CrI3 were the first van der Waals ferromagnetic semiconductors revealed by magneto-optical Kerr microscopy in 2017,3,4 where the intrinsic long-range FM order was discovered in 2D systems. The study of the layer-number dependence of properties showed that bulk Cr2GE2Te6 is a Heisenberg ferromagnet, in which the magnetic moments are orientated in all directions, but the few-layer material reveals a good ferromagnetic ordering with excellent gate-voltage tunability.5 In the case of CrI3, the number of layers and the stacking arrangement affect the magnetic properties of this material, through the competition between direct Cr–Cr exchange and super–superexchange Cr–I–I–Cr interactions.6,7CrSBr belongs to ternary chromium chalcogenide halide compounds (CrXh, where X = S/Se and h = Cl/Br/I) that have recently been widely investigated. CrSBr has attracted attention because its bulk, first synthesised 50 years ago, was diagnosed as an antiferromagnetic (AFM) semiconductor,8,9 with the bulk Néel temperature of TN = 132 ± 1 K.10 Under ambient conditions, CrSBr has an orthorhombic structure with a Pmmn space group. The crystal structure of CrSBr is formed by the two Cr layers bounded by S atoms and passivated by Br layers along the c axes. CrSBr belongs to van der Waals crystals; therefore, it can be easily exfoliated down to the monolayer using conventional mechanical exfoliation techniques. CrSBr has been identified as an extremely interesting and unique van der Waals type magnetic semiconductor, having the band gap in the near-infrared region between 1.25 eV and 1.5 eV, possessing a large magnetic moment (3 μB per Cr atom).10–12 CrSBr exhibits an A-type antiferromagnetic order, with robust FM within the layers, and AFM arrangement of adjacent layers (see Fig. S1 in ESI†).
In this paper, by the use of the combined DFT+U studies and experimental measurements we demonstrate that changes in magnetic phases can be reflected in the optical and electronic properties of the layered CrSBr.
2 Experimental and computational details
CrSBr was investigated by photoreflectance (PR), optical absorption, photoacoustic spectroscopy (PAS), photoluminescence (PL), and Raman measurements in the 10–300 K temperature range. For PR experiments the sample was illuminated with a halogen lamp and the reflected light was dispersed with a 0.55 m focal length single grating monochromator. The signal was detected with a Si photodiode and measured by the lock-in technique. Reflectance was modulated by a chopped (280 Hz) laser beam of a wavelength of 405 nm. Temperature-dependent optical absorption spectra were measured using the same tunable light source as that used for photoreflectance experiments. The intensity of light transmitted through the sample was measured using Si photodiode. Photoluminescence and RAMAN measurements were made in the microregime, where a 532 nm line of a diode-pumped solid state laser (DPSS) was focused on the sample with a long working distance objective (50× magnification, NA = 0.55); the diameter of the laser spot was estimated to be below 2 μm. PL and RAMAN spectra were measured using a single grating 0.55 m focal length monochromator with a multichannel liquid nitrogen cooled Si CCD array detector. During these measurements, the sample was mounted on a cold finger in a closed cycle refrigerator coupled with a programmable temperature controller that allows measurements in the 10–300 K temperature range. The photoacoustic spectrum was measured using the gas-microphone method employing an electret condenser microphone mounted in a sealed aluminium cell with a quartz transmission window. The sample was excited with a tunable light source consisting of a 150 W quartz tungsten halogen lamp and a 300 mm focal length monochromator. The excitation beam was then mechanically modulated at a frequency of 40 Hz and focused on the sample surface. More details about the principles of PAS can be found in ref. 13–15The bulk CrSBr crystal for this study was grown by chemical vapour transport by direct reaction of pure Cr, Br, and S elements in a quartz ampoule. Details of the material synthesis and structural characterisation of CrSBr can be found in ESI† and ref. 16. The magnetic behaviour of the crystal was also tested and found to be antiferromagnetically below 132 K (see the magnetic properties described in ESI†), in concert with data from the literature.8–10
DFT calculations have been performed in Vienna Ab Initio Simulation Package (VASP).17 The electron–ion interaction was modelled using the projector-augmented wave technique (PAW).18 The Perdew–Burke–Ernzerhof (PBE)19 exchange–correlation (XC) functional was employed. A plane wave basis cut-off of 550 eV and a 12 × 12 × 10 Monkhorst–Pack20k-point grid for BZ integrations were set with Gaussian smearing of 0.02 eV for integration in reciprocal space. Non-collinear magnetism and SOC were included in our calculations. A 1 × 1 × 2 unit cell was used to exploit the A-AFM ordering of CrSBr. The semi-empirical D3 Grimme approach21 was used to account for van der Waals forces. The position of the atoms and the lattice parameters were optimised within the DFT+U method.22 This approach accounts for a proper description of the on-site Coulomb repulsion between 3d electrons of transition-metal ions, by using effective Hubbard U parameters. We have carefully checked the dependence of the U parameter on the electronic bands close to the band gap (see ESI†). The electronic structure within the DFT+U approach was then compared with the electronic structure obtained within the hybrid functional HSE06.23U = 3 eV was chosen to calculate the optically active direct transitions and the phonon dispersion curves. The former were determined by calculating direct interband momentum matrix elements using the wave function derivatives within the density functional perturbation theory.24 Phonon dispersion curves were obtained within Phonopy software25 using the Parliński–Li–Kawazoe method,26 applied for the 3 × 3 × 2 supercell to find interatomic force constants within the harmonic approximation.
3 Results and analysis
Fig. 1 presents PR, absorption and PL spectra for a bulk CrSBr acquired at 20 K. Combining these experimental techniques allows us to unambiguously discern the nature of the optical transitions of CrSBr and establish their energy. Two resonances, denoted as E1 and E2, can be observed in the PR spectrum. The origin of these optical transitions will be explained later. Since PR is only sensitive to direct optical transitions and the PR resonances cover the absorption spectrum, we can conclude that all of the measurements presented here reveal the direct character of the optical transition.In order to determine the position of the resonance on the energy scale and its broadening, the PR spectrum was fitted using the Aspnes formula.
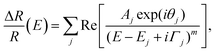 | (1) |
 denotes the energy dependence of the PR signal, Aj is an amplitude of the jth resonance, Ej indicates the energy of the jth optical transition, Γj is the broadening parameter and θj represents the phase of the resonance line.27 The parameter m depends on the character of the optical transition; m = 2.5 is conventionally used for the band-to-band transition, while m = 2 is assigned for the excitonic transition. For a better illustration of the energy transitions, their moduli are plotted in Fig. 1(a) below the PR spectrum (see the blue-shaded peaks at the bottom), which are defined as
denotes the energy dependence of the PR signal, Aj is an amplitude of the jth resonance, Ej indicates the energy of the jth optical transition, Γj is the broadening parameter and θj represents the phase of the resonance line.27 The parameter m depends on the character of the optical transition; m = 2.5 is conventionally used for the band-to-band transition, while m = 2 is assigned for the excitonic transition. For a better illustration of the energy transitions, their moduli are plotted in Fig. 1(a) below the PR spectrum (see the blue-shaded peaks at the bottom), which are defined as | (2) |
PL spectrum exhibits several intriguing features. The broad-flat peak at 1.25 eV we assign to defect-like emission. The doublet at around 1.35 eV comes rather from excitonic emission. Klein et al. have recently suggested that CrSBr behaves like a quasi–1D electronic material manifested by a very narrow exciton and, at low excitation power, appears as a doublet. Such an exciton can inherit the 1D character and show pronounced exciton–phonon coupling effects.28
The temperature dependence of the optical transition of CrSBr has also been comprehensively investigated. For this purpose PR and absorption measurements have been performed in the temperature range from 20 to 300 K. Fig. 1(b) shows the PR spectra and the corresponding fits of CrSBr measured at temperatures between 20 and 300 K in the 1.15–1.65 eV energy range. The transition energies E1 and E2 at each temperature were determined by fitting the spectra with eqn (1). It can be observed that the position of the PR resonances moves toward lower energies and broadens as the temperature increases. Furthermore, for temperatures higher than 140 K the shape of the PR spectra drastically differs from those at lower temperatures.
The absorption spectra obtained at different temperatures for CrSBr are shown in Fig. 1(c). The absorption onsets vary between 1.21 at 300 K and 1.41 eV at 20 K. The plots of α2versus the photon energy exhibit approximately linear behaviour, which is consistent with a direct band gap. No features below the sharp onset of α were observed that would be a strong indication of an indirect transition. Fig. 1(d) shows a comparison of the optical absorption and photoacoustic spectra at room temperature of a bulk CrSBr crystal. Both spectroscopic methods reveal a steep absorption edge in the 1.15–1.3 eV energy range. Note that both methods use monochromatic light illumination with changing wavelengths as opposed to broad-spectrum probing, which can deliver undesirable effects such as excessive sample heating or photovoltaic carrier generation. It is clearly seen that the photoacoustic spectrum follows optical absorption up to 1.3 eV when it saturates, which is a characteristic effect in photoacoustic detection performed at low modulation frequency. PAS does not depend on the analysis of light reflected or passed through the sample and is fundamentally associated with optical absorption. PAS is sensitive to the indirect transition29 and no evidence of the indirect band gap is observed.
To provide insight into the observed optical transitions of the bulk phase below TN, the band structure calculations are presented in Fig. 1(e) along the high-symmetry lines in the first Brillouin zone. Our electronic band gap obtained for A-AFM within the HSE06 functional (1.85 eV, see ESI†) is comparable to previous GW calculations for the monolayer (1.8 eV),11 and experimental measurements using scanning tunneling spectroscopy and PL (1.5 + −0.2 eV).10 The negligible dependence of the Hubbard U on the electronic band gap is predicted (see ESI†). Although the DFT+U approach underestimates the band gap (0.84 eV), this approach reveals a qualitatively similar electronic band dispersion in the vicinity of the Fermi level as the hybrid functional HSE06 and the previous report on the GW calculations.11 Therefore, this method is chosen for further calculations. The valence band maximum (VBM) is located at the Γ point, while the conduction band minimum (CBM) is at the U k-point, resulting in the indirect character of the band gap. Note that the difference between the direct band gap (at the Γ point) and the indirect one is just about 20 meV. The bands are double degenerate, in line with the results obtained for the CrSBr bilayer in the corresponding magnetic ground state.11 The Γ–Z line corresponds to the stacking direction of the layers, thus relatively flat bands (denoted VB1, CB1, CB2 in Fig. 1(e)) are visible in the vicinity of Fermi level, resulting in direct nesting-like transitions. We assign the optical transitions from the VB1 to the CB1, and from the VB1 to the CB2 to respective E1 and E2 resonances, visible in the PR spectrum. Note that the E2 occurs between the Γ and the Z point (nesting-like character), for which non-zero dipole matrix elements are computed, reflecting the probability of the transition. Both the E1 and E2 transitions exhibit linear polarisation of the light pointing along the y direction. The theoretical values of E1 and E2 were found to be 0.82 eV and 0.93 eV, respectively, while the corresponding experimental values are higher 1.39 eV and 1.45 eV (at 20 K). Because these absolute values cannot be directly compared between two different approaches, the differences between the transitions ΔE2−1 = E2 − E1 are determined. Namely, ΔE2−1 has been found to be 0.11 eV, which corresponds to the experimental energy separation of 0.07 eV in PR spectra. In the PR we also found the third resonance around 1.77 at 20 K (denoted as E3 – see Fig. S9 in ESI†), which we assign to the non-zero intensity (see Fig. 1(e)) of the transition from VB3 to CB1 occurring at the Γ point. The energy difference between E1 and E3 (ΔE3−1) from PR has been found to be 0.38 eV. This value corresponds to the DFT value of 0.28 eV, which supports our assignment.
Next, we present the temperature dependence of the optical transitions (E1, E2 and E3) in Fig. 2(a). Filled circles denote results obtained from the PR and Aspnes fitting, while diamonds represent the optical absorption results, where the values were found using standard linear extrapolation to the intersection with the background level of the α2versus hν curves. The temperature evolution of the E1 and E2 transitions has a linear trend with a kink around 140 K, resulting in two linear parts of the temperature dependence. For the 20–140 K temperature range, the E1 transition redshifts from 1.39 to 1.34 eV in the case of PR results and from 1.41 to 1.36 eV in the case of absorption results, which gives the change of ∼4.2 × 10−4 eV K−1. The redshift of E2 in the same temperature range is from 1.45 to 1.41 eV, corresponding to a reduction of ∼3.3 × 10−4 eV K−1. For the 140–300 K temperature range, the E1 transition energy changes from 1.34 eV to 1.20 eV for PR results and from 1.36 eV to 1.20 eV for absorption results, which corresponds to a higher reduction of ∼9.1 × 10−4 eV K−1. For both spectroscopic methods, E1 is 1.20 eV at 300 K, which is consistent with the PAS result. While the redshift of the E1 transition is clearly visible at the 140–300 K temperature range, the evolution of the E2 temperature differs and reaches the plateau, giving a constant value of ∼1.40 eV. The presence of the kink at ∼140 K in Fig. 2(a) nearly coincides with the Néel temperature in the investigated CrSBr crystal, suggesting that the magnetic phase transition occurs and can be observed in optical measurements such as PR or absorption. Furthermore, such a phase transition can influence the shape of the PR spectra; as mentioned above, the shape of the PR spectrum for CrSBr changes for temperatures higher than 140 K.
The temperature-dependent intensity of the PL (TDPL) is shown in Fig. 2(b). Usually, in paramagnetic semiconductors, the PL intensity monotonously decreases as the temperature increases because of the enhancement of phonon–exciton interactions at high temperatures, and the PL position shows a redshift following the conventional Varshni equation. However, when the temperature increases, the intensity of CrSBr PL gradually increases and reaches the maximum value near the Néel temperature, while the intensity of PL becomes weaker at higher temperatures. This suggests that a correlation between light emission and antiferromagnetic ordering might exist in CrSBr. To determine the transition temperature from the temperature-dependent PL spectra, the intensity-temperature curve gradient is calculated and shown in the inset of Fig. 2(b). The slope-temperature curve shows a linear region of 100 to 150 K. The linear fit can be used to extract the maximum intensity temperature of PL when the slope is zero, which is T = 110 ± 33 K. This value agrees well with the Néel transition temperature TN = 131 K of the bulk CrSBr. We also noticed that the PL intensity-temperature crossover is very broad, from 100 to 150 K. A similar correlation between PL intensity and Néel temperature in another antiferromagnetic van der Waals semiconductor MnPS3 was found recently by Zhou et al.30
Next, we present the electronic structure assuming two magnetic states FM and A-AFM of bulk systems (see Fig. 3(a and b)), along the high-symmetry lines in the IBZ. Significant splitting of the conduction bands is visible in the FM case, which is absent in A-AFM arrangement along the Γ–Z direction (see Fig. 3(a)), and to the best of our knowledge have not been reported yet in previous DFT calculations.11,31 This aspect directly reflects the difference between the stacking direction of the magnetic arrangements of the employed states, whereas the Γ–Z direction corresponds to this stacking direction in the first BZ. First, the direct character of the band gap is obtained for the FM case, and the degeneracy of the bands is lifted compared to that of the A-AFM state. The magnetic ordering breaks the time-reversal symmetry (TRS). However, in the case of an A-AFM arrangement, the out-of-plane translation symmetry shift recovers the symmetry in the system, and the bands remain degenerate. Splitting the bands in the FM case results in a wider band dispersion of the conduction bands compared to the AFM case, and in general depends on the overall magnetisation of the system (see Fig. S10 in ESI†). A pronounce splitting of the bands is visible for the conduction bands at Γ, resulting in lowering of the conduction band minimum, and leading to the change in the character of the band gap from the indirect (A-AFM) to direct one (FM). The band gap is lowered by 110 meV for FM compared to the A-AFM case. Due to the splitting of the bands, more transitions might occur for the FM case along the Γ–Z directions (see Fig. 3(e)). In addition, optical matrix elements calculated (see ESI†) for the transitions around the Fermi level reveal the linear polarisation of the light (y component), irrespective to the magnetic ordering. Note that the dominant contribution to the VBM along the Γ–Z direction comes from px,y orbitals of Br (FM) and S (A-AFM) atoms. There is also a difference between the types of hybridized states, namely between the 3dz2 Cr states and p state of Br at CBM for the employed magnetic arrangements (FM – px,y, A-AFM – pz).
These electronic structure changes should be reflected in magnetic interactions for two employed magnetic arrangements. Note that the p orbitals of both ligands (S, Br atoms) are involved in the superexchange mechanism within the layers, as indicated in Fig. 3(c). However, only the p states of Br atoms mediate the magnetic interaction within the super–superexchange mechanism between adjacent layers. Although, it has been shown that in-plane exchanges (J1, J2, J3) are one order of magnitude larger than out-of-plane J0 (schematic picture of exchange couplings in Fig. 3(f)),16,32 the J0 is important and cannot be neglected because it controls overall magnetisation (see Fig. S10 in ESI†). In particular, within the standard superexchange theory16 the J0 is equal to −1.5 meV.
Next, we address how the interlayer magnetic ordering affects the phonon spectra. For this purpose, we compare the theoretical phonon dispersion for the A-AFM and FM phases, with the experimentally obtained Raman spectrum excited at 532 nm and collected at 10 K (see Fig. 4(a)). During the experiment, a sample was tilted with respect to the laser beam - this was forced by the lumpy shape of the sample. This experimental spectrum shows well-defined peaks (in cm−1) at 82, 109, 243, 294, 336, and 357 and two overlapping peaks in the vicinity 188 cm−1 (Table S1 with experimental and theoretical Raman modes can be found in ESI†). This fits the previously reported Raman modes for crystals with Pmmn symmetry, where of the 15 phonon modes, only Ag, B2g, and B3g are Raman-active.33,34 Each peak is fitted by Lorentzian curves. Then we examine the positions of these peaks as a function of temperature (see Fig. 4(b)). We observe strong spin–phonon coupling for the A3g (see Fig. S11(b), ESI†), which have been already observed in previous works. Here, we detect a remarkable splitting for the B22g/B23g (see Fig. 4(c)) modes, which up to the Néel temperature have a constant position difference (5 cm−1) at a temperature close to the Néel temperature, start to move away from each other (up to 15 cm−1 at 220 K). Our theoretical calculations (Fig. 4(e)-(g)) reveal that the difference between the B22g and B23g modes depends on the magnetic order (4 cm−1 for FM, 1 cm−1 for A-AFM), and in the case of FM order the frequency of these modes are blue shifted by 13 cm−1 (B22g) and 18 cm−1 (B23g) compared to A-AFM. Furthermore, the significant change in the position of the out-of-plane A3g mode is obtained experimentally (see Fig. S11(b and c), ESI†), whereas no difference between the position of this mode is revealed for the FM and A-AFM cases (see ESI† and Table S1), excluding the origin in the interlayer magnetism. In fact, our theoretical considerations have corroborated the previous DFT study (ref. 35), which has shown that the change in the position of A3g is sensitive to the in-plane magnetic order, pointing to the strong correlation between spin and phonon.
Finally, we examine the structural changes between the employed magnetic arrangements and consider the interlayer magnetism from the point of view of its structural or electronic origin. The structural difference between the A-AFM and FM orderings is visible in the distance between the layers and the representative angle between Br–Br–Cr (see Fig. 3b)). These quantities are enlarged by 2% and 0.4% in comparison to A-AFM case, respectively, while no structural changes are observed for in-plane lattice parameters and in-plane bond lengths. Note that the out-of-plane optical phonon modes Ag are nearly intact upon magnetic order (see Fig. 4(g)), suggesting that the interlayer structural changes have negligible impact on the magnetic arrangement. However, the significant shift in energy and separation between in-plane B2g and B3g phonon modes at the Γ k point are visible. Thus, we claim that the interlayer magnetism is rather of electronic than structural origin. This result is strongly corroborated by our electronic band structure calculations presented above. Note that there is a significant difference between the states at the top of VB, which are mainly composed of Br px,y (in FM) and S px,y (A-AFM) along the Γ–Z direction. These states are mainly involved in the superexchange mechanism within the layer (see Fig. 3(c)).
4 Summary
The results presented here demonstrate that the magnetic phase transition can be manifested in optical spectra. The temperature dependences of the absorption edge and PR resonances do not follow the trend observed in conventional semiconductors (i.e. the Varshni trend). Here, we observe a distinct kink at Néel temperature, which indicates the change in the magnetic phase of CrSBr. Furthermore, the intensity of PL increases to Néel temperature and then decreases as the temperature increases. This behaviour suggests a correlation between light emission and antiferromagnetic ordering. A careful analysis of the band structure shows that the experimental results are very consistent with the DFT calculations. The energy differences between the experimental optical transitions are in good agreement with the energy differences determined theoretically. A significant difference between the interlayer magnetic order is visible in band structure calculations, along the Γ–Z direction. That is, the band gap is lowered by 110 meV, and the character of the band gap changed from indirect (A-AFM) to direct (FM). The remarkable splitting of the conduction bands is obtained for the non-zero overall magnetisation. Moreover, the in-plane phonon modes (B2g, B3g) are sensitive to the interlayer magnetic ordering, whereas the out-of-plane modes (Ag) are intact to the interlayer magnetic arrangement. In particular, the increase in splitting between B2g and B3g obtained for FM compared to A-AFM correlates with the increase of B2g/B3g splitting measured across the Néel temperature. Therefore, we point out the relevance of other magnetic states, which might be present close to the Néel temperature, as reported in ref. 36 Visible in-plane structural changes (interlayer distances and angles) do not affect out-of-plane phonon modes (Ag). The significant changes are the electronic properties upon the different interlayer magnetic orderings, pointing out the electronic rather than structural origin of the interlayer magnetism in CrSBr.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was carried out under the grant of the National Science Centre, Poland (Grant No. 2019/35/B/ST5/02819). M. B. acknowledges support from the University of Warsaw within the project “Excellence Initiative-Research University” program. Access to computing facilities of PL-Grid Polish Infrastructure for Supporting Computational Science in the European Research Space, the Wroclaw Centre for Networking and of the Interdisciplinary Center of Modeling (ICM), University of Warsaw are gratefully acknowledged. We acknowledge ACK Cyfronet AGH (Poland) for awarding this project access to the LUMI supercomputer, owned by the EuroHPC Joint Undertaking, hosted by CSC (Finland) and the LUMI consortium through Pl-Grid organization (Poland), under the grant entitled: “Electronic, optical and thermoelectric properties of selected layered materials and selected heterostructures”.References
- D. D. Awschalom and M. E. Flatté, Nat. Phys., 2007, 3, 153–159 Search PubMed
.
- S. Chen, C. Huang, H. Sun, J. Ding, P. Jena and E. Kan, J. Phys. Chem. C, 2019, 123, 17987–17993 CrossRef CAS
.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed
.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed
.
- W. Xing, Y. Chen, P. M. Odenthal, X. Zhang, W. Yuan, T. Su, Q. Song, T. Wang, J. Zhong, S. Jia, X. C. Xie, Y. Li and W. Han, 2D Mater., 2017, 4, 024009 CrossRef
.
- N. Sivadas, S. Okamoto, X. Xu, C. J. Fennie and D. Xiao, Nano Lett., 2018, 18, 7658–7664 CrossRef CAS PubMed
.
- R. Xu and X. Zou, J. Phys. Chem. Lett., 2020, 11, 3152–3158 CrossRef CAS PubMed
.
- H. Katscher and H. Hahn, Naturwissenschaften, 1966, 53, 361 CrossRef CAS
.
- O. Göser, W. Paul and H. Kahle, J. Magn. Magn. Mater., 1990, 92, 129–136 CrossRef
.
- E. J. Telford, A. H. Dismukes, K. Lee, M. Cheng, A. Wieteska, A. K. Bartholomew, Y.-S. Chen, X. Xu, A. N. Pasupathy, X. Zhu, C. R. Dean and X. Roy, Adv. Mater., 2020, 32, 2003240 CrossRef CAS PubMed
.
- N. P. Wilson, K. Lee, J. Cenker, K. Xie, A. H. Dismukes, E. J. Telford, J. Fonseca, S. Sivakumar, C. Dean, T. Cao, X. Roy, X. Xu and X. Zhu, Nat. Mater., 2021, 20, 1657–1662 CrossRef CAS PubMed
.
- K. Yang, G. Wang, L. Liu, D. Lu and H. Wu, Phys. Rev. B, 2021, 104, 144416 CrossRef CAS
.
- A. Rosencwaig, Phys. Today, 1975, 28, 23–30 CrossRef CAS
.
- A. Rosencwaig, J. Appl. Phys., 1978, 49, 2905–2910 CrossRef CAS
.
- S. J. Zelewski, Z. Zhou, F. Li, X. Kang, Y. Meng, J. C. Ho and R. Kudrawiec, ACS Appl. Mater. Interfaces, 2019, 11, 19260–19266 CrossRef CAS PubMed
.
- J. Klein, T. Pham, J. D. Thomsen, J. B. Curtis, T. Denneulin, M. Lorke, M. Florian, A. Steinhoff, R. A. Wiscons, J. Luxa, Z. Sofer, F. Jahnke, P. Narang and F. M. Ross, Nat. Commun., 2022, 13, 5420 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- N. A. W. Holzwarth, A. R. Tackett and G. E. Matthews, Comput. Phys. Commun., 2001, 135, 329–347 CrossRef CAS
.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS
.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed
.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS
.
- D. Aspnes, Surf. Sci., 1973, 37, 418 CrossRef CAS
.
- J. Klein, B. Pingault, M. Florian, M.-C. Heißenbüttel, A. Steinhoff, Z. Song, K. Torres, F. Dirnberger, J. B. Curtis, M. Weile, A. Penn, T. Deilmann, R. Dana, R. Bushati, J. Quan, J. Luxa, Z. Sofer, A. Alu, V. M. Menon, U. Wurstbauer, M. Rohlfing, P. Narang, M. Lončar and F. M. Ross, ACS Nano, 2023, 17, 5316–5328 CrossRef CAS PubMed
.
- S. J. Zelewski and R. Kudrawiec, Sci. Rep., 2017, 7, 15365 CrossRef PubMed
.
- Y. Zhou, K. He, H. Hu, G. Ouyang, C. Zhu, W. Wang, S. Qin, Y. Tao, R. Chen, L. Zhang, R. Shi, C. Cheng, H. Wang, Y. Liu, Z. Liu, T. Wang, W. Huang, L. Wang and X. Chen, Laser Photonics Rev., 2022, 16, 2100431 CrossRef CAS
.
- J. Cenker, S. Sivakumar, K. Xie, A. Miller, P. Thijssen, Z. Liu, A. Dismukes, J. Fonseca, E. Anderson, X. Zhu, X. Roy, D. Xiao, J.-H. Chu, T. Cao and X. Xu, Nat. Nanotechnol., 2022, 17, 256–261 CrossRef CAS PubMed
.
- X. Bo, F. Li, X. Xu, X. Wan and Y. Pu, New J. Phys., 2023, 25, 013026 CrossRef
.
- M. Bykov, E. Bykova, S. van Smaalen, L. Dubrovinsky, C. McCammon, V. Prakapenka and H.-P. Liermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014110 CrossRef
.
- T. Zhang, Y. Wang, H. Li, F. Zhong, J. Shi, M. Wu, Z. Sun, W. Shen, B. Wei, W. Hu, X. Liu, L. Huang, C. Hu, Z. Wang, C. Jiang, S. Yang, Q.-M. Zhang and Z. Qu, ACS Nano, 2019, 13, 11353–11362 CrossRef CAS PubMed
.
- X. Xu, X. Wang, P. Chang, X. Chen, L. Guan and J. Tao, J. Phys. Chem. C, 2022, 126, 10574–10583 CrossRef CAS
.
- K. Lee, A. H. Dismukes, E. J. Telford, R. A. Wiscons, J. Wang, X. Xu, C. Nuckolls, C. R. Dean, X. Roy and X. Zhu, Nano Lett., 2021, 21, 3511–3517 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01216f |
| This journal is © The Royal Society of Chemistry 2023 |