Sr₂Sb₂O₇: a novel earth abundant oxide thermoelectric

Abstract

Thermoelectric devices are increasingly proving to be a viable energy recycling method, with oxide thermoelectrics providing an earth abundant and non-toxic alternative to the materials traditionally used in the field. This study conducts a detailed investigation into the thermoelectric properties of the ternary wide band semiconductor Sr₂Sb₂O₇, which has previously been synthesised under high temperature conditions and shown to be thermally stable. Lattice dynamics calculations predict lattice thermal conductivities below 1 W m⁻¹ K⁻¹ at temperatures above 1125 K. The Seebeck coefficient, electrical conductivity and electronic component to the thermal conductivity were calculated via the explicit calculation of the polar optical phonon scattering, acoustic deformation potential scattering and ionised impurity scattering rates within the AMSET code. The obtained results were combined to obtain a maximum ZT of 0.536 at 1400 K, which when nanostructured to 10 nm was increased to 0.71, showing its predicted potential to perform as a high-performance n-type oxide thermoelectric.

---

1 Introduction

The world's demand for energy has seen a steep rise since the 1950s; increasing from 28.5 TW h to 173.3 TW h in 2019.¹ There has been an increase in the generation of energy through renewable sources, but in the first quarter of 2020, these accounted for only 28% of the total energy generated,² as most still originated from traditional fossil fuel sources, the limitations of which are well known. A relatively untapped source of renewable energy is the recycling of excess heat energy. Although the efficiency of power plants has been increased, non-renewable energy sources still only operate with efficiencies ranging between 33 and 39%, with the remaining energy being released as heat.³ Moreover, household items and processes such as cement production have efficiencies which range between 12 and 68%.⁴ The conversion of the released excess heat into electricity is a huge potential source of renewable energy while reducing our energy demands.⁵

Thermoelectric generators convert excess heat energy back into electrical energy through the use of a temperature gradient. This thermal gradient causes the charge carriers to diffuse from the hot side to the cold side, creating an electrical voltage. A thermocouple contains n- and p-type materials which are connected electrically in series and thermally in parallel. The effectiveness of a thermoelectric material is measured by the dimensionless figure of merit, ZT:⁶

where σ is the electrical conductivity, T is the absolute temperature, κ_lat and κ_ele are the lattice and electronic contributions to the thermal conductivity and α is the Seebeck coefficient, which is the voltage generated per unit temperature difference, and the principle behind thermoelectric devices:^7,8where k_B is the Boltzmann constant, m* is the charge carrier effective mass, e is the charge on an electron and n is the carrier concentration. To maximise the ZT, a high absolute Seebeck coefficient is needed. This can be achieved when there is a low concentration of heavy or poorly mobile charge carriers. Conversely, the electrical conductivity has an opposite requirements:where τ is the charge carrier lifetime, m* is their effective mass and μ is their mobility. To optimise this problem, materials are often sought which conduct electricity like a single crystal but conduct heat like an amorphous solid, referred to as “phonon-glass electron-crystal” materials.⁹ Here we also focus on high temperatures, where concentrated heat and higher efficiencies mean less material is required,^10–12 and non-toxic, earth-abundant elements, which are more suitable for widespread use, in contrast to current high-ZT thermoelectrics.^13–19 Oxide thermoelectrics are generally non-toxic and stable in air, making them cheaper to manufacture; and tend to possess superior chemical and thermal stability across a wider temperature range. 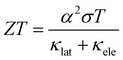Research into oxide thermoelectrics began in the 1990s with the discovery that a single crystal of the of the p-type material NaCo₂O₄ can obtain a very high power factor (∼50 μW m⁻¹ K⁻²) at 300 K.²⁰ Since then, p-type oxide thermoelectric materials have been studied extensively and a range of materials with ZT values above 1 have been found.^21–2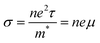3

Recent studies have also shown some promising results for n-type thermoelectric materials, including SrTi_0.8Nb_0.2O₃ which obtained a ZT of 0.37 at 1000 K,²⁴ Sr_0.92La_0.08TiO₃ which also obtained a ZT of 0.37 at 1045 K²⁵ and with x between 0.125 and 0.175 which achieved a ZT of 0.41 at 973 K,²⁶ all of which were obtained experimentally. Effective thermocouples need both the n-type and p-type components to have high ZT values. As seen by the above mentioned recent studies, the ZT for n-type materials are significantly lower, showing the need for further study in this area.

Transparent conducting oxides (TCOs), in particular, have been suggested as a subclass of oxides with great potential as thermoelectrics. As their name suggests, they are electrically conducting, fulfilling one of the criteria for a thermoelectric. Studies into TCO thermoelectric devices have shown high PFs, with the lattice thermal conductivities being the main contributors to the ZTs recorded being as low as 0.04.²⁷ In particular, TCO materials which have cations with an empty s-orbital in their conduction band have been shown to have dispersive conduction band minima and thus high electrical conductivities. These dispersive bands indicate the potential low effective mass of electrons, which if doped can lead to n-type behaviour. The result is a high conductivity but a low Seebeck coefficient, highlighting how challenging it is to find materials which balance both properties. Studies have started looking at complex metal oxides as a way of reducing the lattice thermal conductivity while maintaining the advantages presented above. Materials with heavier cations embedded into these complex structures have been of particular interest as they have been shown to reduce phonon lifetimes and hence the material's lattice thermal conductivity.²⁸

To date the most successful experimentally observed n-type TCO thermoelectric is the doubly doped ZnO ceramic Zn_0.96Al_0.02Ga_0.02O with a maximum ZT of 0.65 at 1247 K.²⁹ The main aspect of this material which enhances its properties to make it a successful thermoelectric is the inclusion of dopants in the structure which reduces the lattice thermal conductivity with respect to that of the undoped structure. The structure was also nanostructured with the same purpose. It was reduced from 40 and 7 W m⁻¹ K⁻¹ for Zn_0.98Al_0.02O to 21 and 5 W m⁻¹ K⁻¹ for Zn_0.96Al_0.02Ga_0.02O at 300 K and 1100 K, respectively. This reduction in the lattice thermal conductivity increased the ZT from 0.36 to 0.65, showing its drastic effect.

The development of Zn_0.96Al_0.02Ga_0.02O is a step in the right direction however it still does not compare to some of the available p-type thermoelectric materials. Examples include Bi_0.94Pb_0.06Cu_0.99Fe_0.01SeO which reached a ZT of 1.46 at 873 K and other doped forms of BiCuSeO, highlighting the need for further study into n-type oxide thermoelectrics.^30–32

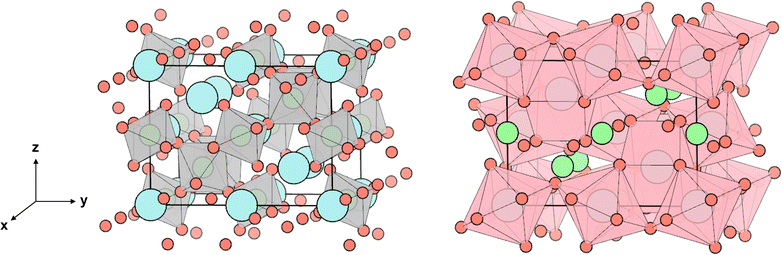
This work focuses on Sr₂Sb₂O₇ as a potential thermoelectric. Sr₂Sb₂O₇ ticks many of the boxes for a good TCO thermoelectric. It is a complex metal oxide with an Imma (74) structure composed of heavy cations (Sb⁵⁺ and Sr²⁺), with the corner and edge sharing Sb–O and Sr–O polyhedra creating a 3D network in the unit cell, shown in Fig. 1. This 3D complex structure should reduce phonon lifetimes while maintaining a good electrical conductivity, as electrons will be conducted via the connectivity of the Sb–O octahedra. The polyhedra can be further divided into two different types for each cation. The Sb–O octahedra can be classified as elongated and compressed octahedra and are shown with their varying bond lengths in Fig. 2. The Sr–O polyhedra differ more significantly between themselves. They are both bonded to eight oxygen atoms, however the first type forms a cube-like structure, whereas the second forms a hexagonal bipyramid structure. Both of these are depicted in Fig. 3. The cube-like polyhedra are connected via edge sharing and the hexagonal bipyramid polyhedra are connected via corner sharing. The two types are connected to each other via edge sharing. Moreover, the Sb⁵⁺ cations have empty 5s⁰ orbitals which should provide a 3-D electronic pathway for a high electrical conductivity.

Fig. 1 The Sr₂Sb₂O₇ conventional unit cell. The strontium atoms are denoted in blue, the antimony atoms in green, and the oxygen atoms in orange. The grey polyhedra correspond to Sb–O octahedra and the pink polyhedra show the connectivity of the Sr–O atoms.

Fig. 2 The distorted SbO₆ octahedra with the Sb–O bond lengths as calculated with the hybrid functional PBE0. The outer octahedra are the compressed octahedra located on the Sb octahedral holes along the x axis and the faces of the cell on the y axis. The central octahedron is elongated and found on Wycoff positions 4c.

Fig. 3 The two types of SrO₈ polyhedra with the Sr–O bond lengths as calculated with the hybrid functional PBE0. The Sr atoms making the cube-like polyhedron on the left are located on Wycoff positions 4d in the unit cell. The Sr atoms making the hexagonal bipyramid polyhedron seen on the right, are located on the edges, corners and in the centre of the cell.

Some materials with similar electronic structures to Sr₂Sb₂O₇ have been studied recently and have shown great potential. These include ZnSb₂O₆,³³ BaBi₂O₆³⁴ and α-Bi₂Sn₂O₇.³⁵ ZnSb₂O₆ was studied with a focus on its TCO properties and was shown to have a high conductivity when doped with gallium. BaBi₂O₆ was recently shown to have potential as an oxide thermoelectric except for its high lattice thermal conductivity.³⁴ BaBi₂O₆ ticked the necessary criteria for a good thermoelectric, including a cation with an empty s orbital, and a network of Bi–O octahedra. Unfortunately, its structure was not stable at high temperatures and it only yielded a ZT of 0.22 at 600 K. Sr₂Sb₂O₇ has a more complex structure than that of BaBi₂O₆, and could therefore have a lower lattice thermal conductivity. α-Bi₂Sn₂O₇ also ticked most of the necessary criteria for an effective thermoelectric. The CBM of α-Bi₂Sn₂O₇ was also composed of an empty s orbital and its complex crystal structure gave it a low lattice thermal conductivity. However, it had a low temperature stability, which meant it was predicted to only serve as a room temperature thermoelectric with a ZT of 0.36 at 385 K.

Sr₂Sb₂O₇ has been studied a number of times with a focus on its photocatalytic properties. It was first investigated for its potential as a UV-photocatalyst in a water splitting mechanism; where it was proposed that the distorted SbO₆ octahedra, which can be seen in Fig. 2, were the source of its photocatalytic efficiency.³⁶ However, they presented no evidence which specifically indicated the involvement of the octahedra in the electron–hole splitting mechanism.³⁷ Lin et al. investigated the photocataytic ability of Sr₂Sb₂O₇ and Ca₂Sb₂O₇ for the degradation of methyl orange.³⁸ They also pointed at Sr₂Sb₂O₇'s more distorted octahedra and open structure as the reason for higher efficiency under UV radiation.

To the best of our knowledge this is the first study into Sr₂Sb₂O₇ with a focus on its potential as an n-type oxide thermoelectric.

2 Computational methodology

This study used Density Functional Theory (DFT) within the Vienna ab initio simulation package (VASP).^39–42 The projector augmented-wave (PAW) pseudopotential method was used to take the interaction between the core and valence electrons into account.^43,44 The kinetic energy cutoff for the plane-wave basis set and the k-point mesh were converged at 500 eV and a 3 × 3 × 3 Γ-centred k-point grid to within 0.01 eV per atom. The convergence of the plane wave cut off and k-point mesh can be found in Fig. S1 (ESI†). A more dense 7 × 8 × 8 Γ-centred mesh was used for all density of states (DOS) calculations. The Perdew–Burke–Ernzerhof Generalised Gradient Approximation (GGA) for solids (PBEsol)^45,46 was used in all lattice dynamics calculations, as it has been shown to be accurate but cheap for these calculations.⁴⁷ This includes calculations to obtain the lattice thermal conductivity, ionic dielectric constant, piezoelectric coefficient, elastic constant and polar optical phonon frequency. The hybrid functional PBE0^46,48,49 which uses 25% Hartree–Fock exchange correlation was used for all DOS, band structure (BS), and high-frequency dielectric constant calculations. PBE0 has been proven to accurately calculate the electronic structure properties of solids to match experimental work and eliminates the band gap underestimation seen when GGA functionals are used.⁵⁰

The structure of Sr₂Sb₂O₇ was optimised so the force on each atom was less than 0.01 eV Å⁻¹ and the total electronic energy converged to less than 1 × 10⁻⁸ eV, with a larger cutoff energy of 650 eV to avoid basis set errors arising from Pulay stress.⁵¹

Computational studies into n-type oxide thermoelectrics have generally been carried out using the constant relaxation time approximation (CRTA) which has now been shown to lead to significantly overestimated ZTs.⁵² For this reason, the electronic transport properties including the conductivity, Seebeck coefficient and electronic thermal conductivity were calculated using the package AMSET.⁵² AMSET provides insight into the contributions to the transport properties from four scattering types including; the polar optical phonon scattering (POP), acoustic deformation potential scattering (ADP), ionised impurity scattering (IMP) and the piezoelectric scattering (PIE). These fit into the ZT equation through the electrical conductivity given in eqn (3) where τ⁻¹ is the scattering rate, meaning that lower total scattering rates should lead to higher electrical conductivities and higher ZTs.

The parameters required as input for AMSET were calculated as follows: DFPT (density functional perturbation theory) with the GGA functional PBEsol was used to calculate the polar-optic phonon frequency, elastic constant and ionic dielectric constant. Hybrid first principles calculations were used to obtain the deformation potential and high frequency dielectric constant, which was added to the ionic dielectric constant to obtain the static dielectric constant. These values can be found in Table S1 (ESI†). Once the transport properties were calculated, they were converged with respect to interpolation factor, and this can be seen in Fig. S2 (ESI†).

Lattice dynamics calculations were carried out using the Phonopy package, which uses a supercell approach with finite displacements to calculate the second order force constants.^53,54 The supercell size was converged with respect to the phonon dispersions along the high symmetry points of the Brillouin zone of the primitive cell. A 2 × 2 × 2 supercell with 198 atoms, was visually deemed as converged, and can be seen in Fig. S3 (ESI†). The atom contributions to the lattice dynamics were determined from the atom-projected phonon density of states which was calculated using Fourier interpolation. The lattice thermal conductivity was calculated using the Phono3py package which also uses a supercell approach to calculate the third order force constants.⁵⁵ A 198 2 × 2 × 2 supercell with 21 140 displacement calculations was also used to calculate the third order force constants. The plots in this paper were plotted with sumo⁵⁶ and ThermoPlotter⁵⁷ and the structures are plotted with vesta,⁵⁸ all of which are open source software.

3 Results and discussion

3.1 Structure and geometry

Sr₂Sb₂O₇ has a 22 atom primitive unit cell which crystallises in the Imma (74) space group. It is composed of two types of SbO₆ octahedra which create a 3D network across the lattice. The bond lengths for the distorted octahedra are reported in Table 1. The unit cell has elongated octahedra located in the tetrahedral holes, while the compressed octahedra are located on the octahedral holes and the faces of the cell and are all connected via corner sharing. An example of the octahedra with their bond lengths can be seen in Fig. 2. The starting structure was obtained from the MaterialsProject database where the structure was relaxed with PBE.⁵⁹Table 1 also shows the relaxed lattice parameters obtained using the PBEsol and PBE0 functionals used in this study and in experiment. The lattice parameters obtained using the PBE0 functional are in all cases closer to those obtained in experiment than those calculated with PBEsol.

Table 1 Lattice parameters of Sr₂Sb₂O₇ and Sb–O bond lengths in the elongated and compressed SbO₆ octahedra calculated with PBEsol, PBE0 and experimentally

Parameter (Å)	PBEsol	PBE0	Experiment^38
a	7.492	7.448	7.456
b	10.401	10.366	10.371
c	7.711	7.702	7.686
Elongated octahedra Sb–O bond lengths	2.0220 (×2); 1.9912 (×4)	2.0017 (×2); 1.9712 (×4)	2.0479 (×2); 2.0091 (×4)
Compressed octahedra Sb–O bond lengths	1.9453 (×2); 2.0384 (×4)	1.9225 (×2); 2.0197 (×4)	2.0330 (×2); 2.0219 (×4)

---

3.2 Electronic structure

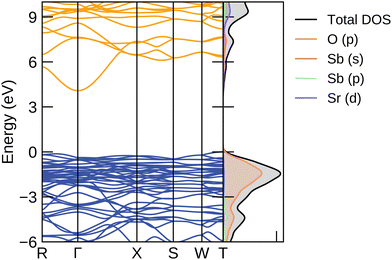
The electronic structure was calculated using the hybrid functional PBE0 from the optimised bulk geometry and plotted with sumo and can be seen in Fig. 4.⁵⁶ The valence band maximum (VBM) is primarily composed of oxygen p-orbitals, a behaviour typical in oxides. The conduction band minimum (CBM) is dominated by antimony s orbitals, giving the disperse character needed for a good electrical mobility, as seen in other TCO materials.²⁷

Fig. 4 The electronic band structure showing the band energy levels along the high symmetry paths in the Brillouin zone, where the conduction bands are shown in orange and the valence bands in blue. The density of states on the right show the orbitals with the most significant contributions at the different energies.

The PBE0-calculated direct band gap is 4.45 eV at the Γ point and the indirect band gap between the T and Γ point is 4.08 eV, making it transparent, in contrast to the PBEsol results of 1.95 eV and 1.60 eV respectively. Two different experimental values for the optical band gap have been reported, which have both been collected using UV-vis diffuse reflectance spectra. The values range between 4.1⁶⁰ and 3.86 eV.³⁸ The difference between the two reported values stems from the crystallinity of the samples which the spectra were carried out upon. The Sr₂Sb₂O₇ sample carried out by Chen et al. which reported an optical band gap of 4.1 eV, was synthesised via a hydrothermal method and resulted in crystals with an average size of 23.9 nm. The sample tested by Lin et al., on the other hand, was prepared via a solid state reaction method and resulted in an average crystallite size of 300 nm and with a band gap of 3.86 eV. Absorption spectra vary significantly depending on the quality of the sample. Crystallite size and thickness play major roles in the accuracy of the observed results. As such, the larger crystal size obtained by Lin et al. seems to suggest their reported optical band gap to be the more reliable one. By comparison, PBEsol majorly underestimates the band gap, with an indirect band gap of 1.60 eV, a direct band gap of 1.95 eV and an optical band gap of 1.94 eV.

There are a range of reasons for the difference between the optical band gap calculated by Lin et al. and our calculated value of 4.49 eV. Excitonic effects can occur when the band edges are flat and result in the lowering of the adsorption energy onset. Another possibility is that vibrational effects, introduced due to the measurements being carried out at room temperature, lower the optical band gap. Finally, it has recently been shown that the PBE0 functional can slightly overestimate band gaps by 3%.³³ All these factors may contribute to the discrepancy observed between our calculated and the reported optical band gaps. As the values are still within a 5% error margin, the PBE0 functional is deemed to provide sufficient detail for this study.

The curvature of the bands gives the inverse of the charge carrier effective mass, which is calculated by sumo using parabolic band fitting with a k-point range of 0.0322. The valence band maximum is flat resulting in a moderate hole effective mass of 1.39 m_e. Typical transparent conductors have effective masses with values below 1 m_e. As Sr₂Sb₂O₇ is expected to be n-type in nature, the electron effective mass is of more interest. The bands at the conduction band minimum (CBM) are considerably disperse, with a low mass of 0.34 m_e, and suggesting that a high conductivity is possible if effectively doped. The R and X point represent points of high symmetry at (0, 0.5, 0) and (0.5, −0.5, 0.5) in the Brillouin zone. This translates to the electron mobility being particularly high between the x and y axis and across the diagonal of the unit cell respectively.

Efficient thermoelectric materials need to display metal-like conduction. A way to determine this is by using the Mott criterion, n_Mott, a value which gives the carrier concentration above which this requirement will be satisfied. It can be calculated from the electron and hole effective masses via the band structure as follows:^61–63

a₀ is the effective Bohr radius and ε₀ is the static dielectric constant. Sr₂Sb₂O₇ has a Bohr radius of 2.57 × 10⁻⁹ m and a Mott criterion of 1.03 × 10¹⁸ cm⁻³. This means that the ZT will only reach significant values above this carrier concentration and is the minimum needed when doping the material.

3.3 Transport properties

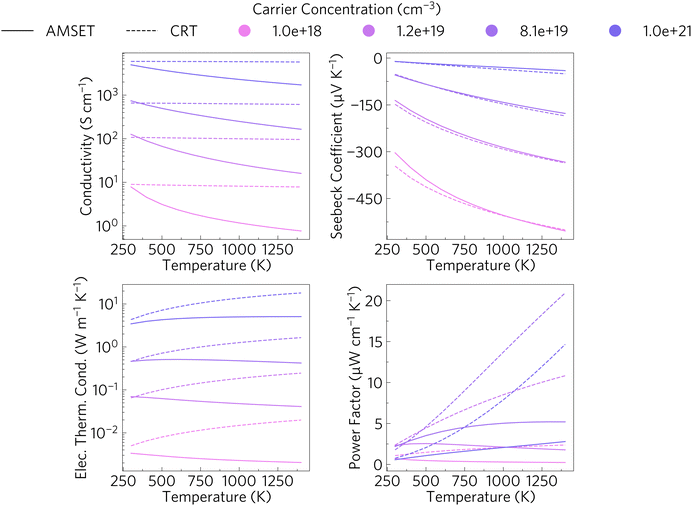
Fig. 5 shows the conductivity, Seebeck coefficient, electrical thermal conductivity and power factor (PF) versus temperature at different carrier concentrations. The PF is the combination of the Seebeck coefficient and the electrical conductivity. The PF is often used for easier comparison between different materials, due to the complex relationship between the Seebeck coefficient and electrical conductivity. The solid lines represent the direction-averaged values obtained when using AMSET and the dashed ones represent those just calculated using the CRTA (constant relaxation time approximation). There is a small degree of anisotropy, with power factor in the z direction being about 8% lower than in the x and y directions at high temperatures due to a small reduction in both electrical conductivity and Seebeck coefficient, as shown in Fig. S4 (ESI†). The discrepancies between the values obtained with AMSET and the CRTA are seen particularly in the bottom right hand graph showing the power factor, highlighting the necessity to explicitly calculate the scattering rates as the CRTA significantly overestimates the conductivity and electrical thermal conductivity, which leads to higher PF values and thus an overestimation of the ZT.

Fig. 5 Calculated transport properties with respect to temperature at a range of carrier concentrations calculated with AMSET (in the solid line) and the constant relaxation time approximation (CRTA) (in the dashed line), highlighting the effect of the two methods.

To put these results into context with other calculated thermoelectric properties we highlight a study into the thermoelectric response of Sr_1−xLa_xTiO₃ by Okuda et al.⁶⁴ SrTiO₃ obtained a Seebeck coefficient of ∼−350 μV K⁻¹ at 300 K which decreased in magnitude to ∼−75 μV K⁻¹ for Sr_0.9La_0.1TiO₃. It is however easier to compare the power factors, which at room temperature ranged between 28 and 36 μW cm⁻¹ K⁻² with carrier concentrations between 0.2 and 2 × 10²¹ cm⁻³ for their range of x values. At our target high temperature range of 1000–1400 K, Sr₂Sb₂O₇ obtained values between 1.78 and 1.79 μW cm⁻¹ K⁻² for carrier concentrations of 10 × 10¹⁹ to 10 × 10²¹ cm⁻³. This is significantly lower than that obtained by Okuda et al., however that report calculated the transport properties using the CRTA, which as can be seen by the dashed lines, yields a much higher range of values than those calculated with AMSET.

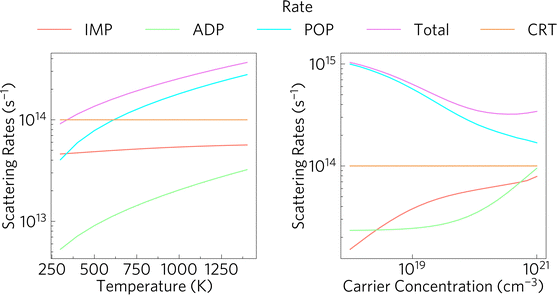
The relationship between the scattering rates and the electrical conductivity can be seen by comparing Fig. 5 and 6. As expected, as the temperature increases, the total scattering rate increases too. The inverse relationship between the scattering rate and the conductivity is highlighted as the conductivity decreases with increasing temperature when calculated with AMSET. This is due to there being increased electron scattering at higher temperatures which reduces the conductivity.

Fig. 6 Contributions from the ionised impurity scattering (IMP), acoustic deformation potential scattering (ADP) and polar optical phonon scattering (POP) at (a) increasing temperatures at a carrier concentration of 1 × 10²⁰ cm⁻³ and (b) at increasing carrier concentrations at 1400 K.

Fig. 6 also provides insight into the contributions from the different types of scattering rates in Sr₂Sb₂O₇. The predominant type of scattering is POP scattering. POP scattering tends to originate from the vibrations of the optical phonon modes creating dipoles which are then scattered across the crystal structure. Optical vibrations result from the out-of-phase motion of atoms in the system. This indicates that the charge carriers are mainly scattered through the out of phase motion of atoms. As previously mentioned, phonon scattering increases with temperature, while the scattering rate decreases with increased carrier concentration, explaining the higher conductivity. At low carrier concentrations, POP is the main scattering type, ADP (acoustic deformation potential) and IMP (ionised impurity scattering) become more significant as the number of charge carriers increases.

Acoustic deformation potential scattering is caused by the coupling of electrons with acoustic phonons. Lattice vibrations cause the displacements of atoms from their lattice sites, modifying the band structure. This modification causes electrons in the conduction band edge to interact with the phonons and scatter them. This explains the steep increase in ADP scattering as the carrier concentration increases, as this will result in a larger number of electrons in the conduction band which can couple with phonons. Similarly, increasing the temperature results in more lattice vibrations and also results in higher quantities of excited electrons due to higher thermal energy in the system. IMP scattering is dominated by the presence of charged defects which, in an n-type material, will scatter electrons in the lattice. Higher carrier concentrations will also lead to more electrons being scattered and to IMP scattering to become more relevant, until it plateaus. IMP is relatively temperature independent.

AMSET also includes contributions from piezoelectric scattering, however, this tends to originate from a lack of a centre of inversion in the unit cell, which Sr₂Sb₂O₇ has, clarifying why it is not present in this system.

3.4 Phonon dispersion and density of states

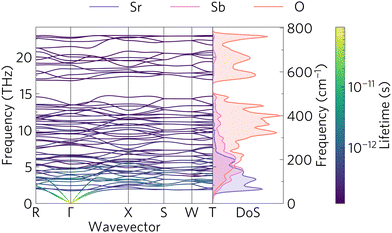
The phonon band structure and PDOS can be seen in Fig. 7 which was calculated with Phonopy and plotted with ThermoPlotter.⁵⁴ The phonon band structure is calculated via 20 finite displacements on a 2 × 2 × 2 supercell, with 176 atoms, and using the PBEsol functional. The primitive cell contains 22 atoms, resulting in 3N = 66 phonon bands at each wavevector. Imaginary modes, indicating dynamic instability would appear as modes with a negative frequency. There are no such modes, indicating that Sr₂Sb₂O₇ is dynamically stable.

Fig. 7 Phonon band structure along the high symmetry points of the Brillouin zone of Sr₂Sb₂O₇ and the atom-projected density of states.

Similar to the charge carrier mobilities in the electronic band structure, phonon group velocities are given by the gradient of the bands. Good thermoelectric materials have low phonon group velocities in order to minimise the lattice thermal conductivity. The phonon band structure shows mostly flat modes. The PDOS gives insight into which atoms contribute to the group velocities. The three bottom modes, also known as acoustic modes which at the Γ point correspond to translations in the x, y and z directions, are dominated by the heavy Sr²⁺ cations. The optical modes correspond to the rest of the higher energy modes. These tend to have significant contribution from oxygen. The plot also shows the phonon lifetimes as a colour gradient with the longer lifetimes appearing as yellow, while the short lifetime phonons are denoted in blue. It is clear that the longer lifetimes are correlated to the phonon group velocities as the larger phonon gradients also correspond to the longer lifetimes. This said, the lifetimes are still comparatively small compared to those seen in other materials, for example, LaZnOP and LaZnOAs have phonon lifetimes which range between 10 × 10⁻¹² and 10 × 10⁻⁹ s.⁶⁵

The phonon band gap between 14.8 and 17 THz originates from the contrast in molecular mass of the oxygen and the heavier strontium and antimony atoms. This band gap has been proven to reduce the thermal conductivity of materials by flattening the phonon modes and reducing the group velocity.^9,66 There are also some avoided crossings between the acoustic modes near the Γ and R and X points and the low energy optical modes. These avoided crossings have been shown to also reduce the phonon group velocities and hence reduce the thermal transport abilities of the material.^67–69 Avoided crossings are common when heavy atoms are present, and are often described as displaying ‘rattling’ behaviour by scattering phonons.⁷⁰ They have also been suggested to originate from symmetry-forbidden transitions.⁷¹ Finally, the high density of the optical modes between 5 and 14.7 THz, which is often seen in complex crystal structures, has been shown to provide scattering channels for the high velocity acoustic modes; further reducing the lattice thermal conductivity.³⁵

3.5 Lattice thermal conductivity

The lattice thermal conductivity can be seen in Fig. 8. Like Phonopy, Phono3py uses a supercell approach to obtain third order force constants. As described in Section 2, a 2 × 2 × 2 cell, with 176 atoms and 21 140 displacements was used to obtain the third order force constant. The lattice thermal conductivity was converged with respect to q-point mesh at 1000 K, and this can be seen in Fig. S5 (ESI†). All calculations were carried out with the PBEsol functional. The plot shows that Sr₂Sb₂O₇ has a moderate lattice thermal conductivity. The lattice thermal conductivities are almost the same in the x and y directions whereas it is lower in the z direction.

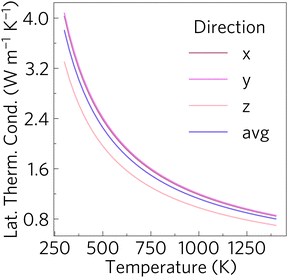Fig. 8 Calculated lattice thermal conductivity with respect to temperature in the x, y and z directions of the lattice, where the values obtained for x and y are almost identical.

Fig. 10 shows the contributions to the phonon projected density of states (PDOS) divided into the different type of cation polyhedra described in the introduction and demonstrates that the first peak at 2 THz corresponds to the cube-like Sr–O polyhedra and is aligned with the very flat bands in the phonon band structure. This suggests that the direction which contains more cube-like Sr–O polyhedra will have a low group velocity and thus a low lattice thermal conductivity. Fig. 9 depicts the polyhedra from the different axis of the conventional unit cell, demonstrating the polyhedra are more densely packed in the z axis, explaining its lower lattice thermal conductivity.

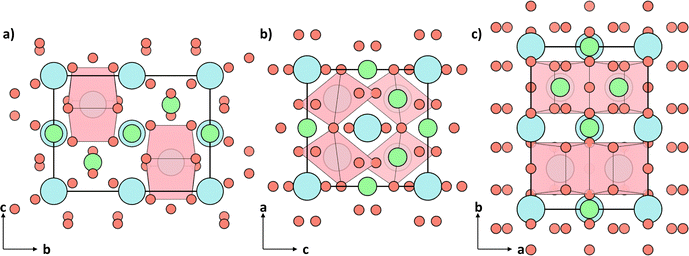Fig. 9 The conventional cell of Sr₂Sb₂O₇ with only the cube-like Sr–O polyhedra shown viewed from the (a) x-axis, (b) y-axis and (c) z-axis.

Fig. 10 Phonon band structure with the projected density of states divided into the different types of cation polyhedra.

The difference between the directions decreases with increasing temperature. This can be attributed to the higher vibrational energy associated with higher temperatures, which will result in the phonons being scattered more equally in all directions. Moreover, the difference between the values obtained for the different directions is small enough to be inconsequential in a real world setting, where the average lattice thermal conductivity dominates. The lattice thermal conductivity reaches values below 1 W m⁻¹ K⁻¹ at temperatures above 1125 K which is much lower than many of the well known n-type oxide thermoelectrics, including Sr_1−3x/₂La_xTiO₃ which obtained a ZT of 0.41 at 973 K with a lattice thermal conductivity of 2.5 W m⁻¹ K^−1 26 and Ca_0.97Bi_0.03MnCu_0.04O_3−δ which had a lattice thermal conductivity of 1.5 W m⁻¹ K⁻¹ at 1073 K and obtained a ZT of 0.44.⁷²

Fig. 11 highlights the potential reduction in lattice thermal conductivity if Sr₂Sb₂O₇ were nanostructured to 10 nm. This dimension was chosen as it was successfully synthesised to an average crystallite size of 6 nm in 2008.⁷³ This shows the significant effect nanostructuring could have on the lattice thermal conductivity by reducing it to a maximum of 0.72 W m⁻¹ K⁻¹ in the c direction. It is interesting to note however, that although the lattice thermal conductivity in the z direction is lower at higher mean free paths, it is higher than in the x and y directions at mean free paths between ∼1 nm and ∼50 nm. This suggests there are more low mean free path phonons which travel in the z direction than in the x and y directions.

Fig. 11 The lattice thermal conductivity in the x, y and z direction plotted with respect to the phonon mean free path. The horizontal line corresponds to 10 nm, showing the potential reduction in lattice thermal conductivity if Sr₂Sb₂O₇ were nanostructured to 10 nm at 1000 K.

3.6 Thermoelectric properties

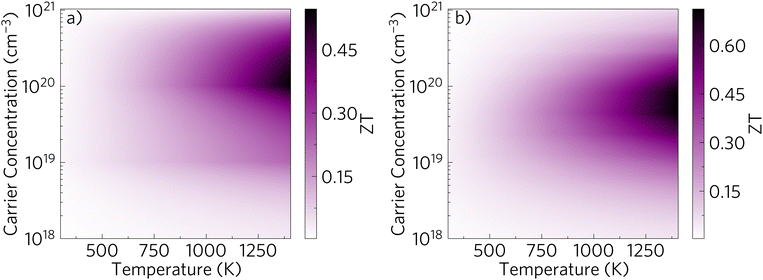
The above properties are combined to obtain the ZT for a range of temperatures and carrier concentrations as seen in Fig. 12(a) in the form of a heatmap. The average ZT is plotted, with a maximum ZT of 0.596 at 1400 K and 8.11 × 10¹⁹ cm⁻³, which breaks down to 0.584, 0.578 and 0.626 in the x, y and z directions respectively. The ZT compares well to the previously mentioned champion Zn_0.96Al_0.02Ga_0.02O with a ZT of 0.65 at 1247 K.²⁹

Fig. 12 Plot showing the ZT as a colour gradient along changing carrier concentrations and temperatures (a) in the z direction with a maximum ZT of 0.536 at 1400 K and 8.11 × 10¹⁹ cm⁻³ and (b) directionally averaged with a maximum ZT of 0.71 at 1400 K and 4.33 × 10¹⁹ cm⁻³ when nanostructured to 10 nm.

For comparison, the ZT was also calculated with the CRT and can be seen in Fig. S6 (ESI†). The maximum ZT obtained with this method is of 1.6, which would make it the best n-type oxide thermoelectric to date. This highlights the extent to which the CRT overestimates ZTs.

3.7 Nanostructuring potential

Fig. 11 showed the potential of nanostructuring on the lattice thermal conductivity at 1000 K. Nanostructuring reduced the lattice thermal conductivity by 50% at 1000 K and by 45% at 1400 K. It reached values below 1 Wm⁻¹ K⁻¹ in all directions at temperatures above 475 K. The full plot of the lattice thermal conductivity vs. temperature, when nanostructured to 10 nm can be seen in Fig. S7 (ESI†). Moreover, this reduction in lattice thermal conductivity does not take into account the phonon scattering contribution from potential external dopants, which will further reduce it. This means that this is still an upper limit, and further decreases in κ_lat may be possible. The reduction in lattice thermal conductivity often results in an increase in the maximum ZT.⁷⁴ To test the effect it would have on the transport properties, AMSET was rerun with nanostructuring to 10 nm included. It was seen that the electronic transport properties reduced, resulting in a power factor reduction of around 15% under optimal doping and temperature (Fig. S8, ESI†), but this is much less than the effect on the thermal conductivity. These transport properties were used to calculate the ZT plot seen in Fig. 12(b). Nanostructuring to 10 nm would lead to a ZT of 0.71 at 1400 K and a carrier concentration of 4.33 × 10¹⁹ cm⁻³. This increase could make Sr₂Sb₂O₇ a world leader in the field of n-type oxide thermoelectrics.

4 Conclusions

In this computational thermoelectric study we have shown the necessity of using approaches which go beyond the constant relaxation time to ensure a more realistic estimation of the ZT. The structural, electronic, electronic transport and lattice dynamic properties were calculated to assess the thermoelectric potential of Sr₂Sb₂O₇ using DFT. The electronic properties showed that the material is transparent with a direct and indirect band gap of 4.45 eV and 4.08 eV, respectively. Analysis of the individual scattering rate contributions to the electronic transport properties showed that polar optical phonon scattering is the predominant type of scattering. This was related to the fact that most of the lattice thermal conductivity originates from the Sr²⁺ cations in the lattice, which also contributed the most to the phonon group velocities. Its lattice thermal conductivity reached a value below 1 W m⁻¹ K⁻¹ at temperatures above 1125 K, which was significantly lower than other materials which obtained ZT of ∼0.4 at similar temperatures. Sr₂Sb₂O₇ has shown huge potential as an oxide thermoelectric with a current predicted maximum ZT of 0.536 at 1400 K and a carrier concentration of 8.11 × 10¹⁹ cm⁻³. When nanostructured to 10 nm, the ZT is predicted to increase to 0.71 at 1400 K and 4.33 × 10¹⁹ cm⁻³, which puts it above the current champion, doubly doped ZnO which has a ZT of 0.65 at 1100 K. If dopable, this could make Sr₂Sb₂O₇ the new leader of n-type oxide thermoelectric materials. The next step is to fully examine Sr₂Sb₂O₇'s defect chemistry to determine whether n-type doping is possible and whether the carrier concentrations needed to reach the maximum ZT are achievable.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Via our membership of the United Kingdoms HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431, EP/T022213), this work used the ARCHER2 U.K. National Supercomputing Service (http://www.archer2.ac.uk) and the U.K. Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is also partially funded by EPSRC (EP/P020194 and EP/T022213). The authors acknowledge the use of the UCL Myriad, and Kathleen and Thomas High Throughput Computing Facilities (Myriad@UCL, Kathleen@UCL and Thomas@UCL) and associated support services in the completion of this work. DOS acknowledges support from the EPSRC (EP/N01572X/1). DOS acknowledges membership of the Materials Design Network.

Notes and references

1. H. Ritchie and M. Roser, Our World in Data, 2020.
2. Global Energy Review, International energy agency technical report, 2020.
3. Is the Cooling of Power Plants a Constraint on the Future of Nuclear Power?, Online, https://www.world-nuclear.org/our-association/publications/technical-positions/cooling-of-power-plants.aspx.
4. Q. Bian, Environ. Syst. Res., 2020, 9, 8.
5. in CRC Handbook of Thermoelectrics, ed. D. Rowe, CRC Press, 2018.
6. A. F. Ioffe, L. S. Stilbans, E. K. Iordanishvili, T. S. Stavitskaya, A. Gelbtuch and G. Vineyard, Phys. Today, 1959, 12, 42.
7. A. Volta, Le opere di Alessandro Volta, Edizione Nazionale, Milano, Ulrico Hoepli, 1918.
8. T. J. Seebeck, Ann. Phys., 1826, 82, 253–286.
9. G. S. Nolas, G. A. Slack, D. T. Morelli, T. M. Tritt and A. C. Ehrlich, J. Appl. Phys., 1996, 79, 4002.
10. S. Parveen, S. V. Vedanayakam and R. P. Suvarna, Int. J. Eng. Technol., 2018, 7, 189.
11. C. Goupil, W. Seifert, K. Zabrocki, E. Müller and G. J. Snyder, Entropy, 2011, 13, 1481–1517.
12. T. Caillat, J.-P. Fleurial, G. Snyder and A. Borshchevsky, Proceedings ICT 2001. 20 International Conference on Thermoelectrics (Cat. No. 01TH8589), 2001.
13. M. H. Francombe, Br. J. Appl. Phys., 1958, 9, 415–417.
14. H. J. Goldsmid, Thermoelectric Refrigeration, Springer, US, 1964.
15. Y. Pei, H. Wang and G. J. Snyder, Adv. Mater., 2012, 24, 6125–6135.
16. D. Beretta, N. Neophytou, J. M. Hodges, M. G. Kanatzidis, D. Narducci, M. Martin-Gonzalez, M. Beekman, B. Balke, G. Cerretti, W. Tremel, A. Zevalkink, A. I. Hofmann, C. Müller, B. Dörling, M. Campoy-Quiles and M. Caironi, Mater. Sci. Eng., R, 2019, 138, 100501.
17. F. Rosi, Solid-State Electron., 1968, 11, 833–868.
18. C. Wood, Rep. Prog. Phys., 1988, 51, 459–539.
19. H. Goldsmid, Materials, 2014, 7, 2577–2592.
20. I. Terasaki, Y. Sasago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R12685–R12687.
21. M. Ito and D. Furumoto, J. Alloys, 2008, 450, 494–498.
22. J. Li, J. Sui, Y. Pei, X. Meng, D. Berardan, N. Dragoe, W. Cai and L.-D. Zhao, J. Mater. Chem. A, 2014, 2, 4903.
23. Z. Liu, X. Guo, R. Li, J. Qin, H. Li, X. Chen and X. Zhou, J. Materiomics, 2019, 5, 649–656.
24. Y. Chen, J. Liu, Y. Li, X. Zhang, X. Wang, W. Su, J. Li and C. Wang, J. Electron. Mater., 2018, 48, 1147–1152.
25. A. Kikuchi, N. Okinaka and T. Akiyama, Scr. Mater., 2010, 63, 407–410.
26. Z. Lu, H. Zhang, W. Lei, D. C. Sinclair and I. M. Reaney, Chem. Mater., 2016, 28, 925–935.
27. K. B. Spooner, A. M. Ganose and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 11948–11957.
28. N. V. Nong, N. Pryds, S. Linderoth and M. Ohtaki, Adv. Mater., 2011, 23, 2484–2490.
29. M. Ohtaki, K. Araki and K. Yamamoto, J. Electron. Mater., 2009, 38, 1234–1238.
30. B. Feng, G. Li, Z. Pan, X. Hu, P. Liu, Z. He, Y. Li and X. Fan, J. Solid State Chem., 2018, 266, 297–303.
31. B. Feng, G. Li, X. Hu, P. Liu, R. Li, Y. Zhang, Y. Li, Z. He and X. Fan, J. Alloys, 2020, 818, 152899.
32. Q. Wen, C. Chang, L. Pan, X. Li, T. Yang, H. Guo, Z. Wang, J. Zhang, F. Xu, Z. Zhang and G. Tang, J. Mater. Chem. A, 2017, 5, 13392–13399.
33. A. J. Jackson, B. J. Parrett, J. Willis, A. M. Ganose, W. W. W. Leung, Y. Liu, B. A. D. Williamson, T. K. Kim, M. Hoesch, L. S. I. Veiga, R. Kalra, J. Neu, C. A. Schmuttenmaer, T.-L. Lee, A. Regoutz, T.-C. Lee, T. D. Veal, R. G. Palgrave, R. Perry and D. O. Scanlon, ACS Energy Lett., 2022, 3807–3816.
34. K. B. Spooner, A. M. Ganose, W. W. W. Leung, J. Buckeridge, B. A. D. Williamson, R. G. Palgrave and D. O. Scanlon, Chem. Mater., 2021, 33, 7441–7456.
35. W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 16405–16420.
36. J. Sato, N. Saito, H. Nishiyama and Y. Inoue, J. Phys. Chem. B, 2003, 107, 7965–7969.
37. J. Sato, N. Saito, H. Nishiyama and Y. Inoue, J. Photochem. Photobiol., A, 2002, 148, 85–89.
38. X. Lin, F. Huang, W. Wang, Y. Wang, Y. Xia and J. Shi, Appl. Catal., A, 2006, 313, 218–223.
39. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
40. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
42. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
43. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
44. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
47. J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 064710.
48. J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102.
49. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
50. J. He and C. Franchini, J. Phys.: Condens. Matter, 2017, 29, 454004.
51. P. Pulay, Mol. Phys., 1969, 17, 197–204.
52. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222.
53. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
54. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
55. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
56. A. M. Ganose, A. J. Jackson and D. O. Scanlon, J. Open Source Software, 2018, 3, 717.
57. K. B. Spooner, M. Einhorn, D. W. Davies and D. O. Scanlon, ThermoPlotter: Streamlined Analysis of Thermoelectric Properties, 2022, https://github.com/SMTG-UCL/ThermoPlotter.
58. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
59. Materials Data on Sr ₂ Sb ₂ O ₇ by Materials Project , 2020.
60. L. Chen, P. Chen, H. Wang, W. Cui, J. Sheng, J. Li, Y. Zhang, Y. Zhou and F. Dong, ACS Appl. Mater. Interfaces, 2021, 13, 5153–5164.
61. N. F. Mott, Rev. Mod. Phys., 1968, 40, 677–683.
62. P. P. Edwards and M. J. Sienko, J. Am. Chem. Soc., 1981, 103, 2967–2971.
63. D. O. Scanlon, A. B. Kehoe, G. W. Watson, M. O. Jones, W. I. F. David, D. J. Payne, R. G. Egdell, P. P. Edwards and A. Walsh, Phys. Rev. Lett., 2011, 107, 246402.
64. T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104.
65. M. Einhorn, B. A. D. Williamson and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 7914–7924.
66. S. M. Kauzlarich, A. Zevalkink, E. Toberer and G. J. Snyder, Energy and Environment Series, Royal Society of Chemistry, 2016, pp. 1–26.
67. M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811–815.
68. H. Lin, G. Tan, J.-N. Shen, S. Hao, L.-M. Wu, N. Calta, C. Malliakas, S. Wang, C. Uher, C. Wolverton and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2016, 55, 11431–11436.
69. W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2021, 9, 20417–20435.
70. J. Dong, O. F. Sankey and C. W. Myles, Phys. Rev. Lett., 2001, 86, 2361–2364.
71. K. Brlec, K. B. Spooner, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2022, 10, 16813–16824.
72. X. Song, S. A. P. Navia, L. Liang, C. Boyle, C.-O. Romo-De-La-Cruz, B. Jackson, A. Hinerman, M. Wilt, J. Prucz and Y. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 39018–39024.
73. H. Xue, Z. Li, H. Dong, L. Wu, X. Wang and X. Fu, Cryst. Growth Des., 2008, 8, 4469–4475.
74. Ø. Prytz, E. Flage-Larsen, E. S. Toberer, G. J. Snyder and J. Taftø, J. Appl. Phys., 2011, 109, 043509.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01003a

---