Magnetic phase separation in the EuPdSn₂ ground state

Abstract

The chemical bonding, structural and magnetic properties of EuPdSn₂ have been investigated by DFT, synchrotron X-ray and neutron powder diffraction and ¹⁵¹Eu Mössbauer spectroscopy. As a result, no structural transition is observed in the thermal range of 5–290 K, whereas ferromagnetic and antiferromagnetic orderings are found to coexist below 12 K and compete in the ground state. This magnetic phase separation is likely triggered by the minimization of the global energy resulting from the coexistence of the different magnetic configurations. Chemical bonding analysis in position space reveals the presence of heteroatomic 4a- and 5a-bonds, involving each species, and two-atomic Eu–Pd polar covalent interactions building up graphite-like distorted honeycomb layers.

---

Introduction

The magnetic behaviour of intermetallic compounds based on Eu²⁺ (electron configuration 4f⁷ and ⁸S_7/2 ground state) is often unexpected. In fact, these compounds constitute a pure spin system with J = S = 7/2 and L = 0 (J: total angular momentum; S: total spin angular momentum; L: total orbital angular momentum) which preclude crystal electric field effects. Consequently, these compounds are expected to show a negligible magnetic anisotropy, although, on the contrary, they frequently exhibit a complex anisotropic magnetic ordering.^1–4

In the course of our systematic investigation on the Eu–Pd–Sn system several novel compounds have been discovered, namely Eu₂Pd₂Sn, EuPd₂Sn₄ and EuPdSn₂; strong indications of a complex magnetism with a divalent state of Eu were found by magnetization, specific heat and resistivity measurements in all these Eu-bearing compounds.^5–7 Neutron diffraction is by far the best method of determining a magnetic structure. However, in the case of europium these measurements are hampered by the rather large absorption cross section for thermal neutrons (4530 b). Recently, it was demonstrated that neutron diffraction patterns of Eu compounds can be successfully collected by using a large-area flat-plane geometry.⁸ In fact, this technique has already been successfully used to determine the incommensurate magnetic structure of EuPdSn.⁴

By magnetic susceptibility and specific heat measurements, a complex magnetic behaviour below 12.5 K was evidenced in EuPdSn₂, where Eu is found in a divalent state.⁷ In particular, the magnetic ordering was found to evolve from a state which is not simply antiferromagnetic to a ferromagnetic state with an increasing external magnetic field. A symptom that indicated that, at zero magnetic field, the ground state is not purely antiferromagnetic, is that the transition does not shift at all strengths by applying a magnetic field between 0 and 0.45, whereas a magnetic field of 0.5 T causes a rearrangement of magnetic moments towards a ferromagnetic state.⁷ These results prompted us to deepen the investigation of the complex and peculiar magnetic behaviour characterizing EuPdSn₂.

In this paper, we combine ¹⁵¹Eu Mössbauer spectroscopy and neutron powder diffraction to show that antiferromagnetic and ferromagnetic domains coexist and compete at low temperature in EuPdSn₂. Our study is complemented by a position-space chemical bonding analysis and synchrotron X-ray powder diffraction measurements.

Experimental

Sample preparation and analyses

Samples were prepared as described in ref. 7. Stoichiometric amounts of pure elements (Eu 99.99 mass % and Sn 99.999 mass % by Smart Elements, Vienna – Austria; Pd 99.5 mass % by Chimet, Arezzo – Italy) were weighed inside a glove box and enclosed in tantalum crucibles sealed by arc welding under a pure argon atmosphere. The reactant mixture was thus melted by using an induction furnace under a stream of pure argon and then annealed in a resistance furnace at 600 °C for two weeks. Finally, the sample was quenched in cold water.

¹⁵¹Eu Mössbauer spectroscopy measurements were carried out using a 4 GBq ¹⁵¹SmF₃ source, driven in the sinusoidal mode. The drive motion was calibrated using a standard ⁵⁷CoRh/α-Fe foil. Isomer shifts are quoted relative to EuF₃ at ambient temperature. The 21.6 keV gamma rays were recorded using a thin NaI scintillation detector. The sample was cooled in a vibration-isolated closed-cycle helium refrigerator with the sample in the helium exchange gas. The spectra were used to fit the parameters describing a sum of Lorentzian lines with the positions and intensities derived from a full solution to the nuclear Hamiltonian.⁹

Synchrotron X-ray powder diffraction (XRPD) analysis was carried out at the high-intensity– high-resolution ID22 beamline of ESRF, using a wavelength λ = 0.3543 Å. XRPD data were collected in the thermal range 5–290 K. A reference pattern from LaB₆ powder (NIST 660a) has been recorded to assess the instrumental line broadening.

Neutron powder diffraction (NPD) analysis was performed at the Institut Laue Langevin (ILL; Grenoble – F) using the high-intensity D20 diffractometer. NPD patterns were collected using a wavelength λ = 2.414 Å in the thermal range 2.5–20 K; in particular higher statistic data were collected at 20 K (in the paramagnetic state) and at 10.7 K and 2.5 K (below the magnetic transition temperature). In order to minimize the strong neutron absorption of natural Eu (σ_abs = 4530 b), a large-area flat-plat geometry sample holder was used;¹⁰ for this purpose, powdered EuPdSn₂ was dispersed and fixed in the single-crystal silicon flat-wafer sample holder by using an alcoholic solution (ethanol) of GE varnish.

Structural refinements were carried out according to the Rietveld method¹¹ using the program FullProf. For XRPD data, a file describing the instrumental resolution function (obtained by analysing a standard LaB₆ sample) and a Thompson–Cox–Hastings pseudo-Voigt convoluted using an axial divergence asymmetry function were used during calculations. In the final cycle, the following parameters were refined: the scale factor; the zero point of detector; the background; the unit cell parameters; the atomic site coordinates not constrained by symmetry; the atomic displacement parameters; the anisotropic microstrain broadening using parameters described in ref. 12 tracing back to an approach introduced in ref. 13. For NPD data, Rietveld refinement was carried out by fitting the difference pattern obtained by subtracting data collected at 2.5 K (where magnetic ordering is complete) minus data collected at 18.5 K, in the paramagnetic regime, that is, by fitting the difference plot constituted of purely magnetic Bragg peaks.

On the XRPD data taken at 4 K, specific checks of different versions of the microstrain broadening model already used in the Fullprof evaluations were carried out applying a parametrization described in ref. 14. These evaluations were performed using the TOPAS software¹⁵ allowing for the use of user-designed line broadening models.

Computational details

Electronic structure calculations were performed using the all-electron full-potential local orbital (FPLO) method,^16,17 using the experimentally determined crystal structure parameters of EuPdSn₂. The LSDA exchange and correlation functional as parametrized by Perdew and Wang¹⁸ was selected. The localized nature of the Eu 4f states resulting in a narrow bandwidth requires LSDA+U calculations for a more accurate treatment. The on-site Coulomb repulsion U was set to 8 eV, which is a characteristic value for 4f electrons in FPLO calculations.^19,20 The atomic limit (AL) method was employed for the double counting correction. Relativistic effects for valence and semi-core states were approximated with a scalar-relativistic treatment. Electronic structure calculations were carried out simulating both ferromagnetic (FM) and antiferromagnetic models (AFM). The AFM calculation was conducted in the C2/m crystallographic space group type (space group no 12) on a 1 × 1 × 2 supercell, reproducing the two inequivalent Eu sites per unit cell actually observed in the experimental AFM structure, crystallizing in the C_c2/c magnetic space group type (see the “Neutron powder diffraction” section). The Brillouin zone was sampled for the Cmcm and C2/m structures, respectively, with the following k-point sets: (14 14 14) and (14 14 8) for total energies; (8 8 8) and (8 8 4) for chemical bonding analysis. For comparative purposes, an electronic structure calculation was also performed for the isostructural CaPdSn₂ intermetallic compound. Structural data published by R. D. Hoffmann et al.²¹ were used. For consistency, the same computational setup employed for the Eu-containing analogue was selected. Position–space chemical bonding analyses were performed by analyzing the electron density (ED) and the electron-localizability indicator (ELI-D)²² calculated in an equidistant grid of ∼0.05 bohr using a dedicated module.²³ The Bader's quantum theory of atoms in molecules (QTAIM)²⁴ constitutes the basis for such investigations. The analysis of the ED within the QTAIM framework gives access to atomic basins and then to effective atomic charges; when the same approach is applied to the ELI-D field, the crystal space is partitioned into chemically sound regions, i.e. core and valence basins. The combined analysis of both ED and ELI-D basins through the intersection techniques²⁵ provides information about atomic contributions in the valence region and bond polarity. The latter may be conveniently quantified by the bond fraction, p(B^X_i).^26,27 Such topological studies were obtained by using the DGrid software.²⁸ Scalar fields and their basins were plotted by means of the ParaView²⁹ visualization application with the aid of dedicated plugins.³⁰

Results and discussion

Crystal structure description

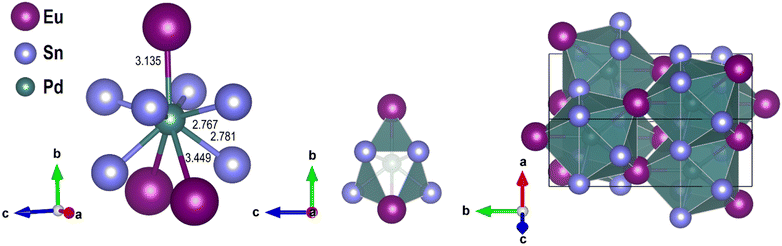
EuPdSn₂ crystallizes in the Cmcm space group type (no. 63) and is isotypical with MgCuAl₂ (Pearson symbol: oS16), as well as the homologous indide EuPdIn₂.³¹ The MgCuAl₂ structure is generally described as being constituted of trigonal prism centred by Cu atoms with two Mg and four Al atoms at vertices. Actually, this description appears biased. In fact, by using the MgCuAl₂ structural data³² and considering the coordination around the central Cu atom, four plus two Al atoms are found at ∼2.54 Å and ∼2.51 Å, respectively, and one plus two Mg atoms at 2.64 Å at 2.83 Å, respectively. In order to obtain a trigonal prism centred by Cu atoms, only the four longer Cu–Al and the two longer Cu–Mg bonds must be considered, disregarding the shorter Cu–Al and Cu–Mg bonds. In EuPdSn₂ the atomic distribution around the central Pd atom (located at the 4c Wyckoff site) is a little bit different, because four Sn atoms are found at a slightly shorter distance (at the 8f Wyckoff site), but also in this case a single Eu atom (at 4c Wyckoff site) is located at the shorter distance (Fig. 1, panel on the left). As a consequence, the crystal structure of EuPdSn₂ can be better described as an ordered network of base-sharing irregular tricapped trigonal prisms stacked along the a-axis of composition [PdEu₃Sn₆] and centred by Pd atoms (Fig. 1, panel at the centre and on the right).

Fig. 1 On the left: The coordination around the central Pd atom (bond distances in Å). At the center: The basic tricapped trigonal prism of composition [PdEu₃Sn₆] centred by Pd and viewed along the main axis. On the right: Overall crystal structure of EuPdSn₂ showing an extended unit cell.

Chemical bonding

The chemical bonding of several intermetallic compounds crystallizing with the MgCuAl₂-type structure has been deeply investigated, paying particular attention to the interactions among the elements occupying the 8f position.^33–38 In fact, they build up a substructure related to lonsdaleite (i.e. hexagonal diamond), which can be easily evidenced when the relationship with the hexagonal CaIn₂ phase is considered.^39–41 Although covalent bonds were often described within such substructures, further interactions among the constituents make the bonding scenarios much more complicated.^33–35 According to the Pearson's crystal database,⁴² only eight stannides show the MgCuAl₂-type structure and the chemical bonding was analyzed for five of them: CaTSn₂ (T = Rh, Pd, Ir)²¹ and AEIrSn₂ (AE = Sr, Ba).⁴³ The case of stannides is chemically intriguing since if the bond is interpreted on the basis of the Zintl formalism, assuming that each Sn–Sn contact is covalent, a neutral lonsdaleite-like network formed by four-bonded tin, (4b) Sn, may be guessed. Focusing on the title EuPdSn₂ compound, an accurate interatomic-distance analysis is sufficient to realize that such description is too simplistic. In fact, Sn–Sn distances within the Sn distorted tetrahedra are 3.01 (d1), 2 × 3.33 (d2) and 3.52 Å (d3). Except for d1, which is close to the shortest one in β-Sn (4 × 3.02 and 2 × 3.18 Å), the others are too long to be interpreted as homopolar interactions. Thus, the lonsdaleite substructure should be merely considered as a geometric feature, devoid of chemical meaning. Such conclusion is in agreement with the strong tin–transition metal bonding for CaTSn₂ (T = Rh, Pd, Ir),²¹ derived from DOS/COOP studies. Aiming to assess the chemical interactions among the constituents for EuPdSn₂, DFT/LSDA+U calculations were effectuated. The FM and the AFM models turn out to have no relevant energy differences (<0.1 meV per atom), hinting toward the formation of a more complex magnetic scenario, whose comprehension is a target of this contribution. The spin magnetic moment is about 7.16μ_B, resulting from s, p, d and f contributions of 0.02, 0.02, 0.12 and 7.00μ_B, respectively. The occupation of ∼7 for the 4f states indicates the presence of divalent Eu. The induced spin moments on Pd and Sn are negligible (<0.01μ_B). It is worth mentioning that the overall bonding scenario is not affected by the magnetic ordering. Bonding results discussed in the following are those obtained for the AFM structure; for the sake of clarity, they are reported in the crystallographic 1 × 1 × 1 cell. The electronic DOS and pDOS for EuPdSn₂ are shown in Fig. 2.

Fig. 2 Total and atom-projected electronic density of states for EuPdSn₂vs. energy; the Fermi energy E_F is indicated by a dashed line.

The non-zero states at the Fermi level indicate that the title phase is a metal, in line with resistivity measurements.⁷ The DOS region below ∼−5.0 eV is mainly contributed by the Sn 5s states; the Sn 5p are located at higher energies where they energetically overlap with the Pd and Eu states hinting toward Sn–Pd/Eu bonding interactions. The Pd 4d states are the main contributors in the energy window from about −5.0 to −2.0 eV. The fact that such states lie below the Fermi energy E_F, and are spread in a quite wide energy range, implies a Pd charge acceptor behaviour and active involvement in chemical bonding. It is worth noting that the Eu 4f states are localised, as shown by their reduced bandwidth, and located around −2.7 eV. The goodness of both the chosen U parameter and structural model for EuPdSn₂ is confirmed when compared with the (p)DOS of CaPdSn₂ (Fig. 2, inset).²¹

Quantum-chemical techniques in position-space were selected to undertake further investigations on the interactions taking place among the constituents. Interesting insights may be obtained from the effective charges (Q^eff) and shapes of the QTAIM atomic basins (see Fig. 3).

Fig. 3 Shapes and effective charges of the Eu (green), Pd (blue) and Sn (orange) QTAIM atomic basins for EuPdSn₂. As a guide to the eye, red sticks evidence the Sn–Sn contacts building up the lonsdaleite like network.

Tin is almost neutral having a Q^eff(Sn) of −0.05. Since the above-described Sn–Sn distances reveal that the formation of four homopolar bonds per Sn atom is unrealistic, the origin of such a low value deserves additional investigations. Interestingly, Eu is the only QTAIM cation (+1.02) and Pd bears a negative effective charge of −0.92, enriching the family of intermetallic compounds containing an anionic late transition metal.^44–50 The Q^eff(Eu) is almost half of the formal one supporting its involvement in covalent interactions. The shapes of the atomic basins are quite characteristic for transition metal rare-earth tetrelides: Eu cations are quite spherical whereas both Pd and Sn display polyhedral shapes, sharing convex surfaces with Eu and flat among them. The ELI-D field possesses three kinds of attractors occupying the 16 h (0.2798, 0.0776, 0.0390), the 4c (0, 0.1872, ¼) and the 8f (0, 0.0936, 0.6277) Wyckoff positions; the related ELI-D basins are shown in Fig. 4 to the left and are indicated with grey, greenish and purple colours, respectively.

Fig. 4 On the left: Shape, electronic population and atomicity of the ELI-D valence basins. On the right: Pd penultimate shell basin represented with its intersection with QTAIM atoms: the blue portion is intersected by Pd whereas the green ones by Eu. Black sticks indicate the Eu–Pd contacts.

Such a distribution confirms the absence of a covalent (4b) Sn network, in line with the aforementioned interatomic-distance considerations. In fact, there are no ELI-D maxima in the vicinity of the Sn–Sn contacts, except for the shortest d1. The valence basin close to d1 (greenish) is indeed the only one intersected by two Sn atoms whereas for the others only one contributes. In addition to the two Sn atoms, the d1-basin is intersected by two Pd and one Eu QTAIM atoms, leading to the following bond fractions: p(B^Sn_i) = 0.35, p(B^Pd_i) = 0.14, p(B^Eu_i) = 0.02. Thus, such a basin may be described as effectively five-atomic (5a-Sn₂Pd₂Eu₁) and not just 2a as it would have been in the case of a classical Sn–Sn homopolar interaction, with a bond fraction per Sn atom of about 0.5. The fact that europium has been included in the atomicity (number of QTAIM atoms contributing to the ELI-D basin population⁵¹) despite its low bond fraction deserves additional comments. In fact, similar values were recently published for the binary CaGe compound describing the Ca–Ge interactions as 5a-Ge₁Ca₄ bonds after the application of a specifically developed method, called Penultimate Shell Corrections (PSC0).²⁷ As a result of this correction, the total bond fraction of 4Ca increased from 0.08 to 0.15. The PSC0 was conceived particularly to account for underestimated valence contributions due to considerable charge storage in the penultimate shell. Both calcium in CaGe and europium in EuPdSn₂ display a core overpopulation of about 0.3 e, suggesting a similar scenario. When elements with an ambiguous oxidation state, like Pd, are involved the PSC0 cannot be employed. The remaining ELI-D valence basins are populated by 1.76 (purple) and 1.44 e (grey) and have almost identical bond fractions: 0.76 for Sn and 0.05 for 2 Eu in both cases, and 0.18 and 0.19 for Pd, respectively. Then, they should be interpreted as 4a-Sn₁Pd₁Eu₂ polar covalent bonds, and not as Sn lone pairs due to the not negligible metal contributions, particularly for Pd.

The Pd penultimate shell basins (see Fig. 4, on the right) show three bulges that extend in the valence region pointing toward the closest Eu species, one at 3.160 Å and two at 3.457 Å (Fig. 4, on the right). In fact, they are intersected by the corresponding Eu QTAIM atoms (see green regions in Fig. 4 to the right). The same kind of feature was recently reported for some ternary La₂TGe₆ germanides (T = Ag, Pd)²⁷ and for LaAuMg₂,³⁸ which is isostructural with the title compound. For these phases, bulges were interpreted as 2a polar covalent metal–metal bonds, also thanks to a complementary analysis of the ELI-D relative Laplacian. Therefore, Pd and Eu form heteropolar interactions realizing ²_∞[EuPd] distorted honeycomb layers parallel to (001), analogously to Au and La within LaAuMg₂. According to our knowledge, this is the first Eu–Pd bond reported so far. Finally, the origin of the almost zero charge of tin may be accounted for. Each Sn realizes four multiatomic covalent bonds practically without transferring its four valence electrons to the metal species, similarly to what happens when homopolar Sn–Sn bonds are formed. In fact, subtracting the Sn ELI-D core basin population from the Sn QTAIM one yields a valence electron number of 4.19 e, very close to the ideal 4.00 value.

Synchrotron X-ray powder diffraction analysis

Rietveld refinements carried out using synchrotron XRPD data confirm that EuPdSn₂ crystallizes in the Cmcm space group type in between 4 K and 290 K (Fig. 5); no evidence for structural transition (selective peak splitting or broadening) can be detected in this thermal range (structural data at 4 K and 290 K are listed in Table 1). Very faint diffraction peaks reveal the presence of very small amounts of secondary unidentified phases; preliminary scanning electron microscopy analysis coupled with energy dispersive X-ray spectroscopy hint at the presence of a novel intermetallic compound with composition Eu₂Pd₃Sn₅.

Fig. 5 Rietveld refinement plot for EuPdSn₂ (synchrotron XRPD data collected at 4 K); the panel on the right shows an enlarged view of the fitting in the high-Q region.

Table 1 Structural data of EuPdSn₂ at 290 K (upper data) and 4 K (lower data) obtained by Rietveld refinement (synchrotron XRPD data); space group type Cmcm (space group no. 63)

Lattice parameters (Å)
a	b	c
4.4575(1)	11.6073(1)	7.4677(1)
4.4480(1)	11.5420(1)	7.4266(1)

---

Atomic positions
Atom	Wyckoff site	x	y	z
Sn	8f	0	0.1483(1)	0.0483(1)
			0.1478(1)	0.0474(1)
Eu	4c	0	0.4339(1)	¼
			0.4340(1)
Pd	4c	0	0.7062(1)	¼
			0.7056(1)

---

Agreement factors
R F-factor	4.59	R Bragg	2.84
	2.37		3.89

---

By using the structural data obtained by the XRPD analysis in the thermal range 4–290 K, the thermal expansion behaviour of EuPdSn₂ was investigated by fitting the cell volume in the whole inspected thermal range, using a Grüneisen second-order approximation for the zero-pressure equation of state:⁵²

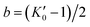where Q = V₀K₀/γ′ and ; γ′ is a dimensionless Grüneisen parameter of the order of unity; K₀ is the compressibility and 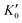its derivative with respect to applied pressure; V₀ is the zero temperature limit of the unit cell volume; and U is the internal energy per unit cell calculated by the Debye approximation:where N is the number of atoms in the unit cell; k_B is the Boltzmann's constant; Θ_D is the Debye temperature and T is the temperature. The fitting was carried out assuming K₀ ∼ 75 GPa (as obtained for MgCuAl₂^53,54) and Θ_D = 245 K reported for the isotypic YbNiGa₂ compound (where no magnetic ordering occurs);⁵⁵γ′ and were free parameters.

Fig. 6 shows the resulting fitting curve: it can be seen that the Grüneisen law reasonably accounts for the observed temperature dependence of the cell volume. Since the curve describes the temperature dependence of the cell volume expected for a nonmagnetic phase, the departure observed at low temperature should account for magnetostriction in the developing magnetic phase.

Fig. 6 Thermal evolution of the cell volume; the solid line shows the best fit to a second-order Grüneisen approximation.

In a previous work on the Ce₂Pd₂In compound,⁵⁶ it was found that magnetic properties are strongly influenced by faint variation of the chemical composition. In particular, excess of Pd favours antiferromagnetism, whereas excess of Ce induces ferromagnetism; moreover, both magnetic transitions occur at the nearly same temperature. Hence, it is fundamental to ascertain if the composition of the analysed EuPdSn₂ sample is homogeneous, without significant chemical fluctuations that could induce different and co-existing magnetic orderings. At this scope, microstructural properties were accurately investigated by analysing the broadening of the diffraction lines and their temperature dependence.

The hkl dependent line widths evident in the XRPD data were calculated in the course of the FullProf evaluations by a widely used anisotropic microstrain model.^12,14 The refined parameters reveal the temperature-dependent line widths along different directions, as shown in Fig. 7(a). Evidently, the most pronounced broadening occurs in the [100] direction and decreases to some degree with increasing temperature.

Fig. 7 (a) Temperature dependent evolution of the width of the microstrain broadening in different directions given by hkl (FullProf evaluations). (b) Tensor surface representing the direction dependence of the microstrain broadening for the 4 K data (TOPAS evaluation) according to the more general model eqn (4) (equivalent to the FullProf evaluations) and (c) according to the more restricted model according to eqn (5). No scale is given; hence the surfaces do not depict the extent but the anisotropy.

In view of exploring the possible origin of the microstrain broadening, its anisotropy was further analyzed by Rietveld refinements within the TOPAS software for the XRPD data recorded at 4 K. The microstrain broadening appeared to be of Lorentzian shape. Refinements were done (in view of the orthorhombic symmetry) using two different models for the anisotropy of the microstrain:

(a) The squared direction-dependent microstrain assumes the usually adopted 4th order polynomial in hkl. That model is equivalent to that used in the FullProf refinements, using, however, a parametrisation detailed in ref. 14. In that case the width of the microstrain broadening (projected on the diffraction vector during a powder-diffraction experiments), e.g. its full width of half maximum B_ε amounts

where d is the d-spacing calculated for the reflection hkl, and the six independent Z_ijpq are model parameters to be fitted. That model assumes a symmetry invariant, more or less correlated microstrain distribution.

(b) The square of the direction-dependent microstrain is proportional to the square of a 2nd order polynomial. In that case

Z_ii are three independent model parameters. It can be shown that eqn (5) is a special case of eqn (4) for which Z_iiii = Z_ii² and Z_iijj = 3Z_iiZ_jj hold.¹⁴

Refinement with the 6 parameters of eqn (4) should always result in a better fitting than refinement using the special case in eqn (5) with only 3 parameters. This is indeed the case. Using the model according to eqn (5), one obtains a weighted profile R value of wR_p = 0.075, whereas it decreases to 0.066 upon use of eqn (4), suggesting the significance of the additional degrees of freedom. The direction dependences from the refined parameters are depicted by the tensor surfaces shown in Fig. 7(b) [eqn (4)] and (c) [eqn (5)]. Both confirm the result of Fig. 7(a), i.e. that the largest microstrain occurs in the [100] direction. The bulges perpendicular to [100] visible in Fig. 7(b) can only be modeled using the degrees of freedom provided by eqn (4).

One possible considered origin of the peculiar two-phase magnetic structure (see what follows) was a possible inhomogeneous character of the sample. As described in ref. 14, anisotropic microstrain broadening due to composition variations should be compatible with eqn (5), which moreover would unlikely show a Lorentzian shape. Hence, we do not associate the anisotropic broadening to an inhomogeneous character of the sample.

¹⁵¹Eu Mössbauer spectroscopy

At 4.8 K the ¹⁵¹Eu Mössbauer spectrum of EuPdSn₂ can be fitted using a single Eu site with an isomer shift of −10.5(1) mm s⁻¹ and a hyperfine field (B_hf) of 25.7(1) T (Fig. 8). These values are typical of divalent Eu-based intermetallic compounds. A modest quadrupole interaction of ∼−8 mm s⁻¹ is also present. At 20 K the spectrum suggests a fully paramagnetic state and the presence of a small (∼1%) trivalent impurity being apparent as a feature near 0 mm s⁻¹. As trivalent europium is non-magnetic the presence of this impurity does not affect the analysis of the Mössbauer spectra. Fig. 8 shows that as the temperature is increased from 4.8 K there is a progressive collapse of the magnetic splitting.

Fig. 8 ¹⁵¹Eu Mössbauer spectra of EuPdSn₂ at several temperatures. The evolution to magnetically split at 4.8 K to paramagnetic by 20 K is clear. The solid lines are full Hamiltonian fits as described in the text.

Tracking the hyperfine field B_hf as a function of temperature (Fig. 9) shows a smooth evolution that can be fitted to a conventional mean-field Brillouin function yielding a transition temperature of 12.9(1) K. However, we had to use J = 1/2 rather than J = 7/2 expected for the Eu²⁺ ion, indicating that the local anisotropy at the europium site has a significant Ising-like character. In particular, a single hyperfine field is detected in the whole thermal range; this result indicates that the amplitude of the magnetic moments is rather homogenous in the whole sample, regardless of whether it belongs to a unique or different magnetic structures.

Fig. 9 Temperature dependence of B_hf for EuPdSn₂. The dashed line through the data is a J = ½ Brillouin function that gives an ordering temperature of 12.9(1) K. Two interleaved data sets are shown (squares and circles) that were taken at different times on the same sample.

Interestingly, a divalent (and therefore moment carrying) component is still detected below ∼12 K. Since this component is associated with the Eu sub-structure, but it behaves paramagnetically (i.e. it does not interact with ordered moments), it should be sited at a zero intensity point of the global molecular field. The amount of these non-interacting ions decreases on cooling and it is definitively suppressed below ∼4 K (Fig. 10).

Fig. 10 Thermal dependence of the Eu²⁺ non-interacting magnetic component below 12 K.

Neutron powder diffraction

Magnetic Bragg peaks are observed below T_m = 13 K in the NPD patterns, in good agreement with previous susceptibility measurements indicating a long-range magnetic phase transition at 12.5 K.⁷Fig. 11 shows the thermal dependence of the magnetic Bragg peaks observed in EuPdSn₂.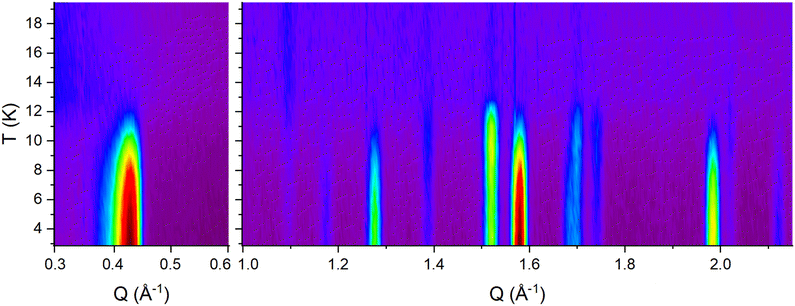

Fig. 11 Temperature dependent evolution of the magnetic Bragg peaks in EuPdSn₂ (NPD data; panels have different colors scales; red: high intensity, violet: low intensity).

Notably, it is possible to distinguish two sets of magnetic peaks. In the first set the peaks are almost saturated at 10.7 K (arrows in Fig. 12); in the second set the intensities progressively increase only on cooling below 12 K. It is not possible to index both sets with the same magnetic propagation vector. Instead it was found that the first set follows k₁ = [0,0,0] while the second set is created through k₂ = [0,0,½].

Fig. 12 On the left: Magnetic Bragg peaks of EuPdSn₂ (T_m = 13 K) at 10.7 K and 2.5 K (difference NPD patterns; magnetic Bragg peaks already saturated at 10.7 K are arrowed). On the right: Temperature-dependent evolution of the magnetic Bragg peak intensities at Q = 1.51 and 1.57 Å⁻¹ (originated by FM and AFM ordering, respectively).

Magnetic symmetry analysis⁵⁷ using the programs BASIREPS^58,59 and MAXMAGN⁶⁰ was employed to determine the allowed magnetic structures. Tables 2 and 3 list the irreducible representations (IR) and their basis vectors (BV) of Eu on the Wyckoff position 4c for k₁ = 0 and k₂ = [0,0,½], respectively. All the magnetic Bragg peaks at 2.5 K are satisfactorily fitted by combining IR5 of k₁ (Table 2) with either one of two different combinations of the BV of the IR2 with k₂ (Table 3). As the propagation vectors associated with the magnetic structures correspond to different points in the Brillouin zone of the crystal structure, hereinafter magnetic structures with k₁ and k₂ are referred to as Γ and Z, respectively; the corresponding IR is indicated as subscript.

Table 2 Basis vectors (BV) of the allowed irreducible representations (IR) for the Wyckoff position 4c of space group Cmcm for k₁ = [0,0,0] ≡ Γ

Eu Atoms	IR2	IR3	IR4	IR5	IR7	IR8
0 y ¼	0 1 0	0 0 1	1 0 0	0 1 0	1 0 0	0 0 1
0 −y ¾	0 −1 0	0 0 1	−1 0 0	0 1 0	1 0 0	0 0 −1

---

Table 3 Basis vectors (BV) of the allowed irreducible representations (IR) for the Wyckoff position 4c of space group Cmcm for k₂ = [0,0,½] ≡ Z

Eu Atoms	IR1		IR2
	BV1	BV2	BV1	BV2	BV3	BV4
0 y ¼	0 0 0	1 0 0	0 1 0	0 0 0	0 0 0	0 0 1
0 −y ¾	−1 0 0	0 0 0	0 0 0	0 0 1	0 1 0	0 0 0

---

As mentioned above, the microstructural analysis provides no clear evidence for significant chemical fluctuations in our sample. As a consequence, two models can be supposed in order to describe the magnetic structure: (1) a magnetic phase constituted of the superposition of the k₁ and k₂ structures (all reflections originate from the same magnetic domain); (2) a magnetic phase coexistence of the ferromagnetic phase following k₁ with the antiferromagnetic phase created through k₂ (the two sets of reflections originate from distinct magnetic domains).

On account of the strong Eu absorption reducing the coherently scattered intensity, Rietveld refinements were carried out by fitting the difference pattern obtained by subtracting the data collected in the paramagnetic regime at 18.5 K from the data collected at 2.5 K (where magnetic ordering is complete; Fig. 13, on the right). As a result, the difference plot is thus constituted of purely magnetic Bragg peaks. The scale-factor needed for the calculation of absolute magnetic moment values is determined from a refinement of the 18.5 K data using the purely nuclear phase (Fig. 13, on the left).

Fig. 13 On the left: Rietveld refinement plot obtained by using data collected in the paramagnetic state (18.5 K); Al peaks from the sample environment are also observed. On the right: Difference plot fitting of the NPD magnetic Bragg peaks at 2.5 K using the Γ₅ + Z₂ magnetic structural models.

The Γ₅ model (IR5 of k₁; Table 2) corresponds to a ferromagnetic ordering belonging to the Cm′cm′ magnetic space group type (#63.464) with magnetic moments aligned along the b-axis (Fig. 14). Two magnetic structural models for Z₂ are created through different combinations of the basis vectors of IR2 for the antiferromagnetic k₂ coupling (Table 3); they belong to magnetic space group types A_ama2 – #40.208 and C_c2/c – #15.90, respectively, and provide similar goodness of fit parameters, preventing a reliable selection based on NPD data only.

Fig. 14 Magnetic moment orderings fulfilling the Γ₅ and Z₂ IRs and corresponding magnetic space group.

The magnetic structure crystallizing in the A_ama2 magnetic space group type is characterized by a non-collinear antiferromagnetic ordering and leads to a large difference of the magnetic moment values for different Eu positions pertaining to the same crystallographic site (Fig. 14). Conversely, in the C_c2/c magnetic structural model the magnetic moments are collinear and are of equal magnitude (Fig. 14). In model 1, the coupling between the ferromagnetic and the antiferromagnetic components leads to a unique multi-k model where both couplings are superposed within the same magnetic phase. As a result, strong variations of the total magnetic moment values are found, as the ferromagnetic component pointing in the b-direction (Fig. 14) will add to or be subtracted from the antiferromagnetic component pointing along the b-direction which is present in both (Fig. 14) of the possible k₂ structures. At lower temperatures, this scenario leads to unphysical large values of the magnetic moment on half of the Eu-sites. As a consequence, this unique multi-k commensurate magnetic structure model must be rejected.

Taking into account the ¹⁵¹Eu Mössbauer spectroscopy outcomes, revealing that magnetic moment values must be of comparable amplitude even though they belong to different orderings, the magnetic structure crystallizing in the C_c2/c magnetic space group type (Fig. 14) should be thus preferred in the magnetic phase coexistence scenario (model 2). Then, by assuming equal magnetic moment amplitudes in both magnetic phases, it results in ∼33% of ferromagnetic phase coexisting with ∼67% of antiferromagnetic phase, with a magnetic moment of about 6.7μ_B at 2.5 K, in fair agreement with magnetization measurements where a saturation of approximately 6.8μ_B was found at 2 K.⁶

The magnetic behaviour of EuPdSn₂ can be thus outlined as follows. The ferromagnetic Γ₅ order parameter develops between 13.4 K and ∼ 10 K (Fig. 12, on the right). Conversely, the antiferromagnetic Z₂ phase (C_c2/c magnetic structural model) grows at a slightly lower temperature, below 12.3 K, and the transition completes below ∼4 K (Fig. 12, on the right). It is interesting to observe that the magnetic peak intensity of the ferromagnetic phase undergoes a slight decrease as the antiferromagnetic phase develops (Fig. 12, on the right), indicating some kind of competition between these phases. The intensity decrease affecting the ferromagnetic peaks on cooling can have two different origins: (1) a decrease of the net magnetic moment of the ferromagnetic phase; and (2) a decrease of the volume percentage of the ferromagnetic phase. This second option should be preferred in our case. In fact, at around 12 K the ¹⁵¹Eu Mössbauer indicates that there is about 10% of paramagnetic phase (Fig. 10) and the hyperfine field is ∼14 T (Fig. 9). This implies that (i) about 90% of the Eu²⁺ in the sample is magnetically ordered and (ii) that the magnetic moment at this temperature is far from saturation, as the hyperfine field significantly increases on cooling down to 4 K, up to over 24 T. Taking into account the fact that the amplitudes of the magnetic moments must be comparable in both phases, the thermal dependence of the hyperfine field indicates that the net magnetic moment increases in both phase fractions, which automatically implies a decrease of the ferromagnetic phase fraction below 10.6 K.

Within this scenario, the neutron diffraction and the Mössbauer data can be consistently explained for the different temperature regions: at 12 K only ferromagnetic ordering (with ∼ 3μ_B) occurs in about 90% of the magnetic Eu sub-structure, the remaining 10% being still in the paramagnetic state. As the temperature is decreased down to 10.7 K, the phase percentage of this ferromagnetic phase decreases down to ∼60%, but its net moment increases up to ∼4.5μ_B; at this same temperature the antiferromagnetic phase percentage would amount then to about 33%, with a net magnetic moment of as well ∼4.5μ_B, whereas the paramagnetic phase percentage decreases down to 7%. For T < 4 K, the paramagnetic phase is no longer present and both magnetic orderings coexist within separated domains in the ground state as described above for the 2.5 K data.

The origin of the FM + AFM phases coexistence deserves further discussion. Indeed, DFT/LSDA+U calculations predict that there are no total energy differences (within the accuracy of DFT) between the FM and the two AFM orderings. On the other hand, faint deviations from the ideal chemical and structural model used for calculations could play a major role in promoting and switching the nature of the experimental magnetic ordering. In the real case, the presence of different inhomogeneities at both chemical and structural level can be hypothesized, such as Eu valence fluctuations, and local compositional or microstructural variation. Indeed, their occurrence would compromise the delicate energy balance characterizing the FM and the AFM states. As a matter of fact, all our analyses found no evidence for any kind of chemical and structural fluctuation. ¹⁵¹Eu Mössbauer spectroscopy indicates that all Eu is found as divalent; no evidence for Eu³⁺ diluted within the magnetic Eu²⁺ sub-structure can be gained, ruling out the possibility that magnetic interactions can be locally affected by this non-interacting ionic species. Indeed, magnetic properties could be strongly influenced by the chemical composition. In the similar intermetallic compound Ce₂Pd₂In two branches of solid solutions are observed, where excess of Pd favours antiferromagnetism, whereas excess of Ce induces ferromagnetism.⁵⁶ In EuPdSn₂ microstructural analysis detected no clear evidence for both compositional (non-stoichiometric composition) and structural (incipient symmetry breaking) fluctuations that could affect the average homogeneity of the crystal composition/symmetry even at the local scale (thus favouring different magnetic interactions). In conclusion, by considering the complementary ¹⁵¹Eu Mössbauer spectroscopy and neutron powder diffraction data, the peculiar magnetic phase coexistence detected in EuPdSn₂ is fully consistent with the DFT/LSDA+U calculation prediction.

Conclusions

EuPdSn₂ crystallizes in the orthorhombic Cmcm space group in the whole inspected thermal range (5–290 K) and Eu is found as Eu²⁺ (no significant amounts of Eu³⁺ can be detected). The ground state of EuPdSn₂ is characterized by the coexistence of antiferromagnetic and ferromagnetic domains below ∼13 K, whereas a significant fraction of non-interacting magnetic Eu²⁺ ions is found down to ∼4 K. No evidence for both valence, chemical and structural fluctuations can be detected in the inspected samples. Such a study is complemented by a chemical bonding analysis in positional space. EuPdSn₂ turned out to be a polar intermetallic where each Sn atom establishes four heteroatomic bonds, i.e. four- and five-atomic, interacting with the surrounding Pd, Eu and, in one case, Sn species. In making these bonds, Sn employs its four valence electrons without transferring them; as a result, Sn is almost neutral which is generally unexpected for intermetallics comprising p-block elements, often described based on the Zintl formalism. Moreover, two-atomic polar covalent bonds have been found, for the first time, between Pd and Eu, forming graphite-like distorted hexagonal layers. In addition, the presence of different magnetic phases observed in the ground state can be ascribed to the closeness of the antiferromagnetic and ferromagnetic configuration energies (as revealed by theoretical calculations); likely, this magnetic phase coexistence minimizes the global energy of the system.

Author contributions

A. Martinelli: XRPD and NPD data analysis. D. Ryan: Mössbauer analysis. J. Sereni: supervision and manuscript revision. C. Ritter: NPD data analysis. A. Leineweber: microstructural analysis. I. Čurlík: supervision and manuscript revision. R. Freccero: computational analysis. M. Giovannini: sample preparation, conceptualization and supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Authors acknowledge the European Synchrotron Radiation Facility (ESRF) for provision of synchrotron radiation facilities under proposal number HC-4363 (DOI: 10.15151/ESRF-ES-447344408) and Institute Laue-Langevin (ILL) for provision of neutron radiation facilities under proposal number DIR-231 (DOI: 10.5291/ILL-DATA.DIR-231). A. M. acknowledges A. Fitch for his kind assistance during data collection at ID22.

Notes and references

1. O. Bednarchuk and D. Kaczorowski, J. Alloys Compd., 2015, 646, 291.
2. S. Seiro and S. C. Geibel, J. Phys.: Condens. Matter, 2014, 26, 046002.
3. D. H. Ryan, J. M. Cadogan, R. Rejali and C. D. Boyer, J. Phys.: Condens. Matter, 2016, 28, 266001.
4. P. Lemoine, J. Cadogan, D. Ryan and M. Giovannini, J. Phys.: Condens. Matter, 2012, 24, 236004.
5. M. Giovannini, I. Curlik, R. Freccero, P. Solokha, M. Reiffers and J. Sereni, Inorg. Chem., 2021, 60, 8085.
6. I. Čurlík, M. Zapotoková, F. Gastaldo, M. Reiffers, J. Sereni and M. Giovannini, Phys. Status Solidi B, 2021, 258, 2000633.
7. I. Čurlík, M. Giovannini, F. Gastaldo, A. M. Strydom, M. Reiffers and J. G. Sereni, J. Phys.: Condens. Matter, 2018, G, 495802.
8. D. H. Ryan and L. M. D. Cranswick, J. Appl. Crystallogr., 2008, 41, 198.
9. C. J. Voyer and D. H. Ryan, Hyperfine Interact., 2006, 170, 91104.
10. M. Potter, H. Fritzsche, D. H. Ryan and L. M. D. Cranswick, J. Appl. Crystallogr., 2007, 40, 489.
11. R. A. Young, The Rietveld Method; IUCr Monographs on Crystallography, Oxford University Press, Oxford, 1993, vol 5.
12. J. Rodriguez-Carvajal and T. Roisnel, Mater. Sci. Forum, 2004, 443–444, 123.
13. J. Rodriguez-Carvajal, M. T. Fernandez-Diaz and J. L. Martinez, J. Phys.: Condens. Matter, 1991, 3, 3215.
14. A. Leineweber, Z. Kristallogr., 2011, 226, 905.
15. 15 TOPAS V5.0, Bruker AXS, Karlsruhe, Germany, 2014.
16. H. Eschrig, K. Koepernik and J. Chaplygin, Solid State Chem., 2003, 176, 482.
17. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
18. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
19. S. Chanakian, R. Weber, U. Aydemir, A. Ormeci, J.-P. Fleurial, S. Bux and G. Snyder, J. Electron. Mater., 2017, 46, 4798.
20. U. Aydemir, I. Kokal, Y. Prots, T. Förster, J. Sichelschmidt, F. M. Schappacher, R. Pöttgen, A. Ormeci and M. Somer, J. Sol. State Chem., 2016, 239, 75.
21. R.-D. Hoffmann, D. Kussmann, U. Ch Rodewald, R. Pöttgen, C. Rosenhahn and B. D. Mosel, Z. Naturforsch., 1999, 54, 709.
22. M. A. Kohout, Int. J. Quantum Chem., 2004, 97, 651.
23. A. Ormeci, H. Rosner, F. R. Wagner, M. Kohout and Y. Grin, J. Phys. Chem. A, 2006, 110, 1100.
24. R. F. W. Bader, Atoms in Molecules-A Quantum Theory, Oxford Univ. Press, New York, 1990.
25. S. Raub and G. A. Jansen, Theor. Chem. Acc., 2001, 106, 223.
26. F. R. Wagner, D. Bende and Y. Grin, Dalton Trans., 2016, 45, 3236.
27. R. Freccero, P. Solokha, S. De Negri, A. Saccone, Y. Grin and F. R. Wagner, Chem. – Eur. J., 2019, 25, 6600.
28. M. Kohout, software DGrid, v. 4.6 and 5.0.
29. U. Ayachit, The ParaView Guide: A Parallel Visualization Application, Kitware, 2015.
30. A. Baranov, Visualization Plugin for ParaView. 2015.
31. Y. V. Galadzhun, R.-D. Hoffmann, G. Kotzyba, B. Künnen and R. Pöttgen, Eur. J. Inorg. Chem., 1999, 975.
32. B. Heying, R.-D. Hoffmann and R. Pöttgen, Z. Naturforsch., 2005, 60b, 491.
33. R.-D. Hoffmann, R. Pöttgen, G. A. Landrum, R. Dronskowski, B. Künnen and G. Kotzyba, Z. Anorg. Allg. Chem., 1999, 625, 789.
34. R.-D. Hoffmann and R. Pöttgen, Chem. – Eur. J., 2001, 7, 382.
35. S. Liu and J. D. Corbett, Inorg. Chem., 2003, 42, 4898.
36. L. Vasylechko, U. Burkhardt, W. Schnelle, H. Borrmann, F. Haarmann, A. Senyshyn, D. Trots, K. Hiebl and Y. Grin, Solid State Sci., 2012, 14, 746.
37. F. Stegemann, T. Block, S. Klenner, Y. Zhang, B. P. T. Fokwa, A. Timmer, H. Mçnig, C. Doerenkamp, H. Eckert and O. Janka, Chem. – Eur. J., 2019, 25, 10735.
38. R. Freccero, S. De Negri and P. Solokha, Dalton Trans., 2020, 49, 12056.
39. A. Iandelli, Z. Anorg. Allg. Chem., 1964, 330, 221.
40. M. Kersting, M. Johnscher, S. F. Matar and R. Pöttgen, Z. Anorg. Allg. Chem., 2013, 639, 707.
41. M. Johnscher and R. Pöttgen, Z. Naturforsch., 2012, 67b, 1221.
42. P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds, ASM International, Materials Park, Ohio, USA, 2021.
43. M. Marshall, L. Xing, Z. Sobczak, J. Blawat, T. Klimczuk, R. Jin and W. Xie, J. Mater. Sci., 2019, 54, 11127.
44. R. Freccero, P. Solokha, D. M. Proserpio, A. Saccone and S. De Negri, Crystals, 2018, 8, 205.
45. R. Freccero, S. De Negri, G. Rogl, G. Binder, H. Michor, P. F. Rogl, A. Saccone and P. Solokha, Inorg. Chem., 2021, 60, 3345.
46. R. Freccero, P. Solokha and S. De Negri, Inorg. Chem., 2021, 60, 10084.
47. L. Agnarelli, Y. Prots, U. Burkhardt, M. Schmidt, P. Koželj, A. Leithe-Jasper and Y. Grin, Inorg. Chem., 2021, 60, 13681.
48. L. Agnarelli, Y. Prots, M. Schmidt, M. Krnel, E. Svanidze, U. Burkhardt, A. Leithe-Jasper and Y. Grin, ChemistryOpen, 2022, 11, e2022001.
49. P. Solokha, R. A. Eremin, T. Leisegang, D. M. Proserpio, T. Akhmetshina, A. Gurskaya, A. Saccone and S. De Negri, Chem. Mater., 2020, 32, 1064.
50. M. Armbrüster, Sci. Technol. Adv. Mater., 2020, 21, 303.
51. Q. Zheng, F. R. Wagner, A. Ormeci, Y. Prots, U. Burkhardt, M. Schmidt, W. Schnelle, Y. Grin and A. Leithe-Jasper, Chem. – Eur. J., 2015, 21, 16532.
52. L. Vočadlo, K. S. Knight, G. D. Price and I. G. Wood, Phys. Chem. Miner., 2002, 29, 132.
53. C. Zhang, Y. Wan, W. Zou, X. Shang and Y. Zhang, Comput. Theor. Chem., 2021, 1201, 113293.
54. Y. Feng, X. Chen, Y. Hao and B. Chen, Vacuum, 2022, 202, 111131.
55. L. Vasylechko, U. Burkhardt, W. Schnelle, H. Borrmann, F. Haarmann, A. Senyshyn, D. Trots, K. Hiebl and Y. Grin, Solid State Sci., 2012, 14, 746.
56. M. Giovannini, H. Michor, E. Bauer, G. Hilscher, P. Rogl, T. Bonelli, F. Fauth, P. Fischer, T. Herrmannsdörfer, L. Keller, W. Sikora, A. Saccone and R. Ferro, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 4044.
57. E. F. Bertaut, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24, 217.
58. J. Rodriguez-Carvajal, BASIREPS: a program for calculating irreducible representations of space groups and basis functions for axial and polar vector properties. Part of the FULLPROF Suite of programs. http://www.ill.eu/sites/fullprof/.
59. C. Ritter, Solid State Phenom., 2011, 170, 263.
60. M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. – Cryst. Mater., 2006, 221, 15.

---