Second-order nonlinear optical organic crystals based on a “click” compound

Abstract

Click chemistry has been widely employed for the construction of many functional materials such as polymers and topological macromolecules, surface modifications and biomaterials. Polymers fabricated via a click reaction have been explored as nonlinear optical (NLO) materials with high NLO hyperpolarizabilities. However, this is very demanding for the thermostability of molecules and chromophores, which might be degenerative at elevated temperatures for processing techniques such as electric poling. Herein, second-order NLO crystals have been fabricated from an organic compound synthesized using facile click chemistry. Two noncentrosymmetric crystal phases of the target compound exhibit promising NLO performances with strong second harmonic generation (SHG) responses, along with high thermal stability and wide optical transparency. This work paves the way for the application of click chemistry in the construction of organic NLO crystals.

---

Introduction

Click chemistry was first proposed by Sharpless et al. in 2001¹ that defined a group of chemical reactions for connecting carbon heteroatoms characterized by high yields, mild reactions, wide scope, high stereospecificity and few byproducts.^2–6 Click chemistry, as an effective synthetic method, has been widely employed for construction of many functional materials such as polymers and topological macromolecules, surface modifications and biomaterials.^7–13 Recently, click chemistry has been also taken advantage of in the fabrication of nonlinear optical (NLO) materials, including linear polymers, hyperbranched polymers, dendrimers and dendritic hyperbranched polymers with high NLO hyperpolarizabilities.^14–19 Second harmonic generation (SHG) is one of the most developed and widely applied second-order NLO effects, which requires noncentrosymmetric molecular arrangements in their aggregated solid state to realize macroscopic NLO activity.^20–23 The aforementioned click polymers require techniques such as electric poling to realize the required noncentrosymmetric alignment of NLO chromophores.^24–26 However, this is very demanding for the thermostability of molecules and chromophores, which might be degenerative at elevated temperatures upon electric poling.^27,28

Organic crystals demonstrate their superiority as NLO materials on account of their rich self-assembly behaviours with synergistic noncovalent interactions.²⁹ Accurate information on crystalline molecules could be obtained with the assistance of single crystal X-ray diffraction analysis, which is highly beneficial for the investigation of structure–performance relationships.^30,31 Among all the NLO materials, organic molecular materials have drawn broad attention owing to their larger nonlinear coefficient, faster response speed, lower relative permittivity, and easier processability than those of inorganic materials.^32,33 In particular, organic π-conjugated molecular systems are widely employed as second-order NLO chromophores owing to their delocalized π-electrons, high optical susceptibilities, and optimal band gaps.^34–41 The delocalized π-electrons and the charge transfer between the electron donor and acceptor groups play a decisive role in the optimization of NLO susceptibility of the organic molecules, but the pursuit of high polarizability often endows the compounds with long absorption edges, leading to the so-called “nonlinearity-transparency tradeoff” effect.^42–44 Therefore, the design and synthesis of organic second-order NLO compounds with a large NLO response and good optical transparency have been one of the hot topics in the molecular engineering of organic NLO materials in recent decades.

Organic small molecules such as urea with chromophoric groups containing only n–π molecular motifs (=C=O, –N=N–, =C=N–, and –N=O) can better balance this “nonlinearity–transparency tradeoff” compared with the extended π-conjugated molecules.⁴⁵ Furthermore, the internal forces between these special units increase the intermolecular interactions and could induce the preferred molecular packing.^46,47 The click reaction is a facile and efficient method to synthesise 1,2,3-triazole analogous compounds, which includes n–π molecular units such as –N=N– and might have promising NLO properties. A few triazole based organic compounds have been indeed reported to be NLO active.^48–50 However, the NLO properties of these triazole based compounds have been mainly studied in the powder form, which limits their practical applications and lacks structure–property correlations. In this work, we have taken advantage of the azide–alkyne click chemistry and synthesized the 1-benzyl-4-phenyl-1,2,3-triazole (BPTA) compound involving n–π motifs. BPTA can be readily fabricated into well-defined crystals with three different polymorphic phases, among which two polymorphs have been identified to be noncentrosymmetric and been demonstrated to exhibit strong second-order NLO responses, along with high thermal stability and wide optical transparency. It is expected that the facile synthetic strategy of click chemistry can be readily expanded to other functional groups and could provide new options for the construction of organic NLO crystals.

Results and discussion

Synthesis and preparation

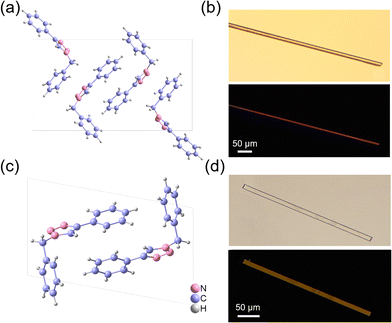
The target compound BPTA was synthesized via a copper-catalysed click reaction of benzyl azide and phenylacetylene in a high yield (see the Experimental section for details in the ESI,† Scheme S1).⁵¹¹H and ¹³C NMR spectroscopy, mass spectrometry (MS), as well as elemental analysis have been utilized to characterize the target compound (Fig. S1, ESI†). The result of thermal gravimetric analysis (TGA) indicates that BPTA does not undergo decomposition until 300 °C (Fig. S2, ESI†), revealing its high thermal stability. Single crystal X-ray diffraction (SCXRD) analysis reveals that three crystal phases of BPTA could be obtained using a solvent-vapour method. Two of these polymorphs are noncentrosymmetric, crystallizing in the Pna2₁ (referred to as the α-phase) and P2₁ space group (referred to as the β-phase), respectively. The α- and β-phase crystals could be facilely obtained by volatilizing the solution of BPTA in toluene and acetone, respectively. The third polymorphic phase of BPTA is centrosymmetric (in the P2₁/c space group, referred to as the γ-phase, Fig. S3, ESI†), which could be obtained by volatilizing its solution in ethyl acetate. The characteristics of the solvent, such as polarity, molecular size and molecular structure might affect the structure and morphology of crystals due to the specific and non-specific interactions between the solvent and the solute molecules.^52,53 The measured powder X-ray diffraction (PXRD) patterns agree well with the simulation patterns (Fig. S4, ESI†), suggesting their high phase purity. Herein, we focused on the study of the α- and β-phases of BPTA because they are noncentrosymmetric and are suitable for second-order NLO applications.

In the α-phase, there are four BPTA molecules in a unit cell (Fig. 1a), connected by C–H⋯π interactions and C–H⋯N hydrogen bonds. There is a net complex C–H⋯π interaction among adjacent molecules, mainly distributed along the aob plane (Fig. S5, ESI†). The intermolecular C–H⋯N hydrogen bonds (2.56 and 2.64 Å) are contributed by the triazole moiety and drive the molecular packing along the crystallographic c-axis (Fig. S6, ESI†). The calculated morphology of the α-phase indicates that the crystal growth direction of the α-phase is preferred along the crystallographic c-axis, where the hydrogen bond is located (Fig. S7, ESI†). This matches well with the experimentally observed microrod-like morphology of the α-phase crystal (Fig. 1b). The β-phase has two BPTA molecules in its unit cell (Fig. 1c). However, the intermolecular interactions of the β-phase are concise and loose, which mainly involve C–H⋯N hydrogen bonds (2.67 and 2.68 Å) between successive BPTA molecules in the aob plane and drive the molecular packing along the crystallographic b-axis (Fig. S8, ESI†). The calculated crystal growth direction is along the building direction connected by hydrogen bonds (Fig. S9, ESI†). The observed microplate-like crystal of the β-phase is also consistent with the calculated morphology (Fig. 1d). Hirshfeld surface analysis shows that the C–H⋯N interactions have a larger proportion in the β-phase (Fig. S10, ESI†).

Fig. 1 Crystal structures and morphologies of the self-assembled polymorphic crystals from BPTA. (a) Molecular packing in a unit cell of the α-phase, viewed along the crystallographic c-axis. (b) The microscopy image of the α-phase crystal and its corresponding polarized microscopy image. (c) Molecular packing in a unit cell of the β-phase, viewed along the crystallographic b-axis. (d) The microscopy image of the β-phase crystal and corresponding polarized microscopy image.

Theoretical calculations

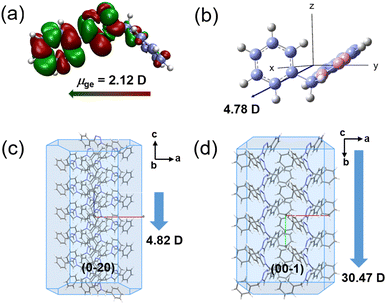
In order to understand the structure–packing–performance relationships of the two polymorphic phases, theoretical calculations have been carried out. First of all, we performed density functional theory (DFT) calculations on the BPTA molecule by using the Gaussian16 program package.⁵⁴ The orbital spatial distributions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) for the BPTA molecule are shown in Fig. 2a. While in the HOMO the electron density of BPTA is mainly localized in the 1,2,3-triazole and phenyl moiety, it is distributed in the whole molecular framework in the LUMO. Such an orbital pattern implies that the HOMO–LUMO transitions for BPTA are accompanied by charge transfer in the 1,2,3-triazole and phenyl moiety, while the benzyl unit shows less distribution of electron clouds. The band gap between the HOMO and the LUMO is calculated to be 5.24 eV, larger than those of the phenyl functionalize fluorenone derivatives.^33,55 The measured absorption spectra of BPTA display an absorption peak at 216 nm in CH₂Cl₂, in agreement with the calculation result (Fig. 2b). The absorption spectrum of the BPTA powder is similar to that experimentally measured in the solution, with a slight shift to 289 nm, revealing its high optical transparency. The transition dipole of the BPTA molecule corresponding to the S₀–S₁ transition is calculated to be 2.12 D (Fig. 3a). Meanwhile, the permanent dipole moment of a single BPTA molecule is calculated to be 4.78 D (Vector: 2.6, −3.43, −2.07; Fig. 3b). Due to these dipole–dipole interactions, molecules in crystal structures tend to self-assemble in anti-parallel arrangements, leading to a zero macroscopic polarizability.⁴⁷ The overall inherent dipole moment in the unit cell of α- and β-phases are calculated to be non-zero (Fig. 3c and d), thanks to the noncentrosymmetric arrangements of BPTA molecules. Corresponding to their crystal structures, the β-phase has a much larger net dipole moment (30.47 D) than that of the α-phase (4.82 D) in a unit cell. In addition, the directions of the overall permanent dipole moment for the two phases are both along the long axes of the microcrystals. According to the simulations, the amplification of the dipole moment of the β-phase at the macroscopic level will facilitate its NLO response.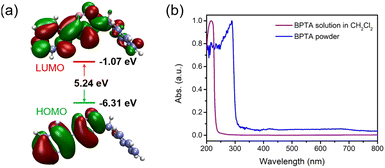

Fig. 2 (a) Calculated electronic structures and band gap of the BPTA molecule. (b) Normalized UV-vis absorption spectra of BPTA in CH₂Cl₂ solution (10⁻⁵ mol L⁻¹) and in powder.

Fig. 3 Simulations. (a) Electric transition dipole moment of the BPTA molecule. (b) Magnitude and direction of permanent dipole moment of the BPTA molecule. Magnitude: 4.78 D. Vector: (2.6, −3.43, −2.07). (c) The calculated overall inherent dipole moment in the unit cell of the α-phase. Magnitude: 4.82 D. Direction: opposite to the crystallographic c-axis. (d) The calculated overall inherent dipole moment in the unit cell of the β-phase. Magnitude: 30.47 D. Direction: along the crystallographic b-axis.

Nonlinear optical properties

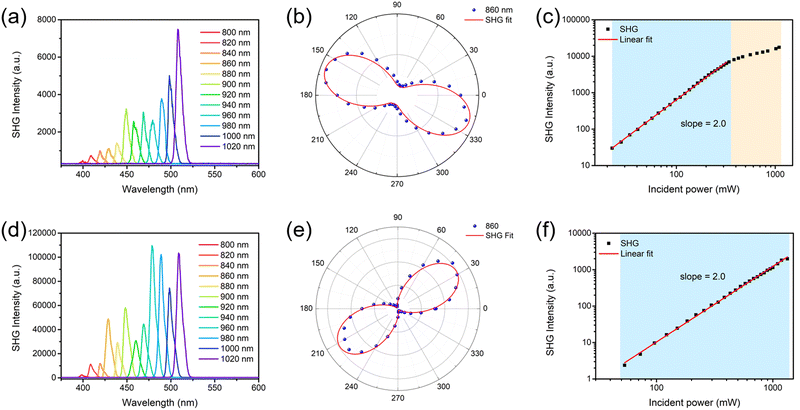
The NLO properties of the α- and β-phase polymorphic crystals of BPTA were studied using a home-built femtosecond laser system in the reflection geometry.⁵⁶ In order to compare their NLO effects, microcrystals of the two polymorphic crystals with similar thicknesses (∼80 μm, Fig. S11 and S12, ESI†) were selected to collect SHG signals under the same measurement conditions. The crystals were perpendicular to the plane of incidence and the incident light was perpendicular to the long axis of the crystals. The SHG mapping presented the overall SHG intensity of the two crystals, which is consistent with crystal morphologies (Fig. S13, ESI†). A spot fixed in the strongest area of each crystal was selected to measure the wavelength-dependent NLO spectra from crystals of the α-phase (Fig. 4a) and β-phase (Fig. 4d) from 800 to 1020 nm (excitation wavelengths). As shown in Fig. 4a and d, both the α- and β-phase crystals exhibit enhanced SHG signals with the increasing of the excitation wavelength. The results suggest that BPTA crystals might be suitable as visible and near-infrared NLO crystals. The SHG intensities of the β-phase crystal are significantly higher than those of the α-phase crystal under all measured wavelengths (Fig. 5). At the excitation wavelength of 860 nm, the intensity ratio of two phases is about 53. The different intermolecular interactions of α- and β-phases are responsible for driving molecules in the two non-centrosymmetric space groups, eventually leading to their distinguishable NLO properties. The SHG measurements show that the α- and β-phase crystals exhibit different and remarkable SHG response that confirms their polarizability arising from the different intermolecular interactions in the crystal packing. This is also consistent with the result of theoretical calculations that the β-phase crystal possesses a larger net inherent dipole moment at the macroscopic level.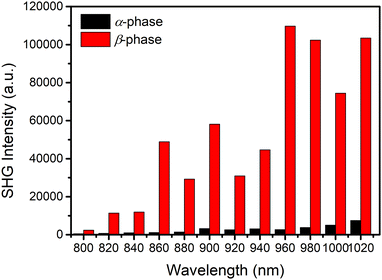

Fig. 4 NLO properties. (a) Wavelength-dependent SHG spectra of the α-phase in a fixed spot. (b) Polarization-dependent SHG spectra of the α-phase at 860 nm. (c) Logarithmic plot of the power-dependent SHG signals of the α-phase at 800 nm. (d) Wavelength-dependent SHG spectra of the β-phase in a fixed spot. The blue region is the quadratic dynamic range. The orange region deviates from the quadratic linear relationship. (e) Polarization-dependent SHG spectra of the β-phase at 860 nm. (f) Logarithmic plot of the power-dependent SHG signals of the β-phase at 800 nm. The red lines for panels (b) and (e) represent the cos⁴ θ fits for SHG. The incident power was 15 mW except for panels (c) and (f). The incident light is perpendicular to the long axis of the crystal.

Fig. 5 The comparison of SHG intensities between the α- and β-phase BPTA crystals at different wavelength under the same measurement conditions. Incident power: 15 mW.

The shapes of polarization-dependent SHG spectra of the two polymorphic phases are both two-lobed and can be well fitted by cos⁴ θ,^57,58 but their optimum polarization angles are different (Fig. 4b and e). For the α-phase crystal, the intensities of SHG reach maxima at 160° and 340°, while the intensities of SHG reach maxima at 40° and 220° in the β-phase crystal. Furthermore, the polarization ratio ρ of the β-phase (94%) is much higher than that of the α-phase (77%), following the formula ρ = (I_max − I_min)/(I_max + I_min), where I_max and I_min are the maximum and minimum values of SHG intensity, respectively. This suggests that the SHG effect of the β-phase BPTA has a higher sensitivity of the polarization angle than the α-phase. The results of power-dependent measurements show that the SHG intensities of both the α- and β-phase crystals follow a quadratic dependence on the incident laser power, owing to the two-photon nature of the nonlinear optical SHG process (Fig. 4c and f). The power-dependent SHG signals of the α-phase pumped at 800 nm follow a quadratic dependence in the blue region and deviate from the quadratic linear relationship in the orange region. The reason for the deviation in the orange region is due to the saturation of the SHG signal strength. The trend of SHG intensity increasing with the increase of incident power indicates that the sample has not been damaged. Both α- and β-phase crystals generate stable SHG signals even at an incident power higher than 1000 mW, suggesting the very high laser damage threshold of BPTA crystals.

We compared the SHG intensity from the β-phase crystal with that of the benchmark potassium dihydrogen (KDP) crystal to evaluate the NLO efficiency of BPTA. The SHG signals from the β-phase BPTA and KDP crystals have been collected at different excitation wavelengths under the same measurement conditions. The thickness of KDP is about 134 μm (Fig. S14, ESI†). The wavelength-dependent SHG spectra of both crystals were measured at the selected spots with strongest NLO responses as shown in their SHG mapping (Fig. S15, ESI†), under optimal polarization directions at different excitation wavelengths. The comparison of SHG intensities between the crystals of the β-phase BPTA and KDP, as shown in Fig. S15a (ESI†), indicates that the SHG intensities of the β-phase crystal are comparable with KDP under the excitation wavelength ranging from 800 to 920 nm. When the excitation changes to longer wavelengths (from 940 to 1040 nm), the β-phase BPTA crystal has obvious superiority in NLO performances (with the SHG intensity about 30 times that of KDP at 1020 nm). Such a highly efficient second-order NLO response of the β-phase BPTA is remarkable in organic crystals, suggesting the promising applications of click compounds as potential NLO materials.

Conclusions

In this work, an organic molecule BPTA has been synthesized by using azide–alkyne click chemistry. The self-assembled polymorphic crystals of BPTA with noncentrosymmetric structures exhibit strong second-order NLO responses, along with good optical transparency and high thermal stability. Especially, the β-phase BPTA crystal exhibits highly efficient SHG response tens of times higher than commercial inorganic material KDP. It is expected that this short and high-yielding synthetic strategy of click chemistry can be expanded to other functional groups and will pave the way for their applications in organic NLO materials and devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the National Natural Science Foundation of China (52172045 and 22035003) and the Fundamental Research Funds for the Central Universities is gratefully acknowledged. Prof. W. Li is acknowledged for the assistance with DFT calculations.

References

1. H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021.
2. G. Meng, T. Guo, T. Ma, J. Zhang, Y. Shen, K. B. Sharpless and J. Dong, Nature, 2019, 574, 86–89.
3. M. Meldal and F. Diness, Trends Chem., 2020, 2, 569–584.
4. G. S. Kumar and Q. Lin, Chem. Rev., 2021, 121, 6991–7031.
5. Q. Zheng, H. Xu, H. Wang, W. H. Du, N. Wang, H. Xiong, Y. Gu, L. Noodleman, K. B. Sharpless, G. Yang and P. Wu, J. Am. Chem. Soc., 2021, 143, 3753–3763.
6. B. D. Fairbanks, L. J. Macdougall, S. Mavila, J. Sinha, B. E. Kirkpatrick, K. S. Anseth and C. N. Bowman, Chem. Rev., 2021, 121, 6915–6990.
7. C. X. Zhao, J. N. Liu, J. Wang, C. Wang, X. Guo, X. Y. Li, X. Chen, L. Song, B. Q. Li and Q. Zhang, Sci. Adv., 2022, 8, eabn5091.
8. P. R. Fitzgerald and B. M. Paegel, Chem. Rev., 2021, 121, 7155–7177.
9. A. K. Agrahari, P. Bose, M. K. Jaiswal, S. Rajkhowa, A. S. Singh, S. Hotha, N. Mishra and V. K. Tiwari, Chem. Rev., 2021, 121, 7638–7956.
10. R. A. Flynn, K. Pedram, S. A. Malaker, P. J. Batista, B. A. H. Smith, A. G. Johnson, B. M. George, K. Majzoub, P. W. Villalta, J. E. Carette and C. R. Bertozzi, Cell, 2021, 184, 3109–3124.
11. L. Taiariol, C. Chaix, C. Farre and E. Moreau, Chem. Rev., 2022, 122, 340–384.
12. V. G. Muir and J. A. Burdick, Chem. Rev., 2021, 121, 10908–10949.
13. N. Z. Fantoni, A. H. El-Sagheer and T. Brown, Chem. Rev., 2021, 121, 7122–7154.
14. X. Zang, H. Liu, Q. Li, Z. A. Li and Z. Li, Polym. Chem., 2020, 11, 5493–5499.
15. W. Wu, R. Tang, Q. Li and Z. Li, Chem. Soc. Rev., 2015, 44, 3997–4022.
16. Z. Li, W. Wu, Q. Li, G. Yu, L. Xiao, Y. Liu, C. Ye, J. Qin and Z. Li, Angew. Chem., Int. Ed., 2010, 49, 2763–2767.
17. X. Deng, K. Wang, Q. Li and Z. Li, Mater. Chem. Front., 2022, 6, 3349–3358.
18. J. Liu and W. Wu, Symmetry, 2022, 14, 882.
19. W. Wu, C. Wang, R. Tang, Y. Fu, C. Ye, J. Qin and Z. Li, J. Mater. Chem. C, 2013, 1, 717–728.
20. J. Chen, C. L. Hu, F. Kong and J. G. Mao, Acc. Chem. Res., 2021, 54, 2775–2783.
21. T. P. Radhakrishnan, Acc. Chem. Res., 2008, 41, 367–376.
22. J. Xu, S. Semin, T. Rasing and A. E. Rowan, Small, 2015, 11, 1113–1129.
23. J. Wu, Z. a Li, J. Luo and A. K. Y. Jen, J. Mater. Chem. C, 2020, 8, 15009–15026.
24. Q. S. Shen and K. Y. Wong, Opt. Commun., 1999, 164, 47–50.
25. W. Wu, Z. Xu and Z. Li, J. Mater. Chem. C, 2014, 2, 8122–8130.
26. H. Sun, Z. a Li, J. Wu, Z. Jiang, J. Luo and A. K. Y. Jen, J. Mater. Chem. C, 2018, 6, 2840–2847.
27. R. Wang, Z. Cheng, X. Deng, W. Zhao, Q. Li and Z. Li, J. Mater. Chem. C, 2020, 8, 6380–6387.
28. X. C. Deng, K. Wang, Q. Q. Li and Z. Li, Mater. Chem. Front., 2022, 6, 3349–3358.
29. Q. Li and Z. Li, Acc. Chem. Res., 2020, 53, 962–973.
30. D. P. Yan and D. G. Evans, Mater. Horiz., 2014, 1, 46–57.
31. D. Yan, Chem. – Eur. J., 2015, 21, 4880–4896.
32. S. J. Kim, B. J. Kang, U. Puc, W. T. Kim, M. Jazbinsek, F. Rotermund and O. P. Kwon, Adv. Opt. Mater., 2021, 9, 2101019.
33. S. Semin, X. Li, Y. Duan and T. Rasing, Adv. Opt. Mater., 2021, 9, 2100327.
34. J. Xu, S. Semin, J. Cremers, L. Wang, M. Savoini, E. Fron, E. Coutino, T. Chervy, C. Wang, Y. Li, H. Liu, Y. Li, P. Tinnemans, P. H. J. Kouwer, T. W. Ebbesen, J. Hofkens, D. Beljonne, A. E. Rowan and T. Rasing, Adv. Opt. Mater., 2015, 3, 948–956.
35. Y. L. Duan, C. G. Ju, G. Yang, E. Fron, E. Coutino-Gonzalez, S. Semin, C. C. Fan, R. S. Balok, J. Cremers, P. Tinnemans, Y. Q. Feng, Y. L. Li, J. Hofkens, A. E. Rowan, T. Rasing and J. L. Xu, Adv. Funct. Mater., 2016, 26, 8968–8977.
36. Y. Nagai, K. Ishiba, R. Yamamoto, T. Yamada, M. A. Morikawa and N. Kimizuka, Angew. Chem., Int. Ed., 2021, 60, 6333–6338.
37. S. Kaur, M. Kaur, P. Kaur, K. Clays and K. Singh, Coord. Chem. Rev., 2017, 343, 185–219.
38. Y. J. Ma, G. Xiao, X. Fang, T. Chen and D. Yan, Angew. Chem., Int. Ed., 2023, 62, e202217054.
39. D. P. Yan, H. J. Yang, Q. Y. Meng, H. Y. Lin and M. Wei, Adv. Funct. Mater., 2014, 24, 587–594.
40. M. Savoini, L. Huber, H. Cuppen, E. Abreu, M. Kubli, M. J. Neugebauer, Y. Duan, P. Beaud, J. Xu, T. Rasing and S. L. Johnson, ACS Photonics, 2018, 5, 671–677.
41. Y. Z. Dong, S. Semin, Y. Q. Feng, J. L. Xu and T. Rasing, Chin. Chem. Lett., 2021, 32, 525–528.
42. L. Su-Yue, L. Zhong-An, Z. Zhi-Chao, Z. Wei, H. Ting, L. Zhen, Y. Cheng and Q. Jin-Gui, Chin. J. Chem., 2008, 26, 328–332.
43. T. G. Zhang, Y. X. Zhao, I. Asselberghs, A. Persoons, K. Clays and M. J. Therien, J. Am. Chem. Soc., 2005, 127, 9710–9720.
44. Z. Cheng, R. Tang, R. Wang, Y. Xie, P. Chen, G. Liu and Z. Li, Polym. Chem., 2018, 9, 3522–3527.
45. F. Q. Meng, M. K. Lu, J. Chen, S. J. Zhang and H. Zeng, Solid State Commun., 1997, 101, 925–928.
46. G. A. Valdivia-Berroeta, E. W. Jackson, K. C. Kenney, A. X. Wayment, I. C. Tangen, C. B. Bahr, S. J. Smith, D. J. Michaelis and J. A. Johnson, Adv. Funct. Mater., 2019, 30, 1904786.
47. R. Zhao, T. Zhu, S. Wang, C. Jarrett-Wilkins, A. M. Najjarian, A. J. Lough, S. Hoogland, E. H. Sargent and D. S. Seferos, Chem. Sci., 2022, 13, 12144–12148.
48. S. Maza, C. Kijatkin, Z. Bouhidel, S. Pillet, D. Schaniel, M. Imlau, B. Guillot, A. Cherouana and E. E. Bendeif, J. Mol. Struct., 2020, 1219, 128492.
49. H. M. Jesudoss, M. Saminathan, R. E. Jesudoss, D. Murugan and P. Alagusundaram, Braz. J. Phys., 2019, 49, 28–43.
50. P. Liang, Z. Li, Y. Mi, Z. Yang, D. Wang, H. Cao, W. He and H. Yang, J. Electron. Mater., 2015, 44, 2883–2889.
51. B. S. P. Anil Kumar, K. Harsha Vardhan Reddy, K. Karnakar, G. Satish and Y. V. D. Nageswar, Tetrahedron Lett., 2015, 56, 1968–1972.
52. S. H. Saraf and R. Ghiasi, Russ. J. Phys. Chem. A, 2020, 94, 1047–1052.
53. R. Ghiasi and A. Peikari, Phys. Chem. Liq., 2016, 55, 421–431.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 16 Gaussian, C.01 Revision, Gaussian, Inc., Wallingford CT, 2016.
55. J. Xu, S. Semin, D. Niedzialek, P. H. Kouwer, E. Fron, E. Coutino, M. Savoini, Y. Li, J. Hofkens, I. H. Uji, D. Beljonne, T. Rasing and A. E. Rowan, Adv. Mater., 2013, 25, 2084–2089.
56. Y. Zheng, J. Xu and X. H. Bu, Adv. Opt. Mater., 2021, 10, 2101545.
57. A. Miniewicz, K. Palewska, L. Sznitko and J. Lipinski, J. Phys. Chem. A, 2011, 115, 10689–10697.
58. L. Moreaux, O. Sandre and J. Mertz, J. Opt. Soc. Am. B, 2000, 17, 1685–1694.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, simulation details, PXRD pattern, thermal stability measurement and crystallographic information. CCDC 2091943–2091945. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc00652b

---