Ferroelectricity in oxygen-deficient perovskite-type oxide Sr₁₀Ga₆Sc₄O₂₅

Abstract

We have investigated the physical properties of an oxygen-deficient perovskite-type Sr₁₀Ga₆Sc₄O₂₅ by means of dielectric permittivity, pyroelectric current, and X-ray diffraction (XRD) measurements using a polycrystalline sample. The real part of the dielectric permittivity shows a clear anomaly around 310 K. Switchable pyroelectric current is also observed around this temperature, indicating a ferroelectric phase transition in the title compound. Synchrotron powder XRD measurements reveal that no discontinuous jump takes place in the temperature dependent cell volume around 310 K, implying that the phase transition is of second order. The candidates of the low and high temperature space groups are discussed based on the group theory.

---

1. Introduction

Most dielectric materials, which are fundamental to state-of-the-art technologies, belong to simple perovskite-type oxides with the chemical formula of ABO₃.^1–6 The proper ferroelectric BaTiO₃, and P(Zr,Ti)O₃ are representative of such compounds.^7–10 On the other hand, rich functionalities have also been discovered in the past decade in compounds which have more complex sublattices. For instance, layered perovskite-type oxides show “improper” ferroelectricity with intriguing cross correlation between polarization, strain, and magnetization.^11–15 The coexistence of ferroelectricity, anti-ferroelectricity, and ion conductivity in a single thermodynamic phase has also been reported in the derived form of a layered perovskite-type oxide.^16–20 A class of aluminate-sodalite-type oxides, which have a cage structure consisting of eco-friendly elements, shows large electromechanical coupling factor and piezoelectric strain coefficient, offering highly efficient pyroelectric power generation and piezoelectric sensing.^21,22 Therefore, searching for ferroelectric materials not only in simple perovskite-type oxides but also in compounds with more complex crystal structures will open a frontier of the fields of ferroelectric and other multifunctional materials.

In this regard, oxygen-deficient perovskite-type oxides with the composition ratio of A:(B,C):O = 1 : 1 : 2.5 are attractive, because in such compounds oxygen vacancies can be ordered in a periodic manner to form a unique long-range order. The quaternary Sr–Sc–Ga–O system, which forms various crystal structures depending on the ratio of B and C, is the representative of such compounds.²³ When Ga : Sc = 3 : 1, a cubic perovskite-type phase is formed as SrGa_0.75Sc_0.25O_2.5. When Ga : Sc = 1 : 1, a brownmillerite-type structure, the framework of which is composed of a two-dimensional ScO₆ octahedral network and one-dimensional (1D) GaO₄ tetrahedral chains, is formed. The structure, which has a lot of gaps to take in oxygen, has recently attracted keen interest as a playground of oxide ion conductors.^24,25 Rom et al. have reported that the brownmillerite-type structure transforms to the simple perovskite-type structure by rare-earth substitution and attains photoluminescent properties.²⁶ Furthermore, Wu et al. have very recently found a dielectric anomaly²⁷ associated with an order-disorder transition of the GaO₄ tetrahedral chains.²⁵

Here, we focus on the dielectric properties of an oxygen-deficient perovskite-type oxide with the composition ratio of Ga : Sc = 6 : 4, Sr₁₀Ga₆Sc₄O₂₅. This compound was first synthesized in 2011, and its crystal structure has been analyzed by means of neutron powder diffraction and Monte Carlo simulation.²³ The same as Sr₂ScGaO₅, the ordering of oxygen vacancies creates ScO₆ octahedral- and GaO₄ tetrahedral-sites, and then they form a new type of long-range order with the space group I4₁/a. Since the dielectric properties of a compound are strongly related to its crystal structure, such novel crystal structure makes us expect unique dielectric properties. In this paper, we report a second-order ferroelectric phase transition associated with a small spontaneous polarization in Sr₁₀Ga₆Sc₄O₂₅ revealed by our dielectric, pyroelectric current, and powder X-ray diffraction measurements.

2. Experiments

Samples of Sr₁₀Ga₆Sc₄O₂₅ ceramics were synthesized by a conventional solid-state reaction method. A stoichiometric mixture of SrCO₃ (99.9%), Sc₂CO₃ (99.9%), and Ga₂O₃ (99.999%) was ground in wet processes with ethanol using an agate mortar and pestle. The powder mixtures were calcined at 1200 °C for 12 h. The resultants were sintered at 1200 °C for 12 h after intermediate regrinding and palletization. The sintered samples were confirmed by powder X-ray diffraction (XRD) measurements at the beamline BL02B2 of SPring-8, Japan.²⁸ The Rietveld refinement was performed by using the Jana2006 program.²⁹ The dielectric measurements were performed by using a Keysight 4284A precision LCR meter with a temperature slope of 10 K min⁻¹. The pyroelectric current was measured by using a Keithley 6430 sub-femto-amp remote source meter. The sample was preliminarily electrically poled on the cooling process and then pyroelectric current was measured on the heating process with a temperature slope of 10 K min⁻¹. The temperatures of the samples were controlled using a LINKAM THMS600 heating/cooling stage for the dielectric and pyroelectric measurements. Dielectric and pyroelectric measurements shown in the main text were performed on the same ceramic pellet, whose diameter and thickness were approximately 10 mm and 200 μm, respectively. The platinum electrodes were sputtered on both surfaces of the samples for the measurements.

3. Results and discussion

Fig. 1 shows the crystal structure of Sr₁₀Ga₆Sc₄O₂₅ visualized by the VESTA code.²⁹ Although this compound has a three-dimensional framework of oxygen-polyhedra, here we treat it as a layered structure that is composed of eight layers. Among them, two layers are symmetrically inequivalent, layer 1 and layer 2 in Fig. 1. In each layer, twelve GaO₄ tetrahedra and eight ScO₆ octahedra exist, namely, Ga and Sc are ordered with the ratio of 3 : 2. The connection of the oxygen-polyhedra differs between the inequivalent two layers. These two layers are rotated by π/2 and moved up by c/4 by the 4₁ screw axis by four times, and then the entire structure is formed. The cell volume of Sr₁₀Ga₆Sc₄O₂₅ is about 100 000 ų, which is roughly 160 times larger than a unit-cell of a simple cubic perovskite-type oxide.

Fig. 1 The crystal structure of Sr₁₀Ga₆Sc₄O₂₅. The detailed description is seen in the main text.

Fig. 2 shows the comparison between the synchrotron powder XRD pattern of Sr₁₀Ga₆Sc₄O₂₅ and simulation pattern by using the previously reported I4₁/a crystal structure.²³ The measured and simulated patterns show good agreement. The inset shows the expanded pattern around the highest intensity peak. We note that there are substantial amounts of impurity Sr₂ScGaO₅ phase. The volume of the impurity phase is about 20% against the main phase.

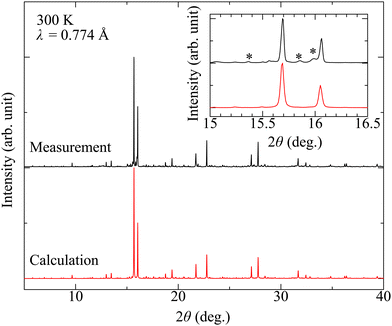Fig. 2 Synchrotron powder X-ray diffraction pattern of polycrystalline Sr₁₀Ga₆Sc₄O₂₅. The simulated pattern by using the reported structure is also shown. The inset shows close view around the highest peak. There are impurity Sr₂ScGaO₅ phases, whose volume is 20% against the Sr₁₀Ga₆Sc₄O₂₅ phase. The structure is visualized by the VESTA code.³⁰

The temperature dependence of the real (ε′) and imaginary (ε′′) part of the dielectric permittivity for Sr₁₀Ga₆Sc₄O₂₅ in the temperature range from 250 to 500 K is shown in Fig. 3(a). The real part ε’ is ∼12 at 500 K, which is the same as ordinary oxides, while the imaginary part ε′′ is small enough in the measurement temperature range, indicating good insulating character of Sr₁₀Ga₆Sc₄O₂₅. Importantly, we observe an anomaly like the Curie–Weiss law in ε′ around 310 K among all measurement frequencies. This is clearly confirmed by the inverse plot of ε′ (the right inset in Fig. 3(a)), which shows linear temperature dependence above 310 K. Although our sample contains impurity Sr₂ScGaO₅, it shows flat temperature dependence and does not show any dielectric anomalies around 310 K.²⁶ Thus, our observation indicates the occurrence of a phase transition in Sr₁₀Ga₆Sc₄O₂₅ around 310 K.

Fig. 3 (a) Temperature dependence of the real (ε′) and imaginary (ε′′) part of the dielectric permittivity of polycrystalline Sr₁₀Ga₆Sc₄O₂₅ in the heating process. The left inset shows the expansion of the dielectric anomalies in the heating and cooling process. The right inset shows the inverse plot of ε′. (b) Temperature dependence of the pyroelectric current under the poling field of ± 11 kV cm⁻¹. The inset shows temperature dependent spontaneous polarization evaluated from the pyroelectric current measurements.

Note that the anomaly is not a single peak but associated with a broad tail which shows frequency dependence and spreads to 250 K. We attribute this structure to the response of polar domains formed below the phase transition in Sr₁₀Ga₆Sc₄O₂₅. Since domain formation depends on defects and/or strain in each polycrystal, the tail structure shows sample-dependence, as shown in Fig. S1 (ESI†). Nevertheless, the 1/T dependence of ε′ above 310 K seems to be almost unchanged between the three different samples, confirming that the anomaly comes from a thermodynamic phase transition in Sr₁₀Ga₆Sc₄O₂₅. Furthermore, the left inset of Fig. 3(a) shows the expansion of the dielectric anomaly in both heating and cooling processes. The peak temperature is the same in both processes, indicating that the phase transition is of the second order.

To investigate the detail of the dielectric phase transition around 310 K, we conducted pyroelectric current measurements. If the structure changes from a non-polar phase to a polar phase associated with the phase transition, the charges accumulated at the sample surface by spontaneous polarization are released when the temperature of the sample reaches the transition temperature from low temperatures, and pyroelectric current is detected. Fig. 3(a) shows the temperature dependence of the pyroelectric current for Sr₁₀Ga₆Sc₄O₂₅. We observe a clear peak like signal with its maximum around 315 K under both positive and negative bias fields. This indicates that switchable spontaneous polarization is formed in the low temperature phase of Sr₁₀Ga₆Sc₄O₂₅, namely the phase transition observed in our dielectric permittivity measurement is a ferroelectric phase transition. Note that this is the first observation of switchable spontaneous polarization in the Sr–Ga–Sc–O quaternary system. In addition, the pyroelectric current emerges diffusively from 340 K to 250 K. Possibly local compositional and/or structural fluctuation originated from the complex crystal structure makes the phase transition diffusive as seen in a disordered perovskite-type ferroelectric material.³¹ The inset of Fig. 3(b) shows the temperature dependent spontaneous polarization evaluated from the pyroelectric current measurements. The spontaneous polarization at 250 K is about 0.05 μC cm⁻², which is 2–3 orders of magnitude smaller than that of ordinary ferroelectric perovskite-oxides.

To further reveal the details of the ferroelectric phase transition, we investigated a structural property. Fig. 4(a) shows the temperature dependent lattice constants from 200 to 520 K. Note that the lattice constants are refined by Rietveld fitting assuming the structural model of I4₁/a²³ among all measured temperatures. Since there are too many refinable structural parameters due to the huge unit cell, we only refined the lattice and profile parameters. The isotropic compression in the a- and c-axes reflects the three-dimensional bonding nature of Sr₁₀Ga₆Sc₄O₂₅, and differs from anisotropic compression of two dimensional Sr₂ScGaO₅.²⁵ The cell volume (V) is an essential thermodynamical parameter, which reflects the nature of the phase transition. We do not find a discontinuous jump in temperature dependent V. Rather it seems to show changes in its slope (dV/dT) around 310 K. Since V is the first derivative of the Gibbs free energy, the change in its derivative confirms the second order phase transition.

Fig. 4 (a) Temperature dependence of the lattice parameters between 200 and 520 K. The value of a, c, and V at 520 K is 17.56 Å, 32.93 Å, and 101 000 ų, respectively. The line on the V data is a guide for the eyes. (b) Colormap composed of multiple powder X-ray patterns measured at 42 temperature points every 10 K from 100 K to 520 K. (c) and (d) Comparison of the raw powder XRD data at various temperatures. The dot line in each picture shows the peak position of 002 and 006 reflections.

Now, let us consider the candidate of the space group for the high and low temperature phases. First, the reported space group I4₁/a is incompatible with our pyroelectric current measurement, since the emergence of pyroelectric current around 310 K proves that the polar space group realizes at 300 K. Nevertheless, the reported crystal structure well reproduces our XRD pattern, namely, the difference between reported and actual crystal structures is expected to be small. Thus, we assume that the space group I4₁/a is realized in the high temperature phase. Since a second order structural phase transition allows only the transformation to the maximum subgroup of I4₁/a, we can predict the low temperature space group from the viewpoint of group theory.

According to ref. 32 the maximum subgroups of I4₁/a are I4₁, I4̄, and C2/a. Fortunately, we can uniquely choose I4₁ as a candidate for the low temperature space group, since the others are nonpolar space groups, which are incompatible with the result of pyroelectric current measurement. We scrutinized whether the space group I4₁ is compatible with our XRD data or not. Fig. 4(b) shows a colormap, which is composed of multiple powder X-ray patterns measured at 42 temperature points every 10 K from 100 K to 520 K. The highest intensity reflection 4 −2 8 and the second highest reflection 6 2 0 are always single peaks and do not show splitting or broadening in the measured temperature range, indicating that the low temperature phase maintains tetragonal symmetry.

Fig. 4(c) and (d) show the comparison of the raw powder XDR data among various temperatures. The dot lines in each picture show the peak position of the 0 0 2 and 0 0 6 reflections, which are prohibited by the 4₁ screw axis symmetry. Thus, if the low temperature phase is either I4̄ or C2/a except for I4₁, additional peaks can emerge at those positions. No additional reflection emerging below 310 K is compatible with the I4₁ space group. We have also checked the generation rule of a-glide symmetry. However, we cannot find clear violation of it. This indicates that the intensity of additional reflections is several orders of magnitude smaller than the intensity of the primary reflections due to small atomic displacement associated with the phase transition.

Note that we have not yet succeeded in the refinement of the I4₁ structure by using the powder XRD data due to too many inequivalent sites (∼100 sites). Here, we guess a possible scenario for the phase transition from the viewpoint of symmetry. At the high temperature phase, there are a- (b-) glide planes at z = 0.25 and 0.75 (z = 0 and 0.5), which give a 1/2 translational operation along the a- (b-) axis and then give mirror operation. Since the mirror symmetry mirrors an upward electric dipole downward, forming macroscopic electric polarization along the c-axis is forbidden. In particular, the layers 3 and 7 (1 and 5) in Fig. 1, which are on the a- (b-) glide planes, cannot form local electric polarization along the c-axis in themselves. In addition, although the layers with even numbers can form local electric polarization in themselves, the glide symmetry cancels out the macroscopic electric polarization. Namely, the disappearance of the a-glide planes can cause local electric polarization in the layers with odd numbers and/or make the cancellation between the local electric polarization imperfect, and then macroscopic nonzero electric polarization emerges. The bending or ordering of the oxygen-polyhedral framework is a candidate of the structural change to break the a-glide planes. It is a future issue to elucidate the crystal structure, phase transition behavior, and microscopic ferroelectric origin by accurate physical property measurements on high-quality single crystals.

In this paper, we have demonstrated that a compound which has a complex long-range order by oxygen vacancies shows ferroelectricity. Although another compound which has the same structure as Sr₁₀Ga₆Sc₄O₂₅ has not been found yet, we may create this type of material from a large number of perovskite-type oxides by oxygen vacancy engineering. We think that the experimental approach to such complex materials is an important issue to open the frontiers of material science, since the state-of-the-art theoretical calculation cannot precisely predict their physical properties. We hope that our findings will accelerate the development of new functional materials in the future.

4. Summary

The ferroelectric phase transition on the oxygen-deficient perovskite-type Sr₁₀Ga₆Sc₄GaO₂₅ has been investigated by means of dielectric, pyroelectric current and synchrotron powder XRD measurements in the present study. The dielectric permittivity shows an anomaly which seems to obey the Curie–Weiss law, around 310 K. The pyroelectric current also exhibits a peak-like structure with its maximum around 315 K, and furthermore, it can be switched when opposite bias fields are applied. The estimated spontaneous polarization P_s at 250 K is around 0.05 μC cm⁻². The continuous change in the cell volume around 310 K indicates a second-order phase transition. The I4₁/a and I4₁ space groups are assigned to high and low temperature phases, respectively, based on the group theory. Further precise structural analyses are needed to clarify the origin of the ferroelectric transition in Sr₁₀Ga₆Sc₄GaO₂₅.

Author contributions

A. N.: conceptualization, formal analysis, funding acquisition, investigation, and writing – original draft. I. T.: resources, supervision, and writing – review & editing. H. T.: resources, supervision, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The present work was partially supported by Nippon Sheet Glass Foundation for Materials Science and Engineering. Powder XRD measurements were conducted with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2019B1089, and 2020A1246). This work was partially supported by JSPS Grants-in-Aid for Transformative Research Areas (A) “Hyper-Ordered Structures Sciences” (Grant No. 20H05878, 20H05879).

References

1. R. E. Cohen, Origin of ferroelectricity in perovskite oxides, Nature, 1992, 358, 136–138.
2. M. Posternak, R. Resta and A. Baldereschi, Phys. Rev. B: Condens. Role of covalent bonding in the polarization of perovskite oxides: The case of KNbO₃, Matter Mater. Phys., 1994, 50, 8911.
3. M. Kunz and I. D. Brown, Out-of-center Distortions around Octahedrally Coordinated d⁰ Transition Metals, J. Solid State Chem., 1995, 115, 395–406.
4. J. B. Goodenough, Jahn–Teller phenomena in solids, Annu. Rev. Mater. Sci., 1998, 28, 1–27.
5. Y. Kuroiwa, S. Aoyagi, A. Sawada, J. Harada, E. Nishibori, M. Takata and M. Sakata, Evidence for Pb–O Covalency in Tetragonal PbTiO₃, Phys. Rev. Lett., 2001, 87, 217601.
6. N. A. Benedek and C. J. Fennie, Why Are There So Few Perovskite Ferroelectrics, J. Phys. Chem. C, 2013, 117, 13339.
7. M. M. Vijatovic, J. D. Bobic and B. D. Stojanovic, History and Challenges of Barium Titanate: Part I, Sci. Sintering, 2008, 40, 155.
8. J. F. Scott and C. A. Paz de Araujo, Ferroelectric memories, Science, 1989, 246, 1400.
9. G. Yi, Z. Wu and M. Sayer, Preparation of Pb(Zr,Ti)O₃ thin films by sol gel processing: Electrical, optical, and electro-optic properties, J. Appl. Phys., 1988, 64, 2717.
10. C. A. Paz de Araujo, L. D. McMillan, B. M. Melnick, J. D. Cuchiaro and J. F. Scott, Ferroelectrics memories, Ferroelectrics, 1990, 104, 241.
11. N. A. Benedek and C. J. Fennie, Hybrid Improper Ferroelectricity: A Mechanism for Contrpllable Polarization- Magnetization Coupling, Phys. Rev. Lett., 2011, 106, 107204.
12. N. A. Benedek, A. T. Mulder and C. J. Fennie, Polar octahedral rotations: A path to new multifunctiona materials, J. Solid State Chem., 2012, 195, 11–20.
13. Y. S. Oh, X. Luo, F.-T. Huang, Y. Wang and S.-W. Cheong, Experimental demonstration of hybrid improper ferroelectricity and the presence of abundant charged walls in (Ca,Sr)₃Ti₂O₇ crystals, Nat. Mater., 2015, 14, 407–413.
14. Y. Wang, F. T. Huang, X. Luo, B. Gao and S. W. Cheong, The first Room-Temperature Ferroelectric Sn Insulator and Its Polarization Switching Kinetics, Adv. Mater., 2017, 29, 1601288.
15. S. Yoshida, H. Akamatsu, R. Tsuji, O. Hernandez, H. Padmanabhan, A. Sen Gupta, A. S. Gibbs, K. Mibu, S. Murai, J. M. Rondinelli, V. Gopalan, K. Tanaka and K. Fujita, Hybrid Improper Ferroelectricity in (Sr,Ca)3Sn2O7 and Beyond: Universal Relationship between Ferroelectric Transition Temperature and Tolerance Factor in n = 2 Ruddlesden-Popper Phases, J. Am. Chem. Soc., 2018, 140, 15690.
16. T. Nagai, H. Shirakuni, A. Nakano, H. Sawa, H. Moriwake, I. Terasaki and H. Taniguchi, Weak Ferroelectricity in n = 2 Pseudo Ruddlesden–Popper-Type Niobate Li₂SrNb₂O₇, Chem. Mater., 2019, 31, 6257–6261.
17. T. Nagai, Y. Mochizuki, H. Shirakuni, A. Nakano, F. Oba, I. Terasaki and H. Taniguchi, Phase Transition from Weak Ferroelectricity to Incipient Ferroelectricity in Li₂Sr(Nb_1−xTa_x)₂O₇, Chem. Mater., 2020, 32, 744–750.
18. Y. Mochizuki, T. Nagai, H. shirakuni, A. Nakano, F. Oba, I. Terasaki and H. Taniguchi, Coexisting Mechanisms for the Ferroelectric Phase Transition in Li₂SrNb₂O₇, Chem. Mater., 2021, 33, 1257–1264.
19. A. Nakano, H. Shirakuni, T. Nagai, Y. Mochizuki, F. Oba, H. Yokota, S. Kawaguchi, I. Terasaki and H. Taniguchi, Phase variation of ferroelectric Li₂Sr_1−xCa_x(Nb_1−xTa_x)₂O₇ by selective reinforcement in the (Nb,Ta)-O covalent bonds, Phys. Rev. Mater., 2022, 6, 044412.
20. X. Xu, F.-T. Huang, K. Du and S.-W. Cheong, Multifunctionality of Li₂SrNb₂O₇: Memristivity, Tunable Rectification, Ferroelasticity, amd Ferroelectricity, Adv. Mater., 2022, 34, 2206022.
21. Y. Maeda, T. Wakamatsu, A. Konishi, H. Moriwake, C. Moriyoshi, Y. Kuroiwa, K. Tanabe, I. Teradaki and H. Taniguchi, Improper Ferroelectricity in Stuffed Aluminate Sodalites for Pyroelectric Energy Harvesting, Phys. Rev. Appl., 2017, 7, 34012.
22. H. Taniguchi, T. Hattori, T. Isobe, A. Nakano, I. Terasaki and M. Hagiwara, A large piezoelectric voltage coefficient in aluminate-sodalite-type improper ferroelectric oxides, J. Mater. Chem. C, 2021, 9, 15649.
23. S. V. Chernov, Y. A. Dobrovolsky, S. Y. Istomin, E. V. Antipov, J. Grins, G. Svensson, N. V. Tarakina, A. M. Abakumov, G. V. Tendeloo, S. G. Eriksson and S. M. H. Rahman, Sr₂GaScO₅, Sr₁₀Ga₆Sc₄O₂₅, and SrGa_0.75Sc_0.25O_2.5: a play in the octahedra to tetrahedra ratio in oxygen-deficient perovskites, Inorg. Chem., 2012, 51, 1094.
24. S. Corallini, M. Ceretti, G. Silly, A. Piovano, S. Singh, J. Stern, C. Ritter, J. Ren, H. Eckert, K. Conder, W. Chen, F. Chou, N. Ichikawa, Y. Shimawakawa and W. Paulus, One-Dimensional Oxygen Diffusion Mechanism in Sr₂ScGaO₅ Electrolyte Explored by Neutron and Synchrotron Diffraction, ¹⁷O NMR, and Density Functional Theory Calculations, J. Phys. Chem. C, 2015, 119, 11447.
25. C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, S. J. Clark, J. S. O. Evans and I. R. Evans, Brownmillerite-Type Sr₂ScGaO₅ oxide Ion Conductor: Local Structure, Phase Transition, and Dynamics, Chem. Mater., 2019, 31, 7395.
26. T. Rom, S. Laha, S. Gadiyaram, P. K. Maji and A. K. Paul, Rare-earth (Nd and Eu) indued structural transformation and optical properties of brownmillerite-type Sr₂ScGaO₅ oxide, J. Solid State Chem., 2022, 317, 123696.
27. Z. J. Wu, B. H. Zhang, X. Q. Liu and X. M. Chen, Crystal structures, dielectric properties, and phase transitions in Sr₂ScGaO₅-based brownmillerite ceramics, Ceram. Int., 2023, 49(3), 5298–5304.
28. S. Kawaguchi, M. Takemoto, K. Osaka, E. Nishibori, C. Moriyoshi, Y. Kubota, Y. Kuroiwa and K. Sugimoto, High-throughput powder diffraction measurement system consisting of multiple MYTHEN detectors at beamline BL02B2 of SPring-8, Rev. Sci. Instrum., 2017, 88, 085111.
29. V. Petricek, M. Dusek and L. Palatinus, Z. Kristallogr, Crystallographic Computing System JANA2006: General features, Cryst. Mater., 2014, 229, 345–352.
30. K. Monma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Cryst., 2008, 41, 653.
31. N. Setter and L. E. Cross, The role of B-site cation disorder in diffuse phase transition behavior of perovskite ferroelectrics, J. Appl. Phys., 1980, 51, 4356.
32. S. Ivantchev, E. Kroumova, G. Madariaga, J. M. Perez-Mato and M. I. Aroyo, SUBGROUPGRAPH: a computer program for analysis of group-subgroup relations between spae group, J. Appl. Cryst., 2000, 33, 1190.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc05118d

---