Equilibration and thermal reversibility in mixtures of model OPV small-molecules and polymers

Abstract

The thermal behaviour of small-molecule/polymer mixtures is of crucial significance in relation to the operational stability of organic photovoltaics, and the equilibration (or otherwise) of domain compositions and interfaces is of key importance for guiding design. Here, model phase-separated mixtures of fullerene and polystyrene are studied in detail in a thin-film bilayer, to robustly examine whether such systems satisfy two key requirements of thermodynamic equilibrium; (i) the attainment of a state (at a given temperature) that minimises the free energy, independent of the starting state of the system, and (ii) the reversibility of transitions between such equilibrium states. In an extensive study using polystyrene molecular weights of 1.86, 4.73, and 278.2 kg mol⁻¹, depth profiles are measured as a function of temperature using in situ neutron reflectivity, with initial sample composition profiles containing layers that are either pure components or blends. Following thermal annealing at sufficiently high temperatures we reproducibly observe changes in layer compositions, layer thicknesses and interfacial roughnesses during temperature cycling that are reversible, irrespective of the starting composition profiles of the samples. This robust demonstration of equilibrium behaviour provides a benchmark for the understanding of mixing in small-molecule/polymer thin-films, with particular relevance to the operation of organic photovoltaic devices.

---

Introduction

Organic photovoltaic (OPV) devices fabricated from mixtures of polymers and small-molecules have achieved substantial increases in efficiency over recent years.^1–5 However, the stability requirements for commercial viability remain a significant challenge,⁶ with the control of structure and morphology within bulk heterojunctions (BHJs) being of key importance (during both fabrication and operation).⁷ The non-equilibrium microstructure within BHJs is highly complex, containing, in general, both amorphous and crystalline domains (potentially of both components)^8,9 in which the sizescale, connectivity and degree of order contribute to the efficiency of charge separation and transport.^10,11 Over recent years, it has been recognised that the composition of mixed amorphous domains¹² within devices is also key, owing to the requirement for small-molecule–acceptor pathways to percolate within the polymer-rich domains and enable efficient charge transport.¹³ Recent attempts have been made to improve the design of BHJs using frameworks based on component molecular mobility and component miscibility within amorphous phases.^13–16 One focus has been on the utilisation of equilibrium theory, such as Flory–Huggins (FH) mean-field theory, to understand domain composition, and directly relate this to device performance.¹³ The establishment of a robust theoretical framework radically enhances design capabilities, in terms of efficiency and (morphological) stability; this is key in relation to the latter given the potential evolution of non-equilibrated (but optimised) domain compositions¹⁷ and morphology¹⁸ over time, leading to device degradation. Of crucial importance when implementing such theories is the ability to obtain predictive capabilities from them, both in terms of structure/device-performance relationships,¹³ and in terms of structural and morphological design/control (via kinetics or thermodynamics^16,19). The aim of the work we report herein is to rigorously probe key aspects of the equilibrium thermodynamics of model OPV-small-molecule/polymer mixtures. In recent work, we investigated the capability of FH theory to describe model amorphous-polymer/small-molecule systems, consisting of narrow molecular-weight-distribution polystyrene (PS) and two different fullerenes, phenyl-C60-butyric acid methyl ester (PCBM) and bis-adduct phenyl-C60-butyric acid methyl ester (bis-PCBM).^20–22 We found that FH theory can indeed be used to quantitatively predict co-existing phase composition as a function of polymer molecular weight (MW) in these systems. In addition, self-consistent-field-theory (SCFT) was used in a semi-quantitative way to interpret increased interfacial width at low MW in PS/PCBM.²⁰ Successful application of equilibrium thermodynamics to thin-film OPV materials is likely to be a key requirement for the ‘rational optimisation’¹³ of OPV devices. However, to enable complete confidence in predictions, a thorough test of the full range of equilibrium behaviour is desirable. To this end we hereby describe a series of experimental investigations into the equilibration of PS/bis-PCBM bilayers, with the specific aim of testing the path-independence of states following extensive mixing, and the reversibility of the transition from one such state to another. These two requirements of equilibrium states are here tested as a function of the starting structure of the films and the temperature, during thermal annealing. In comparison to BHJs, bilayer architectures facilitate simplified compositional analysis and enable investigations of equilibration and reversibility in thin-film geometries. The results from such investigations are of direct relevance to the behaviour of domain compositions within BHJs as, given sufficient molecular mobility, they move in the direction of thermodynamic equilibrium during operation (under thermal cycling).¹⁴In situ neutron reflectometry (NR) is used to measure layer composition and thickness within bilayers, and the buried interfacial width (interfacial roughness) between the two layers, while annealing at elevated temperature. This allows us to investigate any temperature-dependent behaviour in detail, as it eliminates any changes that might occur if the samples were quenched to room temperature and then measured. The low propensity for bis-PCBM to crystallise²³ enables exploration of the liquid–liquid equilibrium state at elevated temperature over extended time periods, while the narrow molecular-weight-distribution of PS enables discrimination between MW-dependent and temperature-dependent phenomena. Firstly, we will demonstrate that, following annealing to sufficiently high temperatures, for a given MW and temperature, these systems do indeed show convergence to a single equilibrium state from different starting points in phase-space. Secondly, we will demonstrate that these systems show significant changes in the composition of the two co-existing phases as a function of temperature, but that once the system is equilibrated, these changes are reversible with temperature. During our investigations we also discovered that equilibrium layer thickness changes will require theories beyond FH to fully understand the measured phenomenon.

Experimental methods

Sample preparation

PS (Agilent, UK) and bis-PCBM (99.5% purity, Solenne, Netherlands) solutions were prepared by dissolving in toluene and chlorobenzene respectively. The PS weight-average molecular weights (M_w) used in this study were 1.86, 4.73, and 278.2 kg mol⁻¹, with polydispersity indices (M_w/M_n, where M_n is the number-average molecular weight) of 1.04, 1.04, and 1.05 respectively. Henceforth these will be referred to as 2k, 5k and 300k. PS/bis-PCBM blends were prepared by first mixing the PS and bis-PCBM at a given mass ratio, and then adding chlorobenzene. The solutions were then left in the dark for several days. Single-side-polished silicon wafers (two-inch diameter, 2.5 mm thickness, from Siltronix, France) with a native oxide layer were sonicated in acetone and then isopropanol (15 minutes each). This was followed by rinsing in de-ionised water, and then drying (by rotating the wafers on a spin-coater at approximately 2 × 10³ revolutions per minute, for one minute). Bis-PCBM solutions were then spin-coated onto the silicon wafers. Top layers (PS and PS/bis-PCBM blends) were prepared by spin-coating solutions onto sheets of freshly cleaved mica (Goodfellow, UK) and then floating the layers onto the surface of a bath of de-ionised water. This floating layer was then deposited onto the silicon/bis-PCBM to make a bilayer sample. The samples were left to dry in the dark, before being placed under vacuum (at room temperature, in the dark) for 24 hours. Further details regarding solution concentrations and spin speeds are given in the ‘Sample list’ section in the ESI.† Two batches of samples were fabricated; (i) batch 1 – fabricated and then measured on the reflectometer D17,²⁴ at the Institut Laue-Langevin (ILL), Grenoble, France in 2021, and (ii) batch 2 – fabricated and then measured on D17 in 2019. The bulk of the results presented in this paper are from batch 1; batch 1 contained nine samples (labelled A-I, with various PS MWs), and batch 2 contained four samples (labelled 1–4, all with 300k PS MW). Sample details are summarised in Table 1.

Table 1 Summary of the initial (starting) top layer compositions of the samples used in batches 1 and 2. The bottom layer was pure bis-PCBM for all samples

Batch 1 samples	Initial top layer composition
Samples A, B and C	Pure 300k PS
Sample D and E	Bis-PCBM/300k PS blend (34 wt% bis-PCBM)
Sample F	Pure 5k PS
Sample G	Bis-PCBM/5k PS blend (33 wt% bis-PCBM)
Sample H and I	Pure 2k PS

---

Batch 2 samples
Samples 1 and 2	Bis-PCBM/300k PS blend (35 wt% bis-PCBM)
Sample 3	Bis-PCBM/300k PS blend (27 wt% bis-PCBM)
Sample 4	Bis-PCBM/300k PS blend (14 wt% bis-PCBM)

---

In situ neutron reflectivity (NR)

Samples were bolted onto the surface of a heater block within a vacuum chamber, as shown in Fig. S1a (ESI†). Extensive calibrations were performed both before and after each experiment on D17, to establish the offset between the heater set-point and the temperature at the surface of the silicon wafers (see ESI,† for details). Experiments on batch 1 were performed using a turbo pump which achieved pressures of approximately 10⁻⁴ mbar during thermal annealing. Experiments on batch 2 were performed using a rotary pump, achieving pressures in the range 2 × 10⁻¹ to 2 × 10⁻² mbar. After the chamber was pumped down, the heater was set to either 80 °C (batch 1) or 100 °C (batch 2), and a ‘full’ NR measurement was taken (with data acquired out to a momentum transfer, q, of around 0.2 Å⁻¹). A full NR measurement consisted of acquisition using a white beam of neutrons in time-of-flight mode at incident angles of 0.8° and 3°. By using a relatively relaxed resolution, Δq/q, of around 2–4% at q = 0.008 Å⁻¹ and around 8% at q = 0.15 Å⁻¹, we were able to collect a full NR curve using a total of 10 minutes acquisition time (2 and 8 minutes acquisition for incident angles of 0.8° and 3° respectively).‡ The heater set-point temperature was then changed in a stepwise fashion. After waiting for a sufficient time after each set-point change for the sample surface temperature to stabilise (during which, several NR measurements were taken at an incident angle of 0.8°), a full NR measurement was taken. A range of different heating protocols were used, involving isothermal annealing, and stepwise temperature cycling; protocol details are given in the Results and discussion and the ESI.†

Throughout the main paper, unless stated otherwise, given temperatures are the sample surface temperatures, rather than heater set-point temperatures (for both batches).

Data reduction and analysis

All NR data was reduced using Cosmos, within the ILL's data manipulation software, Lamp.²⁵ Further details are given in the ‘Data Reduction and Analysis’ section in the ESI.† All NR curves were fitted within refnx²⁶ using two uniform scattering length density (SLD) layers (refnx ‘slabs’) with adjustable thickness and SLD. The sample surface roughness and buried interfacial roughness (between the two layers) were also both adjustable (NB: all roughness parameters are Gaussian,^27,28 and for the 5k and 300k samples were small compared to the two layer thicknesses). A fixed layer (SLD = 2.5 × 10⁻⁶ Å⁻², thickness = 15 Å, roughness = 2 Å) representing the native oxide layer was included in the model between the adjustable layers and the semi-infinite silicon substrate. A fixed background of 10⁻⁷ was also included. The resolution from the data file (calculated in Cosmos from the instrumental settings) was used in all fits. For comparison purposes, a combination of Levenburg–Marquardt, differential evolution and Markov-chain-Monte-Carlo (MCMC) methods were used to fit the data.²⁶ These all gave very similar fit parameters. The error bars plotted in the NR curves represent standard deviations, calculated from the neutron counts. The MCMC uncertainties approximate standard deviations.²⁶ Goodness-of-fit, χ², parameters²⁹ for the (Levenburg–Marquardt/differential evolution) fits to the NR curves are given in Table S5 (ESI†).

Fourier transform infra-red spectroscopy (FTIR)

Prior to annealing, FTIR measurements were carried out on bis-PCBM films to assess whether oxidation of the fullerene was likely to occur under our annealing protocols. Firstly, films of bis-PCBM were made by drop-casting from chlorobenzene solution onto a silicon substrate. The films were then dried and measured using a PerkinElmer Spectrum Two spectrometer equipped with a diamond crystal for measuring in attenuated total reflection (ATR) mode. Annealing was then performed under more harsh conditions than used in the in situ NR experiments (at higher temperatures, for longer times and with lower vacuum). As found previously during our studies on PCBM,²⁰ no evidence of characteristic fullerene oxidation³⁰ was observed (see Fig. S5, ESI†).

Results and discussion

Convergence from different starting points and thermal reversibility

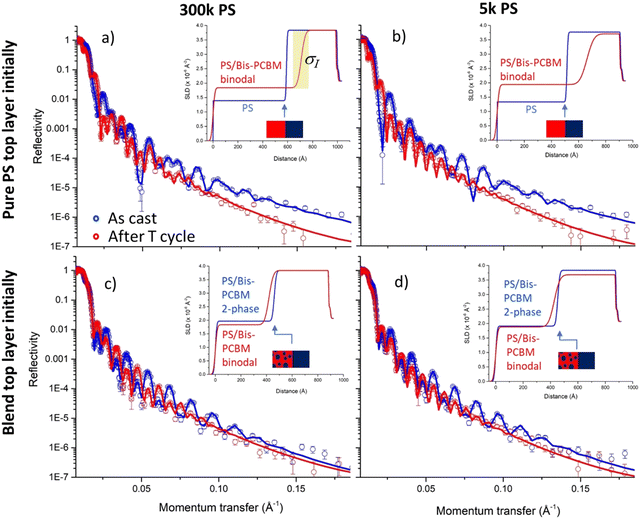
Our experimental methodology is summarised schematically in Fig. 1. To probe the approach to equilibrium from different starting points, two main categories of sample were fabricated on silicon substrates; (i) those with a pure bis-PCBM bottom layer and a pure PS top layer, and (ii) those with a pure bis-PCBM bottom layer and a top layer that was a blend of PS and bis-PCBM. Our aim was to heat the samples up to a sufficiently high temperature, so that the components became mobile, and the structure of the films evolved towards equilibrium. In samples with pure PS top layers, mixing of fullerenes into these layers occurs rapidly (within a few minutes),^20,21 once you approach the reported glass transition temperature (T_g) of the fullerene.³¹ Using our previous knowledge of PS/bis-PCBM systems,^20,21 we mostly chose top layer blend compositions that were expected to be in the two-phase region of phase space.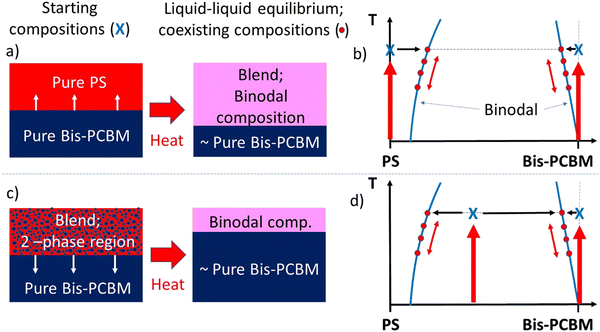

Fig. 1 Schematic representations of the convergent equilibration and thermal reversibility hypotheses tested in this study. (a) and (b) represent a bilayer that initially consists of two pure layers. (c) and (d) represent a bilayer that initially has a PS/bis-PCBM blend top layer (with a composition in the two-phase region of the phase diagram). (a) and (c) show the sample geometries/compositions before and after thermal annealing (with accompanying mass transfer) for sufficiently high MW PS. (b) and (d) show the hypothesised behaviour in relation to the phase-diagram for a typical polymer/small-molecule system; here, idealised as a system with a purely enthalpic FH interaction parameter, χ, displaying an upper-critical-solution-temperature (UCST). In (b) and (d) the red symbols correspond to co-existing compositions at different temperatures during thermal cycling, and the blue crosses correspond to the starting compositions of the top and bottom layers. NB; as we report herein, the PS/bis-PCBM phase-diagrams do not always exhibit the kind of binodals shown schematically in (b) and (d). In the case of sufficiently high MW PS, the change in bottom layer compositions (the right-hand bis-PCBM binodal branches in (b) and (d)) are exaggerated, as these would remain close to pure bis-PCBM,²⁰ and the left-hand binodal branches can exhibit qualitatively different thermal behaviour, depending on MW.

The annealing protocol that was employed was dependent on the category of sample and the batch. Batch 1 samples with pure PS top layers were first heated to 80 °C, at which there is little change in bilayer composition profile (layer thickness, composition or interface/sample-surface roughness) in comparison to room temperature,^20,21 and then measured using NR. They were then heated straight to the maximum temperature used (tens of degrees above the reported T_g of the fullerene), and, after a suitable waiting time, a NR measurement was taken. The temperature was then reduced in steps of approximately 10 °C to a minimum value, and back up to the maximum temperature. The NR was measured at each temperature after a suitable waiting time. Finally, the sample was slowly cooled to 80 °C, at which another NR measurement was taken. For batch 1 samples with PS/bis-PCBM blend top layers initially, the heating protocol was adjusted by inserting an isothermal annealing step of several hours (at temperatures that enable extensive mixing of the components), to allow the system a longer time to evolve towards equilibrium. These ‘initially blend top layer samples’ were then put through the same temperature cycling protocol as the samples with initially pure PS top layers.

The behaviour during thermal annealing in the two categories of sample is represented schematically in Fig. 1a and c; there is mass transfer of bis-PCBM molecules into the top layer for samples that initially had pure PS top layers, but out of the top layer in samples that initially had blend top layers in the two-phase region of the phase diagram. At equilibrium, because of the difference in the molecular sizes between the polymer and fullerene, the bottom layer composition will remain close to pure bis-PCBM for sufficiently high MW PS.^20,32Fig. 1b and d visualise equilibration from the two different starting compositions, for samples that are heated to sufficiently high temperatures.

Typical NR data, fits and model scattering length density (SLD) profiles for the two categories of samples, measured at 80 °C before and after heating to higher temperatures, are shown in Fig. 2. For all measurements we obtain very good fits using bilayer composition profiles, that consist of two uniform layers on top of a silicon substrate. Bilayer composition profiles are parameterised by 6 adjustable fit parameters; a thickness and SLD for each layer, a buried interfacial roughness, and a sample surface roughness. The insets in Fig. 2 show that the layer compositions and interfacial roughnesses following annealing from very different starting profiles (blue curves), appear to converge on similar values (red curves). In keeping with expectations from FH theory, the 300k PS samples also show no significant change in the measured bottom layer SLDs, while the 5k PS samples have slightly lower SLDs following annealing (in comparison to the measurements before annealing). In all four samples, the interfacial roughness, σ_I, also increases following annealing.

Fig. 2 Convergent equilibration; neutron reflectivity (NR) measurements (batch 1). NR data, fits and corresponding SLD profiles (insets) measured at 80 °C, before and 80 °C after thermal annealing (isothermal heating and temperature cycling) of bilayer samples. (a) A sample with an initially pure 300k PS top layer (sample B). (b) A sample with an initially pure 5k PS top layer (sample F). (c) A sample with a top layer that was initially a 300k PS/bis-PCBM blend (34 wt% bis-PCBM; sample D). (d) A sample with a top layer that was initially a 5k PS/bis-PCBM blend (33 wt% bis-PCBM; sample G). The insets plot SLD versus distance from the sample surface.

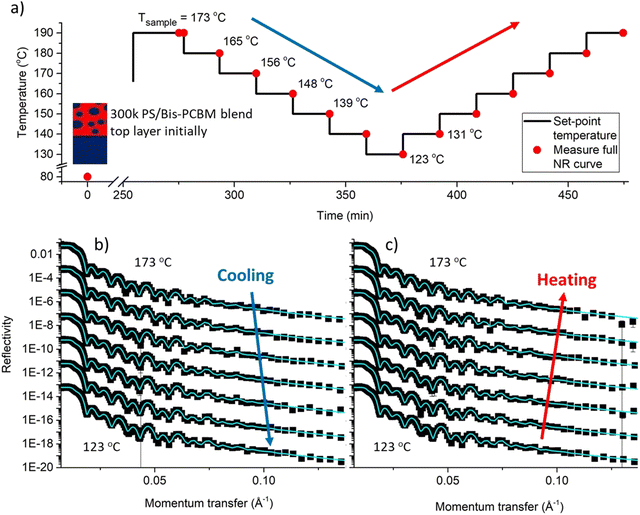
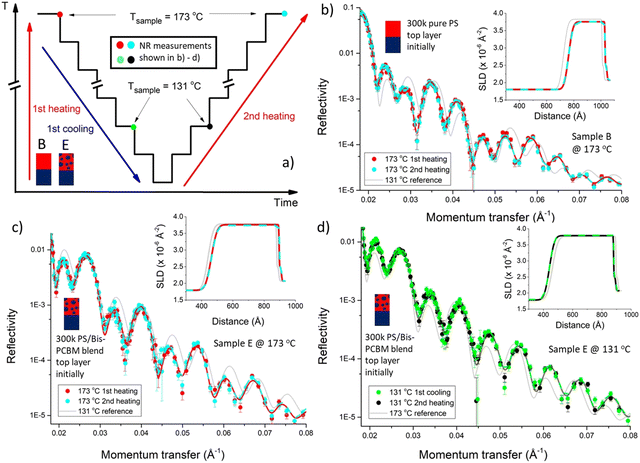
We now examine the in situ annealing of an individual sample. Fig. 3a shows the temperature cycling protocol for a sample that initially had a 300k PS/bis-PCBM top layer (sample D), showing the set-point and sample surface temperatures (see Fig. S2 and S3 for temperature stabilisation and offset calibration data, ESI†). The in situ NR data in Fig. 3b and c show the excellent quality of the bilayer fits, and the reversibility of the NR measurements and fits (this reversibility can be most readily visualised directly in the NR data by looking at the changes in the intensity of neighbouring fringes, on cooling/heating). This can be directly seen by careful inspection of Fig. 3b and c, but is more clearly illustrated by pairwise comparisons of NR curves and SLD profiles on first and second heating. Fig. 4 shows such comparisons for two further samples (B and E), in which we focus on the details of the NR curves within a limited q range. For a sample fabricated with a 300k PS/bis-PCBM blend top layer (sample E), that was cooled from 173 °C to 114 °C and then heated back up to 181 °C, Fig. 4c and d show that the fringe positions in the data and the fits clearly shift between measurements at 173 °C and 131 °C, but then reversibly change back on (re)heating. This reversibility and repeatability is also illustrated in the SLD profile for this sample (see insets to Fig. 4c and d). Although the pattern of fringes is different, due to the different layer thicknesses, similarly reversible behaviour in the reflectivity curve and the SLD profile is shown in Fig. 4b, for a sample that was fabricated with a pure 300k PS top layer (sample B). Having established that thermal reversibility is clearly apparent in the NR data and fits, we now examine the behaviour of the extracted fit parameters across our dataset (batch 1 and batch 2).

Fig. 3 In situ thermal cycling and neutron reflectivity (NR) measurements of an equilibrated sample (sample D; initially with a 34 wt% bis-PCBM/300k PS blend top layer). (a) A typical cooling/heating protocol to test thermal reversibility following equilibration, showing the set-point temperatures (on the y-axis) and the sample surface temperatures (as annotations). Full NR measurements took 10 minutes each, and followed a 6 minute wait after each change in set-point temperature. The red symbols mark the time at the end of each NR measurement. (b) and (c) show NR measurements and fits during the cooling and heating cycles respectively. The thermal cycling for this sample was preceded by isothermal annealing with a sample surface temperature of 139 °C for approximately 250 minutes. The NR curves have been shifted vertically with respect to one another for clarity.

Fig. 4 Reversibility of neutron reflectivity (NR) curves and scattering length density (SLD) profiles. (a) Schematic representation of the measurements of samples B and E shown in this figure. (b) NR curves and fits for a bilayer that was fabricated with a pure 300k PS top layer initially (Sample B). This sample underwent heating to 173 °C, then cooling to 131 °C, and then a second heating to 173 °C. The NR curves and fits in (b) show the two different measurements at 173 °C with a fit at 131 °C as a reference in grey. (c) and (d) show NR curves and fits for a bilayer that was fabricated with a blend top layer initially (Sample E −34 wt% bis-PCBM/300k PS). After isothermal heating at a sample surface temperature of 148 °C, this sample underwent heating to 173 °C, then stepwise cooling to 114 °C, and then a second heating to 181 °C. The NR curves and fits in (c) show the two different measurements at 173 °C with a fit at 131 °C as a reference in grey, and the NR curves and fits in (d) show the two different measurements at 131 °C with a fit at 173 °C as a reference in grey. The insets to (b)–(d) show the SLD profiles (SLD versus distance from the sample surface) corresponding to the fits.

Fig. 5 summarises our findings with regard to convergence from different top layer starting compositions. Fig. 5a shows the extracted fit parameters for seven samples from batch 1, with samples measured at 80 °C before and after thermal cycling (five 300k PS samples, and two 5k PS samples). It is clear that the SLD of the top layer layers, ρ_top, converges on a value of around 1.8 × 10⁻⁶ Å⁻² for the three samples that initially had pure 300k PS top layers and the two samples that initially had 300k PS/bis-PCBM blend top layers, while the bottom layer SLD in these five samples, ρ_bottom, remains at the pure bis-PCBM SLD of around 3.8 × 10⁻⁶ A⁻². Similar convergence in SLD on annealing is seen for the two 5k PS samples, although here, greater miscibility at lower PS MW is evidenced by the slightly higher values of ρ_bottom and slightly lower values of ρ_top. Such a dependence on MW is expected from the equilibrium thermodynamics of polymer/small molecule mixtures³² and predicted/observed in PS/bis-PCBM.²⁰ Quantitatively, the current study offers a fuller characterisation for 5k PS/bis-PCBM bilayers than our previous measurements, as the samples here have been equilibrated by going to elevated temperature before being cooled, and the samples also consist of more complete bilayers, rather than the slightly truncated bilayers shown in Hynes et al.²⁰ For each MW, Fig. S9b (ESI†) also shows similar values for the roughnesses of the buried interface, σ_I, and the sample surface, σ_S, in the two categories of samples (initially with a blend top layer, and initially with a pure PS top layer), after annealing. Higher σ_I values are observed here in the 5k PS samples, compared to the 300k samples, as expected from equilibrium theory.^27,33

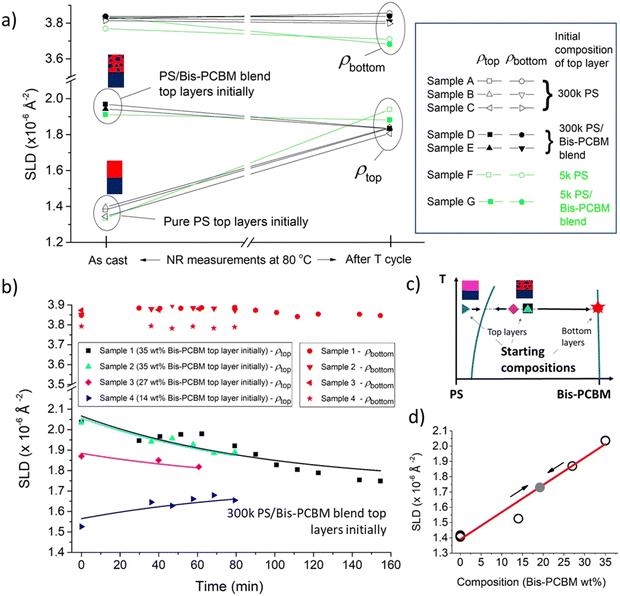Fig. 5 Summary of convergent behaviour. (a) Scattering length densities (SLDs) of top and bottom layers for seven different 300k and 5k PS/bis-PCBM samples, measured at 80 °C before (‘As cast’) and after thermal cycling. These samples were all made from a single batch of silicon blocks (batch 1) and measured during the same experiment (D17;2021). (b) Scattering length density (SLD) as a function of time during in situ annealing, for four samples, all starting with top layers that were initially 300k PS/bis-PCBM blends with various compositions. The data points shown at time zero in (b) represent measurements taken at 99 °C (at which the composition profiles of the samples was essentially the same as at room temperature.²¹ Subsequent measurements were taken at either 147 or 157 °C (see ESI,† for details). The lines in (b) are exponential fits with a single time constant (see ESI,† for further details). The measurements in (b) were all made on a second batch of silicon (batch 2) and measured during a different experiment (D17;2019) to the batch 1 samples shown in Fig. 2–4, 5a and 6–8. The layer thickness fit parameters that accompany (b) are shown in the ESI† (Fig. S10). (c) Schematic phase-diagram showing the starting compositions in (b) in relation to the binodal (blue curves). (d) Initial top layer SLDs versus the initial composition of the top layers for the four samples shown in (b) and three pure PS top layer samples from batch 2 (open circles). The red line in (d) is a linear fit to the SLD v composition data, and the grey point on this line represents the infinite time asymptote of the 4 fits in (b).

While the focus of the current manuscript is not on the kinetics of equilibration, to illustrate the generality of the findings in Fig. 5a we show a single plot of the temporal behaviour of a second batch (batch 2) of in situ annealed bilayers in Fig. 5b. These samples have not been annealed using a protocol similar to that set out in Fig. 3a, but have just been heated from 99 °C (a temperature at which there is no discernible mixing of constituents between layers)²¹ straight to temperatures of approximately 150–160 °C. Fig. 5b shows that the overall picture of composition convergence from different starting points is demonstrated in this batch of samples also; here four samples with different blend ratios of PS and bis-PCBM in the top layer initially (three samples in the two-phase region, and one sample in the one-phase region) all evolve towards a common top layer SLD of around 1.7–1.8 × 10⁻⁶ A⁻², in close proximity to the five equilibrated 300k PS samples in batch 1 (Fig. 5a).

We now investigate the thermal behaviour of equilibrated bilayers, focussing firstly on the five different 300k PS samples after they have been equilibrated at high temperature. Fig. S11 (ESI†) shows the behaviour of the layer SLDs. While there appears to be little systematic change in the SLD of the top layer as a function of temperature between 114 and 173 °C (and also no systematic change in the buried interfacial roughness or the sample surface roughness – see Fig. S11 inset, ESI†), all five samples show a slight, but systematic, reduction in the bottom layer SLD with temperature. This change is similar to that observed for a single bis-PCBM layer (Fig. S12a, ESI†), providing evidence that the bottom layer remains close in composition to pure bis-PCBM. The fact that the SLD of the PS-rich top layer changes much less with temperature than the bis-PCBM bottom layer, is, however, in qualitative disagreement with the expectations of FH theory for an enthalpic interaction parameter, χ.³² Fig. S11 (ESI†) also shows that the changes in SLD, interface roughness and sample surface roughness are all reversible in all samples.

The change in layer SLDs cannot be rationalised in terms of simple thermal expansion of the sample, as the higher thermal expansivity of PS (by a factor of approximately 2–4, in comparison to bis-PCBM; see Fig. 6 and ESI†) would predict that the top layer should show an even larger decrease in SLD than the bottom layer. This is further evidenced by inspection of the layer thickness behaviour in Fig. 6a and b, which sets out the fractional change in the thickness of each layer as a function of temperature (d_top and d_bottom are the thicknesses of the top and bottom layers respectively, and Fig. 6a and b plot the ratio of these thicknesses to the values at 80 °C after annealing). Fig. 6a shows that the change in thickness of the top (PS-rich) layer is actually commensurate with (or slightly larger than) the thermal expansivity of PS melts, and therefore thermal expansion is likely to be a significant contributor to this behaviour. However, the behaviour of the bottom (pure bis-PCBM) layer thickness does not even correspond qualitatively to the thermal expansion of bis-PCBM. Instead, the bottom layer in all five samples reduces in thickness with increasing temperature, once the temperature is around 130–140 °C (approaching the reported T_g of bis-PCBM³¹). The few points below 130 °C in Fig. 6b are actually commensurate with the bis-PCBM thermal expansivity, likely due to the slowing of dynamics or even vitrification in the system and consequent inhibition of mass-transfer between the layers, below this temperature. Bottom layer thickness reduction is most clearly seen in samples A–C, which initially had pure PS top layers, and where the fractional bottom layer thickness changes are larger, but is also evident in samples D and E, which initially had PS/bis-PCBM blend top layers. The reproducibility and reversibility of changes in both layer thicknesses with temperature is also apparent in Fig. 6a and b. The total sample thickness increases with temperature, as would be anticipated from first-order considerations based on the thermal expansivity of the pure components alone. It is clear, however, that to account for our findings, as the system expands with increasing temperature there must be significant transfer of bis-PCBM molecules into the top (PS-rich) layer. Such a change in the composition of the co-existing phases (causing the SLD of the top layer to remain approximately constant with temperature, as its thickness increases) is indicative of UCST-like behaviour over this temperature range. However, to fully understand the thermal behaviour of the system requires an approach beyond FH to account for volume changes in the system. Recent work by Peng et al.³⁴ extending the temperature dependence of the FH χ parameter, based on theoretical considerations of compressibility, has enabled the fitting of binodal curves for polymer/small-molecule OPV mixtures that exhibit both UCST and lower-critical-solution-temperature (LCST) behaviour. However, to achieve predictive capabilities with regard to all of the behaviour that we observe (both layer composition and thickness as a function of temperature) requires a more fundamental approach, such as the locally-correlated-lattice (lcl) theory developed and implemented by Lipson and co-workers.^35,36 Such an approach involves careful measurements of the thermal behaviour of the individual components, fitting of a single datum relating to a mixture and detailed theoretical analysis, and is beyond the scope of the present manuscript. It is left for future workers to try to understand and predict the exact nature of the equilibrium states in these kinds of systems. Our focus here is on establishing whether key criteria for equilibrium behaviour (convergence from different starting points in phase space, and reversibility) are satisfied or not.

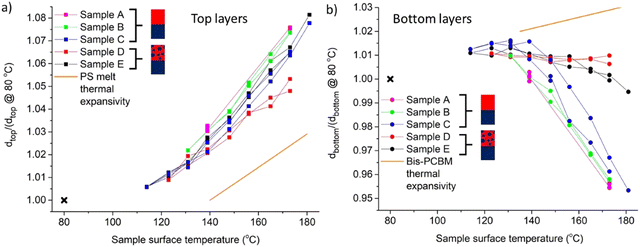Fig. 6 Reversible layer thickness changes during in situ thermal cycling of 5 different 300k PS/bis-PCBM bilayers following equilibration (samples A, B and C had pure PS top layers initially, and samples D and E had PS/bis-PCBM blend top layers initially). The plots show layer thickness as the temperature is cycled from high-to-low-to-high, and finally after cooling to 80 °C (marked by x). (a) Ratio of the thickness of the top (PS/bis-PCBM blend) layer during annealing, to the thickness of the top layer after cooling to 80 °C, versus sample temperature. The orange line in (a) represents the thermal expansivity of PS melt films from the literature (7.2 ± 2 × 10⁻⁴ K⁻¹).³⁷ (b) Ratio of the thickness of the bottom (pure bis-PCBM) layer to the thickness of the bottom layer after cooling to 80 °C, versus sample temperature. The orange line in (b) represents the thermal expansivity of bis-PCBM films (approximately 2 × 10⁻⁴ K⁻¹ see ESI,† for details).

MW-dependence

We now present the thermal behaviour of equilibrated systems containing 5k PS. Fig. 7 shows the parameters extracted from measurements on two different 5k PS samples after the samples have been equilibrated at high temperature. Fig. 7a, c and e show layer thicknesses, layer SLDs and sample roughnesses for a bilayer that initially had a pure 5k PS top layer, and Fig. 7b, d and f show the same parameters for a bilayer that initially had a 5k PS/bis-PCBM blend top layer. The most visible aspects of these measurements are (i) that again we see reversible behaviour with temperature in both samples (with a caveat that the data points at the highest temperature immediately before final cooling to 80 °C do not reproduce the fit parameters extracted at the same temperatures on first heating, as well as occurs at lower temperatures – see ESI,† Section 5 for further details), and (ii) that the behaviour of these two samples is remarkably similar in all aspects. Both samples exhibit the same kind of layer thickness behaviour found for the 300k PS samples, in which the top layer thickness increases and the bottom layer thickness reduces with temperature (and the total sample thickness increases with temperature; again indicative of the need to go beyond FH theory). The sample surface roughnesses of these two samples is very similar to the 300k PS samples across the temperature range, while the buried interface roughness is larger in the 5k PS samples compared to the 300k PS samples, as would be expected at equilibrium.^27,33,38 There is also some indication of a temperature-dependence to the buried interfacial roughness in both 5k PS samples, with evidence of broader interfaces with increasing temperature, above around 140 °C (see Fig. 7e and f). The interfacial roughness measured by NR is in general a combination of the ‘intrinsic’ interfacial width due to molecular mixing of the components, and lateral roughness.^28,39 In an equilibrated liquid–liquid system the intrinsic width will depend on the chemical compatibility of the interacting molecules (the FH χ parameter, in polymeric systems) and the MW of any polymeric constituents,^27,33,38,40 while lateral roughness occurs due to thermally-activated capillary-waves⁴¹ (whose mean-square amplitude scales in inverse proportion to the interfacial tension between the two phases^28,42). As far as we are aware, the magnitude of these two contributions has not been quantitatively predicted in polymer/small-molecule systems. However, in polymer/polymer systems, increases in both of these contributions to the total roughness go hand-in-hand with increases in miscibility^27,28 (for example as a function of temperature or MW). Qualitatively, we would therefore expect that an increase in interfacial roughness would be accompanied by bulk phase that are closer together in composition. This is exactly what we observe here, for both 5k PS samples. Fig. 7c and d show that as the temperature increases, the SLDs of both layers become systematically closer together; the top layer SLD increasing and the bottom layer SLD reducing. We note that a similar narrowing miscibility gap, indicative of UCST-like behaviour is observed in a related PS/fullerene system over this temperature range.³⁴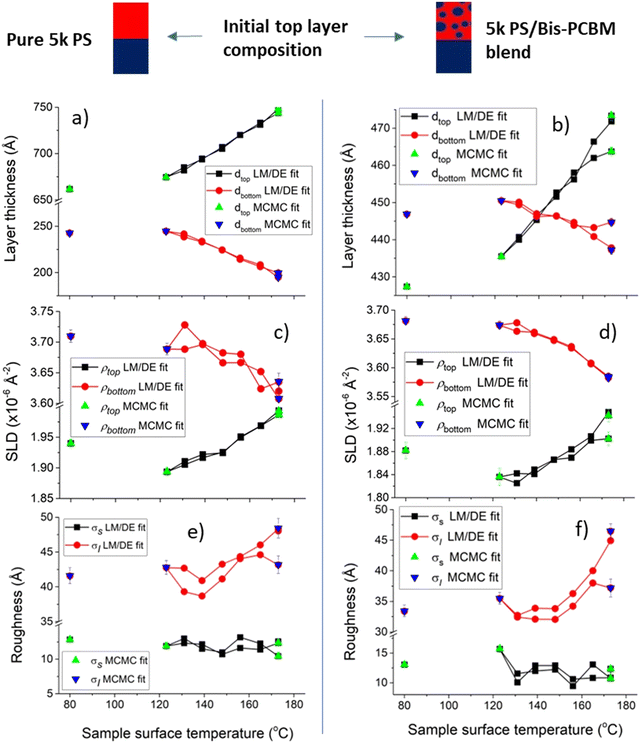

Fig. 7 Reversibility during in situ temperature cycling of two different equilibrated 5k PS/bis-PCBM bilayers. The plots show the six bilayer fit parameters obtained from each neutron reflectivity (NR) measurement, as the temperature is cycled from high-to-low-to-high, and finally after cooling to 80 °C. (a), (c) and (e) set out the layer thicknesses, layer scattering length densities (SLDs) and surface/interfacial roughness of sample F which had a pure PS top layer initially. (b), (d) and (f) set out the layer thicknesses, layer SLDs and surface/interfacial roughness of sample G that had a PS/bis-PCBM blend top layer initially. In addition to the standard Levenberg–Marquardt/differential evolution (LM/DE) fitting procedure, the plots show some data points which correspond to the MCMC²⁶ fitting procedure.

To probe the behaviour of the system further we also fabricated two bilayer samples using 2k PS (samples H and I, both with pure PS top layers). These were annealed using a similar protocol to the 5k and 300k PS samples, except that the investigation was shifted to slightly lower temperatures (due to evidence that the onset of mixing in these PS/fullerene systems is influenced by the MW-dependent molecular-mobility of the PS^21,43). NR data, bilayer fits, SLD profiles and fit parameters for these samples are shown in Fig. S13–S16 (ESI†). As for the 5k and 300k PS samples, changes in the fit parameters with temperature for 2k PS are reversible (see Fig. S13 and S14, ESI†) and show repeatable behaviour as a function of temperature (Fig. S14 and S16, ESI†), indicative of equilibration following heating at sufficiently high temperature. Unfortunately, however, the extent of mass transfer that occurred from the bis-PCBM layer into the PS layer on annealing, resulted in the bottom layer becoming thinner than in the 5k and 300k PS samples. This led to some fitted SLD profiles having interfacial roughnesses that were around half the thickness of the bottom layers (see Fig. S14(a), (c) and S16(a), (c), ESI†), potentially calling into question the use of a bilayer model (in which the interface roughness should be significantly smaller than the thickness of the layers on either side). This necessitates a caveat that some of the fit parameters extracted from the 2k PS bilayer fits as a function of temperature may not be as reliable as for the 5k and 300k PS samples. To assess the robustness of the bilayer fits, we therefore also fitted some NR curves for 2k PS samples using a free-form (spline function) SLD profile (see Fig. S15, ESI†). These showed very similar SLD profiles to the bilayer fits, allowing us to conclude that the bilayer fits do a reasonable job in approximating the binodal compositions for the 2k PS samples. However, we need to be careful with regard to the thermal behaviour and are hesitant to rely on these parameters to accurately quantify the temperature dependence of the binodal compositions. This is because the rather subtle changes observed in the binodal compositions with temperature for the higher MWs are potentially perturbed in the 2k PS samples due to the absence of a truly uniform bottom layer of sufficient thickness in comparison to the buried interface roughness. For this reason the 2k PS data (plotted in grey in Fig. 8) should only be used as an indication of the binodal compositions, in comparison to the 5k and 300k PS samples, with caution applied to the behaviour as a function of temperature. It is though clear that the bilayer fits to the annealed 2k PS samples give layer compositions that are significantly closer to one another than the 5k and 300k PS samples.

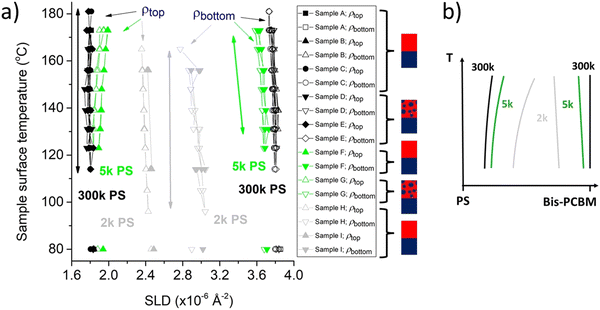Fig. 8 Summary of equilibrated scattering length densities (SLDs), ρ_top and ρ_bottom, as a function of MW and temperature during thermal cycling. (a) SLD parameters obtained during in situ thermal cycling, following equilibration (measured as the temperature is cycled from high-to-low-to-high, and finally after cooling to 80 °C). The plot combines the fit parameters for 5k and 300k PS/bis-PCBM bilayers shown in Fig. 7c, d and Fig. S11 (ESI†) with those for two 2k PS/bis-PCBM bilayers (samples H and I; both initially having pure PS top layers). (b) Schematic diagram illustrating the typical phase behaviour of three different MW polymer/small-molecule systems that exhibit UCST-like behaviour within the framework of FH theory (for an incompressible system with a purely enthalpic FH interaction parameter, χ). NB; We emphasise that the schematic diagram in (b) is included here principally to illustrate the expected dependence as a function of MW.²⁰ As discussed in the text, the temperature dependence of the 2k PS data in (a) needs to be treated with caution, while the 300k PS data in (a) is in qualitative disagreement with the expectations of FH theory for an enthalpic χ parameter (shown in (b)); in the 300k data (shown on its own in Fig. S11 (ESI†)) the SLD of the PS-rich layer changes much less with temperature than the bis-PCBM layer.

To summarise, the overall progression of co-existing compositions with MW, shown in Fig. 8, is qualitatively consistent with the predictions of FH theory made for bis-PCBM/PS as a function of PS MW, on the basis of high MW measurements (on samples annealed ex situ and quenched to room temperature),²⁰ but understanding the temperature dependence (of both the compositions and phase volumes) requires significant further analysis, that is beyond the scope of the present study. The key point, however, with regard to our study is that these thermal annealing measurements robustly demonstrate behaviour that is reproducible, reversible (with temperature) and shows convergence to equilibrium states from different starting points in phase-space.

Conclusions

We have performed an in-depth investigation into PS/bis-PCBM bilayers, as a function of MW, temperature and initial layer composition. We find that the composition profiles comply with the expectations of equilibrium thermodynamics, in two key aspects. Firstly, the state of the system at any given temperature, following thermal annealing at sufficiently high temperature, is independent of the path taken to reach that state. Secondly, the temperature-dependent behaviour of the system is reversible on heating/cooling. That these two aspects of equilibrium behaviour are exhibited across a range of MWs and temperatures in a thin-film geometry, is remarkable. Given the potential for preferential segregation of constituent molecules to the substrate, surface or buried interface, and the potential for dewetting of thin-films, it is notable that these systems form simple layered structures with uniform layer compositions, enabling detailed characterisation of co-existing compositions, and sub-nanometre characterisation of interfacial roughness. The use of low-polydispersity PS enables us to clearly separate out MW-dependent and temperature-dependent behaviour and investigate rather subtle changes in composition profiles with temperature. Behaviour such as interfacial segregation of low-MW fractions^38,44 or fractionation by chain-length within bulk phases^45,46 will potentially be exhibited in addition to that found in the present study in the polydisperse systems typical of conjugated polymers. Given such potential complexity, we believe there are significant benefits in establishing a solid framework based on equilibrium thermodynamics, for understanding behaviour in model small-molecule/polymer OPV systems. Recent work has applied understanding of component molecular mobility and polymer/small-molecule thermodynamics to advance the ‘rational design’ of a range of OPV systems.^13,14 With this in mind, the current study (on approximately spherical small-molecules and low polydispersity amorphous polymers) is relevant as a benchmark in understanding behaviour within OPV blends. Of particular significance with-respect-to non-fullerene acceptor (NFA) systems is the potential requirement for greater understanding of volume changes on mixing, or as a result of temperature cycling during operation. We anticipate that the large aspect-ratios typical of these small-molecule acceptors and the varied molecular structures (with planar or twisted architectures)^3,47–50 may lead to a broad range of different mixing behaviours (as can occur for small-molecule mixtures containing different isomers⁵¹) in comparison to the simpler fullerenes studied herein. Our discovery of properly equilibrated bis-PCBM/PS phases, with a free-energy minimum approached from different starting states and reversible transitions between equilibrium states at different temperatures, is an important finding that enables the application of equilibrium theory to thin-film blends, underpinning the basis for theoretical understanding and robust predictions in OPV mixtures.

Data availability

Data can be downloaded using the DOIs for the two experiments: https://doi.org/http://doi.ill.fr/10.5291/ILL-DATA.9-11-1903 and https://doi.org/http://doi.ill.fr/10.5291/ILL-DATA.9-11-1983 after an embargo period of four years. Requests for data earlier than this should be emailed to the corresponding author.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the ILL for the award of beam time (experiment numbers 9-11-1903 in 2019 and 9-11-1983 in 2021), and the staff of D17 for help during the experiments. We thank the IT group at ILL for establishing remote access to D17, which was used during experiment 9-11-1983. AH thanks Josh Barlow and Ben Harrison at Swansea University for use of their chemistry facilities to host the sample preparation activity, which was necessitated following a fire in Swansea which closed the usual chemistry laboratory for more than a year. AH thanks Andrew Nelson (Ansto, Australia) for help with setting up and troubleshooting refnx, and Andrew Parnell (Sheffield University) and Suzanne Thomas (Swansea University) for performing atomic force microscopy measurements. EH acknowledges Swansea University for funding her studentship. AH acknowledges João Cabral (Imperial College, London) for several useful discussions, and comments on the manuscript.

References

1. L. Zuo, et al., Dilution effect for highly efficient multiple-component organic solar cells, Nat. Nanotechnol., 2021, 17, 53–60,  DOI:10.1038/s41565-021-01011-1.
2. F. W. Zhao, et al., Emerging Approaches in Enhancing the Efficiency and Stability in Non-Fullerene Organic Solar Cells, Adv. Energy Mater., 2020, 10, 2002746,  DOI:10.1002/aenm.202002746.
3. M. Kim, S. U. Ryu, S. A. Park, Y. J. Pu and T. Park, Designs and understanding of small molecule-based non-fullerene acceptors for realizing commercially viable organic photovoltaics, Chem. Sci., 2021, 12, 14004–14023,  10.1039/d1sc03908c.
4. P. Cheng, G. Li, X. W. Zhan and Y. Yang, Next-generation organic photovoltaics based on non-fullerene acceptors, Nat. Photonics, 2018, 12, 131–142,  DOI:10.1038/s41566-018-0104-9.
5. R. Xue, J. Zhang, Y. Li and Y. Li, Organic Solar Cell Materials toward Commercialization, Small, 2018, 14, e1801793,  DOI:10.1002/smll.201801793.
6. W. Li, D. Liu and T. Wang, Stability Of Non-Fullerene Electron Acceptors and Their Photovoltaic Devices, Adv. Funct. Mater., 2021, 31, 2104552,  DOI:10.1002/adfm.202104552.
7. S. Yoon, et al., Progress in morphology control from fullerene to nonfullerene acceptors for scalable high-performance organic photovoltaics, J. Mater. Chem. A, 2021, 9, 24729–24758,  10.1039/d1ta06861j.
8. A. A. Y. Guilbert, et al., Effect of Multiple Adduct Fullerenes on Microstructure and Phase Behavior of P3HT:Fullerene Blend Films for Organic Solar Cells, ACS Nano, 2012, 6, 3868–3875.
9. C. Müller, et al., Binary Organic Photovoltaic Blends: A Simple Rationale for Optimum Compositions, Adv. Mater., 2008, 20, 3510–3515,  DOI:10.1002/adma.200800963.
10. J. W. Kiel, A. P. Eberle and M. E. Mackay, Nanoparticle agglomeration in polymer-based solar cells, Phys. Rev. Lett., 2010, 105, 168701,  DOI:10.1103/PhysRevLett.105.168701.
11. K. Vandewal, S. Himmelberger and A. Salleo, Structural Factors That Affect the Performance of Organic Bulk Heterojunction Solar Cells, Macromolecules, 2013, 46, 6379–6387,  DOI:10.1021/ma400924b.
12. W. Yin and M. Dadmun, A New Model for the Morphology of P3HT/PCBM Organic Photovoltaics from Small-Angle Neutron Scattering: Rivers and Streams, ACS Nano, 2011, 5, 4756–4768.
13. L. Ye, et al., Quantitative relations between interaction parameter, miscibility and function in organic solar cells, Nat. Mater., 2018, 17, 253–260,  DOI:10.1038/s41563-017-0005-1.
14. M. Ghasemi, et al., A molecular interaction-diffusion framework for predicting organic solar cell stability, Nat. Mater., 2021, 20, 525–532,  DOI:10.1038/s41563-020-00872-6.
15. M. Gao, Z. Liang, Y. Geng and L. Ye, Significance of thermodynamic interaction parameters in guiding the optimization of polymer:nonfullerene solar cells, Chem. Commun., 2020, 56, 12463–12478,  10.1039/d0cc04869k.
16. L. Ye, et al., Quenching to the Percolation Threshold in Organic Solar Cells, Joule, 2019, 3, 443–458,  DOI:10.1016/j.joule.2018.11.006.
17. Y. Liu, et al., Aggregation and morphology control enables multiple cases of high-efficiency polymer solar cells, Nat. Commun., 2014, 5, 5293,  DOI:10.1038/ncomms6293.
18. N. Li, et al., Abnormal strong burn-in degradation of highly efficient polymer solar cells caused by spinodal donor-acceptor demixing, Nat. Commun., 2017, 8, 14541,  DOI:10.1038/ncomms14541.
19. Y. Qin, et al., The performance-stability conundrum of BTP-based organic solar cells, Joule, 2021, 5, 2129–2147,  DOI:10.1016/j.joule.2021.06.006.
20. E. L. Hynes, et al., Interfacial width and phase equilibrium in polymer-fullerene thin-films, Commun. Phys., 2019, 2, 112,  DOI:10.1038/s42005-019-0211-z.
21. E. L. Hynes, P. Gutfreund, A. J. Parnell and A. M. Higgins, Liquid-liquid equilibrium in polymer-fullerene mixtures; an in situ neutron reflectivity study, Soft Matter, 2020, 16, 3727–3739,  10.1039/c9sm02337b.
22. D. Môn, et al., Bimodal crystallization at polymer-fullerene interfaces, Phys. Chem. Chem. Phys., 2015, 17, 2216–2227,  10.1039/c4cp04253k.
23. R. K. M. Bouwer, G.-J. A. H. Wetzelaer, P. W. M. Blom and J. C. Hummelen, Influence of the isomeric composition of the acceptor on the performance of organic bulk heterojunction P3HT:bis-PCBM solar cells, J. Mater. Chem., 2012, 22, 15412,  10.1039/c2jm32993j.
24. T. Saerbeck, et al., Recent upgrades of the neutron reflectometer D17 at ILL, J. Appl. Crystallogr., 2018, 51, 249–256.
25. P. Gutfreund, et al., Towards generalized data reduction on a chopper-based time-of-flight neutron reflectometer, J. Appl. Crystallogr., 2018, 51, 606–615.
26. A. R. J. Nelson and S. W. Prescott, refnx: neutron and X-ray reflectometry analysis in Python, J. Appl. Crystallogr., 2019, 52, 193–200,  DOI:10.1107/S1600576718017296.
27. R. A. L. Jones and R. W. Richards, Polymers at Surfaces and Interfaces, Cambridge University Press, 1999.
28. M. Sferrazza, et al., Evidence for capillary waves at immiscible polymer/polymer interfaces, Phys. Rev. Lett., 1997, 78, 3693–3696,  DOI:10.1103/PhysRevLett.78.3693.
29. I. G. Hughes and T. P. Hase, Measurements and their Uncertainties, Oxford University Press, 2010.
30. E. M. Speller, et al., Impact of Aggregation on the Photochemistry of Fullerene Films: Correlating Stability to Triplet Exciton Kinetics, ACS Appl. Mater. Interfaces, 2017, 9, 22739–22747,  DOI:10.1021/acsami.7b03298.
31. D. Leman, et al., In Situ Characterization of Polymer–Fullerene Bilayer Stability, Macromolecules, 2015, 48, 383–392,  DOI:10.1021/ma5021227.
32. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003.
33. H. Tang and K. F. Freed, Interfacial Studies of Incompressible Binary Blends, J. Chem. Phys., 1991, 94, 6307–6322,  DOI:10.1063/1.460419.
34. Z. Peng, N. Balar, M. Ghasemi and H. Ade, Upper and Apparent Lower Critical Solution Temperature Branches in the Phase Diagram of Polymer:Small Molecule Semiconducting Systems, J. Phys. Chem. Lett., 2021, 12, 10845–10853,  DOI:10.1021/acs.jpclett.1c02848.
35. R. P. White, et al., Thermodynamics of Model P alpha MSAN/dPMMA Blend: A Combined Study by SANS, Ellipsometry, and Locally Correlated Lattice (LCL) Theory, Macromolecules, 2020, 53, 7084–7095,  DOI:10.1021/acs.macromol.0c00706.
36. R. P. White, J. E. G. Lipson and J. S. Higgins, New Correlations in Polymer Blend Miscibility, Macromolecules, 2012, 45, 1076–1084,  DOI:10.1021/ma202393f.
37. J. L. Keddie, R. A. L. Jones and R. A. Cory, Size-Dependent Depression of the Glass-Transition Temperature in Polymer-Films, Europhys. Lett., 1994, 27, 59–64,  DOI:10.1209/0295-5075/27/1/011.
38. D. Broseta, G. H. Fredrickson, E. Helfand and L. Leibler, Molecular-Weight and Polydispersity Effects at Polymer Polymer Interfaces, Macromolecules, 1990, 23, 132–139,  DOI:10.1021/ma00203a023.
39. D. James, et al., Measurement of molecular mixing at a conjugated polymer interface by specular and off-specular neutron scattering, Soft Matter, 2015, 11, 9393–9403,  10.1039/c5sm02008e.
40. E. Helfand and Y. Tagami, Theory of Interface Between Immiscible Polymers. 2, J. Chem. Phys., 1972, 56, 3592–3601,  DOI:10.1063/1.1677735.
41. F. P. Buff, R. A. Lovett and F. H. Stillinger, Interfacial density profile for fluids in the critical region, Phys. Rev. Lett., 1965, 15, 621–623.
42. J. S. Rowlinson and B. Widom, Molecular Theory of Capiliarity, Oxford University Press, 1989.
43. P. G. Santangelo and C. M. Roland, Molecular weight dependence of fragility in polystyrene, Macromolecules, 1998, 31, 4581–4585,  DOI:10.1021/ma971823k.
44. P. Mahmoudi, W. S. R. Forrest, T. M. Beardsley and M. W. Matsen, Testing the Universality of Entropic Segregation at Polymer Surfaces, Macromolecules, 2018, 51, 1242–1247,  DOI:10.1021/acs.macromol.7b02474.
45. P. Sollich and M. E. Cates, Projected Free Energies for Polydisperse Phase equilibria, Phys. Rev. Lett., 1998, 80, 1365–1368.
46. P. B. Warren, Combinatorial Entropy and the Statistical Mechanics of Polydispersity, Phys. Rev. Lett., 1998, 80, 1369–1372.
47. J. Hou, O. Inganas, R. H. Friend and F. Gao, Organic solar cells based on non-fullerene acceptors, Nat. Mater., 2018, 17, 119–128,  DOI:10.1038/nmat5063.
48. S. Holliday, et al., A rhodanine flanked nonfullerene acceptor for solution-processed organic photovoltaics, J. Am. Chem. Soc., 2015, 137, 898–904,  DOI:10.1021/ja5110602.
49. C. B. Nielsen, S. Holliday, H. Y. Chen, S. J. Cryer and I. McCulloch, Non-fullerene electron acceptors for use in organic solar cells, Acc. Chem. Res., 2015, 48, 2803–2812,  DOI:10.1021/acs.accounts.5b00199.
50. G. Zhang, et al., Renewed Prospects for Organic Photovoltaics, Chem. Rev., 2022, 122, 14180–14274,  DOI:10.1021/acs.chemrev.1c00955.
51. T. Takigawa, M. Ohba, H. Ogawa and S. Murakami, Thermodynamic properties of binary mixtures of hexane isomer and cyclohexane at 298.15 K, Fluid Phase Equilib., 2003, 204, 119–130.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc04916c

‡ Except for sample 3 in batch 2, which had a reduced sample area. For this sample the beam footprint on the sample was reduced by a factor of two, and the acquisition time was increased to 4 and 16 minutes for incident angles of 0.8° and 3° respectively.

---