Metallic to half-metallic transition driven by pressure and anion composition in niobium oxyfluoride

Abstract

Half-metallic materials play a key role in the development of spintronics, but few suitable materials are known. Continuously varying the ratio of two anions in a single material offers one route to enhance half-metallic behaviour. Here we report the effect of varying the oxide-fluoride ratio in ReO₃-type niobium oxyfluoride NbO_2−xF_1+x using ab initio calculations. Increasing the fluorine content from NbO₂F to NbF₃ leads to a transition from semiconducting, through metallic, to half-metallic behaviour as x increases. The effect of pressure on this behaviour is also investigated, finding a transition from cubic to rhombohedral symmetry for all compositions below a maximum transition pressure of 5 GPa for x = 0.35. Additionally, we reveal that compositions close to NbF₃ are expected to retain rhombohedral symmetry under ambient pressure. The structural phase transition and electronic behaviour are independent for most compositions except those close to NbO_1.65F_1.35. Here, we discover that the application of moderate pressure can drive the material from metallic to half-metallic, offering a new possibility for controlling spin currents.

---

I. Introduction

The next generation of computational devices will require novel materials to meet the technological demands of data processing and storage. Spintronics is concerned with utilising the electron spin degree of freedom, in addition to electron charge, for the development of smaller components and increased data-processing speed whilst also decreasing overall power consumption.¹ The phenomenon of half-metallicity arises in some magnetic materials where the material is conducting for one electron spin direction, either up or down, whilst semiconducting or insulating in the other. This concept was first introduced in 1983 and the spin control properties of these materials play a crucial role in the field of spintronics.² In spite of this long history, most existing half-metals do not meet the needs of functional spintronics devices, therefore better half-metallic candidates need to be developed.

Atomic doping is one strategy known to induce half-metallicity,^3–5 improve thermal stability,⁶ increase conductivity⁷ and increase magnetoresistance.⁸ Solid solutions — where dopant composition can be continuously varied between two parent compounds – provide even greater flexibility in tuning physical properties. One flexible approach towards solid solutions are mixed-anion materials, containing multiple anions in a single phase. This approach offers a route towards tuning composition while maintaining the cationic interactions important for many properties, however, the number of such materials is currently limited.⁹ Niobium oxyfluorides are one particular class of mixed-anionic materials of interest for functional applications: the variable oxidation state of niobium; similar ionic radii of oxygen and fluorine; and higher covalency of Nb–O bonds cf. Nb–F bonds leads to direct control of physical properties through variable oxygen:fluorine ratios. These materials are built around corner-sharing Nb(O,F)₆ octahedra, with a number of shear-related phases also known.^10–12 The simplest structure observed in the family is that of cubic ReO₃ (Fig. 1a) and this structure has been reported across the entire NbO_2−xF_1+x solid solution, ranging from x = 0 (Nb^VO₂F) to x = 2 (Nb^IIIF₃).^13–15 Such ReO₃-type (oxy)fluorides are of wide interest, with a range of properties including lithium incorporation for battery applications^16,17 or negative thermal expansion as in ScF₃.¹⁸ The latter property is linked to a cubic to rhombohedral transition apparent in many ReO₃-type trifluorides,^19–22 caused by octahedral rotation around the [111] crystallographic direction (a⁻a⁻a⁻ in Glazer's tilt notation).²³ Such a transition has also been observed in NbO₂F under a relatively low hydrostatic pressure of 0.47 GPa (Fig. 1b).²⁴

Fig. 1 Structures reported for NbO_2−xF_1+x compositions showing (a) cubic (Pm3̄m) and (b) rhombohedral (R3̄c) polymorphs. Structures are aligned to show the relationship between unit cells (shown as black lines). Nb shown as red spheres/polyhedra, O/F as blue spheres (figures created using VESTA v3.5.7).²⁵

Electronically, NbF₃ has been predicted to be half-metallic,²⁶ with a large minority spin band gap (8.9 eV) that would minimise spin flipping within a real spintronic device.²⁷ In contrast, NbO₂F is known to be a wide band gap semiconductor with a band gap of 3.1 eV.²⁸ However, there is no information on the electronic structure of the intermediate solid solutions. It is therefore unclear how half-metallicity arises in NbF₃ and also how the band structure is modified to reach semiconducting NbO₂F. Here, we report electronic structure calculations across the NbO_2−xF_1+x solid solution to understand the relationship between electronic structure, half-metallicity and anionic composition. In addition, we describe the effect of anionic composition on the cubic to rhombohedral phase transition under applied pressure.

II. Methods

All first-principles calculations were performed using a DFT+U approach implemented in CASTEP (v18.1) by the rotationally invariant approach proposed by Dudarev et al.^29,30 The generalised gradient approximation (GGA) Perdew–Burke–Ernzehof (PBE) exchange–correlation functional was used for all calculations. A Hubbard U parameter of 3.5 eV was chosen to match, as closely as possible, the previously predicted NbF₃ minority spin band gap (Fig. S1, ESI†). The U correction was applied to the niobium d orbitals. The electronic ground state was found by the density-mixing algorithm with a mixing amplitude of 0.6 and 1.5 for the charge and spin density respectively. The default CASTEP (v18.1) ultrasoft pseudopotentials were used for oxygen and fluorine whilst the Materials Studio pseudopotential was used for niobium. The electron wave functions were expanded as plane waves up to a cut-off energy of 850 eV. For the sampling over the Brillouin zone, a Monkhorst–Pack³¹k-point grid spacing of 0.03 Å⁻¹ was used. The cut-off energy and k-point grid spacing were chosen so that the final energy converged to ±4 meV (Fig. S2, ESI†). Geometry optimisation and density of states calculations were performed using single primitive cubic (ICSD #25596) and rhombohedral (ICSD #280539) cells.^24,32–34 To examine antiferromagnetic ordering, single point energy calculations were performed for a cubic 2 × 2 × 2 supercell. Mixed oxygen/fluorine calculations were performed by applying the virtual crystal approximation (VCA) so that anion sites are treated as a stoichiometric mixture of oxygen and fluorine potentials. External pressure values were specified as a tensor within the CASTEP geometry optimisations, with atomic positions and cell geometry optimised with the constraint of either cubic or rhombohedral symmetry. Density of states processing and optical band gap calculations were performed using OptaDOS (v1.2).³⁵ Analysis of octahedral distortion was performed by fitting of a minimum bounding ellipsoid using the PIEFACE (v1.1.0) software package.³⁶

III. Results and discussion

A. Magnetic ordering

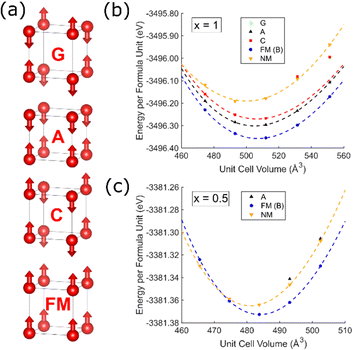
Self-consistent energy calculations at different unit cell volumes for NbOF₂ and NbO_1.5F_1.5 with different magnetic configurations (Fig. 2) were fitted to a third order Birch–Murnaghan equation of state.³⁷ These results indicate that a ferromagnetic (FM) ordering of spins is significantly more stable for both compositions by approximately 0.06 eV and 0.01 eV per formula unit, respectively. This contradicts the previous assertion that FM ordering will be lost on the addition of oxygen to NbF₃,²⁷ although it is unclear whether these previous results relate to surface calculations. Many of the calculations show difficult convergence to the desired magnetic state on account of a shallow potential energy landscape and low magnetic moments; only the FM calculation could be reliably converged at all volumes for both compositions. In particular, antiferromagnetic (AFM) calculations for NbO_1.5F_1.5 (Fig. 2c) often resulted in non-magnetic occupations of Nb t_2g orbitals (Fig. S3, ESI†). Despite this, all AFM or non-magnetic states obtained are significantly higher in energy than the FM state except when extremely compressed.

Fig. 2 (a) Trial magnetic configurations in cubic NbO_2−xF_1+x with corresponding symmetry labels. Nb atoms shown as red spheres, arrows indicate magnetic moment directions. Calculated energy for each configuration, including non-magnetic (NM), at different unit cell volumes is shown for (b) NbOF₂ (x = 1) and (c) NbO_1.5F_1.5 (x = 0.5). Dashed lines show Birch–Murnaghan fits.

B. Electronic band structure

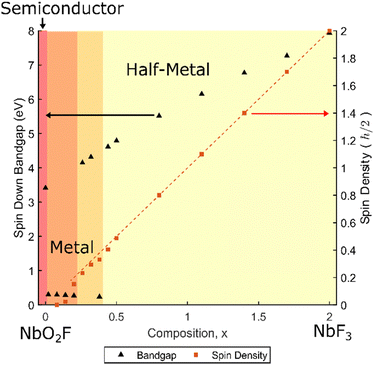
Representative band structures and partial density of states (PDOS) results for NbO_2−xF_1+x are shown in Fig. 3. For each composition x, the cubic ReO₃ lattice parameter was optimised enforcing FM ordering. In each case, the minority spin band gap and overall spin density have been extracted and are summarised in Fig. 4. NbO₂F is correctly predicted to be a semiconductor with a band gap of 3.4 eV, in close agreement to the experimental value of 3.1 eV.²⁸ The PDOS for NbO₂F (Fig. 3a) shows the valence band is dominated by the O 2p states whilst Nb 3d states dominate the conduction band. Comparing this result with the PDOS for NbO_1.8F_1.2 (Fig. 3b), the effect of increasing the fluorine content is to reduce Nb(V) towards Nb(IV), donating electrons into the conduction band. This leads to a transition from semiconductor to metal for small x.

Fig. 3 Selected band structure diagrams and PDOS for (a) semiconducting NbO₂F; (b) metallic NbO_1.8F_1.2 and (c) half-metallic NbO_0.9F_2.1. PDOS (and band structures in (a)) are separated by spin direction with the majority (spin up) spin state on the right and minority (spin down) spin state on the left.

Fig. 4 The variation in minority spin band gap and spin density with composition for cubic NbO_2−xF_1+x. The dashed line indicates the number of unpaired electrons per unit cell indicating the maximum spin density. The semiconducting, metallic and half-metallic phases are indicated by red, orange and yellow shading respectively.

As well as inducing a metallic phase, increasing the fluorine content x increases the number of unpaired electrons per niobium, resulting in an increase in overall spin density (Fig. 4). This leads to an increase in the energy difference between the Nb 3d majority and minority spin bands as the majority band occupation is increasingly stabilised, until a transition to a half-metallic phase occurs between x = 0.20 and x = 0.44. There is some uncertainty in this transition with several borderline half-metal/metal results, indicated by the overlapping shaded area in Fig. 4. This uncertainty reflects the proximity in energy of metallic and half-metallic states in this region, and the corresponding difficulties in achieving a robust self-consistent minimum energy. The splitting between the minority and majority Nb 3d spin states can be seen in Fig. 3c showing the half-metallic state for x = 1.1. Furthermore, Fig. 4 shows an increase in the minority spin band gap as x increases corresponding to this splitting. The dispersive nature of the conduction bands (Fig. 3a) indicate this half-metallic phase should have good conductivity, desirable for spintronics applications.

The dashed line in Fig. 4 corresponds to the number of unpaired electrons per unit cell and therefore the maximum spin density. From this, it is clear the spin density is equal to the number of unpaired Nb electrons for the half-metallic phase. This is due to the presence of only majority spin states close to the Fermi level which leads to a theoretical 100% spin polarisation. However, as the splitting between the spin states decreases and the phase becomes metallic there are also minority spin states at the Fermi level (Fig. 3b). This results in a deviation from the ideal 100% spin polarisation, eventually resulting in a loss of magnetic ordering around x = 0.14.

The electron density distribution for a cross-section of the NbF₃ and NbO₂F unit cells is shown in Fig. 5. As expected, the charge density is more delocalised in NbO₂F due to the more covalent character of the Nb–O bonds. The highly electronegative fluoride, however, results in a more localised charge density for NbF₃.³⁸ The increasing covalency as x decreases corresponds to an increasing anionic contribution to the states near the Fermi level, driving the reduction in minority spin band gap.

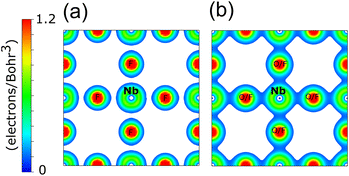Fig. 5 The DFT calculated electron density for (a) cubic NbF₃ and (b) cubic NbO₂F, both for the (100) plane with a minimum isosurface of 0.1 electrons/Bohr³.

C. Crystal structure under external pressure

Given the relatively low-pressure transition to a rhombohedral structure for NbO₂F,³⁹ DFT+U calculations were also performed at elevated external pressures using a rhombohedral unit cell (Fig. 1b) in order to allow additional degrees of freedom for octahedral tilting and distortion during the geometry optimisations. The quality of the rhombohedral geometry optimisations was evaluated by comparison with experimental results for NbO₂F (Fig. S4, ESI†).^24,39 For the cubic structure at ambient pressure there is good agreement between the experimental and computational results. However, at elevated pressure, the lattice parameter is slightly underestimated, and the cell angle overestimated on the order of 2°.

Comparison of the final enthalpy of these optimisations indicate all compositions are predicted to undergo a cubic to rhombohedral phase transition with pressure, while NbO_0.3F_2.7 and NbF₃ are both rhombohedral at ambient pressure. Transition to the rhombohedral structure occurs by a tilting mechanism of the rigid octahedra which can be quantified by an octahedral rotation, , where y is the anion fractional coordinate.⁴⁰ The results of the geometry optimisations in terms of this octahedral rotation are shown for each composition and pressure in Fig. 6a. For higher fluorine compositions, the octahedra also experience a trigonal distortion with equal length Nb–(O/F) bonds no longer oriented at 90° to each other. This distortion can be quantified by fitting a minimum bounding ellipsoid to the octahedra and calculating the standard deviation of its principal radii, σ(R), the results of which are shown in Fig. 6b.³⁶ An attempt to determine the transition pressure using a common tangent approach (Fig. S5 and S6, ESI†) produced large errors at higher x compositions due to the low curvature of the rhombohedral energy against volume, therefore ω was used to identify the transition pressures shown in Fig. 6.

Fig. 6 Structural parameters as a function of pressure and composition for rhombohedral NbO_2−xF_1+x. Results are colour coded by (a) octahedral rotation and (b) octahedral distortion. The red dotted line indicates the cubic to rhombohedral phase transition.

Previous experimental work reported NbF₃ as adopting a cubic ReO₃-type structure,¹⁴ however the present results suggest a rhombohedral phase is more stable. One explanation may be that the synthesised NbF₃ actually contained some quantity of oxygen. The method used for stoichiometric analysis of the final products is unspecified although a titration approach was likely used and could be inaccurate.¹⁴ It has also been suggested that NbF₃ cannot be synthesised without some quantity of oxygen being present.⁴¹

From these results the transition pressure obtains a maximum at approximately x = 0.35, close to one additional electron per three niobium(V) ions. Similar cubic to rhombohedral transitions in other ReO₃-type structures are typically governed by cationic repulsion; the reduction in Nb–Nb distance observed in the rhombohedral structure is unfavourable for highly charged cations.^42–44 As such, the transition pressure is expected to decrease with decreasing cation charge, as is observed for x > 0.35. For x < 0.35 a different energetic contribution must therefore drive the increase in transition pressure with x. We attribute this to the greater covalency of Nb–O bonds cf. Nb–F bonds. The increased covalency drives hybridisation between O 2p and 2s orbitals, which in turn causes the Nb–O–Nb bond angle to shift away from 180° and oxygen lone pairs to occupy the vacant space within the ReO₃ framework. The lone pairs can be seen from electron localisation function (ELF) calculations (Fig. S7, ESI†). This effect is strong enough to reduce the transition pressure for small x, in spite of the significant electrostatic repulsion between adjacent Nb(V) ions.

D. Electronic structures under pressure

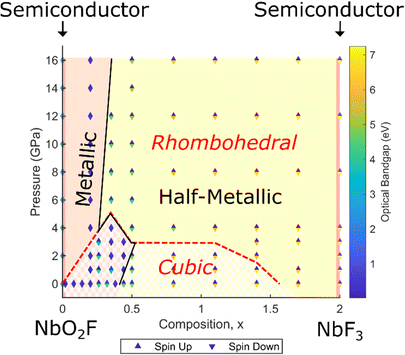
In order to determine the effect of the structural transition and increasing pressure on the electronic structure, a full composition-pressure phase diagram for both cubic and rhombohedral geometries is presented in Fig. 7 (individual cubic and rhombohedral results are shown in Fig. S8, ESI†). The transition from semiconducting NbO₂F to a metallic phase on doping with fluorine is maintained at all pressures, as is the metallic to half-metallic transition with x. NbF₃ is predicted to be semiconducting for the most stable rhombohedral phase (in contrast to previous cubic predictions).

Fig. 7 Summary of structural and electronic results for NbO_2−xF_1+x across the composition range 0 ≤ x ≤ 2 and for pressures up to 16 GPa. Each point represents the magnitude of majority (spin up) and minority (spin down) optical band gaps, while the solid black line indicates the transition between metallic and half-metallic behaviour. The cubic to rhombohedral structural transition is shown by the red dotted line.

For NbO₂F, the structural transition to a rhombohedral phase with pressure has no significant impact on the electronic properties. The phase remains semiconducting with a large band gap between the oxygen 2p and niobium 3d states (Fig. S9, ESI†), although the band gap does show a slight increase (less than 1 eV) with pressure. Additionally, the octahedral splitting in the Nb 3d band is more pronounced for the rhombohedral structure. These effects are due to narrowing of the 3d bands due to the octahedral tilting, caused by the reduced overlap efficiency between niobium 3d t_2g and anion 2p states.^45–47 This is supported by an observed increase in the octahedral splitting with octahedral rotation.

The most significant observation from the phase diagram (Fig. 7) is the co-occurrence of the transition between metallic and half-metallic behaviour with the cubic to rhombohedral phase transition, observed for compositions around x = 0.35 and pressures of 3–5 GPa. This can be understood by comparing the density of states for each symmetry for x = 0.35 (Fig. 8a and b, corresponding band structures in Fig. S10 and S11, ESI†). Increased narrowing of the minority spin 3d bandwidth in the rhombohedral phase causes it to become unoccupied, resulting in a half-metallic state. In contrast, the broader cubic 3d band (driven by more effective overlap between Nb and O orbitals) causes it to be partially occupied, maintaining a metallic state.

Fig. 8 Calculated PDOS for: (a) cubic NbO_1.65F_1.35 at 4 GPa; (b) rhombohedral NbO_1.65F_1.35 at 6 GPa; (c) rhombohedral NbO_0.3F_2.7 at 0 GPa; and (d) rhombohedral NbF₃ at 0 GPa. PDOS are separated by spin direction with the majority (spin up) spin state on the right and minority (spin down) spin state on the left.

Examination of the PDOS for rhombohedral NbO_0.3F_2.7 and NbF₃ (Fig. 8c and d and Fig. S12–S14, ESI†) shows an additional splitting in the niobium 3d states absent at higher oxygen compositions. This is caused by the trigonal distortion of the octahedra discussed previously (Fig. 6b) with the effect that the cubic 3d t_2g states are split into a combination of occupied e_g and unoccupied a_1g states. The resulting electronic gap (0.9 eV) allows NbF₃ to maintain spin polarisation whilst being semiconducting, and contrasts with previous predictions of half-metallic behaviour for x = 2.^14,27

E. Effects of anionic ordering

In order to evaluate the effects of anionic ordering on the electronic structure, we performed calculations based on a 2 × 2 × 2 supercell with different arrangements of oxygen and fluorine across the anion sites. These ordered models do not match the true anion arrangement (which exhibits local O/F ordering without 3-dimensional periodicity) but allow deviations from the VCA model due to anion ordering to be studied.

Calculations for NbO₂F with different anion arrangements reveal that a semiconducting state is retained with anion ordering, but the O_2p and F_2p sub-bands split according to the differing electronegativities of these species (Fig. S15, ESI†). The resulting bandgaps (1–2 eV) are smaller than the experimental value, but will be highly dependent on the Hubbard on-site repulsion term. Similar supercell models for cubic NbO_1.5F_1.5 and NbOF₂ (Fig. 9) show the same splitting of O and F sub-bands, but the half-metallicity observed from the VCA model is retained. Different anion ordering patterns (Fig. S16 and S17, ESI†) result in changes to the width of the anion p-bands, but the half-metallicity occurs as a result of the splitting of niobium 3d states which are independent of anion order. In real materials, we anticipate that the anion disorder will result in a DOS intermediate between the VCA and supercell model results presented here.

Fig. 9 PDOS calculated from an ordered supercell for (a) cubic NbO_1.5F_1.5 and (b) cubic NbOF₂. PDOS are separated by spin direction with the majority (spin up) spin state on the right and minority (spin down) spin state on the left.

IV. Conclusions

Our first-principles calculations have predicted half-metallicity over a wide range of compositions in the NbO_2−xF_1+x solid solution. Half-metallic behaviour is expected to occur in both cubic and rhombohedral structures for 0.44 ≤ x < 2, and could allow the electronic band structure to be continuously tuned by varying anionic composition.

The impact of external pressure on the ReO₃-type structure and the electronic properties of NbO_2-xF_1+x has also been explored. Anionic control over the cubic to rhombohedral phase transition is predicted with a maximum transition pressure of 5 GPa for x = 0.35. The trigonal octahedral distortion expected in NbF₃ is found to produce a spin-polarised semiconducting phase rather than the previously predicted half-metallic cubic phase.²⁷ The cubic to rhombohedral phase transition is also found to be the driving force behind half-metallicity in compositions around x = 0.35. This is caused by a narrowing of the Nb 3d t_2g band as a result of octahedral tilting. This structural control over half-metallicity could potentially be exploited to give materials that could be switched between metallic and half-metallic states under moderate applied pressure. Such behaviour would present a new approach in controlling spin currents for spintronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work used the Cirrus UK National Tier-2 HPC Service at EPCC (http://www.cirrus.ac.uk) funded by the University of Edinburgh and EPSRC (EP/P020267/1). EKD wishes to thank the University of Edinburgh for funding. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.

References

1. S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495.
2. R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027.
3. Y. H. A. Wang, A. Gupta, M. Chshiev and W. H. Butler, Appl. Phys. Lett., 2008, 92, 062507.
4. Y. H. A. Wang, A. Gupta, M. Chshiev and W. H. Butler, Appl. Phys. Lett., 2009, 94, 062515.
5. W. E. Pickett and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1146–1160.
6. Y. Ding, C. Yuan, Z. Wang, S. Liu, J. Shi, R. Xiong, D. Yin and Z. Lu, Appl. Phys. Lett., 2014, 105, 092401.
7. K. G. West, M. Osofsky, I. I. Mazin, N. N. H. Dao, S. A. Wolf and J. Lu, Appl. Phys. Lett., 2015, 107, 012402.
8. N. Tezuka, N. Ikeda, A. Miyazaki, S. Sugimoto, M. Kikuchi and K. Inomata, Appl. Phys. Lett., 2006, 89, 112514.
9. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
10. S. Cordier, T. Roisnel and M. Poulain, J. Solid State Chem., 2004, 177, 3119–3126.
11. S. Andersson, Acta Chem. Scand., 1964, 18, 2339–2344.
12. S. Andersson and A. Åström, Acta Chem. Scand., 1964, 18, 2233–2236.
13. F. J. Brink, L. Norén and R. L. Withers, J. Solid State Chem., 2004, 177, 2177–2182.
14. M. Pouchard, M. R. Torki, G. Demazeau and P. Hagenmuller, C. R. Seances Acad. Sci., Ser. C, 1971, 273, 1093–1096.
15. F. P. Gortsema and R. Didchenko, Inorg. Chem., 1965, 4, 182–186.
16. M. V. Reddy, S. Madhavi, G. V. Subba Rao and B. V. R. Chowdari, J. Power Sources, 2006, 162, 1312–1321.
17. N. H. Bashian, M. B. Preefer, J. Milam-Guerrero, J. J. Zak, C. Sendi, S. A. Ahsan, R. C. Vincent, R. Haiges, K. A. See, R. Seshadri and B. C. Melot, J. Mater. Chem. A, 2020, 8, 12623–12632.
18. B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498.
19. K. S. Aleksandrov, V. N. Voronov, A. N. Vtyurin, A. S. Krylov, M. S. Molokeev, M. S. Pavlovskiĭ, S. V. Goryaĭnov, A. Y. Likhacheva and A. I. Ancharov, Phys. Solid State, 2009, 51, 810–816.
20. C. R. Morelock, L. C. Gallington and A. P. Wilkinson, J. Solid State Chem., 2015, 222, 96–102.
21. S. U. Handunkanda, E. B. Curry, V. Voronov, A. H. Said, G. G. Guzmán-Verri, R. T. Brierley, P. B. Littlewood and J. N. Hancock, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 134101.
22. H. A. Evans, Y. Wu, R. Seshadri and A. K. Cheetham, Nat. Rev. Mater., 2020, 5, 196–213.
23. A. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
24. S. Carlson, A.-K. Larsson and F. E. Rohrer, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2000, 56, 189–196.
25. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
26. J. Wang, S. Qi, X. Song, Y. Qu, W. Li and M. Zhao, Appl. Surf. Sci., 2019, 495, 143623.
27. B. Yang, J. Wang, X. Liu and M. Zhao, Phys. Chem. Chem. Phys., 2018, 20, 4781–4786.
28. H. Mizoguchi, M. Orita, M. Hirano, S. Fujitsu, T. Takeuchi and H. Hosono, Appl. Phys. Lett., 2002, 80, 4732–4734.
29. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
30. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
32. P. Ehrlich, F. Plöger and G. Pietzka, Z. Anorg. Allg. Chem., 1955, 282, 19–23.
33. G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Comput. Sci., 1983, 23, 66–69.
34. A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B, 2002, 58, 364–369.
35. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, Comput. Phys. Commun., 2014, 185, 1477–1485.
36. J. Cumby and J. P. Attfield, Nat. Commun., 2017, 8, 14235.
37. F. Birch, Phys. Rev., 1947, 71, 809–824.
38. A. Agulyansky, in The Chemistry of Tantalum and Niobium Fluoride Compounds, ed. A. Agulyansky, Elsevier Science, Amsterdam, 2004, ch. 1, pp. 1–10.
39. S. Carlson, J. Appl. Crystallogr., 2000, 33, 1175–1176.
40. C. Michel, J.-M. Moreau and W. J. James, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 501–503.
41. H. Schäfer, H. G. Schnering, K. J. Niehues and H. G. Nieder-Vahrenholz, J. Less-Common Met., 1965, 9, 95–104.
42. P. Daniel, A. Bulou, M. Rousseau, J. Nouet and M. Leblanc, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 10545–10552.
43. A. Mogus-Milankovic, J. Ravez, J. P. Chaminade and P. Hagenmuller, Mater. Res. Bull., 1985, 20, 9–17.
44. P. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32–43.
45. P. G. Radaelli, G. Iannone, M. Marezio, H. Y. Hwang, S. W. Cheong, J. D. Jorgensen and D. N. Argyriou, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8265–8276.
46. M. Medarde, J. Mesot, P. Lacorre, S. Rosenkranz, P. Fischer and K. Gobrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9248–9258.
47. T. Zhao, L. M. Daniels, B. Slater, M. J. Rosseinsky and F. Corà, J. Phys. Chem. C, 2020, 124, 13045–13052.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc01563c

---