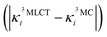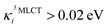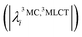Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast 3MLCT quenching and vibrational coherence: excited-state dynamics of the first-discovered Fe(II)–carbene sensitiser resolved†
Mátyás
Pápai
 *,
Tamás
Rozgonyi
*,
Tamás
Rozgonyi
 and
György
Vankó
and
György
Vankó

Wigner Research Centre for Physics, P. O. Box 49, H-1525 Budapest, Hungary. E-mail: papai.matyas@wigner.hu
First published on 13th November 2023
Abstract
The application of N-heterocyclic carbene (NHC) ligands represents a groundbreaking advance towards environment-friendly light-harvesting complexes, yet, even the excited-state dynamics of the first-discovered Fe–NHC photosensitiser [Fe(bmip)2]2+ (bmip = 2,6-bis(3-methyl-imidazole-1-ylidine)-pyridine) remain controversial. Using full-dimensional trajectory surface hopping (TSH) spin-vibronic dynamics simulations, we fully resolve and clarify the deactivation mechanism of [Fe(bmip)2]2+. In agreement with the most recent fs-resolved X-ray experiments, we find that the excited-state population branches into triplet metal-to-ligand charge transfer (3MLCT) and metal-centered states (3MC) on early sub-ps timescales (∼200 fs). The ultrafast 3MLCT quenching by 3MC is driven by multidimensional excited-state ligand motion; it is this deactivation process that ultimately weakens the photosensitising efficiency of [Fe(bmip)2]2+. Crucially, the preservation of vibrational coherence along the covalent Fe–C bonds (∼300 fs vibrational period) and the appearance of resulting coherent oscillations in various time-resolved experimental data unambiguously evidence the presence of the early sub-ps 3MC component.
1 Introduction
Transition metal complexes have received throughout the past decades grand attention due to their fascinating functionalities. Among the variety of functional transition-metal containing molecules, the class of light-harvesting complexes is especially intriguing, being a key component of technologies based on clean and green energy, such as solar energy conversion and photocatalysis.1,2 In both transition-metal based solar cells and photocatalytic assemblies, the process is initiated by a light-induced electron transfer from the metal to the ligand in a photosensitiser, leading to a metal-to-ligand charge transfer (MLCT) excited state.Extensive research efforts have continuously been devoted to developing efficient sensitisers absorbing in the visible range, with the most important aspects being the price and/or toxicity of the metal and the lifetime of the relevant MLCT states.3 An immense achievement was made a decade ago towards replacing photosensitisers based on precious metals, such as Ru and Ir, with Earth-abundant Fe complexes. This breakthrough was obtained owing to the utilisation of strongly σ-donating N-heterocyclic carbene (NHC) ligands,4–6 which destabilise metal-centered (MC) excited states7 that otherwise rapidly, in ca. 100 fs, quench the MLCTs in common Fe complexes such as Fe(II) polypyridines.8–12 Across the years, numerous Fe–NHC complexes have been synthesised and characterised with MLCT lifetimes ranging from 9 ps for the first-discovered Fe(II) sensitiser13 up to 528 ps;14 even higher excited-state lifetimes have been achieved for Fe(II) complexes containing amide donor atoms (2.0–2.7 ns)15 and for ligand-to-metal charge transfer (LMCT) states in an Fe(III)–carbene complex (2 ns).16
Despite the remarkable progress made in the coordination chemistry and photophysics of Fe–carbene complexes, consistent mechanistic understanding of the undergoing excited-state dynamics is often still lacking; this profound knowledge could in fact also be the key for real-life applications for solar cells and photocatalysts. Inconsistencies may typically be rooted in discrepancies in interpretations, stemming from the complexity of data acquired by time-resolved (pump–probe) experiments and/or approximations made in theoretical models for excited-state simulations. For Fe–NHCs, the scenario is best illustrated by the case of the very first discovered Fe–NHC photosensitiser, [Fe(bmip)2]2+ (bmip = 2,6-bis(3-methyl-imidazole-1-ylidine)-pyridine), shown in Fig. 1, right. Utilising transient optical absorption spectroscopy (TOAS) with 485 nm pump excitation, Liu et al.13 identified two timescales, <100 fs and 9 ps, which they attributed to 1MLCT → 3MLCT intersystem crossing (ISC) and 3MLCT → 3MC decay, respectively, see Fig. 1a. Our spin-vibronic17 quantum wavepacket dynamics simulations in highly-reduced nuclear configurational space (4D18 and 5D19) supported this assignment, identifying an ∼100 fs 1MLCT → 3MLCT ISC process, and the 3MLCT → 3MC transition occurring on ps timescales (with time constants of ∼1 ps and ∼4 ps). More recently, utilising fs-resolved X-ray emission spectroscopy (XES) Kunnus et al.20 identified that upon 400 nm excitation, the 3MLCT decay exhibits branching with an ∼110 fs 3MLCT → 3MC component (40%) and an ∼9 ps one (60%), the latter being identical to the 3MLCT lifetime determined by TOAS; we note that a similar branching was observed for a COOH-derivative of [Fe(bmip)2]2+ by vibrational coherence spectroscopy.21 Furthermore, coherent oscillations with a 278 fs period were identified in the time-resolved XES and X-ray solution scattering (XSS) signals, assigned to breathing wavepacket motion in the 3MC state; such oscillations are also apparent in the TOAS data but were not analysed and in no other cases were observed by XES. Clearly, there is a significant difference in these experimental assignments, i.e., TOAS (485 nm excitation) vs. XES (400 nm excitation), as well as the XES data vs. theory in the appearance of the ∼100 fs 3MC component. This ultrafast 3MLCT quenching channel could in fact have a vital role as it challenges the general picture of Fe–carbenes possessing long-lived MLCT states and potentially weakens the complex's photosensitising ability. Crucially, using full-dimensional hybrid quantum-classical excited-state simulations, we herein clarify and explain all important aspects and ambiguities of [Fe(bmip)2]2+, fully resolving its excited-state dynamics.
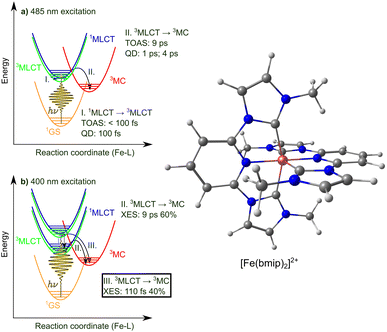 | ||
| Fig. 1 Left: Schematic illustration of the photophysics of [Fe(bmip)2]2+ photoexcited at (a) 485 nm and (b) 400 nm, as concluded from the analysis of time-resolved experiments (TOAS13 and XES20) and QD simulations.18 The focus of this work is (III), i.e., the sub-ps 3MLCT → 3MC process, which is highlighted in panel (b). Right: Molecular structure of the [Fe(bmip)2]2+ complex. | ||
2 Results and discussion
2.1 Theory overview
In the following, we address the ultrafast (sub-ps) quenching of 3MLCT states by 3MC, observed by fs-resolved XES. In fact, this is a remarkable result in light of the known photophysical behaviour of [Fe(bmip)2]2+. This pathway was not considered in the TOAS assignment of Liu et al.13 in their original work reporting [Fe(bmip)2]2+, and also challenges theoretical studies. For the theoretical modelling of this complex, first Fredin et al.7 calculated its potential energy surfaces (PESs) using density functional theory (DFT) and time-dependent DFT (TD-DFT). Subsequently, as mentioned in the Introduction, we performed quantum dynamics22 (QD) simulations18,19 using TD-DFT PESs along 4 and 5 chosen normal modes, which were all identified to possess a dominant Fe–N/Fe–C stretching character. We stress that this means a necessary drastic reduction in nuclear degrees of freedom, albeit the modes were carefully chosen based on calculated ab initio data and symmetry considerations.22 All these results supported the existence of a long-lived 3MLCT state, without any sub-ps 3MC component. Herein, we employ an alternative approach based on trajectory surface hopping (TSH). Importantly, in contrast to QD, which delivers a solution to the time-dependent Schrödinger equation, TSH is not restricted by the number of nuclear degrees of freedom (DoF), as nuclear motion is described classically with electronic transitions approximated by stochastic hops. The dynamics thus occur on the full-dimensional PES and properties are calculated by averaging over numerous trajectories.The electronic structure description of the PES has a decisive impact on the simulated dynamics. For transition metal complexes, in particular in the case of excited states, quantum chemistry faces immense challenges such as the description of electronic degeneracies, high density of states, and charge transfer excited states. Ideally, a balanced multiconfigurational treatment such as multiconfigurational second-order perturbation theory (CASPT2) would be the method of choice, however, computational feasibility issues as well as variance of the utilised active space for the nuclear configurational space explored by the dynamics severely limit its applicability. Herein, we use our efficient DFT/TD-DFT framework based on the B3LYP* exchange-correlation functional,23 which we benchmarked extensively against experimental24,25 and CASPT2 data.12,26 We carry out TSH dynamics simulations both on DFT/TD-DFT PESs, according to a linear vibronic coupling (LVC) harmonic model27 (which allows simulations up to several ps), and full on-the-fly ab initio PESs (in order to assess the validity of the LVC model for short sub-ps timescales). Details of the utilised methodology are described in the Methods section and the ESI.†
2.2 Ultrafast 3MLCT quenching: excited-state population dynamics
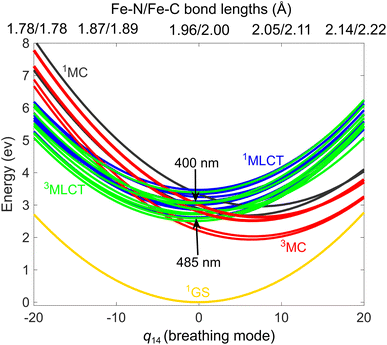
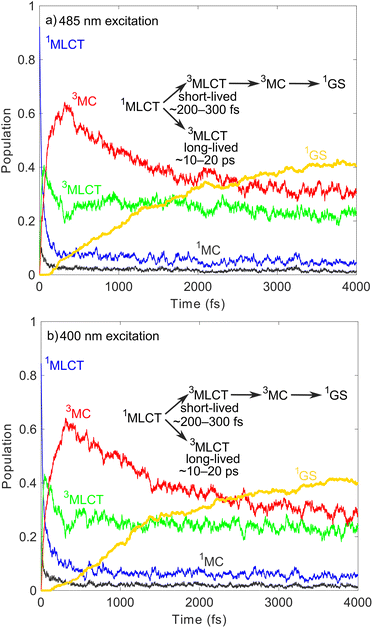
According to the two sets of experiments, i.e., TOAS13/XES,20 we simulate the photoexcitation of [Fe(bmip)2]2+ at 485/400 nm; this is illustrated in Fig. 2, in which we display the ground and excited-state diabatic PESs along the breathing mode ν14,28 known to be the dominant mode for dynamics involving MC states.12,29,30 Our excited-state model includes 11 1MLCT, 3 1MC, 12 3MLCT, and 6 3MC states (we here note that the PESs and electronic couplings can vary for different components of a given manifold such as 1MLCT, etc.) The excitation process is simulated by projection of the ground-state nuclear (Wigner) distribution to the excited-state PES using a 0.1 eV energy window centered at the 2.55/3.10 eV (485/400 nm) excitation energies (see ESI, Section S1,† for further details). As seen in Fig. 2, the two excitation schemes lead to different initial 1MLCT states, with the lower one matching the initial 1MLCT state of our previous QD simulations.18,19Fig. 3 shows the simulated electronic population dynamics for the lower-energy 485 nm (Fig. 3a) and higher-energy 400 nm (Fig. 3b) excitation. We note that we base all further analysis on the diabatic electronic representation, as it is suited for discussion of MLCT–MC dynamics, i.e., it maintains the electronic character at any nuclear geometry. It is clear from Fig. 3 that the pump energy does not have any considerable effect on the simulated dynamics. In both cases, i.e., 485/400 nm, the initial excited state has a dominant 1MLCT character, which is in line with the matching excitation energies and considerable oscillator strengths calculated at the Franck–Condon (FC) equilibrium geometry (see ESI, Table S1†); excitation into 1MC states only appears as a minor component. The 1MLCT population almost promptly, in ∼50 fs, decays to 3MLCT via singlet-triplet ISC. We find that the 3MLCT population consists of two branches: a component converted into 3MC in ∼200–300 fs, which then decays on a ps timescale (in qualitative agreement with the 1.5 ps time constant determined by XES20), repopulating the ground state (1GS), and a second one with a 3MLCT population stable up to well beyond 4 ps. We recall that in our previous QD simulations,18,19 we did observe the latter long-lived (∼few ps) 3MLCT component, but not the former sub-ps 3MLCT → 3MC pathway. Note that in principle, the 3MC states could also be populated directly from the 1MLCTs,21 however, we find that this direct channel is negligible (due to its very low occurrence), as revealed by the inspection of individual trajectories (see ESI, Section S3†); this analysis also confirms that the ground state is dominantly repopulated from the 3MC states (90%) with a minor 3MLCT → 1GS component (10%).
Importantly, our simulated 3MLCT–3MC population dynamics are in excellent agreement with the XES experiment of Kunnus et al.20 with the only discrepancy being in the branching ratio, as we identify the 3MC component as the one with larger weight, whereas in the XES experiment it is 3MLCT. However, the observed early sub-ps 3MC component is missing in the assignment of the TOAS experiment of Liu et al.,13 as well as in our previous QD studies.18,19
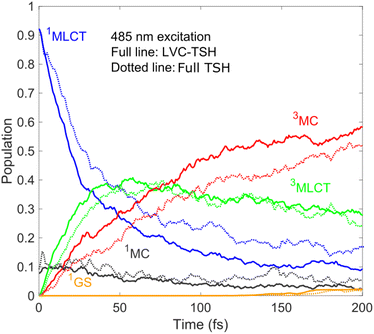
Based on the above, we thus identify a branching electronic relaxation mechanism with two components: (i) 1MLCT → 3MLCT → 3MC → 1GS with a short-lived 3MLCT component (∼200–300 fs), and (ii) 1MLCT → 3MLCT with a long-lived 3MLCT intermediate (∼10 ps or longer lived). The population dynamics up to 200 fs and thus the early appearance of 3MC are supported by our simulation utilising the full (unconstrained) PESs and SOCs calculated on the fly, see Fig. 4; as is clear, the simulated LVC and full dynamics for 485 nm excitation show rather good agreement.
In the following, we analyse the key ultrafast early 3MLCT → 3MC deactivation pathway focusing on nuclear motion and vibrational coherence.
2.3 Ultrafast 3MLCT quenching: nuclear motion
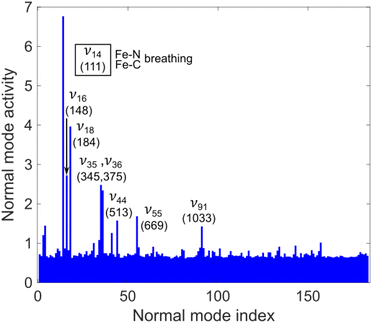
A key aspect of our simulated dynamics is that it unfold in full dimension, thus allowing us to analyse nuclear motion along all 183 modes of [Fe(bmip)2]2+. Fig. 5 shows the mode activity of nuclear motion for the case of 400 nm excitation, calculated as a standard deviation of nuclear displacements projected onto dimensionless mass-frequency weighted normal mode coordinates, see ESI, Section S1.† As is clear from Fig. 5, nuclear motion during the excited-state dynamics of [Fe(bmip)2]2+ is dominated by 5 modes: ν14 (as anticipated, the most dominant one, i.e., we chose this breathing mode to visualize the PESs in Fig. 2), ν16, ν18, ν35, and ν36, which are all identified to possess Fe–N/Fe–C stretching characters; we note that this result is very similar for the case of 485 nm excitation, see ESI, Fig. S1.† Among these 5 modes, 4 are identical to those used in our previous QD simulations (instead of the fifth mode ν35, we used mode ν34, which appears here with smaller mode activity), supporting that we indeed chose the most dominant modes. However, the population dynamics obtained with QD based on these modes are very different from our present full-D TSH results, in particular regarding the appearance of the ∼200–300 fs 3MC component. Our interpretation for this discrepancy is as follows: all identified dominant Fe–N/Fe–C stretching modes are activated and operative in the 3MC states, due to occupation of an antibonding orbital, but for the 3MLCT → 3MC transition, nuclear motion in the 3MLCT states is in fact decisive. However, the MLCT potentials are typically thought to be parallel with respect to the one of the ground state, see Fig. 2; this was indeed the case in our QD simulations utilising Fe–N/Fe–C stretching modes only, with negligible nuclear motion in the MLCT states. This is the reason why the 3MC states were only found to be populated on longer (∼ps) timescales, as the 3MLCT–3MC energy gap near the ground state equilibrium geometry is significantly larger (∼hundreds of meV) than the coupling between the states.
orbital, but for the 3MLCT → 3MC transition, nuclear motion in the 3MLCT states is in fact decisive. However, the MLCT potentials are typically thought to be parallel with respect to the one of the ground state, see Fig. 2; this was indeed the case in our QD simulations utilising Fe–N/Fe–C stretching modes only, with negligible nuclear motion in the MLCT states. This is the reason why the 3MC states were only found to be populated on longer (∼ps) timescales, as the 3MLCT–3MC energy gap near the ground state equilibrium geometry is significantly larger (∼hundreds of meV) than the coupling between the states.
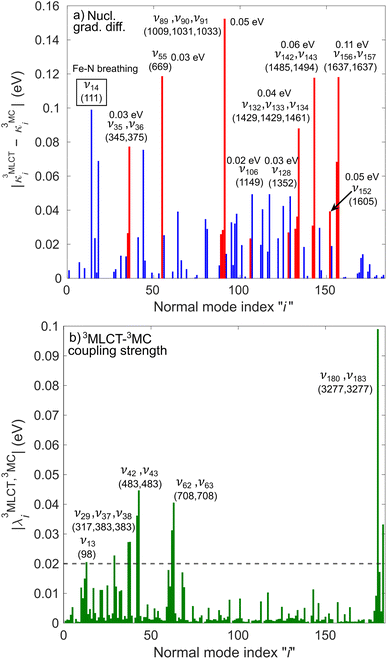
In the following, we show that nuclear motion in the lowest 3MLCT states is non negligible and is in fact the key to the ultrafast 3MLCT quenching mechanism by 3MC states. Nuclear motion and thus excited-state dynamics are dictated by the nuclear gradient of the potential energy for the excited states. The 3MLCT → 3MC dynamics are governed by the difference of 3MLCT–3MC nuclear gradients that mediates the 3MLCT–3MC energy gap. For simplicity, we here analyse the lowest out of the numerous triplet states: Fig. 6 shows the largest differences in nuclear gradients at the FC geometry between the lowest four 3MLCT and three 3MC states; we note that a similar approach to analyse vibronic effects was reported in ref. 22. We here focus on nuclear motion in the 3MLCT states and its effect on the 3MLCT–3MC dynamics, and therefore, in Fig. 6a, we highlight in red the most significant absolute gradient differences (above 0.02 eV; note that all nuclear gradients are given for unit nuclear displacement expressed in dimensionless normal mode coordinates) for which the 3MLCT gradient is also significant (at least 0.02 eV). As seen in Fig. 6a (red bars), excited-state 3MLCT nuclear motion will occur along several modes. Importantly, all these modes, with the exception of ν35 and ν36, will reduce the 3MLCT–3MC energy gap (∼0.16–0.39 eV for the analysed 4 3MLCT and 3 3MC states, see ESI, Table S1†), as movement from the FC region towards the 3MLCT minimum for these modes raises the 3MC energy (for ν35 and ν36, the opposite effect is observed, i.e., the 3MLCT–3MC gap slightly increases upon 3MLCT geometry relaxation). All 13 identified modes possess dominant ligand ring deformation and/or internal ligand bending character, in accordance with nuclear motion triggered by MLCT excitation (for animation of the modes, see the ESI†). Furthermore, we identified 10 additional modes which are the most important to couple the 3MLCT–3MC states (with the absolute value of the off-diagonal coupling constant being larger than 0.02 eV, see Fig. 6b); 8 of these, ν13, ν29, ν42, ν43, ν62, ν63, ν180, and ν183 have a dominant ligand character (out-of-plane twisting, out-of-plane deformation of the middle pyridine ring, C–H stretching), and the remaining two, ν37 and ν38 are characterised by off-center movement of the central Fe atom and bending modes of the ligand rings.
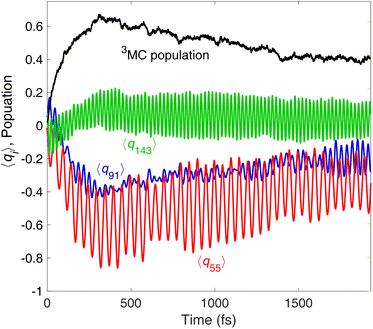
The above analysis clearly demonstrates that in contrast to the general discussion scheme of excited-state transition metal complexes, the 3MLCT PESs of [Fe(bmip)2]2+ are displaced from the ground-state potential along several modes (i.e., the 13 modes identified above by the magnitude of 3MLCT nuclear gradient, see Fig. 6a). All of these modes possess a dominant ligand character, which will be activated by electronic MLCT excitation. As seen above, several of these activated modes should be capable of facilitating the 3MLCT → 3MC conversion either by reducing the 3MLCT–3MC energy gap or by accounting for the 3MLCT–3MC coupling. Equipped with these insights, we now explicitly analyse the interplay of nuclear and 3MLCT–3MC electronic population dynamics. Fig. 7 shows the average trajectory along three out of the above identified ligand modes, as well as the 3MC population, for the simulation with 400 nm excitation. The three modes, selected by the 3MLCT and 3MC nuclear gradients (see Fig. 6a), are ν55 and ν91, which are deformation modes of the middle pyridine rings with symmetric stretching/compression of the Fe–N bonds, and ν143, a more complex mode involving deformation of all ligand rings as well as C–H wagging motion of the methyl groups. As seen in Fig. 7, significant vibrational dynamics occur along all three modes during the initial 0–300 fs period, with the mean displacement along the selected modes continuously shifting towards a structure distorted from the initial equilibrium geometry 〈qi〉 = 0. Crucially, these structural dynamics correlate excellently with the initial 3MC population increase (Fig. 7, black curve), signalling the role of excited-state ligand motion in the sub-ps 3MLCT → 3MC deactivation. We here recall that nuclear motion and electronic coupling can vary for different components of the 3MLCT and 3MC manifolds. Therefore, for certain components and initial conditions, no early 3MLCT → 3MC transition occurs (because, e.g., the 3MLCT ligand motion is not strong enough to significantly decrease the 3MLCT–3MC energy gap), which is the reason for the branching observed in Fig. 3 (i.e., sub-ps 3MLCT → 3MC transition vs. long-lived 3MLCT).
2.4 Vibrational coherence
Importantly, our results are consistent with the time-resolved XES experiment of Kunnus et al.,20 in particular supporting the branching of the excited-state population into 3MLCT and 3MC on early sub-ps timescales. As TOAS, in contrast to XES, is not directly sensitive to the electronic state, it is reasonable to expect that the <100 fs features of the TOAS data should in fact also contain a 3MLCT → 3MC component (although was assigned previously13 solely to 1MLCT → 3MLCT). By analysis of coherent oscillations in the Fe–N/Fe–C bond lengths, we below show that this interpretation should indeed be correct, evidencing that the branching does occur.Both the XES and XSS data for [Fe(bmip)2]2+ photoexcited at 400 nm (ref. 20) show oscillations with the same period of 278 fs and an exponential damping time constant of 500 fs. The XSS oscillations clearly identify coherent vibrational motion along the Fe–N/Fe–C stretching nuclear coordinate. Interestingly, the breathing vibration is also reflected in the oscillatory XES signal;31 based on the XES data, the coherent vibrations were assigned to the 3MC states. Fig. 8 displays the nuclear dynamics averaged over all trajectories (400 nm excitation case) along the Fe–N and Fe–C bonds, as well as projected onto the breathing normal mode ν14. In agreement with the XES/XSS experiments and their assignments, in our simulations, we observe coherent oscillations along the breathing mode with a period of ∼300 fs, which is clear in the Fe–C, but less in the Fe–N bond lengths (in the latter, the oscillations are dominated by faster components). Metal–ligand bonding and covalency has recently been proposed to be a key factor in rationalising the remarkable sensitivity of core-to-core XES to structural changes.20,32 Namely, the Fe–ligand interaction modulates the screening of the relevant core holes (e.g., 1s and 2p, for Kα); as this modulation varies with the Fe–ligand distance, the structural dynamics will be reflected in the time-dependent XES signal. Our results also indicate the importance of covalency, as we clearly observe the coherent oscillations with a period reasonably matching the experimental one for the Fe–C bonds, which are significantly more covalent than the Fe–N. We note that (i) the coherent oscillations are very similar for the case of 485 nm excitation (see ESI, Fig. S6†), and (ii) damping (decoherence) of our oscillations is slower than the experimental one; we attribute this discrepancy to the underestimation of intermode interactions and the absence of solvent in our model. It is important to stress, however, that the appearance of vibrational coherence and the period of oscillations are in good agreement with the XES/XSS experiments, and decoherence does occur, even if it is slower than observed experimentally.
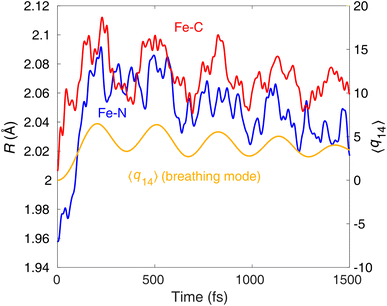 | ||
| Fig. 8 Average trajectories of [Fe(bmip)2]2+ along the Fe–N and Fe–C bond, as well as the breathing normal mode ν14, as obtained from the simulation with 400 nm excitation. | ||
Finally, we analyse the origin of the observed vibrational coherence and the case of the TOAS experiment with 485 nm excitation. The vibrational dynamics along the Fe–N/Fe–C bonds are triggered by electronic structure changes in the 3MC states, dominated by the population of an antibonding 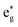 orbital (dx2–y2 or dz2 combined with the corresponding ligand orbitals). Any considerable contribution of MLCT states to such dynamics along the breathing mode (see Fig. 8) is ruled out, since an MLCT excitation does not lead to significant changes in the Fe–N/Fe–C bond lengths (i.e., the case of the nested ground-state and 3MLCT oscillators,21 see also Fig. 2). As seen in Fig. 3, the 3MC population rises fast, within an oscillation period of the breathing mode (∼300 fs), and hence vibrational coherence is preserved, as evidenced by the observation of coherent oscillations (Fig. 8). Therefore, the appearance of coherent oscillations, with a period matching the vibrational period of the breathing mode, can be used as a fingerprint for any significant 3MC component. Importantly, the TOAS data also contain oscillations with a rather similar period to those obtained by XES and XSS (see ref. 13, ESI, Fig. S12†), appearing already at ∼300 fs. Given the connection between the 3MC population rise and the coherent oscillations, this clearly means that the 3MC states have to be populated already at early times (∼100–300 fs), otherwise the coherent oscillations could not have been observed. All this agrees excellently with our simulated dynamics, unambiguously evidencing the existence of the observed early sub-ps 3MC component and thus the branching mechanism of the excited-state population into 3MLCT and 3MC.
orbital (dx2–y2 or dz2 combined with the corresponding ligand orbitals). Any considerable contribution of MLCT states to such dynamics along the breathing mode (see Fig. 8) is ruled out, since an MLCT excitation does not lead to significant changes in the Fe–N/Fe–C bond lengths (i.e., the case of the nested ground-state and 3MLCT oscillators,21 see also Fig. 2). As seen in Fig. 3, the 3MC population rises fast, within an oscillation period of the breathing mode (∼300 fs), and hence vibrational coherence is preserved, as evidenced by the observation of coherent oscillations (Fig. 8). Therefore, the appearance of coherent oscillations, with a period matching the vibrational period of the breathing mode, can be used as a fingerprint for any significant 3MC component. Importantly, the TOAS data also contain oscillations with a rather similar period to those obtained by XES and XSS (see ref. 13, ESI, Fig. S12†), appearing already at ∼300 fs. Given the connection between the 3MC population rise and the coherent oscillations, this clearly means that the 3MC states have to be populated already at early times (∼100–300 fs), otherwise the coherent oscillations could not have been observed. All this agrees excellently with our simulated dynamics, unambiguously evidencing the existence of the observed early sub-ps 3MC component and thus the branching mechanism of the excited-state population into 3MLCT and 3MC.
3 Conclusions
In this work, we resolved the excited-state dynamics of the first-discovered photosensitiser, [Fe(bmip)2]2+, using full-dimensional TSH dynamics simulations. In agreement with the recent XES experiment of Kunnus et al.,20 we observe branching of the excited-state population into 3MLCT and 3MC, on early sub-ps timescales. According to the branching, we identify two main relaxation pathways: (i) 1MLCT → 3MLCT → 3MC → 1GS with a short-lived 3MLCT component (∼200–300 fs), and (ii) 1MLCT → 3MLCT with a long-lived 3MLCT intermediate (∼10 ps or longer lived). Similarly to our recent work12 on the singlet-triplet-quintet dynamics of the [Fe(terpy)2]2 complex (terpy = 2,2′:6′,2′′-terpyridine), we obtain convincing agreement with experimentally resolved dynamics, which justifies the accuracy of the utilised B3LYP* DFT/TD-DFT framework for MLCT–MC energetics and dynamics. Moreover, the consistency achieved for the initial dynamics using LVC and unconstrained full ab initio PESs further validates our results.Based on the analysis of vibronic interactions and nuclear dynamics, we found that the early transition into 3MC states is driven by ligand motion triggered by the MLCT electronic excitation; this challenges the common photophysical 1D picture with the MLCT surfaces parallel to the one of the ground state. We explicitly showed that the early 3MC population increase occurs concurrently with nuclear dynamics along ligand modes, such as deformation of the middle pyridine ring and internal ligand bending/wagging, which reduce the 3MLCT–3MC energy gap and thus facilitate the electronic transition. We explained that this mechanism does not occur for all trajectories, depending on different states of the 3MLCT/3MC manifolds and initial conditions, giving rise to the component of the branching with a long-lived 3MLCT state. As the early sub-ps 3MLCT quenching by 3MC is a highly multidimensional process, it is not likely that this channel can be suppressed by blocking the relevant modes, as there are too many of them; a more efficient strategy would be to further increase the ligand field strength to even more destabilise the 3MC states. We note that in line with this interpretation, in the absence of ligand motion such as the case of the previous QD simulations,18,19 the early 3MC is completely missing.
Finally, we analysed coherent oscillations along the Fe–N/Fe–C bonds in the 3MC states. We emphasise that these oscillations can only be observed, i.e., vibrational coherence is preserved, if the 3MC population rises fast enough with respect to the period of the oscillations (∼300 fs). As both the more recent XES/XSS data by Kunnus et al.20 and the TOAS data from the original work on [Fe(bmip)2]2+ by Liu et al.13 contain the same oscillatory component, appearing already at early times, this means that the 3MC states had to be populated already at early sub-ps timescales; this thus clarifies the branching mechanism. We attribute the lack of the early 3MC component in the TOAS assignment to the lower sensitivity of TOAS to the electronic character. Our simulated coherent oscillations are in good agreement with those extracted from the time-resolved experiments, even if the damping (decoherence) is underestimated. We showed that the coherent oscillations with a period of ∼300 fs stem mostly from nuclear dynamics of the Fe–C bonds, which underlines the effect of covalency that has been identified as a key factor in the sensitivity of core-to-core XES to structural dynamics.20,32
4 Methods
The dynamics were simulated by full-dimensional trajectory surface hopping (TSH) based on Tully's fewest switches33 a three-step propagator technique,34 and local diabatisation,35,36 as implemented in the SHARC2.1 software.37,38 Our model includes the lowest 15 singlet and 18 triplet electronic states of [Fe(bmip)2]2+. The B3LYP*/TZVP DFT/TD-DFT calculations for the LVC and full (on-the-fly) PESs were carried out using the ORCA5.0 quantum chemistry program package.39,40 Further details of the utilised methodology are given in the ESI.†Data availability
Numerical LVC parameters are provided in the ESI† files. Further data are available from the corresponding author upon reasonable request.Author contributions
Mátyás Pápai: conceptualisation, methodology, validation, formal analysis, investigation, data curation, writing – original draft, visualisation, project administration, funding acquisition. Tamás Rozgonyi: writing – review & editing. György Vankó: conceptualisation, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading to the presented results has received funding from the Hungarian National Research, Development and Innovation Fund under grant numbers NKFIH PD 134976 and TKP2021-NVA-04. MP acknowledges support from the János Bolyai Scholarship of the Hungarian Academy of Sciences. Guest access to the central HPC cluster of the Technical University of Denmark is acknowledged.41Notes and references
- H. B. Gray and A. W. Maverick, Science, 1981, 214, 1201–1205 CrossRef CAS PubMed.
- X. Zhang, Y. Hou, X. Xiao, X. Chen, M. Hu, X. Geng, Z. Wang and J. Zhao, Coord. Chem. Rev., 2020, 417, 213371 CrossRef CAS.
- N. Sinha and O. S. Wenger, J. Am. Chem. Soc., 2023, 145, 4903–4920 CrossRef CAS PubMed.
- Y. Liu, P. Persson, V. Sundström and K. Wärnmark, Acc. Chem. Res., 2016, 49, 1477–1485 CrossRef CAS PubMed.
- L. Lindh, P. Chábera, N. W. Rosemann, J. Uhlig, K. Wärnmark, A. Yartsev, V. Sundström and P. Persson, Catalysts, 2020, 10, 315 CrossRef CAS.
- P. Dierks, Y. Vukadinovica and M. Bauer, Inorg. Chem. Front., 2022, 9, 206–220 RSC.
- L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071 CrossRef CAS PubMed.
- C. Brady, J. J. McGarvey, J. K. McCusker, H. Toftlund and D. N. Hendrickson, in Time-Resolved Relaxation Studies of Spin Crossover Systems in Solution, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 1–22 Search PubMed.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. Hadt, R. Hartsock, T. Kroll, K. Kjær, K. Kubiček, H. Lemke, H. Liang, D. Meyer, M. Nielsen, C. Purser, J. Robinson, E. Solomon, Z. Sun, D. Sokaras, T. Van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Pápai, K. B. Møller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundström, K. Wärnmark, P. Persson, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760 RSC.
- T. Rozgonyi, G. Vankó and M. Pápai, Commun. Chem., 2023, 6, 7 CrossRef CAS PubMed.
- Y. Liu, T. Harlang, S. E. Canton, P. Chábera, K. Suárez-Alcántara, A. Fleckhaus, D. A. Vithanage, E. Göransson, A. Corani, R. Lomoth, V. Sundström and K. Wärnmark, Chem. Commun., 2013, 49, 6412–6414 RSC.
- P. Chábera, K. S. Kjær, O. Prakash, A. Honarfar, Y. Liu, L. A. Fredin, T. C. B. Harlang, S. Lidin, J. Uhlig, V. Sundström, R. Lomoth, P. Persson and K. Wärnmark, J. Phys. Chem. Lett., 2018, 9, 459–463 CrossRef PubMed.
- J. D. Braun, I. B. Lozada, C. Kolodziej, C. Burda, K. M. E. Newman, J. van Lierop, R. L. Davis and D. E. Herbert, Nat. Chem., 2019, 11, 1144–1150 CrossRef CAS PubMed.
- K. S. Kjær, N. Kaul, O. Prakash, P. Chábera, N. W. Rosemann, A. Honarfar, O. Gordivska, L. A. Fredin, K.-E. Bergquist, L. Häggström, T. Ericsson, L. Lindh, A. Yartsev, S. Styring, P. Huang, J. Uhlig, J. Bendix, D. Strand, V. Sundström, P. Persson, R. Lomoth and K. Wärnmark, Science, 2019, 363, 249–253 CrossRef PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- M. Pápai, G. Vankó, T. Rozgonyi and T. J. Penfold, J. Phys. Chem. Lett., 2016, 7, 2009–2014 CrossRef PubMed.
- M. Pápai, T. Rozgonyi, T. J. Penfold, M. M. Nielsen and K. B. Møller, J. Chem. Phys., 2019, 151, 104307 CrossRef PubMed.
- K. Kunnus, M. Vacher, T. C. B. Harlang, K. S. Kjær, K. Haldrup, E. Biasin, T. B. van Driel, M. Pápai, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, E. Källman, M. Delcey, R. W. Hartsock, M. E. Reinhard, S. Koroidov, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, L. Sandberg, Z. Németh, D. S. Szemes, É. Bajnóczi, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. B. Møller, M. M. Nielsen, G. Vankó, K. Wärnmark, V. Sundström, P. Persson, M. Lundberg, J. Uhlig and K. J. Gaffney, Nat. Commun., 2020, 11, 634 CrossRef CAS PubMed.
- F. Hainer, N. Alagna, A. Reddy Marri, T. J. Penfold, P. C. Gros, S. Haacke and T. Buckup, J. Phys. Chem. Lett., 2021, 12, 8560–8565 CrossRef CAS PubMed.
- C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43–58 RSC.
- M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- D. Sárosiné Szemes, T. Keszthelyi, M. Papp, L. Varga and G. Vankó, Chem. Commun., 2020, 56, 11831–11834 RSC.
- M. Papp, T. Keszthelyi, A. Vancza, É. G. BajnÓczi, É. Kováts, Z. Németh, C. Bogdán, G. Bazsó, T. Rozgonyi and G. Vankó, Inorg. Chem., 2023, 62, 6397–6410 CrossRef CAS PubMed.
- M. Pápai, G. Vankó, C. de Graaf and T. Rozgonyi, J. Chem. Theory Comput., 2013, 9, 509–519 CrossRef PubMed.
- H. Köppel, W. Domcke and L. S. Cederbaum, in Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, John Wiley & Sons, Ltd, 1984, pp. 59–246 Search PubMed.
- Note that in our previous QD studies,18,19 this mode was denoted as ν6.
- A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstutz, Coord. Chem. Rev., 2006, 250, 1642–1652 CrossRef CAS.
- C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem.–Eur. J., 2013, 19, 17541–17551 CrossRef CAS PubMed.
- Note that core-to-core XES for transition metal complexes is primarily sensitive to the spin of the transition metal atom. So far, the case of [Fe(bmip)2]2+ is the only one for which the structural dynamics are reflected in the core-to-core XES signal.20.
- M. Vacher, K. Kunnus, M. G. Delcey, K. J. Gaffney and M. Lundberg, Struct. Dyn., 2020, 7, 044102 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514 CrossRef PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- DTU Computing Center, DTU Computing Center Resources, 2022, DOI:10.48714/DTU.HPC.0001.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the utilised methodology, linear vibronic coupling (LVC) parameters, supplementary results for population dynamics and Fe–N/Fe–C bond oscillations, animation of key normal modes. See DOI: https://doi.org/10.1039/d3ta05985e |
| This journal is © The Royal Society of Chemistry 2023 |