 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical capacitance measurements reveal the impact of oxygen vacancies on the charge curve of LiNi0.5Mn1.5O4−δ thin films†
Andreas E.
Bumberger
 *a,
Sergej
Ražnjević
b,
Zaoli
Zhang
*a,
Sergej
Ražnjević
b,
Zaoli
Zhang
 b,
Gernot
Friedbacher
a and
Juergen
Fleig
b,
Gernot
Friedbacher
a and
Juergen
Fleig
 a
a
aInstitute of Chemical Technologies and Analytics, TU Wien, Vienna, Austria. E-mail: andreas.bumberger@tuwien.ac.at
bErich Schmid Institute for Materials Science, Leoben, Austria
First published on 16th October 2023
Abstract
The level of oxygen deficiency δ in high-voltage spinels of the composition LiNi0.5Mn1.5O4−δ (LNMO) significantly influences the thermodynamic and kinetic properties of the material, ultimately affecting the cell performance of the corresponding lithium-ion batteries. This study presents a comprehensive defect chemical analysis of LNMO thin films with oxygen vacancy concentrations of 2.4% and 0.53%, focusing particularly on the oxygen vacancy regime around 4 V versus Li+/Li. A set of electrochemical properties is extracted from impedance measurements as a function of state-of-charge for the full tetrahedral-site regime (3.8 to 4.9 V versus Li+/Li). A defect chemical model (Brouwer diagram) is derived from the data, providing a coherent explanation for all important trends of the electrochemical properties and charge curve. Highly resolved chemical capacitance measurements allow a refining of the defect model for the oxygen vacancy regime, showing that a high level of oxygen deficiency not only impacts the amount of redox active Mn3+/4+, but also promotes the trapping of electrons in proximity to an oxygen vacancy. The resulting stabilisation of Mn3+ thereby mitigates the voltage reduction in the oxygen vacancy regime. These findings offer valuable insights into the complex influence of oxygen deficiency on the performance of lithium-ion batteries based on LNMO.
Introduction
Over the past three decades, lithium-ion batteries (LIBs) have emerged as the key energy storage technology for a wide range of applications. In particular, the utilization of LIBs in electric vehicles requires not only high energy densities to ensure a sufficient driving range, but also high power densities to enable fast charging. The overall power density of a Li-ion cell strongly depends on the specific electrochemical properties of the electrode materials (i.e., charge transfer resistance Rct, ionic conductivity σion, volume-specific chemical capacitance CVchem, Li chemical diffusion coefficient![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ). However, detailed studies dealing with the dependence of these properties on the state-of-charge (SOC) are rare. Interestingly, defect chemical models based on dilute-solution thermodynamics can offer valuable insights into the SOC-dependent transport properties of Li storage materials over a surprisingly wide range of charge carrier concentrations.1–3 Nonetheless, defect interactions inevitably come into play when exploiting the full charge/discharge capacity of a given Li storage material.
). However, detailed studies dealing with the dependence of these properties on the state-of-charge (SOC) are rare. Interestingly, defect chemical models based on dilute-solution thermodynamics can offer valuable insights into the SOC-dependent transport properties of Li storage materials over a surprisingly wide range of charge carrier concentrations.1–3 Nonetheless, defect interactions inevitably come into play when exploiting the full charge/discharge capacity of a given Li storage material.
In the search for new cathode materials, the cobalt-free spinel of the nominal composition LiNi0.5Mn1.5O4 (LNMO) has been investigated as a promising candidate due to its potentially low cost, good rate capability and high voltage versus Li+/Li.4–13 In contrast to its isostructural parent material LiMn2O4 (LMO), where Mn is in the mixed valence state of +3.5, Mn in stoichiometric LiNi0.5Mn1.5O4 is fully oxidized to a valence state of +4, while Ni remains in the lower valence state +2. Upon charging, the extraction of Li from the 8a tetrahedral sites is therefore accompanied by the oxidation of Ni to a final valence state of +4 in Ni0.5Mn1.5O4. Thus, the high oxidation potential of Ni2+/3+/4+ is exploited to reach a voltage of approximately 4.7 V versus Li+/Li, compared to 4.0 V in the Mn3+/4+-based LMO.
However, stoichiometric LiNi0.5Mn1.5O4 is difficult to synthesize, due to the material's tendency towards oxygen deficiency, accompanied by partial reduction of Mn4+ to Mn3+.6,10,11,14–20 Due to the exothermal nature of the oxygen incorporation reaction, a high degree of oxidation is favoured by low temperatures and high oxygen partial pressures. Thus, the typical synthesis route towards stoichiometric LNMO ends with a slow cooling step under an oxygen-rich atmosphere to allow the material to equilibrate at the lowest possible temperature. It was shown that a high degree of oxidation in LNMO is closely related to Ni ordering on the octahedral sites. While high levels of oxygen deficiency favour the formation of the disordered phase with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (“d-LNMO”), samples close to the stoichiometric composition LiNi0.5Mn1.5O4 tend to crystallise in the ordered P4332 phase (“o-LNMO”), although the difference between these two phases is hard to resolve by crystallographic experiments.6
m (“d-LNMO”), samples close to the stoichiometric composition LiNi0.5Mn1.5O4 tend to crystallise in the ordered P4332 phase (“o-LNMO”), although the difference between these two phases is hard to resolve by crystallographic experiments.6
From a defect chemical perspective, oxygen deficiency in LNMO can be realized either via oxygen vacancies according to LiNi0.5Mn1.5O4−δ or via metal interstitials according to [LiNi0.5Mn1.5]1+δ/(4−δ)O4. However, these two cases are difficult to distinguish experimentally, because both configurations lead to a donor-doped material of the same chemical composition. Although the metal excess model has been discussed for both LMO and LNMO,21–23 the larger part of literature seems to adopt the viewpoint of oxygen nonstoichiometry,6,17,20 and in this paper we therefore also consider oxygen deficiency in terms of oxygen vacancies in LiNi0.5Mn1.5O4−δ. Charge neutrality then requires the reduction of 2δ formula units of Mn4+ to Mn3+, which can be expressed as LiNi0.5Mn4+1.5−2δMn3+2δO4−δ. As a consequence, a fraction corresponding to 2δ × 100% of the total tetrahedral site capacity is moved from the 4.7 V (Ni2+/3+/4+) to the 4.0 V (Mn3+/4+) regime, resulting in a proportional loss of storable energy due to the lower average voltage.
However, the presence of oxygen vacancies does not simply move part of the total capacity from the high-voltage Ni- to the lower-voltage Mn-regime, but furthermore introduces a variety of possible defect interactions such as defect associates (i.e., electronic and ionic trap states) that influence the material's SOC-dependent electrochemical properties in a nontrivial manner. Although computational studies have suggested a significant impact of such associates (trap states) on the voltage profile of LNMO electrodes,17,24–26 particularly in the oxygen vacancy regime around 4.0 V, there have been little efforts to quantitatively describe the experimentally observed shape of the LNMO charge curve as a function of oxygen vacancy concentration and defect interaction energies. Furthermore, although the overall cycling performances of ordered (low δ) and disordered (high δ) samples have often been compared, the precise variation of their electrochemical transport properties with δ and the state-of-charge is largely unknown.
In this work, we investigate the impact of oxygen vacancies on the electrochemical properties of epitaxial LNMO thin films by means of impedance measurements as a function of electrode potential. We report a full and detailed set of electrochemical properties (charge transfer resistance, ionic conductivity, chemical capacitance and chemical diffusion coefficient) as a function of SOC for two different levels of oxygen deficiency. Particularly the chemical capacitance (i.e., differential capacity) turns out to be a highly valuable source of information regarding both ionic and electronic defect interactions in LNMO and their impact on the charge curve. For the first time, we provide a detailed defect chemical analysis of the charge curve in the oxygen vacancy regime around 4 V versus Li+/Li and show that the level of oxygen deficiency not only determines the amount of redox active Mn3+/4+ but furthermore impacts the defect interactions and hence the shape of the charge curve. More generally, the reported results pave the way towards a better understanding of the oxygen-nonstoichiometry in all Li-ion cathode materials and its effect on electrode performance.
Results
Epitaxial SRO/LNMO thin films
To analyse the effect of oxygen vacancies on the electrochemical properties of LNMO, two types of thin-film sample were prepared – one with a high and one with a low level of oxygen deficiency, as described in the experimental section. Although the post-oxidized sample is still weakly oxygen-deficient (see below), and its space group could not be unambiguously identified as Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m or P4332, its structural and electrochemical properties are close to what is referred to as ordered LNMO in the literature, and we will therefore refer to the samples with high and low oxygen vacancy concentration as d-LNMO and o-LNMO (d = disordered, o = ordered), respectively.
m or P4332, its structural and electrochemical properties are close to what is referred to as ordered LNMO in the literature, and we will therefore refer to the samples with high and low oxygen vacancy concentration as d-LNMO and o-LNMO (d = disordered, o = ordered), respectively.
The structural characterisation of typical d-LNMO and o-LNMO samples is summarised in Fig. 1. As shown in Fig. 1a, LNMO was deposited onto an epitaxial SrRuO3 (SRO) thin-film current collector on a (100)-oriented SrTiO3 (STO) single crystal substrate coated with Ti/Pt on its sides and backside. The θ–2θ X-ray diffractograms in Fig. 1b suggest that both o-LNMO and d-LNMO grow epitaxially on the (100)-oriented SRO thin film. For SRO and the STO substrate, only the (100), (200) and (300) reflexes are visible in the measured range of 2θ, with the SRO reflexes shifted to lower angles with respect to the substrate. For both samples, the SRO (200) reflex appears around 2θ = 45.2°, corresponding to an out-of-plane lattice parameter of approximately 4.01 Å. In a previous study,2 it was confirmed by reciprocal space mapping that SRO grows on STO as a compressively strained, epitaxial thin film, thereby adopting the in-plane lattice parameter of 3.91 Å from the substrate. As shown in Fig. 1c, the LNMO (400) reflex appears at 2θ = 43.9° and 2θ = 44.3° for d-LNMO and o-LNMO, corresponding to out-of-plane lattice parameters of 8.25 Å and 8.18 Å, respectively. This is in good agreement with literature, where a larger lattice parameter is reported for d-LNMO due to the larger ionic radius of Mn3+ compared to Mn4+.18
The epitaxial growth of both d- and o-LNMO on the SRO current collector is confirmed by the high-resolution TEM images in Fig. 1h and i, respectively. The close agreement of the measured out-of-plane lattice parameter with the bulk lattice parameters from literature, together with the large lattice mismatch of 5% between LNMO and SRO, suggests that, for both samples, the epitaxial LNMO film relaxes to its bulk in- and out-of-plane lattice parameter within a short distance from the interface, and does not adopt a significant amount of compressive strain from the substrate.
The AFM images of the d- and o-LNMO surfaces are shown in Fig. 1d and e, respectively, and show a clear difference in morphology between the disordered and ordered spinel samples. The d-LNMO film exhibits an ill-defined surface morphology with some octahedral imprints that hint at the characteristic morphology of (400)-oriented spinel thin films, an RMS roughness of 15 nm and a surface area that is 12% larger than the projected sample area. The o-LNMO film, on the other hand, exhibits a well-defined morphology with a clear preference for exposure of the (111) facets, resulting in an octahedrally imprinted structure with an RMS roughness of 45 nm and a surface area that is 59% larger than the projected area. The difference in morphology between d-LNMO and o-LNMO is even more evident in the corresponding bright-field TEM images in Fig. 1f and g, respectively, with the ordered sample showing clearly defined pyramids, while the disordered sample exhibits a smoother but more irregularly shaped surface.
For the d-LNMO thin film, an average thickness of 70 nm was estimated from the bright-field TEM images. For the o-LNMO film, the estimated average thickness in the cross section shown in Fig. 1g is only 56 nm. However, due to the strong thickness variation in the o-LNMO film, the comparatively small sample size of the TEM image and the fact that the same deposition rate and time were employed for both samples, we use the same average thickness (70 nm) for the data analysis of both d-LNMO and o-LNMO. Owing to the thickness variations, especially in the o-LNMO film, the geometry normalised properties deduced from the impedance spectra have to be regarded as averaged (effective) values. Although the presence of grain boundaries cannot be ruled out, our TEM investigations indicate a largely single-crystalline, dense thin film for both sample types. This is further supported by the Fourier transform (FT) images shown in Fig. S1 of the ESI† together with the corresponding HR-TEM images. For both samples, the FT patterns correspond to a spinel single crystal as viewed along the [010] zone axis with some additional amorphous contributions, which presumably stem from the amorphous surface layer introduced during FIB lamella preparation. For o-LNMO, some minor additional spots are observed, which could originate from the ordered P4332 phase, or a small fraction of crystallites with different orientations. In either case, the films appear dense and largely single-crystalline, and we therefore consider the extracted electrochemical properties as representative also for the corresponding bulk material.
DC measurements
After cell assembly, the two different LNMO samples were characterized by cyclic voltammetry (CV) for 5 cycles at a scan rate of 1 mV s−1, to ensure sufficient electrochemical stability for the subsequent impedance measurements. The fifth cycle CV scans are plotted in Fig. 2a. Both samples exhibit the well-known double peak in current density around 4.7 V versus Li+/Li,6,10,13 corresponding to the removal/insertion of Li+ from the tetrahedral sites upon oxidation/reduction of Ni2+/3+/4+, with o-LNMO showing higher overall current densities for both the forward and the backward scan. While it may be tempting to assign these two peaks to the separate redox couples Ni2+/3+ and Ni3+/4+, the potential difference close to 100 mV between the two peaks is very similar to the double peak observed for LMO, where only one redox species (Mn3+/4+) is active, and the peak splitting has been reported to originate from Li ordering at the composition Li0.5Mn2O4.27–31 It is therefore likely, although experimentally not fully established, that a similar ordering occurs in LNMO and may either cause or at least contribute to the observed peak splitting.10A second, broader and much lower current peak is observed around 4.0 V, which is significantly higher for d-LNMO than for o-LNMO. This peak can be assigned to the removal/extraction of Li+ from the tetrahedral sites upon oxidation/reduction of Mn3+/4+, stemming from the charge compensation of oxygen vacancies. Hence, this peak is the focus of our study. The much lower current densities observed for o-LNMO compared to d-LNMO in the 4.0 V region therefore confirms the successful, although still incomplete, incorporation of additional oxygen into the material in the post-annealing step under oxygen atmosphere.
For both samples, a significant amount of background current is observed, that increases up to approximately 10 μA cm−2 at 4.9 V. This background current presumably originates from side reactions due to either impurities or residual water content in the electrolyte or the onset of electrolyte oxidation at the highest voltages. Although the observed background currents are negligible compared to typical bulk electrode capacities in the mA h range, they are significant in the context of our thin film electrodes with capacities of only a few μA h. Accordingly, they have a noticeable impact on the coulombic efficiency, as discussed below. Cyclic voltammetry was therefore chosen over classical galvanostatic cycling, since the former allows for a better estimation of the background currents contributing to the measured charge/discharge capacities. A comparison of constant–current cycling data of d-LNMO and o-LNMO can be found, for example, in ref. 6, 11, and 16.
By integration, the CV curves in Fig. 2a can also be converted directly into potential versus charge curves, i.e., voltage profiles, as shown in Fig. 2b. The integrated charge/discharge capacities amount to 165/127 mA h g−1 (d-LNMO) and 181/136 mA h g−1 (o-LNMO), with corresponding coulombic efficiencies of 77% and 75%, respectively. As discussed above, side reactions with the electrolyte, indicated by the oxidative background current in the CV scan, negatively impact the coulombic efficiency. Furthermore, these background currents lead to a distortion of the charge/discharge curves towards higher/lower capacities in the high-voltage region above 4.8 V. More generally, the voltage profiles appear particularly distorted in potential regions outside the main storage regime around 4.7 V, where the currents due to reversible Li intercalation/extraction are low and background currents are comparatively higher. Since these potential regions also correspond to stoichiometries with low charge carrier concentrations, where a dilute defect model could be applied to describe the material's electrochemical properties, the DC measurements shown in Fig. 2 do not provide sufficiently accurate data for a quantitative comparison with defect chemical calculations. For further investigations, we therefore resort to impedance measurements, as established in our previous studies on Li1−δCoO2 and Li2−δMn2O4.1,2 This virtually eliminates the effect of background currents and allows us to extract not only the volume-specific chemical capacitance CVchem (i.e., differential capacity), but also the charge transfer resistance Rct, the ionic conductivity σion and the Li chemical diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) as a function of SOC.
as a function of SOC.
Impedance measurements
Impedance spectra for LNMO electrode potentials of 3.80 to 4.90 V versus Li+/Li were measured in increments of 10 mV and are shown in Fig. 3 for both d-LNMO and o-LNMO in increments of 100 mV. For both samples, the frequency-dependent impedance response exhibits a similar variation with electrode potential, with the highest real and imaginary impedances at 3.80 and 4.90 V. The real impedance only shows a strong variation at low and high voltages and appears to remain relatively constant in the intermediate voltage range. The imaginary part of the impedance reaches a first minimum at 4.00 V and a second, more pronounced minimum around 4.70 V. The high-frequency region of the spectra, which is magnified in Fig. 3c (d-LNMO) and Fig. 3g (o-LNMO), consists of two semicircles, one of which exhibits a strong variation with electrode potential, whereas the other remains nearly constant throughout the entire set of measurements. At intermediate voltages, the two semicircles appear to be of similar magnitude and blend into each other, signifying a similar capacitance of the corresponding transport processes. The most notable difference between the d-LNMO and o-LNMO samples can be seen in the low and intermediate voltage region, up to approximately 4.40 V. For d-LNMO, the previously described variation of real and imaginary impedance around 4.00 V is more pronounced than for o-LNMO. For example, the impedance spectrum of o-LNMO at 3.90 V is very similar to the spectrum at 4.90 V, while for d-LNMO, the real and imaginary impedances are significantly lower at 3.90 V. Since both the real and imaginary parts of the electrode impedance are related to charge carrier concentrations in the material (see next section), this hints at a higher capacity of d-LNMO in the Mn-regime, as could already be estimated from the CV curves in Fig. 2a.Fitting of impedance spectra
Impedance spectra of Li storage thin films have conventionally been fitted with Randles' circuit,32,33 which is based on an intuitive combination of an open Warburg element Wo with a charge transfer resistance Rct, a double-layer capacitance Cdl and a high-frequency offset resistance Rhf. More generally, the impedance response of a Li storage electrode can be described by the general transmission line model proposed by Jamnik and Maier, shown in Fig. 4a. This physically derived impedance model considers the one-dimensional transport of mass and charge across a mixed ionic and electronic conductor (MIEC) slab of thickness L by two parallel resistive rails for ions and electrons, coupled by chemical capacitors, with Reon = ∑reon, Rion = ∑rion, and Cchem = ∑cchem.34–38 For a Li storage electrode, the volume-specific chemical capacitance can be defined as39 | (1) |
μLi = μLi,metal + kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aLi, aLi, | (2) |
 | (3) |
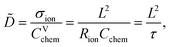 | (4) |
 | ||
| Fig. 4 Stepwise derivation of the equivalent circuit used for impedance fitting. (a) General transmission line with four distinct R/C terminals. (b) Simplified transmission line obtained by (i) neglecting electronic resistances, (ii) assuming an ohmic electronic contact at the SRO/LNMO interface, and (iii) assuming an LNMO/electrolyte interface that allows for both Li+ and electron transfer. (c) Final equivalent circuit used for fitting, obtained by accounting for anomalous diffusion as well as for the contributions of the Li metal counter electrode (CE) and the electrolyte. Circuit elements with fixed parameters are marked in red, and their respective values are summarised in Table 1. | ||
For the present study, we further assume a current collector that presents an ohmic electronic contact to the mixed ionic and electronic conductor (LNMO), i.e., a negligible contact resistance, and an LNMO/electrolyte interface that allows for both charge transfer (transport of Li+ across the interface) and side reactions (i.e., electron transfer to or from the electrolyte, for example due to electrolyte oxidation at high voltages). The charge transfer and side reaction resistances are denoted as Rct and Rs, respectively. The electrochemical double-layer capacitance Cdl at the LNMO/electrolyte interface is placed on the electronic rail terminal to remain consistent with the commonly used Randles' circuit after replacement of the transmission line with an open Warburg element (see below). The resulting equivalent circuit is shown in Fig. 4b.
The remaining portion of the transmission line is identical to an ideal open Warburg element Wo, which describes the impedance transition from semi-infinite to finite-space diffusion with characteristic phase angles of 45° and 90°, respectively. In our previous studies on Li1−δCoO2 and Li2−δMn2O4,1,2 we have shown that the diffusional impedance of real intercalation electrodes can be fitted with an anomalous finite-space diffusion element  embedded in the impedance analysing software EC-Lab (Biologic, France), which is closely related to the anomalous open Warburg element proposed by Bisquert.41 The corresponding impedance expression reads
embedded in the impedance analysing software EC-Lab (Biologic, France), which is closely related to the anomalous open Warburg element proposed by Bisquert.41 The corresponding impedance expression reads
 | (5) |
 The nonideality parameter was found to be in the range of 0.4 to 1. Furthermore, we replace the ideal double-layer capacitance Cdl by a constant-phase element Qdl and add a serial high-frequency offset resistance Rhf to account for the ohmic resistance contributions of the electrolyte and other cell components.
The nonideality parameter was found to be in the range of 0.4 to 1. Furthermore, we replace the ideal double-layer capacitance Cdl by a constant-phase element Qdl and add a serial high-frequency offset resistance Rhf to account for the ohmic resistance contributions of the electrolyte and other cell components.
A two-electrode cell setup is used in this study to avoid distortions of the impedance spectra that are potentially encountered in a three-electrode setup due to slight misalignments of the square-shaped working and counter electrodes. Hence, also the Li metal counter electrode must be included in the equivalent circuit. Its impedance is observed as a nearly invariant high-frequency semicircle, as shown in Fig. 3, and can therefore be accounted for by a RCE/QCE element in series to the remaining equivalent circuit with fixed values of RCE, QCE, and the corresponding constant-phase exponent n. The side-reaction resistance Rs was also found to be nearly constant throughout the series of measurements and was therefore fixed to ensure a meaningful fit in the potential regions of high chemical capacitance, where the low-frequency diffusional tail is too short to allow an unambiguous identification of Rs. The final equivalent circuit used for fitting is shown in Fig. 4c, with the fixed circuit elements marked in red. The corresponding fixed fit parameters for d-LNMO and o-LNMO, which were extracted from the impedance spectra at 3.90 V and 4.50 V, respectively, are summarised in Table 1. Exemplary impedance fits at 3.90 V are shown in Fig. 3d and h for d-LNMO and o-LNMO, respectively. A more extensive overview of the impedance fits is shown in Fig. S2 of the ESI.†
| R s [Ω] | R CE [Ω] | Q CE [F sn−1] | n | |
|---|---|---|---|---|
| d-LNMO | 1.95 × 105 | 206 | 6.48 × 10−6 | 0.836 |
| o-LNMO | 2.45 × 105 | 192 | 8.18 × 10−6 | 0.818 |
Analysis of electrochemical properties
The electrochemical properties obtained by fitting the impedance spectra in Fig. 3 to the equivalent circuit from Fig. 4c are shown in Fig. 5 as a function of Li activity and electrode potential versus Li+/Li. The data sets of d-LNMO and o-LNMO are marked in red and black, respectively. For o-LNMO, impedance spectra at electrode potentials below 3.83 V versus Li+/Li could not be evaluated due to the high values of Rct and Rion, which blend into each other in the low-frequency region and can no longer be distinguished by the fit (see, for example, the impedance spectrum at 3.80 V in Fig. 3e). The entire data set was therefore limited to an electrode potential range of 3.83 V to 4.90 V for both d-LNMO and o-LNMO.The charge transfer resistance, normalised to the electrode surface area measured by AFM, is plotted as the inverse 1/Rct in Fig. 5a to emphasise the similar concentration dependences of σion and 1/Rct. For d-LNMO, Rct decreases from 3.7 kΩ cm2 at 3.83 V to a minimum value of about 80 Ω cm2 at 4.14 V. From 4.05 V to 4.60 V, Rct remains relatively constant around 100 Ω cm2. Above 4.60 V, Rct starts to increase again and reaches a final value of 3.7 kΩ cm2 at 4.90 V. For o-LNMO, Rct decreases from 23 kΩ cm2 at 3.83 V to about 100 Ω cm2 at around 4.33 V and then remains relatively constant up to 4.67 V, where it shows a slight further decrease down to a minimum of 70 Ω cm2, before increasing again up to 6.0 kΩ cm2 at 4.90 V. In the low potential region around 3.83 V to 4.15 V, Rct is almost one order of magnitude higher for o-LNMO than for d-LNMO. From 4.15 V to 4.90 V, however, Rct is very similar for o-LNMO and d-LNMO, with little variation between approximately 4.20 and 4.70 V. Overall, measured values of Rct are in good agreement with literature.42,43
The SOC-dependent ionic conductivity σion is plotted in Fig. 5b and shows a very similar variation with Li activity and electrode potential as Rct for both d-LNMO and o-LNMO. In the range up to roughly 4.15 V, σion is about one order of magnitude lower for o-LNMO than for d-LNMO. For d-LNMO, σion increases by two orders of magnitude from 10−9 S cm−1 at 3.83 V to approximately 10−7 S cm−1 at 3.95 V. For o-LNMO, σion even increases by three orders of magnitude from 10−10 S cm−1 to 10−7 S cm−1 at about 4.15 V. Above 4.15 V the ionic conductivity of both samples is nearly identical, remaining surprisingly constant up to 4.70 V and then decreasing again down to around 10−9.5 S cm−1 at 4.90 V. The broad plateau can be attributed to the presence of oxygen vacancies, as described in the defect chemical discussion. Literature reports of the SOC-dependent ionic conductivity are hard to find, but the value of about 10−9 S cm−1 measured by Amin and Belharouk for a nominally stoichiometric LNMO pellet20 is in good agreement with our results at the lowest electrode potentials (i.e., close to full lithiation of the tetrahedral sites).
To provide a more direct comparison of d-LNMO and o-LNMO rate capabilities, the total effective electrode resistance Rtot = Rion/3 + Rct is plotted in Fig. S3 of the ESI† as a function of electrode potential (Fig. S2a†) and Li content (Fig. S2b†). At low electrode potentials up to about 4.2 V versus Li+/Li, Rtot is about half an order of magnitude lower for d-LNMO than for o-LNMO, indicating a significantly better rate capability and energy efficiency for d-LNMO in this potential region. However, due to the small amounts of charge stored at low potentials, these differences are only significant close to full Li content (i.e., the fully discharged state), as shown in Fig. S2b.†
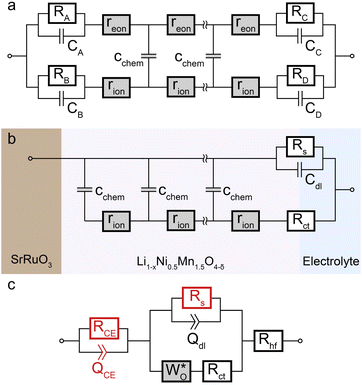
The volume-specific chemical capacitance CVchem of d-LNMO and o-LNMO is shown in Fig. 5c. Up to around 4.30 V versus Li+/Li, values of CVchem are about half an order of magnitude higher for d-LNMO than for o-LNMO. For both samples, CVchem exhibits a broad peak at 4.02 V, reaching a maximum value of 1185 F cm−3 and 382 F cm−3 for d-LNMO and o-LNMO, respectively. Above 4.30 V the data sets of both samples closely match each other, with the only difference being the sharper and higher double peaks of CVchem for o-LNMO at 4.68 V and 4.74 V. The double peaks around 4.7 V strongly resemble the peaks found in LMO, presumably due to ordering of Li ions on the tetrahedral sites at half occupancy. A detailed analysis of these peaks is beyond the scope of this paper, which focusses on the broad peak around 4.0 V caused by oxygen vacancies. The general appearance and magnitude of our CVchem measurements are in good agreement with CV curves and differential capacity plots found in the literature.42–44
The chemical capacitance from impedance fits can be compared to the values obtained from cyclic voltammetry via
 | (6) |
 | ||
| Fig. 6 Comparison of the volume-specific chemical capacitance obtained from impedance fits (EIS) and from cyclic voltammetry (CV) scans for (a) d-LNMO and (b) o-LNMO. | ||
The variation of the chemical diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) with Li activity and electrode potential (Fig. 5d) is more complex than the trends of Rct, σion, and CVchem, and needs to be understood as the ratio between σion and CVchem according to eqn (4). Without going into details of the differences between d-LNMO and o-LNMO, we can state that the
with Li activity and electrode potential (Fig. 5d) is more complex than the trends of Rct, σion, and CVchem, and needs to be understood as the ratio between σion and CVchem according to eqn (4). Without going into details of the differences between d-LNMO and o-LNMO, we can state that the ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) values are very similar above 4.4 V and significantly different for lower voltages. The latter is not surprising, considering the differences in σion and CVchem in the same potential region. The two sharp minima at 4.68 V and 4.74 V reflect the corresponding maxima of CVchem at the same electrode potentials. As expected from the CVchem curve, these minima are sharper and deeper for o-LNMO than for d-LNMO. The shape and magnitude of the variation of
values are very similar above 4.4 V and significantly different for lower voltages. The latter is not surprising, considering the differences in σion and CVchem in the same potential region. The two sharp minima at 4.68 V and 4.74 V reflect the corresponding maxima of CVchem at the same electrode potentials. As expected from the CVchem curve, these minima are sharper and deeper for o-LNMO than for d-LNMO. The shape and magnitude of the variation of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) with SOC agree excellently with other literature reports, although values below 4.3 V are rarely reported.42,44,45
with SOC agree excellently with other literature reports, although values below 4.3 V are rarely reported.42,44,45
Overall, the d-LNMO and o-LNMO samples behave similarly in the high-voltage region above approximately 4.30 V, where reversible Li+ release/insertion occurs at the tetrahedral Li sites upon oxidation/reduction of Ni2+/3+/4+. At potentials below 4.30 V, on the other hand, the strongly deviating electrochemical properties of the two samples clearly reflect the higher charge carrier concentrations of d-LNMO in the Mn3+/4+ regime due to a higher level of oxygen deficiency, which was already evident from the CV curves in Fig. 2a. We define the oxygen vacancy regime as the electrode potential region below 4.37 and 4.21 V for d-LNMO and o-LNMO, respectively, which corresponds to the position of the respective CVchem minima in Fig. 6. By integrating the chemical capacitance according to
 | (7) |
Discussion
Defect chemical model for oxygen-deficient LNMO
The material parameters deduced so far describe the kinetics of Li insertion (Rct, σion,![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) and its thermodynamics (CVchem). For σion, and CVchem, a more or less straightforward relation to defect chemical properties and considerations can be expected. Particularly a defect chemical analysis of CVchem may be a powerful tool for understanding and interpreting the impact of oxygen vacancies on the charge/discharge behaviour of LNMO. This is shown in the remaining part of the paper. First, we introduce the basic defect chemical model of stoichiometric and oxygen-deficient LNMO, which already qualitatively explains many features of the measured CVchem (and σion) dependences on voltage. In a second step, we specify the defect model for the additional storage regime introduced by oxygen vacancies (oxygen vacancy regime). Finally, we compare the measured chemical capacitance with the model and refine the model such that all essential features (absolute value of CVchem and slope shapes at both sides of the CVchem peak) can be explained. This refined consideration leads to important conclusions with respect to the local chemical environment of oxygen vacancies and defect interactions between oxygen vacancies, lithium vacancies and electrons. Thus, it substantially improves the understanding of LNMO voltage profiles.
) and its thermodynamics (CVchem). For σion, and CVchem, a more or less straightforward relation to defect chemical properties and considerations can be expected. Particularly a defect chemical analysis of CVchem may be a powerful tool for understanding and interpreting the impact of oxygen vacancies on the charge/discharge behaviour of LNMO. This is shown in the remaining part of the paper. First, we introduce the basic defect chemical model of stoichiometric and oxygen-deficient LNMO, which already qualitatively explains many features of the measured CVchem (and σion) dependences on voltage. In a second step, we specify the defect model for the additional storage regime introduced by oxygen vacancies (oxygen vacancy regime). Finally, we compare the measured chemical capacitance with the model and refine the model such that all essential features (absolute value of CVchem and slope shapes at both sides of the CVchem peak) can be explained. This refined consideration leads to important conclusions with respect to the local chemical environment of oxygen vacancies and defect interactions between oxygen vacancies, lithium vacancies and electrons. Thus, it substantially improves the understanding of LNMO voltage profiles.
In a recent study on LMO thin films,2 it was shown that the defect chemistry of spinel cathode materials, i.e., the ionic and electronic point defect concentrations and chemical capacitance as a function of electrode potential, can be described by dilute-solution thermodynamics over a surprisingly wide Li stoichiometry range when taking site restriction effects into account. By solving the set of mass action laws defined by the available octahedral and tetrahedral lattice sites, together with the appropriate charge neutrality expression, the corresponding point defect concentrations as a function of Li activity (i.e., a Brouwer diagram) can be obtained. As long as only one type of Li site and one type of redox couple need to be considered, an analytical expression for CVchem can be derived, which depends only on the relevant defect concentrations. As soon as two or more lattice sites become relevant, such as the octahedral and tetrahedral sites in a typical spinel material, CVchem can only be calculated viaeqn (1) and therefore requires detailed knowledge of the Li chemical potential μLi and its defect concentration dependences. For oxygen-deficient LNMO, this defect chemical description is further complicated by (i) the presence of a second type of transition metal redox couple Ni2+/3+/4+ in addition to Mn3+/4+ (ii) the presence of oxygen vacancies that act as donor dopants and (iii) the potential of these oxygen vacancies to engage in charge trapping (i.e., defect association) reactions. The general formalism for calculating (i) the total Li chemical potential, and thus also CVchem, for multiple Li sites, multiple redox couples and variable doping states, as well as (ii) the relevant defect concentrations as a function of electrode potential is detailed in Section 4 of the ESI.† Herein, we restrict ourselves to a qualitative discussion of the resulting Brouwer diagrams under certain assumptions.
To simplify our brief discussion of the Ni regime around 4.7 V, we consider neither separate Ni2+/3+ and Ni3+/4+ redox regimes nor Li ordering. We treat Ni as a single type of redox couple contributing to the total capacity with one electron per formula unit, instead of considering it as two different redox couples, each contributing 0.5 electrons per formula unit. In the following analysis, an electron  on Mn corresponds to Mn3+ and an electron
on Mn corresponds to Mn3+ and an electron  on Ni corresponds to
on Ni corresponds to  , with
, with  and c0 being the concentration of formula units. In a first step, we discuss the defect concentrations as a function of Li activity (i.e., the Brouwer diagram), assuming a single tetrahedral site regime without ordering effects. For the sake of illustration, we also include a continuous octahedral site regime without any two-phase regions, even though this is not observed in experiments. The resulting Brouwer diagram is shown in Fig. 7a.
and c0 being the concentration of formula units. In a first step, we discuss the defect concentrations as a function of Li activity (i.e., the Brouwer diagram), assuming a single tetrahedral site regime without ordering effects. For the sake of illustration, we also include a continuous octahedral site regime without any two-phase regions, even though this is not observed in experiments. The resulting Brouwer diagram is shown in Fig. 7a.
 | ||
Fig. 7 Calculated Brouwer diagrams of (a) stoichiometric and (b) oxygen-deficient LNMO, neglecting Li ordering on tetrahedral sites and thus the characteristic double peak at 4.7 V. For both diagrams, charge carrier concentrations were calculated via eqn (S6), (S7), (S10), and (S11) in the ESI.†CVchem was calculated from eqn (1) by inserting μLi as derived in the ESI (eqn (S3)–(S9)).† The values  , , 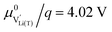 , ,  , and , and  were chosen such that the chemical capacitance peaks of the defect model occur around the same electrode potentials as observed experimentally. For the defect model of oxygen-deficient LNMO, an oxygen deficiency of δ = 0.1 was inserted into eqn (S10).† Please note that the continuous octahedral regime around 2.9 V is not observed experimentally due to the presence of a two-phase region. were chosen such that the chemical capacitance peaks of the defect model occur around the same electrode potentials as observed experimentally. For the defect model of oxygen-deficient LNMO, an oxygen deficiency of δ = 0.1 was inserted into eqn (S10).† Please note that the continuous octahedral regime around 2.9 V is not observed experimentally due to the presence of a two-phase region. | ||
As also shown for LMO,2 the Brouwer diagram of stoichiometric LNMO features two main storage regimes that correspond to the octahedral and tetrahedral sites. However, in LNMO there are two different transition metals (Mn and Ni) with redox capacities of 1.5 and 1 electron per formula unit, respectively, rather than a single transition metal (Mn) that covers the total storage capacity of two formula units in LMO. As a consequence, the voltage-dependent concentrations of electrons show a similar site-restricted behaviour as the ionic charge carriers, that is, Li vacancies and Li+ on the Li sites. In the tetrahedral site regime without ordering (around 4.7 V), the Brouwer diagram of stoichiometric LNMO resembles that of a generic layered oxide (see ref. 2, Fig. 7a). At high and low tetrahedral site occupancy,  and
and  vary with slopes of ½ and −½, respectively, with a corresponding CVchem peak in the transition region around half site occupancy, where
vary with slopes of ½ and −½, respectively, with a corresponding CVchem peak in the transition region around half site occupancy, where  . Hence, the chemical capacitance peak originates from the site restriction of both Li vacancies on the tetrahedral sites and electrons on Ni. In the hypothetical octahedral site regime around 2.9 V,
. Hence, the chemical capacitance peak originates from the site restriction of both Li vacancies on the tetrahedral sites and electrons on Ni. In the hypothetical octahedral site regime around 2.9 V,  increases with a slope of 1 at high site occupancy with [Mn4+] ≈ 0.5c0, while [Li+(O)] ≈ [Mn3+] varies with a slope of −½ at low site occupancy. These slopes are again reflected in the corresponding CVchem peak. It is also straightforward to include Li ordering in the tetrahedral regime by considering two energetically different tetrahedral sites. This was extensively discussed for pure LMO and can explain the experimentally observed characteristic double peak around 4.7 V.2 In this study, however, we focus on the effects introduced by oxygen vacancies, i.e., donor doping.
increases with a slope of 1 at high site occupancy with [Mn4+] ≈ 0.5c0, while [Li+(O)] ≈ [Mn3+] varies with a slope of −½ at low site occupancy. These slopes are again reflected in the corresponding CVchem peak. It is also straightforward to include Li ordering in the tetrahedral regime by considering two energetically different tetrahedral sites. This was extensively discussed for pure LMO and can explain the experimentally observed characteristic double peak around 4.7 V.2 In this study, however, we focus on the effects introduced by oxygen vacancies, i.e., donor doping.
Fig. 7b displays the Brouwer diagram for such an oxygen-deficient material, again without Li ordering on the tetrahedral sites. Assuming that oxygen vacancies are electronically compensated by Mn3+ according to  for LiNi0.5Mn4+1.5−2δMn3+2δO4−δ, the tetrahedral site regime is split into a low-voltage Mn (4.0 V) and a high-voltage Ni (4.7 V) subregime, as shown in Fig. 7b. Interestingly, the CVchem peaks now are no longer caused solely by Li and/or electron site restriction, but reflect transitions from ionically to electronically dominated charge compensation of the oxygen vacancies. More specifically, in the oxygen vacancy regime around 4.0 V, charge compensation switches from [Mn3+] to
for LiNi0.5Mn4+1.5−2δMn3+2δO4−δ, the tetrahedral site regime is split into a low-voltage Mn (4.0 V) and a high-voltage Ni (4.7 V) subregime, as shown in Fig. 7b. Interestingly, the CVchem peaks now are no longer caused solely by Li and/or electron site restriction, but reflect transitions from ionically to electronically dominated charge compensation of the oxygen vacancies. More specifically, in the oxygen vacancy regime around 4.0 V, charge compensation switches from [Mn3+] to  , with slopes of 1 and −1, respectively, and a corresponding peak in CVchem. The total storage capacity of this regime is defined by the oxygen vacancy concentration. Please note that this situation is fully analogous to the chemical capacitance peak observed in acceptor-doped mixed conducting oxides, where charge compensation switches from oxygen vacancies to electron holes when increasing the oxygen chemical potential.46
, with slopes of 1 and −1, respectively, and a corresponding peak in CVchem. The total storage capacity of this regime is defined by the oxygen vacancy concentration. Please note that this situation is fully analogous to the chemical capacitance peak observed in acceptor-doped mixed conducting oxides, where charge compensation switches from oxygen vacancies to electron holes when increasing the oxygen chemical potential.46
In the tetrahedral-site Ni regime around 4.7 V, the oxygen vacancies remain compensated by Li vacancies, resulting in slopes of 1 and −1 for [Ni4+] and [Li+(T)], being the minority charge carriers at high and low site occupancy, respectively. At intermediate site occupancies, where  and
and  , the slopes flatten from 1 and −1 to ½ and −½ for
, the slopes flatten from 1 and −1 to ½ and −½ for  and
and  , respectively. For the entire hypothetical octahedral site regime, oxygen vacancies remain compensated by [Mn3+], resulting in a steepening of the slope of [Li+(O)] from −½ to −1 for
, respectively. For the entire hypothetical octahedral site regime, oxygen vacancies remain compensated by [Mn3+], resulting in a steepening of the slope of [Li+(O)] from −½ to −1 for  . Since a total of 1.5 Mn4+ are available per formula unit compared to only 1 octahedral Li site, the total capacity of the octahedral regime is not affected for realistic levels of oxygen deficiency.
. Since a total of 1.5 Mn4+ are available per formula unit compared to only 1 octahedral Li site, the total capacity of the octahedral regime is not affected for realistic levels of oxygen deficiency.
Qualitatively, the tetrahedral regime (approximately 3.7 V to 5.0 V) of the Brouwer diagram for oxygen-deficient LNMO in Fig. 7b can explain several key features of the experimental data presented in Fig. 5. The inverse charge transfer resistance and the ionic conductivity both increase and decrease at low and high electrode potentials, respectively, but remain nearly constant at intermediate potentials from about 4.1 V to 4.6 V. This constancy of 1/Rct and σion is remarkably consistent with the almost constant concentration of the relevant ionic charge carrier  between the 4.0 V and 4.7 V regimes. Both 1/Rct and σion are lower for o-LNMO than for d-LNMO in the low-voltage region due to the lower oxygen vacancy and hence lower Li vacancy concentrations in this potential region. The fact that this difference almost vanishes at intermediate electrode potentials suggests a difference in the concentration-dependence of the respective ionic mobilities of d-LNMO and o-LNMO.
between the 4.0 V and 4.7 V regimes. Both 1/Rct and σion are lower for o-LNMO than for d-LNMO in the low-voltage region due to the lower oxygen vacancy and hence lower Li vacancy concentrations in this potential region. The fact that this difference almost vanishes at intermediate electrode potentials suggests a difference in the concentration-dependence of the respective ionic mobilities of d-LNMO and o-LNMO.
As predicted by Fig. 7b, CVchem exhibits two main peaks corresponding to the tetrahedral-site Mn and Ni regimes around 4.0 V and 4.7 V, respectively, the former being lower for o-LNMO due to the lower oxygen vacancy concentration. As already discussed above, the pronounced double peak measured at 4.68/4.74 V is attributed to Li ordering on tetrahedral sites, as for pure LMO.2 This effect is not included in the calculations of Fig. 7b and beyond the scope of this paper. However, at the onset of the Ni regime, around 4.6 V, both samples show a CVchem slope of ½, in agreement with Fig. 7b for high charge carrier concentrations. The region of low [Ni4+], where a slope of 1 would be expected, is not visible in the experimental data due to an overlap with the smeared out low-voltage oxygen vacancy regime (see below). In the following, we analyse the impact of oxygen deficiency on the defect chemistry of LNMO in more detail and therefore focus on the oxygen vacancy regime (Mn regime) below 4.5 V.
Defect chemical model for the oxygen vacancy regime
We start by isolating the oxygen vacancy regime (i.e., the tetrahedral-site Mn regime introduced through charge compensation of oxygen vacancies) from the full defect chemical model in Fig. 7b. Since only one Li site (tetrahedral site) and one redox couple (Mn3+/4+) are relevant in this regime, an explicit expression for the Li chemical potential can easily be derived, without resorting to the more complicated multi-site formalism in Section 4 of the ESI.† For this purpose, we consider the Li insertion equilibrium | (8) |
 corresponding to Mn3+. To account for different capacities, and thus also different site restrictions, of lattice sites and redox species, we write the site occupancy xj of species j as
corresponding to Mn3+. To account for different capacities, and thus also different site restrictions, of lattice sites and redox species, we write the site occupancy xj of species j as | (9) |
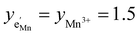 and yNi4+ = 0.5. The balance of chemical potentials can then be written as
and yNi4+ = 0.5. The balance of chemical potentials can then be written as | (10) |
 and
and  are the individual site-restricted chemical potentials of tetrahedral vacancies and electrons (or Mn3+), which are related to the respective site occupancies according to
are the individual site-restricted chemical potentials of tetrahedral vacancies and electrons (or Mn3+), which are related to the respective site occupancies according to | (11) |
 | (12) |
 | (13) |
 | (14) |
 and Li+(T) are related via
and Li+(T) are related via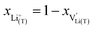 | (15) |
 | (16) |
 and yMn3+ = yMn4+ = 1.5. The system of equations defined by eqn (13)–(16) can then be solved for the four individual point defect concentrations as a function of Li activity if Kins or the corresponding standard chemical potentials μ0j are known.
and yMn3+ = yMn4+ = 1.5. The system of equations defined by eqn (13)–(16) can then be solved for the four individual point defect concentrations as a function of Li activity if Kins or the corresponding standard chemical potentials μ0j are known.
Furthermore, the chemical capacitance can be obtained by inserting eqn (9)–(12) and (14) into eqn (1). For realistic oxygen vacancy concentrations, i.e., for δ ≪ 1, site restriction of  and
and  can be neglected and eqn (11) and (12) can be simplified by assuming
can be neglected and eqn (11) and (12) can be simplified by assuming  and
and  . In this case, the chemical capacitance can be expressed as37
. In this case, the chemical capacitance can be expressed as37
 | (17) |
 and Mn3+
and Mn3+ .
.
The resulting point defect concentrations and chemical capacitance are shown in a log–log plot versus −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aLi (i.e., a Brouwer diagram) in Fig. 8a for
aLi (i.e., a Brouwer diagram) in Fig. 8a for  and Kins = 10−67.8. The value of
and Kins = 10−67.8. The value of 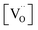 is taken from the integration of the d-LNMO CVchem data of impedance fits below 4.37 V (see eqn (7) and following paragraph). Kins is chosen such that the CVchem peak of the defect model appears at the same electrode potential versus Li+/Li as in the experimental results. Due to the clear separation of the octahedral (2.9 V), oxygen vacancy (4.0 V) and Ni tetrahedral (4.7 V) regimes in Fig. 7b, the isolated defect model of the oxygen vacancy regime (Fig. 8a) is virtually identical to the full defect model (Fig. 7b) of oxygen-deficient LNMO in the selected potential region. The Brouwer slopes of 1 and −1 in the chemical capacitance result from the corresponding variation of
is taken from the integration of the d-LNMO CVchem data of impedance fits below 4.37 V (see eqn (7) and following paragraph). Kins is chosen such that the CVchem peak of the defect model appears at the same electrode potential versus Li+/Li as in the experimental results. Due to the clear separation of the octahedral (2.9 V), oxygen vacancy (4.0 V) and Ni tetrahedral (4.7 V) regimes in Fig. 7b, the isolated defect model of the oxygen vacancy regime (Fig. 8a) is virtually identical to the full defect model (Fig. 7b) of oxygen-deficient LNMO in the selected potential region. The Brouwer slopes of 1 and −1 in the chemical capacitance result from the corresponding variation of  and [Mn3+]
and [Mn3+]  , respectively, while [Li+(T)] and [Mn4+] remain nearly constant on a logarithmic scale.
, respectively, while [Li+(T)] and [Mn4+] remain nearly constant on a logarithmic scale.
 | ||
Fig. 8 (a) Brouwer diagram and chemical capacitance of the oxygen vacancy regime extracted from Fig. 7b for  and Kins = 10−67.8. (b) Brouwer diagram and chemical capacitance of the oxygen vacancy regime, assuming energetically non-equivalent LiT* and Mn* sites, for and Kins = 10−67.8. (b) Brouwer diagram and chemical capacitance of the oxygen vacancy regime, assuming energetically non-equivalent LiT* and Mn* sites, for  and Kins = 10−68. and Kins = 10−68. | ||
A direct comparison of the chemical capacitance from impedance fits (black dots) and from the defect model in Fig. 8a (orange line) is shown in Fig. 9a and b for d-LNMO  and o-LNMO
and o-LNMO  , respectively. For both o-LNMO and d-LNMO, the defect model from Fig. 8a predicts a CVchem peak, the position of which reflects the value of Kins. The total charge contained within the CVchem peak corresponds to
, respectively. For both o-LNMO and d-LNMO, the defect model from Fig. 8a predicts a CVchem peak, the position of which reflects the value of Kins. The total charge contained within the CVchem peak corresponds to  , and enters the defect chemical calculation as a fixed parameter derived via integration of the experimental CVchem curve up to the minimum between the oxygen vacancy and Ni regimes viaeqn (7). Although the calculated CVchem curve appears to be in the same order of magnitude as the experimental data in terms of total charge (i.e., area under the peak), the calculated curve exhibits steeper slopes and significantly higher peak values for both d-LNMO and o-LNMO. Furthermore, the model fails to describe the particularly flat slope of the experimental data between 4.0 and 4.3 V. In the following, we refine the defect model by including different Li site energies close to oxygen vacancies.
, and enters the defect chemical calculation as a fixed parameter derived via integration of the experimental CVchem curve up to the minimum between the oxygen vacancy and Ni regimes viaeqn (7). Although the calculated CVchem curve appears to be in the same order of magnitude as the experimental data in terms of total charge (i.e., area under the peak), the calculated curve exhibits steeper slopes and significantly higher peak values for both d-LNMO and o-LNMO. Furthermore, the model fails to describe the particularly flat slope of the experimental data between 4.0 and 4.3 V. In the following, we refine the defect model by including different Li site energies close to oxygen vacancies.
 | ||
Fig. 9 Calculated chemical capacitance of three different defect models (continuous lines) compared to the data from impedance fits (black dots). (a) d-LNMO: experimental data and calculated chemical capacitances from Fig. 8a, b and from the multi-site model for  , p1 = 0.66, p2 = 0.21, p3 = 0.13, , p1 = 0.66, p2 = 0.21, p3 = 0.13, 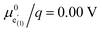 , ,  , , 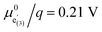 , and , and  . (b) o-LNMO: experimental data and calculated chemical capacitances from Fig. 8a, b and from the multi-site model for . (b) o-LNMO: experimental data and calculated chemical capacitances from Fig. 8a, b and from the multi-site model for  , p1 = 0.86, p2 = 0.14, , p1 = 0.86, p2 = 0.14,  , ,  , and , and  . . | ||
Chemical capacitance indicating modified tetrahedral Li sites in the oxygen vacancy regime
The defect model in Fig. 8a assumes that the tetrahedral Li sites and Mn3+/4+ redox centres being active in the oxygen vacancy regime around 4.0 V are indistinguishable from the tetrahedral Li sites involved in the tetrahedral-site Ni regime around 4.7 V and the remaining Mn sites, respectively. In other words, it is assumed that the local chemical environments surrounding each point defect are unaffected by the oxygen vacancies. However, owing to electrostatic considerations, it is reasonable to assume that Li vacancies and Mn3+ are significantly stabilized in vicinity to an oxygen vacancy. This leads us to conclude that a suitable defect chemical model for d-LNMO has to consider not only the presence of Mn3+ due to charge compensation of the oxygen vacancies, but also the different local chemical environments of the ionic and electronic point defects involved in the corresponding oxygen vacancy regime.As a first step to include defect interactions, we adapt our defect model to treat the tetrahedral Li sites and Mn3+/4+ species involved in the oxygen vacancy regime as energetically non-equivalent to the remaining Li sites and Mn redox centres. Accordingly, we assume that Li storage in the oxygen vacancy regime is locally restricted to the lattice sites in immediate proximity to the oxygen vacancies. In a first approximation, this can simply be done by relating the number of available tetrahedral lattice sites T* or electronic sites Mn* per formula unit to the oxygen nonstoichiometry δ according to yT* = yMn* = 2δ, where the asterisk denotes the non-equivalence of  , Mn4+,
, Mn4+,  , Li+(T*) and the corresponding defect species in Fig. 8a. Eqn (8)–(16) are then still valid for species j*, and can again be solved for the individual point defect concentrations [j*], with the additional condition
, Li+(T*) and the corresponding defect species in Fig. 8a. Eqn (8)–(16) are then still valid for species j*, and can again be solved for the individual point defect concentrations [j*], with the additional condition
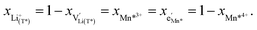 | (18) |
 | (19) |
For 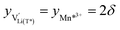 , eqn (19) simplifies into
, eqn (19) simplifies into
 | (20) |
 and Kins = 10−68. While in the original defect model in Fig. 8a, only
and Kins = 10−68. While in the original defect model in Fig. 8a, only  and [Mn3+] vary significantly and cause a relatively sharp CVchem peak with slopes of 1 and −1, the concentrations
and [Mn3+] vary significantly and cause a relatively sharp CVchem peak with slopes of 1 and −1, the concentrations  and
and  vary in concert in the adapted defect model in Fig. 8b, resulting in a relatively broad CVchem peak with slopes of ½ and −½. The total storage capacity, i.e., the total area under the CVchem curves, is the same for both models and is defined by the oxygen vacancy concentration in the material. Please note that due to the asymmetry of the defect model in Fig. 8a, the peak of CVchem appears at −log
vary in concert in the adapted defect model in Fig. 8b, resulting in a relatively broad CVchem peak with slopes of ½ and −½. The total storage capacity, i.e., the total area under the CVchem curves, is the same for both models and is defined by the oxygen vacancy concentration in the material. Please note that due to the asymmetry of the defect model in Fig. 8a, the peak of CVchem appears at −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aLi > −log
aLi > −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kins, while in the adapted (now symmetric) defect model the CVchem peak position is defined by −log
Kins, while in the adapted (now symmetric) defect model the CVchem peak position is defined by −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aLi = −log
aLi = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kins. We therefore chose a slightly lower Kins value for the defect model in Fig. 8a so that for both models the CVchem peak is located at approximately −log
Kins. We therefore chose a slightly lower Kins value for the defect model in Fig. 8a so that for both models the CVchem peak is located at approximately −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aLi = 68 (ELNMO ≈ 4.02 V versus Li+/Li), where it is observed experimentally.
aLi = 68 (ELNMO ≈ 4.02 V versus Li+/Li), where it is observed experimentally.
The comparison of the two different defect models with the experimental CVchem data is shown in Fig. 9a and b for d-LNMO and o-LNMO, respectively. The adapted defect model clearly fits the experimental data better, in terms of both CVchem slopes and absolute values. In the low-potential region below 4.0 V versus Li+/Li, the adapted model comes remarkably close to the experimental data, although the absolute values predicted by the model are slightly higher.
Interestingly, the Mn(*)3+/4+ transition and thus the CVchem peak of the oxygen vacancy regime in LNMO is very close, in terms of electrode potential, to the main Mn3+/4+ transition in LMO. This requires very similar Kins values. However, we already discussed that significant stabilisation of Li vacancies and electrons in the vicinity of oxygen vacancies are required to explain our measured CVchem data. According to eqn (13), a similar equilibrium constant Kins of LNMO and LMO despite very different standard chemical potentials  and
and  is only possible if changes of the two standard chemical potentials are very similar.
is only possible if changes of the two standard chemical potentials are very similar.
However, in the high-potential region above 4.0 V, there are still substantial deviations of the model from the measured CVchem values, with the calculated peak value being significantly higher and the slope being steeper than the experimental data. Especially for d-LNMO, the measured CVchem peak appears smeared-out towards high potentials, with a slope that is significantly flatter than predicted by both defect models in Fig. 8. It is worth mentioning that this smeared-out CVchem peak of d-LNMO is also seen in various other studies in the literature,11,13,47–49 but has received relatively little attention so far. In the following, we explain these deviations by leaving the assumption of only one  level.
level.
Chemical capacitance as a fingerprint of stabilised Mn3+
So far, our defect model explains the absolute values of the CVchem peak as well as its flattened slope close to ½ for voltages below 4.0 V. We still have to understand the even smaller slope above 4.0 V and the very broad decrease for the d-LNMO sample with a high concentration of oxygen vacancies.In principle, we face a complex situation with multiple-defect interaction including (at least) oxygen vacancies 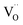 , lithium vacancies
, lithium vacancies  or occupied Li sites Li+(T*), and electrons Mn*3+. Different concepts may be employed for dealing with defect interactions, for example, activity coefficients or defect association equilibria. Owing to the complex situation with three relevant particles/defects, we choose a third approach to extend the given model with modified site energies around an oxygen vacancy. We simply introduce a finite number of different standard defect energies and thus different μ0 terms.
or occupied Li sites Li+(T*), and electrons Mn*3+. Different concepts may be employed for dealing with defect interactions, for example, activity coefficients or defect association equilibria. Owing to the complex situation with three relevant particles/defects, we choose a third approach to extend the given model with modified site energies around an oxygen vacancy. We simply introduce a finite number of different standard defect energies and thus different μ0 terms.
In this manner, we consider the existence of multiple energetically different lattice sites in proximity to oxygen vacancies, where Li storage is assumed to be located for the oxygen vacancy regime. The variations in the local chemical environments of these sites can modulate the stabilizing effect of the oxygen vacancy on both Li vacancies and electrons (Mn*3+). Additional stabilization of Li vacancies would move part of the chemical capacitance to lower electrode potentials, as the corresponding Li+(T*) is more easily removed from the lattice. For electrons, on the other hand, additional stabilization would shift part of the chemical capacitance to higher electrode potentials, as the stabilized Mn*3+ is less easily oxidised. Since the defect model in Fig. 8b is already in good agreement with the measured data below 4 V, but still shows significant deviations above 4 V, especially for d-LNMO (c.f.Fig. 9a), we refine the defect model only for electrons to account for different local chemical environments in vicinity to an oxygen vacancy.
For this purpose, we resort to the multi-site formalism described in Section 4 of the ESI.† More specifically, we consider the presence of three (d-LNMO) or two (o-LNMO) types of Mn* sites, each  site having a different value of
site having a different value of 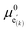 , and derive the corresponding multi-site-restricted electron chemical potential μe′ from eqn (S7) and (S9).† Since the total number of available Li(T*) and Mn* sites is the same and no additional doping effects need to be considered within the oxygen vacancy regime itself, the correction term c in eqn (S9)† can be set to zero. To assign each of the Mn* sites a fraction of the total oxygen vacancy regime capacity 2δ, the number of available lattice sites per formula unit can be defined as
, and derive the corresponding multi-site-restricted electron chemical potential μe′ from eqn (S7) and (S9).† Since the total number of available Li(T*) and Mn* sites is the same and no additional doping effects need to be considered within the oxygen vacancy regime itself, the correction term c in eqn (S9)† can be set to zero. To assign each of the Mn* sites a fraction of the total oxygen vacancy regime capacity 2δ, the number of available lattice sites per formula unit can be defined as 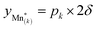 , with 0 ≤ pk ≤ 1, ∑pk = 1, and
, with 0 ≤ pk ≤ 1, ∑pk = 1, and  . Thus, the pk factors indicate the fraction of the total oxygen vacancy regime capacity that is attributed to each
. Thus, the pk factors indicate the fraction of the total oxygen vacancy regime capacity that is attributed to each  site. The resulting μe' can then be inserted into eqn (10), together with the unchanged
site. The resulting μe' can then be inserted into eqn (10), together with the unchanged  from eqn (11), to obtain the total Li chemical potential μLi and finally the chemical capacitance viaeqn (1).
from eqn (11), to obtain the total Li chemical potential μLi and finally the chemical capacitance viaeqn (1).
The resulting chemical capacitance curves (green line) are shown in comparison to the experimental data and the previous defect models in Fig. 9a and b for d-LNMO (δ = 0.095) and o-LNMO (δ = 0.021), respectively. The corresponding subregimes for each  site are indicated as dotted lines. For both plots, the values of
site are indicated as dotted lines. For both plots, the values of  and pk were chosen manually to approximate the experimental data, as indicated in the figure caption. Please note that, although a mathematical fitting algorithm could in principle be applied to obtain the closest approximation, the conclusions of our qualitative discussion would remain the same. For both d-LNMO and o-LNMO, the calculated CVchem curves are in good agreement with the experimental data for the entire relevant voltage range (up to 4.37 and 4.21 V versus Li+/Li for d-LNMO and o-LNMO, respectively).
and pk were chosen manually to approximate the experimental data, as indicated in the figure caption. Please note that, although a mathematical fitting algorithm could in principle be applied to obtain the closest approximation, the conclusions of our qualitative discussion would remain the same. For both d-LNMO and o-LNMO, the calculated CVchem curves are in good agreement with the experimental data for the entire relevant voltage range (up to 4.37 and 4.21 V versus Li+/Li for d-LNMO and o-LNMO, respectively).
As expected for a multi-site model, the CVchem peaks are now split into three/two sub-peaks for d-/o-LNMO. For both samples, the model features sub-peaks at 4.02 V and 4.17 V, with d-LNMO having an additional sub-peak at 4.28 V. Each sub-peak corresponds to a different  , with the total capacity remaining the same as for defect models from Fig. 8a and b. The relative capacities of the peaks were set to p1 = 0.66, p2 = 0.21, p3 = 0.13 for d-LNMO, and p1 = 0.86, p2 = 0.14 for o-LNMO.
, with the total capacity remaining the same as for defect models from Fig. 8a and b. The relative capacities of the peaks were set to p1 = 0.66, p2 = 0.21, p3 = 0.13 for d-LNMO, and p1 = 0.86, p2 = 0.14 for o-LNMO.
For d-LNMO, the multi-site model correctly describes the smeared-out chemical capacitance curve towards higher electrode potentials, although the calculated curve still exhibits a wavier profile than the experimental data. In principle, this could be corrected by assuming a larger number of  sites with slightly different values of
sites with slightly different values of  . Given the large variety of possible local chemical environments of oxygen vacancies in disordered LNMO,17 this would be a plausible assumption.
. Given the large variety of possible local chemical environments of oxygen vacancies in disordered LNMO,17 this would be a plausible assumption.
For o-LNMO, the multi-site model also gives a good fit of the experimental data, with the peak at 4.17 V being significantly diminished compared to d-LNMO and the third peak at 4.28 V being completely obsolete. Thus, while the CVchem curve of d-LNMO in the oxygen vacancy regime is stretched out towards higher electrode potentials due to additional stabilisation of Mn*3+, the o-LNMO sample largely follows the single-site behaviour from Fig. 8b. This suggests that the two samples differ not only in their oxygen vacancy concentrations, but also in the variety of local chemical environments surrounding each oxygen vacancy, which excellently agrees with the well-established correlation of Ni-disorder and oxygen-deficiency.17
Finally, we can illustrate the impact of oxygen vacancies on the shape of charge curves, which are obtained by integration of CVchem according to eqn (7). First, we compare the capacity-normalised charge curves of the oxygen vacancy regime for d-LNMO, o-LNMO and the ideal defect model in Fig. 8b. As shown in Fig. 10a, the additional stabilising defect interactions of oxygen vacancies and Mn*3+ in the multi-site model lead to an upwards shift of the charge curve towards higher electrode potentials, thereby raising the average voltage in the oxygen vacancy regime. As expected from the respective distributions of CVchem in Fig. 9, this effect is more pronounced for d-LNMO than for o-LNMO. The corresponding increase in energy density is marked in Fig. 10b as the area between the calculated charge curves with and without multi-site electron (Mn*3+) stabilisation. Not only is the additional stabilisation of Mn*3+ stronger for d-LNMO than for o-LNMO, but the total impact on the average voltage, and hence energy density, is further scaled up by the higher level of oxygen deficiency (δ) in d-LNMO.
 | ||
| Fig. 10 (a) Charge curves of the oxygen vacancy regime calculated by integration of CVchemviaeqn (7) for the single-site model in Fig. 8b and the multi-site models in Fig. 9. Capacities were normalised by 2δ to allow a direct comparison between d-LNMO and o-LNMO. (b) Calculated charge curves of d-LNMO and o-LNMO showing the impact of oxygen deficiency and additional Mn*3+ stabilisation in the multi-site model. (c) Impact of oxygen deficiency and defect interactions on the calculated energy density of LNMO compared to stoichiometric LNMO for 0 ≤ x ≤ 1. For the Ni regime (2δ ≤ x ≤ 1), an average electrode potential of 4.72 V vs. Li+/Li was assumed. | ||
On the other hand, an increase in δ also reduces the average voltage of the overall tetrahedral-site regime by moving part of its capacity from the high-voltage Ni to the lower-voltage Mn (oxygen vacancy) region. This leads to a trade-off between charge compensation by Mn*3+, which lowers the average voltage, and the additional multi-site stabilisation of Mn*3+ by oxygen vacancies, which again compensates at least part of the voltage loss. As shown in Fig. 10c, the lower energy density of the o-LNMO sample compared to ideal stoichiometric LNMO is still dominated by the level of charge compensation due to oxygen deficiency, and only a very small fraction of this loss is regained by multi-site electron stabilisation. For d-LNMO, on the other hand, a significant fraction of the energy density loss is compensated, thus mitigating the negative impact of oxygen vacancies on the average voltage.
These considerations raise the question whether oxygen vacancies and the accompanying electron (Mn3+) stabilisation might also increase the average voltage and energy density in LiMn2O4−δ cathodes. In fact, Wang et al. recently reported differential capacity curves of oxygen-deficient LMO samples, which appear shifted by more than +50 mV with respect to nearly stoichiometric LMO,50 and are therefore consistent with our results for oxygen-deficient LNMO.
Experimental
Sample preparation
Thin films of SrRuO3 (SRO) and LiNi0.5Mn1.5O4−δ (LNMO) were deposited onto the polished side of (100)-oriented SrTiO3 (STO) single crystal substrates of dimensions 10 × 10 × 0.5 mm3 (MaTecK, Germany) by means of radio-frequency magnetron sputtering in a custom-built deposition chamber (Huber Scientific, Austria), using commercial 2′′ targets obtained from Advanced Engineering Materials (China) and Loyaltarget (China), respectively. To ensure a good electrical contact around the edges to the backside, the substrate edges were roughened with fine sandpaper and sputter-coated with a 5/200 nm bilayer of Ti/Pt by means of DC sputtering (room temperature, Ar atmosphere, 0.7/2.0 Pa, 5 mA cm−2) prior to SRO/LNMO deposition. The nominal substrate temperature was determined via a power-temperature calibration of the heating stage using a polished (100)-oriented Y:ZrO2 single crystal (9.5 mol% Y2O3, CrysTec, Germany) and an optical pyrometer, assuming a surface emissivity of ε = 0.9. SRO was deposited in a gas mixture of Ar![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 = 3
O2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at a total pressure of 2.5 Pa, a nominal substrate temperature of 650 °C, and a power of 60 W, resulting in a film thickness of approximately 80 nm, as estimated by TEM. LNMO was deposited under oxygen atmosphere at a pressure of 2.5 Pa, a nominal substrate temperature of 550 °C, and a power of 60 W, resulting in a film thickness of approximately 70 nm, as estimated by TEM. For d-LNMO, the sample was cooled down at a rate of 30 °C min−1 immediately after deposition while maintaining an oxygen partial pressure of 2.5 Pa. For o-LNMO, the nominal substrate temperature was kept at 550 °C after deposition while gradually flooding the deposition chamber with oxygen over the course of 5 h. For this purpose, a separate temperature calibration at atmospheric pressure was used. Finally, the o-LNMO sample was kept at 550 °C under 1 atm of oxygen for 1 h, followed by a cool-down at 15 °C min−1. After LNMO deposition, the sample backside was sputter coated with another Ti/Pt bilayer to ensure a good electrical contact to the steel plunger of the electrochemical measuring cell. Due to the characteristic concentric variation of the deposition rate during magnetron sputtering and the large substrate area compared to the target size, a certain degree of thickness variation in the SRO and LNMO thin films across the sample is expected, and the film thicknesses measured by TEM can only be taken as approximate values for the whole sample.
1 at a total pressure of 2.5 Pa, a nominal substrate temperature of 650 °C, and a power of 60 W, resulting in a film thickness of approximately 80 nm, as estimated by TEM. LNMO was deposited under oxygen atmosphere at a pressure of 2.5 Pa, a nominal substrate temperature of 550 °C, and a power of 60 W, resulting in a film thickness of approximately 70 nm, as estimated by TEM. For d-LNMO, the sample was cooled down at a rate of 30 °C min−1 immediately after deposition while maintaining an oxygen partial pressure of 2.5 Pa. For o-LNMO, the nominal substrate temperature was kept at 550 °C after deposition while gradually flooding the deposition chamber with oxygen over the course of 5 h. For this purpose, a separate temperature calibration at atmospheric pressure was used. Finally, the o-LNMO sample was kept at 550 °C under 1 atm of oxygen for 1 h, followed by a cool-down at 15 °C min−1. After LNMO deposition, the sample backside was sputter coated with another Ti/Pt bilayer to ensure a good electrical contact to the steel plunger of the electrochemical measuring cell. Due to the characteristic concentric variation of the deposition rate during magnetron sputtering and the large substrate area compared to the target size, a certain degree of thickness variation in the SRO and LNMO thin films across the sample is expected, and the film thicknesses measured by TEM can only be taken as approximate values for the whole sample.
Structural characterisation
Out-of-plane X-ray diffractograms were recorded from 2θ = 15° to 80° on an Empyrean X-ray diffractometer (Malvern Panalytical, UK) using a hybrid Kα monochromator of type 2XGe(220) on the incident beam side and a GaliPIX3D area detector in scanning line mode on the diffracted beam side. AFM images of the sample surface were acquired on a Nanoscope V multimode setup (Bruker) and analysed using the open-source software Gwyddion.51 Electron-transparent lamellae for TEM investigations were prepared by standard lift-out techniques on a Thermo Fisher Scios 2 DualBeam FIB/SEM operating with a Ga-ion beam at 30 kV accelerating voltage. Final thinning and low-voltage polishing steps were carried out at 5 kV and 2 kV to reduce the amount of surface amorphization on the lamellae. All TEM imaging was carried out on a JEOL JEM-2100F field-emission gun microscope equipped with an image-side spherical aberration corrector, operating at an accelerating voltage of 200 kV. TEM images were acquired on a Gatan Orris SC1000 CCD camera. High-resolution TEM images were further processed using an average background subtraction filter (ABSF).Electrochemical characterisation
For electrochemical measurements, the thin-film samples were assembled in a two-electrode cell (PAT-Cell, EL-CELL, Germany) using a 260 μm glass-fibre separator (EL-CELL), 80 μL of a standard organic liquid electrolyte (1 M LiPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ethylene carbonate and dimethyl carbonate, Aldrich, USA), and a Li metal counter electrode (10 × 10 × 0.6 mm3, Goodfellow, Germany). All electrochemical measurements were carried out at room temperature on a SP200 Biologic potentiostat with a built-in impedance analyser. Cyclic voltammetry was carried out with a scan rate of 1 mV s−1 in the voltage range of 3.7 to 4.9 V versus Li+/Li for 5 cycles before starting the series of impedance measurements. Potential-controlled impedance spectra were acquired in the frequency range of 200 kHz to 10 mHz (6 points per decade) using a perturbation amplitude of 10 mV. In the voltage range of 3.8 to 4.9 V versus Li+/Li, spectra were recorded in increments of 10 mV with intermittent equilibration (i.e., constant voltage) steps of 5 min. The sufficiency of this equilibration time was verified by monitoring the flattening out of the exponential current decrease in response to an applied voltage step and comparing impedance spectra measured after various equilibration times. Since the measured current decreases to virtually static levels within 5 min and no significant changes of the impedance spectra are observed for longer equilibration times, we regard this time as sufficient to reach equilibrium.
1 mixture of ethylene carbonate and dimethyl carbonate, Aldrich, USA), and a Li metal counter electrode (10 × 10 × 0.6 mm3, Goodfellow, Germany). All electrochemical measurements were carried out at room temperature on a SP200 Biologic potentiostat with a built-in impedance analyser. Cyclic voltammetry was carried out with a scan rate of 1 mV s−1 in the voltage range of 3.7 to 4.9 V versus Li+/Li for 5 cycles before starting the series of impedance measurements. Potential-controlled impedance spectra were acquired in the frequency range of 200 kHz to 10 mHz (6 points per decade) using a perturbation amplitude of 10 mV. In the voltage range of 3.8 to 4.9 V versus Li+/Li, spectra were recorded in increments of 10 mV with intermittent equilibration (i.e., constant voltage) steps of 5 min. The sufficiency of this equilibration time was verified by monitoring the flattening out of the exponential current decrease in response to an applied voltage step and comparing impedance spectra measured after various equilibration times. Since the measured current decreases to virtually static levels within 5 min and no significant changes of the impedance spectra are observed for longer equilibration times, we regard this time as sufficient to reach equilibrium.
Conclusions
The electrochemical properties (charge transfer resistance Rct, ionic conductivity σion, specific chemical capacitance CVchem and chemical diffusion coefficient![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) of LiNi0.5Mn1.5O4−δ thin films were investigated by cyclic voltammetry and impedance spectroscopy as a function of SOC for high (d-LNMO) and low (o-LNMO) levels of oxygen deficiency δ. The extracted properties vary by up to three orders of magnitude, with the most notable differences between d-LNMO and o-LNMO being observed in the oxygen vacancy regime below approximately 4.3 V versus Li+/Li, where d-LNMO exhibits significantly higher values of 1/Rct, σion, CVchem, and (up to 4.15 V)
) of LiNi0.5Mn1.5O4−δ thin films were investigated by cyclic voltammetry and impedance spectroscopy as a function of SOC for high (d-LNMO) and low (o-LNMO) levels of oxygen deficiency δ. The extracted properties vary by up to three orders of magnitude, with the most notable differences between d-LNMO and o-LNMO being observed in the oxygen vacancy regime below approximately 4.3 V versus Li+/Li, where d-LNMO exhibits significantly higher values of 1/Rct, σion, CVchem, and (up to 4.15 V) ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) than o-LNMO. Overall, the measured electrochemical properties are in excellent agreement with a defect chemical model based on ionic and electronic lattice site restrictions, with oxygen vacancies acting as a donor dopant.
than o-LNMO. Overall, the measured electrochemical properties are in excellent agreement with a defect chemical model based on ionic and electronic lattice site restrictions, with oxygen vacancies acting as a donor dopant.
Closer analysis of the oxygen vacancy regime revealed that oxygen vacancies are not merely charge-compensated by Mn3+ or Li vacancies, but are involved in defect interactions that significantly impact the charge curve. For both d-LNMO and o-LNMO, the charge curve below 4.0 V is accurately described by a single-site defect model that treats the tetrahedral Li sites T* and Mn sites (Mn*) as locally restricted to the proximity of an oxygen vacancy due to stabilisation (i.e., trapping) of electrons and Li vacancies. For a high level of oxygen deficiency (d-LNMO), the charge curve in the oxygen vacancy regime bends upwards towards higher electrode potentials, thus mitigating the voltage suppression introduced through to the presence of Mn*3+. This characteristic feature of the charge curve suggests that the oxygen vacancy concentration not only affects the amount of redox active Mn*3+/4+, but also causes multiple energetically different electron sites in the vicinity of an oxygen vacancy.
Overall, these results reveal the complexity of effects introduced by oxygen vacancies in oxide-based Li insertion materials, but also the power of chemical capacitance measurements to understand and interpret the corresponding phenomena. Moreover, this study once more highlights the relevance of defect chemical concepts for understanding the complex interplay of ionic and electronic charge carriers in all battery materials.
Author contributions
A. E. Bumberger: conceptualization (equal), investigation (lead), writing – original draft, S. Raznjevic: investigation (supporting), Z. Zhang: funding acquisition, M. Kubicek: funding acquisition, G. Friedbacher: investigation (supporting), J. Fleig: supervision, conceptualization (equal), writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by Austrian Science Fund (FWF) project P31654-N37 is gratefully acknowledged.References
- A. E. Bumberger, C. Steinbach, J. Ring and J. Fleig, Chem. Mater., 2022, 34, 10548–10560 CrossRef CAS PubMed.
- A. E. Bumberger, C. Boehme, J. S. Ring, S. Raznjevic, Z. Zhang, M. Kubicek and J. Fleig, Chem. Mater., 2023, 35, 5135–5149 CrossRef CAS PubMed.
- Y. Zhu and J. Maier, Adv. Mater., 2023, 35, 2304666 CrossRef CAS PubMed.
- Y. Gao, K. Myrtle, M. J. Zhang, J. N. Reimers and J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16670–16675 CrossRef CAS PubMed.
- M. Hu, X. L. Pang and Z. Zhou, J. Power Sources, 2013, 237, 229–242 CrossRef CAS.
- J. H. Kim, S. T. Myung, C. S. Yoon, S. G. Kang and Y. K. Sun, Chem. Mater., 2004, 16, 906–914 CrossRef CAS.
- A. Kraytsberg and Y. Ein-Eli, Adv. Energy Mater., 2012, 2, 922–939 CrossRef CAS.
- J. C. Li, C. Ma, M. F. Chi, C. D. Liang and N. J. Dudney, Adv. Energy Mater., 2015, 5, 1401408 CrossRef.
- D. Pritzl, A. E. Bumberger, M. Wetjen, J. Landesfeind, S. Solchenbach and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, A582–A590 CrossRef CAS.
- R. Santhanam and B. Rambabu, J. Power Sources, 2010, 195, 5442–5451 CrossRef CAS.
- L. P. Wang, H. Li, X. J. Huang and E. Baudrin, Solid State Ionics, 2011, 193, 32–38 CrossRef CAS.
- T. F. Yi, Y. Xie, M. F. Ye, L. J. Jiang, R. S. Zhu and Y. R. Zhu, Ionics, 2011, 17, 383–389 CrossRef CAS.
- Q. M. Zhong, A. Bonakdarpour, M. J. Zhang, Y. Gao and J. R. Dahn, J. Electrochem. Soc., 1997, 144, 205–213 CrossRef CAS.
- J. Cabana, M. Casas-Cabanas, F. O. Omenya, N. A. Chernova, D. L. Zeng, M. S. Whittingham and C. P. Grey, Chem. Mater., 2012, 24, 2952–2964 CrossRef CAS PubMed.
- J. Xiao, X. L. Chen, P. V. Sushko, M. L. Sushko, L. Kovarik, J. J. Feng, Z. Q. Deng, J. M. Zheng, G. L. Graff, Z. M. Nie, D. W. Choi, J. Liu, J. G. Zhang and M. S. Whittingham, Adv. Mater., 2012, 24, 2109–2116 CrossRef CAS PubMed.
- J. M. Zheng, J. Xiao, X. Q. Yu, L. Kovarik, M. Gu, F. Omenya, X. L. Chen, X. Q. Yang, J. Liu, G. L. Graff, M. S. Whittingham and J. G. Zhang, Phys. Chem. Chem. Phys., 2012, 14, 13515–13521 RSC.
- P. V. Sushko, K. M. Rosso, J. G. Zhang, J. Liu and M. L. Sushko, Adv. Funct. Mater., 2013, 23, 5530–5535 CrossRef CAS.
- E. Y. Hu, S. M. Bak, J. Liu, X. Q. Yu, Y. N. Zhou, S. N. Ehrlich, X. Q. Yang and K. W. Nam, Chem. Mater., 2014, 26, 1108–1118 CrossRef CAS.
- J. H. Kim, A. Huq, M. F. Chi, N. P. W. Pieczonka, E. Lee, C. A. Bridges, M. M. Tessema, A. Manthiram, K. A. Persson and B. R. Powell, Chem. Mater., 2014, 26, 4377–4386 CrossRef CAS.
- R. Amin and I. Belharouk, J. Power Sources, 2017, 348, 311–317 CrossRef CAS.
- M. Hosoya, H. Ikuta, T. Uchida and M. Wakihara, J. Electrochem. Soc., 1997, 144, L52–L53 CrossRef CAS.
- Y. Koyama, I. Tanaka, H. Adachi, Y. Uchimoto and M. Wakihara, J. Electrochem. Soc., 2003, 150, A63–A67 CrossRef CAS.
- H. Shiiba, N. Zettsu, M. Nakayama, S. Oishi and K. Teshima, J. Phys. Chem. C, 2015, 119, 9117–9124 CrossRef CAS.
- Z. K. Tang, Y. F. Xue, G. Teobaldi and L. M. Liu, Nanoscale Horiz., 2020, 5, 1453–1466 RSC.
- J. H. Kim, J. W. Jung, S. H. Cho, I. D. Kim, Y. C. Park, D. H. Seo and H. S. Kim, Small, 2022, 18, 2201134 CrossRef CAS PubMed.
- J. Cen, B. Zhu, S. R. Kavanagh, A. G. Squires and D. O. Scanlon, J. Mater. Chem. A, 2023, 11, 13353 RSC.
- Y. Gao, J. N. Reimers and J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3878–3883 CrossRef CAS PubMed.
- B. Ammundsen, J. Roziere and M. S. Islam, J. Phys. Chem. B, 1997, 101, 8156–8163 CrossRef CAS.
- J. Barker, R. Koksbang and M. Y. Saidi, Solid State Ionics, 1995, 82, 143–151 CrossRef CAS.
- R. J. Gummow and M. M. Thackeray, J. Electrochem. Soc., 1994, 141, 1178–1182 CrossRef CAS.
- K. Ooi, Y. Miyai, S. Katoh, H. Maeda and M. Abe, Langmuir, 1989, 5, 150–157 CrossRef CAS.
- Y. H. Rho, K. Dokko and K. Kanamura, J. Power Sources, 2006, 157, 471–476 CrossRef CAS.
- J. Xie, K. Kohno, T. Matsumura, N. Imanishi, A. Hirano, Y. Takeda and O. Yamamoto, Electrochim. Acta, 2008, 54, 376–381 CrossRef CAS.
- M. Adamic, S. D. Talian, A. R. Sinigoj, I. Humar, J. Moskon and M. Gaberscek, J. Electrochem. Soc., 2018, 166, A5045–A5053 CrossRef.
- J. Jamnik and J. Maier, J. Electrochem. Soc., 1999, 146, 4183–4188 CrossRef CAS.
- J. Jamnik and J. Maier, Phys. Chem. Chem. Phys., 2001, 3, 1668–1678 RSC.
- J. Jamnik, J. Maier and S. Pejovnik, Electrochim. Acta, 1999, 44, 4139–4145 CrossRef CAS.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS.
- J. Maier, Solid State Phenom., 1994, 39–40, 35–60 Search PubMed.
- J. Maier, Z. Naturforsch., B: J. Chem. Sci., 2020, 75, 15–22 CrossRef CAS.
- J. Bisquert and A. Compte, J. Electroanal. Chem., 2001, 499, 112–120 CrossRef CAS.
- M. Mohamedi, A. Makino, K. Dokko, T. Itoh and I. Uchida, Electrochim. Acta, 2002, 48, 79–84 CrossRef CAS.
- M. Gellert, K. I. Gries, J. Zakel, A. Ott, S. Spannenberger, C. Yada, F. Rosciano, K. Volz and B. Roling, Electrochim. Acta, 2014, 133, 146–152 CrossRef CAS.
- H. Xia, Y. S. Meng, L. Lu and G. Ceder, J. Electrochem. Soc., 2007, 154, A737–A743 CrossRef CAS.
- A. Ito, D. Li, Y. Lee, K. Kobayakawa and Y. Sato, J. Power Sources, 2008, 185, 1429–1433 CrossRef CAS.
- A. Schmid, G. M. Rupp and J. Fleig, Phys. Chem. Chem. Phys., 2018, 20, 12016–12026 RSC.
- S. H. Park, S. W. Oh, S. H. Kang, I. Belharouak, K. Amine and Y. K. Sun, Electrochim. Acta, 2007, 52, 7226–7230 CrossRef CAS.
- Y. Wang, Q. Peng, G. Yang, Z. Yang, L. C. Zhang, H. Long, Y. H. Huang and P. X. Lu, Electrochim. Acta, 2014, 136, 450–456 CrossRef CAS.
- C. L. Lin, J. X. Yin, S. R. Cui, X. Huang, W. Liu and Y. C. Jin, ACS Appl. Mater. Interfaces, 2023, 15, 16778–16793 CrossRef CAS PubMed.
- J. Wang, H. Y. Xing, W. Q. Hou and Y. L. Xu, Phys. Chem. Chem. Phys., 2023, 25, 18903–18914 RSC.
- D. Necas and P. Klapetek, Cent. Eur. J. Phys., 2012, 10, 181–188 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05086f |
| This journal is © The Royal Society of Chemistry 2023 |




