Thermoelectric properties of the aliovalent half-Heusler alloy Zn_0.5Ti_0.5NiSb with intrinsic low thermal conductivity

Abstract

Using mixtures of aliovalent elements to achieve a valence balanced electronic state is a rapidly emerging area in half-Heusler thermoelectric materials research. Here, we report on Zn_0.5Ti_0.5NiSb, a combination of ZnNiSb and TiNiSb, which by adjusting the Zn/Ti-ratio can be made p- and n-type, achieving peak zT = 0.18 at 793 K and zT = 0.33 at 700 K, respectively. These promising values are underpinned by a low lattice thermal conductivity, κ_L = 2.7 W m⁻¹ K⁻¹ at 340 K, similar for all samples, decreasing to 1.25 W m⁻¹ K⁻¹ at 793 K. Transport data reveal similar weighted electronic mobilities for p- and n-type samples, suggesting similar zT should be possible. For both polarities, a transition to degenerate conduction is observed, superposed on intrinsic semiconducting behaviour with a bandgap E_g = 0.4 eV. Neutron and synchrotron X-ray diffraction experiments, including total scattering, indicate the absence of interstitial metals and do not reveal strong local structural variations. The absence of substantial mass disorder and lattice strain points towards bond disorder as a possible origin for the low κ_L. This work describes a new materials system and provides further insight into the impact of aliovalent alloying in the half-Heusler structure.

---

1. Introduction

Thermoelectric technology has applications in waste heat recovery, energy scavenging and thermal management.^1–8 The thermoelectric performance of a material is given by its figure of merit, zT = (S²/ρκ)T, where S is the absolute Seebeck coefficient, ρ is the electrical resistivity and κ the thermal conductivity, which has lattice (κ_L) and electronic (κ_E) components, and T is the absolute temperature.³ Half-Heusler (HH) alloy materials are leading contenders for application in mid-temperature power generation applications. In addition to good thermoelectric performance, they satisfy important engineering requirements, including mechanical strength, stability, facile electrical and thermal contacting, and they are based on sustainable raw materials if the use of Hf can be avoided.^9–14 Within the already substantial class of HH materials a new direction has recently emerged, focusing on valence balanced mixtures of aliovalent elements that achieve a semiconducting electron count.¹⁵ This approach greatly expands the number of possible HH materials and has led to a significant new research activity,^15–29 extending to high entropy compositions when mixing >5 components.^30–32 Archetypal HH materials with XYZ composition, such as ZrNiSn and NbFeSb are characterized by large power factors (S²/ρ = 5–10 mW m⁻¹ K⁻²) and high κ_L = 10–20 W m⁻¹ K⁻¹, reflecting their symmetric “tetrahedral” structure with strong chemical bonds.^14,33–37 The new aliovalent compositions have intrinsically low κ_L (e.g. ∼6.5 W m⁻¹ K⁻¹ at 340 K for TiFe_0.5Ni_0.5Sb compared to ∼15 W m⁻¹ K⁻¹ for TiCoSb) and modest S²/ρ (e.g. ∼1.5 mW m⁻¹ K⁻² for TiFe_0.5Ni_0.5Sb).¹⁶ The origin of this intrinsic low κ_L is not fully explained. Initial work considered ordered variants, i.e. a lower symmetry structure with Fe and Ni arranged in a checkerboard pattern.¹⁵ Calculations showed reduced phonon velocities and increased Umklapp scattering, consistent with a low κ_L.¹⁵ However, there is no experimental evidence for ordering of the aliovalent metals in any of the studied systems, and it is unclear if the results of these calculations carry over into the real (disordered) materials. The lack of ordering implies that the sometimes-used nomenclature of double (or triple, etc.) HHs is something of a misnomer, as noted in the original publication.¹⁵ Mechanical properties and velocity of sound are not markedly different compared to XYZ compositions, indicating that the observed low κ_L and compromised S²/ρ are due to disorder that reduces the phonon and electron mean free path.^16,19 The usual contributors to atomic-scale disorder are mass fluctuations and lattice strain due to size differences of the elements present.³⁸ However, these disorder effects are small for most of the aliovalent compositions as they contain elements with similar mass and size. In some compositions, vacancies and/or interstitials have been observed, and this would cause large disorder,^39–42 but it remains unclear if this occurs for all aliovalent HH alloys.^21,25

Most work on aliovalent HHs has focused on compositions with mixtures of Y-site elements. In case of Zn_0.5Ti_0.5NiSb, the aliovalent mixing (formal oxidation states of Zn²⁺ and Ti⁴⁺) occurs on the X-site, which is octahedrally coordinated by Sb.⁹ This local structure contrasts with the Y-site, which has 4 X and 4 Z neighbours, each in tetrahedral coordination.⁹ To date, two other X-site aliovalent HH alloys have been investigated. Both contain 17-electron MgNiSb, combined with TiNiSb (19 electrons) or VNiSb (20 electrons) to yield valence balanced 18-electron Mg_0.5Ti_0.5NiSb and Mg_0.67V_0.33NiSb compositions.^20,25 Both compositions have low κ_L with 340 K values ∼4.5 W m⁻¹ K⁻¹ for Mg_0.5Ti_0.5NiSb and ∼2.5 W m⁻¹ K⁻¹ for Mg_0.67V_0.33NiSb, substantially lower than found for Y-site systems like TiFe_0.5Ni_0.5Sb. This suggests that the disorder introduced by aliovalent X-site mixing is stronger than for the Y-site systems. In case of Mg_1−xTi_xNiSb, peak zT ∼0.4 is found for both p- (x = 0.48) and n-type (x = 0.6) compositions at 950 K.²⁵ Mg_0.67V_0.33NiSb has a lower peak zT ∼0.17 at 750 K, but has not yet benefitted from an optimisation study.²⁰ The largest zT values for the aliovalent HH alloys, without additional Hf alloying, are found for TiFe_1−xNi_xSb with zT = 0.7 (p-type, x = 0.4) and zT = 0.5 (n-type, x = 0.6) at 973 K, reflecting a better trade-off between electronic mobility and low κ_L.¹⁶

Zn_0.5Ti_0.5NiSb is an analogue of Mg_0.5Ti_0.5NiSb combining 17-electron ZnNiSb and 19-electron TiNiSb to form a stable 18-electron semiconducting composition. This is schematically illustrated in Fig. 1a, including its relationship to a regular 18-electron XYZ HH alloy, ScNiSb in this example. Adjusting the Zn/Ti ratio can be used to control the carrier polarity, with Zn donating two electrons and Ti four electrons. Stable Zn_1−xTi_xNiSb compositions can be prepared between 0.35 ≤ x ≤ 0.65. The most significant feature of these materials is the low κ_L ∼2.7 W m⁻¹ K⁻¹ at 340 K, which occurs without substantial mass and size disorder from our diffraction and total scattering data. In terms of electronic properties, Zn_1−xTi_xNiSb shows a transition from semiconducting (x ∼0.5) to degenerately doped behaviour for both n- (x > 0.5) and p-type doping (x < 0.5). Competitive highest zT values of 0.18 (793 K) and 0.33 (700 K) are observed for p- and n-type compositions. It is worth noting that TiNiSb, the x = 1 end-member of the Zn_1−xTi_xNiSb series, forms with large amounts of Ti vacancies. Based on electron counting, Ti_0.75NiSb has 18 valence electrons. Experimentally strongly n-type doped compositions near Ti_0.8NiSb are found.^43–45 The large concentration of Ti vacancies strongly impacts on the thermoelectric properties with low κ_L values observed. However, for Ti_0.8NiSb, this is likely linked to the large mass disorder caused by the vacancies.

Fig. 1 (a) Schematic phase diagram linking 17 electron ZnNiSb, 19 electron TiNiSb and 18 electron ScNiSb. (b) Stacked X-ray powder diffraction datasets for the Zn_1−xTi_xNiSb samples prepared in this study. The * and ▼ symbols represent graphite and an unknown impurity in the x = 0.35 sample. (c) Evolution of the half-Heusler lattice parameter; linear extrapolation reveals a continuous change towards Ti_0.8NiSb indicating that further substitution of Ti is possible and that Ti vacancies are introduced; the plateau in the direction of ZnNiSb reveals the limit of Zn solubility under the used synthetic conditions. (d) Rietveld fit to neutron powder diffraction data collected on a Ti_0.5Zn_0.5NiSb sample, confirming that Zn/Ti are located on the X-site, and not giving any indication of the presence of interstitial metals.

2. Results

2.1 Phase stability and crystal structure

Fig. 1 gives an overview of the phase behaviour of the Zn_1−xTi_xNiSb samples. Samples were successfully prepared between x = 0.35 (Zn rich) and x = 0.65 (Ti rich), i.e. extending 0.15 holes/electrons away from the 18-electron x = 0.5 composition (Fig. 1b). The evolution of the lattice parameter (Fig. 1c) confirms that, at the Zn-rich end, x = 0.40 corresponds to the solubility limit under the used synthetic conditions. At the Ti-rich side, linear extrapolation of the lattice parameter beyond x = 0.65 matches with the reported value for Ti_0.8NiSb,⁴⁴ suggesting (1) that larger x values are accessible and (2) that Ti vacancies are gradually introduced for x > 0.5. SEM-EDX analysis showed samples to be highly homogeneous with no compositional segregation at the micrometre length scale (Fig. S1 and S2 in the ESI†). Minor Ti impurities occur at grain boundaries, most obvious for the Ti-rich compositions, while Zn-rich samples show slight reaction towards the Ta foil used for sample containment. Zn-rich samples show less damage after polishing, suggesting that polycrystalline domains are bonded stronger. Overall, SEM-EDX confirms the purity of the prepared samples with compositions in agreement with nominal values (Table S1†). The presence of minor Ti impurities for x > 0.5 is consistent with the gradual introduction of Ti vacancies, as predicted from the lattice parameter evolution (Fig. 1c). Assuming a linear increase of Ti vacancies, our x = 0.65 composition could have a vacancy fraction near 0.04, which is difficult to confirm from site occupancy analysis in Rietveld fits of laboratory X-ray diffraction data. Another outstanding question is the location of Zn in the crystal structure. According to its +2 formal oxidation state and similarity in behaviour to Mg, it is expected to occupy the X-site. However, its location in the periodic table after Ni suggests that it could also be accommodated on the Y-site.¹⁵ Neutron powder diffraction, which offers good scattering contrast between Ti (b = −3.4 fm), Zn (b = 5.68 fm), Ni (b = 10.3 fm) and Sb (5.57 fm), was used to investigate the distribution of metals in the structure (Fig. 1d). This showed that in a nominal x = 0.5 sample, Zn and Ti occupy the X-site, with the fits indicating a slightly Zn-rich Ti_0.45(1)Zn_0.55(1)NiSb composition (Table 1). Attempts to include interstitial metals, vacancies or incorporate site disorder (X-, Y-site swapping) did not lead to improvements to the fit, suggesting that these defects are absent. One notable feature is the order of magnitude larger thermal displacement parameter for the Ti/Zn-site, which could signal structural disorder (Table 1). However, the near null coherent scattering factor for Ti/Zn could also be driving this behaviour by making the site near invisible. Synchrotron X-ray diffraction data does not show this large disorder effect with similar displacement parameters for all sites (Table 1). A final feature of the NPD pattern is the slightly asymmetric peak shape, extending towards higher d-spacings, which cannot fully be described by the pseudo-Voigt function. This indicates a degree of inhomogeneity, possibly related to short range-clustering of the X-site metals, although no evidence for this was found from the pair distribution function (PDF) analysis below.

Table 1 Lattice parameters (a), site occupancies (occ), thermal displacement parameters (U_iso) and fit statistics for the Rietveld refinements against neutron (Zn_0.5Ti_0.5NiSb) and synchrotron X-ray (Zn_0.4Ti_0.6NiSb) powder diffraction data

	Zn0.5Ti0.5NiSb (NPD)	Zn0.4Ti0.6NiSb (SXRD)
a HH (Å)	5.9186(1)	5.9121(1)
X occ	Zn – 0.55(1)	Zn – 0.4
	Ti – 0.45(1)	Ti – 0.6
U iso (Å^2)	0.031(4)	0.007(1)
Y occ	Ni – 1	Ni – 1
U iso (Å^2)	0.0046(2)	0.0043(1)
Z occ	Sb – 1	Sb – 1
U iso (Å^2)	0.0029(4)	0.0029(1)
wRp (%)	7.6	5.9
R f ^2 (%)	4.7	9.5
R p (%)	5.2	5.6

---

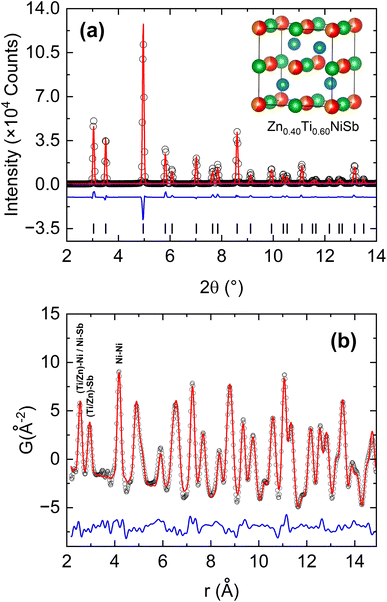
Total scattering and PDF analysis is a powerful probe of local structure, looking at distributions of bond distances. This can yield information beyond the average unit cell, e.g. the observation of different Ti–Ni and Zn–Ni bond distances, whereas only an average value can be obtained from diffraction. The results from PDF analysis of a Zn_0.4Ti_0.6NiSb sample is summarised in Fig. 2. The diffraction pattern can be fitted well by the HH structure with nominal composition (Fig. 2a and Table 1). Trial fits provided no evidence for structural point defects, confirming the absence of interstitials, in agreement with the NPD analysis. The resulting structural model was used to fit the experimental PDF data, yielding good agreement with the observed intensities (Fig. 2b). The absence of peak splitting in the PDF data, e.g. due to different Ti–Ni and Zn–Ti bond distances confirms that the local structure is close to the average from the Rietveld analysis. In other words, the local coordination is similar to that expected based on the average structure, within the experimental resolution. The limited X-ray scattering contrast between Zn and Ti means the experiment is not sensitive to picking up evidence of short-range clustering and this may occur in these samples. However, this does not lead to large deviations from the average bond distances.

Fig. 2 Synchrotron X-ray total scattering investigation of Zn_0.4Ti_0.6NiSb. (a) Rietveld fit to the diffraction dataset, revealing good agreement between the average unit cell structure and the experimental data. (b) Fit to the pair distribution function, which gives additional insight into the local structure, which is adequately described by the average unit cell structure with mixing of Ti and Zn on the X-site without any interstitial metals. The inset in panel (a) shows the structure used to fit both XRD and PDF datasets (Zn/Ti: mixed orange/red; Ni: blue; Sb: green).

2.2 Electrical transport

The evolution of S, ρ and S²/ρ with temperature and composition (at 340 K), split by conduction type are shown in Fig. 3 and 4. The x = 0.5 sample is p-type with S_340K = 55 μV K⁻¹, with the crossover to n-type behaviour occurring for x = 0.55 (Fig. 4a). Samples close to x = 0.5 are characterised by low S and bipolar conduction. As the composition moves away from the crossover point, becoming more electron rich, S_340K initially decreases to −115 μV K⁻¹ for x = 0.6 and then increases for x = 0.65. The Zn-rich samples (x = 0.45 and x = 0.4) are p-type conductors with similar S_340K ∼50 μV K⁻¹ (Fig. 4a). The highest doped n- and p-type samples have or tend towards metal-like ρ(T), as expected for increasing carrier doping levels. Compositions closer to x = 0.5 have a semiconducting ρ(T), consistent with being lightly doped and intrinsic conduction via carrier excitation across the bandgap. This significant change in behaviour is illustrated by the rapid drop in ρ_340K (Fig. 4b) as the composition moves away from x = 0.5. It can also be seen in the ρ_793K/ρ_340K resistivity ratio, which changes from values <1 (i.e. semiconducting) near x = 0.5 to values approaching or >1 (degenerate system) for higher doped samples (Fig. 4c).

Fig. 3 Temperature dependence of the Seebeck coefficient (S), electrical resistivity (ρ) and power factor (S²/ρ) split by carrier polarity. Panels (a–c) show data for the n-type and (d–f) for the p-type Zn_1−xTi_xNiSb samples. Solid lines to ρ(T) are fits as described in the text. Solid symbols are used throughout for n-type samples, open symbols for p-types.

Fig. 4 Composition dependence of (a) the Seebeck coefficient (S_340K), (b) the electrical resistivity (ρ_340K), (c) the ratio of the high-to low-temperature resistivity (ρ_793K/ρ_340K) and (d) the weighted mobility (μ_w) for the Zn_1xTi_xNiSb samples. The black dashed line corresponds to the approximate p-to n-type transition.

The semiconducting ρ(T) is not described well by a thermally activated (gapped semiconductor) or variable range hopping model (typical for conduction between localised states in disordered materials at band edges) as shown in Fig. S3.† However, a model allowing for parallel degenerate (ρ_deg) and semiconducting (ρ_int) channels can describe the data very well. This uses the following expression:⁴⁶

ρ_deg(T) = ρ₀ + BT^1.5

ρ(T) = [(ρ_deg(T))⁻¹ + (ρ_int(T))⁻¹]⁻¹

Here, ρ₀ is the residual resistivity, B captures the strength of acoustic phonon scattering, E_g is the electronic bandgap and A is a scaling factor. The final fit to ρ(T) is shown in Fig. 3b and e and the fit parameters are summarised in Table S2.† All data is fitted using a consistent bandgap, E_g = 0.39(2) eV. In case of the semiconducting compositions, inclusion of ρ₀ is essential to fit the data, but there is little temperature dependence in the degenerate term. The degenerate term dominates the transport in the most highly doped n- and p-type compositions, furthest away from x = 0.5. 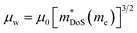The weighted mobility, is a measure of the electronic quality of a thermoelectric material.⁴⁷ Here, μ₀ is the intrinsic carrier mobility and 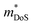is the density of states effective mass, related to the band mass and degeneracy of the bandstructure. The calculated μ_w(T) is shown in Fig. S4,† and the 340 K values are shown in Fig. 4d. This reveals that the most highly doped compositions have similar μ_w(T), with the p-types performing slightly better at high temperature. The implication is that both polarities can support similar S²/ρ, only requiring optimisation of the doping level. At high temperatures μ_w(T) follows an approximate T^−1.5 dependence, consistent with acoustic phonon scattering limited charge transport. There is no crossover to grain boundary or ionised impurity scattering, which both have a positive Tⁿ dependence.⁴⁷ The deviation from T^−1.5 near room temperature likely reflects the large ρ₀ for these samples (Table S2†). Highly doped p- and n-type materials achieve the best S²/ρ = 0.9 mW m⁻¹. K⁻² at 793 K (x = 0.4) and 1.2 mW m⁻¹. K⁻² at 700 K (x = 0.6), respectively.

2.3 Thermal transport

The temperature dependence of κ, κ_L = κ-LT/ρ and zT is given in Fig. 5. All compositions have low total κ = 2.7–3.7 W m⁻¹ K⁻¹ at 340 K, typically increasing upon heating, due to increasing electronic and bipolar contributions. The only exception is the heavily n-type doped x = 0.65 sample that has a negligible bipolar term (Fig. 5b) and which shows a gradual decrease with temperature. At 340 K, all samples have a low κ_L = 2.5–3 W m⁻¹ K⁻¹ (Fig. 5b), which is remarkable for a HH composition using only first row transition metals, without any heavy alloying elements. The Ti_0.8NiSb vacancy HH system has similar low κ_L,340K = 2–3 W m⁻¹ K⁻¹, but here mass disorder plays a substantial role,⁴⁴ unlike in the Zn_1−xTi_xNiSb samples. On heating, κ_L follows a T⁻ⁿ dependence with 0.5 ≤ n ≤ 0.7 up to 550–600 K, above which bipolar thermal conduction becomes dominant. This result is consistent with samples near x = 0.5 having a large intrinsic semiconducting component from ρ(T) fitting. The more highly doped samples have a larger degenerate contribution, and hence an imbalance in p- and n-type carrier concentrations, suppressing the thermal bipolar term, leading to the observation of a very low κ_L = 1.25 W m⁻¹ K⁻¹ at 793 K for the x = 0.65 sample. Resonant ultrasound spectroscopy measurements reveal slightly reduced elastic moduli, and reduced transverse (v_t) and longitudinal (v_l) velocities of sound (Table 2). Compared to TiCoSb, a ∼20% reduction in v_t and v_l is found, and a ∼10% reduction compared to TiFe_0.5Ni_0.5Sb. This reduction partly explains the low κ_L for the Zn_1−xTi_xNiSb samples (i.e. from 15 W m⁻¹ K⁻¹ for TiCoSb to 11 W m⁻¹ K⁻¹) but is not sufficient to explain it fully. As was the case for the other aliovalent HH materials, the low κ_L is therefore not fully explained by a reduced v_t and v_l but has to be partially attributed to additional channels causing phonon scattering, linked to the mixing of aliovalent elements.

Fig. 5 Thermal properties and figure of merit of the Zn_1−xTi_xNiSb series. Temperature dependence of (a) total thermal conductivity (κ), (b) lattice thermal conductivity (κ_L = κ − LσT) and (c) dimensionless figure of merit zT.

Table 2 Elastic properties for Zn_0.5Ti_0.5NiSb from resonant ultrasound spectroscopy. RUS determines elastic moduli, from which the tabulated values are calculated.⁵⁶ Data from the literature is based on measured velocity of sound data, from which elastic moduli are calculated¹⁴

	Zn0.5Ti0.5NiSb	Ti0.8NiSb^44	TiFe0.5Ni0.5Sb^16	TiCoSb^16
Longitudinal sound velocity, νl (m s^−1)	4720	5301	5300	5750
Shear sound velocity, νt (m s^−1)	2623	2873	3060	3230
Average sound velocity, νs (m s^−1)	2921	3206	3397	3594
Shear modulus, G (GPa)	47.3	59	68	78
Bulk modulus, B (GPa)	90.2	123	114	144
Young's modulus, E (GPa)	121	153	170	198
Debye temperature, θD	324	360	376	401
Poisson ratio, ν	0.28	0.29	0.25	0.27
Grüneisen parameter, γ	1.66	1.72	1.5	1.6

---

The zT values achieved in these materials compare well to other aliovalent HH compositions investigated. A peak n-type zT = 0.33 at 700 K was for Zn_0.4Ti_0.6NiSb and for the p-types, zT = 0.18 at 793 K was found in Zn_0.6Ti_0.4NiSb (Fig. 5c). Hence, both best performing compositions occur 0.1 hole/electrons away from the stable 18 valence electron count of the x = 0.5 composition. Compared to the TiFe_1−xNi_xSb system, our samples have somewhat lower S²/ρ but also lower κ_L values, enabling similar zT values, when comparing like-for-like in terms of operating temperature. The lower S²/ρ and κ_L suggest that there is a stronger “disorder” effect in these X-site aliovalent materials that affects both carrier and phonon lifetime.

3. Discussion

We have successfully prepared a new X-site aliovalent HH materials system based on a 50 : 50 mixture of ZnNiSb and TiNiSb. We find an appreciable range of stability in the Zn_1−xTi_xNiSb series, extending from 0.4 ≤ x ≤ 0.65. The solid-solution towards x = 1 is readily accessible, while the boundary for Zn-rich (x = 0.4) appears to be a hard limit. This difference in response is related to the reducing electron count, below 18 for x < 0.5. This destabilises the HH structure, despite the existence of stable ZnNiSb. For x < 0.5, there may be a miscibility gap between metallic (ZnNiSb) and semiconducting (close to x = 0.5) HH structures. In principle higher synthesis temperature can be used to extend the solubility limit, but this is limited by the low sublimation temperature of Zn. For x > 0.5, the stable end-member is the Ti_0.8NiSb composition with intrinsic Ti vacancies,⁴⁴ which is an 18-electron composition. The x = 0.5 to x = 1 line therefore connects two stable semiconducting HH phases, removing any electronic driving force for immiscibility. Globally the thermoelectric response follows the electron count of the materials with x = 0.5 showing intrinsic semiconducting behaviour, transitioning to degenerate p- and n-type conduction for x < 0.5 (Zn rich) and x > 0.5 (Ti rich). All samples are characterised by relatively low μ_w, S²/ρ and κ_L, as is typical for aliovalent HH compositions. A comparison of the measured κ_L and zT with selected literature samples is given in Fig. 6. This confirms that these materials possess very low κ_L, only matched by Mg_0.67V_0.33NiSb, another X-site aliovalent system. As already noted, the Ti_0.8NiSb end-member with intrinsic vacancies also has comparable low κ_L, = 2–3 W m⁻¹ K⁻¹.⁴⁴ This shows that there are two routes to achieve low κ_L without using heavy alloying elements.¹⁴ Both involve the X-site and involve either using mixtures of aliovalent elements (e.g. Zn/Ti, Mg/Ti or Mg/V) or creating vacancies. In case of X-site vacancies, a large part of the κ_L reduction is likely to be linked to mass disorder, but the bond disorder that is important in the aliovalent systems may well play a role in the vacancy compositions. The zT values of Zn_1−xTi_xNiSb are competitive with other aliovalent HH materials systems, considering the temperature at which they occur.

Fig. 6 Comparison of (a) κ_L at 340 K and (b) largest zT values for selected aliovalent half-Heusler compositions. Red histogram bars are for XY′_0.5Y′′_0.5Z compositions, green bars are for XYZ′_0.5Z′′_0.5 compositions and blue bars are for X′_0.5X′′_0.5YZ compositions. Hatched (solid) indicates p-type (n-type) samples. Data taken from: TiFe_1−xNi_xSb/Ti_0.8Hf_0.2Fe_0.6Ni_0.4Sb,¹⁶ TiFe_0.5+xCo_0.25Cu_0.25−xSb,²⁴ Zr_0.9Ni_0.9In_0.5Sb_0.5/Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6,²¹ Mg_0.5±0.5xTi_0.5±0.5xNiSb,²⁵ and Mg_0.67V_0.33NiSb.²⁰

The description of electronic and thermal transport in these aliovalent HH compositions is not yet well understood. Intuitively, mixing aliovalent elements with different orbital energies will lead to a degree of inherent disorder in the electronic structure. This disorder is expected to reduce carrier mobility, consistent with the low values for μ_w and S²/ρ. Similarly, there is a large suppression of κ_L that is also related to a disorder effect. Analysis of the PDF from synchrotron X-ray total scattering reveals that the local structure for Zn_1−xTi_xNiSb is not substantially different from the average structure. This means that there are no large differences in bond distances (e.g. Zn–Ni versus Ti–Ni) that might give rise to a large lattice strain effect. In addition, there is no evidence for other point defects, such as interstitials, leaving the origin of the low κ_L unresolved. On balance it seems likely that the low κ_L has to be related to a form of bond/electronic disorder that is introduced by the mixing of aliovalent Zn and Ti. For example, the slightly reduced elastic moduli may reflect a mixture of stronger and weaker bonds (e.g. Ti–Ni versus Zn–Ni) that leaves the average v_l, and v_t largely unaffected (v_l, and v_t are governed by long wavelength phonons) but would cause substantial local bond disorder. If this manifested itself similar to lattice strain, then a 10–20% bond strength mismatch could substantially reduce κ_L. The absence of a clear compositional dependence of κ_L also points towards bond disorder, as lattice strain is known to remain large over a broad composition range near the maximum alloyed (x = 0.5) composition.³⁸ Further investigation of the local structure in these materials, e.g. using high annular dark field imaging in scanning transmission electron microscopy, and modelling beyond the periodic electron and phonon bandstructure, is needed to elucidate the microscopic origin for low mobilities and thermal conductivity.

To conclude, we have investigated the structure and properties of a new aliovalent HH materials system based on mixing 17-electron ZnNiSb and 19-electron TiNiSb. These materials show promising thermoelectric performance in both polarities, tuneable by adjusting the Zn/Ti ratio, offering the possibility of devices with n- and p-type legs of nearly identical composition. Understanding the electrical and thermal transport in aliovalent HH materials is a vital next step for rational design of further performance improvements.

4. Experimental

Zn_1−xTi_xNiSb (0.35 ≤ x ≤ 0.65) samples were prepared on a 5 g scale by solid–state reaction of elemental powders purchased from Alfa Aesar and Merck Scientific of ≥99.99% purity. The powders were mixed with an agate mortar and pestle for ∼20 minutes, then cold pressed into ∼13 mm diameter disks. The disks were cut in half using bolt cutters, wrapped in tantalum foil, sealed in evacuated silica ampoules, and annealed for 48 hours at 1073 K, followed by annealing at 1123 K for 48 hours. This two-step profile was chosen to minimise Zn loss due to sublimation. The annealed pellets were ball milled for 30 minutes to produce a fine powder. The powders were hot-pressed using an in-house apparatus for 20 minutes at 1123 K with an applied pressure of 80 MPa, yielding densities ≥97% for all hot-pressed disks (Table S3†). An additional Ti_0.5Zn_0.5NiSb sample was prepared for Neutron powder diffraction (NPD), with the analysis carried out on a pulverized annealed pellet. All manipulation of powders was done in an argon filled glovebox to prevent exposure to oxygen and moisture.

All samples were initially characterized using powder X-ray diffraction (XRD). Data was collected over 30 minutes using a Malvern Panalytical Empyrean diffractometer, with Cu K_α1 and K_α2 radiation. Room temperature NPD data was collected on ∼3.5 g of finely ground powder, on the D2B instrument, ILL, Grenoble, France. Rietveld fitting of XRD and NPD data were carried out using the General Structure Analysis System II (GSAS-II) suite of programs, whilst qualitative peak matching was carried out using the Malvern Panalytical Highscore Plus software and the ICDD database.^50,51

Scanning electron microscopy (SEM) of the hot pressed Zn_1−xTi_xNiSb disks was performed using a Quanta 650 FEG SEM, equipped with an Oxford Instruments X-max 150 mm detector for EDX spectroscopy. Prior to measurements, all samples were polished first with SiC sandpaper, then with subsequent 15 μm, 5 μm and 1 μm diamond polish pastes to produce a reflective mirror finish. Polished surfaces were thoroughly washed with propan-1-ol to remove any SiC or diamond paste residue. Quantitative analysis of selected areas was performed using the Oxford Instruments Aztec Large Area Maps software.

Total scattering synchrotron X-ray data was collected on the ID15A beamline⁵² at the ESRF (European Synchrotron Research Facility, Grenoble, France) using a Dectris Pilatus 2 M CdTe detector. X-ray energy was 68.5 keV (wavelength 0.1810 Å) and sample-detector distance 185.0 mm. Detector images were averaged and azimuthally integrated using pyFAI⁵³ and the resulting integrated intensities were converted to PDF using GudrunX.⁵⁴ Fitting of the XRD dataset was carried out using the GSAS-II software, whilst the PDF fits were undertaken using the PDFfit2 and PDFGui software.⁵⁵

The electrical resistivity ρ and absolute Seebeck coefficient S were measured using a Linseis LSR-3 instrument on bar-shaped specimens (∼1.5 × 2 × 10 mm³), under a static He atmosphere. The thermal diffusivity α was measured using a Linseis LFA-1000 laser flash instrument on hot-pressed disks of ∼13 mm diameter and ∼1.5 mm thickness, under dynamic vacuum conditions. The thermal conductivity κ was then calculated from the equation κ = αC_pρ, with C_p the specific heat of the nominal composition estimated from the Dulong Petit Law and ρ the disk density obtained using the Archimedes method (Table S3†).

Resonance ultrasound spectroscopy (RUS) was used to measure the natural frequencies of the Zn_0.5Ti_0.5NiSb sample using a RUS008 system.⁵⁶ The spectrum was collected using the open-source RUSpy software. A parallelepiped sample of dimensions 4.7 × 5.8 × 1.3 mm³ was used to measure the spectrum. An isotropic model was used to calculate the independent elastic constants C11 and C44 from the spectrum using the RusCal program, which implements an inverse numerical analysis.⁵⁷

Data availability

The research data underpinning this publication can be accessed at https://doi.org/10.17630/b9b0eaac-bd76-4ac9-8455-af7c1b735de1.⁵⁸

Author contributions

Materials synthesis, data acquisition and analysis, manuscript writing – original draft (B. F. K.); data acquisition and analysis (S. A. J. K., S. C., E. S., A. K. M. A. S., A. Z., J. B.), Conceptualisation, funding, project supervision, manuscript writing - review & editing (J. -W. G. B).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The EPSRC is acknowledged for funding the research into new half-Heusler materials, through award (EP/N01717X/1) and for a PhD studentship for B. F. K. The ILL is acknowledged for easy-access beam time on the super-D2B instrument.⁴⁸ The ESRF is acknowledged for provision of inhouse beamtime (proposal IH-HC-3871).⁴⁹

References

1. Materials, Preparation, and Characterization in Thermoelectrics, ed. D. M. Rowe, CRC Press, Boca Raton, 2012.
2. Thermoelectric Energy Conversion, ed. R. Funahashi, Woodhead Publishing, 2021.
3. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
4. T. J. Zhu, Y. T. Liu, C. G. Fu, J. P. Heremans, J. G. Snyder and X. B. Zhao, Adv. Mater., 2017, 29, 1605884.
5. X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515.
6. Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054.
7. Q. Y. Yan and M. G. Kanatzidis, Nat. Mater., 2022, 21, 503–513.
8. V. Pecunia, S. R. P. Silva, J. D. Phillips, E. Artegiani, A. Romeo, H. Shim, J. Park, J. H. Kim, J. S. Yun, G. C. Welch, B. W. Larson, M. Creran, A. Laventure, K. Sasitharan, N. Flores-Diaz, M. Freitag, J. Xu, T. M. Brown, B. Li, Y. Wang, Z. Li, B. Hou, B. H. Hamadani, E. Defay, V. Kovacova, S. Glinsek, S. Kar-Narayan, Y. Bai, D. B. Kim, Y. S. Cho, A. Žukauskaitė, S. Barth, F. R. Fan, W. Wu, P. Costa, J. del Campo, S. Lanceros-Mendez, H. Khanbareh, Z. L. Wang, X. Pu, C. Pan, R. Zhang, J. Xu, X. Zhao, Y. Zhou, G. Chen, T. Tat, I. W. Ock, J. Chen, S. A. Graham, J. S. Yu, L.-Z. Huang, D.-D. Li, M.-G. Ma, J. Luo, F. Jiang, P. S. Lee, B. Dudem, V. Vivekananthan, M. G. Kanatzidis, H. Xie, X.-L. Shi, Z.-G. Chen, A. Riss, M. Parzer, F. Garmroudi, E. Bauer, D. Zavanelli, M. K. Brod, M. A. Malki, G. J. Snyder, K. Kovnir, S. M. Kauzlarich, C. Uher, J. Lan, Y.-H. Lin, L. Fonseca, A. Morata, M. Martin-Gonzalez, G. Pennelli, D. Berthebaud, T. Mori, R. J. Quinn, J.-W. G. Bos, C. Candolfi, P. Gougeon, P. Gall, B. Lenoir, D. Venkateshvaran, B. Kaestner, Y. Zhao, G. Zhang, Y. Nonoguchi, B. C. Schroeder, E. Bilotti, A. K. Menon, J. J. Urban, O. Fenwick, C. Asker, A. A. Talin, T. D. Anthopoulos, T. Losi, F. Viola, M. Caironi, D. G. Georgiadou, L. Ding, L.-M. Peng, Z. Wang, M.-D. Wei, R. Negra, M. C. Lemme, M. Wagih, S. Beeby, T. Ibn-Mohammed, K. B. Mustapha and A. P. Joshi, J. Phys. Mater., 2023, 6, 042501.
9. J. W. G. Bos and R. A. Downie, J. Phys. Condens. Matter, 2014, 26, 433201.
10. T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588.
11. L. H. Huang, Q. Y. Zhang, B. Yuan, X. Lai, X. Yan and Z. F. Ren, Mater. Res. Bull., 2016, 76, 107–112.
12. S. J. Poon, J. Phys. D: Appl. Phys., 2019, 52, 493001.
13. J.-W. G. Bos, in Thermoelectric Energy Conversion, ed. R. Funahashi, Woodhead Publishing, 2021, pp. 125–142,  DOI:10.1016/B978-0-12-818535-3.00014-1.
14. R. J. Quinn and J.-W. G. Bos, Mater. Adv., 2021, 2, 6246–6266.
15. S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238.
16. Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29, 1905044.
17. S. Guo, Z. Liu, Z. Feng, T. Jia, S. Anand, G. J. Snyder and Y. Zhang, J. Mater. Chem. A, 2020, 8, 23590–23598.
18. Y. Liu, X. Xu, W. Fang, S. Teng, X. Xie, L. Li, S. Fan, J. Li and J. Li, J. Alloys Compd., 2021, 858, 157689.
19. W. Ren, X. Shi, Z. Wang and Z. Ren, Mater. Today Phys., 2022, 25, 100704.
20. K. Imasato, P. Sauerschnig, S. Anand, T. Ishida, A. Yamamoto and M. Ohta, J. Mater. Chem. A, 2022, 10, 18737–18744.
21. S. He, A. Bahrami, P. Ying, L. Giebeler, X. Zhang, K. Nielsch and R. He, J. Mater. Chem. A, 2022, 10, 13476–13483.
22. P. Luo, Y. Mao, Z. Li, J. Zhang and J. Luo, Mater. Today Phys., 2022, 26, 100745.
23. S. R. Mishra, L. P. Tan, V. Trivedi, M. Battabyal, P. S. Sankara Rama Krishnan, D. V. M. Repaka, S. K. Yadav, R. V. Ramanujan and B. S. Murty, ACS Appl. Energy Mater., 2023, 6, 6262–6277.
24. P.-F. Luo, S. Dai, Y. Zhang, X. Liu, Z. Li, J. Zhang, J. Yang and J. Luo, J. Mater. Chem. A, 2023, 11, 9125–9135.
25. A. Li, M. K. Brod, Y. Wang, K. Hu, P. Nan, S. Han, Z. Gao, X. Zhao, B. Ge, C. Fu, S. Anand, G. J. Snyder and T. Zhu, Adv. Sci., 2023, 2302086.
26. J. N. Kahiu, S. K. Kihoi, H. Kim, U. S. Shenoy, D. K. Bhat and H. S. Lee, ACS Appl. Energy Mater., 2023, 6, 4305–4316.
27. R. Hasan, S. Jo, W. Shi, S. Y. Lee, W.-S. Seo, V. C. S. Theja, R. A. L. Vellaisamy, K. T. Kim, S.-i. Kim, S. W. Kim, H.-S. Kim and K. H. Lee, J. Alloys Compd., 2023, 938, 168572.
28. A. Ojha, R. K. Sabat, A. N. Gandi and S. Bathula, J. Electron. Mater., 2023, 52, 5473–5484.
29. S. R. Mishra, A. Karati, S. Ghosh, R. C. Mallik, R. Shabadi, P. S. S. R. Krishnan, S. K. Yadav, R. V. Ramanujan and B. S. Murty, J. Mater. Sci., 2023, 58, 10736–10752.
30. J. Yan, F. Liu, G. Ma, B. Gong, J. Zhu, X. Wang, W. Ao, C. Zhang, Y. Li and J. Li, Scr. Mater., 2018, 157, 129–134.
31. K. Chen, R. Zhang, J.-W. G. Bos and M. J. Reece, J. Alloys Compd., 2022, 892, 162045.
32. S. Li, K. Chen, Y. Wang, T. Saunders, R. Zhang, J.-W. G. Bos and M. J. Reece, Temperature and Doping Insensitivity of Thermoelectric Properties of High-Entropy Half-Heusler Compounds, SSRN, 2023,  DOI:10.2139/ssrn.4526733.
33. C. G. Fu, S. Q. Bai, Y. T. Liu, Y. S. Tang, L. D. Chen, X. B. Zhao and T. J. Zhu, Nat. Commun., 2015, 6, 8144.
34. J. W. Zhou, H. T. Zhu, T. H. Liu, Q. C. Song, R. He, J. Mao, Z. H. Liu, W. Y. Ren, B. L. Liao, D. J. Singh, Z. F. Ren and G. Chen, Nat. Commun., 2018, 9, 1721.
35. Q. Ren, C. Fu, Q. Qiu, S. Dai, Z. Liu, T. Masuda, S. Asai, M. Hagihala, S. Lee, S. Torri, T. Kamiyama, L. He, X. Tong, C. Felser, D. J. Singh, T. Zhu, J. Yang and J. Ma, Nat. Commun., 2020, 11, 3142.
36. H. Zhu, W. Li, A. Nozariasbmarz, N. Liu, Y. Zhang, S. Priya and B. Poudel, Nat. Commun., 2023, 14, 3300.
37. S. Guo, S. Anand, M. K. Brod, Y. Zhang and G. J. Snyder, J. Mater. Chem. A, 2022, 10, 3051–3057.
38. J. Yang, G. P. Meisner and L. Chen, Appl. Phys. Lett., 2004, 85, 1140–1142.
39. R. He, T. Zhu, Y. Wang, U. Wolff, J.-C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood, Z. Liu, L. Feng, N. P. Rodriguez, G. J. Snyder, J. C. Grossman, K. Nielsch and G. Schierning, Energy Environ. Sci., 2020, 13, 5165–5176.
40. D. A. Ferluccio, J. E. Halpin, K. L. MacIntosh, R. J. Quinn, E. Don, R. I. Smith, D. A. MacLaren and J.-W. G. Bos, J. Mater. Chem. C, 2019, 7, 6539–6547.
41. S. A. Barczak, J. E. Halpin, J. Buckman, R. Decourt, M. Pollet, R. I. Smith, D. A. MacLaren and J.-W. G. Bos, ACS Appl. Mater. Interfaces, 2018, 10, 4786–4793.
42. S. A. Barczak, R. J. Quinn, J. E. Halpin, K. Domosud, R. I. Smith, A. R. Baker, E. Don, I. Forbes, K. Refson, D. A. MacLaren and J. W. G. Bos, J. Mater. Chem. A, 2019, 7, 27124–27134.
43. V. V. Romaka, P. Rogl, L. Romaka, Y. Stadnyk, N. Melnychenko, A. Grytsiv, M. Falmbigl and N. Skryabina, J. Solid State Chem., 2013, 197, 103–112.
44. F. Luo, J. Wang, C. Zhu, X. He, S. Zhang, J. Wang, H. Liu and Z. Sun, J. Mater. Chem. A, 2022, 10, 9655–9669.
45. R. Kainuma, R. Umino, X. Xu, K. Han and T. Omori, J. Phase Equilib. Diffus., 2020, 41, 116–122.
46. R. J. Quinn, G. B. G. Stenning and J.-W. G. Bos, J. Phys. Energy, 2022, 4, 024005.
47. G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537.
48. J. W. G. Bos and E. Suard, Dataset, 2023 DOI:10.5291/ILL-DATA.EASY-1108.
49. S. Checchia, M. Di Michiel and G. Vaughan, Dataset, 2023 DOI:10.15151/ESRF-ES-1089938161.
50. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
51. T. Degen, M. Sadki, E. Bron, U. König and G. Nénert, Powder Diffr., 2014, 29, S13–S18.
52. G. B. M. Vaughan, R. Baker, R. Barret, J. Bonnefoy, T. Buslaps, S. Checchia, D. Duran, F. Fihman, P. Got, J. Kieffer, S. A. J. Kimber, K. Martel, C. Morawe, D. Mottin, E. Papillon, S. Petitdemange, A. Vamvakeros, J.-P. Vieux and M. Di Michiel, J. Synchrotron Radiat., 2020, 27, 515–528.
53. J. Kieffer, V. Valls, N. Blanc and C. Hennig, J. Synchrotron Radiat., 2020, 27, 558–566.
54. A. K. Soper, GudrunN and GudrunX: Programs for Correcting Raw Neutron and X-ray Diffraction Data to Differential Scattering Cross Section, Science & Technology Facilities Council, Swindon, UK, 2011.
55. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
56. F. F. Balakirev, S. M. Ennaceur, R. J. Migliori, B. Maiorov and A. Migliori, Rev. Sci. Instrum., 2019, 90, 121401.
57. J. Torres, A. Flores-Betancourt and R. P. Hermann, J. Acoustical Soc. Am., 2022, 151, 3547–3563.
58. B. F. Kennedy, S. A. J. Kimber, S. Checchia, A. K. M. A. Shawon, A. Zevalkink, E. Suard, J. Buckman and J.-W. G. Bos, Dataset, 2023 DOI:10.17630/b9b0eaac-bd76-4ac9-8455-af7c1b735de1.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta04514e

---