Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A single-phase gadolinium-doped ceria cathode for highly efficient CO2 electrolysis†
Ahmad
Shaur
 a,
Michel
Drazkowski
a,
Michel
Drazkowski
 a,
Shaochen
Zhu
a,
Shaochen
Zhu
 a,
Bernard
Boukamp
a,
Bernard
Boukamp
 b and
Henny J. M.
Bouwmeester
b and
Henny J. M.
Bouwmeester
 *acd
*acd
aElectrochemistry Research Group, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE, Enschede, The Netherlands. E-mail: h.j.m.bouwmeester@utwente.nl
bInorganic Materials Science Group, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE, Enschede, The Netherlands
cCAS Key Laboratory of Materials for Energy Conversion, Department of Materials Science and Engineering, University of Science and Technology of China, Hefei, 230026, P. R. China
dForschungszentrum Jülich GmbH, Institute of Energy and Climate Research-IEK-1, Leo- Brandt-Str. 1, D-52425, Jülich, Germany
First published on 3rd November 2023
Abstract
High-temperature solid-oxide CO2 electrolysers enable high-efficiency conversion of electrical energy to valuable fuels and chemicals and as such facilitate a sustainable-energy technology. Conventional cermet-based fuel electrodes used in such solid-oxide cells (SOCs) like nickel–yttria-stabilized zirconia (Ni–YSZ) suffer from morphological degradation and destructive carbon deposition. In recent years, there has been an increasing interest in employing single-phase ceria-based fuel electrodes, which are known to exhibit excellent carbon deposition resistance. Under sufficiently reducing conditions, doped ceria (substituted with trivalent cations such as samarium or gadolinium to generate mobile oxygen vacancies) becomes a mixed ionic–electronic conductor, showing appreciable electronic conductivity. Here, we show for the first time stable high performance in CO2 electrolysis using a ceria-based SOC. The single full cell incorporating a 10 mol% gadolinium-doped ceria (GCO) fuel electrode delivers a current density as high as 1.51 A cm−2 at 800 °C during pure CO2 electrolysis, which is the best electrode performance reported to date among all-ceramic cathode materials. We demonstrate that the electrode performance in CO2 electrolysis is linked with the electronic conductivity, and hence, with the electronic charge carrier concentration in GCO. The results of the present work pave the way for development of robust, nickel-free SOCs for direct CO2 electrolysis.
Introduction
In the global effort to develop efficient and carbon-neutral alternatives to fossil fuels, SOCs currently attract extensive attention due to their high faradaic efficiencies, wide fuel flexibility, and low pollutant emission. They can be operated reversibly, converting chemical fuels to electricity (fuel cell mode) and vice versa (electrolysis cell mode), at high efficiencies and with zero emissions.1,2 Operating in the electrolysis cell mode, SOCs which can be thermally integrated with downstream chemical processing can be employed to convert surplus electricity generated from renewables to a wide range of storable synthetic fuels and chemicals.3 In particular, there is a growing worldwide interest in the direct electrochemical conversion of the greenhouse gas CO2.4,5Fig. 1 demonstrates the overall reaction scheme for CO2 electrolysis in a solid oxide electrolysis cell (SOEC), where CO2 is converted to CO at the cathode (fuel electrode), while the formed oxygen ion migrates via the electrolyte to the anode (air/oxygen electrode), where it is oxidized to O2.6,7In Kröger–Vink notation, the CO2 reduction reaction may be written as
 ,
, 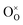 , and e′ denote a doubly ionized oxygen vacancy, a regular lattice oxygen and an electron, respectively.
, and e′ denote a doubly ionized oxygen vacancy, a regular lattice oxygen and an electron, respectively.  and e′ are the charge carriers being transported to the surface reaction site, where gaseous CO2 is reduced to CO. The state-of-the-art SOEC cathode is the nickel–yttria stabilized zirconia (Ni–YSZ) cermet electrode.8,9 Here, the electrode reaction is confined to the near vicinity of the triple-phase boundary (3PB), where the gas phase, the ionic conductor and the catalytically active metal phase are in simultaneous contact with each other. However, Ni–YSZ electrodes are inherently redox unstable and prone to issues like re-oxidation, morphological degradation, and coking.10,11 Moreover, a flow of safety gas (reducing gas, e.g., H2/CO) premixed with the CO2 feed gas needs to be supplied to the electrode during start-up and/or to avoid (re-)oxidation of Ni to NiO in the event of an incidental shut-down.12 To overcome these drawbacks or limitations, researchers still endeavour to find alternative electrode materials, thereby focusing on mixed ionic–electronic conducting oxides (MIECs) with high stability under reducing conditions.8 The use of an MIEC as electrode material extends the active area over the entire electrode surface, thus potentially enhancing the overall reaction rate.13 Amongst others, mixed-conducting perovskite-type oxides such as La0.75Sr0.25Cr0.5Mn0.5O3−δ (LSCrMn),7,14,15 LaxSr1−xTiO3−δ (LST),16–18 SrTi0.3Fe0.7O3−δ (STF),19 La0.6Sr0.4FeO3−δ (LSF),20,21 Sr2Fe1.5Mo0.5O6−δ (SFMo),9 Sr2Fe1.4Mn0.1Mo0.5O6−δ (SFMnMo),9 and Sr2Fe1.5Mo0.5O6−δF0.1 (F-SFMo),22 have been tested for use as a cathode for CO2 electrolysis.6,23,24 Infiltration, fluorine-doping, and/or in situ exsolution of reducible transition metal cations have been applied to enhance the performance of the perovskites electrodes.1,6,8 For some of the perovskite-structured electrodes strontium segregation and subsequent carbonation have been found to induce passivation, resulting in performance degradation over time.25–27 The best performance in the open literature has been reported to date for the fluorine-doped SFM fuel electrode, incorporated in a 250 μm-thick La0.9Sr0.1Ga0.8Mg0.2O3−δ (LSGM) electrolyte-supported cell, showing a current density of 1.38 A cm−2 at an applied potential of 1.5 V at 800 °C, using pure CO2 as feed gas.22
and e′ are the charge carriers being transported to the surface reaction site, where gaseous CO2 is reduced to CO. The state-of-the-art SOEC cathode is the nickel–yttria stabilized zirconia (Ni–YSZ) cermet electrode.8,9 Here, the electrode reaction is confined to the near vicinity of the triple-phase boundary (3PB), where the gas phase, the ionic conductor and the catalytically active metal phase are in simultaneous contact with each other. However, Ni–YSZ electrodes are inherently redox unstable and prone to issues like re-oxidation, morphological degradation, and coking.10,11 Moreover, a flow of safety gas (reducing gas, e.g., H2/CO) premixed with the CO2 feed gas needs to be supplied to the electrode during start-up and/or to avoid (re-)oxidation of Ni to NiO in the event of an incidental shut-down.12 To overcome these drawbacks or limitations, researchers still endeavour to find alternative electrode materials, thereby focusing on mixed ionic–electronic conducting oxides (MIECs) with high stability under reducing conditions.8 The use of an MIEC as electrode material extends the active area over the entire electrode surface, thus potentially enhancing the overall reaction rate.13 Amongst others, mixed-conducting perovskite-type oxides such as La0.75Sr0.25Cr0.5Mn0.5O3−δ (LSCrMn),7,14,15 LaxSr1−xTiO3−δ (LST),16–18 SrTi0.3Fe0.7O3−δ (STF),19 La0.6Sr0.4FeO3−δ (LSF),20,21 Sr2Fe1.5Mo0.5O6−δ (SFMo),9 Sr2Fe1.4Mn0.1Mo0.5O6−δ (SFMnMo),9 and Sr2Fe1.5Mo0.5O6−δF0.1 (F-SFMo),22 have been tested for use as a cathode for CO2 electrolysis.6,23,24 Infiltration, fluorine-doping, and/or in situ exsolution of reducible transition metal cations have been applied to enhance the performance of the perovskites electrodes.1,6,8 For some of the perovskite-structured electrodes strontium segregation and subsequent carbonation have been found to induce passivation, resulting in performance degradation over time.25–27 The best performance in the open literature has been reported to date for the fluorine-doped SFM fuel electrode, incorporated in a 250 μm-thick La0.9Sr0.1Ga0.8Mg0.2O3−δ (LSGM) electrolyte-supported cell, showing a current density of 1.38 A cm−2 at an applied potential of 1.5 V at 800 °C, using pure CO2 as feed gas.22
Besides its use as electrolyte or as diffusion barrier layer, doped ceria (typically gadolinium- or samarium-doped ceria) is commonly employed as an additive to SOC fuel electrodes, either as an (impregnated) catalyst28 or as a dispersed phase to enhance the overall 3PB length.9,29–31 Acceptor-doped ceria exhibits electronic conductivity to become a mixed ionic–electronic conductor under reducing conditions.32,33 Chueh et al.34 used ceria-metal cermet electrodes to investigate the kinetics of the H2 oxidation reaction. The authors showed that the reaction pathway is dominated by electrocatalysis at the oxide/gas interface (2PB) with only a minimal contribution from the oxide/metal/gas boundaries (3PBs).34 Nenning et al.35 found excellent kinetics for thin-film single-phase Gd-doped ceria (GCO) electrodes tested in both H2/H2O and CO/CO2 atmospheres using electrochemical impedance spectroscopy on symmetrical cells, while Skafte et al.36 showed selective CO2 to CO conversion for thin-film ceria-based electrodes well beyond the thermodynamic carbon deposition threshold. These studies clearly point towards the potential of single-phase doped ceria for use as fuel electrode. Here, we demonstrate for the first time exceptional performance of single-phase porous GCO electrodes in pure CO2 electrolysis, achieving a current density of 1.51 A cm−2 in electrolyte-supported cells operated at 1.5 V at 800 °C. We further demonstrate that the performance arises in response of the high electronic conductivity in the ceria-based electrode being linked with the Nernstian chemical potential associated with the applied overpotential. Symmetrical cell tests are conducted to probe the electrode polarization and the effective electrolyte resistance.
Results and discussion
Electrolysis cell and performance
Here, an electrolyte-supported SOEC was fabricated by screen-printing a 20 μm-thick GCO (Gd0.1Ce0.9O2−δ) layer on a 150 μm-thick 8 mol% yttria-stabilized zirconia (8YSZ) electrolyte disc (Fig. S1†). Screen-printed La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF) was used as the oxygen electrode. A dense 2 μm-thin diffusion-barrier layer of GCO obtained by pulsed layer deposition (PLD) was applied between the 8YSZ electrolyte and the LSCF electrode to prevent the formation of secondary phases. Different CO/CO2 gas mixtures were fed to the GCO cathode, whereas synthetic air (21% oxygen with nitrogen balance) was supplied to the anode side of the cell. Fig. 2a shows current–voltage (I–V) curves for pure CO2 electrolysis in the range of 700–800 °C, while Fig. 2b shows corresponding curves, at 750 °C, in atmospheres with different CO2/CO volume ratios. There is virtually no hysteresis in the I–V curves, which were recorded from open-circuit voltage (OCV) to about 1.6 V, indicating high reversibility of the cell within the constraints of the experiment. A current density as high as 1.51 A cm−2 at 1.5 V, at 800 °C, is found for pure CO2 electrolysis, which to our knowledge is the highest value reported to date for single-phase oxide electrode materials (Fig. 2c). Fig. 2d shows the CO production rate (VCO) and faradaic efficiency as a function of current density, at 750 °C, for pure CO2 electrolysis. The value of VCO increases to 18.0 ml min−1 cm−2 as the current density increases to 0.75 A cm−2 (which is reached at a cell voltage of 1.32 V). The faradaic efficiency remains close to 100%. Next, we proceeded to perform pure CO2 electrolysis, at 750 °C, at an applied voltage of 1.2 V. A stable performance is found for 300 h (Fig. 2e). Post mortem scanning electron microscopy (SEM) did not show any sign of degradation of the electrode microstructure (Fig. S1c†). The obtained results in this study clearly demonstrate that GCO holds great promise for stable and selective CO2 electrolysis.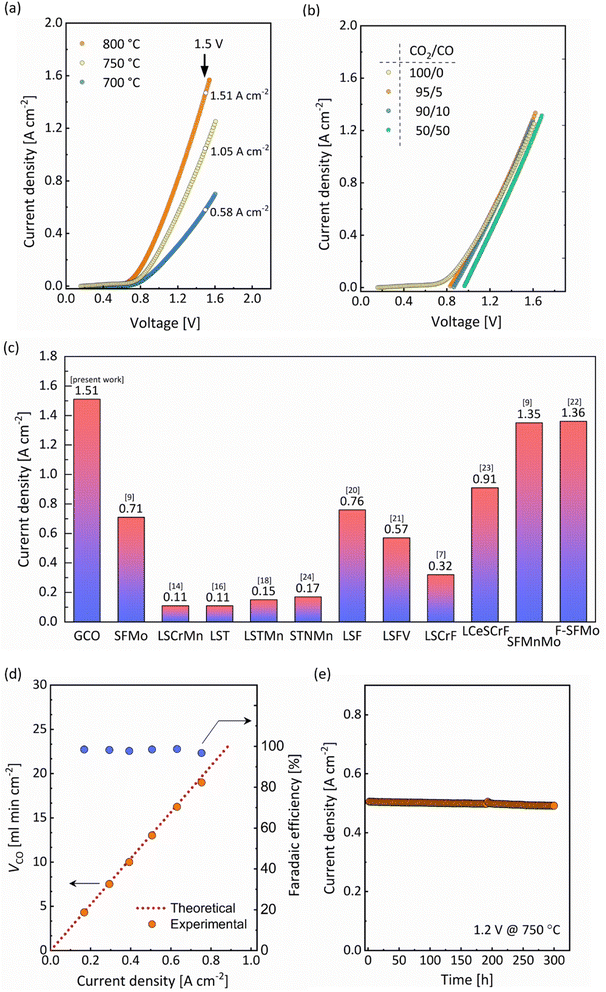 | ||
| Fig. 2 Single-cell performance for the electrolyte-supported SOEC LSCF|GCO|8YSZ|GCO, incorporating a single-phase GCO cathode (a) I–V curves for pure CO2 electrolysis collected at different temperatures. (b) I–V curves of the cell operated at 750 °C in different CO2/CO atmospheres. (c) Comparison of the cell performance at 800 °C and at 1.5 V under pure CO2 electrolysis with that of cells based on different single-phase oxide cathode materials: La0.6Sr0.4FeO3−δ (LSF),20 Sr2Fe1.5Mo0.5O6−δ (SFMo),9 Sr2Fe1.4Mn0.1Mo0.5O6−δ (SFMnMo),9 Sr2Fe1.5Mo0.5O6−δF0.1 (F-SFMo),22 La0.6Sr0.4TiO3−δ(LST),16 La0.6Sr0.4Ti0.8Mn0.2O3−δ (LSTMn),18 La1.2Sr0.8Cr0.5Mn0.5O4 (LSCrMn),14 La0.6Sr0.4Fe0.5V0.5O3−δ (LSFV),21 La0.70Sr0.3Cr0.5Fe0.5O3−δ (LSCrF),7 Sr0.95Ti0.80Nb0.10Mn0.10O3−δ (STNMn)24 and La0.65Ce0.05Sr0.3Cr0.5Fe0.5O3−δ (LCeSCrF).23 (d) CO production rate and corresponding faradaic efficiency as a function of applied current density of the cell operated at 750 °C under pure CO2 electrolysis. (e) Long-term durability test at 1.2 V and 750 °C under pure CO2 electrolysis. | ||
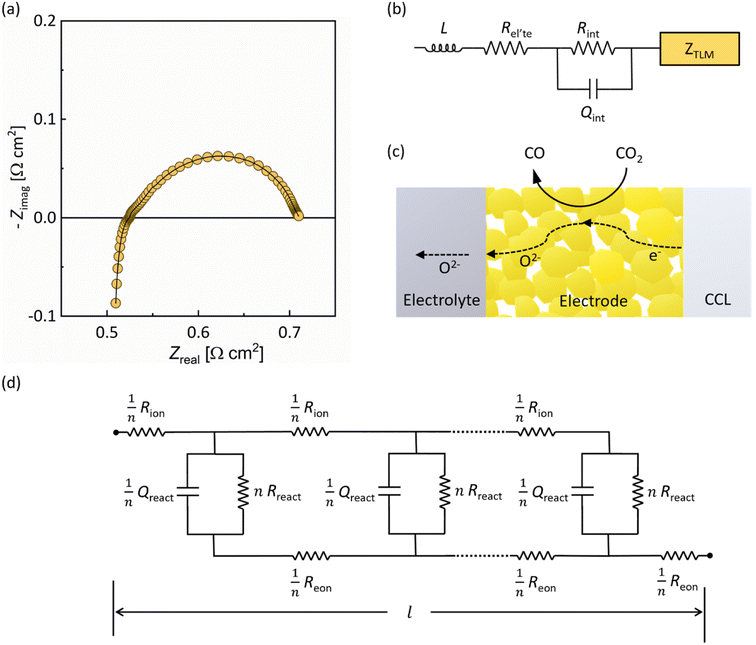
Electrochemical impedance spectroscopy
Electrochemical impedance spectroscopy (EIS) was performed on electrolyte-supported symmetrical cells, GCO|8YSZ|GCO, at different temperatures in CO2/CO 50/50, and in different CO2/CO atmospheres at 750 °C. To this end, GCO layers 20 μm thick were screen-printed on both sides of a 150 μm-thick 8YSZ electrolyte disc. A typical impedance spectrum obtained from measurements is shown in Fig. 3a. All impedance spectra were analyzed with an effective equivalent circuit model incorporating a transmission line model (TLM) for the electrode responses (Fig. 3b). The TLM consists of two rails accounting for the transport of electrons and oxygen ions to and from discrete reaction sites (Fig. 3c and d). These reaction sites are distributed along the thickness of the porous GCO electrode. The descriptive parameters for transport are the effective ionic resistance (Rion) and the effective electronic resistance (Reon), which in addition to their corresponding intrinsic values of GCO, are affected by the porosity (ε) of the electrode and the tortuosity (τ) of the conduction pathways. Electrode parameters and equations used for estimating values of Rion and Reon for fitting are provided in Table S1.† The coupling between ionic and electron charge carriers through the electrochemical reaction is represented by the parallel combination of a surface reaction resistance (Rreact) and a constant phase element or CPE (Qreact), with admittance YCPE(ω) = Qreact(jω)αreact where Qreact and 0 < αreact < 1 are characteristic parameters and ω is the angular frequency.37 For a symmetrical cell, the impedance response of the electrodes is twice that of a single electrode. Throughout this text, electrode parameters obtained from equivalent circuit fitting are presented for individual electrodes.The expression for the impedance of the TLM model as was first derived in the PhD thesis by De Boer38 is given by
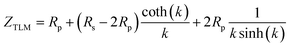 | (1) |
 . In derivation of eqn (1), gas phase diffusion limitations in the porous electrode are ignored. The quantities Rion, Reon, Rreact (Ω cm2) and Qreact (F sαreact−1 cm−2) correspond to the whole electrode thickness. It may be shown that eqn (1) is mathematically equivalent to that derived by Bisquert et al.39 Additional elements in the equivalent circuit shown in Fig. 3b include: (i) an inductance (L) related to the wiring and instruments, (ii) the ionic resistance of the 8YSZ electrolyte (Rel'te), (iii) the ion transfer resistance (Rint) and (iv) associated CPE (Qint) of the interface between electrolyte and electrode layer. Excellent fits of the impedance spectra are obtained over the entire frequency range (Fig. 3a and 4). To avoid over-parameterization, values for Rion and Reon were estimated from data of electrical conductivity (discussed below). Best-fit parameters obtained from equivalent circuit fitting of the impedance spectrum shown in Fig. 3a are listed in Table S2.†
. In derivation of eqn (1), gas phase diffusion limitations in the porous electrode are ignored. The quantities Rion, Reon, Rreact (Ω cm2) and Qreact (F sαreact−1 cm−2) correspond to the whole electrode thickness. It may be shown that eqn (1) is mathematically equivalent to that derived by Bisquert et al.39 Additional elements in the equivalent circuit shown in Fig. 3b include: (i) an inductance (L) related to the wiring and instruments, (ii) the ionic resistance of the 8YSZ electrolyte (Rel'te), (iii) the ion transfer resistance (Rint) and (iv) associated CPE (Qint) of the interface between electrolyte and electrode layer. Excellent fits of the impedance spectra are obtained over the entire frequency range (Fig. 3a and 4). To avoid over-parameterization, values for Rion and Reon were estimated from data of electrical conductivity (discussed below). Best-fit parameters obtained from equivalent circuit fitting of the impedance spectrum shown in Fig. 3a are listed in Table S2.†
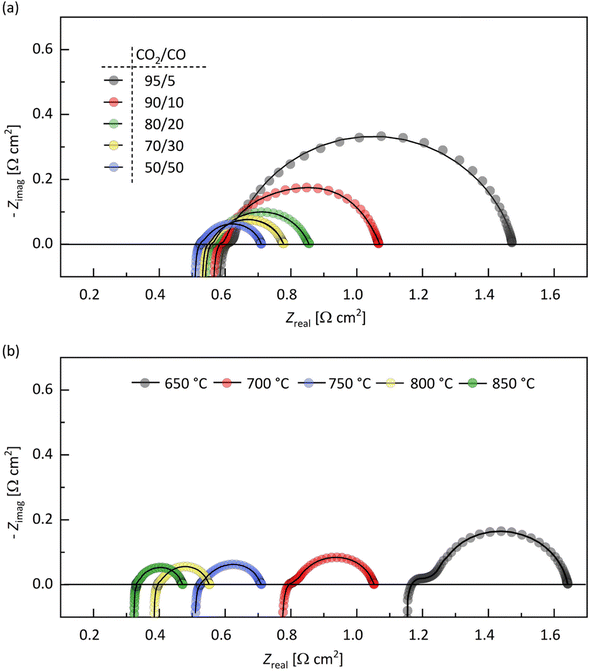 | ||
| Fig. 4 Impedance spectra of the electrolyte-supported symmetrical cell GCO|8YSZ|GCO. Spectra recorded at (a) 750 °C in different CO2/CO gas mixtures and (b) at different temperatures in CO2/CO 50/50. The solid lines are from equivalent circuit fitting. Corresponding resistance values from fitting are given in Tables S4 and S5 (ESI†), respectively. | ||
The value of the high-frequency cut-off resistance, R∞, in impedance spectra is normally solely determined by the electrolyte resistance, Rel'te. At constant temperature, however, R∞ in this work is found to decrease with decreasing CO2/CO ratio (Fig. 4a and Table S3†), i.e., with the drop of pO2, which indicates that the GCO electrode contributes to R∞. This is in accordance with the n-type electronic conductivity of GCO under reducing conditions, increasing with decreasing pO2. The high-frequency cut-off resistance becomes R∞ = Rel'te + 2Rp, where Rp corresponds to the high-frequency limit of eqn (1). The calculated values of Rel'te in different CO2/CO gas mixtures, at 750 °C, remain essentially constant (within 2%; Table S3†), as expected. Fig. S2† compares the Arrhenius plot of the ionic conductivity of 8YSZ calculated using data of Rel'te (Table S4†) obtained from equivalent circuit fitting of the impedance spectra measured at different temperatures in CO2/CO 50/50 with literature data. The overall matching is good, though some discrepancy is noted at the highest temperatures. It can, therefore, not be excluded that Rel'te is a lumped parameter containing contributions of bulk ionic conductivity and possibly interfacial transfer.
At DC conditions (ω → 0), the resistance of the transmission line model (ZTLM|ω→0) can be calculated by means of eqn (1) using  . The contribution of Rint to the area-specific resistance ASR (=Rint + ZTLM|ω→0) of the GCO electrode is within range 2–7%, depending on temperature and applied CO2/CO gas mixture (Tables S3 and S4†). The activation energy of 0.88 ± 0.06 eV estimated from the Arrhenius plot of 1/Rint (Fig. S3a†) is regarded as the energy barrier for interfacial oxygen ion transfer between 8YSZ and GCO. Values of the effective capacitance associated with the CPE, calculated using
. The contribution of Rint to the area-specific resistance ASR (=Rint + ZTLM|ω→0) of the GCO electrode is within range 2–7%, depending on temperature and applied CO2/CO gas mixture (Tables S3 and S4†). The activation energy of 0.88 ± 0.06 eV estimated from the Arrhenius plot of 1/Rint (Fig. S3a†) is regarded as the energy barrier for interfacial oxygen ion transfer between 8YSZ and GCO. Values of the effective capacitance associated with the CPE, calculated using  ,40 range from 0.40 × 10−3 F cm−2 at 650 °C to 1.12 × 10−3 F cm−2 at 850 °C in CO2/CO 50/50 (Fig. S3c†). These values are typical for interfacial capacitances at solid/solid boundaries, generally of the order of 10−3 F cm−2 to 10−5 F cm−2.13,41 From the observed αint values (0.83 < αint < 0.87) we learn that Qint approaches ideal capacitive behavior.
,40 range from 0.40 × 10−3 F cm−2 at 650 °C to 1.12 × 10−3 F cm−2 at 850 °C in CO2/CO 50/50 (Fig. S3c†). These values are typical for interfacial capacitances at solid/solid boundaries, generally of the order of 10−3 F cm−2 to 10−5 F cm−2.13,41 From the observed αint values (0.83 < αint < 0.87) we learn that Qint approaches ideal capacitive behavior.
A prominent contribution to the ASR of the GCO electrode originates from the surface reaction resistance Rreact, depending on temperature and CO2/CO gas mixture (Fig. S4a and b†). Note that when the resistances associated with ionic and electronic transport can be ignored, it follows that ASR = Rint + Rreact. The relatively large values observed for Creact, from 0.10 F cm−2 at 650 °C to 0.65 F cm−2 at 850 °C in CO2/CO 50/50 (Fig. S4c†) as calculated by conversion of Qreact , are attributed to the bulk chemical capacitance of GCO, due to its ability to store electrical charge in response to changes in the oxygen chemical potential.40 Values of αreact are found to vary between 0.80 < αreact < 0.87. The interfacial capacitance of the GCO electrode/gas interface and the dielectric capacitance will in principle also contribute to the apparent value of Creact, though their impact is judged to be negligible.
, are attributed to the bulk chemical capacitance of GCO, due to its ability to store electrical charge in response to changes in the oxygen chemical potential.40 Values of αreact are found to vary between 0.80 < αreact < 0.87. The interfacial capacitance of the GCO electrode/gas interface and the dielectric capacitance will in principle also contribute to the apparent value of Creact, though their impact is judged to be negligible.
The expression for the chemical capacitance of GCO can by derived from the change of oxygen stoichiometry with change in oxygen chemical potential (i.e., inverse thermodynamic factor). Assuming local charge electroneutrality and dilute charge carrier concentrations, this expression can be evaluated as42
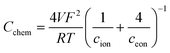 | (2) |
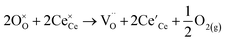 | (3) |
 represents the Ce3+ cations, or small electron polarons, and
represents the Ce3+ cations, or small electron polarons, and  represents the Ce4+ cations. Fig. S5† shows that the electron carrier concentration,
represents the Ce4+ cations. Fig. S5† shows that the electron carrier concentration,  , determined using the chemical capacitance values exhibits good agreement with the expected pO2−1/4 dependence. Furthermore, excellent agreement is found with values of
, determined using the chemical capacitance values exhibits good agreement with the expected pO2−1/4 dependence. Furthermore, excellent agreement is found with values of 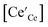 evaluated from oxygen nonstoichiometry data reported by Bishop et al.43 (Fig. S5†).
evaluated from oxygen nonstoichiometry data reported by Bishop et al.43 (Fig. S5†).
Comparison with literature values reported for other single-phase oxide electrode materials investigated for potential use in high-temperature CO2 electrolysis shows that GCO exhibits the lowest ASR values in a wide temperature range (Fig. 5).44–48 In calculation of the ASR values the GCO electrode at different temperatures in CO2/CO 50/50 and, at 750 °C, in different CO2/CO gas mixtures, the DC resistance of the TLM model (ZTLM|ω→0) has been evaluated from the fitted parameters (see Tables S3 and S4,† respectively). It is recalled that these parameters correspond to the whole electrode thickness (dexp) instead of being specified per unit thickness. Thicker electrodes reduce the activation overpotential, through their larger surface area, but increase the ohmic losses. The optimal electrode thickness (dopt) can be evaluated by plotting ZTLM|ω→0 as a function of electrode thickness (d), which requires rescaling of the fitted parameters Rion, Reon and Rreact with factor d/dexp. Fig. S6† shows that ZTLM|ω→0 at 750 °C in CO2/CO 50/50 exhibits a shallow minimum at around 32 μm. The precise value of dopt can be calculated using,
 | (4) |
 | ||
| Fig. 5 Comparison of the area-specific resistance (ASR) of different single-phase oxide cathode materials used for high-temperature CO2 electrolysis: La0.6Sr0.4FeO3−δ (LSF),21 La0.6Sr0.4Fe0.95Mo0.05O3−δ (LSFMo),45 Sr2Fe1.5Mo0.5O6−δ (SFMo),9 La0.3Sr0.7Cr0.3Fe0.7O3−δ (LSCrF),47 La1.2Sr0.8Co0.4Mn0.6O4 (LSCoMn),43 La0.9Sr0.8Co0.4Mn0.6O3.9−δF0.1 (F-LSCoMn),44 Sr2Fe1.5Mo0.5O6−δF0.1 (F-SFMo),22 Sr2Fe1.4Mn0.1Mo0.5O6−δ (SFMnMo),9 La0.6Sr0.4Fe0.8Ni0.2O3−δ (LSFN).46 The gas phase composition is CO2/CO 50/50 in all cases. | ||
Importance of electron carrier concentration to cell performance
To elucidate the role of electronic conductivity or, equally, the electronic carrier concentration on the performance of GCO as electrode material for CO2 electrolysis, the total electrical conductivity (σtot) of GCO was measured at different temperatures as a function of pO2, using different O2/N2 and CO2/CO gas mixtures. The obtained data extend the data set previously measured for the related composition Sm0.15Ce0.85O2−δ by Haile et al.41 to higher temperatures and clearly demonstrate that GCO is an ionic conductor under moderately oxidizing conditions and becomes a mixed conductor under reducing conditions (Fig. 6). The experimental data can be fitted to σtot = σion + σeon = σion + σ0eonpO2m, assuming that the concentration of oxygen vacancies and, hence, the ionic conductivity (σion) in GCO is fixed by the Gd-dopant concentration. At moderate temperatures, the electronic contribution to the conductivity exhibits an m = −1/4 power law dependence on pO2 as may be inferred from defect chemical considerations assuming ideal solution behavior. At higher temperatures, the absolute value of m begins to deviate from this dependence to slightly higher values, i.e., from m = −0.249 ± 0.008 at 650 °C to m = −0.291 ± 0.011 at 850 °C (Table S5†). Consistent with previous findings,49–51 these observations can be accounted for by a decrease in the enthalpy of reduction of non-stoichiometric doped ceria due to defect interactions, easing the formation of electrons and oxygen vacancies upon lowering pO2.50,51 A detailed discussion on the electrical conductivity of GCO is beyond the scope of this paper and will be presented elsewhere.52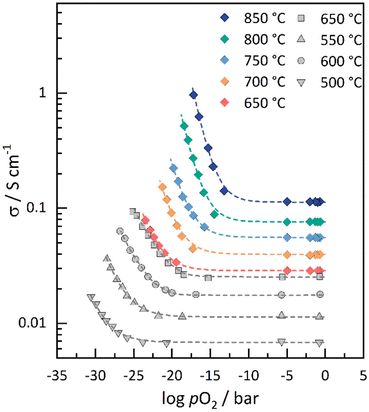 | ||
| Fig. 6 Total electrical conductivity of GCO at different temperatures as a function of oxygen partial pressure. Also shown are data of the total electrical conductivity for Sm0.15Ce0.85O2−δ, taken from Lai et al.41 Dashed lines represent the fit of the experimental data to σtot = σion + σ0eonpO2m. | ||
Fig. 7a shows the electrolysis current density of the full cell (synthetic air) LSCF|GCO|8YSZ|GCO (CO2/CO), at 750 °C, in different CO2/CO atmospheres alongside with the bulk electronic conductivity of GCO at this temperature as a function of the effective pO2 within the GCO electrode. The latter is estimated using the Nernst equation,53–55
 | (5) |
 localized electron concentration derived from literature oxygen non-stoichiometry data,49 showing a linear relationship between both parameters (Fig. S8†).
localized electron concentration derived from literature oxygen non-stoichiometry data,49 showing a linear relationship between both parameters (Fig. S8†).
 | ||
| Fig. 7 Bulk electronic conductivity of GCO and electrolysis current density of the cell (synthetic air) LSCF|GCO|8YSZ|GCO (CO2/CO) as functions of the (IR-corrected) cell voltage log(pO2 (GCO)) (top axis) or effective pO2 within the GCO electrode (bottom axis) in (a) different CO2/CO atmospheres, at 750 °C, and (b) for pure CO2 electrolysis at different temperatures. The dashed lines in (a) refer to the theoretical OCV values in corresponding gas mixtures. The effective pO2 within the GCO electrode is calculated using Nernst's equation (eqn (5)). | ||
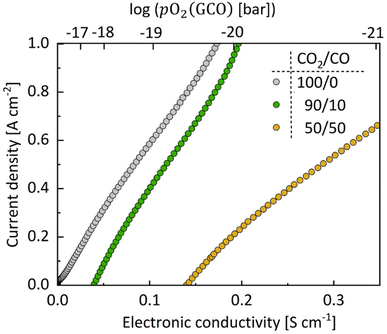 | ||
| Fig. 8 CO2 electrolysis current density at 750 °C as functions of log(pO2 (GCO)) (top axis) or bulk electronic conductivity of GCO (bottom axis) in different CO2/CO atmospheres. The effective pO2 within the GCO electrode has been calculated from the applied (IR-corrected) cell voltage via Nernst's equation (eqn (5)). The associated bulk electronic conductivity is calculated using σeon = σ0eonpO2m. Values of σ0eon and m obtained from fitting experimental data of the total conductivity (Fig. 6) are listed in Table S5.† | ||
Above observations can be rationalized in terms of a simple reaction scheme for CO2 dissociation on the GCO surface as has been proposed earlier by Feng et al.55
Step 1
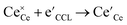 | (6) |
Step 2
 | (7) |
Step 3
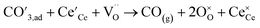 | (8) |
 represents an electron from the metal current collecting layer (CCL) and
represents an electron from the metal current collecting layer (CCL) and  an adsorbed carbonate ion. It is assumed that the transport of mobile charge carriers within the GCO layer to the surface reaction site does not impose any rate limitations. Step 1 involves the electron transfer from the CCL to the GCO bulk. Step 2 is the chemisorption of CO2 onto a surface oxygen ion. The chemisorption involves electron transfer from a small polaron site at the surface to the adsorbed CO2 molecule, generating a surface monodentate carbonate species
an adsorbed carbonate ion. It is assumed that the transport of mobile charge carriers within the GCO layer to the surface reaction site does not impose any rate limitations. Step 1 involves the electron transfer from the CCL to the GCO bulk. Step 2 is the chemisorption of CO2 onto a surface oxygen ion. The chemisorption involves electron transfer from a small polaron site at the surface to the adsorbed CO2 molecule, generating a surface monodentate carbonate species  . In reaction step 3, a second electron transfer from the oxide surface leads to dissociation of the carbonate intermediate and formation of gaseous CO. Here, we may speculate that step 2 is rate determining as it predicts, in line with the results presented in Fig. 8, a current which is proportional to both the concentration of
. In reaction step 3, a second electron transfer from the oxide surface leads to dissociation of the carbonate intermediate and formation of gaseous CO. Here, we may speculate that step 2 is rate determining as it predicts, in line with the results presented in Fig. 8, a current which is proportional to both the concentration of  and the partial pressure of CO2 in the gas phase. However, our proposal contradicts with the work of Feng et al.55 Using ambient pressure X-ray photoelectron spectroscopy (AP-XPS), these authors observed that the coverage of the surface carbonate intermediates on samarium-doped ceria (Sm0.2Ce0.8O2−δ) increases with the surface concentration of
and the partial pressure of CO2 in the gas phase. However, our proposal contradicts with the work of Feng et al.55 Using ambient pressure X-ray photoelectron spectroscopy (AP-XPS), these authors observed that the coverage of the surface carbonate intermediates on samarium-doped ceria (Sm0.2Ce0.8O2−δ) increases with the surface concentration of  , as was found in an earlier study on pure ceria.56 Based upon this observation, Feng et al.55 postulated quasi-equilibration of the surface carbonate coverage due to a high rate constant for reaction step 2 relative to step 3. There is consensus in literature that CO2 electrolysis on oxide surfaces proceeds via carbonate intermediates. In fact, various binding configurations of surface carbonates have been reported.57 Noting that step 3 is a concerted reaction, our observations could equally well be explained by rate determining formation of a bidentate carbonate configuration (by adsorption of
, as was found in an earlier study on pure ceria.56 Based upon this observation, Feng et al.55 postulated quasi-equilibration of the surface carbonate coverage due to a high rate constant for reaction step 2 relative to step 3. There is consensus in literature that CO2 electrolysis on oxide surfaces proceeds via carbonate intermediates. In fact, various binding configurations of surface carbonates have been reported.57 Noting that step 3 is a concerted reaction, our observations could equally well be explained by rate determining formation of a bidentate carbonate configuration (by adsorption of  onto a nearby oxygen vacancy site) prior to electron transfer and dissociation of the formed surface complex. Clearly more research is needed to unambiguously address the mechanism of CO2 dissociation on ceria-based oxide surfaces.
onto a nearby oxygen vacancy site) prior to electron transfer and dissociation of the formed surface complex. Clearly more research is needed to unambiguously address the mechanism of CO2 dissociation on ceria-based oxide surfaces.
Conclusions
Our findings support that doped ceria has a great promise for use as a fuel electrode for CO2 electrolysis in SOECs. A current density of 1.51 A cm−2 has been achieved in pure CO2 electrolysis using electrolyte-supported cells operated at 1.5 V at 800 °C. This performance exceeds that of other single-phase oxide cathodes currently reported in literature. It is believed that there is still scope for improvement of the performance by optimizing the microstructure, to enhance the exposed surface area, and electrode thickness. Furthermore, full cell designs with lower overall resistance than the electrolyte-supported cell used in this study can be considered. The almost-linear correlation of the current density with electronic conductivity observed in different CO2/CO atmospheres suggests that electron transfer between ceria and adsorbed CO2 is likely rate determining. However, more research is needed to unambiguously address the mechanism of CO2 dissociation.Experimental
Materials and cell fabrication
Dense 8 mol% yttria-stabilized zirconia (8YSZ) electrolyte substrates of 150 μm thickness were purchased from Kerafol (Germany). Precursor electrode powders of GCO (Gd0.1Ce0.9O2−δ) and LSCF (La0.6Sr0.4Co0.2Fe0.8O3−δ) were purchased from Fuelcellmaterials (USA). Electrode powder slurries were prepared by mixing 2 g precursor powder with 2 g dispersant (6 wt% ethyl-cellulose dissolved in terpineol) with a mortar and pestle before screen-printing onto the 8YSZ substrate. First, a 2 μm-thin GCO diffusion-barrier layer (between the LSCF electrode and 8YSZ substrate) was grown on one side of the 8YSZ substrate using PLD, employing a KrF laser (Lambda Physik, Germany) with a wavelength of 248 nm. The growth parameters of the GCO film were: laser repetition frequency 10 Hz, target–substrate distance 50 mm, substrate temperature 600 °C, fluency 2.5 J cm−2 and O2 background pressure 10−3 mbar. Subsequently, a GCO electrode layer was screen printed on the opposite side of the 8YSZ substrate, followed by drying at 100 °C for 1 h and annealing in air at 1200 °C for 3 h. Hereafter, the LSCF oxygen electrode was screen-printed onto the GCO barrier layer and annealed in air at 1000 °C for 3 h, resulting in the complete single full cell LSCF|GCO|8YSZ|GCO. Brush-painted gold functioned as current collecting layer (CCL) on both sides of the cell. The top surface of the GCO fuel electrode and the cross-section of the cell after annealing were examined using a scanning electron microscope (SEM, JEOL JSM-6010 LA, Japan). The thickness of the GCO electrode after sintering was 20 μm. Symmetrical cells GCO|8YSZ|GCO were prepared using procedures like those as described above.Electrochemical testing
Electrochemical testing was accomplished using a home-made test rig. A single full cell was mounted onto an alumina test tube with a ceramic sealant (Ceramabond 552, Aremco Products Inc.). A flow of CO2/CO was supplied to the GCO fuel electrode, while a flow of oxygen (balanced with nitrogen) was supplied to the LSCF oxygen electrode. For symmetrical cell testing, the same CO2/CO gas mixture was supplied to both sides of the cell, which was mounted onto the test tube using a perforated alumina disc. Measurements were performed under various conditions. The total flow rates were 200 ml min−1 and in all cases the CO2 utilization was less than 4% at all current densities. The concentration of gases was controlled by mass flow controllers (GF40, Brooks Instruments). I–V curves were collected by cyclic voltammetry from OCV to 1.6 V at a scan rate of 20 mV s−1 using a potentiostat (Gamry reference 3000, Gamry Instruments). The Faraday efficiency was evaluated by analyzing the fuel outlet gas using online gas chromatography (Compact GC 4.0, Interscience). The long-term durability of the full cell was tested at 1.2 V for 300 h supplying pure CO2 to the GCO electrode and 21% oxygen (balanced with nitrogen) to the LSCF electrode. Impedance spectra of the full cell were recorded, at 750 °C, with CO2/CO 90/10 supplied to the fuel side and different concentrations of oxygen to the oxygen side. Impedance spectra on symmetrical cells were recorded at different temperatures in CO2/CO 50/50, and at 750 °C in different CO2/CO gas mixtures. Impedance data were collected in the frequency range 10 mHz to 100 kHz frequency range and were validated by a Kramers–Kronig test using the Gamry Echem Analyst software package (Gamry Instruments). Equivalent circuit analysis of the impedance spectra was carried out using the ZView software package (Scribner Associates Inc.).Electrical conductivity testing
Powders of GCO were pelletized by uniaxially pressing at 25 MPa followed by isostatic pressing at 400 MPa. Subsequently, the pellets were sintered at 1400 °C in air for 4 h with heating/cooling rates of 2 °C min−1. The relative density of the pellets after sintering was 96.3% of the theoretical value as measured by Archimedes' method. Thin rectangular bars were cut out of the sintered pellets using a cutting machine (Secotom-50, Struers LLC). The obtained bars were ground by abrasive plates and subsequently polished (Tegramin-20, Struers LLC) to final dimensions 15 × 6 × 0.9 mm3. Electrical conductivity data were collected by a standard four-probe dc technique using platinum wires (Fiaxell SOFC Technologies, 0.25 mm in diameter) wrapped around the bar to act as electrodes. Platinum ink (Fuelcellmaterials) was applied on the sample surface directly underneath the platinum wires. Prior to measurements, the bar was in situ annealed in synthetic air at 900 °C for 1 h to establish a proper adhesion between the platinum wires and the bar's surface. The pO2 during measurements was controlled by mixing oxygen and nitrogen or CO2 and CO in the desired ratios using Brooks GF40 mass flow controllers (Brooks Instruments Inc.).Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
Financial support from the Dutch Technology Foundation (STW, now part of NWO; Project No. 15325) is gratefully acknowledged.References
- A. Atkinson, S. Barnett, R. J. Gorte, J. Irvine, A. J. McEvoy, M. Mogensen, S. C. Singhal and J. Vohs, Nat. Mater., 2004, 3, 17–27 CrossRef CAS PubMed
.
- S. P. Jiang and S. H. Chan, J. Mater. Sci., 2004, 39, 4405–4439 CrossRef CAS
.
- A. Hauch, R. Küngas, P. Blennow, A. B. Hansen, J. B. Hansen, B. V. Mathiesen and M. B. Mogensen, Science, 2020, 370, eaba6118 CrossRef CAS PubMed
.
- Y. Zheng, W. Zhang, Y. Li, J. Chen, B. Yu, J. Wang, L. Zhang and J. Zhang, Nano Energy, 2017, 40, 512–539 CrossRef CAS
.
- S. D. Ebbesen, S. H. Jensen, A. Hauch and M. B. Mogensen, Chem. Rev., 2014, 114, 10697–10734 CrossRef CAS PubMed
.
- Y. Song, X. Zhang, K. Xie, G. Wang and X. Bao, Adv. Mater., 2019, 31, 1902033 CrossRef CAS PubMed
.
- X. Yue and J. T. S. Irvine, J. Electrochem. Soc., 2012, 159, F442–F448 CrossRef CAS
.
- P. I. Cowin, C. T. Petit, R. Lan, J. T. Irvine and S. Tao, Adv. Energy Mater., 2011, 1, 314–332 CrossRef CAS
.
- Y. Jiang, Y. Yang, C. Xia and H. J. M. Bouwmeester, J. Mater. Chem. A, 2019, 7, 22939–22949 RSC
.
- C. Graves, S. D. Ebbesen, S. H. Jensen, S. B. Simonsen and M. B. Mogensen, Nat. Mater., 2015, 14, 239–244 CrossRef CAS PubMed
.
- Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602–1644 RSC
.
- G. Tsekouras, D. Neagu and J. T. S. Irvine, Energy Environ. Sci., 2013, 6, 256–266 RSC
.
- W. Jung, J. O. Dereux, W. C. Chueh, Y. Hao and S. M. Haile, Energy Environ. Sci., 2012, 5, 8682–8689 RSC
.
- X. Zhang, Y. Song, F. Guan, Y. Zhou, H. Lv, Q. Liu, G. Wang and X. Bao, J. Power Sources, 2018, 400, 104–113 CrossRef CAS
.
- F. Bidrawn, G. Kim, G. Corre, J. Irvine, J. M. Vohs and R. J. Gorte, Electrochem. Solid-State Lett., 2008, 11, B167 CrossRef CAS
.
- L. Ye, C. Pan, M. Zhang, C. Li, F. Chen, L. Gan and K. Xie, ACS Appl. Mater. Interfaces, 2017, 9, 25350–25357 CrossRef CAS PubMed
.
- G. Tsekouras and J. T. S. Irvine, J. Mater. Chem., 2011, 21, 9367–9376 RSC
.
- W. Qi, Y. Gan, D. Yin, Z. Li, G. Wu, K. Xie and Y. Wu, J. Mater. Chem. A, 2014, 2, 6904–6915 RSC
.
- J. H. Zhang, F.-Z. Han, C.-X. Li and S.-L. Zhang, J. Eur. Ceram. Soc., 2022, 42, 5801–5812 CrossRef CAS
.
- A. K. Opitz, A. Nenning, C. Rameshan, M. Kubicek, T. Götsch, R. Blume, M. Hävecker, A. Knop-Gericke, G. n. Rupprechter and B. Klötzer, ACS Appl. Mater. Interfaces, 2017, 9, 35847–35860 CrossRef CAS PubMed
.
- Y. Zhou, Z. Zhou, Y. Song, X. Zhang, F. Guan, H. Lv, Q. Liu, S. Miao, G. Wang and X. Bao, Nano Energy, 2018, 50, 43–51 CrossRef CAS
.
- Y. Li, Y. Li, Y. Wan, Y. Xie, J. Zhu, H. Pan, X. Zheng and C. Xia, Adv. Energy Mater., 2019, 9, 1803156 CrossRef
.
- Y. Q. Zhang, J. H. Li, Y. F. Sun, B. Hua and J. L. Luo, ACS Appl. Mater. Interfaces, 2016, 8, 6457–6463 CrossRef CAS PubMed
.
- J. Zhang, K. Xie, H. Wei, Q. Qin, W. Qi, L. Yang, C. Ruan and Y. Wu, Sci. Rep., 2014, 4, 7082 CrossRef PubMed
.
- Đ. Tripković, J. Wang, R. Küngas, M. B. Mogensen, B. Yildiz and P. V. Hendriksen, Chem. Mater., 2022, 34, 1722–1736 CrossRef
.
- C. Zhang, J. Sunarso and S. Liu, Chem. Rev., 2017, 46, 2941–3005 CAS
.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS
.
- R. Price, J. G. Grolig, A. Mai and J. T. S. Irvine, Solid State Ionics, 2020, 347 CrossRef CAS
.
- P. Kim-Lohsoontorn and J. Bae, J. Power Sources, 2011, 196, 7161–7168 CrossRef CAS
.
- V. Singh, H. Muroyama, T. Matsui, S. Hashigami, T. Inagaki and K. Eguchi, J. Power Sources, 2015, 293, 642–648 CrossRef CAS
.
- C. Gaudillere, L. Navarrete and J. M. Serra, Int. J. Hydrogen Energy, 2014, 39, 3047–3054 CrossRef CAS
.
- S. Wang, T. Kobayashi, M. Dokiya and T. Hashimoto, J. Electrochem. Soc., 2000, 147, 3606–3609 CrossRef CAS
.
- R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. Rupp, Chem. Soc. Rev., 2020, 49, 554–592 RSC
.
- W. C. Chueh, Y. Hao, W. Jung and S. M. Haile, Nat. Mater., 2011, 11, 155–161 CrossRef PubMed
.
- A. Nenning, M. Holzmann, J. Fleig and A. K. Opitz, Mater. Adv., 2021, 2, 5422–5431 RSC
.
- T. L. Skafte, Z. Guan, M. L. Machala, C. B. Gopal, M. Monti, L. Martinez, E. Stamate, S. Sanna, J. A. Garrido Torres, E. J. Crumlin, M. García-Melchor, M. Bajdich, W. C. Chueh and C. Graves, Nat. Energy, 2019, 4, 846–855 CrossRef CAS
.
- B. A. Boukamp, Solid State Ionics, 1986, 18, 136–140 CrossRef
.
-
B. De Boer, PhD thesis, University of Twente, Enschede, The Netherlands, 1998
.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and A. Compte, Electrochem. Commun., 1999, 1, 429–435 CrossRef CAS
.
- D. Chen, S. R. Bishop and H. L. Tuller, ECS Trans., 2013, 57, 1387 CrossRef
.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS
.
- J. S. Lee, J. Jamnik and J. Maier, Monatsh. Chem., 2009, 140, 1113–1119 CrossRef CAS PubMed
.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Acta Mater., 2009, 57, 3596–3605 CrossRef CAS
.
- S. Park, Y. Kim, H. Han, Y. S. Chung, W. Yoon, J. Choi and W. B. Kim, Appl. Catal., B, 2019, 248, 147–156 CrossRef CAS
.
- S. Park, H. Han, W. Yoon, J. Choi, Y. Kim, H. Kim and W. B. Kim, ACS Sustainable Chem. Eng., 2020, 8, 6564–6571 CrossRef CAS
.
- S. Wang, H. Jiang, Y. Gu, B. Yin, S. Chen, M. Shen, Y. Zheng, L. Ge, H. Chen and L. Guo, Electrochim. Acta, 2020, 337, 135794 CrossRef CAS
.
- S. Liu, Q. Liu and J.-L. Luo, J. Mater. Chem. A, 2017, 5, 2673–2680 RSC
.
- P. Addo, B. Molero-Sanchez, M. Chen, S. Paulson and V. Birss, Fuel cells, 2015, 15, 689–696 CrossRef CAS
.
- S. Bishop, K. Duncan and E. Wachsman, Electrochim. Acta, 2009, 54, 1436–1443 CrossRef CAS
.
- S. Grieshammer and M. Martin, J. Mater. Chem. A, 2017, 5, 9241–9249 RSC
.
- S. Grieshammer, Phys. Chem. Chem. Phys., 2021, 23, 10321–10325 RSC
.
- A. Shaur and H. J. M. Bouwmeester, to be published.
- T. Kawada, J. Suzuki, M. Sase, A. Kaimai, K. Yashiro, Y. Nigara, J. Mizusaki, K. Kawamura and H. Yugami, J. Electrochem. Soc., 2002, 149, E252 CrossRef CAS
.
- A. Schmid, G. M. Rupp and J. Fleig, Phys. Chem. Chem. Phys., 2018, 20, 12016–12026 RSC
.
- Z. A. Feng, M. L. Machala and W. C. Chueh, Phys. Chem. Chem. Phys., 2015, 17, 12273–12281 RSC
.
- Y. Yu, B. Mao, A. Geller, R. Chang, K. Gaskell, Z. Liu and B. W. Eichhorn, Phys. Chem. Chem. Phys., 2014, 16, 11633–11639 RSC
.
- W. Taifan, J.-F. Boily and J. Baltrusaitis, Surf. Sci. Rep., 2016, 71, 595–671 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta03977c |
| This journal is © The Royal Society of Chemistry 2023 |