Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First principles study of layered transition metal dichalcogenides for use as electrodes in Li-ion and Mg-ion batteries†
Conor Jason
Price
 *,
Edward Allery David
Baker
*,
Edward Allery David
Baker
 and
Steven Paul
Hepplestone
and
Steven Paul
Hepplestone
 *
*
Department of Physics, University of Exeter, Stocker Road, Exeter, EX4 4QL, UK. E-mail: cjp225@exeter.ac.uk; S.P.Hepplestone@exeter.ac.uk
First published on 18th May 2023
Abstract
We present a first principles investigation of lithium- and magnesium-intercalation into each of the layered transition metal dichalcogenides. Using a consistent and thorough methodology, we investigate 84 TMDC materials (transition metals, Group XIV, and S, Se, Te chalcogens) as potential electrode materials, evaluating their T and H phases. We show generally low volume expansions and provide direct estimates of the theoretical capacity based on thermodynamic arguments. We find that many offer capacities in excess of 200 mA h g−1 (400 mA h g−1) with Li (Mg) intercalation and show a range of voltage profiles. For both Li and Mg, we show that the Group VIII and IX are promising electrode materials, and in particular highlight ScS2 as a promising cathode material. We also show that sulfides are generally better for electrode materials.
1 Introduction
Lithium ion batteries, as a result of their high specific energy density and capacity, have a vital role in sustainable energy storage, driven in recent years by the rising popularity of electric vehicles, flexible electronics, and the ever-increasing demand for more powerful portable devices. Beyond intercalation with lithium, other ionic species have also been considered. Group II elements such as magnesium and calcium in particular have received attention as possible successors to lithium. Whilst these elements offer twice the number of valence electrons of lithium, and hence twice the charge available for transfer, this larger charge leads to issues in the stability of the electrodes and electrolytes being used.1 However, they have been shown to be safer due to non-dendritic metal deposition.2The electrodes are a crucial component of batteries, determining voltages, capacity, and cost. The anode is required to have a low voltage with respect to the redox level of the intercalant species (e.g. vs. Li/Li+), with a particularly successful material being graphite, showing lithium intercalation occurring between 0.2 and 0.01 V vs. Li/Li+. However, graphite suffers from a capacity being limited to LiC6 (equivalent to 372 mA h g−1)3 and the low intercalation potential results in the decomposition of organic electrolytes. This has led to materials such as silicon,4 lithium titanate,5 and other metal oxide materials being considered.6,7 Cathodes, on the other hand, need to offer high intercalation potentials typically in excess of 3 V.8 Following the success of LiCoO2, many transition metal-based oxides have been investigated and have demonstrated their own successes. NMC, NCA, and their variants,9–14 several phosphates,15–17 and spinel oxides such as Mn2O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18,19 have each offered high voltages, and layered van der Waals (vdW) structures have been shown to offer lower volume expansions20 upon intercalation as they can more readily accept intercalants.21–23
18,19 have each offered high voltages, and layered van der Waals (vdW) structures have been shown to offer lower volume expansions20 upon intercalation as they can more readily accept intercalants.21–23
There are many transition metal chalcogenide materials which do offer the desired layered structure, and have also been shown to be electrochemically active and have shown good cyclability.24,25 One particularly diverse group of layered materials are the transition metal dichalcogenides (TMDCs),26–28 with general formula MX2. The presence of a transition metal M allows us to utilise the redox levels that have led to the successes of the transition metal oxides, the choice of chalcogen X means that electrolytes that are not oxygen-based (such as sulfur-based electrolytes) may now be a more viable option, and the different possible M–X pairings allow us to consider the wide range of properties that have been demonstrated within the TMDC family. Many TMDC compounds do not possess a layered structure, exhibiting a pyrite, marcasite, or rock salt phase, and chalcopyrite or spinel phases when intercalated with a foreign ion.29–31 Fortunately, various techniques can be employed to encourage the growth of the layered structure, such as through careful choice of a substrate, the use of specific growth conditions, or specific techniques.32,33
Many members of the TMDC family and their intercalated structures have already received a lot of attention, being the subject of intense study over the last few decades.21,34–36 TiS2 was identified as early as the 1970s37,38 for showing a lithium-intercalation voltage of 2 V and a reversible capacity of 240 mA h g−1. However, due to the sensitivity of TiS2 to moisture (releasing H2S gas on contact with water), the inclusion of a dangerous, shock-sensitive electrolyte, and the use of metallic lithium, device manufacture was found to be expensive and complex. Nonetheless, it inspired works of magnesium intercalation into TiS2,39,40 and prompted investigations into the Zr41–44 and Hf41,45 analogues. The large inter-layer spacing in VS2 has been shown to allow rapid insertion and extraction of alkali-metal intercalants,46 and recently it was proposed47 for magnesium-based cathodes, delivering a reversible discharge capacity of 235 mA h g−1. The Nb- and Ta-based materials41 have been intercalated to similar levels, but their heavier masses result in lower theoretical capacities below 170 mA h g−1. Of course, the ubiquitous MoS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48–53 is a favourite within the study of layered materials and has been the subject of many of its own investigations, demonstrating an intercalation voltage of 2 V with a capacity of 167 mA h g−1. This material, along with some others, can exhibit multiple TMDC phases, and has been observed to undergo transitions between them with intercalation.54,55 Other materials, such as CrS2
48–53 is a favourite within the study of layered materials and has been the subject of many of its own investigations, demonstrating an intercalation voltage of 2 V with a capacity of 167 mA h g−1. This material, along with some others, can exhibit multiple TMDC phases, and has been observed to undergo transitions between them with intercalation.54,55 Other materials, such as CrS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56,57 and ScS2,58,59 are not stable without intercalants, though it is possible to synthesise them in their intercalated forms. ScS2 in particular has recently been suggested as a promising electrode,60 promising an ideal cathode voltage of 4.5 V and a reversible capacity of 183 mA h g−1. The post-transition metal sulfide SnS2 has also been the subject of many studies,61–70 however it has been shown to readily undergo conversion to Li2S and elemental tin.
56,57 and ScS2,58,59 are not stable without intercalants, though it is possible to synthesise them in their intercalated forms. ScS2 in particular has recently been suggested as a promising electrode,60 promising an ideal cathode voltage of 4.5 V and a reversible capacity of 183 mA h g−1. The post-transition metal sulfide SnS2 has also been the subject of many studies,61–70 however it has been shown to readily undergo conversion to Li2S and elemental tin.
For several of these materials, the intercalation capacity is dictated by the formation of the Li2S (or equivalent) compound, a conversion product which can result in the irreversible loss or amorphisaton of the layered TMDC structure.55 Typically, the breakdown of LiaMX2 into Li2X occurs for 0 < a < 1, as has been observed for MoS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50,53 and WS2.71 Though this conversion reaction allows for further charging of the cell, facilitated by subsequent reactions involving Li2S or lithium polysulfides to elemental lithium and sulfur, the metal species of the host material is inert.49,71
50,53 and WS2.71 Though this conversion reaction allows for further charging of the cell, facilitated by subsequent reactions involving Li2S or lithium polysulfides to elemental lithium and sulfur, the metal species of the host material is inert.49,71
Recent works have looked at improving many of the properties offered by these materials, with the aim of extending device operation, increasing the intercalant capacities, and improving operating voltages. Dimension reduction72–74 provides greater surface area and thus a higher surface reactivity, allowing for faster ionic and electronic transport. To a similar effect, morphology control48,75,76 and composite formation,46,77–82 particularly through the inclusion of graphitic carbon or other layered materials, has been used to improve electrical and ionic conductivity, provide mechanical support, and improve the resultant capacity. Coating and encapsulation has been used to protect both the electrolyte and electrode from mutual decomposition, stabilisation of surfaces and prevention of reactions between the electrolyte and the electrode surface.83 Finally, doping and functionalisation84–88 can improve chemical and thermal stability, and allow for some control of the operating voltage.60 However, to understand the improvements that arise from each of these methods, an understanding of the fundamental electrochemical properties of the bulk structures is first needed. Properties such as the volumetric expansion, the intercalation voltage, and the intercalation capacity need to be established in a consistent manner as these are vital for discussions of electrode materials. Further, much of this family is yet to be investigated, meaning there are still many materials that could offer ideal voltages or higher capacities, or alternatively demonstrate other properties that could be advantageous to a wide range of other applications.
In this article, we report on a theoretical modelling of TMDC layers with a focus on their properties for use as electrode materials in lithium and magnesium ion cells. We present the material voltage profiles, and discuss how the thermodynamic stability of these materials upon intercalation can be used as a way to calculate the charge storage capacity from reversible intercalation. We also examine other properties that are important for consideration when discussing possible electrode materials, such as the volumetric expansion that arises from intercalation, and the resultant electronic structure which is important for efficient electronic conduction. Further details and discussions that go towards supporting the work presented in this article are presented in the ESI.†
2 Methods
2.1 First-principles methods
In this work, first principles techniques based on density functional theory were used to determine structural, energetic, and electronic properties of layered MX2 materials intercalated with varying levels of either lithium or magnesium. These calculations were performed using the Vienna Ab initio Simulation Package (VASP).89–92 The projector augmented wave method93 was used to describe the interaction between core and valence electrons, and a plane-wave basis set was used with an energy cutoff of 700 eV. The valence electrons included for each species are indicated in ESI Section I.A.† vdW interactions have been addressed using the zero damping DFT-D3 method of Grimme.94This study focuses on 1T-phase TMDCs, as many of the TMDCs exhibit the 1T-phase.34,95–97 Not only are they known to have superior electrical conductivities over their 2Hc-phase counterparts,98 making them better suited to electrode application, but alternative phases often undergo a phase transition to the T-phase under intercalation.99,100 However, the Hc-phase is found to be important for several TMDCs. As such, comparisons have been made with the 2Hc-phase for such TMDCs, as is discussed later in the article. Though transition metal dichalcogenide compounds can exhibit a wide range of different structural phases beyond the layered structures considered here,29 we focus on the T- and Hc-phases to utilise their ideal layered structures.
For comparisons of intercalant site and of the T- and Hc-phases, primitive cells of each of the TMDCs were used. However, for a more thorough consideration of these materials with finer sampling of intercalant concentrations, supercells of (2 × 2 × 1) and (2 × 2 × 2) unit cells (corresponding to 24 atoms, eight MX2 formula units, and two TMDC layers) of 2Hc- and 1T-phase MX2, respectively, were generated and structurally relaxed. These were then used as the bulk unit cells into which lithium and magnesium were intercalated for evaluation of voltages and thermodynamic stability. Further details are presented in the ESI Section I.B.†
All structural relaxations (allowing for both ionic and unit cell optimisation) were completed using the Perdew–Burke–Ernzerhof (PBE)101 functional form of the generalised gradient approximation (GGA), and converged to a force tolerance of 0.01 eV Å−1, while electronic self-consistency was considered to an accuracy of 10−7 eV. Monkhorst–Pack grids102 of k-points equivalent to a 6 × 6 × 6 grid in the supercells are used throughout. Due to the possibility of unpaired electrons in d and f orbitals in transition metal compounds, we have allowed for collinear spin-polarized calculations for all materials considered, without specifying any initial spin configuration. To account for the inaccurate calculation of exchange in GGA functionals, the HSE06 hybrid functional103–105 has also been used for a selection of systems. For these systems, geometric relaxations were performed on the primitive cell to the same force and energy tolerance as used with the PBE functional, though a coarser k-point grid was used due to the increased computational cost of the hybrid functional.
Nudged elastic band (NEB) methods, as employed in VASP, were used to consider transition states for intercalant diffusion through the system106,107 (using the PBE functional). This method uses a series of interpolated ‘images’ along a specified path to determine the activation energies for diffusion. For these calculations, we formed 2 × 2 bilayers of selected TMDCs and fixed the positions of the transition metal species with intercalant species occupying high-coordination sites. NEB relaxations were considered to a force tolerance of 0.01 eV per Å per atom, electronic self-consistency was considered to an accuracy of 10−7 eV, and Monkhorst–Pack grids of 6 × 6 × 1 k-points were used.
2.2 Methods for material evaluation
When assessing a material for its suitability as an electrode material, there are many key properties that need to be determined. Quantities such as the volumetric expansion and electronic band gaps can be directly obtained from DFT calculations, however there are many other properties that need careful attention. The intercalation voltage gives a measure of the energy associated with intercalation of a given ion, whereas the intercalation capacity gives a limit on how much of a given intercalant can be introduced to a host material before secondary reactions that degrade the material occur. Here, we outline how we approach these challenges using a first principles approach.To compare different levels of lithium/magnesium-intercalated MX2 the voltage, V, can be calculated using,108,109
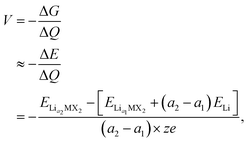 | (1) |
In some situations, however, taking the difference between two equivalent structures of consecutive intercalant contents does not always give the most accurate representation of what happens in reality. For example, lithium has been found to cluster in some materials rather than distributing evenly throughout.65,67,113,114 In these cases, it is more accurate to consider combinations of different lithium concentrations; for example, it might be favourable for lithium to fill one cell to Li0/8MX2 and an adjacent cell to Li8/8MX2, rather than filling a both cells to Li4/8MX2. This would be indicative of clustering or phase separation, and so has been considered in the evaluation of TMDC voltages. Further details of this have been given in the ESI Section I.C.†
The stability of TMDCs with intercalation depends heavily on how favourable the formation of secondary products is, for example Li2X or MgX. Generally, these conversion products are not desired for intercalation electrodes as they indicate the loss of the layered TMDC structure, and limits the reversibility of cell charging. By assessing the relative stability of these conversion products against the intercalated phases, one can construct phase diagrams indicating the viability of the intercalated structure at different intercalant concentrations.115 We can then determine the maximum intercalant capacity that can be reached, and hence the reversible charge capacity, a key metric for assessing the viability of electrode materials. For lithium intercalation, we express this limit as,
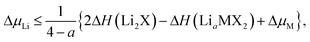 | (2) |
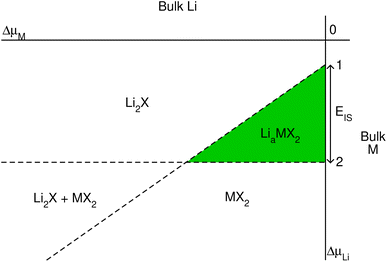 | ||
| Fig. 1 Schematic phase diagram for lithium intercalated TMDCs, constructed using eqn (2)–(4). | ||
Further limits can be considered on the chemical potential, which are expressed as
| ΔμLi,M,X ≤ 0, | (3) |
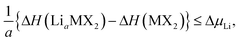 | (4) |
We can quantitatively compare the phase diagrams for the different concentrations considered by evaluating the difference between the intercepts of lines ‘1’ and ‘2’ with the vertical ΔμLi-axis. We define this as,
| EIS = Δμ(1)Li(ΔμM = 0) − Δμ(2)Li(ΔμM = 0), | (5) |
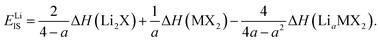 | (6) |
Each of the enthalpy of formation values should be negative for them to be thermodynamically stable with respect to their atomic constituents. When the value of EIS is negative, the first two terms dominate, and line ‘1’ intercepts below line ‘2’ so no stability region exists. Consequently, any intercalation is followed by the conversion of the host material. When the value of EIS is positive, however, ΔH(LiaMX2) dominates and the intercalated MX2 material is stable. For magnesium intercalation, we have an equivalent expression,
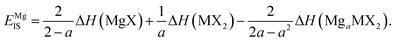 | (7) |
Thus, we have a metric to describe the limit of intercalation, and hence a direct calculation on the reversible intercalation charge capacity.
2.3 Determination of structure
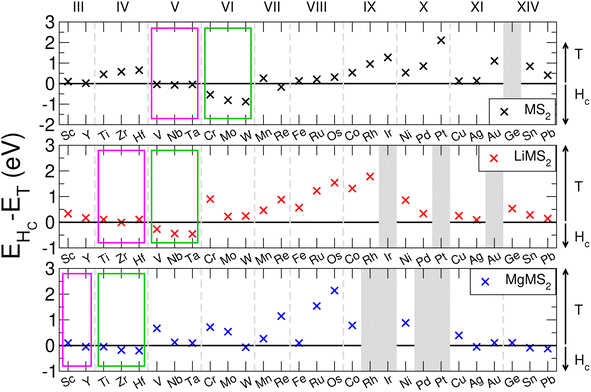
The family of TMDCs have been shown to exhibit multiple polymorphs of the layered structure, most commonly the 1T-phase and 2Hc-phase.96,97 T-phase TMDCs have D3d symmetry, and form degenerate dz2,x2−y2 and degenerate dxy,yz,zx orbitals. This leads to the non-bonding d-bands splitting into two orbitals, with the dxy,yz,zx orbitals lower in energy than the dz2,x2−y2 orbitals. Hc-phase TMDCs have D3h symmetry, and form three sets of degenerate orbitals: dz2, dx2−y2,xy and dyz,zx, in increasing energy order.26 As the Group number of the transition metal is changed, the number of d-electrons is increased, and so a change in the preference of phase can be seen.98 As the phase of the host TMDC material can have some effect on the operating voltage, material stability, and hence the overall energy capacity, it is important that the correct phase be determined first.We evaluate the energetic ordering of these phases in the pristine bulk by taking the difference between the Hc-phase energy (EHc) and the T-phase energy (ET). The results of this are presented in Fig. 2 for the TMDC sulfides, where positive values indicate a more favourable T-phase and negative values indicate a more favourable Hc-phase. We find that most of the TMDCs prefer the T-phase, with the exception of those composed of Group V and Group VI transition metals which prefer to exhibit the Hc-phase, agreeing with many other works.96–98 Some data has been omitted from Fig. 2 as they structurally relax out of any Hc-like phase, further details of which, along with equivalent results for the TMDC selenides and tellurides, are presented in the ESI Section I.E.†
Upon intercalation, charge donation from the intercalated species increases the effective number of d-electrons on the transition metal, and so the effective transition metal Group is increased. This can result in a phase transition between the two phases, as has been demonstrated by many materials, but most notably by MoS2.55,100 With lithium intercalation, we note that the electron count of Group VI metal sulfides has effectively increased by one, resulting in them being ‘Group VII-like’ and reproducing the H → T transition seen in MoS2.100 When Group V materials are intercalated with lithium the extra electron results in ‘Group VI-like’ behaviour (with the H phase being preferred), and upon magnesium intercalation the Group IV materials become ‘Group VI-like’. This behaviour, and the favourability of the Hc-phase over the T-phase, is indicated with the green boxes in Fig. 2. We see that the pristine Group V materials show little difference in energy between the T- and Hc-phases (with EHc − ET being close to 0 eV). When intercalated with lithium, the Group IV materials lose their clear preference for the T-phase and become ‘Group V-like’, as do the Group III materials when intercalated with magnesium. This progression of Group V behaviour is indicated with the magenta boxes in Fig. 2. From these results we conclude that (i) the T-phase is the preferred phase in the pristine, lithium-intercalated, and magnesium-intercalated forms for most of the TMDCs considered in this work, with the exception of those materials composed of early transition metals, and (ii) the additional electrons from lithium causes Group VI TMDCs to undergo a H → T transition, and similarly the addition electrons from magnesium causes Group IV TMDCs to undergo a T → H transition. We therefore also consider the Hc-phase TMDCs only for the Group IV, V, and VI TMDCs.
2.4 Intercalation site
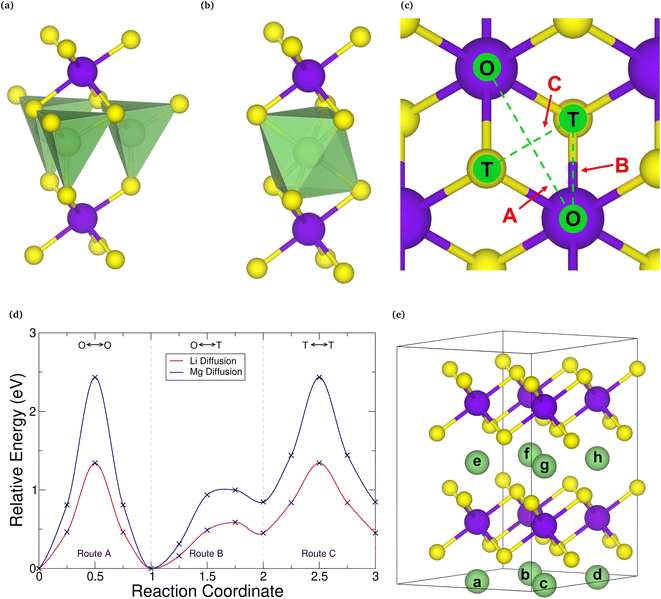
Before assessing the intercalation properties of a host material, and hence its suitability for electrode applications, it is important to first determine the correct intercalation site within it. The two sites often considered in investigations of intercalated TMDCs are the octahedrally coordinated site and the tetrahedrally coordinated site directly above the chalcogen. Whilst the octahedrally coordinated site has been shown to be the preferred site for many TMDC-like structures intercalated with lithium9,110,116,117 and magnesium,40,117 for consistency, we examine this here. First, we compare the relative energy from intercalation into each of these sites of the primitive cell for both lithium and magnesium intercalation, the results of which are presented in the ESI Section I.F.† For most of the TMDCs, we find that the tetrahedrally coordinated site (Fig. 3a) is higher in energy than the octahedrally coordinated site (Fig. 3b) by ∼0.5 eV. This is due to the octahedral site having a higher coordination between the intercalant and chalcogen species than the tetrahedral site. We do identify some exceptions, such as LiYS2, LiYSe2, MgWSe2, MgAuSe2, and MgGeSe2, where the tetrahedral site is lower in energy, though a closer investigation of these using larger unit cells show a transition in favourability of the two sites: for concentrations of a in LiaMX2 and MgaMX2 greater than 0.5 the tetrahedral site is indeed energetically preferred, but for concentrations lower than 0.5 the octahedral is preferred. Thus, if these TMDC materials are intercalated from MX2, the octahedral site will be occupied first, and promote further filling of octahedral sites as more intercalants are added.Whilst these high-symmetry, high-coordination intercalation sites are frequently considered for investigations of intercalation into TMDCs, we have performed nudged elastic band (NEB) calculations between these sites on selected systems, to confirm that there are no lower-energy sites within these materials. The three routes investigated are (a) between two octahedrally-coordinated sites, depicted by route A in Fig. 3c, (b) between one octahedrally-coordinated site and one tetrahedrally-coordinated site, depicted by route B, and (c) between two tetrahedrally-coordinated sites, depicted by route C. A typical NEB diffusion barrier is shown in Fig. 3d for SnSe2 for lithium (red) and magnesium (blue) diffusion. As can be seen from this figure, for both intercalants the octahedral and tetrahedral coordination sites are local minima along the diffusion routes, as was found in the discussion above from direct intercalation into both of these sites, and there are no intermediate sites that are lower in energy.
From the results presented here, it is clear that the preferred site of intercalation is the octahedrally-coordinated site above the transition metal of the host material. As such, we use this site for the following study. For the 2 × 2 × 2 supercells used in this work, there are eight different sites available for intercalation (indexed a–h in Fig. 3e) and 23 unique intercalant configurations for intercalation. Each of these configurations were considered, and further details are presented in the ESI Section I.B.†
Though the octahedral site is found to be lower in energy than the tetrahedral site for both lithium and magnesium, diffusion directly between these sites (along route A) provides the largest activation energy. For SnSe2, this is 1.34 eV for lithium and 2.43 eV for magnesium. The lowest diffusion barrier is actually found along route B, where the barriers are 0.59 eV and 1.01 eV for lithium and magnesium, respectively. This agrees with other works on TMDC intercalation,34,40,56 and is found for other TMDCs considered in this work (see ESI Section I.F†). As the rate of diffusion is Arrhenius-like, diffusion of both lithium and magnesium would occur at a higher rate along route B than along route A. The diffusion barriers for magnesium are higher than those for lithium, a result of the double valency resulting in a larger charge on the magnesium ion and hence stronger interaction between the positively charged magnesium and the negatively charged chalcogen of the host.
3 Results
3.1 Charge analysis
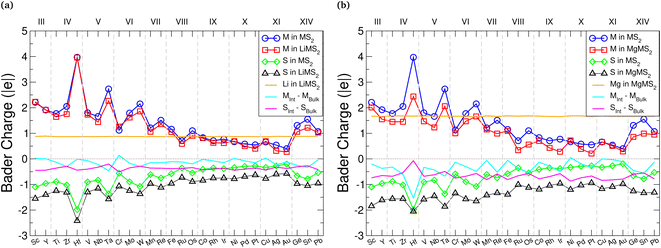
Charge transfer from the intercalant species to the host material is the fundamental mechanism for energy storage in electrode materials, and the distribution of charge within the material can affect how the structure transforms during intercalation, dictating the resultant volumetric expansion. It is therefore important to consider both the magnitude and direction of any charge transfer. To this end, we utilise two different approaches for assessing charge transfer: Bader charge analysis, and evaluation of differences in the charge density.Bader charge analysis118–122 was performed on both the pristine TMDCs and the fully intercalated (LiMX2 and MgMX2) TMDCs, and the average charges of the M, X, Li, and Mg atoms are all displayed in Fig. 4 for the TMDC sulfides. Firstly, we note that the charge of the intercalant ion in an intercalated TMDC structure maintains an almost constant value, independent of the host material. Lithium maintains a charge of +0.86 (±0.02)|e| across all TMDCs considered, agreeing with Bader charges reported for the same materials with the chalcopyrite structure30 and in graphite.123 For magnesium intercalation, the magnesium ion maintains a charge of +1.63 (+0.05−0.07)|e| across the materials considered. On average, the magnesium ions posses a charge 1.89 times greater than that of the intercalated lithium, close to the double valency of the magnesium ion.
Generally, the M species has a small reduction in its charge, as indicated by the cyan line in Fig. 4. There is a larger reduction for magnesium intercalation than there is for lithium intercalation, demonstrating that the reduction in the charge of the metal arises from the intercalant. This charge transfer to the metal species is increased as the atomic number of the chalcogen increases, due to the greater number of electrons already present and hence the reduced electronegativity of the chalcogen. There is a greater transfer of electronic charge to the chalcogen species compared to the charge transferred to the metal, as indicated by the magenta line in Fig. 4. As the chalcogen species is both closer to the intercalant and more electronegative than the metal species, this is unsurprising. Again, there is a greater charge transfer to the chalcogen species with magnesium intercalation than with lithium intercalation. We identify a gradual decrease in the absolute charge on both the transition metal and chalcogen in the intercalated states, as the Group of the transition metal is increased, which has also been noted for the chalcopyrite structure.30 Selenide and telluride data show the same trends, as shown in ESI Section II.A.†
Alongside the average values presented in Fig. 4, we have also evaluated the charges on the individual ions with different intercalant concentrations and configurations. These results are presented in ESI Section II.B,† where we see almost no change to the charges of the intercalant ions. The transition metal and chalcogen species, on the other hand, follow a roughly linear trend between the values shown in the pristine bulk and fully intercalated structures, and demonstrate a wide range (as high as 0.5|e|) of values depending on the intercalant configuration. This spread is naturally larger for the chalcogen, as the ions are closest to the intercalant ions and receive most of the donated electronic charge.
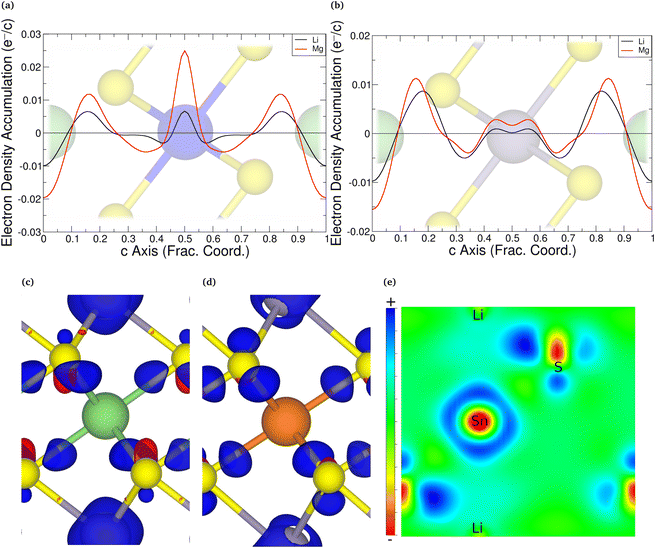
An alternative evaluation of the charge transfer can be achieved by analysing the differences in the charge density before and after intercalation. Keeping the positions of the ions the same as in the intercalated material, the electronic charge densities were obtained. By comparing the charge density of the full structure with those of the TMDC and lithium (or magnesium),124i.e. Δρ = ρLiMX2 − [ρLi + ρMX2], it is possible to comment on the charge transfer upon intercalation. An example is shown in Fig. 5, where we present the planar-averaged values of Δρ for ZrS2 (Fig. 5a) and SnS2 (Fig. 5b), which are representative of the TMDC materials. In these, the metal species of the host TMDC (blue, purple) is positioned at c = 0.5, the host chalcogens (yellow) are at c = 0.25 and c = 0.75, and the intercalant species (green) is at c = 0 with its periodic image at c = 1. We can see there is significant electron depletion from the location of intercalant (c = 0, 1), which is to be expected as the intercalated species donate their valence electrons to the host material. These donated electrons are shown to be partially donated into the Li–S and Mg–S bonding regions. These extra electrons in the vicinity of the chalcogen species repel the electrons that are present in the M–X bond closer to the metal of the host/reduce the number of electrons required for donation from the metal to the chalcogen. Hence we observe negative Δρ values in the ranges c = 0.3–0.4 and c = 0.6–0.7, and the positive values of Δρ on the metal site itself. This agrees with the reduction in Sn and Zr Bader charges presented above. This is further supported with the 3D visualisations of the charge transfer, presented in Fig. 5c and d for lithium and magnesium intercalation into SnS2. The isosurfaces chosen are the chosen by the ratio of intercalant Bader charges 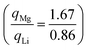 . Fig. 5e shows a 2D slice through the (1 1 0) plane of the LiSnS2 charge-difference distribution, passing through the tin, sulfur, and lithium atoms. In each of the 3D and 2D visualisations, red isosurfaces show electron depletion and blue isosurfaces show electron accumulation. Finally, we note the increased charge transfer, both with the planar-averaged charge transfer plots and the 3D visualisation, for magnesium intercalation compared to lithium. Due to the double valency this is to be expected, and is in line with the results of the Bader analysis.
. Fig. 5e shows a 2D slice through the (1 1 0) plane of the LiSnS2 charge-difference distribution, passing through the tin, sulfur, and lithium atoms. In each of the 3D and 2D visualisations, red isosurfaces show electron depletion and blue isosurfaces show electron accumulation. Finally, we note the increased charge transfer, both with the planar-averaged charge transfer plots and the 3D visualisation, for magnesium intercalation compared to lithium. Due to the double valency this is to be expected, and is in line with the results of the Bader analysis.
3.2 Volumetric expansion
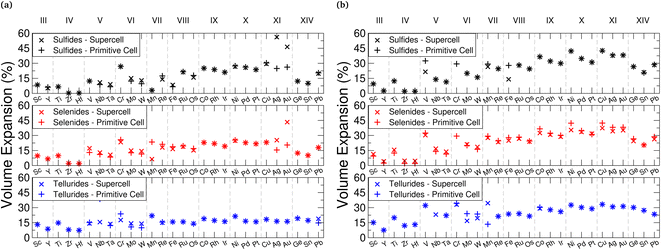
For intercalation electrodes, it is important to consider the volumetric expansion that arises from the intercalation of ions, as significant expansion during cycling can result in degradation of the electrode material, ultimately leading to device failure. We therefore present in Fig. 6a and b the volumetric expansion associated with lithium and magnesium intercalation, respectively. This is calculated using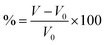 , for fully intercalated (LiMX2 and MgMX2) volume V and volume of the unintercalated structure V0.
, for fully intercalated (LiMX2 and MgMX2) volume V and volume of the unintercalated structure V0.
We note that as the transition metal Group increases, there is a larger volume expansion upon intercalation, with the Group III, IV, and V metal TMDC sulfides not exceeding 15% expansion with lithium intercalation. ZrS2 and HfS2 in particular demonstrate expansions of less than 1%. These expansions are comparable to many market leaders which possess a layered structure, including LiCoO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 125,126 (2–3.25%), NMC127 (8.44%), and graphite128 (13.2%). Conversely, Group IX, X, and XI metal TMDC sulfides undergo expansions over 20%. We see the volume expansion of all of the TMDCs remaining below 60%, with most materials remaining below 30%. Whilst these are larger than expansions demonstrated by other layered materials, they remain exceptionally low compared to many materials that have been considered for electrode applications, such as tin129 (300%) and silicon130 (380%). Across the family of TMDCs the expansion that arises from magnesium intercalation is comparable to that with lithium intercalation, and considering the ionic radii of both lithium and magnesium, this is not surprising.
125,126 (2–3.25%), NMC127 (8.44%), and graphite128 (13.2%). Conversely, Group IX, X, and XI metal TMDC sulfides undergo expansions over 20%. We see the volume expansion of all of the TMDCs remaining below 60%, with most materials remaining below 30%. Whilst these are larger than expansions demonstrated by other layered materials, they remain exceptionally low compared to many materials that have been considered for electrode applications, such as tin129 (300%) and silicon130 (380%). Across the family of TMDCs the expansion that arises from magnesium intercalation is comparable to that with lithium intercalation, and considering the ionic radii of both lithium and magnesium, this is not surprising.
Looking at the expansion of the a- and c-lattice vectors can not only be useful for determining the origin of the volume expansion, but also for the pairing of materials in superlattice structures. We present in ESI Section II.C† the lattice constants for each of the TMDCs without an intercalant, when intercalated with lithium, and when intercalated with magnesium. With intercalation, most TMDCs show an out-of-plane lattice expansion. For Group III–VIII, this expansion remains below ∼15%, with some TMDCs showing out-of-plane contraction with magnesium intercalation. Later Groups, however, demonstrate expansions exceeding 15%, reaching as high as 45%. This expansion is shown to be due to a lengthening of the M–X bond, and an increase in the vertical separation between chalcogens on opposing sides of the vdW gap. For lithium intercalation, most of the TMDCs exhibit in-plane lattice expansion of 5–10%, with a few of the early-transition metal TMDCs surprisingly contracting. We notice greater expansion of the in-plane lattice constants with magnesium intercalation, with some TMDC tellurides exhibiting expansions close to 20%.
Unintercalated structures show a large spread in the in-plane lattice constants, but upon intercalation the spread in lattice constants of the TMDCs is reduced. To highlight this, the TMDC with the largest lattice constant of the pristine T-phase sulfides is shown to be YS2 with a = 4.07 Å and the smallest lattice constant is CrS2 with a = 3.04 Å, giving a range of 1.03 Å. However, upon intercalation to LiMS2 the largest lattice constant is PbS2 with a = 3.84 Å and the smallest is WS2 with a = 3.24 Å. This gives a smaller range of 0.60 Å. Similarly, upon intercalation with magnesium to MgMS2 the largest lattice constant is PbS2 with a = 3.86 Å and the smallest is WS2 with a = 3.27 Å, giving a range of 0.61 Å. Clearly, the largest lattice constant is reduced and the smallest lattice constant is increased. This is likely due to the intercalated ions straining the TMDCs such that the nearest-neighbour distance of the intercalated species is close to the nearest-neighbour distance in the bulk form of the intercalant.
Along with the changes in lattice vectors and volume of these materials, there are also small changes to the atomic structure of the host material. Upon intercalation, we typically see an increase in the in-plane metal–metal distance, following the increase of the in-plane lattice constants, and a smaller increase in the metal–chalcogen bond length. These increases are more significant for the magnesium intercalant than they are for lithium. We also note a vertical stretching/contraction of the TMDC sheets: this is identified by both an increase/decrease in the vertical separation between the transition metal and nearest six chalcogen ions, and by an increase/decrease in the vertical separation between intralayer chalcogen ions on opposing basal planes of a TMDC layer. The bond length between the magnesium and the chalcogen species is found to be longer than the bond length between lithium and the chalcogen species. Further details of ionic geometry is given in ESI Section II.D.†
3.3 Energetics
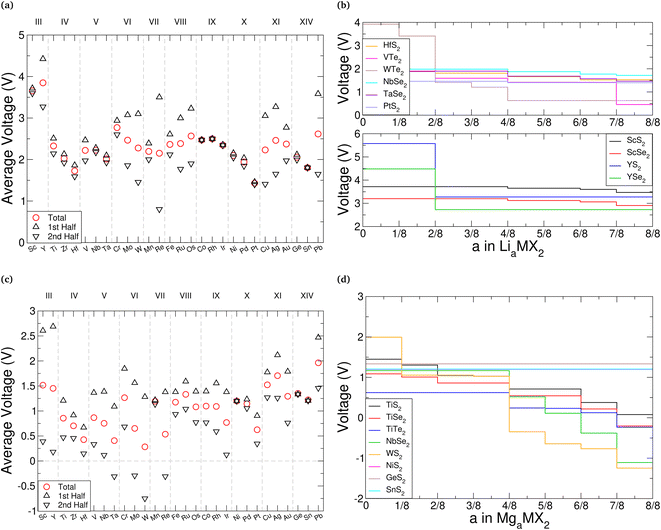
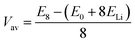 . As the intercalant concentration varies the voltage can change, and does in many of these materials. To highlight the variation, we have also indicated the average potential for the first half of the intercalation range (0 < a < 0.5) and the average potential for the second half (0.5 < a < 1). Equivalent data for the selenide and telluride materials are presented in ESI Section II.E.† Comparing these values, we see a clear reduction in the average voltage as the atomic number of the chalcogen species is increased. In general, most of the sulfide (selenide|telluride) values lie in the 2–2.5 V (1.5–2 V|1–1.5 V) range.
. As the intercalant concentration varies the voltage can change, and does in many of these materials. To highlight the variation, we have also indicated the average potential for the first half of the intercalation range (0 < a < 0.5) and the average potential for the second half (0.5 < a < 1). Equivalent data for the selenide and telluride materials are presented in ESI Section II.E.† Comparing these values, we see a clear reduction in the average voltage as the atomic number of the chalcogen species is increased. In general, most of the sulfide (selenide|telluride) values lie in the 2–2.5 V (1.5–2 V|1–1.5 V) range.
Anode materials should have well-defined voltage plateaus lower than 2 V vs. Li/Li+, ideally in the range 0.5–1.5 V.131 Based solely on this, telluride materials appear best suited with most voltages being around 1.5 V. We highlight this with VTe2 and WTe2 in Fig. 7b, which have average voltages of 1.46 V and 1.56 V, respectively. However, the voltage profiles of these materials vary significantly across the concentration range. Other telluride materials offer the low voltages ideal for anodes but with a more plateau-like voltage profile, such as those composed of the Group IV, X, and XIV metals, each varying by less than 0.5 V. Unfortunately, the atomic mass of tellurium is much larger than sulfur and selenium, the other chalcogen species used in TMDC materials, which would significantly increase the mass of an electrode host-material, and thus reduce the gravimetric capacity. Though there are fewer sulfide and selenide materials that have ideal voltage profiles for anodes, there are still many (such as HfS2, PtS2, NbSe2, and TaSe2 as shown in Fig. 7b) which also have relatively flat voltages below 2 V. Conversely, cathode materials should possess much higher voltages, with current cathodes offering voltages above 3 V.132 We demonstrate this in Fig. 7b with scandium and yttrium sulfide and selenide materials, which are seen to have voltages exceeding 3 V (in the case of the selenides) and 3.5 V (in the case of the sulfides). The promise of ScS2 has recently been presented elsewhere.60
In a similar manner we consider magnesium intercalation, with eqn (1) allowing us to obtain the average magnesium intercalation potentials vs. Mg/Mg2+. We present the results for the TMDC sulfides in Fig. 7c, with selenide and telluride data being presented in ESI Section II.E.† Due to the double valency of magnesium, one can expect different intercalation behaviours to manifest in the profiles of the TMDCs, corresponding to different changes to the oxidation state of the host material. At a concentration of a = 0.5, the two electrons from each of the magnesium ions are donated to the host material, with one electron effectively being donated to each MX2 unit. Past a = 0.5, further electron donation results in another change to the oxidation states of the MX2 unit. We therefore show in Fig. 7 the average voltages for the first stage (0 < a < 0.5) and second stage (0.5 < a < 1) of intercalation with upward-pointing and downward-point triangles, respectively. This helps highlight the voltage variation a given material possesses.
As was observed for lithium intercalation, we note the reduction in intercalation potential with increased atomic number of the chalcogen species, and highlight it in Fig. 7d with the TiX2 materials: TiS2 has an average voltage of 0.86 V, TiSe2 a voltage of 0.61 V, and TiTe2 a voltage of 0.37 V. For most of the TMDCs, there is a significant drop in the magnesium intercalation potential for the second half of the intercalation range. This is dramatically shown with WS2, where the initial intercalation potential is 1.99 V and the final intercalation potential is −1.24 V, demonstrating a drop of over 3 V. This drop results in many of the TMDC materials presenting negative voltages (see ESI Section II.E†). As this does not always occur at a = 0.5, we have also included in the ESI† the average voltage calculated over the range that the voltage remains positive.
We observe that TMDCs composed of early-transition metals have a greater range in the magnesium intercalation voltage than the late-transition metals/post-transition metals. There are some of the materials which show very little change to the intercalation potential, with NiS2, GeS2 and SnS2 each varying by 0 V. These are presented in Fig. 7d. This constant voltage is due to the fact that, for each of the concentrations, it is energetically preferred for the magnesium to separate into regions with no magnesium (with an energy of E0) and regions that are fully intercalated (with and energy of E8). For example, the lowest energy for Mg1/8SnS2 is given by 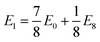 , and the lowest energy for Mg2/8SnS2 is given by
, and the lowest energy for Mg2/8SnS2 is given by 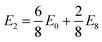 . As the difference between consecutive concentrations is a constant
. As the difference between consecutive concentrations is a constant 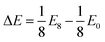 , the voltage is also constant across the range. Further discussion of such clustering or phase separation is presented in ESI Section II.F.†
, the voltage is also constant across the range. Further discussion of such clustering or phase separation is presented in ESI Section II.F.†
For magnesium intercalation, none of the TMDCs achieve voltages greater than 3 V, and so do not offer much promise as cathode materials. However, many of them have voltages below 1.5 V, indicating their potential as anode materials. Further, we can highlight those materials with little difference between the two stages of their intercalation to ensure we have a well-defined voltage plateau.131 However, we do not need to rule out those materials with a large difference between the two stages. Due to the double valency of magnesium, the total charge transferred from the magnesium in either the range 0 < a < 0.5 or 0.5 < a < 1, and hence the total energy stored, is comparable to the charge transferred across the full 0 < a < 1 range using lithium intercalation. As such, in situations where the there is a large difference between the two charging stages, we can utilise just part of the intercalation range. For example, TMDCs composed of the Group III, IV, and V metals show voltages below 0.5 V in the range 0.5 < a < 1, which is ideal for anodes.
The results presented here find good agreement with many experimental works. In particular, we see good agreement between the 2–2.5 V intercalation voltage identified for LiTiS2,34,37,38 and the 1.6–1.9 V intercalation voltage of LiZrS2.42,44 The intercalation voltage of T-MoS2 has been identified in the range 1.9–2.5 V which agrees with the results we have presented,48,52 and we reproduce the 1.8 V intercalation potential seen for intercalation of SnS2.65,67 Of course, many transition metal dichalcogenide compounds do not exhibit the layered structure that has been considered in this work,29 most commonly the pyrite structure as for FeS2,133 MnS2, and CoS2. Comparison with experiment with such materials is therefore not appropriate.
Whilst we have shown good agreement with experiment, validating our choice of functional, previous studies have shown that the choice of functional can lead to differences in predictions for properties important to electrode materials.134,135 To account for the inaccurate calculation of exchange in GGA functionals such as PBE, and to evaluate the differences that can arise from choice of functional, the HSE06 hybrid functional103–105 has used for a selection of systems (see ESI Section II.G†). With the use of the HSE06 hybrid functional, some materials, such as ZrS2, HfS2, and GeSe2, exhibit very little change to the voltage compared to the equivalent system using the PBE functional. Conversely, some materials show significant increases. For example, the LiTiS2 voltage was increased by 0.17 V, the LiMoS2 voltage was increased by 0.25 V, and the LiIrS2 voltage was increased by 0.58 V compared to the PBE functional. This increase in intercalation voltage with use of a hybrid functional (as well as with using GGA + U corrections) has been shown for a range of transition metal oxides commonly used as electrode materials.134,135 We also note, in general, a larger effect on the voltage, as shown with the MoX2 series of TMDCs, with the telluride have a larger increase (1.03 V) than the selenide (0.46 V), which has a larger increase than the sulfide (0.25 V). As we have achieved good agreement with experiment using the PBE functional, however, we have not performed an exhaustive study using the HSE06 alternative.
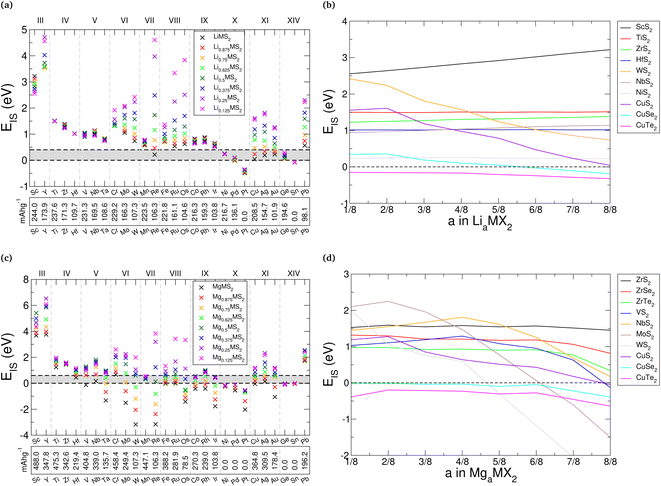
Fig. 8a presents the values of EIS for lithium intercalation of the sulfides, with specific examples being highlighted in Fig. 8b. Equivalent figures are presented in ESI Section II.H† for the selenide and telluride materials. In general, we see a reduction in the stability of the TMDCs as the concentration of lithium is increased. The size of this effect varies across the periodic table, with the TMDCs composed of the central Group VI, VII, and VIII metals showing the largest variation. This is highlighted with WS2 in Fig. 8b, where EIS drops from 2.42 eV at a concentration of Li0.125WS2, to 2.23 eV at a concentration of Li0.25WS2, to 1.57 eV at a concentration of Li0.5WS2, finally to 0.74 eV at a concentration of LiWS2. However, those TMDCs composed of metals from Groups IV, V, IX, and X having a relatively constant values of EIS. For example, as shown in Fig. 8b, TiS2 demonstrates a constant EIS = 1.51 eV at both LiTiS2 and Li0.125TiS2, HfS2 has a minor decrease from 1.02 eV (LiHfS2) to 1.01 eV (Li0.125HfS2), and for NiS2 it retains the same value of EIS = 0.23 eV. Whilst most TMDCs are shown to destabilise with increased lithium content, we do highlight in Fig. 8b some examples that prove exceptions, such as ScS2, ZrS2, and NbS2, whose values of EIS increase with lithium content.
With increasing atomic number of the chalcogen species, there is a gradual reduction in the stability (indicated by a reduction in EIS). This is shown best with the Group XI TMDCs (CuX2, AgX2, and AuX2), where the sulfides are stable across the concentration range investigated, the selenides become unstable when the lithium concentration exceeds a = 0.5, but none of the tellurides are for any of the intercalant concentrations. The data for the CuX2 materials is presented in Fig. 8b to highlight this. This can be explained with the reduced electronegativity for larger atomic numbers, as the greater number of electrons already present at the chalcogen site lowers the favourability of additional electrons being donated. There is no easily-identifiable trend seen for changing the transition metal species, however, with some Groups showing an increase in EIS as the atomic number of the transition metal is increased (e.g. Groups III and VIII) and some showing a decrease (e.g. Groups IV and X).
An alternative but equivalent way to assess the stability of a TMDC material against conversion is to consider the two contributions to the material stability: the formation energy of the pristine TMDC material and the binding energy of the intercalant with the host material.115 The formation energy of a TMDC gives an indication of the strength of the M–X bond and hence its ability to resist conversion, whereas the intercalant binding energy implies the strength of the interaction between the intercalant and the host TMDC in LiaMX2 or MgaMX2. To resist the conversion reaction, therefore, a TMDC should possess a large formation energy, a large intercalant binding energy, or ideally both. Further discussion of this is left to ESI Section II.I,† but it is clear to see that materials that are unstable against intercalation (such as PdS2, SnS2, or CuTe2) are those with low TMDC formation energy and low lithium binding energy.
Overall, the Group III (Sc, Y), IV (Ti, Zr, Hf), V (V, Nb, Ta), and VI (Cr, Mo, W) materials offer the greatest stability, which is unsurprising given that these materials have been investigated the most thoroughly over the past 50 years. However, we also highlight the Group VIII (Fe, Ru, Os) and IX (Co, Rh, Ir) sulfides as potential lithium-intercalation materials as they show stability over the intercalation range considered here.
Comparing our results here with experimental studies we find good agreement, particularly for the Group IV TMDCs. For each of the Group IV dichalcogenides, we find a positive value of EIS, indicating their stability against conversion. Experimentally, TiS2 has been shown to be stable over a range of lithium concentrations up to a = 1 in LiaTiS2, as have the ZrX2 and HfX2 materials.41,56 SnS2 is shown here to have a negative EIS, indicating it is not stable to intercalation and hence susceptible to conversion. This agrees with experimental works62–65 where SnS2 is observed to readily undergo conversion reactions to Li2S or an alloy of Sn and Li. We are also able to show the Hc-MoS2 → T-MoS2 transition arising from lithium intercalation: the phase diagram for Hc-MoS2 has no window of stability, and so would be likely to undergo conversion, whereas the T-phase shows a sizeable EIS (see ESI Section II.J†).
For magnesium intercalation we see similar results, as shown in Fig. 8c for the sulfides, with specific examples are presented in Fig. 8d. The selenide and telluride results are also presented in ESI Section II.H.† We typically see a reduction in the stability with increased magnesium concentration. Again, we highlight this with WS2, where EIS drops from 1.99 eV at a concentration of Mg0.125WS2, to 1.06 eV at a concentration of Mg0.25WS2, to 0.60 eV at a concentration of Mg0.5WS2, finally to −3.17 eV at a concentration of MgWS2. We note this large reduction in EIS between intercalation concentrations of a = 0.5 and a = 1, which is greater than what was demonstrated for lithium intercalation. This is also seen for other materials, including VS2, NbS2, and MoS2, as shown in Fig. 8d. We attribute this large reduction to the second donated electron from the magnesium: the electrons donated in the range 0 ≤ a ≤ 0.5 with magnesium intercalation stimulate the same transition in oxidation state as that of the electrons donated in the range 0 ≤ a ≤ 1 with lithium intercalation. Any further charge donation triggers different changes in oxidation state, as more than one electron is then being donated to each of the MX2 units. However, despite this larger drop for greater magnesium concentrations, many of the TMDCs still possess positive values of EIS, including TMDCs containing Group III, IV, or V metals. As with lithium intercalation, we note a gradual reduction in stability of the TMDCs as the atomic number of the chalcogen species is increased, and demonstrate this with both the ZrX2 and CuX2 TMDCs in Fig. 8d. Despite these causes for stability reduction, however, there still remain several TMDCs that are predicted to be resilient with magnesium intercalation: the Group III (Sc, Y), IV (Ti, Zr, Hf), and V (V, Nb, Ta) sulfides again offer the greatest stability to intercalation. Though many of the other materials show a susceptibility to conversion with intercalation, the Group VIII (Fe, Ru, Os) and IX (Co, Rh, Ir) sulfides offer stability over a significant intercalant concentration range (0 < a < 0.5), which corresponds to significant charge transfer when noting the double valency of magnesium.
Whilst some works have achieved intercalant contents greater than a = 1, such as with Li2VSe2,41 Li3TiS2,136 and Li3.48NbSe2,137 we have not investigated beyond this limit here. However, we have shown for these cases that EIS remains positive with lithium concentration, with values of EIS = 0.63 eV, EIS = 1.51 eV, and EIS = 0.70 eV for LiVSe2, LiTiS2, and LiNbSe2, respectively. These positive values, therefore, still allow for further intercalation towards the concentrations that have been observed experimentally.
It should also be noted that we have not considered the effects of surface formation or how microscopic morphology can play a role. Experimental works have shown that lithium deposition onto the surface of these TMDC materials can lead to conversion even for TMDCs that are stable to intercalation,95,138 and first principles methods have been used to confirm that the formation of a surface can reduce the size of the stability window,115 therefore reducing EIS and making these materials more susceptible to conversion reactions.
The values of EIS presented here are only for the geometrically relaxed structure where the intercalant occupies the lowest-energy intercalation site. Of course, during the cycling of the electrode an intercalant is expected to occupy not only higher-energy intercalation sites, but also intermediate points (e.g. along routes A, B and C in Fig. 3c). As such, the host material will undergo local distortions that will increase its energetic state, and hence reduce the corresponding stability indicated by EIS. However, accurate mapping of the energy space for intercalant diffusion remains a challenge due to current limits on cell sizes. Further, obtaining a sufficient number of interpolated NEB images at different intercalant concentrations for each of the TMDCs would be computationally demanding. As such, we use the difference in energy between the intercalant occupying the octahedral and tetrahedral sites rather than the activation barrier height. We rationalise this further by considering the coordination between the intercalant and chalcogen species which is reduced for intermediate positions and so limits the available ions for conversion to the appropriate Li2X or MgX compound. Finally, the time scales associated with an intercalant ion being in an intermediate position are significantly shorter than the time scales associated with occupation of an octahedral or a tetrahedral site.
The difference in energy between lithium in the octahedral and tetrahedral sites is approximately 0.4 eV across each of the TMDCs, whereas it is typically slightly higher at 0.6 eV for magnesium (see ESI Section I.F†). Whilst there are examples of both higher and lower energies, we can use these typical values as a further limit on EIS. For lithium intercalation, only a few of the sulfides are affected by this new limit, with the fully intercalated ReS2 becoming susceptible to conversion, along with the Group X, XI, and XIV materials. However, there is a more dramatic consequence for magnesium intercalation due to the second donated electron. Almost all of the TMDC sulfides demonstrate a reduction in their capacity, arising from the higher magnesium concentrations being falling within the new limit on EIS, indicated by the shaded region in Fig. 8c.
3.4 Electronic structure
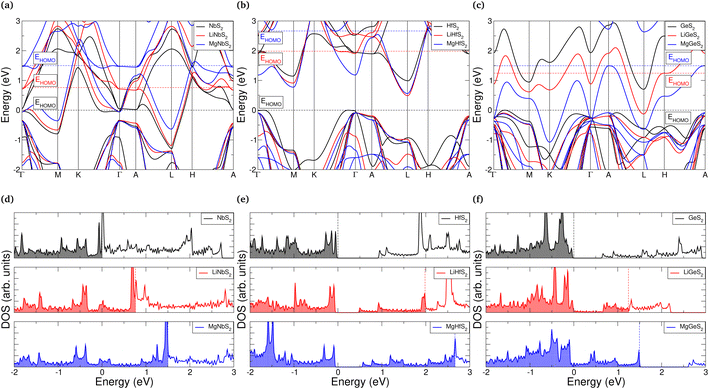
One of the attractive features of the TMDC family is the wide range of electronic properties that have been reported.26,27,139 For electrodes, it is desirable for the host material to be conductive so that the compensating electrons can more easily conduct throughout the host material, and to remove the need for additives such as graphitic carbon. However, upon the addition of intercalant species it can be expected that the electronic structure and properties are modified. As it is desirable for this conductive nature to endure across the range of intercalation, we here present the changes to the electronic structure with intercalation.We summarise in ESI Section II.L† the electronic band gap of the pristine bulk, lithium-intercalated, and magnesium-intercalated TMDCs in the T-phase, where we find that most of the materials considered are found to be metallic in the three levels of intercalation. This is ideal for electrode applications where the conduction of electrons is required. However, TMDCs composed of Group III, VII, IX, and XIV metals undergo transitions between conducting and semiconducting/insulating states, and so conductive additives would be necessary to facilitate charge transfer. In fact, we identify four different cases describing how the electronic structure can change with intercalation: either the TMDC (i) retains a conductive nature with intercalation, (ii) undergoes a semiconductor-to-conductor transition, (iii) undergoes a conductor-to-semiconductor transition, or (iv) possesses an insulating nature before intercalation and at the a = 1 intercalation level. We highlight some examples of these in Fig. 9, where the electronic band structures and associated density of states (DOS) are presented. We have qualitatively aligned the high-energy occupied states of the pristine and intercalated structures at Γ, allowing us to comment on the position of the highest occupied molecular orbital (HOMO).
For materials such as NbS2, the HOMO level lies in the middle of a band, as shown in see Fig. 9a and d. The addition of lithium donates electronic charge to the host, and so the HOMO level rises accordingly. Similarly, with magnesium intercalation the HOMO level rises but by a greater amount due to the larger electronic charge that is donated to the host. We note some small changes to the positions and shape of the individual bands due to local electric fields arising from charge transfer (as was shown in Fig. 5), which can be identified by considering the bands positions at Γ. Otherwise, the general features of the bands can easily be tracked. No new bands, which would be associated with the intercalant species, are introduced into the regions presented. For materials such as HfS2 which undergo a transition from a semiconducting to conducting, we see much the same behaviour, with the addition of a larger jump in the position of the HOMO level due to the presence of the host band gap. Once this band gap has been overcome, however, population of the conduction band states can occur and a conducting nature is achieved (see Fig. 9b and e). Conversely, ScS2 is an example of a material which loses its conductive nature once fully intercalated, further discussion of this has been presented elsewhere.60 In this situation, the addition of electrons fills states until the next band gap is reached. Finally, in Fig. 9c and f we highlight an example of a material which is an insulator before intercalation, becomes conducting under intercalation with lithium (or partial intercalation with magnesium), but once fully intercalated with magnesium recovers a band gap. The cause of this is the gradual downwards shift in the position of the GeS2 conduction band that is dispersive across the energy range 1 eV to 3 eV. Once intercalated with lithium, this band becomes partially occupied and is reduced in energy by ∼1 eV at Γ. When intercalated with magnesium, the band is fully occupied and we see a further energy drop of ∼1 eV at Γ. This ability to control both the material conductivity and position of the HOMO level through intercalation could be useful in a range of applications.
By decomposing the DOS into contributions from the different ionic orbitals (see ESI Section II.L†), we find that TMDCs composed of main-block transition metals have conduction bands dominated by the d-orbital of the metal, with a significantly smaller contribution from the p-orbitals of the chalcogen. For TMDCs composed of Group XIV metals, however, the conduction band is instead composed of metal s-orbitals and chalcogen p-orbitals. The contributions from these states are almost equal, with the chalcogen contributing slightly more. This difference in the character of the conduction band is likely the origin for the difference of its behaviour under intercalation, (as demonstrated for GeS2 in Fig. 9c and f).
Evidently, some of these materials, despite offering ideal volume expansion, voltages, and/or thermodynamic stability, possess a band gap that would be detrimental to the cycling of a cell. For example, the zirconium- and hafnium-based sulfides and selenides, whilst offering other desirable properties, have band gaps of up to 1 eV. Using the idea of progressive filling of bands with intercalant concentration, however, we can avoid the problem of a band gap by ensuring a small intercalant concentration is always present within the host, i.e. not removing any lithium beyond LiδMX2 where δ is a small value. This can therefore provide another limit to intercalation, alongside thermodynamic stability or the assessment of phonon band structures. Alternatively, dopants140,141 or conductive additives could be used to ensure that conductivity issues are minimised. In fact, graphene has previously been suggested as an additive in works into zirconium- and hafnium-based sulfides and selenides,43,45 and was shown to remove the electronic band gap.
We emphasise that these electronic band structures (and the corresponding band gaps) were obtained using the PBE functional. Use of a hybrid functional would likely increase the band gaps of those materials that are semiconducting, and also introduce a band gap into those materials that are metallic. Whilst the PBE functional is known to underestimate band gaps, previous work has suggested that hybrid functionals over-estimate the band gap for TMDC materials.142 Finally, in Fig. 9, we have only shown materials that do no have spin-split electronic structures. Further discussion of the materials which display magnetic moments are presented in ESI Section II.M.†
4 Discussion
In the evaluation of any given electrode material, there are many metrics that need to be considered to determine the promise of that material. We find that all of the layered TMDC materials offer volumetric expansion below 60%, with many early-transition metal compounds (Group III–VI TMs) offering expansions below 15%. Though we identify that the electronic structure can behave differently with intercalation, most of the materials are conductive in their pristine and intercalated forms and thus reduce the need for conductive additives in a functional device. For lithium intercalation, sulfide materials offer the highest intercalation voltages, typically in the range 2–2.5 V, with the selenide and telluride materials offering lower voltages that are better suited for anodes. It is also desired that electrode materials offer voltage profiles that offer little spread across the intercalant concentration, and we find that materials composed of early transition metals and transition metals from Groups IX, X, and XIV demonstrate little spread. For magnesium intercalation, there is a much more significant spread in the voltage profiles due to the double valency of magnesium. However, almost all of the TMDCs offer voltages that are below ∼1.5 V, making them well-suited as anode materials. There are no materials that offer high voltages (>3 V) with magnesium intercalation. Using thermodynamic phase diagrams to assess the resistance of the intercalated TMDCs against conversion reactions, we find that many are stable with lithium intercalation, though the Group X and XI TMDCs do become susceptible to conversion with increasing lithium content. There is a dramatic reduction in the stability of the TMDCs with magnesium intercalation, however, with most becoming unstable for magnesium concentrations greater than a ∼ 0.5. We note that for magnesium intercalation ScS2 and PbS2 both show potential to reach a = 1. For both intercalants, there is a gradual reduction in the stability of the TMDCs with increasing atomic mass of the chalcogen. Due to the lower atomic masses of TMDCs composed of early transition metals and sulfides, they are able to offer high charge capacities. Though there are many selenide and telluride materials can offer performance improvements such as reduced volumetric expansion, improved conductivity, or better-placed voltages, these performance improvements are not sufficient to outweigh the fact that they suffer from a lower stability and have larger chalcogen masses which result in a lower gravimetric charge capacity. In Table 1, we summarise these properties along with the materials which offer desired behaviour, and conclude that in general early transition metal sulfides provide the best candidate for both lithium and magnesium intercalation electrodes. We also highlight the Group VIII and IX sulfide materials for their relatively high voltages and positive values of EIS.| Desired property | Lithium intercalation | Magnesium intercalation |
|---|---|---|
| Low volumetric expansion | Group III–VI TMs | Group III–V TMs |
| Low gravimetric density | Period IV TMs | Period IV TMs |
| Sulfides | Sulfides | |
| Thermodynamic stability | Group III–VI TMs | Group III–V and XI TMs |
| Sulfides and selenides | Sulfides | |
| High charge capacity | Period IV TMs | Period IV, Group III-V TMs |
| Sulfides | Sulfides | |
| Anodic voltage (<1.5 V) | Tellurides | Group IV, V, VIII–X TMs |
| Selenides and tellurides | ||
| Cathodic voltage (>3 V) | Group III TM sulfides | — |
| Constant voltage | Group IV, V, IX, X, XIV TMs | Group IV, X, XI, XIV TMs |
| Electrical conductivity | Group V–VIII, X, XI TMs | Group V, VI, X, XI TMs |
| Tellurides | Tellurides |
5 Conclusion
We have presented the results of an investigation of lithium- and magnesium-intercalation into each of the layered transition metal dichalcogenides. By comparing the two polymorphs of the layered TMDC structures, we have shown that the T-phase is typically the preferred phase. However, phase changes can be induced with intercalation, particularly for the Group IV, V, and VI materials. The layered phase of the TMDCs is ideal for intercalation due to the presence of vdW gaps, providing natural space for intercalation with minimal need for volumetric expansion. All of the TMDCs present expansions lower than 60%, with many of the early transition metal structures expanding by less than 15%. Most of this expansion comes from an increase in the out-of-plane lattice constant, though we also identify minor changes to the in-plane structure.Using thermodynamic phase diagrams, we evaluate the stability of intercalated TMDCs to conversion reactions and thus provide an estimate of the reversible capacity. We find that most TMDCs are stable with lithium intercalation, though this stability is reduced for magnesium intercalation due to the extra charge of the intercalant. Compounds composed of heavier chalcogens also suffer a reduction in stability due to the reduced electronegativity of the chalcogen leading to a reduction in the M–X bonding strength. From the range over which the materials are stable, we determine the gravimetric charge density, and find that many of the Period IV transition metal sulfides offer capacities in excess of 200 mA h g−1 with lithium intercalation, and over 400 mA h g−1 with magnesium intercalation. These materials have shown a range of voltage profiles as well. For lithium intercalation, sulfide materials offer the largest voltages (in the range of 2–2.5 V), with a gradual decrease as the mass of the chalcogen is increased, though many of these values are lower than voltages typically required for successful cathodes, and higher than those typically required for successful anodes. There is further reduction in the voltage for intercalation with magnesium, with most materials offering voltages lower than ∼1.5 V, and a significant spread across the range of magnesium concentration.
We find that most of the TMDCs retain a conductive nature across the range of intercalant concentrations considered, though some materials do become insulating at concentrations of a = 1 in LiaMX2 or MgaMX2. Many key features of the band structure can be easily tracked with the inclusion of intercalants, and there is a gradual shift upwards of the HOMO level due to the charge that is donated to the host material. The Group XIV materials do deviate from this behaviour slightly, but we can attribute this to the difference in character of the conduction band compared to main-block TMDCs.
In general, we find that the TMDC sulfides are the best for lithium intercalation, and we highlight the Group IV, V, and VI in particular for their low volumetric expansion, moderate intercalation voltages, and high stability against conversion reactions. We also highlight ScS2 and YS2 as promising cathode materials, which offer high voltages close to 4 V, and high intercalation stability allowing for theoretical capacities of 243.99 mA h g−1 and 173.91 mA h g−1, respectively. Finally, we suggest that the Group VIII and IX materials are also worthy of further investigation. For magnesium intercalation, we again show that the early transition metals offer the best performance as anodes, but also show that many other materials show ideal voltages and sufficient thermodynamic stability over a significant concentration range. The comprehensive and consistent study here shows both the promise of the TMDCs as electrodes and provides a repository of data for future studies of these materials.
Author contributions
C. J. Price: conceptualization, data curation, formal analysis, methodology, writing – original draft, review and editing. E. A. D. Baker: data curation, formal analysis, methodology, writing - original draft, review and editing. S. P. Hepplestone: conceptualization, funding acquisition, supervision, writing – original draft, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge financial support from the EPSRC (United Kingdom), (Grant No. EP/L015331/1) and the Materials Chemistry Consortium, (EP/L000202, EP/R029431, EP/X035859). The authors acknowledge the use of the University of Exeter HPC facility. This work used the Isambard 2 UK National Tier-2 HPC Service (https://gw4.ac.uk/isambard/) operated by GW4 and the UK Met Office, and funded by EPSRC (EP/T022078/1). We wish to acknowledge the use of the EPSRC funded Physical Sciences Data-science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1. Finally, the authors would also like the thank Dr F. Davies and Dr N. Taylor for their useful discussions.References
- P. Saha, M. K. Datta, O. I. Velikokhatnyi, A. Manivannan, D. Alman and P. N. Kumta, Prog. Mater. Sci., 2014, 66, 1–86 CrossRef CAS.
- C. Ling, D. Banerjee and M. Matsui, Electrochim. Acta, 2012, 76, 270–274 CrossRef CAS.
- J. Asenbauer, T. Eisenmann, M. Kuenzel, A. Kazzazi, Z. Chen and D. Bresser, Sustainable Energy Fuels, 2020, 4, 5387–5416 RSC.
- A. Franco Gonzalez, N.-h. Yang and R.-s. Liu, J. Phys. Chem. C, 2017, 121, 27775–27787 Search PubMed.
- C. P. Sandhya, B. John and C. Gouri, Ionics, 2014, 20, 601–620 CrossRef CAS.
- J. Jiang, Y. Li, J. Liu and X. Huang, Nanoscale, 2011, 3, 45–58 RSC.
- A. R. Armstrong, C. Lyness, P. M. Panchmatia, M. S. Islam and P. G. Bruce, Nat. Mater., 2011, 10, 223–229 CrossRef CAS PubMed.
- M. D. Bhatt and C. O'Dwyer, Phys. Chem. Chem. Phys., 2015, 17, 4799–4844 RSC.
- D. Y. Wan, Z. Y. Fan, Y. X. Dong, E. Baasanjav, H.-B. Jun, B. Jin, E. M. Jin and S. M. Jeong, J. Nanomater., 2018, 2018, 1–9 CrossRef.
- J. Kasnatscheew, S. Röser, M. Börner and M. Winter, ACS Appl. Energy Mater., 2019, 2, 7733–7737 CrossRef CAS.
- G. W. Nam, N. Y. Park, K. J. Park, J. Yang, J. Liu, S. C. Yoon and K.-Y. Sun, ACS Energy Lett., 2019, 4, 2995–3001 CrossRef CAS.
- W. Li, S. Lee and A. Manthiram, Adv. Mater., 2020, 32, 2002718 CrossRef CAS PubMed.
- N. D. Phillip, A. S. Westover, C. Daniel and G. M. Veith, ACS Appl. Energy Mater., 2020, 3, 1768–1774 CrossRef CAS.
- R. N. Ramesha, D. Bosubabu, M. G. Karthick Babu and K. Ramesha, ACS Appl. Energy Mater., 2020, 3, 10872–10881 CrossRef CAS.
- A. S. Andersson, Electrochem. Solid-State Lett., 2000, 3, 66 CrossRef CAS.
- L. Liao, P. Zuo, Y. Ma, X. Chen, Y. An, Y. Gao and G. Yin, Electrochim. Acta, 2012, 60, 269–273 Search PubMed.
- B. Lung-Hao Hu, F. Y. Wu, C. T. Lin, A. N. Khlobystov and L. J. Li, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- W. K. Pang, C.-Z. Lu, C.-E. Liu, V. K. Peterson, H.-F. Lin, S.-C. Liao and J.-M. Chen, Phys. Chem. Chem. Phys., 2016, 18, 17183–17189 RSC.
- H. Ji, J. Wu, Z. Cai, J. Liu, D. H. Kwon, H. Kim, A. Urban, J. K. Papp, E. Foley, Y. Tian, M. Balasubramanian, H. Kim, R. J. Clément, B. D. McCloskey, W. Yang and G. Ceder, Nat. Energy, 2020, 5, 213–221 CrossRef CAS.
- Y. Sun, N. Liu and Y. Cui, Nat. Energy, 2016, 1, 1–12 Search PubMed.
- M. S. Whittingham, J. Electrochem. Soc., 1976, 123, 315–320 CrossRef CAS.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Solid State Ionics, 1981, 3–4, 171–174 CrossRef CAS.
- L. Shi and T. Zhao, J. Mater. Chem. A, 2017, 5, 3735–3758 RSC.
- X. Xu, W. Liu, Y. Kim and J. Cho, Nano Today, 2014, 9, 604–630 CrossRef CAS.
- T. Lu, S. Dong, C. Zhang, L. Zhang and G. Cui, Coord. Chem. Rev., 2017, 332, 75–99 Search PubMed.
- M. Chhowalla, H. S. Shin, G. Eda, L.-j. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed.
- S. J. McDonnell and R. M. Wallace, Thin Solid Films, 2016, 616, 482–501 CrossRef CAS.
- S. Fan, X. Zou, H. Du, L. Gan, C. Xu, W. Lv, Y. B. He, Q. H. Yang, F. Kang and J. Li, J. Phys. Chem. C, 2017, 121, 13599–13605 CrossRef CAS.
- C. Rao and K. Pisharody, Prog. Solid State Chem., 1976, 10, 207–270 CrossRef.
- Z. M. Xu, S. H. Bo and H. Zhu, ACS Appl. Mater. Interfaces, 2018, 10, 36941–36953 CrossRef CAS PubMed.
- R. Besse, M. P. Lima and J. L. F. Da Silva, ACS Appl. Energy Mater., 2019, 2, 8491–8501 CrossRef CAS.
- J. H. Han, M. Kwak, Y. Kim and J. Cheon, Chem. Rev., 2018, 118, 6151–6188 CrossRef CAS PubMed.
- J. Zhou, C. Zhu, Y. Zhou, J. Dong, P. Li, Z. Zhang, Z. Wang, Y.-c. Lin, J. Shi, R. Zhang, Y. Zheng, H. Yu, B. Tang, F. Liu, L. Wang, L. Liu, G.-B. Liu, W. Hu, Y. Gao, H. Yang, W. Gao, L. Lu, Y. Wang, K. Suenaga, G. Liu, F. Ding, Y. Yao and Z. Liu, Nat. Mater., 2022 Search PubMed.
- M. Whittingham, Prog. Solid State Chem., 1978, 12, 41–99 CrossRef CAS.
- Y.-P. Gao, X. Wu, K.-J. Huang, L.-L. Xing, Y.-Y. Zhang and L. Liu, CrystEngComm, 2017, 19, 404–418 Search PubMed.
- Y.-P. Gao, J. Xu, K.-J. Huang, H. Lu, Y.-X. Pang and G.-q. Li, CrystEngComm, 2021, 23, 7546–7564 RSC.
- M. S. Whittingham, Science, 1976, 192, 1126–1127 CrossRef CAS PubMed.
- A. H. Thompson, Phys. Rev. Lett., 1978, 40, 1511–1514 Search PubMed.
- A. Emly and A. Van der Ven, Inorg. Chem., 2015, 54, 4394–4402 CrossRef CAS PubMed.
- D. S. Tchitchekova, A. Ponrouch, R. Verrelli, T. Broux, C. Frontera, A. Sorrentino, F. Bardé, N. Biskup, M. E. Arroyo-de Dompablo and M. R. Palacín, Chem. Mater., 2018, 30, 847–856 CrossRef CAS.
- D. W. Murphy, F. J. Di Salvo, G. W. Hull and J. V. Waszczak, Inorg. Chem., 1976, 15, 17–21 Search PubMed.
- W. McKinnon, J. Dahn and C. Levy-Clement, Solid State Commun., 1984, 50, 101–104 CrossRef CAS.
- G. W. Kingori, C. N. M. Ouma, G. O. Amolo and N. W. Makau, Surf. Interfaces, 2021, 24, 101036 CrossRef CAS.
- S. Kim, Y. J. Kim and W.-h. Ryu, Appl. Surf. Sci., 2021, 547, 149029 CrossRef CAS.
- G. W. Kingori, C. N. M. Ouma, A. K. Mishra, G. O. Amolo and N. W. Makau, RSC Adv., 2020, 10, 30127–30138 RSC.
- H. Qi, L. Wang, T. Zuo, S. Deng, Q. Li, Z. Liu, P. Hu and X. He, ChemElectroChem, 2020, 7, 78–85 CrossRef CAS.
- R. Sun, C. Pei, J. Sheng, D. Wang, L. Wu, S. Liu, Q. An and L. Mai, Energy Stor. Mater., 2018, 12, 61–68 Search PubMed.
- H. Li, W. Li, L. Ma, W. Chen and J. Wang, J. Alloys Compd., 2009, 471, 442–447 CrossRef CAS.
- X. Fang, C. Hua, X. Guo, Y. Hu, Z. Wang, X. Gao, F. Wu, J. Wang and L. Chen, Electrochim. Acta, 2012, 81, 155–160 CrossRef CAS.
- T. Stephenson, Z. Li, B. Olsen and D. Mitlin, Energy Environ. Sci., 2014, 7, 209–231 RSC.
- J. Xia, J. Wang, D. Chao, Z. Chen, Z. Liu, J. L. Kuo, J. Yan and Z. X. Shen, Nanoscale, 2017, 9, 7533–7540 RSC.
- L. Zhang, D. Sun, J. Kang, J. Feng, H. A. Bechtel, L.-W. Wang, E. J. Cairns and J. Guo, Nano Lett., 2018, 18, 1466–1475 CrossRef CAS PubMed.
- A. Nadar, Y. Arora, P. Thakur, T. Narayanan, A. Bhattacharya and D. Khushalani, Electrochem. Commun., 2022, 139, 107313 CrossRef CAS.
- K. Leng, Z. Chen, X. Zhao, W. Tang, B. Tian, C. T. Nai, W. Zhou and K. P. Loh, ACS Nano, 2016, 10, 9208–9215 CrossRef CAS PubMed.
- M. Wang, S. Xu and J. J. Cha, Adv. Energy Sustainability Res., 2021, 2, 2100027 CrossRef CAS.
- R. Friend and A. Yoffe, Adv. Phys., 1987, 36, 1–94 CrossRef CAS.
- J. Peng, Y. Liu, Y. Pan, J. Wu, Y. Su, Y. Guo, X. Wu, C. Wu and Y. Xie, J. Am. Chem. Soc., 2020, 142, 18645–18651 CrossRef CAS PubMed.
- M. van Dijk and C. Plug, Mater. Res. Bull., 1980, 15, 103–106 CrossRef CAS.
- L. Havlák, J. Fábry, M. Henriques and M. Dušek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 623–630 Search PubMed.
- C. J. Price, J. Pitfield, E. A. D. Baker and S. P. Hepplestone, Phys. Chem. Chem. Phys., 2023, 25, 2167–2178 RSC.
- J. Morales, C. Perez-Vicente and J. L. Tirado, Solid State Ionics, 1992, 51, 133–138 CrossRef CAS.
- J. W. Seo, J. T. Jang, S. W. Park, C. Kim, B. Park and J. Cheon, Adv. Mater., 2008, 20, 4269–4273 CrossRef CAS.
- J. Zai, K. Wang, Y. Su, X. Qian and J. Chen, J. Power Sources, 2011, 196, 3650–3654 CrossRef CAS.
- B. Luo, Y. Fang, B. Wang, J. Zhou, H. Song and L. Zhi, Energy Environ. Sci., 2012, 5, 5226–5230 RSC.
- Q. Zhang, R. Li, M. Zhang, B. Zhang and X. Gou, Electrochim. Acta, 2014, 115, 425–433 Search PubMed.
- A. S. Hassan, K. Moyer, B. R. Ramachandran and C. D. Wick, J. Phys. Chem. C, 2016, 120, 2036–2046 CrossRef CAS.
- P. Gao, L. Wang, Y. Y. Zhang, Y. Huang, L. Liao, P. Sutter, K. Liu, D. Yu and E. G. Wang, Nano Lett., 2016, 16, 5582–5588 Search PubMed.
- M. Wang, Y. Huang, Y. Zhu, X. Wu, N. Zhang and H. Zhang, J. Alloys Compd., 2019, 774, 601–609 CrossRef CAS.
- A. Jin, N. Kang, J. H. Um, I. H. Ko, M. S. Kim, K. Kim, S. H. Kim, S. H. Yu and Y. E. Sung, Chem. Commun., 2020, 56, 8095–8098 RSC.
- R. Li, C. Miao, M. Zhang and W. Xiao, Ionics, 2020, 26, 1239–1247 CrossRef CAS.
- X. Li, Z. Liu, D. Zhu, Y. Yan and Y. Chen, Nanoscale, 2022, 14, 5869–5875 RSC.
- M. Kan, J. Y. Wang, X. W. Li, S. H. Zhang, Y. W. Li, Y. Kawazoe, Q. Sun and P. Jena, J. Phys. Chem. C, 2014, 118, 1515–1522 CrossRef CAS.
- Y. Yu, G. Li, L. Huang, A. Barrette, Y.-q. Cai, Y. Yu, K. Gundogdu, Y.-w. Zhang and L. Cao, ACS Nano, 2017, 11, 9390–9396 CrossRef CAS PubMed.
- A. Al Roman, M. M. Rahman, K. Hossain, S. Das and F. Ahmed, Solid State Commun., 2022, 352, 114828 CrossRef CAS.
- Q. Wang, L. Jiao, Y. Han, H. Du, W. Peng, Q. Huan, D. Song, Y. Si, Y. Wang and H. Yuan, J. Phys. Chem. C, 2011, 115, 8300–8304 CrossRef CAS.
- Y. Song, J. Liao, C. Chen, J. Yang, J. Chen, F. Gong, S. Wang, Z. Xu and M. Wu, Carbon, 2019, 142, 697–706 CrossRef CAS.
- X. Xu, C. S. Rout, J. Yang, R. Cao, P. Oh, H. S. Shin and J. Cho, J. Mater. Chem. A, 2013, 1, 14548–14554 RSC.
- Y. Liu, M. Zhu and D. Chen, J. Mater. Chem. A, 2015, 3, 11857–11862 Search PubMed.
- G. K. Sung, K. J. Jeon and C. M. Park, ACS Appl. Mater. Interfaces, 2016, 8, 29543–29550 CrossRef CAS PubMed.
- E. Pomerantseva and Y. Gogotsi, Nat. Energy, 2017, 2, 17089 CrossRef CAS.
- D. K. Bediako, M. Rezaee, H. Yoo, D. T. Larson, S. Y. Zhao, T. Taniguchi, K. Watanabe, T. L. Brower-Thomas, E. Kaxiras and P. Kim, Nature, 2018, 558, 425–429 CrossRef CAS PubMed.
- Z. Xiang Huang, B. Liu, D. Kong, Y. Wang and H. Ying Yang, Energy Stor. Mater., 2018, 10, 92–101 Search PubMed.
- H. S. Kim, Y. H. Chung, S. H. Kang and Y. E. Sung, Electrochim. Acta, 2009, 54, 3606–3610 CrossRef CAS.
- R. Bhandavat, L. David and G. Singh, J. Phys. Chem. Lett., 2012, 3, 1523–1530 CrossRef CAS PubMed.
- Y. Koyama, H. Arai, I. Tanaka, Y. Uchimoto and Z. Ogumi, J. Mater. Chem. A, 2014, 2, 11235–11245 RSC.
- Z. Yu, S.-L. Shang, M. L. Gordin, A. Mousharraf, Z.-K. Liu and D. Wang, J. Mater. Chem. A, 2015, 3, 17376–17384 RSC.
- F. Wu, C. Zhao, S. Chen, Y. Lu, Y. Hou, Y.-S. Hu, J. Maier and Y. Yu, Mater. Today, 2018, 21, 960–973 CrossRef CAS.
- J. H. Jeong, S. Kang, N. Kim, R. Joshi and G.-H. Lee, Phys. Chem. Chem. Phys., 2022, 24, 10684–10711 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Kamaratos, D. Vlachos, C. A. Papageorgopoulos, A. Schellenberger, W. Jaegermann and C. Pettenkofer, J. Phys.: Condens. Matter, 2002, 14, 8979–8986 Search PubMed.
- H. Katzke, P. Tolédano and W. Depmeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–8 CrossRef.
- J. Ribeiro-Soares, R. M. Almeida, E. B. Barros, P. T. Araujo, M. S. Dresselhaus, L. G. Cançado and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115438 CrossRef.
- Y. Xiao, M. Zhou, J. Liu, J. Xu and L. Fu, Sci. China Mater., 2019, 62, 759–775 CrossRef CAS.
- M. Jakhar, J. Singh, A. Kumar and R. Pandey, J. Phys. Chem. C, 2020, 124, 26565–26571 CrossRef CAS.
- Y. Wu, J. Wang, Y. Li, J. Zhou, B. Y. Wang, A. Yang, L.-W. Wang, H. Y. Hwang and Y. Cui, Nat. Commun., 2022, 13, 3008 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(8207), 2006, DOI:10.1063/1.2204597.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 Search PubMed.
- M. Mayo, K. J. Griffith, C. J. Pickard and A. J. Morris, Chem. Mater., 2016, 28, 2011–2021 CrossRef CAS.
- A. N. Enyashin and G. Seifert, Comput. Theor. Chem., 2012, 999, 13–20 CrossRef CAS.
- M. Aydinol, A. Kohan and G. Ceder, J. Power Sources, 1997, 68, 664–668 CrossRef CAS.
- M. K. Aydinol and G. Ceder, J. Electrochem. Soc., 1997, 144, 3832–3835 CrossRef CAS.
- A. Van der Ven, J. Bhattacharya and A. A. Belak, Acc. Chem. Res., 2013, 46, 1216–1225 CrossRef CAS PubMed.
- Y. Lu, J. Li, Y. Zhao and X. Zhu, ACS Omega, 2019, 4, 20612–20617 CrossRef CAS PubMed.
- T. Zhao, H. Shu, Z. Shen, H. Hu, J. Wang and X. Chen, J. Phys. Chem. C, 2019, 123, 2139–2146 CrossRef CAS.
- Z. Liu, H. Deng and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2015, 7, 4000–4009 CrossRef CAS PubMed.
- M. D. Radin and A. Van der Ven, Chem. Mater., 2016, 28, 7898–7904 CrossRef CAS.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 Search PubMed.
- Y. Qi, H. Guo, L. G. Hector and A. Timmons, J. Electrochem. Soc., 2010, 157, A558 CrossRef CAS.
- D. Tristant, P. Puech and I. C. Gerber, Phys. Chem. Chem. Phys., 2015, 17, 30045–30051 RSC.
- Y. Qi, L. G. Hector, C. James and K. J. Kim, J. Electrochem. Soc., 2014, 161, F3010–F3018 CrossRef CAS.
- J. Luo, C. Dai, Z. Wang, K. Liu, W. Mao, D. Fang and X. Chen, Measurement, 2016, 94, 759–770 CrossRef.
- M. Woodcox, R. Shepard and M. Smeu, J. Power Sources, 2021, 516, 230620 CrossRef CAS.
- S. Schweidler, L. de Biasi, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2018, 122, 8829–8835 CrossRef CAS.
- L. Y. Beaulieu, S. D. Beattie, T. D. Hatchard and J. R. Dahn, J. Electrochem. Soc., 2003, 150, A419 CrossRef CAS.
- D. Uxa, B. Jerliu, E. Hüger, L. Dörrer, M. Horisberger, J. Stahn and H. Schmidt, J. Phys. Chem. C, 2019, 123, 22027–22039 Search PubMed.
- A. Eftekhari, Energy Stor. Mater., 2017, 7, 157–180 Search PubMed.
- A. Manthiram, Nat. Commun., 2020, 11, 1550 CrossRef CAS PubMed.
- D. Zhang, Y. J. Mai, J. Y. Xiang, X. H. Xia, Y. Q. Qiao and J. P. Tu, J. Power Sources, 2012, 217, 229–235 CrossRef CAS.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–8 Search PubMed.
- V. L. Chevrier, S. P. Ong, R. Armiento, M. K. Chan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–11 CrossRef.
- E. A. Suslov, O. V. Bushkova, E. A. Sherstobitova, O. G. Reznitskikh and A. N. Titov, Ionics, 2016, 22, 503–514 CrossRef CAS.
- E. Hitz, J. Wan, A. Patel, Y. Xu, L. Meshi, J. Dai, Y. Chen, A. Lu, A. V. Davydov and L. Hu, ACS Appl. Mater. Interfaces, 2016, 8, 11390–11395 CrossRef CAS PubMed.
- B. Liu, T. Luo, G. Mu, X. Wang, D. Chen and G. Shen, ACS Nano, 2013, 7, 8051–8058 CrossRef CAS PubMed.
- Z. Hu, Z. Wu, C. Han, J. He, Z. Ni and W. Chen, Chem. Soc. Rev., 2018, 47, 3100–3128 RSC.
- S. Chowdhury, P. Venkateswaran and D. Somvanshi, Superlattices Microstruct., 2020, 148, 106746 CrossRef CAS.
- S. Li, J. Hong, B. Gao, Y. Lin, H. E. Lim, X. Lu, J. Wu, S. Liu, Y. Tateyama, Y. Sakuma, K. Tsukagoshi, K. Suenaga and T. Taniguchi, Adv. Sci., 2021, 8, 2004438 CrossRef CAS PubMed.
- E. A. D. Baker, J. Pitfield, C. J. Price and S. P. Hepplestone, J. Phys.: Condens. Matter, 2022, 34, 375001 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta00940h |
| This journal is © The Royal Society of Chemistry 2023 |