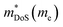Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recent progress in phosphide materials for thermoelectric conversion
Robert J.
Quinn
 and
Jan-Willem G.
Bos
and
Jan-Willem G.
Bos
 *
*
Institute of Chemical Sciences and Centre for Energy Storage and Recovery, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: j.w.g.bos@hw.ac.uk
First published on 31st March 2023
Abstract
Thermoelectric materials allow for the interconversion of heat and electricity. Rapid progress has been made in materials performance but there is a continuing need for the exploration of new materials and disruptive thermoelectric effects. Metal phosphides are currently gaining increasing attention as potential thermoelectric materials. Structural complexity often leads to low thermal conductivity despite the low atomic mass of P, which underpins promising thermoelectric figures of merit, zT. Despite the ability of phosphorus to form strong covalent bonds, including polyanion bonding, a key challenge remains to embed better electrical properties and large power factors. A highest zT = 0.9 has been observed in n-type Cd3P2, whilst promising performance under applied fields has been observed in topological materials, e.g. in the Dirac metal TaP. In this review, we summarise recent materials developments and analyse some of the underlying thermoelectric parameters of metal phosphide materials.
1. Introduction
Thermoelectric technology can be used in power generation, mW-scale ambient heat scavenging and in thermal management, where the benefits of durability and absence of moving parts outweigh high costs and modest efficiencies.1,2 A good example is the radioisotope thermoelectric generators (TEGs) used by NASA to power satellites and rovers. There continues to be a need for improved thermoelectric materials, based on sustainable elements and processing, lowering costs, and increasing power outputs and cooling performance of devices. For a single material, the thermoelectric performance is quantified by its figure of merit (zT):3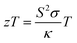 | (1) |
Sustainability considerations and energy security have led to an enormous research effort to develop better thermoelectric materials.5–9 This has been driven by new design concepts such as the phonon-glass electron-crystal, nanostructuring, electronic bandstructure engineering and by improved experimental characterisation of electrical and heat transport.5–9 This has resulted in gradual increases in zT for a range of materials with highest values approaching zT = 3 for SnSe,10–13 greatly exceeding the traditional limit of zT = 1. The wide range of heat sources (temperatures) means there is a need for a range of thermoelectric materials. These also need to satisfy engineering requirements such as good electrical and thermal contacting, long term stability and mechanical strength, as well as matched thermal expansion for the n- and p-type legs that make up the basic thermoelectric couples in devices.5–9 As yet, there is no leading thermoelectric n/p-type couple that would enable widespread cost-effective power generation or replace Bi2Te3 for ambient harvesting or cooling applications. For example, most of the very high zT materials considered for power generation, including Bi2Te3 itself,14,15 PbTe16–20 and GeTe21,22 use tellurium, which is rare and hence expensive. SnSe has exceptional zT based on its ultralow κ and good electronic properties when doped,23–25 but has limited high temperature stability.26 Half-Heuslers boast large power factors (S2σ) but their overall zT continues to be limited by large intrinsic thermal conductivity.27,28
There is considerable interest in Zintl thermoelectrics based on Sb, with antimonide skutterudites reported with large S2σ and zT29–33 and more recently Mg3Sb2 phases with high zT near room temperature in n-type samples.34–38 There are several excellent reviews and book chapters covering Sb-based thermoelectrics,39–44 which support very good zT values, often substantially exceeding unity.
Metal phosphides have attracted limited attention as thermoelectrics but is a group of materials with high potential.45 As will be shown, structural complexity often leads to intrinsically low lattice thermal conductivities, hence providing a platform for potentially large zT values. In fact, for many of the explored materials the challenge is to improve the electrical properties and increase S2σ. From a chemical perspective, the wide range of accessible phosphorous anionic oxidation states allows for a range of structure types and chemical bonding. This includes P0/P− with a high degree of covalent bonding and polyanion formation, and the isolated P3− anion which affords more familiar ionic structure types. In addition to its chemical versatility, phosphorus is highly abundant (11th most abundant element in the earth's crust)46 and relatively low-cost. It also has a lower atomic mass (20 amu) than most other common anions in thermoelectric compounds, offering potential advantages in terms of gravimetric power output. Metal phosphide structures include analogues of well-known thermoelectric candidate materials (in particular of skutterudites, clathrates and tetrahedrites), but also comprise a range of unique structures, with semiconducting or semimetallic bandstructures which are of interest for thermoelectric exploration.
One reason for the limited historical interest in metal phosphide thermoelectrics is through association with white phosphorus.46 This material consists of weakly linked P4 molecules and is highly pyrophoric, reacting violently with oxygen to form P2O5 and further with water to form H3PO4. The formation of highly toxic PH3 gas is also a concern in synthesis involving phosphorus.46 However, red phosphorus, effectively consisting of (P4)n oligomers, has much better stability and is commonly used for synthesis.46 Once formed, metal phosphides can exhibit excellent stability,47–50 in particular if more electropositive alkali and alkaline earth elements are avoided.
This review will start with an overview of the reported thermoelectric properties from the recent literature, and it will discuss some of the underlying electronic and thermal parameters. In subsequent sections a more detailed overview of the structures and properties of highlighted promising materials are given, including novel thermoelectric effects based on topological states. The review concludes with an outlook for the field. All structures shown in this review were drawn using the VESTA programme and are based on published crystallographic data.51
2. Evaluation of performance and underlying thermoelectric parameters
The electronic bandstructures of many known metal phosphide structures can be accessed via databases such as the Materials Project,52 and the electronic properties have been the subject of a recent review.45 From a chemical bonding (Zintl) perspective, it is anticipated that the valence band has a large anion (P) component with conduction band more heavily weighted towards the metal orbitals. Most metal-phosphides are experimentally found to be p-type, consistent with small cation deficiencies leaving a shortage of electrons to fill the anion derived conduction band, hence leaving holes, and causing p-type conduction. Notable exceptions are the high zT phase Cd3P2 and the topological material TaP.53–56An overview of the reported thermoelectric parameters for a range of metal phosphides is given in Fig. 1. These include S2σ(T), κL(T) and zT(T), and the weighted mobility (μw), which was calculated from reported S(T) and σ(T) using an empirical model.62 The power output of a thermoelectric generator is related to S2σ, and as such it is an important engineering parameter. The materials reported so far have modest S2σ, typically achieving values between 0.8 and 1.2 mW m−1 K−2 above 300 K (Fig. 1a). A notable exception is CaCuP with S2σ = 1.75 mW m−1 K−2, possibly linked to its simple crystal structure.50 Low values are found for Zn0.75Cu2P8,59,63 rich in P–P bonds and the clathrate Ba8Cu14Ge6P26,57 which are both limited to S2σ < 0.4–0.6 mW m−1 K−2. In all cases, the reported S2σ are much smaller than state-of-the-art materials, that typically achieve power factors >4 mW m−1 K−2 and up to 10 mW m−1 K−2 for some low-defect half-Heusler phases.27
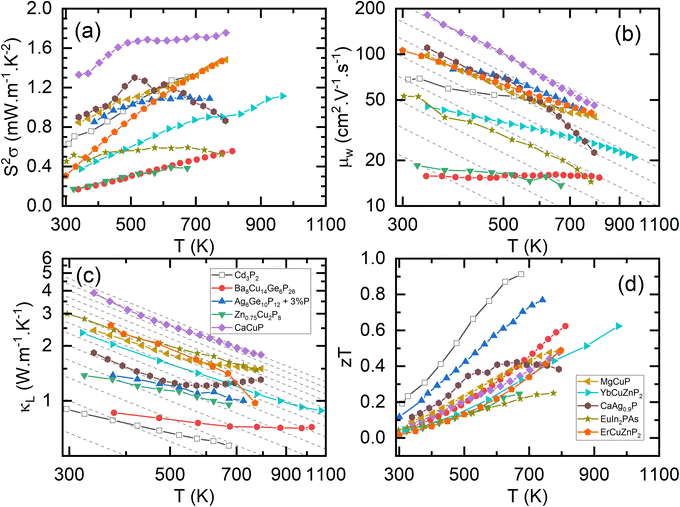 | ||
| Fig. 1 Summary of the thermoelectric properties of promising metal phosphides. Panel (a) shows the power factor (S2σ), (b) shows the weighted mobilities (μw); the dashed lines show a T−1.5 acoustic phonon scattering dependence, (c) shows the lattice thermal conductivity (κL); the dashed lines show a T−1 Umklapp scattering dependence, and (d) shows the figure of merit (zT). Please note that panel (b) and (c) are plotted on a log–log scale (Cd3P2,55 Ba8Cu14Ge6P26,57 Ag6Ge10P12,58 Zn0.75Cu2P8,59 CaCuP,50 MgCuP,50 YbCuZnP2,47 CaAg0.9P,60 EuIn2PAs,61 ErCuZnP2.49). | ||
The weighted mobility μw gives the fundamental electronic performance of a material, independent of carrier doping, and is defined as follows:62
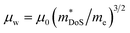 | (2) |
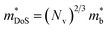 | (3) |
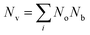 | (4) |
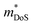 is the density of states effective mass, which determines the magnitude of
is the density of states effective mass, which determines the magnitude of 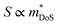 , and
, and 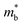 is the effective band mass of the charge carriers. Nv is the total valley degeneracy of the valence or conduction band extrema, which is the product of the degeneracy arising due to symmetry (No) and the degeneracy arising due to different bands (Nb). In the acoustic phonon scattering model μ0 scales as
is the effective band mass of the charge carriers. Nv is the total valley degeneracy of the valence or conduction band extrema, which is the product of the degeneracy arising due to symmetry (No) and the degeneracy arising due to different bands (Nb). In the acoustic phonon scattering model μ0 scales as 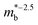 , meaning μw scales as
, meaning μw scales as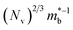 .64,65 As such thermoelectric materials should ideally have light charge carriers
.64,65 As such thermoelectric materials should ideally have light charge carriers 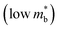 , and a highly converged bandstructure near the Fermi energy (high Nv).7
, and a highly converged bandstructure near the Fermi energy (high Nv).7
Electronic bandstructure information available for metal phosphide phases is summarised in Table 1. Most compositions have band extrema at the Γ-point, which has the lowest possible No = 1. For example, n-type Cd3P2 has a single band at the Γ-point, with an exceptionally low 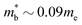 leading to the highest Hall mobilities observed with μH ∼1600 cm2 V−1 s−1 at room temperature.55 The semimetallic p-type skutterudite CoP3 is the only material in Table 1 that has similar low
leading to the highest Hall mobilities observed with μH ∼1600 cm2 V−1 s−1 at room temperature.55 The semimetallic p-type skutterudite CoP3 is the only material in Table 1 that has similar low 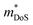 and high mobilities (Table 1).66 The low
and high mobilities (Table 1).66 The low 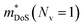 for Cd3P2 results in a relatively low S, yielding modest μw, similar to the A(CuZn)P2 122-phases (Fig. 1b). The large zT observed for Cd3P2 is therefore mostly due to its low κL (Fig. 1c).
for Cd3P2 results in a relatively low S, yielding modest μw, similar to the A(CuZn)P2 122-phases (Fig. 1b). The large zT observed for Cd3P2 is therefore mostly due to its low κL (Fig. 1c).
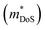 derived using the single parabolic band model with acoustic phonon dominated scattering, reported Hall carrier concentrations (nH) and mobilities (μH)
derived using the single parabolic band model with acoustic phonon dominated scattering, reported Hall carrier concentrations (nH) and mobilities (μH)
| Composition | Type | Band | n H (cm−3) | μ H (cm2 V−1 s−1) | |
|---|---|---|---|---|---|
| a see Section 3.2 on tetrahedrites. | |||||
| Ag6Ge10−xGaxP1267 | p | Multiplea | 7.7–16.5 | 1.1–11 × 1020 | 1.11–1.84 |
| CaCuP50,68 | p | Γ (Nv = 2) | 1.0 | 1.6 × 1020 | 101 |
| MgCuP50,68 | p | Γ (Nv = 1) | 1.7 | 2.4 × 1020 | 29 |
| Cd3P2−δ55 | n | Γ (Nv = 1) | 0.09 | 3.6–10.5 × 1017 | 950–1690 |
| Cd3P1−xAsx53,54 | n | Γ (Nv = 1) | 0.05–0.11 | 6.1–28 × 1017 | 850–9400 |
| ErCuZnP249 | p | Γ (Nv = 2 to 3) | 0.88 | 2.7 × 1020 | 53 |
| YbCuZnP247 | p | — | 0.60 | 2.4 × 1020 | 11.8 |
| CoP366 | p | Γ (Nv = 1) | 0.11 | 3.26 × 1019 | 748 |
| CeFe4P1266 | p | — | 0.16 | 1.42 × 1019 | 24.9 |
| CeRu4P1266 | p | — | 2.26 | 1.8 × 1020 | 6.0 |
The best electronic performance so far is found for CaCuP, in part due to its second valence band (Nb = 2) at the Γ-point,68 which affords a better trade-off between 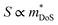 and mobility
and mobility 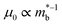 . Not all phosphide bandstructures are trivial. For example the tetrahedrite Ag6Ge10P12 has a complex electronic structure, with multiple hole pockets in low symmetry positions, associated with lone pairs on Ge2+ cations.67,69 Low dispersion (heavy) bands along the G–F and maxima located just outside the high symmetry Γ–H direction yield
. Not all phosphide bandstructures are trivial. For example the tetrahedrite Ag6Ge10P12 has a complex electronic structure, with multiple hole pockets in low symmetry positions, associated with lone pairs on Ge2+ cations.67,69 Low dispersion (heavy) bands along the G–F and maxima located just outside the high symmetry Γ–H direction yield 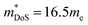 for Ag6Ge9.875Ga0.125P12.67 The electronic quality of the Ag6Ge10P12-based tetrahedrite phases is similar to Cd3P2 and the 122 phases (Fig. 1b).
for Ag6Ge9.875Ga0.125P12.67 The electronic quality of the Ag6Ge10P12-based tetrahedrite phases is similar to Cd3P2 and the 122 phases (Fig. 1b).
An overview of the measured lattice thermal conductivities (κL) is given in Fig. 1c. Within the kinematic theory of heat transport, κL is given by:
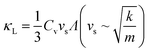 | (5) |
Using elastic properties from the Materials Project (Bulk and Shear moduli B and G),52,75 initial approximations of κL for phosphide materials can be made. Longitudinal, transverse and average sound velocities (vl, vt and vs), Debye temperatures (θD) and Grüneisen parameters (γ) were calculated27 and are listed in Table 2.
| Composition | Materials project reference | ρ (g cm−3) | B (GPa) | G (GPa) | v l (m s−1) | v t (m s−1) | v s (m s−1) | θ D (K) | γ | κ L (W m−1 K−1)/ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| CaCuP | mp-8432 | 4.01 | 74 | 51 | 5951 | 3566 | 3946 | 443 | 1.36 | 4.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
| CaAgP | mp-12277 | 4.89 | 61 | 43 | 4919 | 2965 | 3279 | 358 | 1.34 | 2.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
| MgCuP | mp-7352 | 4.41 | 94 | 48 | 5986 | 3299 | 3677 | 445 | 1.67 | 2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
| SrCuP | mp-16321 | 4.81 | 66 | 46 | 5145 | 3092 | 3420 | 369 | 1.35 | 2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 71 |
| Zn3P2 | mp-2071 | 4.54 | 65 | 35 | 4959 | 2777 | 3090 | 345 | 1.61 | 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
| CaZn2P2 | mp-9569 | 3.98 | 67 | 46 | 5678 | 3400 | 3762 | 417 | 1.37 | 3.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73 73 |
| Cd3P2 | Ref. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
5.60 | 64 | 18 | 3950 | 1760 | 1980 | 203 | 2.35 | 0.91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
| Ag6Ge10P12 | mp-17862 | 5.09 | 65 | 36 | 4712 | 2659 | 2958 | 323 | 1.58 | 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
| CoP3 | mp-1944 | 4.38 | 149 | 115 | 8308 | 5124 | 5653 | 692 | 1.26 | 15.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 66 |
| CeFe4P12 | mp-16272 | 5.17 | 161 | 132 | 8074 | 5053 | 5565 | 689 | 1.21 | 14.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 66 |
| CeRu4P12 | mp-10069 | 5.74 | 167 | 110 | 7392 | 4378 | 4849 | 578 | 1.41 | 8.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 66 |
| AgP2 | mp-8200 | 4.86 | 62 | 26 | 4460 | 2313 | 2589 | 287 | 1.88 | 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 74 |
A plot of experimental κL against the calculated vs is given in Fig. 2. This shows a very clear correlation between calculated vs and measured κL, as expected from eqn (5). The high-zT material Cd3P2 has vs ∼2000 m s−1 and has κL < 1 W m−1 K−1 at 300 K. The next lowest κL < 2 W m−1 K−1 materials are AgP2 (vs ∼ 2600 m s−1), Zn3P2 (vs ∼ 3100 m s−1) and tetrahedrite Ag6Ge10P12 (vs ∼ 3000 m s−1), whilst CaCuP with its large μw has vs ∼ 4000 m s−1 and κL ∼ 4 W m−1 K−1 at 300 K.
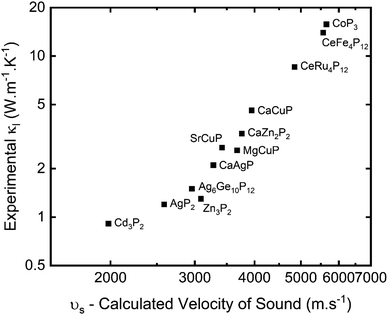 | ||
| Fig. 2 Measured lattice thermal conductivity (κL) plotted against calculated velocity of sound (vs) for selected metal phosphide thermoelectrics (see Table 2 for source data). | ||
In general, a large vs is caused by strong responses to compression and shear strain (large B and G, and hence strong bonds) and when material density is low. Inspection of Table 2 suggests that the trend in vs (κL) is driven by the elastic moduli with changes in density having a smaller role. We note that these calculated values provide a general guide to the elastic properties but are far from exact and need confirmation from measurements.
Another important parameter is the bonding anharmonicity, quantified by the Grüneisen parameter (γ), which is a measure of the strength of phonon Umklapp scattering. For Cd3P2 the calculated γ from fitting the phonon bandstructure is 2.3–2.4, highlighting substantial anharmonic bonding, which combined with heavier mass of Cd results in the low observed κL.55 Compared to CaCuP, with γ ∼1.35 and its much higher vs, the relatively large κL can be attributed to stronger bonds with reduced anharmonicity. A final point is that the phosphide skutterudites have by far the largest bulk moduli, coupled to low γ, leading to the highest vs and κL values in Table 2.
Fig. 1d shows the figures of merit for leading phosphide materials. The highest reported zT = 0.9 at 673 K was reported for n-type Cd3P2 in 2022, linked to decent μw but largely driven by its low κL.55 The best performance amongst the larger group of p-type materials is zT ∼ 0.7 at 750 K for the tetrahedrite Ag6Ge10P12, benefitting from several optimisation studies58,69 since the original report in 2017.48 Clathrates based on Ba8Cu16P30 have been reported with zT ∼ 0.6 at 800 K.57,76 The A(CuZn)P2 122-phases reach zT = 0.6 at 800–1000 K,47,49 whilst 111 phases, including CaCuP reach zT = 0.5 at 800 K.50
3. Phosphide thermoelectric materials
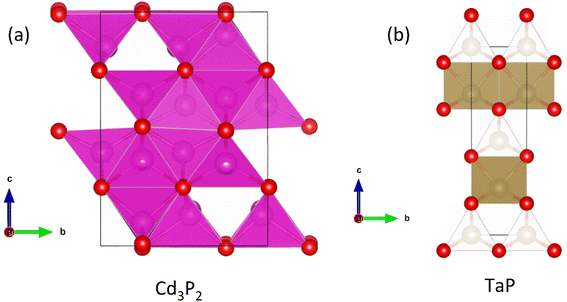
In this section, we will examine the leading phosphide materials in more detail, focusing on their crystal structure and bonding characteristics as well as thermoelectric performance. This will start with ZnCu2P8, a structure dominated by P–P bonding in Section 3.1. Section 3.2 will cover phosphide analogues of established phonon-glass electron-crystal systems (clathrate, skutterudite and tetrahedrite). Section 3.3 and 3.4 will focus on materials with 122 and 111 compositions, which do not exhibit P–P bonding. Section 3.5 will examine the n-type phases Cd3P2 and TaP, which display exceptional thermoelectric properties at high and low temperatures respectively.3.1 ZnCu2P8 – a low-cost material with P–P bonding
ZnCu2P8, first reported in 2020,15 is a good illustration of the range of bonding that phosphorus can exhibit. From an electron counting perspective, assuming Zn2+ and Cu+ (both closed shell d10), the P atoms must average to [P8]4−, requiring a large amount of P–P bonding.The P–P network is quite complex (Fig. 3), although at its simplest, half the P atoms have three single P–P bonds and a single lone pair (i.e. P0), and the other half have two P–P bonds with two lone pairs (i.e. P−). Zn exists in a relatively uniform tetrahedral P coordination, while Cu has a more heavily deformed tetrahedral P environment. This neat separation of Zn and Cu sites may not be present in real samples however, with Cu+/Zn2+ cation disorder being attributed to electronic and thermal transport features.63
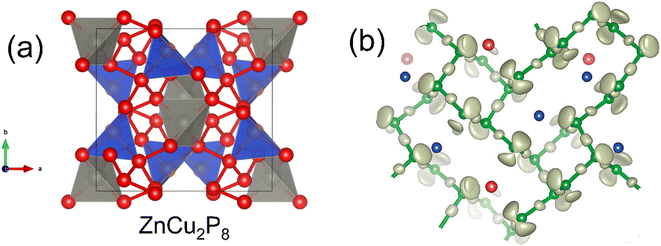 | ||
| Fig. 3 Crystal structure of ZnCu2P8. Panel (a) shows the tetrahedral coordination of Zn (grey), Cu (blue) and the P–P network (red). Panel (b) shows the lone pair behavior of P (green), where P atoms with one lone pair coordinate to Cu (blue), and P atoms with 2 lone pairs bond to Zn (red). Panel (b) reproduced with permission from Nuss et al., Zeitschrift für Anorganische und Allgemeine Chemie, 2020.63 | ||
Ab initio calculations show a strong dependence of the electronic structure and bandgap on Cu/Zn inversion.63 This is reflected in the measured properties in the two studies on this material. ZnCu2P8 prepared using ball milling has an order of magnitude larger ρ300 K,59 compared to high-temperature synthesis, which is found to have metal-like ρ(T) and S(T) above 100 K (but still with relatively high ρ300 K ∼50 mΩ cm, S300 K ∼200 μV K−1),63 suggesting a higher level of p-type doping, potentially linked to different Cu/Zn inversion or subtle deviations from nominal stoichiometry.63 Overall, the performance of ZnCu2P8 is limited by a large ρ(T) with highest observed S2σ = 0.11 mW m−1 K−2 at 673 K.59 In order to optimise the thermoelectric performance, the Cu+/Zn2+ ratio was varied in the nominal Zn1−xCu2+xP8 (−0.25 ≤ x ≤ 0.25) series.59 For x < 0 (increasing Zn – adding electrons), an increase in ρ(T) was observed, yielding a highly resistive material. For x > 0 improvements to S2σ were found to be possible. To minimise CuP2 impurities observed in the Cu-rich Zn1−xCu2+xP8 samples, Zn0.75Cu2P8 was synthesised, yielding S2σ = 0.38 mW m−1 K−2 at 673 K, and a highest reported zT673 K = 0.25. The most promising feature of ZnCu2P8 is its very low κ = 1.05–1.60 W m−1 K−1 at 300 K, decreasing to as low as ∼0.8 W m−1 K−1 at 673 K. Despite the modest overall performance, ZnCu2P8 is a fascinating thermoelectric material with complex chemical bonding offering further possibilities for optimisation. It is based on abundant low-cost elements and has good stability under ambient conditions.59,63
3.2 Phosphide analogues of high-zT phonon-glass electron-crystal thermoelectrics: tetrahedrite, clathrate and skutterudite materials
The phonon-glass electron-crystal concept (PGEC) is one of the key guiding ideas of modern thermoelectrics research.77 Its aim is to unite the low thermal transport of a structural glass with the good electrical properties of a crystalline material.Key thermoelectric materials exhibiting PGEC behaviour are the skutterudites (e.g. LaFe3CoSb12)78 and clathrates (e.g. Ba8Ga16Ge30)79 consisting of a conducting framework and rattling ions (La3+/Ba2+ in the compositions above), causing glass-like κL, whilst the materials are crystalline. Tetrahedrites are chalcogenides (e.g. Cu12Sb4S13)80 with complex structures, characterised by extremely low κL linked to out-of-plane rattling vibrations of three-fold coordinated Cu ions.81 There are phosphide analogues of all three of these important thermoelectric structure types, as illustrated in Fig. 4. These are discussed below in the following sections.
Ag6Ge10P12 can be written as Ag6(Ge4Ge2)Ge4P12Vac to match the tetrahedrite formula, where Vac is a vacancy in the structure. The presence of this vacancy is significant because it leads to the formation of an isolated [Ag6]4+ cluster.87 Valence balancing to reach a semiconducting state requires a mixture of oxidation states for Ge, leading to a formal assignment of [Ag6]4+(Ge42+Ge24+)Ge44+P123−.48
Ag6Ge10P12 is a p-type conductor, with semiconducting ρ(T) and large S300 K ∼ 250 μV K−1 (over 350 μV K−1 in single crystals48).48,58,88 Hole concentrations are sensitive to non-stoichiometry, controlled by nominal excess of P during synthesis. In one study 3% excess yielded the best electronic properties with largest S2σ ∼ 1.1 mW m−1 K−2 above 500 K.58 Higher P excess leads to increased impurity phases, increased κL and degraded thermoelectric performance. Isovalent alloying with Cu and Sn in Ag6-xCuxGe10−ySnyP12 has been found to lead to a reduction in κL, but the level of Cu substitution is limited due to deterioration of the electronic performance.88 Hole doping using Ga in Ag6Ge10−xGaxP12 is effective and can control the hole concentration, with some additional suppression of κL.67
The 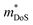 is rather large for Ag6Ge10−xGaxP12, between 8 and 16me depending on the Fermi level, due to the combination of a low dispersion band in the G–F direction and the contribution of a lower energy valence band in the Γ–H direction.67 The complex band structure and measured
is rather large for Ag6Ge10−xGaxP12, between 8 and 16me depending on the Fermi level, due to the combination of a low dispersion band in the G–F direction and the contribution of a lower energy valence band in the Γ–H direction.67 The complex band structure and measured 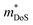 values are illustrated in Fig. 5.
values are illustrated in Fig. 5.
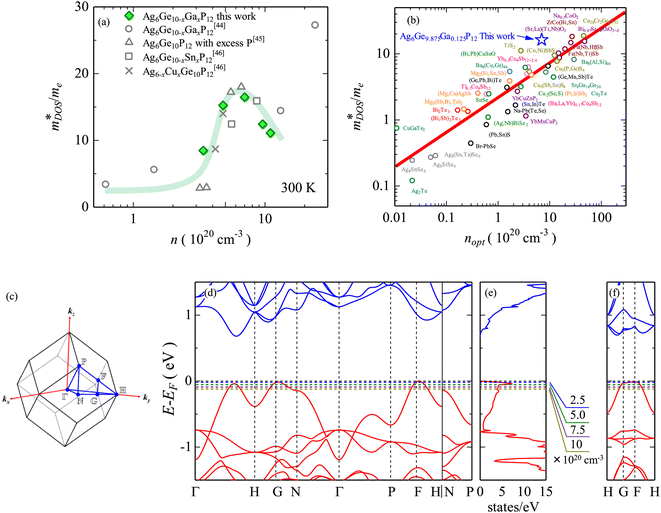 | ||
Fig. 5 Illustration of band convergence in Ag6Ge10−xGaxP12. Panel (a) highlights the dependence of 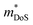 on the hole concentration (Fermi energy). Panel (b) compares on the hole concentration (Fermi energy). Panel (b) compares 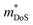 against optimal doping for a range of thermoelectric systems. Panels (c–f) show the multiple bands that contribute to thermoelectric performance at different doping levels. Reproduced under a Creative Commons CC-BY license from Namiki et al., Materials Today Sustainability, 2022.67 References in Panel (a) correspond to the original manuscript. against optimal doping for a range of thermoelectric systems. Panels (c–f) show the multiple bands that contribute to thermoelectric performance at different doping levels. Reproduced under a Creative Commons CC-BY license from Namiki et al., Materials Today Sustainability, 2022.67 References in Panel (a) correspond to the original manuscript. | ||
As is the case for most phosphide materials, high performance in the tetrahedrites is derived from low thermal transport. In single crystal Ag6Ge10P12, κL ∼ 1.75 W m−1 K−1 is observed at 300 K, which is reduced to 1.3 W m−1 K−1 for polycrystalline samples, with lowest observed values ∼0.8 W m−1 K−1 in Ag5.7Cu0.3Ge10P12.48,67,88 One explanation for the low κL is the weak interaction between the covalent Ge–P framework and the enclosed [Ag6Ge4] clusters, in which large thermal displacement parameters give Ag+ a liquid-like behaviour.48 Alternatively, the [Ag6]4+ cluster has been considered to act as a low energy “rattler”, leading to suppression of acoustic phonon modes and low sound velocities.58,69
At present, the highest reported figures of merit are for Ag6Ge10P12 + 3% P and the Ag6Ge10−xGaxP12 series, which have zT750 K ∼ 0.7.58,69
Unfilled CoP3 is an unusual material with a semiconducting ρ(T) but with a magnitude typical of conductive metallic samples (∼3 μΩ m between 5–1000 K), which is consistent with the low reported S(T) of no more than 40 μV K−1.66,96 Early band structure calculations into CoX3 skutterudite materials observed highly linear valence bands crossing a pseudo-band gap,97,98 as illustrated for CoP3 in Fig. 6. This unusual semimetallic bandstructure 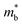 may be the cause of poor thermoelectric performance in CoP3.30,31 The material is further held back by a large κ, although κL can be suppressed through the addition of La as “rattlers” in the vacant site,96 with a reported reduction in κL from ∼15.8 W m−1 K−1 in CoP3 to ∼3 W m−1 m−1 for La0.24CoP3.
may be the cause of poor thermoelectric performance in CoP3.30,31 The material is further held back by a large κ, although κL can be suppressed through the addition of La as “rattlers” in the vacant site,96 with a reported reduction in κL from ∼15.8 W m−1 K−1 in CoP3 to ∼3 W m−1 m−1 for La0.24CoP3.
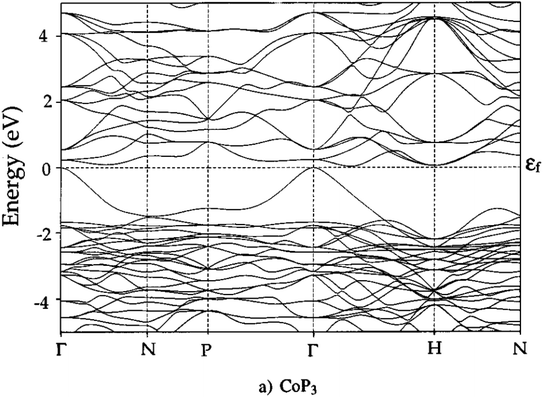 | ||
| Fig. 6 Electronic band structure of skutterudite CoP3. The material is largely gapped between −2 and 0 eV, but has one highly disperse quasi linear valence band at the Γ-point. Reproduced with permission from Llunell et al., Physical Review B, 1996.98 | ||
More promising is p-type CeFe4P12, where Co has been replaced by Fe to balance the charge donation from the Ce4+ rattlers, maintaining a semiconducting electron count.66,99 Interestingly, below 200 K S(T) is slightly negative, with thermal excitations leading to p-type conduction at higher temperatures. The peak S2σ900 K = 0.7 mW m−1 K−2 is substantially larger than for CoP3, although κ remains large at all temperatures, limiting zT to ∼0.08 at 800 K.99 CeRu4P12 similarly shows strong p-type semiconducting properties, with the decrease of S(T) on heating pointing to a more significant bipolar character than the Fe analogue.66 Analysis of room temperature Hall data using the SPB model assuming acoustic phonon scattering, reveals that the switch from Co(Fe) to Ru leads to a substantial increase in  from 0.11–0.16me to 2.26me as shown in Table 1.
from 0.11–0.16me to 2.26me as shown in Table 1.
3.3 The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 phases – EZn2P2 and derivatives
2 phases – EZn2P2 and derivatives
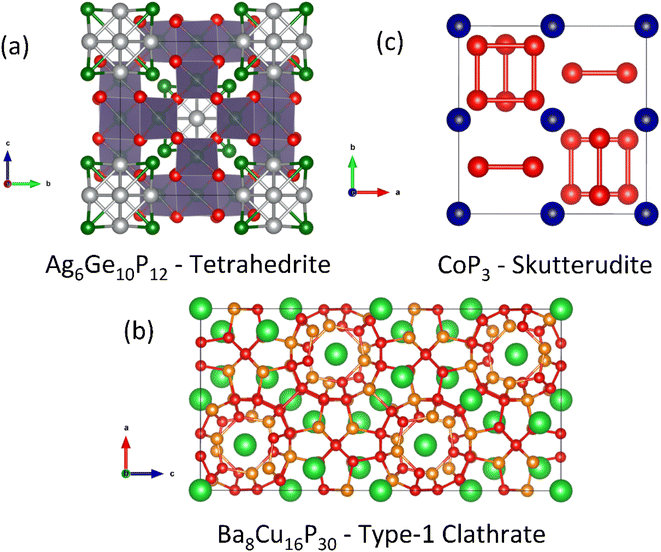
A substantial number of EM2P2 compositions have been reported, with much interest generated on the back of the discovery of high-temperature superconductivity in the Fe pnictides. Generally compositions with M = Zn and Mn are found to be semiconducting. The two most common structure types are hexagonal CaAl2Si2 (illustrated in Fig. 7a) and tetragonal ThCr2Si2/CeGa2Al2 (shown in Fig. 7c).
In terms of thermoelectric performance, most work has focused on hexagonal p-type CaZn2P2 and YbCuZnP2 derived compositions. In these materials the valence states can be simplified as Ca2+(Zn2+)2(P3−)2 and Yb3+Cu+Zn2+(P3−)2.47 The tetragonal ThCr2Si2 structure-type has more potential for intralayer P–P bonding, which would lead to a decrease in the oxidation state from P3−. Observation of this structure with P–P bonding is limited to larger E cations, such as Ba.
As-synthesized CaZn2P2 has a high ρ ∼ 2 Ω.m and S ∼ 300 μV K−1 at 300 K, consistent with a large bandgap and little intrinsic doping,47 with the Goldsmid-Sharp approximation suggesting Eg ∼ 0.6 eV, although recent DFT calculations expect Eg = 1.4 eV.100 Attempts to p-type dope via Cu substitution lead to a decrease in ρ(T) at all temperatures, but S(T) is also heavily suppressed at low temperatures, keeping S2σ < 0.02 mW m−1 K−2.73 However, a sharp (and so far unexplained) increase in S above 600 K leads to a moderate S2σ970 K = 0.5 mW m−1 K−2 in CaZn1.9Cu0.1P2.73 A similar temperature dependence has also been observed in Cu-doped Zn3P2, with sharp increases in S occurring above 600 K, coinciding with a discontinuity in σ(T).72 Mn2+ can be used instead of Zn2+ due to localisation of the 3d5 electrons, also yielding semiconducting materials with similar behaviour but a lower max zT,73 but brings the prospect of coupling to magnetism.101,102
The performance of YbCuZnP2-based compositions with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of Cu+ and Zn2+ (valence balanced through incorporation of Yb3+) is much more promising. YbCuZnP2 was found to have near constant ρ(T) ∼ 22 μΩ m (5 orders of magnitude smaller than CaZn2P2) above 300 K and a high temperature S ∼ 160 μV K−1 at 970 K, leading to S2σ970 K ∼ 1.1 mW m−1 K−2. More recently the thermoelectric properties of other RECuZnP2 materials (RE = Pr, Nd, Er) have been explored, in a study combining theory and experiment.49 While not directly reported by the authors, ErCuZnP2 displayed the largest S2σ of any reported phosphide material at that time, with S2σ780 K ∼ 1.5 mW m−1 K−2.49
1 mixtures of Cu+ and Zn2+ (valence balanced through incorporation of Yb3+) is much more promising. YbCuZnP2 was found to have near constant ρ(T) ∼ 22 μΩ m (5 orders of magnitude smaller than CaZn2P2) above 300 K and a high temperature S ∼ 160 μV K−1 at 970 K, leading to S2σ970 K ∼ 1.1 mW m−1 K−2. More recently the thermoelectric properties of other RECuZnP2 materials (RE = Pr, Nd, Er) have been explored, in a study combining theory and experiment.49 While not directly reported by the authors, ErCuZnP2 displayed the largest S2σ of any reported phosphide material at that time, with S2σ780 K ∼ 1.5 mW m−1 K−2.49
Also promising is the low κL for this structure type, consistently below 3 W m−1 K−1 at 300 K, approaching 1 W m−1 K−1 at 1000 K in the case of CaZn2P2 (Fig. 1). At present, YbCuZnP2 has the largest reported zT970 K ∼ 0.63 in this family of materials,47 although at 800 K ErCuZnP2 is reported with larger zT = 0.5.49 Controlled doping (particularly in CaZn2P2) and employing isovalent alloying strategies may lead to further improvements.
There are a number of other interesting 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 compositions that do not have the CaAl2Si2 structure type. LaMnCuP2 for example crystallises in the BaCu2S2-type structure (Fig. 7b), with the large La3+ cation stabilised by the an increased coordination number (CN) of 7 by phosphide ions.103 This is supported by the existence of α-BaZn2P2 which also forms with the BaCu2S2-type structure.104 Through higher temperature reaction conditions, β-BaZn2P2 was produced with the tetragonal ThCr2Si2-type structure which places Ba in a higher CN = 8 environment.104 Initial thermoelectric property measurements of the α-phase confirm semiconducting ρ(T) and S300 K > 120 μV K−1. With these observations in mind, there should be a large compositional and structural range for further investigation.
2 compositions that do not have the CaAl2Si2 structure type. LaMnCuP2 for example crystallises in the BaCu2S2-type structure (Fig. 7b), with the large La3+ cation stabilised by the an increased coordination number (CN) of 7 by phosphide ions.103 This is supported by the existence of α-BaZn2P2 which also forms with the BaCu2S2-type structure.104 Through higher temperature reaction conditions, β-BaZn2P2 was produced with the tetragonal ThCr2Si2-type structure which places Ba in a higher CN = 8 environment.104 Initial thermoelectric property measurements of the α-phase confirm semiconducting ρ(T) and S300 K > 120 μV K−1. With these observations in mind, there should be a large compositional and structural range for further investigation.
One final composition of note is EuIn2As2−xPx, which differs from the above structures because it has direct In–In bonding (Fig. 7d).61 Focussing on the P-rich compositions, the samples are degenerate semiconductors, with a largely temperature independent S2σ ∼ 0.5 mW m−1 K−2 between 300–800 K. Alloying leads to a substantial reduction in κL, consistent with mass and strain disorder, with a reduction from κL 300 K = 6.7 W m−1 K−1 in EuIn2P2 to ∼3 W m−1 K−1 in alloyed EuIn2PAs. With this beneficial alloying contribution, zT773 K ∼ 0.25 is achieved. Other isoelectronic EuIn2P2-type phosphides have been shown to exist experimentally,105 which may also have promising thermoelectric properties.
3.4 The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 phases – CaCuP, CaAgP and derivatives
1 phases – CaCuP, CaAgP and derivatives
A number of semiconducting phosphides with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
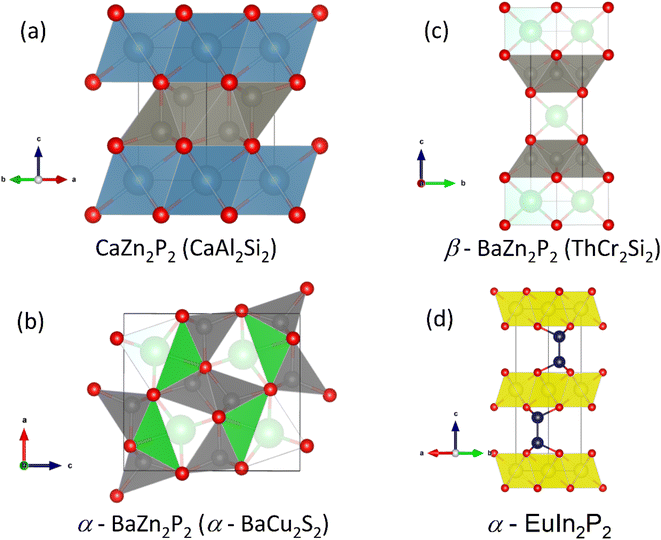
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 composition have been reported. Assuming ionic P3−, the electron donating metals are required to have formal +1 and +2 oxidation states. One larger group of materials satisfying this requirement is the Nowotny-Juza I-II-V phases, which are cubic semiconductors with a valence electron count of 8.106 Their structures are closely related to the heavily investigated half-Heusler thermoelectrics,27 differing only in preferred site occupancies.106 An example of a phosphide Nowotny-Juza phase is LiZnP,107 whose structure is shown in Fig. 8a. Here electronegative P occupies the pseudo-cubic site, whereas late transition metals such as Ni occupy this position in the 18 electron half-Heusler structure.106 Unfortunately, exploration of these phases is difficult, with the alkali metal leading to instability in ambient conditions. A phosphide analogue of MgAgSb, with zT ∼ 1.4 at temperatures below 550 K,108,109 and good initial device properties,110 would be of interest but has not been reported.
1 composition have been reported. Assuming ionic P3−, the electron donating metals are required to have formal +1 and +2 oxidation states. One larger group of materials satisfying this requirement is the Nowotny-Juza I-II-V phases, which are cubic semiconductors with a valence electron count of 8.106 Their structures are closely related to the heavily investigated half-Heusler thermoelectrics,27 differing only in preferred site occupancies.106 An example of a phosphide Nowotny-Juza phase is LiZnP,107 whose structure is shown in Fig. 8a. Here electronegative P occupies the pseudo-cubic site, whereas late transition metals such as Ni occupy this position in the 18 electron half-Heusler structure.106 Unfortunately, exploration of these phases is difficult, with the alkali metal leading to instability in ambient conditions. A phosphide analogue of MgAgSb, with zT ∼ 1.4 at temperatures below 550 K,108,109 and good initial device properties,110 would be of interest but has not been reported.
The remainder of this section will focus on the thermoelectric properties of the 111-compositions CaAg0.9P, MgCuP, CaCuP and SrCuP.
The silver phosphide CaAgP has recently attracted interest as a possible nodal-line Direct semimetal,111,112 although the presence of a predicted band-gap depended on the exchange correlation functional, with PBE-GGA giving a semimetallic bandstructure,111,112 whereas a hybrid-functional gives a low band-gap semiconductor.113 The CaAgP structure, originally discovered in 1979,114 consists of edge-linked CaP5 square based pyramids (Fig. 8b).
In our report, we observe large S(T) values supporting a semiconducting bandstructure, with the metallic ρ(T) likely arising due to Ag vacancies introducing holes into the material, with nominal CaAgP containing 3% Ag impurity and an Ag-site occupancy of ∼0.9 from PXRD data.60S2σ(T) values in the targeted off-stoichiometric CaAg0.9P composition reach a peak of 1.25 mW m−1 K−2 at 550 K, decreasing at higher temperatures due to a bipolar decrease in S(T). The thermal properties of CaAg0.9P are promising, with a low κL 340 K ∼ 1.8 W m−1 K−1 decreasing to a minimum of κL 600 K ∼ 1.2 W m−1 K−1, although it appears that there is a significant bipolar contribution to κ at higher temperatures. Moderate electronic performance and low κL leads to a peak zT600 K ∼ 0.43, which is promising for a largely unoptimized system. The thermoelectric properties of CaAgP have recently (the paper appeared during the proof stages of this review) been the subject of a computational study, confirming experimental findings.115
Following on from CaAgP, we reported the thermoelectric properties of MgCuP and CaCuP, based on sustainable elements and with low gravimetric densities.50 These compositions each have different crystal structures (shown in Fig. 8c and d) and are different from CaAgP, again highlighting the structural diversity of the phosphides. CaCuP forms with hexagonal [CuP]2− layers isostructural with graphene or BN layers, separated by Ca2+ cations.116 Where CaCuP can be viewed as pseudo-2D, the MgCuP structure consists of chains of edge-linked CuP4 tetrahedra in the b-direction giving a pseudo-1D character to the structure (Fig. 8d).117 Electronic bandstructure calculations for both phases exist in the literature, with calculated Eg > 1 eV for both phases.68 An experimental follow-up, in the context of transparent semiconductors, found degenerate p-type behaviour arising due to Cu deficiency in CaCuP,118 consistent with our observations.
Both CaCuP and MgCuP are p-type and have a very similar zT between 300–800 K, reaching ∼0.5 at 790 K, although CaCuP has much better electronic properties while MgCuP has a lower κL.50 At present CaCuP boasts the largest high temperature S2σ of any phosphide material reported in the literature, with a maximum S2σ790 K = 1.75 mW m−1 K−2 (Fig. 1a) and an average value of 1.62 mW m−1 K−2 between 340–790 K, which is helpful for power generation. Unsurprisingly, CaCuP has one of the larger κL covered in this review, with κL 340 K ∼ 3.9 W m−1 K−1, compared to 2.4 W m−1 K−1 for MgCuP, decreasing to 1.8 W m−1 K−1 and 1.5 W m−1 K−1 at 790 K respectively. From a thermoelectric perspective, CaCuP is the more promising of the two phases due to its better electronic performance and the absence of detrimental bipolar carrier effects at high temperatures.50 A further complication with the MgCuP phase was found with increased amounts of Cu3P and CuP2 impurity phases observed upon heating, pointing to partial decomposition of the majority phases.50 However, this effect appears to be reversible on cooling with observation of reversible hysteretic effects in the measured S(T) and ρ(T) on temperature cycling.
During review of this manuscript, Moll et al. reported on the thermoelectric properties of SrCuP,71 which is isostructural to CaCuP. SrCuP was prepared using a mechanical alloying route and is more susceptible to oxidation than CaCuP with substantial Sr10(PO4)6O impurities and visible degradation of the SPS pellet in ambient conditions. In terms of its thermoelectric performance, SrCuP is a p-type degenerate semiconductor with peak S2σ700 K = 0.7 mW m−1 K−2 and a minimum κL 600 K ∼ 1.3 W m−1 K−1. The highest zT reported was zT600 K = 0.2, but improvements should be possible if better quality samples can be produced.
3.5 n-type compositions – Cd3P2 and topological magneto–thermoelectric TaP
A recent report on n-type Cd3P2 found the best thermoelectric performance for a phosphide material reported thus far, with zT673 K ∼ 0.91.55 Promising performance with zT300 K = 0.2 was originally reported as early as 1968 by Masumoto and Isomura,53,54 where alloying with As was found to lead to zT300 K ∼ 0.33, in large part due to suppression of κL. The crystal structure of Cd3P2 is a distortion of the cubic Ag2O3-type structure, with symmetry lowered from cubic to tetragonal. The structure consists of edge and vertex linked CdP4 tetrahedra (Fig. 9a), while there are three distinct 6-coordinate environments for the P3− anions.At present, temperature dependent thermoelectric property data is only available from the 2022 study.55μH has been confirmed to be quite high from multiple sources,53–55,119 with values ∼1500 cm2 V−1 s−1 at room temperature due to a low  , although μH can be lower when grain boundaries are present.55 This low electron mass arises from a single highly dispersive conduction band minima at the Γ-point. Typical nH values are on the order of 1017–1018 cm−3 at 300 K,53–55 which is on the lower end for thermoelectric materials. As expected from low extrinsic carrier doping, these materials have substantial intrinsic carrier effects, with a highly temperature dependent nH(T) and a strong bipolar decrease in S(T) with increasing temperature.55 The calculated band gap for the material is 0.46 eV. In the most highly doped sample, S2σ reaches large values for a system with such low
, although μH can be lower when grain boundaries are present.55 This low electron mass arises from a single highly dispersive conduction band minima at the Γ-point. Typical nH values are on the order of 1017–1018 cm−3 at 300 K,53–55 which is on the lower end for thermoelectric materials. As expected from low extrinsic carrier doping, these materials have substantial intrinsic carrier effects, with a highly temperature dependent nH(T) and a strong bipolar decrease in S(T) with increasing temperature.55 The calculated band gap for the material is 0.46 eV. In the most highly doped sample, S2σ reaches large values for a system with such low  , with a maximum of 1.3 mW m−1 K−2 at 673 K.
, with a maximum of 1.3 mW m−1 K−2 at 673 K.
As already discussed, the real driver behind the high zT is that κL < 1 W m−1 K−1 at all temperatures in the most recent report,55 (or ∼2 W m−1 K−1 in the original reports53,54). First principles calculations and acoustic measurements find low vs are largely responsible for low κL.55 In the phonon density of states, the acoustic phonon behaviour is dominated by the vibration of Cd atoms, while P atoms contribute more heavily to optical phonons.
Alloying in the Cd3P1−xAsx solid solution was carried out in the 1970,53,54 confirming the formation of a complete solid solution. Across the solid solution, all samples are n-type and degenerately doped. The alloying dependence of κL shows a decrease from either end member consistent with expected alloying behaviour, however an increase near x = 0.5 suggests partial ordering on the P/As site. The thermoelectric properties of single crystal Cd3As2 are interesting, showing strong magneto–thermoelectric effects attributed to linear dispersion in the conduction band.120 The room temperature thermoelectric values for Cd3P2 with zero applied field are better however, so an examination of Cd3P2 in applied fields could prove to be interesting.
On the subject of magneto–thermoelectric effects, n-type TaP displays particularly interesting properties,56 perhaps not in the context of power generation, but rather with the observation of the ‘quantised thermoelectric Hall effect’ (QTHE). In short, Weyl Semi-Metals (WSM) benefit from an energy independent density of states g(E) which increases with applied magnetic fields, protected by the topological behaviour of the Weyl nodes. Since S is proportional to the logarithmic derivative of g(E), the application of a magnetic field allows an applied field to induce large S(B). In single crystal TaP, the QTHE has successfully been demonstrated, with Sxx(9T) > 1000 μV K−1 observed at ∼45 K (Fig. 10b). As a semimetal, the applied field induced a substantial magnetoresistance in the sample, but at the maximum reported field of 9T, the power factor Sxx2σ exceeded 50 mW m−1 K−2 at ∼45 K (Fig. 10f).56 Such values are not ordinarily obtained for thermoelectric materials in thermodynamic equilibrium. The practicality of harvesting heat or applying the Peltier effect at 45 K under a 9T magnetic field is challenging and may prevent exploitation, however the results are exceptional.
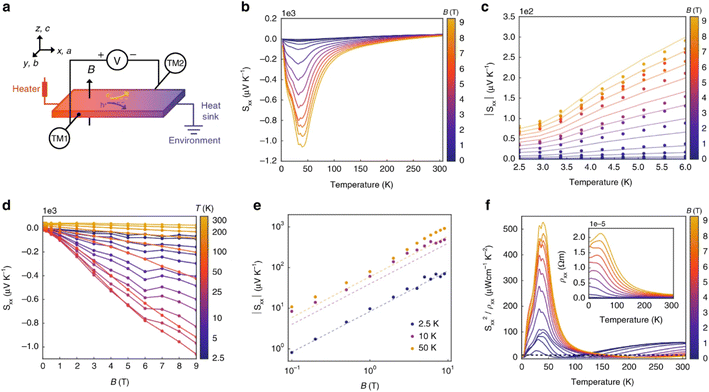 | ||
| Fig. 10 Magneto–thermoelectric effect in TaP. Panel (a) illustrates the experimental setup used to measure the Seebeck coefficient in the x-direction (Sxx). Panel (b) shows the temperature dependence of Sxx at applied fields Bz between 2.5–300 K, and panel (c) highlights the 2.5–6 K region. Panel (d) shows the dependence of Sxx on the applied field at fixed temperatures, with panel (e) showing the same data on logarithmic axes. Finally, panel (f) shows the power factor in the x-direction as a function of temperature at fixed magnetic fields, showing the very large Sx×2/ρxx > 50 mWm−1 K−2 near 45 K in 9T. Reproduced under a Creative Commons CC BY license from Han et al., Nature Communications, 2020.56 | ||
4. Discussion
Metal phosphides are gaining increasing attention with a larger selection of materials now being investigated for their thermoelectric performance. This has enabled more detailed insight into the underlying thermoelectric properties of metal phosphides. The current highest figures of merit are zT673 K = 0.9 for n-type Cd3P2 and zT750 K = 0.7 for p-type tetrahedrite Ag6Ge10GaP12. In both cases, the performance is underpinned by low κL and relatively modest electronic properties (compared to the best performing thermoelectrics, such as Bi2Te3, SnSe, PbTe, GeTe, skutterudites and half-Heuslers).5,7,9 Besides these two compositions, there are several other p-type compositions that reach zT = 0.5–0.6 at 700 K, including 111-type CaCuP and 122-type YbCuZnP2. As observed for antimonide Zintl compositions, n-type conduction is relatively rare in metal phosphides. This is likely linked to the relative ease for metal deficiency in these compositions. One major conclusion is that despite the low atomic mass of P, low κL is commonly observed. This is linked to relatively “weak” chemical bonding (low k in eqn. (5)) in these materials, with a clear correlation between calculated vs and measured κL (Fig. 2). Searching for crystal structures with low bulk moduli (weak and anharmonic bonding) is therefore a promising route towards finding higher zT materials. Where calculations are not available, searching for crystal structures with mixtures of shorter and longer bonds as part of a single coordination environment might be a fruitful route.24From the overview presented here, the main challenge is to improve the thermoelectric power factor in metal phosphides. Table 1 shows that investigated phosphides have 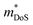 and μH values that are typical for semiconducting materials. The main issue appears to be that μ0 (for a given
and μH values that are typical for semiconducting materials. The main issue appears to be that μ0 (for a given 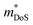 ) lags behind that of thermoelectrics with large S2σ,62 hence compromising μw. Several materials have μw around 50–100 cm2 V−1 s−1, with the clear outlier being CaCuP with 180 cm2 V−1 s−1 which outperforms every other phosphide reported at all temperatures (Fig. 1b). However, even for CaCuP, the μw is only about 1/3 of high-power factor materials, such as the half-Heuslers27,121–123 and antimonide skutterudites.30–33 For CaCuP, the high μw is likely linked to its relatively simple crystal structure. The observation of large μw(T) for tetrahedrite Ag6Ge10P12 is unexpected given its complex structure with unusual separation into weakly interacting [Ag6Ge4] clusters within a [Ge6P12] framework.48 This suggests that the framework of vertex-sharing GeP4 tetrahedra is effective in promoting hole transport. The low μw(T) for the two structures containing high degrees of P–P bonding (Ba8Cu14Ge6P26 and Zn0.75Cu2P8), suggests that electrons in P–P bonds are localised and that this is not favourable for obtaining good electrical properties. There are several theoretical predictions of high thermoelectric performance, including in CuP2,124 and BaAu2P4.125 These compositions or the features supporting good properties (bond hierarchy and low κL for BaAu2P4) are worthy of further investigation. Another interesting composition that was mentioned in the context of low κL is AgP2 (Section 2). As prepared, this material is too insulating, but it could be of interest if it could be doped. Hall data reveal a low
) lags behind that of thermoelectrics with large S2σ,62 hence compromising μw. Several materials have μw around 50–100 cm2 V−1 s−1, with the clear outlier being CaCuP with 180 cm2 V−1 s−1 which outperforms every other phosphide reported at all temperatures (Fig. 1b). However, even for CaCuP, the μw is only about 1/3 of high-power factor materials, such as the half-Heuslers27,121–123 and antimonide skutterudites.30–33 For CaCuP, the high μw is likely linked to its relatively simple crystal structure. The observation of large μw(T) for tetrahedrite Ag6Ge10P12 is unexpected given its complex structure with unusual separation into weakly interacting [Ag6Ge4] clusters within a [Ge6P12] framework.48 This suggests that the framework of vertex-sharing GeP4 tetrahedra is effective in promoting hole transport. The low μw(T) for the two structures containing high degrees of P–P bonding (Ba8Cu14Ge6P26 and Zn0.75Cu2P8), suggests that electrons in P–P bonds are localised and that this is not favourable for obtaining good electrical properties. There are several theoretical predictions of high thermoelectric performance, including in CuP2,124 and BaAu2P4.125 These compositions or the features supporting good properties (bond hierarchy and low κL for BaAu2P4) are worthy of further investigation. Another interesting composition that was mentioned in the context of low κL is AgP2 (Section 2). As prepared, this material is too insulating, but it could be of interest if it could be doped. Hall data reveal a low  and μH = 50 cm2 V−1 s−1.74 Another potentially interesting silver phosphide is Ag3SnP7, which has a low κL = 1.5 W m−1 K−1 with no further thermoelectric characterisation.126
and μH = 50 cm2 V−1 s−1.74 Another potentially interesting silver phosphide is Ag3SnP7, which has a low κL = 1.5 W m−1 K−1 with no further thermoelectric characterisation.126
Assuming that electrical transport is dominated by acoustic phonon scattering (APS), the magnitude of μ0 within the SPB model is related to the longitudinal velocity of sound, (vl), the band mass 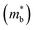 , the inertial carrier mass (mI) and the deformation potential (Edef):27
, the inertial carrier mass (mI) and the deformation potential (Edef):27
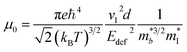 | (6) |
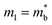 , and using the vl from Table 2 enables an estimate of Edef. For CaCuP and MgCuP Edef = 13.4 eV and 7.9 eV respectively. For Cd3P2 and YbCuZnP2 values come out closer to 40 eV, although in both cases the temperature dependence of σ and μH don't match a typical degenerate semiconductor. At this point it is unclear if acoustic phonon scattering is indeed the dominant scattering mechanism, with optical phonon and ionised impurity scattering also likely to contribute, but the obtained values of Edef are fairly large for thermoelectric materials.28,127–129 Further work on understanding electronic transport (carrier scattering) in these materials is needed and can provide avenues for further materials discovery and optimisation.
, and using the vl from Table 2 enables an estimate of Edef. For CaCuP and MgCuP Edef = 13.4 eV and 7.9 eV respectively. For Cd3P2 and YbCuZnP2 values come out closer to 40 eV, although in both cases the temperature dependence of σ and μH don't match a typical degenerate semiconductor. At this point it is unclear if acoustic phonon scattering is indeed the dominant scattering mechanism, with optical phonon and ionised impurity scattering also likely to contribute, but the obtained values of Edef are fairly large for thermoelectric materials.28,127–129 Further work on understanding electronic transport (carrier scattering) in these materials is needed and can provide avenues for further materials discovery and optimisation.
There are considerations for thermoelectric materials beyond zT, which limit application in popular thermoelectric systems. This includes finding matching n- and p-types, good mechanical properties, electrical and thermal contacting, stability under temperature cycling and during exposure to high temperatures.5,9 Most of the phosphides discussed in this review are at least stable on the bench in ambient conditions, but it seems likely that some sort of encapsulation is needed for high-temperature operation.
A number of studies report thermogravimetric (TGA) and differential scanning calorimetry (DSC) data, generally under inert conditions (typical gas flow for TGA/sealed cups for DSC). For example, SrCuP is stable up to 1273 K from DSC,71 but as discussed in Section 3.5, does readily oxidise in ambient conditions. By contrast MgCuP and CaCuP have good stability on the bench,50 but a (reversible) decomposition occurs for MgCuP above 573 K. The Ba8Cu14Ge6P26 clathrate has good stability in inert conditions up to its melting point at 1100 K.57 Investigation of Ag6Ge10P12 in an open atmosphere showed decomposition above 750 K due to the evolution of P4 gas.48 By contrast, this composition is stable up to the melting point of 1000 K when heated inside a sealed quartz tube. Similarly Cd3P2 shows significant mass loss above 700 K in TGA. However, the sample can be consolidated using hot-pressing at 923 K.55 ZnCu2P8 shows no thermal events during DSC measurements up to 960 K, above which mass loss is detected consistent with P4 gas loss leaving behind the maximum oxidation state phases Cu3P and Zn3P2.63
Materials design can be used to remedy stability issues as demonstrated for Cu2Se, where Cu ion conduction can be suppressed, improving stability under operating conditions.130 The high zT in Cd3P2 is an outstanding result showing that good performance is possible, but it won't be possible to use this composition due to the toxicity of Cd. Some of the 122 and 111 phase contain more abundant and benign constituent elements. With further exploration of phosphide materials, electrical contacting, and measurement of mechanical and thermal properties will be essential to determining viability for device application.
5. Outlook
Metal phosphides have only very recently started to attract attention and are now approaching figures of merit, zT = 1 in both p- and n-type compositions. Whilst the overall performance lags behind those of state-of-the-art materials, this is a promising starting point for further exploration. Metal phosphides comprise a large class of materials with great structural and compositional (bonding) diversity afforded by the flexible oxidation state of P, from covalent P0/P−1 to more ionic materials with P3− anions. Hence, there is huge scope to discover better performing thermoelectrics.The current best performing metal phosphides have low κL and are limited by relatively low μw. The low μw in the materials studied so far appears due to a relatively poor mobility (μ0), when compared to thermoelectric materials with high S2σ. When analysed within the APS limit, large Edef are found, suggesting a strong coupling with the lattice. Even if APS is not the dominant scattering mechanism, this result demonstrates that the carrier scattering is relatively high, compared to materials with comparable 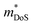 . This leaves improving μw through
. This leaves improving μw through 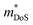 , and in particular by increasing Nv as increasing
, and in particular by increasing Nv as increasing 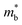 degrades the mobility, as the most direct route to improve performance (eqn (2)–(4)). Investigation of high-zT tetrahedrite Ag6Ge10P12 has found a highly converged band structure, whilst the large compositional range of 122- and 111-phases could afford opportunities for increasing Nv through solid-solution formation. It is also likely that materials with weaker APS (reduced electronic scattering) can be prepared. Targeted design of these materials would require a better understanding of the various carrier relaxation mechanisms. The observation of huge thermoelectric responses in the Weyl semimetal TaP, although driven by field induced increases in S, suggests that large power factors are possible in metal phosphides. Other now more routinely used optimisation strategies focused on defect-engineering,6,8 including finding optimal dopants, control of intrinsic defects, nanostructuring, etc, have also not yet been widely applied to metal phosphides.
degrades the mobility, as the most direct route to improve performance (eqn (2)–(4)). Investigation of high-zT tetrahedrite Ag6Ge10P12 has found a highly converged band structure, whilst the large compositional range of 122- and 111-phases could afford opportunities for increasing Nv through solid-solution formation. It is also likely that materials with weaker APS (reduced electronic scattering) can be prepared. Targeted design of these materials would require a better understanding of the various carrier relaxation mechanisms. The observation of huge thermoelectric responses in the Weyl semimetal TaP, although driven by field induced increases in S, suggests that large power factors are possible in metal phosphides. Other now more routinely used optimisation strategies focused on defect-engineering,6,8 including finding optimal dopants, control of intrinsic defects, nanostructuring, etc, have also not yet been widely applied to metal phosphides.
To conclude, metal phosphides remain a largely unexplored frontier area for thermoelectrics research, with many structures left to be discovered and explored. There is a clear need to improve understanding of the interplay between structure, bonding, and thermoelectric properties in metal phosphides, so that materials exploration can be accelerated. This should include using materials informatics and effective descriptors for high performance and first principles work focused on gaining microscopic understanding. There is no fundamental reason why higher zT values cannot be achieved. Given the established issues with high-temperature stability, this should focus on sub-ambient, room and moderate temperature applications.
Author contributions
Data analysis and visualisation (R. J. Q); manuscript writing – original draft (R. J. Q); conceptualisation, funding, project supervision, manuscript writing–review & editing (J. W. G. B.).Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The Leverhulme Trust is acknowledged for funding the research on metal phosphide thermoelectrics (RPG-2020-177).References
- D. M. Rowe, CRC Handbook of Thermoelectrics, CRC Press, 1995 Search PubMed.
- R. Funahashi, Thermoelectric Energy Conversion, Elsevier, 2021 Search PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- G. J. Snyder and A. H. Snyder, Energy Environ. Sci., 2017, 10, 2280–2283 RSC.
- Q. Yan and M. G. Kanatzidis, Nat. Mater., 2022, 21, 503–513 CrossRef CAS PubMed.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z. Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 RSC.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed.
- X. Su, P. Wei, H. Li, W. Liu, Y. Yan, P. Li, C. Su, C. Xie, W. Zhao, P. Zhai, Q. Zhang, X. Tang and C. Uher, Adv. Mater., 2017, 29, 1602013 CrossRef PubMed.
- X. L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515 CrossRef CAS PubMed.
- L. D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144 CrossRef CAS PubMed.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z. Z. Luo, H. Lee, B. Ge, Y. L. Lee, X. Chen, J. Y. Lee, O. Cojocaru-Mirédin, H. Chang, J. Im, S. P. Cho, M. Wuttig, V. P. Dravid, M. G. Kanatzidis and I. Chung, Nat. Mater., 2021, 20, 1378–1384 CrossRef CAS PubMed.
- C. Chang, M. H. Wu, D. S. He, Y. L. Pei, C. F. Wu, X. F. Wu, H. L. Yu, F. Y. Zhu, K. D. Wang, Y. Chen, L. Huang, J. F. Li, J. Q. He and L. D. Zhao, Science, 2018, 360, 778–782 CrossRef CAS PubMed.
- B. C. Qin, D. Y. Wang, X. X. Liu, Y. X. Qin, J. F. Dong, J. F. Luo, J. W. Li, W. Liu, G. J. Tan, X. F. Tang, J. F. Li, J. Q. He and L. D. Zhao, Science, 2021, 373, 556 CrossRef CAS PubMed.
- S. I. Kim, K. H. Lee, H. A. Mun, H. S. Kim, S. W. Hwang, J. W. Roh, D. J. Yang, W. H. Shin, X. S. Li, Y. H. Lee, G. J. Snyder and S. W. Kim, Science, 2015, 348, 109–114 CrossRef CAS PubMed.
- H. Y. Lv, H. J. Liu, J. Shi, X. F. Tang and C. Uher, J. Mater. Chem. A, 2013, 1, 6831–6838 RSC.
- Y. Wu, P. Nan, Z. Chen, Z. Zeng, R. Liu, H. Dong, L. Xie, Y. Xiao, Z. Chen, H. Gu, W. Li, Y. Chen, B. Ge and Y. Pei, Adv. Sci., 2020, 7, 1902628 CrossRef CAS PubMed.
- J. Zhang, D. Wu, D. He, D. Feng, M. Yin, X. Qin and J. He, Adv. Mater., 2017, 29, 1703148 CrossRef PubMed.
- L. Fu, M. Yin, D. Wu, W. Li, D. Feng, L. Huang and J. He, Energy Environ. Sci., 2017, 10, 2030–2040 RSC.
- G. Tan, F. Shi, S. Hao, L. D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167 CrossRef CAS PubMed.
- K. Biswas, J. Q. He, I. D. Blum, C. I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- A. Suwardi, J. Cao, L. Hu, F. Wei, J. Wu, Y. Zhao, S. H. Lim, L. Yang, X. Y. Tan, S. W. Chien, Y. Yin, W. X. Zhou, W. L. Mun Nancy, X. Wang, S. H. Lim, X. Ni, D. Li, Q. Yan, Y. Zheng, G. Zhang and J. Xu, J. Mater. Chem. A, 2020, 8, 18880–18890 RSC.
- X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, Joule, 2020, 4, 986–1003 CrossRef CAS.
- L. D. Zhao, S. H. Lo, Y. S. Zhang, H. Sun, G. J. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373 CrossRef CAS PubMed.
- S. R. Popuri, M. Pollet, R. Decourt, M. L. Viciu and J. W. G. Bos, Appl. Phys. Lett., 2017, 110, 253903 CrossRef.
- I. Loa, S. R. Popuri, A. D. Fortes and J. W. G. Bos, Phys. Rev. Mater., 2018, 2, 085405 CrossRef CAS.
- S. R. Popuri, M. Pollet, R. Decourt, F. D. Morrison, N. S. Bennett and J. W. G. Bos, J. Mater. Chem. C, 2016, 4, 1685–1691 RSC.
- R. J. Quinn and J. W. G. Bos, Mater. Adv., 2021, 2(19), 6246–6266 RSC.
- R. J. Quinn, G. B. G. Stenning and J. W. G. Bos, J. Phys.: Energy, 2022, 4(2), 024005 Search PubMed.
- V. Shields, T. Caillat, J. P. Fleurial, A. Zoltan, L. Zoltan and M. Tuchscherer, Twenty-first International Conference on Thermoelectronics, Proceedings ICT'02, 2002, pp. 64–67 Search PubMed.
- G. Rogl, A. Grytsiv, P. Heinrich, E. Bauer, P. Kumar, N. Peranio, O. Eibl, J. Horky, M. Zehetbauer and P. Rogl, Acta Mater., 2015, 91, 227–238 CrossRef CAS.
- G. Rogl, A. Grytsiv, K. Yubuta, S. Puchegger, E. Bauer, C. Raju, R. C. Mallik and P. Rogl, Acta Mater., 2015, 95, 201–211 CrossRef CAS.
- G. Rogl and P. Rogl, Curr. Opin. Green Sustainable Chem., 2017, 4, 50–57 CrossRef.
- G. Rogl, A. Grytsiv, F. Failamani, M. Hochenhofer, E. Bauer and P. Rogl, J. Alloys Compd., 2017, 695, 682–696 CrossRef CAS.
- H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187 CrossRef CAS PubMed.
- J. Mao, J. Shuai, S. Song, Y. Wu, R. Dally, J. Zhou, Z. Liu, J. Sun, Q. Zhang, C. Dela Cruz, S. Wilson, Y. Pei, D. J. Singh, G. Chen, C. W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10548–10553 CrossRef CAS PubMed.
- X. Shi, X. Wang, W. Li and Y. Pei, Small Methods, 2018, 2, 1800022 CrossRef.
- J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Nat. Commun., 2017, 8, 13901 CrossRef CAS PubMed.
- J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498 CrossRef CAS PubMed.
- S. M. Kauzlarich, S. R. Brown and G. J. Snyder, Dalton Trans., 2007,(21), 2099–2107, 10.1039/B702266B.
- E. S. Toberer, A. F. May and G. J. Snyder, Chem. Mater., 2010, 22, 624–634 CrossRef CAS.
- S. M. Kauzlarich, A. Zevalkink, E. Toberer and G. J. Snyder, in Thermoelectric Materials and Devices, ed. I. Nandhakumar, N. M. White and S. Beeby, The Royal Society of Chemistry, 2016, 10.1039/9781782624042-00001.
- J. Shuai, J. Mao, S. Song, Q. Zhang, G. Chen and Z. Ren, Mater. Today Phys., 2017, 1, 74–95 CrossRef.
- K. F. Liu and S. Q. Xia, J. Solid State Chem., 2019, 270, 252–264 CrossRef CAS.
- J. W. G. Bos, in Inorganic Thermoelectric Materials: from Fundamental Concepts to Materials Design, ed. A. V. Powell, The Royal Society of Chemistry, 2021, 10.1039/9781788019590-00216.
- J. H. Pöhls, A. Faghaninia, G. Petretto, U. Aydemir, F. Ricci, G. Li, M. Wood, S. Ohno, G. Hautier, G. J. Snyder, G. M. Rignanese, A. Jain and M. A. White, J. Mater. Chem. C, 2017, 5, 12441–12456 RSC.
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Butterworth-Heinemann, Oxford, 2nd edn, 1997 Search PubMed.
- V. Ponnambalam, S. Lindsey, W. Xie, D. Thompson, F. Drymiotis and T. M. Tritt, J. Phys. D: Appl. Phys., 2011, 44, 155406 CrossRef.
- J. Nuss, U. Wedig, W. Xie, P. Yordanov, J. Bruin, R. Hübner, A. Weidenkaff and H. Takagi, Chem. Mater., 2017, 29, 6956–6965 CrossRef CAS.
- J. H. Pöhls, S. Chanakian, J. Park, A. M. Ganose, A. Dunn, N. Friesen, A. Bhattacharya, B. Hogan, S. Bux, A. Jain, A. Mar and A. Zevalkink, Mater. Horiz., 2021, 8, 209–215 RSC.
- R. J. Quinn, C. Stevens, H. Leong, A. D. Huxley and J. W. G. Bos, Chem. Commun., 2022, 58, 11811–11814 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- K. Masumoto and S. Isomura, J. Jpn. Inst. Met., 1968, 32, 1116–1120 CrossRef CAS.
- K. Masumoto and S. Isomura, Energy Convers., 1970, 10, 129–133 CrossRef.
- L. Fan, K. Peng, Z. Zhou, Y. Yan, C. Ran, H. Wang, G. Han, B. Zhang, X. Lu, G. Wang and X. Zhou, Chem. Mater., 2022, 34, 1620–1626 CrossRef CAS.
- F. Han, N. Andrejevic, T. Nguyen, V. Kozii, Q. T. Nguyen, T. Hogan, Z. Ding, R. Pablo-Pedro, S. Parjan, B. Skinner, A. Alatas, E. Alp, S. Chi, J. Fernandez-Baca, S. Huang, L. Fu and M. Li, Nat. Commun., 2020, 11, 6167 CrossRef CAS PubMed.
- J. Wang, O. I. Lebedev, K. Lee, J. A. Dolyniuk, P. Klavins, S. Bux and K. Kovnir, Chem. Sci., 2017, 8, 8030–8038 RSC.
- A. Suwardi, L. Hu, X. Z. Wang, X. Y. Tan, D. V. M. Repaka, L. M. Wong, X. P. Ni, W. H. Liew, S. H. Lim, Q. Y. Yan, J. W. Xu, Y. Zheng and K. Hippalgaonkar, ACS Appl. Mater. Interfaces, 2020, 12, 9150–9157 CrossRef CAS PubMed.
- J. Mark and T. Mori, ACS Appl. Energy Mater., 2021, 4, 4861–4866 CrossRef CAS.
- R. J. Quinn and J. W. G. Bos, Appl. Phys. Lett., 2022, 120, 073903 CrossRef CAS.
- K. Shinozaki, Y. Goto, K. Hoshi, R. Kiyama, N. Nakamura, A. Miura, C. Moriyoshi, Y. Kuroiwa, H. Usui and Y. Mizuguchi, ACS Appl. Energy Mater., 2021, 4, 5155–5164 CrossRef CAS.
- G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537 CrossRef CAS PubMed.
- J. Nuss, U. Wedig, K. Philippi and H. Takagi, Z. Anorg. Allg. Chem., 2020, 646, 1144–1150 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- C. B. Vining, J. Appl. Phys., 1991, 69, 331–341 CrossRef CAS.
- A. Watcharapasorn, R. C. Demattei, R. S. Feigelson, T. Caillat, A. Borshchevsky, G. J. Snyder and J. P. Fleurial, Jpn. J. Appl. Phys., 2000, 39, 14 CrossRef CAS.
- H. Namiki, M. Kobayashi, K. Nagata, Y. Saito, N. Tachibana and Y. Ota, Mater. Today Sustainability, 2022, 18, 100116 CrossRef.
- B. A. D. Williamson, J. Buckeridge, J. Brown, S. Ansbro, R. G. Palgrave and D. O. Scanlon, Chem. Mater., 2017, 29, 2402–2413 CrossRef CAS.
- X. Shen, Y. Xia, G. Wang, F. Zhou, V. Ozolins, X. Lu, G. Wang and X. Zhou, J. Mater. Chem. A, 2018, 6, 24877–24884 RSC.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed.
- A. Moll, A. Hamidou, J. C. Crivello, J. M. Joubert, E. Alleno and C. Barreteau, J. Alloys Compd., 2023, 942, 169123 CrossRef CAS.
- Y. Nagamoto, K. Hino, H. Yoshitake and T. Koyanagi, Seventeenth International Conference on Thermoelectrics. Proceedings ICT98, 1998, pp. 354–357, DOI:10.1109/ICT.1998.740393.
- V. Ponnambalam and D. T. Morelli, J. Electron. Mater., 2014, 43, 1875–1880 CrossRef CAS.
- M. Miyata and M. Koyano, Mater. Res. Express, 2022, 9, 055901 CrossRef.
- M. De Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. K. Ande, S. Van Der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Sci. Data, 2015, 2, 1–13 Search PubMed.
- J. A. Dolyniuk, J. Wang, M. A. T. Marple, S. Sen, Y. Cheng, A. J. Ramirez-Cuesta and K. Kovnir, Chem. Mater., 2018, 30, 3419–3428 CrossRef CAS.
- G. A. Slack, in CRC Handbook of Thermoelectrics, ed. D. M. Rowe, CRC Press, Boca Raton, FL, 1995, p. 407 Search PubMed.
- B. C. Sales, D. Mandrus and R. K. Williams, Science, 1996, 272, 1325–1328 CrossRef CAS PubMed.
- M. Christensen, S. Johnsen and B. B. Iversen, Dalton Trans., 2010, 39, 978–992 RSC.
- X. Lu, D. T. Morelli, Y. Xia, F. Zhou, V. Ozolins, H. Chi, X. Zhou and C. Uher, Adv. Energy Mater., 2013, 3, 342–348 CrossRef CAS.
- S. O. Long, A. V. Powell, S. Hull, F. Orlandi, C. C. Tang, A. R. Supka, M. Fornari and P. Vaqueiro, Adv. Funct. Mater., 2020, 30, 1909409 CrossRef CAS.
- C. Biagioni, L. L. George, N. J. Cook, E. Makovicky, Y. Moëlo, M. Pasero, J. Sejkora, C. J. Stanley, M. D. Welch and F. Bosi, Am. Mineral., 2020, 105, 109–122 CrossRef.
- J. Heo, G. Laurita, S. Muir, M. A. Subramanian and D. A. Keszler, Chem. Mater., 2014, 26, 2047–2051 CrossRef CAS.
- J. Wang, M. Gu, Y. Bao, X. Li and L. Chen, J. Electron. Mater., 2016, 45, 2274–2277 CrossRef CAS.
- H. Hu, H. L. Zhuang, Y. Jiang, J. Shi, J. W. Li, B. Cai, Z. Han, J. Pei, B. Su, Z. H. Ge, B. P. Zhang and J. F. Li, Adv. Mater., 2021, 33, 2103633 CrossRef CAS PubMed.
- P. Vaqueiro, G. Guélou, A. Kaltzoglou, R. I. Smith, T. Barbier, E. Guilmeau and A. V. Powell, Chem. Mater., 2017, 29, 4080–4090 CrossRef CAS.
- H. G. von Schnering and K. G. Hausler, Rev. Chim. Miner., 1976, 13, 71–81 CAS.
- H. Namiki and Y. Ota, Jpn. J. Appl. Phys., 2020, 59, 075508 CrossRef CAS.
- J. Wang, J. A. Dolyniuk and K. Kovnir, Acc. Chem. Res., 2018, 51, 31–39 CrossRef CAS PubMed.
- D. Huo, T. Sasakawa, Y. Muro and T. Takabatake, Appl. Phys. Lett., 2003, 82, 2640–2642 CrossRef CAS.
- J. Dünner and A. Mewis, Z. Anorg. Allg. Chem., 1995, 621, 191–196 CrossRef.
- J. Fulmer, O. I. Lebedev, V. V. Roddatis, D. C. Kaseman, S. Sen, J. A. Dolyniuk, K. Lee, A. V. Olenev and K. Kovnir, J. Am. Chem. Soc., 2013, 135, 12313–12323 CrossRef CAS PubMed.
- J. A. Dolyniuk, J. Wang, K. Lee and K. Kovnir, Chem. Mater., 2015, 27, 4476–4484 CrossRef CAS.
- J. Wang, J. A. Dolyniuk, E. H. Krenkel, J. L. Niedziela, M. A. Tanatar, E. I. Timmons, T. Lanigan-Atkins, H. Zhou, Y. Cheng, A. J. Ramirez-Cuesta, D. L. Schlagel, U. S. Kaluarachchi, L. L. Wang, S. L. Bud’ko, P. C. Canfield, R. Prozorov, O. Delaire and K. Kovnir, Chem. Mater., 2020, 32, 7932–7940 CrossRef CAS.
- G. Rogl, A. Grytsiv, P. Rogl, N. Peranio, E. Bauer, M. Zehetbauer and O. Eibl, Acta Mater., 2014, 63, 30–43 CrossRef CAS.
- R. S. Feigelson, Preparation and Evaluation of Phosphide Skutterudites, Geballe Laboratory for Advanced Materials, 2001 Search PubMed.
- D. J. Singh and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11235–11238 CrossRef CAS PubMed.
- M. Llunell, P. Alemany, S. Alvarez, V. P. Zhukov and A. Vernes, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 10605–10609 CrossRef CAS PubMed.
- A. Watcharapasorn, R. C. DeMattei, R. S. Feigelson, T. Caillat, A. Borshchevsky, G. J. Snyder and J. P. Fleurial, J. Appl. Phys., 1999, 86, 6213–6217 CrossRef CAS.
- G. Murtaza, N. Yousaf, M. Yaseen, A. Laref and S. Azam, Mater. Res. Express, 2018, 5, 016304 CrossRef.
- F. H. Sun, S. F. Ma, W. Y. Zhao, C. C. Li, X. H. Sang, P. Wei and Q. J. Zhang, Rep. Prog. Phys., 2021, 84, 096501 CrossRef CAS PubMed.
- S. Hébert, R. Daou, A. Maignan, S. Das, A. Banerjee, Y. Klein, C. Bourgès, N. Tsujii and T. Mori, Sci. Technol. Adv. Mater., 2021, 22, 583–596 CrossRef PubMed.
- S. S. Stoyko, P. E. R. Blanchard, K. K. Ramachandran and A. Mar, J. Solid State Chem., 2019, 269, 100–106 CrossRef CAS.
- A. Balvanz, S. Baranets, M. O. Ogunbunmi and S. Bobev, Inorg. Chem., 2021, 60, 14426–14435 CrossRef CAS PubMed.
- J. Rauscher, C. Condron, T. Beault, S. Kauzlarich, N. Jensen, P. Klavins, S. MaQuilon, Z. Fisk and M. Olmstead, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, i69–i73 CrossRef CAS PubMed.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- B. W. Montag, M. A. Reichenberger, K. R. Arpin, M. Sunder, K. A. Nelson, P. B. Ugorowski and D. S. McGregor, J. Cryst. Growth, 2015, 412, 103–108 CrossRef CAS.
- Z. Liu, J. Mao, J. Sui and Z. Ren, Energy Environ. Sci., 2018, 11, 23 RSC.
- Y. Zheng, C. Liu, L. Miao, C. Li, R. Huang, J. Gao, X. Wang, J. Chen, Y. Zhou and E. Nishibori, Nano Energy, 2019, 59, 311–320 CrossRef CAS.
- P. Ying, L. Wilkens, H. Reith, N. P. Rodriguez, X. Hong, Q. Lu, C. Hess, K. Nielsch and R. He, Energy Environ. Sci., 2022, 15, 2557–2566 RSC.
- A. Yamakage, Y. Yamakawa, Y. Tanaka and Y. Okamoto, J. Phys. Soc. Jpn., 2016, 85, 013708 CrossRef.
- Y. Okamoto, T. Inohara, A. Yamakage, Y. Yamakawa and K. Takenaka, J. Phys. Soc. Jpn., 2016, 85, 123701 CrossRef.
- N. Xu, Y. T. Qian, Q. S. Wu, G. Autes, C. E. Matt, B. Q. Lv, M. Y. Yao, V. N. Strocov, E. Pomjakushina, K. Conder, N. C. Plumb, M. Radovic, O. V. Yazyev, T. Qian, H. Ding, J. Mesot and M. Shi, Phys. Rev. B, 2018, 97, 161111R CrossRef.
- A. Mewis, Z. Naturforsch., B: J. Chem. Sci., 1979, 34, 14–17 CrossRef.
- U.-G. Jong, C. Ryu, C.-J. Kang and C.-J. Yu, Appl. Phys. Lett., 2023, 122, 133905 CrossRef CAS.
- A. Mewis, Z. Naturforsch., B: J. Chem. Sci., 1978, 33, 983–986 CrossRef.
- A. Mewis, Z. Naturforsch., B: J. Chem. Sci., 1979, 34, 1373–1376 CrossRef.
- J. Willis, I. Bravić, R. R. Schnepf, K. N. Heinselman, B. Monserrat, T. Unold, A. Zakutayev, D. O. Scanlon and A. Crovetto, Chem. Sci., 2022, 13, 5872–5883 RSC.
- W. Żdanowicz and A. Wojakowski, Phys. Status Solidi B, 1965, 8, 569–575 CrossRef.
- H. Wang, X. Luo, W. Chen, N. Wang, B. Lei, F. Meng, C. Shang, L. Ma, T. Wu, X. Dai, Z. Wang and X. Chen, Sci. Bull., 2018, 63, 411–418 CrossRef CAS PubMed.
- J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313 CrossRef.
- W. Ren, H. Zhu, J. Mao, L. You, S. Song, T. Tong, J. Bao, J. Luo, Z. Wang and Z. Ren, Adv. Electron. Mater., 2019, 5, 1900166 CrossRef.
- H. B. Kang, B. Poudel, W. Li, H. Lee, U. Saparamadu, A. Nozariasbmarz, M. G. Kang, A. Gupta, J. J. Heremans and S. Priya, Mater. Today, 2020, 36, 63–72 CrossRef CAS.
- U. G. Jong, C. H. Ri, C. J. Pak, C. H. Kim, S. Cottenier and C. J. Yu, New J. Chem., 2021, 45, 21569–21576 RSC.
- K. Pal, J. G. He and C. Wolverton, Chem. Mater., 2018, 30, 7760–7768 CrossRef CAS.
- M. Miyata, J. Appl. Phys., 2021, 130, 035104 CrossRef CAS.
- H. Wang, Y. Pei, A. D. LaLonde and G. J. Snyder, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 9705–9709 CrossRef CAS PubMed.
- H. Wang, R. Gurunathan, C. Fu, R. Cui, T. Zhu and G. J. Snyder, Mater. Adv., 2022, 3, 734–755 RSC.
- P. Graziosi, C. Kumarasinghe and N. Neophytou, ACS Appl. Energy Mater., 2020, 3, 5913–5926 CrossRef CAS.
- D. Yang, X. Su, J. Li, H. Bai, S. Wang, Z. Li, H. Tang, K. Tang, T. Luo, Y. Yan, J. Wu, J. Yang, Q. Zhang, C. Uher, M. G. Kanatzidis and X. Tang, Adv. Mater., 2020, 32, 2003730 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |