DOI:
10.1039/D3TA00415E
(Paper)
J. Mater. Chem. A, 2023,
11, 7617-7628
Synthesis and characterization of sodium hafnium oxide (Na2HfO3) and its high-temperature CO2 sorption properties†
Received
23rd January 2023
, Accepted 22nd February 2023
First published on 23rd February 2023
1 Introduction
In order to combat the ever-increasing atmospheric CO2 concentration, scientists and engineers are continuously developing methods to decrease the emission of CO2 due to human activities. Such methods include the transition to non-fossil fuel-based sustainable energy generation, and the application of carbon capture, utilization and storage (CCUS). Many different types of solid materials with diverse chemistries have been investigated as sorbents for greenhouse gas separation or sorption. The use of solid sorbents for CO2 capture has been investigated for point sources of CO2 emission such as coal-fired power plants, steel works and other fossil fuel combustion sites. A range of solid-based physisorbents and chemisorbents, such as polymeric membranes,1 metal–organic frameworks (MOFs),2 zeolites,3,4 porous carbon,5 and oxide-based sorbents6–9 all have shown promising CO2 uptake properties.10 Polymeric membranes offer high gas permeability, high energy efficiency, low application (equipment) cost, and simple operation and are scalable. Arguably, polymeric membranes have relatively low gas selectivity and low thermal stability.11 MOFs are porous solid physisorbents constructed from organic ligands coordinated to metal ions. MOFs offer extensive structural diversity and variable surface chemistries. Although MOFs have shown high CO2 selectivity and capacity at high pressure, they typically have low thermal and moisture stability as compared to many other sorbents.2,12,13 Porous carbon and zeolites, also a type of physisorbent, offer low production costs and a diverse range of structures.3,5 Zeolites can have high CO2 uptake capacity and selectivity, but their strong hydrophilic nature is a major drawback in real-life applications.14,15 Inorganic oxides are solid chemisorbents that work well at capturing CO2 at moderate (around 200 °C or above) to high temperatures (over 600 °C).9 They have been regarded as potential low-cost and “easy to fabricate” sorbents for applications such as energy storage, pre-combustion carbon capture or CO2 capture in high-temperature industrial processes such as steel production.16,17 Furthermore, the high operating temperature (i.e. CO2 uptake temperature or carbonation) of some inorganic oxides would eliminate the need to cool the flue gas. The regeneration (calcination) of these high-temperature CO2 sorbents typically takes place at over 800 °C. In such cases, the available energy from a typical fossil fuel combustion or steel production process can be utilized for sorbent regeneration. On the other hand, the long-term cycling stability of these oxide sorbents can often be poor. The CO2 uptake capacity of inorganic oxide sorbents would typically decrease upon cycling due to sintering. Sintering reduces the accessible surface area available for the reaction between CO2 and the sorbent, which decreases the CO2 uptake capacity.18 In order to improve the performance of inorganic oxide sorbents, researchers have focused their research on (1) preventing sintering by adding a thermal stabilizer to the sorbents19–23 or (2) developing sorbents with high cycling stability.24–26
Zirconium-based inorganic oxides such as Na2ZrO3, Li2ZrO3, and K2ZrO3 have attracted attention in recent decades as potential CO2 sorbents. These mixed-metal oxides stand out as they are easy to synthesize, and have good CO2 uptake capacity and excellent cycling stability.27–29 Specifically, mixed-metal oxides have demonstrated better cycling stability than typical high-temperature sorbents such as calcium oxide (CaO). The high stability and high CO2 uptake of mixed-metal oxides are partly due to the mobility of the cations (i.e. Na+, Li+ and K+) within the material.25,30–32 According to previous studies, cation mobility occurs on/under the surface of the sorbent. Upon reaction between the mixed-metal oxides and CO2, a carbonate layer would form first on the surface of the sorbent. Cation mobility within the materials allows carbonate formation to continue between the unreacted oxides below the carbonate layer.30,33 The theoretical CO2 uptake capacity of Na2ZrO3, Li2ZrO3, and K2ZrO3 can be calculated based on the reaction M2ZrO3 + CO2 ⇌ M2CO3 + ZrO2 (M = Na, Li, and K). Such calculations show that the theoretical CO2 uptake capacities of Na2ZrO3, Li2ZrO3, and K2ZrO3 are 23.76, 28.75, and 20.24 wt%, respectively. However, DFT calculations by Duan et al. demonstrated that the total energy change (ΔEDFT) of the reaction between M2ZrO3 and CO2 (forward direction) was most thermodynamically favourable for K2ZrO3 (−223.158 eV, vs. −140.862 eV and −146.648 eV for Na2ZrO3 and Li2ZrO3).34,35 The DFT results were supported by experimental values; experimentally recorded heats of carbonation/calcination (ΔH) also confirmed that ΔH for the reaction between CO2 and K2ZrO3 was larger than between CO2 and Na2ZrO3 or Li2ZrO3. The difference in ΔH also meant that the calcination/regeneration (backward reaction) of K2ZrO3 would require more energy than Na2ZrO3 and Li2ZrO3. Therefore, K2ZrO3 is theoretically a less attractive CO2 sorbent than Na2ZrO3 and Li2ZrO3, as Na2ZrO3 and Li2ZrO3 both offer higher theoretical CO2 uptake with lower energy demand for regeneration than K2ZrO3. The promising CO2 uptake properties of Na2ZrO3 have been reported for three phases: monoclinic, hexagonal, and cubic.30,36,37
Hafnium (Hf) analogues of Zr compounds usually share similar chemistries to the Zr counterparts. Both hafnium oxide (HfO2) and zirconium oxide (ZrO2) have high thermostability, high enthalpy of formation and high dielectric constant.38–40 In this study, the solid-state synthesis of a sodium hafnium oxide (or sodium hafnate; Na2HfO3) CO2 sorbent is presented. Structural analysis of the synthesized Na2HfO3 was carried out using powder X-ray diffraction (PXRD) and transmission electron microscopy (TEM), in particular 3-dimensional electron diffraction (3D ED). We explore the high-temperature CO2 sorption characteristics of the synthesized Na2HfO3. The effect of various synthesis conditions, such as heating rate, reaction temperature, and synthesis time on the CO2 uptake properties, was investigated. In addition, the CO2 sorption kinetics of Na2HfO3 is investigated in order to understand the underlying CO2 uptake mechanism using five different kinetic models. Furthermore, 3D printing of the starting materials is employed as a possible method to structure the Na2HfO3 CO2 sorbent.
2 Results and discussion
2.1 Characterisation of Na2HfO3 obtained by solid-state synthesis
In the synthesis of Na2HfO3, the Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 molar ratio was varied from 0.5–1.5
HfO2 molar ratio was varied from 0.5–1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Here, the samples are referred to as NHO-X, where X is the molar ratio of Na2CO3 with respect to HfO2. Regardless of the Na2CO3
1. Here, the samples are referred to as NHO-X, where X is the molar ratio of Na2CO3 with respect to HfO2. Regardless of the Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratio, the weight loss recorded during the synthesis of NHO-X corresponded reasonably well to the expected values (Table S1, Fig. S4†), and the slight differences noted were related to minor deviations in weighing and mixing. The differences led to a small fluctuation in the real stoichiometry of the reaction mixture. Note that for NHO-1, NHO-1.25 and NHO-1.5, the mass of the reaction mixture showed a consistent decrease with time during synthesis at 900 °C. This decrease in weight was related to the melting and evaporation of the stoichiometric excess Na2CO3 that was present in the reaction mixture. The PXRD patterns of NHO-Xs synthesized at 900 °C for 3 h under N2 are shown in Fig. 1.
HfO2 ratio, the weight loss recorded during the synthesis of NHO-X corresponded reasonably well to the expected values (Table S1, Fig. S4†), and the slight differences noted were related to minor deviations in weighing and mixing. The differences led to a small fluctuation in the real stoichiometry of the reaction mixture. Note that for NHO-1, NHO-1.25 and NHO-1.5, the mass of the reaction mixture showed a consistent decrease with time during synthesis at 900 °C. This decrease in weight was related to the melting and evaporation of the stoichiometric excess Na2CO3 that was present in the reaction mixture. The PXRD patterns of NHO-Xs synthesized at 900 °C for 3 h under N2 are shown in Fig. 1.
 |
| | Fig. 1 PXRD patterns of the synthesized NHO-Xs (a) NHO-0.5 (b) NHO-0.75 (c) NHO-1 (d) NHO-1.25 (e) NHO-1.5, peaks related to Na2HfO3 and HfO2 marked with ● and ○, respectively. | |
Two distinct types of PXRD patterns could be observed as shown in the figure. (1) The PXRD patterns of NHO-0.5 and NHO-0.75 (Fig. 1a and b), which showed more peaks, and (2) the PXRD patterns of NHO-1, NHO-1.25 and NHO-1.5 (Fig. 1c–e). In all cases, the presence of Na2HfO3 was identified by new peaks which appeared at 2θ ∼16.2, 17.6, 18.5, 32.5, 39, and 42.5°. The new peaks were comparable to the PXRD pattern of chemically similar Na2ZrO3 in terms of peak positions. The intensity of the observed Na2HfO3 (marked with ○ symbols in Fig. 1.) and HfO2 peaks (marked with ● symbols in Fig. 1) in NHO-Xs was reflected by the molar ratios of the reaction mixture. With NHO-0.5 and NHO-0.75, HfO2 was in excess in the reaction mixture, which was reflected by the presence of the PXRD peaks attributed to HfO2 (Fig. S5†). The PXRD patterns of NHO-1, NHO-1.25 and NHO-1.5 show peaks related to Na2HfO3 with high intensities. No significant presence of HfO2 was detected in any of the samples. The crystallinity of NHO-1.5 appeared lower than that of NHO-1 and NHO-1.25 according to their PXRD patterns. The SEM images of NHO-Xs are shown in Fig. 2. Similar to the observations made from the PXRD patterns, the SEM images of NHO-0.5 and NHO-0.75 (Fig. 2a and b) showed similarities – two different types of particle morphologies were observed. The first type (type I) of particles was small and globular-shaped (Fig. 2a and b, insets) with similar morphology to HfO2 (Fig. 2g). The second type of particles (type II) was polyhedral-like particles which had aggregated (Fig. 2a and b). These particles had dimensions up to around 1–2 μm with some small nanoparticles that had adhered on the surface. The morphology of NHO-1 and NHO-1.25 (Fig. 2c and d) was similar to the type II morphology also found on NHO-0.5 and NHO-0.75, but no presence of type I (HfO2) was noted. The morphology of NHO-1.5 (Fig. 2e) appeared distinctively different from other NHO-Xs with no presence of globular or polyhedral particles. The particles of NHO-1.5 were highly aggregated and covered the surface, similar in appearance to pure Na2CO3 (Fig. 2f). This observation was also reflected in the BET-specific surface area of NHO-1.5 (2.83 m2 g−1, obtained by N2 sorption), which was lower than that of other NHO-Xs (3.83, 3.77, 3.51 and 3.66, respectively, for NHO-0.5, NHO-0.75, NHO-1, and NHO-1.25, Table S2.†). As shown earlier in Fig. 1, the PXRD patterns of NHO-Xs had peaks with similar peak positions to Na2ZrO3, which suggested that these two compounds have similar structures. Na2ZrO3 has been reported as separate phases (monoclinic, hexagonal and cubic), and these phases have shown differences in their CO2 uptake performance. It is, therefore, important to investigate if similar findings could be expected for Na2HfO3. 3D electron diffraction (3D ED) data on NHO-1.25 are presented in Fig. 3. The 3D reconstructed data comprise both distinct reflections as well as lines of diffuse scattering. Such scattering features are typical to disordered materials with stacking faults. The distinct reflections were indexed with the unit cell parameters a = b = 3.37 Å, c = 17.16 Å, α = β = 90°, and γ = 120° with systematic absence of reflections consistent with the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.
 |
| | Fig. 2 SEM images of the synthesized NHO-Xs and the starting materials (a) NHO-0.5 (b) NHO-0.75 (c) NHO-1 (d) NHO-1.25 (e) NOH-1.5 (f) Na2CO3 (g) HfO2. The insets in (a) and (b) show the polyhedral-like particles and globular-shaped particles that have not aggregated, the scalebars for (a) and (b) apply to the respective insets. | |
 |
| | Fig. 3 3D ED data viewed slightly off-axis from c*, showing well-resolved reflections (black) that can be indexed to a rhombohedral cell (a = 3.4 Å, c = 16.6 Å), as well as streaks (grey) along the c*-axis, highlighted by the inset showing a magnified part (*) of the figure. | |
The overall structure of Na2HfO3 appeared to be comparable to a number of known disordered mixed metal oxides with the general formula M2+M4+O3, such as Li2MnO3, Li2TiO3, and others.41 According to the 3D ED data, all Na+ and Hf4+ are octahedrally coordinated to O2−. Na2HfO3 is constructed of two different types of metal cation layers sandwiched by oxide (O2−) layers (Fig. 4a).42 One type of metal layer contains only Na+, and the other contains a mixture of both Na+ and Hf4+. It was presumed that the mixed metal layer contains 2/3 of Hf4+ and 1/3 of Na+ at the metal sites (Fig. 4b) as is the case with other mixed metal oxides such as Li2MnO3.43 One unit cell comprises three such mixed metal layers stacked along the c-axis. The stacking of these mixed metal layers can occur differently, with four different stacking sequences presented in Fig. 4c–f. These different stacking sequences, in pure form, would result in Na2HfO3 with either the space groups P3112, P3212 (trigonal), C2/m or C2/c (monoclinic). The simulated PXRD patterns of Na2HfO3 with these four ideal structures (Fig. S6†), which assume consistent stacking in each case, appeared to be visually identical to one another. The similarities in the simulated PXRD patterns make it difficult to distinguish between the different stacking modes within one sample of Na2HfO3. For the Na2HfO3 samples studied here, it appears that there is not just one form of stacking or symmetry, but instead more than one type of stacking sequence that exists within each crystal resulting in a disordered structure with stacking faults, which is what causes the diffuse scattering along the c*-axis (Fig. 3). Similar disordered structures are known for chemically similar M2+M4+O3 compounds such as Li2TiO3, Li2MnO3 and Li2SnO3.41–44 The stacking of the layers in Na2HfO3 would be very challenging to control via solid-state synthesis. Nonetheless, we found that very consistent PXRD patterns were obtained when the same synthesis procedures were used. In contrast to the literature on Na2ZrO3 sorbents, the NHO-Xs synthesized here did not adopt one particular type of ordered crystal structure. This disorder could potentially be beneficial and may create high-energy CO2 sorption sites. In the rest of this study, the discussion will focus more on the CO2 uptake properties of NHO-Xs obtained by different synthesized procedures and Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratios in the reaction mixture.
HfO2 ratios in the reaction mixture.
 |
| | Fig. 4 Structures and various stacking sequences of Na2HfO3 (a) the average structure (b) a single ordered Na+Hf4+ layer (c–f) various stacking sequences. Arrows indicate the translation between neighbouring layers in the stacking sequence. | |
2.2 CO2 uptake on NHO-Xs
2.2.1 The effect of different carbonation temperatures.
In order to investigate the reaction between CO2 and Na2HfO3, we performed the majority of the CO2 uptake experiments using pure CO2 gas (with N2 for regeneration). The CO2 uptake under mixed gas conditions (20% vol CO2 in N2) was also investigated and presented in the ESI.† The CO2 uptake curves of NHO-Xs between 600 and 800 °C with a 50 °C interval are individually presented in Fig. S7† and Table 1. The CO2 uptake rate varied depending on the carbonation temperatures; with 750 and 800 °C generally showing the fastest CO2 uptake rates for all samples. The CO2 uptake capacity of NHO-Xs remained comparable at all tested carbonation temperatures. NHO-1 and NHO-1.25 showed the highest CO2 uptake capacity of all NHO-Xs at all temperatures. At 750 °C, the CO2 uptake capacity of NHO-Xs was in the order NHO-1 > NHO-1.25 > NHO-0.75 > NHO-0.5 > NHO-1.5 and varied from 14.54 wt% for NHO-1 down to 8.54 wt% for NHO-1.5 (the CO2 uptake wt% values are quoted with respect to the weight of the sorbent directly after synthesis). According to the TGA curves in Fig. S4† and the PXRD analysis, all of the HfO2 reacted with Na2CO3 to form Na2HfO3 during synthesis. The observed CO2 uptake capacities of the NHO-Xs could be compared with the theoretical maximum uptake of the NHO-X. The comparison in Table 1 shows that in all cases except for NHO-1.5, NHO-Xs reached close to 100% of the maximum theoretical CO2 uptake capacity. In contrast, most of the other mixed metal oxide CO2 sorbents e.g. Na2ZrO3, Li4SiO4 and Na4SiO4 at moderate/high temperatures are unable to reach capacities close to their theoretical maximum CO2 uptake.
Table 1 The CO2 uptake capacity of the mixed metal oxides and the synthesized NHO-Xs at the different carbonation temperatures. For NHO-0.5 and 0.75, the “over 100%” theoretical uptake observed is likely due to the variation in the true Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratio in the synthesis mixture, also see Fig. S4
HfO2 ratio in the synthesis mixture, also see Fig. S4
| Sorbent |
Carbonation temperature [°C] |
Recorded CO2 uptake [wt%] |
Recorded uptake vs. theoretical uptake [%] |
Ref. |
| NHO-0.5 |
600 |
8.84 |
97.14 |
This work |
| 650 |
9.65 |
106.04 |
| 700 |
9.79 |
107.58 |
| 750 |
9.86 |
108.35 |
| 800 |
9.84 |
108.13 |
| NHO-0.75 |
600 |
12.9 |
100.78 |
| 650 |
13.16 |
102.81 |
| 700 |
13.42 |
104.84 |
| 750 |
13.52 |
105.63 |
| 800 |
13.52 |
105.63 |
| NHO-1 |
600 |
14.26 |
88.57 |
| 650 |
14.65 |
90.99 |
| 700 |
14.1 |
87.58 |
| 750 |
14.54 |
90.31 |
| 800 |
14.19 |
88.14 |
| NHO-1.25 |
600 |
13.8 |
93.88 |
| 650 |
13.99 |
95.17 |
| 700 |
14.31 |
97.35 |
| 750 |
14.41 |
98.03 |
| 800 |
14.28 |
97.14 |
| NHO-1.5 |
600 |
7.12 |
52.74 |
| 650 |
8.17 |
60.52 |
| 700 |
8.66 |
64.15 |
| 750 |
8.54 |
63.26 |
| 800 |
8.6 |
63.70 |
| Na2ZrO3 |
400 |
17.6 |
73.95 |
31
|
| Na2ZrO3 |
800 |
22.77 |
95.67 |
45
|
| Na2ZrO3 |
575 |
17 |
71.43 |
45
|
| Na4SiO4 |
844 |
19.2 |
80.33 |
46
|
| Li4SiO4 |
700 |
32.5 |
88.56 |
47
|
| Li4SiO4 |
640 |
8 |
21.80 |
48
|
| Li6CoO4 |
500 |
22.1 |
27.63 |
33
|
| Li6CoO4 |
400 |
42.4 |
53 |
33
|
| SrO |
1100 |
12.6 |
29.65 |
49
|
2.2.2 The effect of molar ratios between Na2CO3 and HfO2.
The TGA curves of NHO-X over five CO2 uptake (750 °C) and regeneration cycles are shown in Fig. 5a. The CO2 uptake capacity of NHO-1 and NHO-1.25 were very comparable in the 1st cycle, both close to 15 wt% (the slight differences between these CO2 uptake capacities and those listed in Table 1 were related to variations between different synthesis batches, as discussed earlier). The high CO2 uptake capacity of NHO-1 and NHO-1.25 was believed to be related to the high purity of the Na2HfO3 sorbent formed. According to the PXRD and SEM analysis discussed earlier, these two samples showed the homogeneous morphology of all NHO-X with no observed HfO2 peaks in the PXRD pattern. The CO2 uptake capacity of these two sorbents in the 1st cycle effectively showed that these two sorbents were equivalent in terms of CO2 uptake capacity. The CO2 uptake rate of NHO-Xs displayed in Fig. 5b and c shows that the CO2 uptake rates by NHO-0.75, NHO-1 and NHO-1.25 were also very comparable. These three NHO-Xs also reached over 80% of their maximum observed uptake in around 250 s. The CO2 uptake capacity of NHO-0.5, 0.75, 1, 1.25, and 1.5 after 250 s exposure to CO2 were 4.98, 10.05, 10.70, 13.80, and 4.04 wt%, respectively. NHO-0.5 and NHO-1.5 showed noticeably slower CO2 uptake kinetics than the other NHO-Xs. Detailed analysis of the CO2 uptake kinetics is presented later in this study. XPS spectra of all NHO-Xs after five cycles are shown in Fig. S8.† The Na 1s XPS spectra of all NHO-Xs had only one peak at ∼1071.3 eV, and this peak was related to Na2CO3. In contrast, four peaks were observed in the Hf 4f spectra at 18.34, 17.74, 16.64, and 16.04 eV. These peaks were assigned to Hf 4f7/2 (at 16.04 and 16.64 eV) and Hf 4f5/2 (at 17.74 and 18.34 eV). The different Hf species were related to the two different forms of Hf present in NHO-X – HfO2 and Na2HfO3. The O1s spectra showed species related to metal oxide and metal carbonate (CO3). The peaks at ∼531.2 and 529.7 eV were related to HfO2 and Na2CO3, respectively. In the C1s spectra, two peaks were observed at ∼289.4 and 284.85 eV which were assigned to CO3 and C–C. The peak related to CO3 in the C1s XPS spectra showed a higher intensity for NHO-1 and NHO-1.25 than other NHO-Xs, which fits with the observation that these two samples had the highest CO2 uptake capacity.
 |
| | Fig. 5 The CO2 uptake capacity of the synthesized NHO-Xs. (a) Five carbonation/calcination cycles at 750/900 °C, (b) 1st cycle of the five carbonation/calcination cycles, and (c) the normalized curves of the 1st cycle. | |
2.2.3 The effect of synthesis time/heating rate.
The effect of different synthesis conditions was investigated. Fig. 6 and Table S3† show the effect of synthesis holding time at 900 °C. There was a slight difference in the optimal synthesis holding time for different NHO-Xs. Fig. 6f shows a comparison of the CO2 uptake capacity of NHO-Xs, each synthesized with its respective optimal synthesis holding time. The CO2 uptake capacity was in the order NHO-1.25 (3 h) > NHO-1 (2 h) > NHO-0.75 (3 h) > NHO-0.5 (1 h) > NHO-1.5 (2 h) with 15.18, 15.1, 13.03, 11.91, and 9.95 wt%, respectively. Although the CO2 uptake capacity of NHO-Xs varied depending on the synthesis holding time, the PXRD pattern showed that the synthesis of Na2HfO3 was completed after 1 h. It was interesting to note that with a synthesis holding time of 4 h, both NHO-1 (4 h) and NHO-1.25 (4 h) performed worse than those obtained with a synthesis time of less than 4 h. The reason behind the clear difference in performance was unclear to us and was somewhat unexpected. PXRD and SEM images of the 4 h synthesis holding time NHO-Xs did not appear noticeably different from the other samples (i.e. 1–3 h). Note that we performed these experiments multiple times as well as on different instruments in order to confirm the reproducibility of the presented data. We found that 4 h synthesis holding time consistently produced NHO-1 and NHO-1.25 with poor CO2 uptake performance. Overall, NHO-1 (2 h) and NHO-1.25 (3 h) showed the highest CO2 uptake capacity at 650 and 750 °C of all NHO-Xs obtained using different synthesis conditions. These two NHO-Xs will, therefore, be the focus of the rest of this study. Fig S9† shows the effect of the synthesis heating rate of NHO-1 and NHO-1.25 on their respective CO2 uptake performance. For NHO-1, very little difference in the CO2 uptake performance (capacity and rate) was observed between the different synthesis heating rates. The difference was more noticeable on NHO-1.25 – a heating rate of 10 °C min−1 gave the highest and fastest CO2 uptake.
 |
| | Fig. 6 The CO2 uptake capacity of the synthesized NHO-Xs with different synthesis times. (a) NHO-0.5, (b) NHO-0.75, (c) NHO-1, (d) NHO-1.25, (e) NHO-1.5, (f) comparison of all NHO-Xs with synthesis time that yielded the highest CO2 uptake. | |
2.2.4 The effect of carbonation time and its product.
It was assumed that the CO2 uptake/regeneration cycles of NHO-Xs proceed by the equilibrium reaction described using eqn (1). To confirm this, the PXRD patterns of NHO-1 and NHO-1.25 exposed to CO2 at 650 °C for 3, 5, 15, and 20 min were recorded (Fig. 7). Fig. 7a and e show that even after a short carbonation time of 3 min, peaks related to Na2CO3 and HfO2 (the carbonation products of NHO-Xs according to eqn (1)) appeared in the PXRD patterns of NHO-1.25 and NHO-1. Furthermore, the PXRD peaks related to Na2HfO3 around 2θ at 16.2, 32.5, and 39° reduced in intensity to a fraction of that before carbonation. After 15 min the peaks around 2θ at 16.2 and 32.5° were no longer visible; however, the CO2 uptake capacity had not reached the equilibrium value. This observation suggested that although the surface of the NHO-X particle may have fully reacted with CO2, carbonation continued as the inside of the NHO-X particles was still in the unreacted state. Previous literature on the CO2 uptake mechanism on Na2ZrO3 has suggested that the CO2 uptake can continue even after all of the Na2ZrO3 surfaces had reacted and formed Na2CO3. Such CO2 uptake mechanisms consider the mobility of Na+ within Na2ZrO3 or possibly CO2 diffusion through the Na2CO3 outer layer to the inner Na2ZrO3 core.24,26 The CO2 uptake kinetics of NHO-X suggested that their CO2 uptake mechanism is comparable to that of Na2ZrO3 as discussed later. After 20 min, the CO2 uptake capacity had reached close to equilibrium. The PXRD patterns of NHO-X after carbonation showed only Na2CO3 and HfO2, with no presence of by-products. This confirmed that carbonation proceeded according to eqn (1).
 |
| | Fig. 7 PXRD pattern of NHO-1.25 with different carbonation times for (a) 3 min, (b) 5 min, (c) 15 min, (d) 20 min and NHO-1 for (e) 3 min, (f) 5 min, (g) 15 min, (h) 20 min, peaks related to Na2HfO3, HfO2, and Na2CO3 marked with ●, ○, and + respectively. | |
2.3 Cycling stability
Cycling performance and stability of NHO-1 and NHO-1.25 were tested for 100 carbonation/calcination cycles. We tested the cycling stability of NHO-1 and NHO-1.25 at different carbonation temperatures in order to gain a deeper understanding of the performance of these two sorbents. NHO-1 was subjected to 100 carbonation/calcination cycles with carbonation at 650 °C (this was chosen as NHO-1 showed good CO2 uptake capacity and uptake rate at 650 °C, comparable to that at other CO2 uptake temperatures, see Fig. S7†). NHO-1.25 underwent the same test twice at two carbonation temperatures – 750 and at 800 °C. Both NHO-1 and NHO-1.25 remained stable after 100 cycles regardless of the carbonation temperature (see Fig. S10–12† for raw TGA curves of 100 cycles).
PXRD patterns of regenerated NHO-1 and NHO-1.25 after 100 cycles showed identical peak positions with only a slight difference in relative peak intensities (Fig. S13†). Fig. 8c shows that the CO2 uptake capacity of NHO-1 increased during the first few cycles, then stabilized with a very minor decrease up to 100 cycles. At the 100th cycle, the CO2 uptake was 4.87% (0.76 wt%) less than that of the 1st cycle. NHO-1.25 performed well at both 750 and 800 °C; after 100 cycles the CO2 uptake decreased by 2.68 and 2.63% (0.4 and 0.37 wt%), respectively, compared to the first cycle. The minor decrease in the CO2 uptake on NHO-1 and NHO-1.25 after 100 cycles can be compared with other high-temperature CO2 sorbents – Na2ZrO3 showed a 30 and 36% decrease in CO2 uptake capacity after 70 and 20 cycles with carbonation at 700 and 800 °C, respectively.24,30 Similarly, Li4SiO4 was found to have a CO2 uptake capacity loss of 40.31% after 15 cycles with carbonation at 700 °C.47 On the other hand, modified Li4SiO4 (the double shell of Li4SiO4 and Li2SiO3) showed good cycling stability, with only 3.5% loss of CO2 uptake capacity after 40 cycles with carbonation at 550 °C.50 Li2ZrO3 showed also good cycling stability of 3% after 30 cycles at 500 °C. Modified CaCO3 and MgCO3 also showed high stability with 1% loss in CO2 uptake capacity after 23 cycles.19
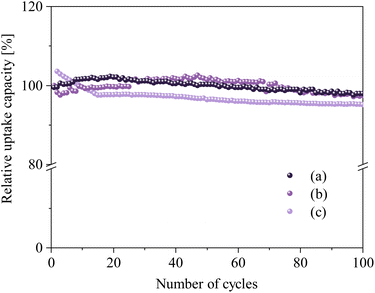 |
| | Fig. 8 Relative CO2 uptake capacity over 100 cycles under the optimized carbonation conditions (a) NHO–1.25 (3 h of synthesis time, heating rate 10 °C min−1, and carbonation at 750 °C), (b) NHO–1.25 (3 h of synthesis time, heating rate 10 °C min−1, and carbonation at 800 °C), and (c) NHO–1 (2 h of synthesis time, heating rate 5 °C min−1, and carbonation at 650 °C). The regeneration was performed at 900 °C for 20 min. | |
Overall, NHO-1 and 1.25 can be considered to be chemically and structurally stable after repeated carbonation and calcination when compared with other sorbents. We are aware that as our experiments were performed using pure CO2 and N2, they cannot be considered to be realistic for real-life applications. The results of CO2 uptake and regeneration experiments using only a mix gas containing 20 vol% CO2 in N2 can be found in the ESI.† The CO2 uptake under mixed gas conditions appeared to have a significantly reduced uptake rate. The data shown in Fig. S15† suggest that Na2HfO3 (NHO-X) would require further development for real-life applications.
2.4 Kinetic analysis of NHO-Xs
The mechanisms and kinetics of the CO2 uptake process are important aspects of CO2 sorbent development. The CO2 uptake kinetics of all NHO-Xs were analyzed using five different kinetic models; pseudo-first order (PFO), pseudo-second order (PSO), Elovich, Avrami and Avrami–Erofeev models. These were used to fit the time-resolved CO2 uptake curves obtained by TGA. The linear and non-linear fits of the chosen kinetic models are shown for the 1st and 5th carbonation cycles on NHO-1.25 (Fig. 9). The curve fittings and the correlation coefficients (R2) for other NHO-Xs (both the 1st and 5th cycles) can be found in Fig. S16 and Table S4.† The PFO model, which assumes that the rate of a reaction depends on the availability of one reactant, failed to describe the CO2 uptake kinetics on all NHO-Xs – no straight-line dependencies were not observed from the PFO linear plots (even though the correlation coefficient (R2) for the PFO model fit was high for all NHO-X samples). The PFO model has been observed to be unsuitable for describing CO2 uptake on other similar oxide sorbents.30,51,52 The reaction between CO2 and NHO-Xs could then be assumed to depend on the availability of both compounds. The PSO model, which assumes that the abundance of more than one reactant affects the rate of the reaction, showed good fits for all NHO-Xs for both the 1st and the 5th CO2 uptake cycles. Linear trends could be observed on the PSO linear plots with high R2 values (R2 > 0.99747 for all NHO-Xs). This was expected as the PSO model has been considered as a good model for describing the sorption of CO2 on chemisorbents similar to NHO-Xs. Specifically, the PSO model suggests that the reaction rate is governed by both the abundance of CO2 as well as sorption/reaction sites on NHO-Xs. The Elovich model suggests that the reaction rate would decrease as the surface coverage increases, which could already be observed to be an inaccurate description by considering the CO2 uptake data shown in Fig. 9. The rate of CO2 uptake did not change until close to saturation since no change in the gradient of the curve was observed until saturation. As a result, the linear plots for the Elovich model showed an obvious deviation from a straight line and had low R2 value for all NHO-Xs (both the 1st and 5th cycles). The Elovich model was also concluded to be not ideal for describing the reaction between CO2 and NHO-Xs.
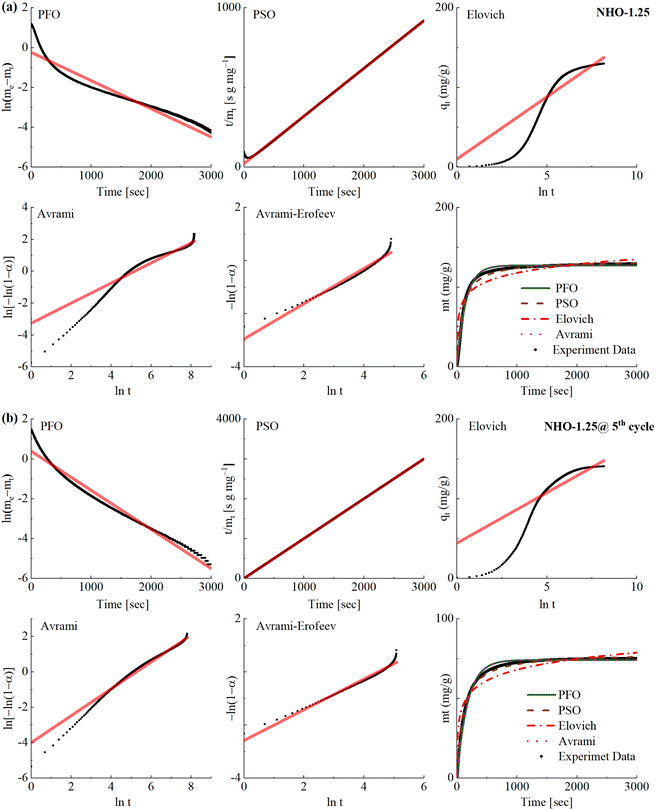 |
| | Fig. 9 The CO2 uptake kinetics at (a) 1st cycle and (b) 5th cycle on the synthesized NHO-1.25 fitted using five different kinetic models; the pseudo-first order (PFO) model, pseudo-second order (PSO) model, the Elovich model, the Avrami model and the Avrami–Erofeev. | |
The mechanism of the reaction between mixed metal oxides (e.g. Na2ZrO3 and Li2SiO4) and CO2 has been described in the literature as a two-step process: (1) CO2 chemisorption occurs on the surface of the sorbent, forming a carbonate layer (often referred to as a carbonate shell). The formation of the carbonate layer is considered as the crystal growth of the reaction product over the sorbent. (2) when the carbonate layer has formed, the mobility of Na+ ions can facilitate further reaction between the unreacted sorbent below the carbonate layer (often referred to as the core) and CO2. This chemical reaction between Na+ and CO2 would occur at high-energy nucleation sites.24,26 The Avrami model is typically used to describe the process of crystal growth, and the Avrami–Erofeev model describes the process of crystal growth and nucleation in chemical reactions.30,51,52 When fitted with the Avrami and Avrami–Erofeev models, the kinetic data showed high R2 values for most of the NHO-Xs (Table S4†). However, the linear plot of the Avrami model appears to have deviated from the straight-line dependency at a certain point on all samples except NHO-1.5 for the first carbonation cycle. In all cases except NHO-1, the shape of the linear plot of the Avrami model changed between the 1st and 5th cycles. Therefore, the Avrami model may not accurately describe the reaction between CO2 and NHO-X. The Avrami–Erofeev model better described the CO2 uptake process of NHO-Xs as a whole when compared to the Avrami model. Interestingly, the linear Avrami–Erofeev plot of NHO-1.25 showed slight differences in the shape of the line after 5 cycles – a better linear line was observed for the 5th CO2 uptake cycle than for the 1st cycle. On the other hand, the reverse trend was observed for NHO-1.5. Crystal growth of the reaction product/phase transformation during CO2 uptake on NHO-Xs was observed in this study by PXRD (Fig. 7), which supports the description of the Avrami–Erofeev model. In short, the Avrami–Erofeev model may be the most reasonable kinetic model of the ones considered here for describing the CO2 uptake on NHO-Xs.
2.5 Additive manufacturing of NHO-1
In addition to optimizing NHO-X sorbents for high-temperature CO2 uptake, it is also important to consider the possible methods which can be used to structure the NHO-X sorbents into adaptable shapes for different potential applications. The SSE-based 3D-printing technique was employed to structure the powder NHO-1 sorbent by printing a formulation that contained equimolar amounts of Na2CO3 and HfO2. Fig. 10a and b show two 3D-printed structures with two different designs. Fig. 10c and d show that these 3D-printed structures retained their respective shapes after heating in the same way as used for the synthesis of NHO-1 as discussed earlier. PXRD and SEM (Fig. S17 and 18†) confirmed the formation of NHO-1 with comparable morphology to the powder NHO-1. Furthermore, the CO2 uptake capacity of the 3D-printed NHO-1 sorbent was comparable to that of the powder NHO-1 (Fig. S19†). Interestingly, the 3D-printed NHO-1 showed slightly faster CO2 uptake when compared to the powder NHO-1. Speculatively, the faster CO2 uptake rate could possibly be related to the structure of the 3D-printed NHO-1. The presence of polymer in the 3D-printed structure could have created a distance between individual NHO-1 particles. In fact, the recorded specific surface area (BET or Langmuir) of the 3D-printed NHO-1 was higher than that of the powder NHO-1 (Table S6†). When the polymer was burnt off by heating, voids may have been created which reduce the possibility of particle sintering. Further investigation into the differences in CO2 uptake properties, in particular the CO2 uptake rate of the 3D-printed NHO-X, will be needed to fully understand the observation noted here, as 3D printing is a relatively new method for post-synthesis processing of powder materials.
 |
| | Fig. 10 3D-printed NHO-1 before synthesis (a and c) and after synthesis (b and d). | |
3 Conclusion
Na2HfO3 has been synthesized by solid-state synthesis using Na2CO3 and HfO2 and its reaction with CO2 at high temperature was investigated. The Na2CO3 : HfO2 ratio was varied between 0.5–1.5 : 1. The obtained Na2HfO3 (NHO-X) shows a similar powder X-ray diffraction pattern as the Na2ZrO3 counterpart but structural disorder was observed by 3D electron diffraction. NHO-1 and NHO-1.25 (Na2CO3 : HfO2 = 1 : 1 and 1 : 1.25) were further optimized synthetically and these NHO-X showed high CO2 uptake capacity of ∼15 wt% within the tested temperature range of 650–800 °C. The observed CO2 uptake capacities of these two NHO-X were close to the theoretical maximum CO2 uptake. NHO-X also showed high cyclic stability with minimal capacity loss even after 100 CO2 uptake/regeneration cycles. Kinetic analysis of the CO2 uptake rate suggests that the pseudo second order (PSO) and the Avrami–Erofeev model may describe the CO2 uptake mechanism well. We showed here that NHO-X can be structured into shapes by 3D printing (3DP) without compromising the CO2 uptake performance. This study demonstrated the CO2 uptake properties of Na2HfO3. Na2HfO3 could be further developed into a candidate CO2 sorbent for high temperature application after further optimization. It would be interesting to further optimize the 3DP parameters to focus on the mechanical properties of the printed NHO-X sorbents, as well as to investigate the effect of 3DP on the CO2 uptake performance in detail. With further optimization, 3DP could be an innovative way to structure sorbents for real-life application.
4 Experimental
4.1 Synthesis of sodium hafnium oxide Na2HfO3
Na2HfO3 was synthesized using hafnium oxide (HfO2) and sodium carbonate (Na2CO3) according to eqn (1) by solid-state synthesis.| | Na2CO3(s) + HfO2(s) ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Na2HfO3(s) + CO2(g) Na2HfO3(s) + CO2(g) | (1) |
In particular, HfO2, (98%) and Na2CO3 (anhydrous for analysis EMSURE®ISO) were purchased from Sigma-Aldrich and dried at 130 °C for 3 h before use. HfO2 and Na2CO3 with molar ratios of Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 = 0.5
HfO2 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.75
1, 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1.25
1, 1.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1.5
1, and 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were mechanically mixed by hand. The mixture was heated to 900 °C for 1–4 h using a Mettler Toledo TGA2 thermogravimetric analyzer (Schwerzenbach, Switzerland) with heating rates of 2, 5, or 10 °C min−1 under a constant flow rate of nitrogen (N2) at 50 cm3 min−1). Different synthesis temperatures (800, 850, 900, and 1050 °C) were tested, but only the products obtained at 900 °C could be identified as Na2HfO3 by PXRD (Fig. S1†). Therefore, 900 °C was chosen as the synthesis temperature used in this study. In addition, we attempted to synthesize Li2HfO3 and K2HfO3 using the same synthesis procedures (with Li2CO3
1 were mechanically mixed by hand. The mixture was heated to 900 °C for 1–4 h using a Mettler Toledo TGA2 thermogravimetric analyzer (Schwerzenbach, Switzerland) with heating rates of 2, 5, or 10 °C min−1 under a constant flow rate of nitrogen (N2) at 50 cm3 min−1). Different synthesis temperatures (800, 850, 900, and 1050 °C) were tested, but only the products obtained at 900 °C could be identified as Na2HfO3 by PXRD (Fig. S1†). Therefore, 900 °C was chosen as the synthesis temperature used in this study. In addition, we attempted to synthesize Li2HfO3 and K2HfO3 using the same synthesis procedures (with Li2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 and K2CO3
HfO2 and K2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 molar ratios of 1
HfO2 molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). We were unable to confirm the successful synthesis of Li2HfO3 or K2HfO3 under the synthesis conditions tested (Fig. S2 and S3†).
1). We were unable to confirm the successful synthesis of Li2HfO3 or K2HfO3 under the synthesis conditions tested (Fig. S2 and S3†).
4.2 Characterization of sodium hafnium oxide Na2HfO3
PXRD patterns of the synthesized Na2HfO3 were collected using a Bruker D8 powder diffractometer (Karlsruhe, Germany) with Cu-Kα radiation (λ = 1.54 Å), 40 kV, and 40 mA. The PXRD patterns were recorded in the 2θ range between 10 and 60° of with 0.01° step size at ambient temperature. Scanning electron microscopy (SEM) images were taken using a Zeiss Merlin field emission scanning electron microscope (Oberkochen, Germany) using an acceleration voltage of 2.5 kV and a probe current of 80 pA. All samples were coated with a gold/palladium sputter coater (Polaron SC7640, Thermo VG Scientific) for 20 s under 20 mA before imaging. TEM and 3D ED were used to examine the synthesized Na2HfO3 using a JEOL JEM-2100 TEM equipped with a Timepix detector from Amsterdam Scientific Instruments. The 3D ED data were collected using Instamatic and analysed using REDp.53,54 Specific surfaces areas using the Brunauer–Emette Teller (BET) method were calculated using the N2 sorption isotherms recorded at −196 °C using a Micromeritics ASAP 2020 surface area analyzer (Norcross, GA, USA). Prior to the analysis, the samples were degassed under dynamic vacuum (1 × 10−4 Pa) at 140 °C for 90 min. X-ray photoelectron spectroscopy (XPS) was performed using a PHI Quantera II Scanning XPS Microprobe to collect chemical information on the surface of all samples. All samples were cleaned by sputtering with argon ions for 30 s before XPS measurements. The energy-resolved spectra of C, O, Hf, and Na were collected and calibrated with the C–C peak of C1s.
4.3 CO2 uptake measurements
CO2 uptake measurements were performed using a Mettler Toledo TGA2 thermogravimetric analyzer (Schwerzenbach, Switzerland) directly after synthesis. CO2 uptake experiments were performed by exposing the as-synthesized Na2HfO3 at 600, 650, 700, 750 or 800 °C for up to 60 min under a CO2 flow of 50 cm3 min−1. Regeneration (calcination) between CO2 uptake cycles was carried out at 900 °C for 30 min under an N2 flow of 50 cm3 min−1. CO2 uptake and regeneration experiments were also performed with a CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 (20
N2 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 vol.) gas mixture for selected samples. The CO2
80 vol.) gas mixture for selected samples. The CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 gas mixture was used both in carbonation and regeneration. The CO2 uptake and regeneration steps were reduced to 20 min each for the long-term stability (100 cycles) test. The CO2 sorption kinetics were analyzed using five different kinetic models: pseudo-first order (PFO), pseudo-second order (PSO), Elovich, Avrami and Avrami–Erofeev. These kinetic models were chosen as they are based on a chemisorption process. The non-linear and linear versions of these kinetic models can be summarized with the following equations:55–57
N2 gas mixture was used both in carbonation and regeneration. The CO2 uptake and regeneration steps were reduced to 20 min each for the long-term stability (100 cycles) test. The CO2 sorption kinetics were analyzed using five different kinetic models: pseudo-first order (PFO), pseudo-second order (PSO), Elovich, Avrami and Avrami–Erofeev. These kinetic models were chosen as they are based on a chemisorption process. The non-linear and linear versions of these kinetic models can be summarized with the following equations:55–57| | | Pseudo-first order non-linear: qt=qe(1 − ek1t) | (2) |
| |  | (3) |
| |  | (4) |
| |  | (5) |
| |  | (6) |
| |  | (7) |
| | Avrami![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) non-linear: ln[ln(qe/qe − qt)] = n non-linear: ln[ln(qe/qe − qt)] = n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k + n k + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t | (8) |
| | | Linear: Vv = 1 − exp(−ktn) | (9) |
| | Avrami–Erofeev non-linear: ln[−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 − α)] = ln 1 − α)] = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k + n k + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t t | (10) |
4.4 Structuring sodium hafnium oxide Na2HfO3 by 3D printing
The semi-solid extrusion (SSE) method was selected as the technique for the scaffold manufacturing process. A modified ToolChanger and Motion system (E3D-online Ltd, Chalgrove, United Kingdom) was used as a base for the 3D-printing system. An additional syringe pump was integrated as an active tool head for SSE printing. 5 mL Luer Lock tip syringes (Terumo Corporation, Tokyo, Japan) were used as a prefilled cartridge mounted into the active tool head. SmoothFlow 0.41 mm gauge tapered tips (Nordson AB, Malmö, Sweden) were used as extrusion nozzles. The 3DP ink formulation contained approximately 30 wt% of a Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 = 1
HfO2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, 1.4 wt% of Carbopol 940 homopolymer, and 68.6 wt% of water. The 3D-printed structures were first heat treated at 650 °C in air for 1 h before the same synthesis steps as described above for Na2HfO3 were adopted. Additional information related to 3D-printing parameters and the print structure model can be found in the ESI.†
1 mixture, 1.4 wt% of Carbopol 940 homopolymer, and 68.6 wt% of water. The 3D-printed structures were first heat treated at 650 °C in air for 1 h before the same synthesis steps as described above for Na2HfO3 were adopted. Additional information related to 3D-printing parameters and the print structure model can be found in the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank the Swedish Research Council (grant no. 2020-04029), Swedish Research Council for Sustainable Development (FORMAS, Grant No. 2018-00651) and the Swedish Foundation for Strategic Research (SSF) for their financial support. Michelle Åhlén is acknowledged for her help with 3D printing.
References
- C. Castel, R. Bounaceur and E. Favre, Front. Chem. Eng., 2021, 3, 668867–668882 CrossRef.
- T. Ghanbari, F. Abnisa and W. M. A. W. Daud, Sci. Total Environ., 2020, 707, 135090–135117 CrossRef CAS PubMed.
- O. Cheung and N. Hedin, RSC Adv., 2014, 4, 14480–14494 RSC.
- O. Cheung, Z. Bacsik, Q. Liu, A. Mace and N. Hedin, Appl. Energy, 2013, 112, 1326–1336 CrossRef CAS.
- C. Song, B. Zhang, L. Hao, J. Min, N. Liu, R. Niu, J. Gong and T. Tang, Green Energy Environ., 2022, 7, 411–422 CrossRef CAS.
- M. T. Dunstan, F. Donat, A. H. Bork, C. P. Grey and C. R. Müller, Engrxiv, 2021, 121, 12681–12745 CAS.
- A. M. Kierzkowska, R. Pacciani and C. R. Müller, ChemSusChem, 2013, 6, 1130–1148 CrossRef CAS PubMed.
- W. Liu, H. An, C. Qin, J. Yin, G. Wang, B. Feng and M. Xu, Energy Fuels, 2012, 26, 2751–2767 CrossRef CAS.
- R. Chang, X. Wu, O. Cheung and W. Liu, J. Mater. Chem., 2022, 10, 1682–1705 RSC.
- R. L. Siegelman, P. J. Milner, E. J. Kim, S. C. Weston and J. R. Long, Energy Environ. Sci., 2019, 12, 2161–2173 RSC.
- M. R. Cerón, L. S. Lai, A. Amiri, M. Monte, S. Katta, J. C. Kelly, M. A. Worsley, M. D. Merrill, S. Kim and P. G. Campbell, J. Membr. Sci., 2018, 567, 191–198 CrossRef.
- H. Demir, G. O. Aksu, H. C. Gulbalkan and S. Keskin, Carbon Capture Sci. Technol., 2022, 2, 100038 CrossRef.
- M. Ding, R. W. Flaig, H. L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783–2828 RSC.
- G. Li, P. Xiao, P. Webley, J. Zhang, R. Singh and M. Marshall, Adsorption, 2008, 14, 415–422 CrossRef CAS.
- S. Kumar, R. Srivastava and J. Koh, J. CO2 Util., 2020, 41, 101251–101266 CrossRef CAS.
- A. Coppola and F. Scala, Energies, 2020, 13, 2176–2185 CrossRef CAS.
- H. C. Mantripragada and E. S. Rubin, Energy Procedia, 2014, 63, 2199–2206 CrossRef CAS.
- C. Wang, X. Zhou, L. Jia and Y. Tan, Ind. Eng. Chem. Res., 2014, 53, 16235–16244 CrossRef CAS.
- M. Vall, J. Hultberg, M. Strømme and O. Cheung, RSC Adv., 2019, 9, 20273–20280 RSC.
- H. Guo, S. Yan, Y. Zhao, X. Ma and S. Wang, J. Chem. Eng., 2019, 359, 542–551 CrossRef CAS.
- S. M. Hashemi, D. Karami and N. Mahinpey, Fuel, 2020, 269, 117432–117442 CrossRef CAS.
- A. Kurlov, A. Armutlulu, F. Donat, A. R. Studart and C. R. Müller, Ind. Eng. Chem. Res., 2019, 59, 7182–7188 CrossRef.
- A. H. Soleimanisalim, M. H. Sedghkerdar, D. Karami and N. Mahinpey, J. Nat. Gas Sci. Eng., 2016, 36, 1056–1061 CrossRef CAS.
- L. M. dlCruz and H. Pfeiffer, J. Solid State Chem., 2013, 204, 298–304 CrossRef.
- P. S. Camacho, I. C. R. Ibarra and H. Pfeiffer, J. CO2 Util., 2013, 3–4, 14–20 CrossRef.
- I. A. Corte, E. F. Israel and H. Pfeiffer, J. Phys. Chem. C, 2008, 112, 6520–6525 CrossRef.
- Q. Xiao, Y. Liu, Y. Zhong and W. Zhu, J. Mater. Chem., 2011, 21, 3838–3842 RSC.
- H. R. Radfarnia and M. C. Iliuta, Ind. Eng. Chem. Res., 2011, 50, 9295–9305 CrossRef CAS.
- A. Iwan, H. Stephenson, W. C. Ketchie and A. A. Lapkin, J. Chem. Eng., 2009, 146, 249–258 CrossRef CAS.
- S. Munro, M. Åhlén, O. Cheung and A. Sanna, J. Chem. Eng., 2020, 388, 124284–124300 CrossRef CAS.
- L. M. dlCruz and H. Pfeiffer, J. Phys. Chem. C, 2012, 116, 9675–9680 CrossRef.
- J. I. Ida and Y. S. Lin, Environ. Sci. Technol., 2003, 37, 1999–2004 CrossRef CAS PubMed.
- E. B. Pablo, F. P. Hernández, A. Y. Aulestia and H. Pfeiffer, J. Chem. Eng., 2020, 384, 123291–123299 CrossRef.
- D. Yuhua, J. Renewable Sustainable Energy, 2012, 4, 013109–013117 CrossRef.
- Y. Duan, J. Renewable Sustainable Energy, 2010, 3, 013102–013117 CrossRef.
- T. Zhao, E. O. Fernández, M. Rønning and D. Chen, Chem. Mater., 2007, 19, 3294–3301 CrossRef CAS.
- H. R. Radfarnia and M. C. Iliuta, Sep. Purif. Technol., 2012, 93, 98–106 CrossRef CAS.
- B. H. Lee, L. Kang, R. Nieh, W. J. Qi and J. C. Lee, Appl. Phys. Lett., 2000, 76, 1926–1928 CrossRef CAS.
- V. Cosnier, P. Besson, V. Loup, L. Vandroux, S. Minoret, M. Cassé, X. Garros, J. M. Pedini, S. Lhostis, K. Dabertrand, C. Morin, C. Wiemer, M. Perego and M. Fanciulli, Microelectron. Eng., 2007, 84, 1886–1889 CrossRef CAS.
- D. Shin and Z. K. Liu, Scr. Mater., 2007, 57, 201–204 CrossRef CAS.
- N. V. Tarakina, R. B. Neder, T. A. Denisova, L. G. Maksimova, Y. V. Baklanova, A. P. Tyutyunnik and V. G. Zubkov, Dalton Trans., 2010, 39, 8168–8176 RSC.
- V. G. Lang, Z. Anorg. Allg. Chem., 1966, 348, 246–256 CrossRef.
- J. Bréger, M. Jiang, N. Dupré, Y. S. Meng, Y. S. Horn, G. Ceder and C. P. Grey, J. Solid State Chem., 2005, 178, 2575–2585 CrossRef.
- T. J. Bastow, M. E. Hobday, M. E. Smith and H. J. Whitfield, Solid State Nucl. Magn. Reson., 1994, 3, 49–57 CrossRef CAS PubMed.
- G. Ji, M. Z. Memon, H. Zhuo and M. Zhao, J. Chem. Eng., 2017, 313, 646–654 CrossRef CAS.
- J. Liu, Z. Wang, Z. Wang, J. Song, G. Li, Q. Xu, J. You, H. Cheng and X. Lu, Phys. Chem. Chem. Phys., 2019, 21, 13135–13143 RSC.
- X. Chen, Z. Xiong, Y. Qin, B. Gong, C. Tian, Y. Zhao, J. Zhang and C. Zheng, Int. J. Hydrogen Energy, 2016, 41, 13077–13085 CrossRef CAS.
- H. A. L. García, O. O. Encinia, J. O. Landeros, E. Lima and H. Pfeiffer, J. Mater. Chem., 2019, 7, 4153–4164 RSC.
- F. Miccio, A. N. Murri and E. Landi, Ind. Eng. Chem. Res., 2016, 55, 6696–6707 CrossRef CAS.
- X. Yang, W. Liu, J. Sun, Y. Hu, W. Wang, H. Chen, Y. Zhang, X. Li and M. Xu, ChemSusChem, 2016, 9, 2480–2487 CrossRef CAS PubMed.
- Z. Qi, H. Daying, L. Yang, Y. Qian and Z. Zibin, AIChE Symp. Ser., 2013, 59, 901–911 CAS.
- X. Yan, Y. Li, X. Ma, J. Zhao and Z. Wang, Int. J. Mol. Sci., 2019, 20, 928–950 CrossRef CAS PubMed.
- M. O. Cichocka, J. Ångström, B. Wang, X. Zou and S. Smeets, J. Appl. Crystallogr., 2018, 51, 1652–1661 CrossRef CAS PubMed.
- W. Wan, J. Sun, J. Su, S. Hovmöller and X. Zou, J. Appl. Crystallogr., 2013, 46, 1863–1873 CrossRef CAS PubMed.
-
G. W. Kajjumba, S. Emik, A. Öngen, H. K. Özcan and S. Aydın, in Advanced Sorption Process Applications, ed. S. Edebali, Intechopen, London, UK, 2019, DOI:10.5772/intechopen.80495.
- E. D. Revellame, D. L. Fortela, W. Sharp, R. Hernandez and M. E. Zappi, Chem. Eng. Technol., 2020, 1, 100032–100044 Search PubMed.
- J. R. C. Guimarães, P. R. Rios and A. L. M. Alves, Mater. Res., 2019, 22, 5 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Erik
Svensson Grape
a,
Erik
Svensson Grape
 b,
Teva
Clairefond
a,
Evgenii
Tikhomirov
a,
A. Ken
Inge
b,
Teva
Clairefond
a,
Evgenii
Tikhomirov
a,
A. Ken
Inge
 b and
Ocean
Cheung
b and
Ocean
Cheung
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hf ratio (between 0.5 and 1.5
Hf ratio (between 0.5 and 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), synthesis temperature, time and heating rate, were investigated to optimize CO2 sorption properties of Na2HfO3. The Na2HfO3 sorbent showed comparable CO2 uptake capacity, reaction rate and excellent cycling stability compared to other metal oxide sorbents. Na2HfO3 with Na
1), synthesis temperature, time and heating rate, were investigated to optimize CO2 sorption properties of Na2HfO3. The Na2HfO3 sorbent showed comparable CO2 uptake capacity, reaction rate and excellent cycling stability compared to other metal oxide sorbents. Na2HfO3 with Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hf = 1
Hf = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1.25
1 and 1.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 showed the highest CO2 uptake among all Na2HfO3 samples obtained, with a CO2 uptake capacity of around 15 wt% (at 650–800 °C). The CO2 uptake rate of NHO-1 and NHO-1.25 was fast with over 80% of the equilibrium uptake reached within 250 s. Na2HfO3 remained stable even after 100 cycles with less than 3% difference in the CO2 uptake capacity between the 1st and 100th cycles. We performed kinetic analysis on the CO2 sorption data and found that the Avrami–Erofeev model fitted the kinetic data best among the kinetic models used. Apart from sorbent optimization, we showed that 3D-printing of Na2HfO3
1 showed the highest CO2 uptake among all Na2HfO3 samples obtained, with a CO2 uptake capacity of around 15 wt% (at 650–800 °C). The CO2 uptake rate of NHO-1 and NHO-1.25 was fast with over 80% of the equilibrium uptake reached within 250 s. Na2HfO3 remained stable even after 100 cycles with less than 3% difference in the CO2 uptake capacity between the 1st and 100th cycles. We performed kinetic analysis on the CO2 sorption data and found that the Avrami–Erofeev model fitted the kinetic data best among the kinetic models used. Apart from sorbent optimization, we showed that 3D-printing of Na2HfO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 mixtures can be used to produce structured Na2HfO3 sorbents with a slightly improved CO2 uptake rate and the same CO2 uptake capacity as the powder-based solid-state synthesized Na2HfO3 sorbent.
HfO2 mixtures can be used to produce structured Na2HfO3 sorbents with a slightly improved CO2 uptake rate and the same CO2 uptake capacity as the powder-based solid-state synthesized Na2HfO3 sorbent.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 molar ratio was varied from 0.5–1.5
HfO2 molar ratio was varied from 0.5–1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Here, the samples are referred to as NHO-X, where X is the molar ratio of Na2CO3 with respect to HfO2. Regardless of the Na2CO3
1. Here, the samples are referred to as NHO-X, where X is the molar ratio of Na2CO3 with respect to HfO2. Regardless of the Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratio, the weight loss recorded during the synthesis of NHO-X corresponded reasonably well to the expected values (Table S1, Fig. S4†), and the slight differences noted were related to minor deviations in weighing and mixing. The differences led to a small fluctuation in the real stoichiometry of the reaction mixture. Note that for NHO-1, NHO-1.25 and NHO-1.5, the mass of the reaction mixture showed a consistent decrease with time during synthesis at 900 °C. This decrease in weight was related to the melting and evaporation of the stoichiometric excess Na2CO3 that was present in the reaction mixture. The PXRD patterns of NHO-Xs synthesized at 900 °C for 3 h under N2 are shown in Fig. 1.
HfO2 ratio, the weight loss recorded during the synthesis of NHO-X corresponded reasonably well to the expected values (Table S1, Fig. S4†), and the slight differences noted were related to minor deviations in weighing and mixing. The differences led to a small fluctuation in the real stoichiometry of the reaction mixture. Note that for NHO-1, NHO-1.25 and NHO-1.5, the mass of the reaction mixture showed a consistent decrease with time during synthesis at 900 °C. This decrease in weight was related to the melting and evaporation of the stoichiometric excess Na2CO3 that was present in the reaction mixture. The PXRD patterns of NHO-Xs synthesized at 900 °C for 3 h under N2 are shown in Fig. 1.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.
m.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratios in the reaction mixture.
HfO2 ratios in the reaction mixture.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 ratio in the synthesis mixture, also see Fig. S4
HfO2 ratio in the synthesis mixture, also see Fig. S4
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Na2HfO3(s) + CO2(g)
Na2HfO3(s) + CO2(g)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 = 0.5
HfO2 = 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.75
1, 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1.25
1, 1.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1.5
1, and 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were mechanically mixed by hand. The mixture was heated to 900 °C for 1–4 h using a Mettler Toledo TGA2 thermogravimetric analyzer (Schwerzenbach, Switzerland) with heating rates of 2, 5, or 10 °C min−1 under a constant flow rate of nitrogen (N2) at 50 cm3 min−1). Different synthesis temperatures (800, 850, 900, and 1050 °C) were tested, but only the products obtained at 900 °C could be identified as Na2HfO3 by PXRD (Fig. S1†). Therefore, 900 °C was chosen as the synthesis temperature used in this study. In addition, we attempted to synthesize Li2HfO3 and K2HfO3 using the same synthesis procedures (with Li2CO3
1 were mechanically mixed by hand. The mixture was heated to 900 °C for 1–4 h using a Mettler Toledo TGA2 thermogravimetric analyzer (Schwerzenbach, Switzerland) with heating rates of 2, 5, or 10 °C min−1 under a constant flow rate of nitrogen (N2) at 50 cm3 min−1). Different synthesis temperatures (800, 850, 900, and 1050 °C) were tested, but only the products obtained at 900 °C could be identified as Na2HfO3 by PXRD (Fig. S1†). Therefore, 900 °C was chosen as the synthesis temperature used in this study. In addition, we attempted to synthesize Li2HfO3 and K2HfO3 using the same synthesis procedures (with Li2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 and K2CO3
HfO2 and K2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 molar ratios of 1
HfO2 molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). We were unable to confirm the successful synthesis of Li2HfO3 or K2HfO3 under the synthesis conditions tested (Fig. S2 and S3†).
1). We were unable to confirm the successful synthesis of Li2HfO3 or K2HfO3 under the synthesis conditions tested (Fig. S2 and S3†).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 (20
N2 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 vol.) gas mixture for selected samples. The CO2
80 vol.) gas mixture for selected samples. The CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 gas mixture was used both in carbonation and regeneration. The CO2 uptake and regeneration steps were reduced to 20 min each for the long-term stability (100 cycles) test. The CO2 sorption kinetics were analyzed using five different kinetic models: pseudo-first order (PFO), pseudo-second order (PSO), Elovich, Avrami and Avrami–Erofeev. These kinetic models were chosen as they are based on a chemisorption process. The non-linear and linear versions of these kinetic models can be summarized with the following equations:55–57
N2 gas mixture was used both in carbonation and regeneration. The CO2 uptake and regeneration steps were reduced to 20 min each for the long-term stability (100 cycles) test. The CO2 sorption kinetics were analyzed using five different kinetic models: pseudo-first order (PFO), pseudo-second order (PSO), Elovich, Avrami and Avrami–Erofeev. These kinetic models were chosen as they are based on a chemisorption process. The non-linear and linear versions of these kinetic models can be summarized with the following equations:55–57




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) non-linear: ln[ln(qe/qe − qt)] = n
non-linear: ln[ln(qe/qe − qt)] = n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k + n
k + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t
t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 − α)] = ln
1 − α)] = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k + n
k + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t
t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HfO2 = 1
HfO2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, 1.4 wt% of Carbopol 940 homopolymer, and 68.6 wt% of water. The 3D-printed structures were first heat treated at 650 °C in air for 1 h before the same synthesis steps as described above for Na2HfO3 were adopted. Additional information related to 3D-printing parameters and the print structure model can be found in the ESI.†
1 mixture, 1.4 wt% of Carbopol 940 homopolymer, and 68.6 wt% of water. The 3D-printed structures were first heat treated at 650 °C in air for 1 h before the same synthesis steps as described above for Na2HfO3 were adopted. Additional information related to 3D-printing parameters and the print structure model can be found in the ESI.†









