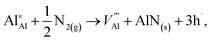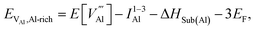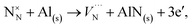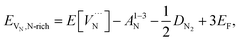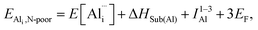Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational study of native defects and defect migration in wurtzite AlN: an atomistic approach†
Lei
Zhu
 a,
C. Richard A.
Catlow
a,
C. Richard A.
Catlow
 *ac,
Qing
Hou
*ac,
Qing
Hou
 ab,
Xingfan
Zhang
ab,
Xingfan
Zhang
 a,
John
Buckeridge
d and
Alexey A.
Sokol
a,
John
Buckeridge
d and
Alexey A.
Sokol
 *a
*a
aDepartment of Chemistry, University College London, London, WC1H 0AJ, UK. E-mail: c.r.a.catlow@ucl.ac.uk; a.sokol@ucl.ac.uk
bInstitute of Photonic Chips, University of Shanghai for Science and Technology, Shanghai, China
cSchool of Chemistry, Cardiff University, Park Place, Cardiff CF10 1AT, UK
dSchool of Engineering, London South Bank University, London, SE1 6NG, UK
First published on 19th June 2023
Abstract
We derive an empirical, lattice energy consistent interatomic force field model for wurtzite AlN to predict consistently a wide range of physical and defect properties. Using Mott–Littleton techniques, we calculate formation energies of vacancies and interstitials, which show good agreement with previous ab initio calculations at the edge of the band gap. A novel N3− interstitialcy configuration is proposed to be of lower energy than the octahedral-channel-centred counterpart. With the assistance of the QM/MM method, our potential can predict a VBM level (−7.35 eV) comparable to previous experimental measurements. We further investigate the migration mechanisms and energy barriers of the main intrinsic defects. For the vacancy migration, the axial migration barrier is found to be lower than the basal migration barrier, in contrast to previous calculations. Two interstitialcy migration mechanisms for the interstitial defects are proposed, the “knock-out” mechanism for Al interstitial and the “hand-over” mechanism for N interstitialcy defects. The new force field model proposed here demonstrates that the empirical two-body interatomic potential is still effective for the study of defect properties, electronic states, and other extended systems of III/V semiconductors and further can be employed with QM/MM embedded techniques.
1. Introduction
Aluminium nitride (AlN), together with gallium nitride (GaN) and indium nitride (InN) and in solid solution with various compositions of group-III nitrides (AlGaN, etc.), is one of the key materials for solid-state light sources. Having had the least attention among the three nitrides, AlN has started to gain more interest owing to its application in deep ultraviolet (wavelength shorter than 300 nm) light-emitting diodes (LEDs),1–3 due to its very wide band gap (6.2 eV, equivalent of 200 nm). The state-of-the-art AlN-based deep-UV lab LED was successfully made with the lowest possible wavelength of 210 nm (5.9 eV),3 the potential of which has stimulated great interest in the material. Some additional advantages, such as good thermal conductivity (285 W m−1 K−1) and high thermal stability,4–7 make AlN increasingly important for energy and electrical devices.8 Recently, single photon emission was observed in an AlN thin film,9 showing AlN to be amongst the most promising materials for applications in quantum technology.10Defects plays a key role in the optical properties of AlN. Early experimental work by Slack and McNelly showed that defects, which are mainly formed during crystal growth, show a strong correlation with the optical properties of AlN.11 Since then, photoluminescence (PL) peaks from red light to deep-UV region have been assigned to various types of defects: Al vacancy and N vacancy being the mostly commonly associated ones.12–21 Meanwhile, computational studies on defects in AlN have been predominantly based on the ab initio techniques, primarily density functional theory (DFT).22–31 The source of the observed optical properties in AlN has now become clearer owing to these computational studies, as the accuracy of the calculations has improved, by the usage of higher level of exchange–correlation energy functionals from local density approximation (LDA) to hybrid functionals.
However, these ab initio techniques are not favourable for large systems of thousands of atoms, due to their computational expense and scaling performance. Although our future work will explore the use of such methods, particularly employing quantum mechanical/molecular mechanical (QM/MM) methods, less computationally demanding methods based on interatomic potential models are essential to explore much larger systems and a wider range of configurations. Though such classical approach will not give information directly on electronic structure, given an accurate set of potential models, we can obtain reliable defect energies and geometries as has been demonstrated by a large number of studies of oxides.32–35 They allow us to establish the overall nature of the defect structure of the materials, with the subsequent (QM/MM) focusing on electronic and spectroscopic properties of key defects using our newly derived interatomic potential in the hybrid QM/MM approaches. Moreover, a robust interatomic potential model is very beneficial in investigating disordered systems and the solid solutions.
Since the first reported interatomic potential model for wurtzite AlN,36 there have been a number of evolutions of the models. The earliest pair-wise Coulomb and Buckingham potential implementations were based on the ionic model of AlN;36,37 such models require only a small number of empirical parameters and allow the prediction of defect energetics and the physical properties including lattice constants and dielectric constants.37 Later studies shifted focus to lattice dynamics, with more emphasis on the covalent components of the bonding of the material, with molecular mechanical rather than an ionic approach to the development of the potential model. These models, including bond order Tersoff potential models,38–43 three-body potential models44,45 and other many-body models,46 have allowed accurate modelling of the physical properties of the material. However, the more complex interatomic potentials require more parameters; moreover, their use is difficult in modelling defect and surface properties of the material. More recently, a machine learning interatomic potential model was developed for silicon, reproducing wide range of DFT results including elastic properties, surface energies, defect formation energies and defect migration barriers.47 However, the data-driven model lacks proper description of long-range interactions and suffers from its intrinsic feature of high dimensionality in exchange of transferability (the so-called “curse of dimensionality”).47,48 A simple empirically fitted interaction potential model still proves to be effective in investigating defect energetics, and transferable to a wide range of structures and physical properties.
In this work, we propose a new pairwise and a 3-body interatomic potential models for wurtzite AlN, from which we will present a comprehensive study of intrinsic defect structure of the material. The new interatomic potential can accurately predict a wide range of physical properties including lattice constants, elastic constants and dielectric constants. The interatomic potential models presented are designed to be lattice energy consistent for reproducing the energies of electronic states accurately. The Mott–Littleton method is implemented for the electron/hole ionization energy and intrinsic defects in wurtzite AlN, focusing on the formation of vacancies and interstitials, which have been previously studied using DFT techniques. While maintaining high calculation efficiency for systems of thousands of atoms, our force field is the first AlN interatomic potential model that can be used to calculate defect formation energies accurately. A novel configuration of a highly charged nitrogen “interstitialcy” defect is found to be more stable than the channel-centred counterpart. With further investigation into the defect migration, our results give new insights into the vacancy migration barriers and the interstitialcy migration mechanisms of Al and N interstitial defects. Our results are of relevance to all III–V nitride systems and indeed to all the wurtzite structured materials.
2. Methodology
2.1 Interatomic potential
The first interatomic potentials for AlN were reported by Cormack,36 using a shell model with formal charges. Later models include those of Chisholm37 which employed partial charges. In both studies, only a Buckingham potential was used whereas in our work, we employ a more complex multi-functional model, giving a more accurate and smooth potential profile, which has been successfully applied to oxides lately.33 The parameterisations of the potential models in this work were completed using the General Utility Lattice Program (GULP) code.49The interatomic potential model in this work is based on the Born model50 of the ionic solid, as both the wurtzite structure adopted by AlN, and the dielectric properties of the material are consistent with the use of the ionic model. To obtain a precise and smooth profile of interatomic potentials across short-range and long-range distances, we fitted a combination of pairwise long-range Coulomb, and short-range Buckingham, Lennard-Jones, and polynomial potentials to experimental data including lattice constants, elastic constants, dielectric constants, piezoelectric constants and phonon frequencies.
Regarding the short-range potentials, for the interaction between the cation and anion, here, we employ the Buckingham potential with respect to internuclear distance r:
where n is the index of summation and Cn are polynomial coefficients.
A repulsive r−12 potential (implemented as a Lennard-Jones type without the attractive term) is applied covering the whole interatomic short range between cation and anion, to prevent atoms from accessing unphysically short separations:
where concept of separately treating the 1st and the 2nd neighbouring anions adopted here is achieved in a condense form. A, ρ, C12, and the polynomial an, bn, Cn constants are all variable parameters that are adjusted during the fitting process. The chosen values for these parameters is discussed below.
In this model, we first apply the pair potential approximation, which is commonly used for ionic solids. In addition, polarisation of the nitride ions is included via the shell model,51 which provides a simple mechanical model of polarizability in which the ion is divided into a core linked by an harmonic spring to a shell, and which has proved effective in modelling dielectric properties of ionic materials. In the harmonic approximation, the polarizability of an ion in vacuo is given by:
As noted, in our model, the aluminium ion is treated as unpolarizable, i.e., core only (charge +3), whereas the nitride ion is polarisable with both a core (charge +1.4) and a shell (charge (Y) −4.4). Two main short-range interactions are considered, i.e., “Al-core–N-shell” and “N-shell–N-shell”. Between “N core” and “N shell”, the interactions are controlled solely by harmonic spring (including square and quartic terms).
For many ionic materials, the Buckingham potential still proves to be an effective model. The parameters of the potential for “Al-core–N-shell” interaction are all fitted empirically against experimental properties. As the Al ion is considered here to have a negligible polarizability, the dispersion term of “Al-core–N-shell” interaction is omitted (C = 0). Parameters of the repulsive “N-shell–N-shell” interaction, A and ρ in the Buckingham potential, are transferred from a widely used “O-shell–O-shell” potential,52 which successfully predicts defect properties and defect diffusion energies for a range of oxide materials.53 The transferability of the potential can be justified by the isoelectronic Ne10 structure of nitride and oxide ions and the minor role of this potential in our simulations. In particular, this potential affects the calculated defect properties only slightly and serves mostly in preventing unphysical configurations with short anion–anion separation distances. For the attractive dispersion parameter C in the “N-shell–N-shell” Buckingham potential, we applied the theory first introduced in the work by Pyper54 and made our approximation previously applied for GaN.55 According to the Slater–Kirkwood formula,56 the dispersion parameter for anion–anion interaction can be determined from the frozen in-crystal polarizability, which is calculated by taking the spring constants fitted to reproduce the high-frequency dielectric constants.
The coefficients of the polynomial functions are calculated to connect all the regions in the Buckingham potentials, under the condition that the 1st and 2nd derivatives at both end points must be matched. The parameters of zero-degree polynomial functions control the vertical offsets of the Buckingham potential, which is adjusted according to the lattice energy. These zero-gradient offsets do not affect the physical properties but can tune the lattice energy, a key term for obtaining our electron affinities and in turn calculating the defect formation energies. The cut-off distances of the short-range potentials are 10 Å, which extends potentials beyond nearest and next-nearest neighbours where the interactions are still significant but allows for a smooth and rapid transition to zero thus reducing the computational costs. The fitted parameters are reported in Table 1.
| Species | Potential functions | Parameters | r min − rmax (Å) |
|---|---|---|---|
| Al core–N shell | Buckingham | A = 1400.00 eV | 0.0–2.2 |
| ρ = 0.3350 Å | |||
| C = 0 eV Å6 | |||
| Polynomial | C 0 = 0.213 eV | 0.0–2.2 | |
| Polynomial | C 0 = 1501.16 eV | 2.2–2.8 | |
| C 1 = −2915.25 eV Å−1 | |||
| C 2 = 2281.18 eV Å−2 | |||
| C 3 = −895.66 eV Å−3 | |||
| C 4 = 176.029 eV Å−4 | |||
| C 5 = −13.83 eV Å−5 | |||
| Buckingham | A = 640.00 eV | 2.8–3.3 | |
| ρ = 0.382 Å | |||
| C = 0 eV Å6 | |||
| Polynomial | C 0 = −0.07 eV | 2.8–3.3 | |
| Polynomial |
C
0 = 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385.05 eV 385.05 eV |
3.3–3.5 | |
| C 1 = −201312.93 eV Å−1 | |||
C
2 = 118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829.78 eV Å−2 829.78 eV Å−2 |
|||
| C 3 = −35061.77 eV Å−3 | |||
| C 4 = 5171.23 eV Å−4 | |||
| C 5 = −305.00 eV Å−5 | |||
| Lennard-Jones | C 12 = 10.42 eV Å−12 | 0.0–10.0 | |
| N shell–N shell | Buckingham-4 |
A = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764.3 eV 764.3 eV |
0.0–10.0 (rcut1 = 2.0, rcut2 = 2.5, rcut3 = 5.0) |
| ρ = 0.1490 Å | |||
| C = 74.00 eV Å6 | |||
| N core–N shell | Spring k2 | 63.00 eV Å−2 | |
| Spring k4 | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.00 eV Å−4 000.00 eV Å−4 |
The resulting structural parameters, physical properties and lattice energy are obtained using the GULP code and shown in Table 2: the lattice constants and dielectric constants agree well with experimental and other ab initio computational results, although there are significant discrepancies in the off-diagonal elastic constants. We note that other work had reported better reproduction of the off-diagonal elastic constants by employing three-body, bond-order, or other many-body types of interatomic potential models.38–46 All these models, however, employ partial ionic charges, which can be problematic in defect calculations. We also note that although the previous two-body interatomic potential model presented a slightly better fitting of elastic constants, the lattice energy was particularly low,37 as a result of the choice of partial charge leading to a much lower Madelung potential. A reliable lattice energy value is crucial in our calculation of defect energy as presented in the following sections.
| Property | Present | Experimental | Other IP | DFT | |
|---|---|---|---|---|---|
| 2-body | 3-body | ||||
| a Ref. 37. b Ref. 57. c Ref. 58. d Ref. 59. e Ref. 60. f Ref. 61. g Ref. 62. h Ref. 63. i Ref. 36. j Ref. 45. k Ref. 42. l Ref. 44. m Ref. 46. n Ref. 64. o Ref. 65. p Ref. 66. q Ref. 67. | |||||
| Lattice constant, a (Å) | 3.11 | 3.10 | 3.11a | 3.11a | 3.11o |
| Lattice constant, c (Å) | 4.98 | 4.98 | 4.98a | 5.00i, 4.97a, 4.98j, 5.07k, 5.04m | 4.97o |
| Special position, u (Å) | 0.380 | 0.379 | 0.382b | 0.380j, 0.375k | 0.382o |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Elastic constants | |||||
| C 11 (GPa) | 517.0 | 364.6 | 345c, 411 ± 10d | 417a, 293j, 392k, 435l, 463m | 464n, 398n, 396n |
| C 12 (GPa) | 275.3 | 117.0 | 125c, 99 ± 4d | 178a, 161j, 137k, 148l, 92m | 149n, 140n, 137n |
| C 13 (GPa) | 261.3 | 103.5 | 120c, 99 ± 4d | 152a, 151j, 101k, 108l, 104m | 116n, 127n, 108n |
| C 33 (GPa) | 567.4 | 462.2 | 395c, 389 ± 10d | 432a, 303j, 428k, 356l, 437m | 409n, 382n, 373n |
| C 44 (GPa) | 137.9 | 137.3 | 118c, 125 ± 5d, 122 ± 1e | 125a, 96j, 114k, 81l, 194m | 128n, 96n, 116n |
| C 66 (GPa) | 120.9 | 123.8 | 120a, 129j, 128k, 144l | ||
| Bulk modulus, B0 (GPa) | 354.9 | 202.8 | 201c, 210d | 248a, 202j, 210k, 211l, 218m | 228n, 218n, 207n |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Dielectric constants | |||||
| ε 011 | 10.50 | 9.77 | 8.8a, 9.14f, 8.5g, 8.0h | 8.07a | |
| ε 033 | 11.84 | 10.50 | 9.5h | 11.22a | |
| ε ∞11 | 4.62 | 4.60 | 4.7a, 4.84f, 4.6g | 4.46a | |
| ε ∞33 | 4.74 | 4.70 | 4.85a | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Piezoelectric constants | |||||
| e 33 (C m−2) | 3.92 | 1.35 | 1.55h | 1.80p, 1.50p, 1.50q | |
| e 31 (C m−2) | −2.45 | −4.63 | −0.58h | −0.64p, −0.53p, −0.60q | |
| Lattice energy (eV) | −91.93 | −90.19 | −98.209i, −43.50a | ||
To demonstrate that the 3-body interatomic potential improves substantially the prediction of elastic constants while still using formal charges, we fit another set of parameters by adding a 3-body potential to the same 2-body ones. Here the 3-body interatomic potential takes the form of:
| Species | Potential functions | Parameters | r min − rmax (Å) |
|---|---|---|---|
| Al core–N shell | Buckingham | A = 1776.79 eV | 0.0–2.2 |
| ρ = 0.3270 Å | |||
| C = 0 eV Å6 | |||
| Polynomial | C 0 = 0.35 eV | 0.0–2.2 | |
| Polynomial | C 0 = 2032.03 eV | 2.2–2.8 | |
| C 1 = −3965.36 eV Å−1 | |||
| C 2 = 3110.78 eV Å−2 | |||
| C 3 = −1222.38 eV Å−3 | |||
| C 4 = 240.12 eV Å−4 | |||
| C 5 = −18.84 eV Å−5 | |||
| Buckingham | A = 2222.25 eV | 2.8–3.3 | |
| ρ = 0.3277 Å | |||
| C = 0 eV Å6 | |||
| Polynomial | C 0 = −0.07 eV | 2.8–3.3 | |
| Polynomial | C 0 = −16719.30 eV | 3.3–3.5 | |
C
1 = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150.45 eV Å−1 150.45 eV Å−1 |
|||
| C 2 = −13939.89 eV Å−2 | |||
| C 3 = 4019.23 eV Å−3 | |||
| C 4 = −578.88 eV Å−4 | |||
| C 5 = 33.32 eV Å−5 | |||
| Lennard-Jones | C 12 = 10.42 eV Å12 | 0.0–10.0 | |
| N shell–N shell | Buckingham-4 |
A = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764.3 eV 764.3 eV |
0.0–10.0 (rcut1 = 2.0, rcut2 = 2.5, rcut3 = 5.0) |
| ρ = 0.1490 Å | |||
| C = 74.00 eV Å6 | |||
| Al core–N shell 1–N shell 2 | 3-Body exponentials | K = −0.1442 eV | 0.0–12.00 (for both bonds) |
| ρ 3B = 4.73 Å−1 | |||
| R 0 3B = 1.89 Å | |||
| N core–N shell | Spring k2 | 63.00 eV Å−2 | |
| Spring k4 | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.00 eV Å−4 000.00 eV Å−4 |
2.2 Mott–Littleton and QM/MM calculations
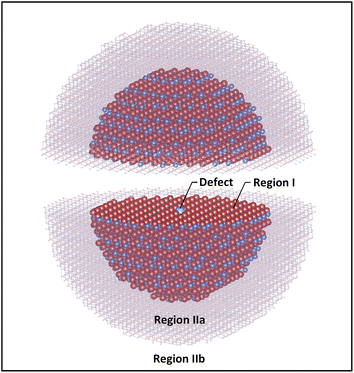
Our potential is implemented in Mott–Littleton68 calculations of defect energies. The method which is discussed in detail in ref. 49 divides the lattice around the central defect into 3 regions (Fig. 1). In the inner region (region I), displacements of the atoms are calculated by explicit energy minimisation. Secondly, the displacement of atoms in the middle region (region IIa) is calculated within the harmonic approximation for interactions with respect to the central defect, with explicit calculation of the interaction energy with region I. Response by the ions of the outer region (IIb) to the Coulomb field of the central defect is treated using a dielectric continuum model but the lattice summation performed explicitly. In this work, the radii of region I and region IIa are 21 Å (around 3600 atoms) and 36 Å (around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms), respectively; with these values all defect energies have converged to within 0.1 eV or better with respect to subsequent expansion. All the calculations were again undertaken using the GULP code.69
000 atoms), respectively; with these values all defect energies have converged to within 0.1 eV or better with respect to subsequent expansion. All the calculations were again undertaken using the GULP code.69
In this study, we also make use of calculated ionisation energies obtained using the hybrid QM/MM embedded cluster method as implemented in the ChemShell software.70,71 The QM/MM method employed here contains three levels of theory. In the central cluster region where the electron ionization occurs, the DFT method is applied with the hybrid functional PBE072,73 and Def2-TZVP74 basis sets. The QM cluster region is surrounded by a large MM environment controlled by the same 2-body interatomic potential. Between the QM and MM region, there is a transition layer balancing the different forces from both sides by the fitted electron localising pseudopotentials (PP).75 Compared to the DFT method using the periodic boundary condition, the QM/MM method can calculate the ionization potential as it has unambiguous definition of the vacuum level. This theory is explained in more detail in other work.70,71,76,77 Further detail of the settings for QM/MM calculations can be found in the ESI.†
3. Results
In this section, we apply our interatomic potential model and the Mott–Littleton method to calculate defect energies and the energies of electron and hole formation. We first compare the defect energies calculated by the 2-body and the 3-body models. We then obtain estimates of electron and hole formation energies, which facilitate the calculation of formation energies for both vacancy and interstitial species. Lastly, we model defect migration processes.3.1 Defect energies from Mott–Littleton calculations
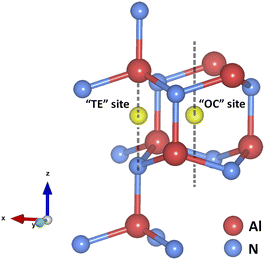
The intrinsic point defect energies of AlN are presented in Table 4. As we use the Mott–Littleton approach, all point defect energies are calculated with their formal charges. We note that the energies are given with respect to the perfect lattice and ions at infinity. For both defect species and charge carriers we use the Kröger–Vink notation.| Defect type | Present work | Previous work36 | |
|---|---|---|---|
| 2-body | 3-body | ||
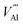
|
53.54 | 53.12 | 63.00 |
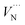
|
53.64 | 53.40 | 52.11 |

|
−34.06 | −32.18 | −40.69 |

|
−34.19 | N/A | −12.56 |

|
−33.95 | −32.37 | −12.56 |
There are two distinct high-symmetry sites, or voids, for interstitials in the wurtzite structure adopted by AlN: the tetrahedral (TE) and octahedral (OC) sites (Fig. 2). An interstitial at the TE site has four cations and four anions as the nearest neighbours, while that at the OC site has six nearest neighbours (three cations and three anions). We may also consider the OC interstitial sites from the perspective of the z-axis, where the interstitial at the OC site is situated at the centre of the “channel”. Previous calculation found the Al interstitial at the OC site is more stable than at the TE site in AlN,26 with analogous results found for GaN.28,78 In our work, when the Al3+ interstitial is initially located at a TE site it moves during the relaxation towards the OC site. Hence, only the results for this configuration of Al3+ interstitial defect are presented here.
 | ||
| Fig. 2 Tetrahedral (TE) and octahedral (OC) sites for interstitial defect in wurtzite AlN. The z axis is oriented along the c crystallographic direction. | ||
For the N3+ interstitial, two distinct stable configurations are found: the octahedral-central (OC-central) configuration and the “interstitialcy” configuration. Our calculations show the defect energy of OC-central type N interstitial is close to its cation counterpart with less than 1% difference in energy (Table 4). Such a configuration is consistent with the previous ab initio simulations of GaN79,80 and InN81 – the only reports obtaining the stable OC-central N interstitial in charge state −3 in wurtzite structured nitride systems.
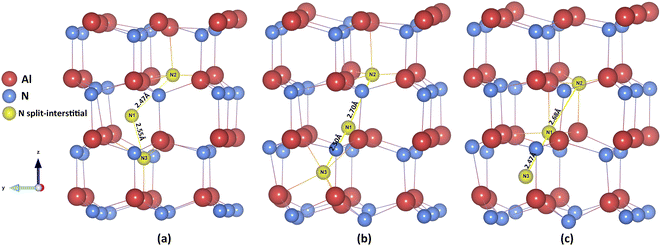
The N3− defect is found to have another stable “interstitialcy” configuration in the system. The new configuration is obtained by first relaxing the OC-central configuration defect, and then adjusting the positions of the defect and its surrounding neighbouring N3− ions. After complete relaxation, the introduced N3− ion (N1 in Fig. 3(a)) is displaced from the ideal OC site (by 0.34 Å) in the lattice basal plane towards one of the three nearest neighbouring N3− ions. The on-site N3− ion (N2 in Fig. 3(a)) is then nudged from its original position (by 0.62 Å) towards the axial direction along the line interconnecting the defect and the on-site ion (Fig. 3(b) and (c)). The two N ions comprise a special “interstitialcy” or split-interstitial configuration, in which two N ions straddle the same N lattice site at the distance of 2.40 Å, forming an interstitial-vacancy-interstitial defect complex structure. We calculated the defect energy of such configuration to be 0.24 eV lower than the OC-central type (Table 4), suggesting that the OC-central N interstitial is a local energy minimum configuration in the system.
The latter type of N interstitial defect has been widely overlooked by other studies of III–V nitride system. The term “split-interstitial” was used in another configuration reported in many previous ab initio studies,26,31,65,82 where their N split-interstitial defects have a form of N2 molecule positioned at the N vacancy site. The bonding in those N–N structure shows a strong covalency nature, which were found to be stable in the charge state from +3 to −1 due to the electronic occupancy at their antibonding-πp-like orbitals.82 We note that our novel ionic N3− interstitialcy defect is a separate configuration from those covalent split-interstitial discussed previously. In the case of our N interstitialcy defect in charge state −3, the two N3− ions are rearranged at the lowest energy configuration as a result of the Madelung potential (electrostatic interactions) and the short-range interatomic potential, which is purely an ionic response. The defect structure of anion interstitial in formal charge is not new in other material system (see examples in alkali halides83 and oxides84). In particular, our N3− interstitialcy defect shows the closest resemblance to the O2− interstitial defect in UO2,52 where the O2− interstitial distorted from body-centre position by 0.2 Å and 0.27 eV lower in energy compared to the symmetric counterpart.
Similar electrostatically-driven reconstruction of interstitial point defect has recently been discussed in another report.85 The authors stated and proved that high-symmetry relaxation methodology adopted by many computational defect studies could easily lead to metastable state (local minima) rather than the global minimum,86 which can be found using their novel symmetry-breaking technique with standard DFT calculations. They found the defect energy of Te2− split-interstitial is 0.2 eV lower than the higher symmetric tetrahedral Te2− interstitial in CdTe, which is consistent with our lower symmetric N3− interstitialcy defect configuration. Different configurations of interstitialcy defects, including OC–OC, TE–TE, and OC–TE types, have also been explored in our system, but all of them are unstable in our simulations. Our N3− interstitialcy configuration has also been confirmed by the QM/MM calculation, which will be presented in full detail in our subsequent paper.
The same defect calculation proves to be problematic for our 3-body potential model. We found that the Mott–Littleton defect calculation cannot converge for all four intrinsic defects without an additional correction in the force field. The pre-exponential parameter K is fitted empirically to be negative (Table 3), which indicates the 3-body potential acts as an attractive force. As a defect is introduced, the cluster is likely to contract due to the additional attractive force, which leads to abnormally high potential gradients at energy minimum position. As a result, a repulsive term must be added in the force field to counteract the force for convergence (see ESI† for more detail). However, the compensation term results in the physical properties deteriorating. Therefore, the 2-body potential is chosen to be more effective for the defect calculation, as the defect energies are close to the ones from our 3-body potential (Table 4). All subsequent calculations use solely the 2-body potential.
3.2 Electron and hole formation
Computational models based on interatomic potentials cannot provide accurate estimates of electronic energies, but a useful estimate of hole and electron energies is still possible. We assume that the conduction band minimum (CBM) can be represented by an electron localising on a cation (Al) and the valence band maximum (VBM) by a hole on an anion (N), i.e., the electron state is thus approximated as a localised Al2+ state, and the hole state as a localised N2− state. (Material's electron affinity and ionisation potential determine the absolute position of CBM and VBM below vacuum level set at zero.) By using our interatomic potential model and Mott–Littleton method in GULP, defect energies of Al2+ and N2− are calculated. To model optical excitations, only shells are relaxed during these calculations, i.e., there is no relaxation of the cores. In addition, we must include appropriate intra-atomic terms. Here, we make another simplification that such intra-atomic energies are equal to their respective ionisation energies as free ions. The third ionisation potential of Al is available from experiment. The third electron affinity of N is not a measurable quantity but has been calculated using the QM/MM techniques.70 All the energy terms are collected in Table 5.| Present (eV) | |
|---|---|
| Al2+ | 33.14 |
| N2− | 34.80 |
| Al2+ → Al3+ + e′ | −29.89 |
| N2− + e′ → N3− | 27.45 |
| Calculated CBM (localising e′) | 3.25 |
| Calculated VBM (localising ḣ) (−Eh) | −7.35 |
| Calculated band gap | 10.60 |
| Experimental low temperature band gap87 | 6.23 |
| Revised CBM (−Ee) | −1.12 |
The calculated VBM is 0.85 eV higher than that based on the experimental ionization potential on the AlN surface of 8.2 eV.88 We obtain a higher band gap energy (10.60 eV) than reported experimentally (6.23 eV at low temperatures87). The calculated large positive value for the CBM is clearly inaccurate, which can be attributed to our assumption of a localised Al2+ state representing a CBM state. The experimental value of the electron affinity of AlN is uncertain with estimates, ranging from 0.25–1.9 eV,88–90 but our calculated CBM value is far from these values. As our approach appears to be more reliable for estimating a hole state, we can estimate the revised CBM value by adding the experimental band gap energy at low temperatures to our VBM value. The revised CBM now falls within the range of experimental values.
3.3 Defect reaction energies
The reaction forming an Al vacancy in the AlN lattice is represented by the following equations depending on the Al and N chemical potentials:
in the AlN lattice is represented by the following equations depending on the Al and N chemical potentials:
N-rich/Al-poor:
N-poor/Al-rich:
The “N-rich/Al-poor” or “N-poor/Al-rich” conditions indicate the respective reactions occurring in the case of either “N2(g) excess/Al(s) deficiency” or “N2(g) deficiency/Al(s) excess”. Considering thermodynamic equilibrium in the Al–N binary systems, the formation of solid AlN imposes a bound on their respective chemical potentials:
The neutral aluminium vacancy created will initially accept three electrons resulting in forming three holes in the system. The energy of forming electrons and holes in the following analysis is determined by the electron chemical potential, or Fermi level, EF, whose values in the material would typically lie in the band gap, between VBM and CBM, −Eh ≤ EF ≤ −Ee (see Table 5), although the heavily doped system can also fall outside this range.
Using the Born–Haber cycles for these reactions, we obtain:
Al-poor (N-rich):
Al-rich (N-poor):
 is the defect energy of Al vacancy in Table 4, ΔHSub(Al) heat of sublimation of Al solid (3.43 eV (ref. 91)) and I1−3Al the ionisation energy of Al atom to Al3+ ion. The experimental ionisation energies of Al can be extracted from the database (53.26 eV (ref. 91) for the sum of the 3 valence shell electrons).
is the defect energy of Al vacancy in Table 4, ΔHSub(Al) heat of sublimation of Al solid (3.43 eV (ref. 91)) and I1−3Al the ionisation energy of Al atom to Al3+ ion. The experimental ionisation energies of Al can be extracted from the database (53.26 eV (ref. 91) for the sum of the 3 valence shell electrons).
Applying the same approach to the N vacancy, Al interstitial, and N interstitial, the following defect reactions can be formulated:
(N-rich/Al-poor):
(N-poor/Al-rich):
(N-rich/Al-poor):
(N-poor/Al-rich):
(N-rich/Al-poor):
(N-poor/Al-rich):
And the respective formation energies are as following:
where A1−3N is the sum of the three electron affinities of N atom. The experimental electron affinity energies of nitrogen atom are not readily available and would, in fact, depend on the stabilising environment of the triply negatively charged species, but we can estimate the sum of three electron affinities via the Born–Haber cycle, for AlN formation, using our calculated 2-body lattice energy in Table 2. Our resulting estimate of the sum of the energies of the three electron affinities of N atom is 27.04 eV. The experimental value of the dissociation energy of N2, DN2, used for these calculations is 9.79 eV.91
Table 6 summarises our calculated formation energies. For vacancy defects, formation energy  is higher in N-rich condition, while the formation energy of
is higher in N-rich condition, while the formation energy of  is higher in Al-rich condition, which is as expected and agrees with other studies using first-principles methods.23,27,30,65,92,93 The comparison with earlier electronic structure calculations is not straightforward as the latter are typically reported as a function of the position of the Fermi level and only in a graphical form, so, in Table 6, we compare reported calculated formation energies for Fermi levels at the band edges. The energies for the N vacancy and Al vacancy in either environment condition agree well with previous DFT calculations at the same Fermi level positions. It was predicted in the previous ab initio calculations that the
is higher in Al-rich condition, which is as expected and agrees with other studies using first-principles methods.23,27,30,65,92,93 The comparison with earlier electronic structure calculations is not straightforward as the latter are typically reported as a function of the position of the Fermi level and only in a graphical form, so, in Table 6, we compare reported calculated formation energies for Fermi levels at the band edges. The energies for the N vacancy and Al vacancy in either environment condition agree well with previous DFT calculations at the same Fermi level positions. It was predicted in the previous ab initio calculations that the  is the most stable defect close to the VBM,26,30,65 which indicates its strong correlation to donor species in AlN. For interstitial defects, the formation energy of
is the most stable defect close to the VBM,26,30,65 which indicates its strong correlation to donor species in AlN. For interstitial defects, the formation energy of  in Al-rich condition is, however, not as close to previous DFT results. The greater value in N-rich condition can be attributed to a lower enthalpy of AlN formation used in the other work.94 Further, there is no available data for
in Al-rich condition is, however, not as close to previous DFT results. The greater value in N-rich condition can be attributed to a lower enthalpy of AlN formation used in the other work.94 Further, there is no available data for  in the literature, as the formally charged N interstitial defect is reported to be not as stable as lower charged states of the N interstitial at the CBM.
in the literature, as the formally charged N interstitial defect is reported to be not as stable as lower charged states of the N interstitial at the CBM.
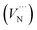 , Al vacancy
, Al vacancy  , N interstitialcy
, N interstitialcy  , and Al interstitial
, and Al interstitial  . (The calculation results from other studies are obtained approximately from their defect transition energy figures (“Fig. 1” in ref. A;65 “Fig. 2” in ref. B;30 “Fig. 2” in ref. C;23 “Fig. 1” in ref D94)
. (The calculation results from other studies are obtained approximately from their defect transition energy figures (“Fig. 1” in ref. A;65 “Fig. 2” in ref. B;30 “Fig. 2” in ref. C;23 “Fig. 1” in ref D94)
| GULP (Present) | Previous DFT calculations | ||||
|---|---|---|---|---|---|
| Ref. A65 | Ref. B30 | Ref. C23 | Ref. D94a | ||
| a The defect formation energies of Al interstitial in “Fig. 1” in ref. D94 appear in the opposite chemical condition. Here we transpose the two values to their opposite conditions. | |||||

|
|||||
| Al-poor/N-rich | −3.07 | −2.79 | −3.33 | −3.31 | −7.06 |
| Al-rich/N-poor | 0.22 | 0.45 | 0.15 | 0.02 | −5.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||

|
|||||
| Al-poor/N-rich | −0.36 | 0.14 | 0.25 | 0.24 | −2.36 |
| Al-rich/N-poor | −3.66 | −3.10 | −2.93 | −3.06 | −4.42 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||

|
|||||
| Al-poor/N-rich | 4.61 | 0.36 | 3.13 | ||
| Al-rich/N-poor | 1.32 | −2.88 | 1.07 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||

|
|||||
| Al-poor/N-rich | 1.12 | ||||
| Al-rich/N-poor | 4.42 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||

|
|||||
| Al-poor/N-rich | 1.36 | ||||
| Al-rich/N-poor | 4.66 | ||||
The results demonstrate our interatomic potential model can obtain accurate defect formation energies, which reproduce well those are calculated using first-principles methods. Note our model requires a much lighter computational load (more detail about the benchmarking is presented in ESI†).
3.4 Formation of Frenkel and Schottky defect pairs
From the energies reported in (Table 4) we can calculate energies of the Schottky and Frenkel pairs listed below:Schottky defect:
Anti-Schottky defect:
Anion Frenkel defect:
Cation Frenkel defect:
All the energies are summarised in Table 7.
For AlN, Schottky disorder has the lowest energy, suggesting that Al and N vacancies will be the dominant disorder type in the material. Cormack36 and Chisholm37 arrived at the same conclusion using interatomic potential methods, but they did not report results for the “Anti-Schottky” energy. The considerably higher Schottky defect energy here compared with that reported by Chisholm et al. reflects the choice of interatomic potential, especially the differences in ionic charges. The higher anti-Schottky and N Frenkel defect energies reported by Cormack can be attributed to the different N interstitial structure, as discussed above.
So far, by accurately predicting the physical properties, the electron/hole states, the defect energetics/structures, and the defect formation, we have tested the robustness of our interatomic potential model. The potential model can provide a reliable embedded environment for our QM/MM system, where a full scope of AlN point defect investigation will be carried out. We should note that our interatomic potential model has not been designed to simulate point defects in other charge states or other covalent defects, which may be a drawback for particular applications, and caution should be applied when modelling, e.g., N diffusion using molecular dynamics.
3.5 Point defect migration
The motion of native defects and surrounding ions controls atomic transport and is fundamental to the understanding of material growth and degradation. However, there is very little information on such processes in AlN, despite extensive interest in III-V nitride semiconductor materials over the last few decades. Experimental studies have been limited to oxygen95 or dopant diffusion,96,97 with none on intrinsic self-diffusion. After Limpijumnong & Van de Walle's comprehensive theoretical study on intrinsic defect migration in GaN using DFT, several other studies followed.31,98–102 But there has not been a detailed computational investigation on intrinsic defect migration in AlN, only some comparisons with GaN.31,101 Here we will present our computational results of a systematic study of defect migration in AlN and compare with currently available data from studies on GaN and InN.Our approach is to perform a comprehensive search of the energy landscape for the migrating species. Along each path, 10–20 points with equal distance are marked and rational function optimization calculations are conducted at each point until a suitable transition state is identified. The transition states are further confirmed by identifying a single imaginary vibrational mode frequency related to the defect. A final check involves a steepest descent optimisation with a small step size from each transitional state in both directions (to initial and final states). Hence, we define a valid migration path as that involving a continuous route which can be successfully connected by steepest descent minimisation via one or multiple transitional states. We note the need for the Mott–Littleton defect cluster centre, to avoid bias, to be at the mid-point of the path so that the activation energies are accurate and reliable.
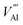 and
and  in the wurtzite AlN lattice in the axial direction (out-of-plane) and basal direction (in-plane, perpendicular to c axis, Fig. 4). In Table 8 we present our calculated activation energies and other currently available data from the literature on AlN, GaN, and InN for comparison.
in the wurtzite AlN lattice in the axial direction (out-of-plane) and basal direction (in-plane, perpendicular to c axis, Fig. 4). In Table 8 we present our calculated activation energies and other currently available data from the literature on AlN, GaN, and InN for comparison.
 | ||
| Fig. 4 Axial and basal directions of vacancy migration in wurtzite AlN (note that these arrows are not actual paths, merely an illustration of migration directions). | ||
Our results show an energy barrier of 1.67 eV with Al migrating in the axial direction and 2.62 eV in the basal direction (Table 4). The initial ground state positions, transition state positions and the interatomic distances are presented in Fig. 5. Previous calculations of the vacancy defect migration present conflicting conclusions. Our higher basal barrier of Al vacancy migration matches the results from the work of Aleksandrov et al.,101 where by using a first-principles method the barrier for the Al vacancy migration was found to be higher than that for the Ga vacancy migration in GaN. However, Warnick et al.99 found a lower barrier (1.6 eV) for Al vacancy migration in AlGaN alloy than in pure GaN, which agrees with our lower barrier results. We found a similar mechanism for N vacancy migration. Our calculated N vacancy migration barrier is 2.92 eV and 2.20 eV in the basal and axial directions respectively. Even though there are no available data for AlN with which to compare, our results are higher than the calculated activation energies in GaN, which agrees with the reported higher barrier trend of N vacancy in the AlGaN alloy99 and the previous DFT calculation results.31 Compared with the ionic radii of Al3+ and Ga3+ ions, that of the N3− ion is much bigger (by a factor of three compared with Al3+ and of two for Ga3+), so it should be expected that the migration will be more hindered in AlN, with higher migration barriers. Previous studies of vacancy self-diffusion in similar materials were reported to be isotropic.78,99,100 A more recent DFT defect calculation in InN shows an anisotropic migration behaviour, but the trend is inverse to ours with higher barrier in the axial direction.103 To our knowledge, no experimental data are available for direct comparison to date.
As stated in Section 3.3, Al interstitials are stable at the OC site. Therefore, the migration path between two nearest neighbour OC sites can either be along the hexagonal channel (along the c-axis) or horizontally passing the TE site. Here we apply the same methodology as for the vacancies where the steepest descent search follows valid saddle point identification. The latter motion involves an “interstitialcy” migration mechanism in which the migrating Al interstitial knocks off and replaces a host Al ion, with the “knocked-out” Al ion becoming a new interstitial defect moving towards its closest neighbouring OC site (Fig. 6). This horizontal migration is energetically more favourable than the vertical migration through the hexagonal channel (Table 9). Our activation energy is very close to that of Ga interstitial migration in GaN, which again supports our reasoning in Section 3.5.1.
 | ||
| Fig. 6 Atomic visualisation of horizontal Al Interstitial defect (green) migration: (a) initial ground state; (b) transitional state (saddle point). | ||
| This work | GaN78,100 | ||
|---|---|---|---|
| Cation interstitial | c-axis channel path | 1.42 | 3.00 |
| Interstitialcy mechanism | 0.93 | 0.90, 0.7 | |
| Anion interstitial | c-axis channel path | 2.04 | |
| Interstitialcy mechanism | 1.32 | 1.4 |
We find that migration of the N interstitial occurs via a more complex mechanism. The N interstitial is easily pulled or dragged by other on-site N ions resulting in the distortion around the defect. Like the investigation of the Al interstitial migration, we assume that there could also be parallel and perpendicular motion for N interstitial migration with respect the c axis, so saddle point and initial/final stable states searches are also undertaken here for both. A more detailed account of the procedure is given below.
For the migration through the hexagonal channel, at the saddle point three nearest neighbouring N ions are pushed away by the defect with different bond lengths—all three are shorter than the stable interstitialcy defect (Fig. 7). This interaction between three N ions makes it more difficult for the defect to return to the initial/final stable configuration, inducing a higher migration barrier.
 | ||
| Fig. 7 Atomic visualisation of the transition state of N Interstitial defect migration through hexagonal channel: see from x-axis (left); see from z-axis (right). | ||
For the other migration mechanism, we found a path in a single conventional unit cell with a much lower barrier. Here we applied an iterative approach to find the transition state. At first, we located two close stable interstitialcy defect configurations at neighbouring lattice layers. These two configurations are rotationally symmetric around the 3-fold wurtzite c axis running through a hexagonal channel, so they are likely to be the initial and final states of the path. Initially, the interstitial N defect (N1 in Fig. 8) was moved along the straight line from N2 to N3. N1 was kept fixed on the path, as we relaxed only the surrounding ions to give us potential energy surface with respect to N1. Afterwards, we conducted Rational Functional Optimisation (RFO) transition state searches on each resulting configuration until a transition state (proved by the identification of a single imaginary vibrational mode frequency) was found, resulting in a new possible migration path of two straight lines connecting three points (N1 to N2 and N1 to N3). Subsequently, we again moved the defect along this new path and repeated the same process iteratively until the highest saddle point was found. Finally, as with all other types of migration, a steepest descent optimisation was conducted to verify the path.
 | ||
| Fig. 8 Atomic visualisation of the “hand-over” mechanism of N Interstitial defect migration (looking from x-axis): (a) initial state; (b) transitional state (saddle point); (c) final state. | ||
The resultant migration motion is illustrated in Fig. 8 and is close to previous reports on GaN.78 The path has two rotationally symmetric interstitialcy defects as its initial and final stable configurations. At the saddle point, another nearest neighbouring N ion (N3) is pushed away from its original position while the initial interstitialcy configuration is maintained with a stretched bond. As the defect approaches its final position forming a new stable pair, the “left-over” N (N2) ion slowly moves back to the closest lattice site. This “hand-over” motion between three N ions is significantly different from the “knock-on” mechanism of the Al interstitial, where the former involves three N ions and the latter one only involves two Al ions.
The migration barriers/activation energies for both mechanisms are presented in Table 9. Our result shows the interstitialcy migration mechanism is energetically more favourable than the hexagonal channel migration. This barrier is also comparable to the result of the same migration mechanism in GaN, which supports the earlier reasoning related to the N ion size.
A comprehensive atomistical investigation of point defect migration suggests that the energy barriers and migration paths of self-diffusion behaviour in AlN are overall close to their counterparts in GaN. The migration barrier of the Al vacancy is 1.67 eV, at least 0.23 eV lower than the calculated Ga vacancy migration barrier in GaN. Contrary to previous calculations, the vacancy migration is not found to be isotropic in our analysis. Different heights of migration barriers are assigned to the axial and the basal directions. For the interstitial defect migration, the energy barrier of c-channel Al interstitial migration is 1.42 eV, which is 1.58 eV lower than that for the GaN counterpart. Different “interstitialcy” migration mechanisms are seen in cation and anion interstitial migration. For the Al interstitial: the on-site Al atom can be “knocked-out” and replaced by the approaching interstitial defect. And for the N interstitial, to maintain the stable interstitialcy configuration, the interstitial first bonded with one on-site N atom is handed over to the other closest on-site N atom. The study of point defect migration here provides further confirmation of the integrity of our new interatomic potential model.
4. Summary and conclusions
We have presented an interatomic potential model for AlN, which we have used to calculate both lattice and defect properties. Physical properties, including lattice constants, and dielectric constants can be reproduced and agree well with experimental data and other theoretical results; the results for the elastic constants and bulk moduli show poorer agreement. We improve the elastic properties by utilizing an additional 3-body interatomic potential, but it performs poorly for the defect calculation without the additional correction, which in turn worsens our physical property prediction. The classical Mott–Littleton method has been employed to investigate formation energies of formally charged native vacancy defects, interstitial defects, and Frenkel and Schottky defect pairs. We gain generally good agreement with previous classical and electronic structure calculations, although in some cases there are significant differences. We propose a new ground state N3− interstitialcy configuration, in which an on-site N atom is nudged away from its original position as a response to the Madelung potential and the short-range force from the N3− defect. A comprehensive investigation of point defect migration suggests that the energy barriers of self-diffusion in AlN are very close to the counterparts in GaN. We found lower migration barriers for vacancy migration in the axial direction than in basal direction. This result contrasts with previous DFT calculations. We propose two interstitialcy migration mechanisms for the interstitial defects: the “knock-out” mechanism for Al interstitial and the “hand-over” mechanism for N interstitialcy defects, both of which are more favourable than c-axis channel migration. The detailed mechanisms of defect migration uncovered in this work would play a significant role across the whole class of wurtzite structured material. Furthermore, with the assistance of the QM/MM method, the model can predict the VBM (−7.35 eV) accurately compared with experimental data, which shows the approach here still has use for electronic structure calculations. Future work will employ the hybrid QM/MM method to investigate other problems including defect formation energy with different electronic charge states and their donor/acceptor behaviour.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the use of the computer system (Faraday/Xenon) at Chemistry Department, UCL, the UCL Kathleen High Performance Computing Facility (Kathleen@UCL), and associated support services, in the completion of this work. We are grateful for the generous help to Julian Gale. For the QM/MM calculation, we acknowledge the use of ARCHER (http://www.archer.ac.uk) and ARCHER2 (http://www.archer2.ac.uk) UK National Supercomputing Service, via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431, EP/T022213, EP/X035859). For the VASP benchmarking calculations, we acknowledge the use of MMM Hub Thomas via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/P020194 and EP/T022213). The co-author Qing Hou acknowledges funding from Shanghai Pujiang Program (grant 22PJ1411300).References
- T. Takano, T. Mino, J. Sakai, N. Noguchi, K. Tsubaki and H. Hirayama, Deep-ultraviolet light-emitting diodes with external quantum efficiency higher than 20% at 275 nm achieved by improving light-extraction efficiency, Appl. Phys. Express, 2017, 10, 31002 CrossRef.
- M. Kneissl, T. Y. Seong, J. Han and H. Amano, The emergence and prospects of deep-ultraviolet light-emitting diode technologies, Nat. Photonics, 2019, 13, 233–244 CrossRef CAS.
- Y. Taniyasu, M. Kasu and T. Makimoto, An aluminium nitride light-emitting diode with a wavelength of 210 nanometres, Nature, 2006, 441, 325–328 CrossRef CAS PubMed.
- G. A. Slack, Nonmetallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS.
- G. A. Slack and S. F. Bartram, Thermal expansion of some diamondlike crystals, J. Appl. Phys., 1975, 46, 89–98 CrossRef CAS.
- D. Gerlich, S. L. Dole and G. A. Slack, Elastic properties of aluminum nitride, J. Phys. Chem. Solids, 1986, 47, 437–441 CrossRef CAS.
- G. A. Slack, R. A. Tanzilli, R. O. Pohl and J. W. Vandersande, The intrinsic thermal conductivity of AIN, J. Phys. Chem. Solids, 1987, 48, 641–647 CrossRef CAS.
- R. Hahn, V. Glaw, A. Ginolas, M. Töpfer, K. Wittke and H. Reichl, High performance liquid cooled aluminium nitride heat sinks, Microelectron. Int., 1999, 16, 21–26 CrossRef CAS.
- Y. Xue, H. Wang, N. Xie, Q. Yang, F. Xu, B. Shen, J. Shi, D. Jiang, X. Dou, T. Yu and B. Sun, Single-Photon Emission from Point Defects in Aluminum Nitride Films, J. Phys. Chem. Lett., 2020, 11, 2689–2694 CrossRef CAS PubMed.
- J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. de Walle and D. D. Awschalom, Quantum computing with defects, Proc. Natl. Acad. Sci. U.S.A., 2010, 107, 8513–8518 CrossRef CAS PubMed.
- G. A. Slack and T. F. McNelly, Growth of high purity AlN crystals, J. Cryst. Growth, 1976, 34, 263–279 CrossRef CAS.
- M. Lamprecht, V. N. Jmerik, R. Collazo, Z. Sitar, S. v Ivanov and K. Thonke, Model for the deep defect-related emission bands between 1.4 and 2.4 eV in AlN, Phys. Status Solidi B, 2017, 254, 1600714 CrossRef.
- G. Liu, C. Yan, G. Zhou, J. Wen, Z. Qin, Q. Zhou, B. Li, R. Zheng, H. Wu and Z. Sun, Broadband White-Light Emission from Alumina Nitride Bulk Single Crystals, ACS Photonics, 2018, 5, 4009–4013 CrossRef CAS.
- I. A. Aleksandrov, V. G. Mansurov, V. F. Plyusnin and K. S. Zhuravlev, Time-resolved photoluminescence characterization of 2 eV band in AlN, Phys. Status Solidi C, 2015, 12, 353–356 CrossRef CAS.
- A. Sedhain, L. Du, J. H. Edgar, J. Y. Lin and H. X. Jiang, The origin of 2.78 eV emission and yellow coloration in bulk AlN substrates, Appl. Phys. Lett., 2009, 95, 262104 CrossRef.
- S. Tojo, R. Yamamoto, R. Tanaka, Q. T. Thieu, R. Togashi, T. Nagashima, T. Kinoshita, R. Dalmau, R. Schlesser, H. Murakami, R. Collazo, A. Koukitu, B. Monemar, Z. Sitar and Y. Kumagai, Influence of high-temperature processing on the surface properties of bulk AlN substrates, J. Cryst. Growth, 2016, 446, 33–38 CrossRef CAS.
- S. M. Evans, N. C. Giles, L. E. Halliburton, G. A. Slack, S. B. Schujman and L. J. Schowalter, Electron paramagnetic resonance of a donor in aluminum nitride crystals, Appl. Phys. Lett., 2006, 88, 62112 CrossRef.
- J.-M. Mäki, I. Makkonen, F. Tuomisto, A. Karjalainen, S. Suihkonen, J. Räisänen, T. Y. Chemekova and Y. N. Makarov, Identification of the VAl-ON defect complex in AlN single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 81204 CrossRef.
- J. S. Harris, J. N. Baker, B. E. Gaddy, I. Bryan, Z. Bryan, K. J. Mirrielees, P. Reddy, R. Collazo, Z. Sitar and D. L. Irving, On compensation in Si-doped AlN, Appl. Phys. Lett., 2018, 112, 152101 CrossRef.
- S. Ichikawa, M. Funato and Y. Kawakami, Dominant Nonradiative Recombination Paths and Their Activation Processes in AlxGa1−xN-related Materials, Phys. Rev. Appl., 2018, 10, 64027 CrossRef CAS.
- D. Alden, J. S. Harris, Z. Bryan, J. N. Baker, P. Reddy, S. Mita, G. Callsen, A. Hoffmann, D. L. Irving, R. Collazo and Z. Sitar, Point-Defect Nature of the Ultraviolet Absorption Band in AlN, Phys. Rev. Appl., 2018, 9, 54036 CrossRef CAS.
- R. Collazo, J. Xie, B. E. Gaddy, Z. Bryan, R. Kirste, M. Hoffmann, R. Dalmau, B. Moody, Y. Kumagai, T. Nagashima, Y. Kubota, T. Kinoshita, A. Koukitu, D. L. Irving and Z. Sitar, On the origin of the 265 nm absorption band in AlN bulk crystals, Appl. Phys. Lett., 2012, 100, 191914 CrossRef.
- B. E. Gaddy, Z. Bryan, I. Bryan, R. Kirste, J. Xie, R. Dalmau, B. Moody, Y. Kumagai, T. Nagashima, Y. Kubota, T. Kinoshita, A. Koukitu, Z. Sitar, R. Collazo and D. L. Irving, Vacancy compensation and related donor-acceptor pair recombination in bulk AlN, Appl. Phys. Lett., 2013, 103, 161901 CrossRef.
- T. Mattila and R. M. Nieminen, Point-defect complexes and broadband luminescence in GaN and AlN, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 9571–9576 CrossRef CAS.
- I. Gorczyca, A. Svane and N. E. Christensen, Theory of point defects in GaN, AlN, and BN: Relaxation and pressure effects, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8147–8157 CrossRef CAS.
- C. Stampfl and C. G. Van de Walle, Theoretical investigation of native defects, impurities, and complexes in aluminum nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155212 CrossRef.
- K. Laaksonen, M. G. Ganchenkova and R. M. Nieminen, Vacancies in wurtzite GaN and AlN, J. Phys.: Condens. Matter, 2009, 21, 15803 CrossRef CAS PubMed.
- C. G. van de Walle and J. Neugebauer, First-principles calculations for defects and impurities: applications to III-nitrides, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- M. A. Caro, S. Schulz and E. P. O'Reilly, Hybrid functional study of the elastic and structural properties of wurtzite and zinc-blende group-III nitrides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 14117 CrossRef.
- Q. Yan, A. Janotti, M. Scheffler and C. G. Van de Walle, Origins of optical absorption and emission lines in AlN, Appl. Phys. Lett., 2014, 105, 111104 CrossRef.
- Y. Gao, D. Sun, X. Jiang and J. Zhao, Point defects in group III nitrides: a comparative first-principles study, J. Appl. Phys., 2019, 125, 215705 CrossRef.
- A. Walsh, C. R. A. Catlow, A. A. Sokol and S. M. Woodley, Physical Properties, Intrinsic Defects, and Phase Stability of Indium Sesquioxide, Chem. Mater., 2009, 21, 4962–4969 CrossRef CAS.
- Q. Hou, J. Buckeridge, T. Lazauskas, D. Mora-Fonz, A. A. Sokol, S. M. Woodley and C. R. A. Catlow, Defect formation in In2O3 and SnO2: a new atomistic approach based on accurate lattice energies, J. Mater. Chem. C, 2018, 6, 12386–12395 RSC.
- A. Walsh, S. M. Woodley, C. R. A. Catlow and A. A. Sokol, Potential energy landscapes for anion Frenkel-pair formation in ceria and india, Solid State Ionics, 2011, 184, 52–56 CrossRef CAS.
- X. Zhang, L. Zhu, Q. Hou, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Toward a Consistent Prediction of Defect Chemistry in CeO2, Chem. Mater., 2023, 35, 207–227 CrossRef CAS PubMed.
- A. N. Cormack, Intrinsic Disorder in Aluminum Nitride, J. Am. Ceram. Soc., 1989, 72, 1730–1732 CrossRef CAS.
- J. A. Chisholm, D. W. Lewis and P. D. Bristowe, Classical simulations of the properties of group-III nitrides, J. Phys. Condens. Matter, 1999, 11, L235–L239 CrossRef CAS.
- F. Benkabou, H. Aourag, P. J. Becker and M. Certier, Molecular Dynamics Study of Zinc-Blende GaN, AIN and InN, Mol. Simul., 2000, 23, 327–341 CrossRef CAS.
- F. Benkabou, M. Certier and H. Aourag, Elastic Properties of Zinc-blende GaN, AlN and InN from Molecular Dynamics, Mol. Simul., 2003, 29, 201–209 CrossRef CAS.
- S. Goumri-Said, M. B. Kanoun, A. E. Merad, G. Merad and H. Aourag, Prediction of structural and thermodynamic properties of zinc-blende AlN: molecular dynamics simulation, Chem. Phys., 2004, 302, 135–141 CrossRef CAS.
- D. Powell, M. A. Migliorato and A. G. Cullis, Optimized Tersoff potential parameters for tetrahedrally bonded III-V semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115202 CrossRef.
- J. Kioseoglou, P. Komninou and T. Karakostas, Interatomic potential calculations of III(Al, In)–N planar defects with a III-species environment approach, Phys. Status Solidi B, 2008, 245, 1118–1124 CrossRef CAS.
- M. Tungare, Y. Shi, N. Tripathi, P. Suvarna and F. (Shadi) Shahedipour-Sandvik, A Tersoff-based interatomic potential for wurtzite AlN, Phys. Status Solidi A, 2011, 208, 1569–1572 CrossRef CAS.
- P. Vashishta, R. K. Kalia, A. Nakano and J. P. Rino, Interaction potential for aluminum nitride: A molecular dynamics study of mechanical and thermal properties of crystalline and amorphous aluminum nitride, J. Appl. Phys., 2011, 109, 33514 CrossRef.
- P. Ruterana, B. Barbaray, A. Béré, P. Vermaut, A. Hairie, E. Paumier, G. Nouet, A. Salvador, A. Botchkarev and H. Morkoç, Formation mechanism and relative stability of the {112�0} stacking fault atomic configurations in wurtzite (Al,Ga,In) nitrides, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15917–15925 CrossRef CAS.
- K. Choudhary, T. Liang, K. Mathew, B. Revard, A. Chernatynskiy, S. R. Phillpot, R. G. Hennig and S. B. Sinnott, Dynamical properties of AlN nanostructures and heterogeneous interfaces predicted using COMB potentials, Comput. Mater. Sci., 2016, 113, 80–87 CrossRef CAS.
- A. P. Bartók, J. Kermode, N. Bernstein and G. Csányi, Machine Learning a General-Purpose Interatomic Potential for Silicon, Phys. Rev. X, 2018, 8, 41048 Search PubMed.
- L. C. Erhard, J. Rohrer, K. Albe and V. L. Deringer, A machine-learned interatomic potential for silica and its relation to empirical models, npj Comput. Mater., 2022, 8, 90 CrossRef.
- J. D. Gale and A. L. Rohl, The General Utility Lattice Program (GULP), Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, 1998 Search PubMed.
- B. G. Dick and A. W. Overhauser, Theory of the Dielectric Constants of Alkali Halide Crystals, Phys. Rev., 1958, 112, 90–103 CrossRef.
- C. R. A. Catlow, Point defect and electronic properties of uranium dioxide, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1977, 353, 533–561 CAS.
- G. v Lewis and C. R. A. Catlow, Potential models for ionic oxides, J. Phys. C Solid State Phys., 1985, 18, 1149–1161 CrossRef.
- N. C. Pyper and A. D. Buckingham, Relativistic AB Initio calculations of the properties of ionic solids, Phil. Trans. Roy. Soc. Lond. Math. Phys. Sci., 1986, 320, 107–158 CrossRef CAS.
- M. Miskufova, PhD thesis, University College of London, 2011.
- J. C. Slater and J. G. Kirkwood, The Van Der Waals Forces in Gases, Phys. Rev., 1931, 37, 682–697 CrossRef CAS.
- H. Schulz and K. H. Thiemann, Crystal structure refinement of AlN and GaN, Solid State Commun., 1977, 23, 815–819 CrossRef CAS.
- K. Tsubouchi, K. Sugai and N. Mikoshiba, in 1981 Ultrasonics Symposium, 1981, pp. 375–380 Search PubMed.
- L. E. Mcneil, C. Hill, N. Carolina and R. H. French, Vibrational Spectroscopy of Aluminum Nitride, J. Am. Ceram. Soc., 1993, 76, 1132–1136 CrossRef CAS.
- G. Bu, D. Ciplys, M. Shur, L. J. Schowalter, S. Schujman and R. Gaska, Surface acoustic wave velocity in single-crystal AlN substrates, IEEE Trans. Ultrason. Ferroelectrics Freq. Control, 2006, 53, 251–254 Search PubMed.
- A. T. Collins, E. C. Lightowlers and P. J. Dean, Lattice vibration spectra of aluminum nitride, Phys. Rev., 1967, 158, 833–838 CrossRef CAS.
- M. E. Levinshtein, S. L. Rumyantsev, M. Shur, V. Bougrov and A. Zubrilov, Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe, John Wiley Sons Inc, New York, 1st edn, 2001 Search PubMed.
- L. Xinjiao, X. Zechuan, H. Ziyou, C. Huazhe, S. Wuda, C. Zhongcai, Z. Feng and W. Enguang, On the properties of AlN thin films grown by low temperature reactive R.F. sputtering, Thin Solid Films, 1986, 139, 261–274 CrossRef.
- A. F. Wright, Elastic properties of zinc-blende and wurtzite AIN, GaN, and InN, J. Appl. Phys., 1997, 82, 2833–2839 CrossRef CAS.
- I. A. Aleksandrov and K. S. Zhuravlev, Luminescence line shapes of band to deep centre and donor–acceptor transitions in AlN, J. Phys.: Condens. Matter, 2020, 32, 435501 CrossRef CAS PubMed.
- A. Zoroddu, F. Bernardini, P. Ruggerone and V. Fiorentini, First-principles prediction of structure, energetics, formation enthalpy, elastic constants, polarization, and piezoelectric constants of AlN, GaN, and InN: comparison of local and gradient-corrected density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 45208 CrossRef.
- I. Supryadkina, K. Abgaryan, D. Bazhanov and I. Mutigullin, Ab initio study of macroscopic polarization of AlN, GaN and AlGaN, Phys. Status Solidi C, 2014, 11, 307–311 CrossRef CAS.
- N. F. Mott and M. J. Littleton, Conduction in polar crystals. I. Electrolytic conduction in solid salts, Trans. Faraday Soc., 1938, 34, 485–499 RSC.
- J. D. Gale, GULP: a computer program for the symmetry-adapted simulation of solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- A. A. Sokol, S. T. Bromley, S. A. French, C. R. A. Catlow and P. Sherwood, Hybrid QM/MM embedding approach for the treatment of localized surface states in ionic materials, Int. J. Quantum Chem., 2004, 99, 695–712 CrossRef CAS.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, QUASI: a general purpose implementation of the QM/MM approach and its application to problems in catalysis, J. Mol. Struct., 2003, 632, 1–28 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Buckeridge, C. R. A. Catlow, M. R. Farrow, A. J. Logsdail, D. O. Scanlon, T. W. Keal, P. Sherwood, S. M. Woodley, A. A. Sokol and A. Walsh, Deep vs shallow nature of oxygen vacancies and consequent n-type carrier concentrations in transparent conducting oxides, Phys. Rev. Mater., 2018, 2, 54604 CrossRef CAS.
- Y. Lu, M. R. Farrow, P. Fayon, A. J. Logsdail, A. A. Sokol, C. R. A. Catlow, P. Sherwood and T. W. Keal, Open-Source, Python-Based Redevelopment of the ChemShell Multiscale QM/MM Environment, J. Chem. Theory Comput., 2019, 15, 1317–1328 CrossRef CAS PubMed.
- ChemShell, a Computational Chemistry Shell, https://www.chemshell.org/ Search PubMed.
- S. Limpijumnong and C. G. van de Walle, Diffusivity of native defects in GaN, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 35207 CrossRef.
- A. F. Wright, Interaction of hydrogen with nitrogen interstitials in wurtzite GaN, J. Appl. Phys., 2001, 90, 6526–6532 CrossRef CAS.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, M. R. Farrow, D. O. Scanlon, S. M. Woodley and A. A. Sokol, Donor and acceptor characteristics of native point defects in GaN, J. Phys. D Appl. Phys., 2019, 52, 335104 CrossRef CAS.
- A. Janotti, J. L. Lyons and C. G. Van de Walle, Hybrid functional calculations of native point defects in InN, Phys. Status Solidi A, 2012, 209, 65–70 CrossRef CAS.
- A. Szállás, K. Szász, X. T. Trinh, N. T. Son, E. Janzén and A. Gali, Characterization of the nitrogen split interstitial defect in wurtzite aluminum nitride using density functional theory, J. Appl. Phys., 2014, 116, 113702 CrossRef.
- D. K. Rowell and M. J. L. Sangster, Calculations of intrinsic defect energies in the alkali halides, J. Phys. C Solid State Phys., 1981, 14, 2909 CrossRef CAS.
- M. J. L. Sangster and D. K. Rowell, Calculation of defect energies and volumes in some oxides, Philos. Mag. A, 1981, 44, 613–624 CrossRef CAS.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, Identifying the ground state structures of point defects in solids, npj Comput. Mater., 2023, 9, 25 CrossRef CAS.
- I. Mosquera-Lois and S. R. Kavanagh, In search of hidden defects, Matter, 2021, 4, 2602–2605 CrossRef.
- I. Vurgaftman, J. R. Meyer and L. R. Ram-Mohan, Band parameters for III–V compound semiconductors and their alloys, J. Appl. Phys., 2001, 89, 5815–5875 CrossRef CAS.
- C. I. Wu and A. Kahn, Electronic states at aluminum nitride (0001)-1×1 surfaces, Appl. Phys. Lett., 1999, 74, 546–548 CrossRef CAS.
- S. P. Grabowski, M. Schneider, H. Nienhaus, W. Mönch, R. Dimitrov, O. Ambacher and M. Stutzmann, Electron affinity of AlxGa1−xN(0001) surfaces, Appl. Phys. Lett., 2001, 78, 2503–2505 CrossRef CAS.
- M. Mishra, S. Krishna, N. Aggarwal and G. Gupta, Influence of metallic surface states on electron affinity of epitaxial AlN films, Appl. Surf. Sci., 2017, 407, 255–259 CrossRef CAS.
- J. R. Rumble, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, USA, 102nd edn, 2020 Search PubMed.
- A. Fara, F. Bernardini and V. Fiorentini, Theoretical evidence for the semi-insulating character of AlN, J. Appl. Phys., 1999, 85, 2001–2003 CrossRef CAS.
- D. F. Hevia, C. Stampfl, F. Viñes and F. Illas, Microscopic origin of n-type behavior in Si-doped AlN, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 85202 CrossRef.
- Y. Zhang, W. Liu and H. Niu, Native defect properties and p-type doping efficiency in group-IIA doped wurtzite AlN, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 35201 CrossRef.
- M. Sterntzke and G. Müller, EELS Study of Oxygen Diffusion in Aluminum Nitride, J. Am. Ceram. Soc., 1994, 77, 737–742 CrossRef.
- E. N. Mokhov, M. K. Rabchinskiy, S. S. Nagalyuk, M. R. Gafurov and O. P. Kazarova, Effect of the Beryllium Acceptor Impurity upon the Optical Properties of Single-Crystal AlN, Semiconductors, 2020, 54, 278–281 CrossRef CAS.
- S. S. Dohyung Kim, H. Lee and Y. Naoi, High Temperature Diffusion in AlxGa1-xN and P-Type AlGaN by Al4C3, Int. J. Mater. Sci. Appl., 2014, 3, 177–182 Search PubMed.
- M. G. Ganchenkova and R. M. Nieminen, Nitrogen Vacancies as Major Point Defects in Gallium Nitride, Phys. Rev. Lett., 2006, 96, 196402 CrossRef CAS PubMed.
- K. H. Warnick, Y. Puzyrev, T. Roy, D. M. Fleetwood, R. D. Schrimpf and S. T. Pantelides, Room-temperature diffusive phenomena in semiconductors: The case of AlGaN, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 214109 CrossRef.
- A. Kyrtsos, M. Matsubara and E. Bellotti, Migration mechanisms and diffusion barriers of carbon and native point defects in GaN, Phys. Rev. B, 2016, 93, 245201 CrossRef.
- I. A. Aleksandrov, T. v Malin, K. S. Zhuravlev, S. v. Trubina, S. B. Erenburg, B. Pecz and Y. v. Lebiadok, Diffusion in GaN/AlN superlattices: DFT and EXAFS study, Appl. Surf. Sci., 2020, 515, 146001 CrossRef CAS.
- C. G. van de Walle, S. Limpijumnong and J. Neugebauer, First-principles studies of beryllium doping of GaN, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245205 CrossRef.
- R. Hrytsak, P. Kempisty, E. Grzanka, M. Leszczynski and M. Sznajder, DFT study on point defects migration through the pseudomorphic and lattice-matched InN/GaN interfaces, Comput. Mater. Sci., 2021, 186, 110039 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09503c |
| This journal is © The Royal Society of Chemistry 2023 |