Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion transport and growth behavior of solid electrolyte interphases on Li and Na with liquid electrolytes based on impedance analysis†‡
Kyungmi
Lim
,
Jelena
Popovic§
 * and
Joachim
Maier
* and
Joachim
Maier
Max Planck Institute for Solid State Research, 70569 Stuttgart, Germany. E-mail: popovic@fkf.mpg.de; jelena.popovic-neuber@uis.no
First published on 13th February 2023
Abstract
Electrochemical impedance spectroscopy (EIS) is an irreplaceable tool for investigating ion transport mechanism and growth of solid electrolyte interphases (SEIs) on Li or Na electrodes. Nevertheless, studies providing understanding of the EIS response and establishing a proper equivalent circuit models for SEIs are rare. In this study, using already published and new data, we develop a most simplified, but suitable EIS model by focusing not only on the measured resistances but also on the corresponding activation energies of ion transport and the respective capacitances. The equivalent circuit model takes account of channels filled with liquid electrolyte in parallel with the more resistive bulk parts of the SEI. The growth of initially porous SEIs proceeds at the liquid/solid interface in the channel, where an additional thin passivation layer (for example native film) may exist. The channels (in reality pores of solid SEI) are either eventually filled, or, if the products from the reaction between liquid electrolytes and alkali metals possess a very different molar volume compared to the already-existing material (Li or Na), another internally porous SEI structure forms. The first scenario seems rather typical for Li, in particular at longer growth times. The latter potentially self-similar-growth behavior seems to apply for contacts of glyme-based liquid electrolyte with Na. Inclusion of the lateral compaction effects in an extended model allows for remarkably good description for the Na/glyme scenario.
1. Introduction
Battery technology continuously changes our lives by enabling the easier use of portable electronic devices and electric vehicles, as well as enabling fossil fuel-free economy.1,2 Despite the substantial improvement of energy density of batteries over the years, the fundamental understanding of the exact physical origin of the overpotential in the battery cells is still insufficient.3–5 The overpotential is determined by a variety of kinetic factors including ohmic drop, charge transfer at interfaces, charge transport within the crystal structure of materials (solid-state diffusion), concentration polarization in electrolytes and additional parasitic reactions.4,6,7 Electrochemical impedance spectroscopy (EIS) is a powerful technique for achieving a more detailed understanding of the electrical transport, since it allows decoupling of kinetic processes with different relaxation times by measurement at a wide frequency range (MHz to mHz).8–11 In particular, EIS is an indispensable method for the investigation of the solid electrolyte interphase (SEI), the organic/inorganic thin passivation layer formed by the (electro)chemical decomposition of electrolyte in contact with the respective electrode.12–14 The experimental difficulties of SEI studies include air-sensitivity and the inherently complex and fragile SEI morphology composed of many chemical compounds with variable mechanical properties and sometimes non-negligible amount of pores.15–23 The above mentioned problems pose even greater challenges for the studies of SEIs on the reactive Li/Na metals, currently considered to be the attractive anode materials for future-generation batteries.24–28 Although novel experimental strategies such as cryo-transmission electron microscopy (TEM),29–32 X-ray-based analytical tools33–35 and nuclear magnetic resonance (NMR) spectroscopy have been recently applied in SEI research,32,36–40 EIS offers particular advantages, as it enables us to distinguish between different electrochemical transport processes in situ and in a non-destructive way.10,41–43Recently, we collected evidence that SEIs on the alkali metals are porous, especially for the Na case.44 The corresponding equivalent circuit model based on the so far not published data, as well as their growth mechanisms will be discussed in this paper. Very general models, such as a transmission line model, have frequently been used to treat the ionic transport in porous electrodes. However, given the high complexity of the system, the parametrization of such models remains difficult.45–50 Rather than applying such a deductive approach, we follow an inductive approach, which is based on a most simplified equivalent circuit which contains a minimum number of circuit elements. Guided by the values of activation energy and relaxation times, which enable us to identify the major transport pathways, we chose the basic motif to be as simple as possible, and make it more complex only if it appears unavoidable. In addition to studying initial structures, we follow and discuss the growth behavior of SEIs on Li/Na over time under open circuit potential (OCP) from the EIS data and give suggestions about the feasible morphological changes of the SEI. Using such simple concepts, the growth behavior of the systems under concern can be described amazingly well on a semi-quantitative level. We highlight the importance of measuring the activation energy (Ea) and inspecting the capacitances, since these parameters provide insight into the dominant ionic transport pathways and the morphology of the SEIs.
2. Results and discussion
2.1. Equivalent circuit model for ion transport in the SEI
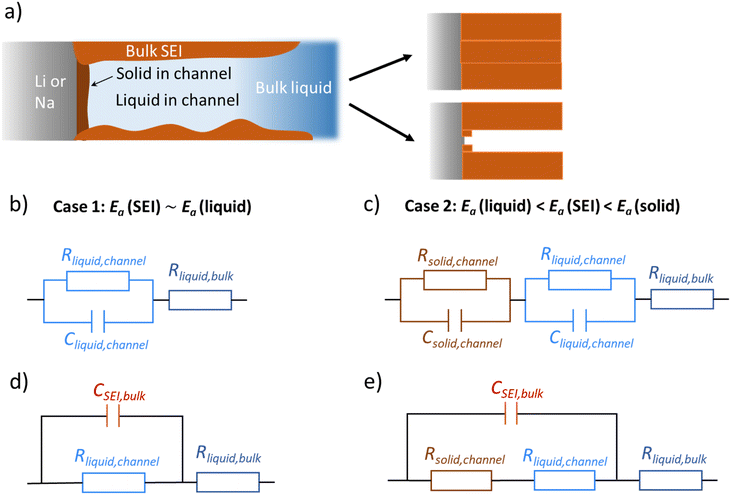
Li and Na electrodes were contacted with two types of liquid electrolytes (glyme-based and carbonate-based) and the resulting symmetric cells were measured with EIS. The experimental details were given in a previous publication and can also be found in the ESI.‡44 The initial impedance spectra are shown in the ESI (Fig. S1‡), where only a single semicircle is observed in the Nyquist plot for the measured frequency range (106∼1 Hz). The semicircle corresponds to transport in the SEI as supported by the values of capacitances which are in the range of 10−7 to 10−6 F cm−2,51 and the values of relaxation times (Fig. 2, will be discussed later), which do not correspond to the ion transport in bulk liquid electrolyte or to the concentration polarization (e.g. in bulk liquid electrolyte or in liquid electrolyte inside of open-pores, see Fig. S1‡ for more details). However, for the situation when some or many pores are closed (e.g. liquid electrolyte encapsulated in solid SEI), such concentration polarization may not be negligible. We also neglect current constriction phenomena, as we expect a large number of closely packed pores. In our previous study, we proved that SEIs on Na metal electrodes formed by the contact with glyme- and carbonate-based salt-in-solvent electrolytes are porous directly after assembly, and remain porous even after the symmetric electrochemical cell was aged under OCP for 600 hours.44 This finding was supported by the measured activation energy of ionic transport in the SEI (Ea(SEI)) (0.15–0.3 eV for the initial storage with Na, showing values close to the ones of the respective liquid electrolyte). Further corroboration stems from focused-ion beam-scanning electron microscopy (FIB-SEM) images, where a number of larger pores (ca. 50 nm) were visible.44 Thus, the SEI semicircle observed for SEI on Na metal should not be interpreted as just a contribution of composite material of several solid phases, as previously suggested for Li metal.52–54 Such SEI semicircle rather corresponds to a complex transport through a solid–liquid composite material.In order to model our EIS data, we start out with the most meaningful parameter as far as the identification of the rate determining step of ion transport through the SEI is concerned, namely the Ea, derived from the temperature dependence of the (temperature)/(diameter of the semicircle arc) from our previous publication. The most striking difference between the Li and Na SEIs is the contrasting value of Ea(SEI) measured at the early stages of the SEI formation (Table 1). The measured Ea values support the claim that Na SEIs are more porous than Li SEIs, since the Ea values of solid-state SEI compounds are much higher than and the ones of the liquid electrolytes (see ESI, Tables S1 and S2‡). Furthermore, the measured effective ionic conductivities of the SEI (σSEI) calculated from the SEI geometry (Table 1) and the measured resistance in the systems are at least four orders of magnitude higher than the ionic conductivity values of Li/Na single inorganic SEI compounds (Tables S1 and S2‡). As already mentioned in our previous work, the higher porosity of the Na SEI in contrast to the Li SEI is most likely attributable to the volume effects during the passivation layer formation characterized by the Pilling–Bedworth ratios (RPB, the molar volume ratio between the SEI compounds and the metal). These are smaller than unity for the relevant Na SEI compounds.44 Naturally, the liquid electrolyte in the channel (termed channel liquid) is not expected to be thermodynamically stable against the alkali metals, giving rise to reaction layers at the metal surface. However, such layers must be thin, in particular initially, so that their resistance contribution remains negligible.
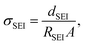 where dSEI is SEI thickness, RSEI is the measured SEI resistance and A is the known geometric surface area of the electrode. Note that Ea, RSEI and dSEI values are from our previous study, ref. 44. Cm was calculated from
where dSEI is SEI thickness, RSEI is the measured SEI resistance and A is the known geometric surface area of the electrode. Note that Ea, RSEI and dSEI values are from our previous study, ref. 44. Cm was calculated from 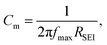 where f is the peak frequency in which the |ZIm| value becomes a maximum for the semicircle corresponding to RSEI
where f is the peak frequency in which the |ZIm| value becomes a maximum for the semicircle corresponding to RSEI
| System | E a(SEI)/eV | σ SEI/S cm−1 | C m/F |
|---|---|---|---|
| Li|1 M LiTf in triglyme|Li | 0.52 | 2.20 × 10−7 | 8.33 × 10−7 |
| Li|1 M LiTf in EC/DMC|Li | 0.55 | 1.92 × 10−7 | 8.79 × 10−7 |
| Na|1 M NaTf in triglyme|Na | 0.15 | 5.24 × 10−5 | 5.52 × 10−6 |
| Na|1 M NaTf in EC/DMC|Na | 0.30 | 4.64 × 10−7 | 1.25 × 10−6 |
Let us start with the general morphological conception which will later serve as an adequate guide for the two cases (Li, Na) we refer to experimentally. We consider an alkali metal electrode in contact with an electrolyte, which gives rise to formation of a passivation layer (e.g. SEI) which – for simplicity – we assume to be chemically homogeneous. We assume that there is an opening in the SEI in which again an unprotected contact of the electrolyte to the electrode occurs and SEI forms within the opening. Let us now discuss the fate of this layer. We distinguish between two extreme scenarios, in an ideal case dictated by the molar volume change during the SEI formation reaction. In the first case, if the opening in the SEI is small, it plays a role of a film perturbation. Then, in a diffusion-controlled SEI growth case, where growth decreases with the layer thickness, the opening is quickly filled, and a continuous smooth layer is formed. The opposite occurs in the second case, if the molar volume change is significant. Here such an opening in the SEI occurs by necessity, namely, to accommodate the mismatch of the molar volumes. The newly formed product at the fresh contact will face the same mechanical problem leading to a formation of smaller openings in this thin internal layer. As the argument applies to even smaller dimension in this extremely simplified scenario, a self-similar structure is expected. Of course, the reality will restrict this self-similarity to a few steps only, and the growth will be additionally affected by island formation. Below we will put the model on a more realistic footing by inclusion of lateral agglomeration of initially formed islands.
Fig. 1a provides the simplified schematics of the SEI structure showing an opening (channel) in the SEI in which liquid electrolyte infiltrates into the bulk SEI. Bulk SEI represents the thick and resistive SEI. In the channels both the solid and liquid parts are present. The resistances and capacitances corresponding to these contributions are noted as RSEI,bulk, CSEI,bulk (for bulk SEI), Rsolid,channel, Csolid,channel (for the solids in channel), and Rliquid,channel, Cliquid,channel (for the liquid electrolyte in channel). Depending on the Ea(SEI) values of the investigated system (Table 1), two different cases of the equivalent circuit model are taken into account, as shown in Fig. 1b and c. The first case applies for the Ea(SEI) value which is comparable to the one of the liquid electrolyte, in our case for Na|1 M NaTf in triglyme|Na, where Rsolid,channel ≪ Rliquid,channel is valid. Thereby, the contributions from both Rsolid,channel and Csolid,channel may be neglected (see ESI, Fig. S2‡ for more details) and the equivalent circuit model is given in Fig. 1b. The second case can be applied for the Ea(SEI) values between Ea(liquid electrolyte) and the Ea(solid SEI compounds), where both the contribution from the solid and the liquid in the channel should be taken into account (Fig. 1c). In both cases, an apparent conductivity of the liquid in the channel (σliquid,channel) can be estimated based on the measured frequency range (Fig. S1‡), and turns out to be three orders of magnitude lower than the one of bulk liquid electrolyte (σliquid,channel = 2πε0εfpeak < 1.7 × 10−6 S cm−1), where fpeak is a peak frequency in which the |ZIm| value becomes a maximum and ε0 is the vacuum permittivity. ε is the dielectric constant of liquid electrolyte, which is typically smaller than 30.55,56 As such a low value of ionic conductivity of liquid electrolyte seems unlikely, the so far neglected solid parallel part of the SEI should be taken into account in the equivalent circuit. Its conductance (1/RSEI,bulk) must still be negligible, as the measured liquid-like activation energy indicates. If the resistance is considered, the discrepancy between σliquid,channel and σliquid,bulk would be even larger. However, the parallel capacitance (CSEI,bulk) should matter, as the area fraction of the parallel channels is expected to be small. If the CSEI,bulk is taken into account, as shown in Fig. 1b and c (bottom), the conductivities of the channel-liquid and bulk-liquid become more similar. According to the measured SEI resistance values, Cliquid,channel is estimated to be in the order of 10−13 to 10−10 F 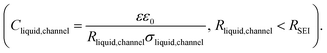 The measured capacitance values
The measured capacitance values 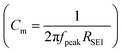 are listed in Table 1, which are four to six orders or magnitude higher than the Cliquid,channel values. This implies that most of the capacitance stem from the solid bulk SEI, meaning that the relaxation time is determined by the resistance of the liquid channel and the capacitance of the solid bulk SEI (τ ≅ RchannelCSEI,bulk, see Fig. 1d and e). Detailed understanding of the pore geometry and distribution, which could possibly be achieved with cryo-TEM, would be the next logical step towards full characterization. This proved to be difficult until now, as the typical Ga ion beam FIB-SEM sample preparation technique available in our lab has not yielded suitable results due to reactivity of SEI, melting of the substrate (e.g. Li, Na) under the ion beam, and sample thickness limitations (ESI, Fig. S3‡). Indeed, these seem to be the typical problems other groups encounter when characterizing microstructure of SEIs on alkali metals, which may be circumvented by electrodeposition of metals on Cu TEM grid, or by using in situ cryo-TEM cells.57–59 However, in these cases, the SEI structures imaged may defer from the ones occurring in real battery cells due to the differences in the cell pressure and electrolyte to electrode volume ratio.
are listed in Table 1, which are four to six orders or magnitude higher than the Cliquid,channel values. This implies that most of the capacitance stem from the solid bulk SEI, meaning that the relaxation time is determined by the resistance of the liquid channel and the capacitance of the solid bulk SEI (τ ≅ RchannelCSEI,bulk, see Fig. 1d and e). Detailed understanding of the pore geometry and distribution, which could possibly be achieved with cryo-TEM, would be the next logical step towards full characterization. This proved to be difficult until now, as the typical Ga ion beam FIB-SEM sample preparation technique available in our lab has not yielded suitable results due to reactivity of SEI, melting of the substrate (e.g. Li, Na) under the ion beam, and sample thickness limitations (ESI, Fig. S3‡). Indeed, these seem to be the typical problems other groups encounter when characterizing microstructure of SEIs on alkali metals, which may be circumvented by electrodeposition of metals on Cu TEM grid, or by using in situ cryo-TEM cells.57–59 However, in these cases, the SEI structures imaged may defer from the ones occurring in real battery cells due to the differences in the cell pressure and electrolyte to electrode volume ratio.
In the second case, the resistance stemming from the channel (Rchannel) can be described by a function of the resistance from the solid SEI in the channel (Rsolid,channel) and the one from the liquid in the channel (Rliquid,channel) as follows:
| Rchannel = Rsolid,channel + Rliquid,channel. | (1) |
Since 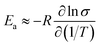 (where R is the gas constant, T is the temperature), eqn (1) can – using the identity
(where R is the gas constant, T is the temperature), eqn (1) can – using the identity 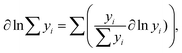 60 – be transformed into
60 – be transformed into
 | (2) |
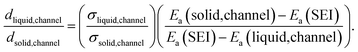 | (3) |
Upon additional assumption that the SEI resistance is solely dominated by the channel (RSEI = Rchannel), the thickness ratio 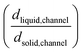 can be plotted as a function of Ea(solid,channel) and σsolid,channel (Fig. S4‡). The obtained results indicate that the thickness of the liquid channel is orders of magnitude higher than the one of solid part in the liquid channel, unless the solid is conductive enough (σsolid,channel > 10−6 S cm−1, Ea(solid,channel) < 0.5 eV).
can be plotted as a function of Ea(solid,channel) and σsolid,channel (Fig. S4‡). The obtained results indicate that the thickness of the liquid channel is orders of magnitude higher than the one of solid part in the liquid channel, unless the solid is conductive enough (σsolid,channel > 10−6 S cm−1, Ea(solid,channel) < 0.5 eV).
2.2. SEI growth under open circuit potential condition
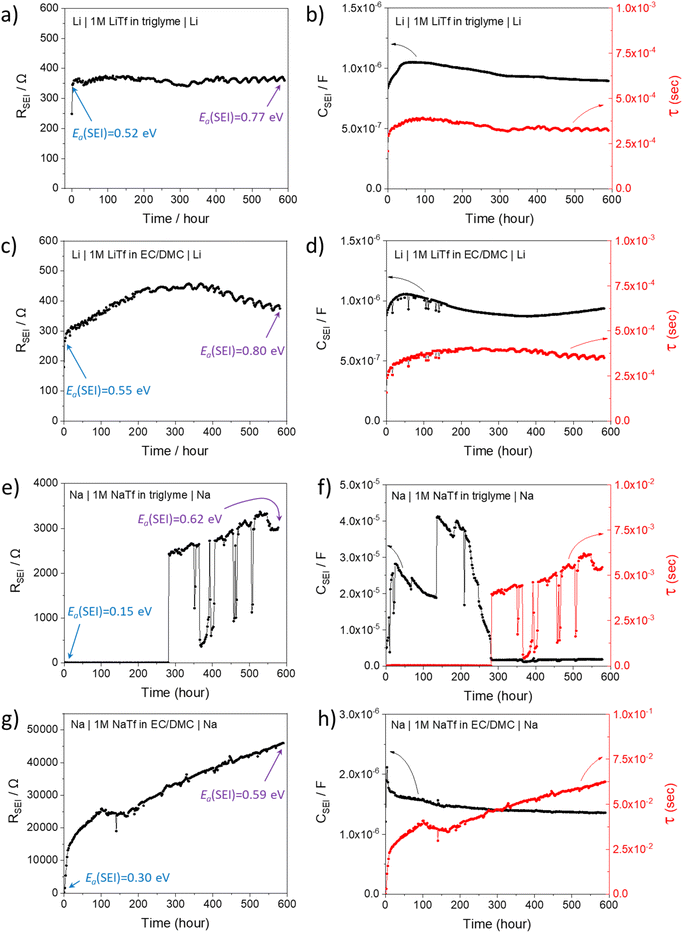
In order to better understand the growth specific kinetics, the model needs refinement. Let us first consider Fig. 2 which shows the time evolution of SEI resistance (RSEI), SEI capacitance (CSEI, derived in the same way as it was done for Cm in Table 1) and relaxation times (τ = RSEICSEI) recorded under open-circuit conditions for approximately 600 hours for four characteristic systems in Fig. 2. Classic thin film growth laws are typically parabolic (diffusion-controlled) and linear (interfacially-controlled),61,62 but the real situation might deviate from the models owing to the chemical and morphological complexity. Compared to the case of Li where relatively mild changes of RSEI and CSEI over time were observed (Fig. 2a–d), the Na system experiences striking changes of RSEI and τ, while CSEI varies less (Fig. 2e–h). We ascribe the distinguished behavior of Na compared to Li to the Pilling–Bedworth ratio as mentioned previously, implying that pores are continuously created, leading to continuous infiltration of the liquid and subsequent chemical reaction, whenever the liquid meets the naked alkali metal. For the SEI forming on Li where RPB is greater than unity (in the case of several SEI compounds such as Li2CO3 (1.35), LiOH (1.26) and Li2S (1.06)), more morphologically-uniform and denser SEI (compared to Na SEI) seems to be realized. The local chemical reaction at the metal/liquid contacts will lead to the SEI growth and thus to the increase of the Ea. Fig. 2 shows such an increase of RSEI and Ea(SEI) values upon aging for all Li/Na symmetric cells under consideration, regardless of the used electrolytes.The most interesting SEI growth behavior was observed in the Na symmetric cell with glyme-based electrolyte (Fig. 2e). The initial behavior of RSEI (t < 280 hours) shows a long period of low resistance (few ohms) where the Ea tells us that the ion transport mechanism through liquid phase is dominant, followed by an abrupt increase of the SEI resistance and subsequent intermittent interruptions. For the purpose of examining the reproducibility of data, six Na–glyme cells were assembled and measured with the identical experimental method (ESI, Fig. S5‡). All cells showed similar RSEI behavior over time (small RSEI values until 100–200 hours and abrupt increase, followed by intermittent RSEI drops). The increase can be ascribed to the situation in which transport in the pore-solid becomes the rate determining step, while the abruptness may be attributable to the densification of the pores in a lateral direction, caused by the ongoing reaction in the pores or external pressure built up in the cell. The following intermittent resistance drop indicates partial channel formation connected with the newly formed as a result of the (i) analogous mechanical instability discussed above, (ii) dissolution of the SEI,63–65 or (iii) mechanical detachment in the course of continuous chemical reaction. If the RPB values of the reaction products in the liquid channel are similar to the ones of the initial SEI formation, a continuous pore formation with a certain degree of self-similarity can be expected. This means that the sequence of infiltration, reaction, growth and cracking can be continued on a continuously smaller scale. A self-similar evolution of SEI would demand continuously lower SEI growth periods and continuously higher residual resistances, a feature that despite the oversimplification seems to be met in Fig. 3. The interpretation of the growth mechanism of SEI on Na in glyme-based electrolytes used in this study is as follows: The Na SEI is initially porous, thus the resistance is dominated by the ion transport in the liquid channel. Blocking within the liquid channels by newly formed reaction products at the Na surface connected with densification leads to the abrupt increase in resistance. The SEI-forming reaction progresses with mechanical instability of the SEI, and seemingly in a self-similar manner. Note that this picture is strongly simplified and additional kinetic pathways are possible.
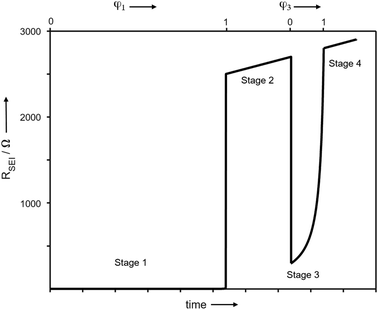 | ||
| Fig. 3 Modelling of the thin film growth where volume changes are such that islands occur. Such islands grow together laterally to form a more compact film (stage 1), which then grows according to a linear growth law (stage 2). After a mechanical instability, the film cracks, and in the opening, the same scenario repeats (stage 3) etc. The detailed parameters are given in ESI,‡ but the comparison with Fig. 2e shows the remarkable reproduction of all the basic growth features. | ||
Let us put this on a more quantitative level by also including lateral morphological effects. For the system under concern, we expect the formation of islands soon after contact of the electrolyte with the metal. The islands are initially isolated, but in the course of time they will form an increasingly dense layer. In this stage, this portion of a surface film can be treated as a composite of solid and liquid portions with increasing volume fraction of the solids. We then can approximate the overall resistance RSEI as
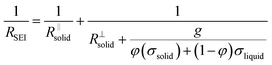 | (4a) |
The right-hand term in the denominator of the second summand takes account of this composite contribution, with σsolid, σliquid describing the conductivities of the two phases, while g is a geometrical factor standing the ratio for thickness (d) and area (A) of the composite (in the channels). 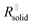 is short for the resistance parallel to the channels;
is short for the resistance parallel to the channels; 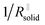 is negligible in the very beginning where the compaction affects the entire contact area, but becomes increasingly important at later stages.
is negligible in the very beginning where the compaction affects the entire contact area, but becomes increasingly important at later stages. 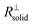 is the series contribution of compact film portions within the channels. It can be neglected in the following. With a slight rearrangement we write
is the series contribution of compact film portions within the channels. It can be neglected in the following. With a slight rearrangement we write
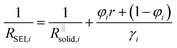 | (4b) |
After the abrupt R-increase (now the islands have formed a resistive, comparatively closed layer), RSEI increases linearly within time (stage 2). The linearity indicates that the product formation is not determined by the flux through the product but rather by liquid transport. Note that the highly resistive film (realized in stage 2) is still not as resistive as a very dense film and exhibits an activation energy which is still lower than that of the pure solid, indicating remaining porosity. This is also seen by comparison with the resistance values of Fig. 2g. (The fact that RSEI is higher than in Fig. 2a reflects the lower conductivity of the Na-compounds compared to the Li-compounds (see ESI‡)). This porous film then reaches a thickness where cracking occurs (the low mechanical strength can be attributed to the porosity). The resistance drops to a level (stage 3) that is higher than in stage 1 as the area in which now island formation occurs is much smaller, while the other parts are taken care of by 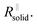 Again eqn (4a) can describe the further evolution, even the curved behavior in stage 3 is well reproduced even if r remains unchanged. This is a consequence of the
Again eqn (4a) can describe the further evolution, even the curved behavior in stage 3 is well reproduced even if r remains unchanged. This is a consequence of the 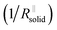 term: initially, i.e., at φ3 ≃ 0 its influence is minimal but becomes increasingly significant with increasing time (φ3) as the channels become more resistive. After the channel has become (partially) filled, the parallel resistance is the dominant contributor. This filling has to happen more quickly than in stage 1, as the area fraction of the channels is less than 1. If we assume d3 = d1 and σsolid to remain constant, an area fraction of 10−4 follows for which the observed filling time appears even too long. However, one can certainly assume that the channels are not completely filled (d3 < d1) and that the final film is porous (σsolid becoming higher) leading to a greater area fraction. The resistance of the porous SEI is nonetheless similar to that at the end of stage 2 (probably a little higher owing to the increased mass). In stage 4, linear growth dominates again, and the observed slope is similar so that the upper parts of the resistance could overall follow a linear growth law. This growth is interrupted due to mechanical instability which occurs earlier than in stage 2, owing to a higher overall inhomogeneity. As outlined before, this scenario may be expected to be continued roughly self-similarly. A more detailed analysis is given in the ESI,‡ here we just show the result for such fitting of Fig. 2e for 4 stages revealing the remarkable agreement. A more detailed description is pointless since in contrast to these characteristic patterns the details are not exactly reproduced.
term: initially, i.e., at φ3 ≃ 0 its influence is minimal but becomes increasingly significant with increasing time (φ3) as the channels become more resistive. After the channel has become (partially) filled, the parallel resistance is the dominant contributor. This filling has to happen more quickly than in stage 1, as the area fraction of the channels is less than 1. If we assume d3 = d1 and σsolid to remain constant, an area fraction of 10−4 follows for which the observed filling time appears even too long. However, one can certainly assume that the channels are not completely filled (d3 < d1) and that the final film is porous (σsolid becoming higher) leading to a greater area fraction. The resistance of the porous SEI is nonetheless similar to that at the end of stage 2 (probably a little higher owing to the increased mass). In stage 4, linear growth dominates again, and the observed slope is similar so that the upper parts of the resistance could overall follow a linear growth law. This growth is interrupted due to mechanical instability which occurs earlier than in stage 2, owing to a higher overall inhomogeneity. As outlined before, this scenario may be expected to be continued roughly self-similarly. A more detailed analysis is given in the ESI,‡ here we just show the result for such fitting of Fig. 2e for 4 stages revealing the remarkable agreement. A more detailed description is pointless since in contrast to these characteristic patterns the details are not exactly reproduced.
The behavior in Fig. 2g is strikingly different; here approximately a square root behavior is seen, i.e. the film growth is rather homogeneous and determined by the flux through the film. It may be assumed that the different electrolyte chemistry renders the film mechanically tougher and probably denser due to the difference in polymeric contributions. Accordingly, the resistance is higher even though the similar activation energy may suggest still the presence of liquid-filled pores that electrically contribute. The behaviour of the capacitance (Fig. 2f) is also interesting as the absolute variations are smaller and it exhibits structures already in stage 1, before it decreases by about one order of magnitude. Such structure is expected due to the lateral phenomena discussed above. The lower values at later stages reflect the fact that parallel solid parts determine the capacitance in agreement with the equivalent circuit model (Fig. 1). The somehow opposite behavior when compared to the resistance is rooted in the opposite geometric dependence when compared to the resistance.
3. Conclusion
In this work, we treated the time-dependent impedance spectroscopy results in the light of our previous study on ion transport in SEIs concerning Li/Na storage. The striking differences between Li and Na are reflected by the Ea(SEI) values indicating the presence of large amount of liquid channels in the latter case. Based on this fact and the corresponding relaxation times of the SEI processes, we propose a very simple equivalent circuit model that takes account of channels within the SEI structure which are at least partially filled with the liquid electrolyte. As long as the solid SEI layers in the channels are highly resistive compared to the liquid in the channels, impedance is dominated by the liquid transport. Parallel contributions by the surrounding solid are then negligible in terms of the resistance, but dominate the capacitive part of the impedance. In the course of time, the reaction layers within the channels grow and the overall resistance becomes more solid-like. If the reaction layer exhibits a decreased molar volume, a self-similar growth mode may be applicable. This minimal motif of partially liquid-filled channels within a resistive but dielectrically active matrix is not only relevant for the Na cases. It can also be applied to the more coherent layers; here the motif represents perturbations that, in the course of time, get ‘ironed out’ (the surface flattens) because the channel solid grows faster than the surrounding (due to its thickness) until the channel is closed. Extending the model by explicitly including lateral film compaction due to agglomeration of islands can explain all the characteristic features of the complex SEI growth.Our finding is critical especially since previous reports on Na in combination with glyme-based electrolytes suggest that the initially low values of RSEI are an indication of chemo-mechanically stable and conductive SEI.66–68 However, we show that the low values of RSEI does not per se originate from the dense, thin and ionically conductive SEI, but in this case rather from the initially porous SEI, where the major transport pathway is the one through the liquid electrolyte in the pores, finally resulting in the SEI growth and densification. These conclusions were only possible only through detailed analysis of the impedance data. We are convinced that the experimentally based and inductively obtained description of the impedance response will help to better understand the complex issue of passivation layers in alkali metal batteries.
Data availability
The datasets supporting this article are given in previous publication (https://pubs.acs.org/doi/full/10.1021/acsami.1c15607) and in the ESI.‡Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate the help of Uwe Traub in data fitting.References
- H. L. F. Kawamura, M. LaFleur, K. Iversen and H. W. J. Cheng, Frontier Technology Issues: Lithium-Ion Batteries: A Pillar for a Fossil Fuel-Free Economy?https://www.un.org/development/desa/dpad/publication/frontier-technology-issues-lithium-ion-batteries-a-pillar-for-a-fossil-fuel-free-economy/#:%7E:text=Lithium%2Dion%20batteries%20have%20indeed,or%20wind%20power%20is%20used, 2022 Search PubMed.
- J. Ma, Y. Li, N. S. Grundish, J. B. Goodenough, Y. Chen, L. Guo, Z. Peng, X. Qi, F. Yang, L. Qie, C.-A. Wang, B. Huang, Z. Huang, L. Chen, D. Su, G. Wang, X. Peng, Z. Chen, J. Yang, S. He, X. Zhang, H. Yu, C. Fu, M. Jiang, W. Deng, C.-F. Sun, Q. Pan, Y. Tang, X. Li, X. Ji, F. Wan, Z. Niu, F. Lian, C. Wang, G. G. Wallace, M. Fan, Q. Meng, S. Xin, Y.-G. Guo and L.-J. Wan, J. Phys. D: Appl. Phys., 2021, 54, 183001 CrossRef CAS.
- J. Moskon, S. Drvarič Talian, R. Dominko and M. Gaberscek, J. Electrochem. Sci. Eng., 2020, 10, 79–93 CrossRef CAS.
- M. Weiss, R. Ruess, J. Kasnatscheew, Y. Levartovsky, N. R. Levy, P. Minnmann, L. Stolz, T. Waldmann, M. Wohlfahrt-Mehrens, D. Aurbach, M. Winter, Y. Ein-Eli and J. Janek, Adv. Energy Mater., 2021, 11, 2101126 CrossRef CAS.
- Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550 CrossRef.
- A. M. Colclasure, A. R. Dunlop, S. E. Trask, B. J. Polzin, A. N. Jansen and K. Smith, J. Electrochem. Soc., 2019, 166, A1412–A1424 CrossRef CAS.
- B. S. Vishnugopi, E. Kazyak, J. A. Lewis, J. Nanda, M. T. McDowell, N. P. Dasgupta and P. P. Mukherjee, ACS Energy Lett., 2021, 6, 3734–3749 CrossRef CAS.
- K. Mc Carthy, H. Gullapalli, K. M. Ryan and T. Kennedy, J. Electrochem. Soc., 2021, 168, 080517 CrossRef CAS.
- H. Nara, T. Yokoshima and T. Osaka, Curr. Opin. Electrochem., 2020, 20, 66–77 CrossRef CAS.
- M. Gaberšček, Nat. Commun., 2021, 12, 6513 CrossRef.
- N. Meddings, M. Heinrich, F. Overney, J.-S. Lee, V. Ruiz, E. Napolitano, S. Seitz, G. Hinds, R. Raccichini, M. Gaberšček and J. Park, J. Power Sources, 2020, 480, 228742 CrossRef CAS.
- W. Huang, D. T. Boyle, Y. Li, Y. Li, A. Pei, H. Chen and Y. Cui, ACS Nano, 2019, 13, 737–744 CrossRef CAS.
- E. Barsoukov, J. H. Kim, J. H. Kim, C. O. Yoon and H. Lee, J. Electrochem. Soc., 1998, 145, 2711–2717 CrossRef CAS.
- S. Eijima, H. Sonoki, M. Matsumoto, S. Taminato, D. Mori and N. Imanishi, J. Electrochem. Soc., 2019, 166, A5421–A5429 CrossRef CAS.
- J.-F. Ding, R. Xu, C. Yan, B.-Q. Li, H. Yuan and J.-Q. Huang, J. Energy Chem., 2021, 59, 306–319 CrossRef CAS.
- A. M. Tripathi, W.-N. Su and B. J. Hwang, Chem. Soc. Rev., 2018, 47, 736–851 RSC.
- P. Verma, P. Maire and P. Novák, Electrochim. Acta, 2010, 55, 6332–6341 CrossRef CAS.
- E. Peled and S. Menkin, J. Electrochem. Soc., 2017, 164, A1703–A1719 CrossRef CAS.
- M. Nojabaee, D. Kopljar, N. Wagner and K. A. Friedrich, Batteries Supercaps, 2021, 4, 909–922 CrossRef CAS.
- J. Popovic, in Frontiers of Nanoscience, ed. R. Raccichini and U. Ulissi, Elsevier, 2021, vol. 19, pp. 327–359 Search PubMed.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao, F. Wei, J.-G. Zhang and Q. Zhang, Adv. Sci., 2016, 3, 1500213 CrossRef.
- W. Liu, P. Liu and D. Mitlin, Adv. Energy Mater., 2020, 10, 2002297 CrossRef CAS.
- A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15 CrossRef.
- E. Matios, H. Wang, C. Wang and W. Li, Ind. Eng. Chem. Res., 2019, 58, 9758–9780 CrossRef CAS.
- X. Shan, Y. Zhong, L. Zhang, Y. Zhang, X. Xia, X. Wang and J. Tu, J. Phys. Chem. C, 2021, 125, 19060–19080 CrossRef CAS.
- H. Wu, H. Jia, C. Wang, J.-G. Zhang and W. Xu, Adv. Energy Mater., 2021, 11, 2003092 CrossRef CAS.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Adv. Energy Mater., 2021, 11, 2002689 CrossRef CAS.
- Z. Zhang, Y. Li, R. Xu, W. Zhou, Y. Li, S. T. Oyakhire, Y. Wu, J. Xu, H. Wang, Z. Yu, D. T. Boyle, W. Huang, Y. Ye, H. Chen, J. Wan, Z. Bao, W. Chiu and Y. Cui, Science, 2022, 375, 66–70 CrossRef CAS.
- M. J. Zachman, Z. Tu, S. Choudhury, L. A. Archer and L. F. Kourkoutis, Nature, 2018, 560, 345–349 CrossRef CAS.
- B. Han, Z. Zhang, Y. Zou, K. Xu, G. Xu, H. Wang, H. Meng, Y. Deng, J. Li and M. Gu, Adv. Mater., 2021, 33, 2100404 CrossRef CAS.
- A. C. Thenuwara, P. P. Shetty, N. Kondekar, S. E. Sandoval, K. Cavallaro, R. May, C.-T. Yang, L. E. Marbella, Y. Qi and M. T. McDowell, ACS Energy Lett., 2020, 5, 2411–2420 CrossRef CAS.
- V. Vanpeene, J. Villanova, J.-P. Suuronen, A. King, A. Bonnin, J. Adrien, E. Maire and L. Roué, Nano Energy, 2020, 74, 104848 CrossRef CAS.
- Z. Shadike, H. Lee, O. Borodin, X. Cao, X. Fan, X. Wang, R. Lin, S.-M. Bak, S. Ghose, K. Xu, C. Wang, J. Liu, J. Xiao, X.-Q. Yang and E. Hu, Nat. Nanotechnol., 2021, 16, 549–554 CrossRef CAS.
- C. Cao, M. F. Toney, T.-K. Sham, R. Harder, P. R. Shearing, X. Xiao and J. Wang, Mater. Today, 2020, 34, 132–147 CrossRef CAS.
- A. J. Ilott and A. Jerschow, J. Phys. Chem. C, 2018, 122, 12598–12604 CrossRef CAS.
- M. Nie, D. P. Abraham, Y. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 13403–13412 CrossRef CAS.
- A. B. Gunnarsdóttir, S. Vema, S. Menkin, L. E. Marbella and C. P. Grey, J. Mater. Chem. A, 2020, 8, 14975–14992 RSC.
- Y.-C. Hsieh, J. H. Thienenkamp, C.-J. Huang, H.-C. Tao, U. Rodehorst, B. J. Hwang, M. Winter and G. Brunklaus, J. Phys. Chem. C, 2021, 125, 252–265 CrossRef CAS.
- Y. Xiang, G. Zheng, Z. Liang, Y. Jin, X. Liu, S. Chen, K. Zhou, J. Zhu, M. Lin, H. He, J. Wan, S. Yu, G. Zhong, R. Fu, Y. Li and Y. Yang, Nat. Nanotechnol., 2020, 15, 883–890 CrossRef CAS.
- F. T. Krauss, I. Pantenburg and B. Roling, Adv. Mater. Interfaces, 2022, 9, 2101891 CrossRef CAS.
- R. R. Gaddam, L. Katzenmeier, X. Lamprecht and A. S. Bandarenka, Phys. Chem. Chem. Phys., 2021, 23, 12926–12944 RSC.
- R. K. Koch, R. Kuhn, I. Zilberman and A. Jossen, Presented in Part at the 16th European Conference on Power Electronics and Applications, 2014 Search PubMed.
- K. Lim, B. Fenk, J. Popovic and J. Maier, ACS Appl. Mater. Interfaces, 2021, 13, 51767–51774 CrossRef CAS PubMed.
- R. de Levie, Electrochim. Acta, 1963, 8, 751–780 CrossRef.
- R. de Levie, Electrochim. Acta, 1964, 9, 1231–1245 CrossRef CAS.
- M. Adamič, S. D. Talian, A. R. Sinigoj, I. Humar, J. Moškon and M. Gaberšček, J. Electrochem. Soc., 2018, 166, A5045–A5053 CrossRef.
- S. Drvarič Talian, J. Bobnar, A. R. Sinigoj, I. Humar and M. Gaberšček, J. Phys. Chem. C, 2019, 123, 27997–28007 CrossRef.
- N. Kaiser, S. Spannenberger, M. Schmitt, M. Cronau, Y. Kato and B. Roling, J. Power Sources, 2018, 396, 175–181 CrossRef CAS.
- I. D. Raistrick, J. R. Macdonald and D. R. Franceschetti, in Impedance Spectroscopy, 2018, pp. 21–105, DOI:10.1002/9781119381860.ch2.
- E. Peled, D. Golodnitsky, G. Ardel and V. Eshkenazy, Electrochim. Acta, 1995, 40, 2197–2204 CrossRef CAS.
- E. Peled, D. Golodnitsky and G. Ardel, J. Electrochem. Soc., 1997, 144, L208–L210 CrossRef CAS.
- J. Thevenin, J. Power Sources, 1985, 14, 45–52 CrossRef CAS.
- A. Zaban, E. Zinigrad and D. Aurbach, J. Phys. Chem., 1996, 100, 3089–3101 CrossRef CAS.
- N. Yao, X. Chen, X. Shen, R. Zhang, Z.-H. Fu, X.-X. Ma, X.-Q. Zhang, B.-Q. Li and Q. Zhang, Angew. Chem., 2021, 60, 21473–21478 CrossRef CAS.
- I. N. Daniels, Z. Wang and B. B. Laird, J. Phys. Chem. C, 2017, 121, 1025–1031 CrossRef CAS.
- Y. Li, Y. Li, A. Pei, K. Yan, Y. Sun, C.-L. Wu, L.-M. Joubert, R. Chin, A. L. Koh, Y. Yu, J. Perrino, B. Butz, S. Chu and Y. Cui, Science, 2017, 358, 506–510 CrossRef CAS.
- X. Wang, Y. Li and Y. S. Meng, Joule, 2018, 2, 2225–2234 CrossRef CAS.
- B. Han, Y. Zou, Z. Zhang, X. Yang, X. Shi, H. Meng, H. Wang, K. Xu, Y. Deng and M. Gu, Nat. Commun., 2021, 12, 3066 CrossRef CAS.
- J. Maier and G. Schwitzgebel, Mater. Res. Bull., 1982, 17, 1061–1069 CrossRef CAS.
- K. R. Lawless, Rep. Prog. Phys., 1974, 37, 231–316 CrossRef CAS.
- M. Nojabaee, K. Küster, U. Starke, J. Popovic and J. Maier, Small, 2020, 16, 2000756 CrossRef CAS.
- L. A. Ma, A. J. Naylor, L. Nyholm and R. Younesi, Angew. Chem., 2021, 60, 4855–4863 CrossRef CAS.
- M. Mandl, J. Becherer, D. Kramer, R. Mönig, T. Diemant, R. J. Behm, M. Hahn, O. Böse and M. A. Danzer, Electrochim. Acta, 2020, 354, 136698 CrossRef CAS.
- R. Mogensen, D. Brandell and R. Younesi, ACS Energy Lett., 2016, 1, 1173–1178 CrossRef CAS.
- Z. W. Seh, J. Sun, Y. Sun and Y. Cui, ACS Cent. Sci., 2015, 1, 449–455 CrossRef CAS.
- L. Lutz, D. Alves Dalla Corte, M. Tang, E. Salager, M. Deschamps, A. Grimaud, L. Johnson, P. G. Bruce and J.-M. Tarascon, Chem. Mater., 2017, 29, 6066–6075 CrossRef CAS.
- M. Goktas, C. Bolli, J. Buchheim, E. J. Berg, P. Novák, F. Bonilla, T. Rojo, S. Komaba, K. Kubota and P. Adelhelm, ACS Appl. Mater. Interfaces, 2019, 11, 32844–32855 CrossRef CAS.
Footnotes |
| † Dedicated to Prof. Doron Aurbach for his 70th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09189e |
| § Current address: University of Stavanger, Department of Energy and Petroleum Engineering, Stavanger, Norway. |
| This journal is © The Royal Society of Chemistry 2023 |