Proton migration barriers in BaFeO_3−δ – insights from DFT calculations

Abstract

Proton migration in the triple conducting perovskite BaFeO_3−δ is investigated using first-principles density functional theory calculations. Oxygen-deficient BaFeO_3−δ exhibits pronounced lattice distortions that entail different chemical environments of lattice oxygen ions and thus different proton migration pathways. We systematically sampled these proton pathways and identified key structural parameters determining the height of the migration barrier. The calculated average migration barrier for proton transfer in Jahn–Teller distorted BaFeO₃ is 0.22 eV. Analysis of geometric changes and chemical bonding in individual proton trajectories indicates that proton transfer occurs as a two-step process: an early stage where the energy change is mainly governed by the approach of donor and acceptor oxygen ions (the O–H bond is hardly stretched), and a second stage near the transition state where the O–H bond is broken. The calculated average migration barrier in oxygen deficient BaFeO_2.75 is 0.18 eV, with a broad range of different barriers due to the increased lattice distortions caused by oxygen vacancies. The decrease in migration barrier with increasing oxygen deficiency could be attributed to the annihilation of oxygen (ligand) holes rather than to volume expansion upon reduction. Considering all calculated barriers in BaFeO₃ and BaFeO_2.75 we find important correlations of the migration barrier height with the initial separation of donor and acceptor oxygen ions, and the O–H bond length. While this co-dependence reflects the two-step nature of proton transfer, it is also helpful for the optimization of triple conducting oxides for various electrochemical applications.

---

1. Introduction

The perovskite BaFeO₃ can be considered as an undoped parent material representing a large variety of differently doped triple conducting perovskites, in which electron holes, oxygen vacancies and protons contribute to the total electrical conductivity. Such triple conducting materials are required for several (electro)chemical applications, particularly as an air electrode in protonic ceramic fuel/electrolysis cells, and for hydrogen permeation membranes.^1–4 In this contribution, we explore the mobility of protons in BaFeO_3−δ as a function of oxygen deficiency and identify key material properties that determine the height of the proton migration barrier.

BaFeO₃ adopts different crystal structures depending on the synthesis conditions. The most stable structure is hexagonal, which can be transformed into a metastable cubic perovskite structure under certain conditions.⁵ The cubic perovskite structure is stabilized by slight doping and is typically used in (electro)chemical applications. The electronic structure of cubic BaFeO₃ is characterized by a negative charge transfer and an associated dominating d⁵L̲ (L̲ = ligand hole) configuration. This implies that electron holes are more associated with oxygen ions (i.e. the ligands, following the nomenclature used in X-ray spectroscopy) and that Fe has a relatively invariant oxidation state of 3+. The formation of oxygen vacancies occurs at the expense of electron holes and is accompanied by pronounced lattice distortions, rendering the crystal structure pseudo cubic.

Proton uptake can occur by dissociative water incorporation into oxygen vacancies (acid–base reaction), as well as by a redox reaction at the expense of electron holes, depending on external conditions (see e.g. ref. 6 and 7). The incorporated protons lead to the formation of OH groups on O lattice sites. At elevated temperature, i.e., 300–700 °C, protons become mobile and migrate through the oxygen sublattice, giving rise to long range proton conductivity.

In contrast to triple conducting perovskites, proton migration in perovskites with predominant proton conductivity (i.e. protonic ceramic electrolyte materials such as BaZrO₃) has been investigated in detail.^8–14 Proton migration in these materials proceeds by a Grotthuss mechanism, involving rotational diffusion within the OH group, and proton transfer to a neighboring oxygen ion along the edge of the [BO₆] octahedron. The proton transfer is assisted by phonons that produce shorter transient O–O distances lowering the energy barrier for the actual proton transfer.⁸ Both experimental and theoretical studies have identified proton transfer (rather than rotational diffusion within the OH group) as the rate limiting step for long range proton conductivity with energy barriers for BaZrO₃ ranging between 0.1 and 0.4 eV.^13,15–20

The proton mobility (and conductivity) in triple conducting perovskites is more challenging to be measured because the electronic conductivity is typically more than 3 orders of magnitude higher, and it also has to be separated from the oxygen ion conductivity.^1,2,6 Typical approaches such as hydrogen permeation, H/D tracer diffusion, or proton-selective electrodes encounter specific issues (e.g. crack formation, limited materials stability in reducing conditions, incomplete suppression of electronic conductivity etc.). The few available experimental data for BaFeO₃-related perovskites indicate that the proton mobility in triple conducting perovskites might be moderately lower than in Ba(Zr,Ce,Y,Yb)O_3−z electrolytes, see e.g. ref. 6; SIMS analysis after deuterium exchange of the double perovskite PrBaCo₂O_5+δ yielded a hard to interpret profile containing a shallow part and a long tail.²¹ Some proton migration barriers in triple conducting oxides have been obtained from density functional theory (DFT) calculations, e.g. ref. 22–28. However, a systematic investigation as a function of cation composition, and correlations with other materials parameters (certain atom distances etc.) in the perovskite structure are not available so far.

A priori qualitative considerations are not able to predict whether the proton mobility is generally higher or lower in triple conducting perovskites compared to electrolyte materials, since there are arguments in both directions. (1) Triple conducting perovskites often have a higher oxygen vacancy concentration which leads to local lattice distortions (even if the average crystallographic structure remains cubic), and decreased symmetry typically decreases the proton mobility.^29,30 (2) Triple conducting perovskites have smaller lattice parameters than Ba(Zr,Ce,Y,Yb)O_3−z electrolytes. This increases the repulsion of the proton in the transition state with the B-site cation, and is expected to increase the barrier (cf. increased barrier in BaCeO₃ under hydrostatic pressure³¹). (3) The transition metal cations in triple conductors are usually in a lower average oxidation state than in electrolyte perovskites, which decreases such a repulsion.

In the present study, we investigate proton migration barriers in BaFeO_3−δ as a function of oxygen deficiency by DFT+U calculations (defect formation energies in (Ba,Sr)FeO_3−δ have been calculated in ref. 32). We separate the effects of volume expansion and formal iron oxidation state on the height of the proton migration barrier. The results are compared to calculated barriers in the electrolyte BaZrO₃, elucidating whether triple conductors and electrolyte materials exhibit fundamental differences in migration barriers. The migration barriers are investigated by nudged elastic band calculations – this allows systematic screening of different proton trajectories more efficiently than computationally much more demanding ab initio molecular dynamics (force-field MD is considered less suitable for materials with mixed-valent cations). We briefly explore also validity of the observed correlations of proton binding sites and migration barriers when using a range-separated hybrid DFT functional instead of DFT+U.

2. Computational details

2.1. Ab initio calculations

Density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP, v.6.1.2)^33–35 together with the projector augmented wave (PAW) method³⁶ and scalar relativistic pseudopotentials with 10 valence electrons on Ba, 14 electrons on Fe, 6 electrons on O, and 1 electron on H. The wave functions were expanded in terms of plane waves with a constant energy cutoff of 500 eV and optimized with a break condition for the self-consistent loop of 10⁻⁵ eV. Structural optimizations were performed until residual forces fell below 10⁻⁴ eV Å⁻¹. The Brillouin zone of the 5-atom primitive unit cell was sampled with an 8 × 8 × 8 Monkhorst–Pack k-point mesh.³⁷ Exchange–correlation was treated with the Perdew–Burke–Ernzerhof (PBE) functional,³⁸ together with the rotationally-invariant Dudarev's form of the so-called DFT+U_eff approach as implemented in the VASP code.³⁹ The U_eff-parameter (hereafter, U) was fixed to 4.0 eV for the Fe 3d-orbitals to take into account strong correlation effects. As found in our previous studies,^32,40 this value represents a good compromise between reproducing experimental values, e.g., magnetic moment, and falling in the range of U values typically employed for Fe-containing perovskites (see, e.g., ref. 41–43). For comparison, we performed calculations with the hybrid HSE06 functional,^44,45 intermixing 25% of exact exchange and a screening parameter of 0.2, of both protonated supercells in the ground state and proton migration barriers. Both functionals yield the same trend in total energy of the protonated supercells where the proton is attached to different oxygen ions. The migration barriers increase by approx. 0.1 eV when calculated by HSE06, but again the key trends (correlation of barrier height with O–H and O⋯O distances) remain unaltered. More details and some discussion on this comparison are provided in Section S17 of the ESI.†

To investigate transition states and minimum-energy pathways of proton transfer, we used the climbing-image nudged elastic band (CI-NEB) method.^46,47 In particular, we used 11 images (including initial and end points) to model proton transfer between initial and final proton positions, and increased this number further in a few cases. This guarantees a step width in the order of ≈0.1 Å of the transferring proton. The convergence parameters for the electronic and ionic relaxation during the NEB calculation were 10⁻⁵ eV and 10⁻² eV Å⁻¹, respectively. The starting geometry of each NEB calculation was fully relaxed with respect to atomic coordinates, volume and shape. In this way, the chemical expansion upon oxygen vacancy formation is taken into account. During a NEB trajectory, we keep the volume and shape of the supercell fixed to that of the initial state (only atomic coordinates relaxed). This prevents complications originating from possible modifications of the overall lattice distortion pattern in the supercell which might impede the energy convergence (in particular in cells with several point defects). NEB test calculations with full relaxation of atom positions, cell volume and shape indicate this restriction has only a minor effect on the barrier height (ESI S1,† barrier difference ≈0.01 eV). In several configurations, the total energies of initial and final states differ significantly, which leads to different barrier heights in forward ΔE = E^TS − E^I and backward direction ΔE = E^TS − E^F (E^TS is the supercell total energy in the transition state, E^I, E^F the total energy in the initial or final state). For such situations it has been suggested to calculate the average of forward and backward barrier (“kinetically resolved activation barrier” KRA⁴⁸). For barriers with a large energy difference between initial and final state, the O–H (covalent bond) and O⋯H (hydrogen bond) distances in the NEB image with the highest energy (i.e. the transition state) show a perceptible difference of ≈0.1 Å.

For a chemical interpretation of the electronic structures of the various supercells, the optimized PAW wave functions were projected onto an auxiliary local basis set using the Local-Orbital Basis Suite Towards Electronic-Structure Reconstruction (LOBSTER) package.^49–55 with Ba 5s 6s 5p, Sr 4s 5s 4p, Fe 4s 3p 3d, and O 2s 2p as valence band configurations. Chemical bonding analysis was carried out using the projected Crystal Orbital Hamilton Population (COHP), which essentially weighs the DOS of a pair of atomic orbitals by their corresponding off-site Hamiltonian matrix element (see e.g. ref. 40 for more details). The energy-integrated COHP (ICOHP) up to the valence band maximum is used as a quantitative measure for the electronic energy associated with the chemical bond covalency.

To assess the quality of linear fitting, we use the Pearson's correlation coefficient, R, ranging between −1 and 1, where negative values indicate negative correlations and positive values indicate positive correlations. The closer the correlation factor is to +1 or −1, the stronger the dependence of the variables.

2.2. Supercells

We apply the supercell approach. The 2 × 2 × 2 supercell (perfect stoichiometry Ba₈Fe₈O₂₄ with 40 atoms) consists of 8 FeO₆ corner-sharing octahedra and allows us to calculate variations in oxygen non-stoichiometry from δ = 0 to 0.5 in BaFeO_3−δ. In the present study aiming mainly at proton migration, we focus on two prototypical cases of δ = 0 and δ = 0.25 with one hydrogen atom present, i.e. BaFeO_3−δH_0.125, in which the formal Fe oxidation states are +3.875 and +3.375. The 2 × 2 × 2 supercell size suffices for obtaining defect energetics and describing all necessary properties. Even the Jahn–Teller distortion can be accounted for.³² However, BaFeO₃ is characterized by only slight Jahn–Teller distortion due electron transfer from O to Fe (d⁵L̲ configuration,³² see also analysis of electronic density of states below). In ref. 32 we had systematically calculated all possible oxygen vacancy arrangements in BaFeO_3−δ cells, and also explored a large number of possible proton positions to find the global energy minima (the list of low energy configurations is given in Table S2 † in ref. 32). Point defects reduce the cubic supercell symmetry, thus in the present calculations the supercells containing interstitial hydrogen atoms possess the symmetry corresponding to the point group C₁. We performed additional calculations which vary the formal Fe oxidation state by adding excess electrons to the supercell (compensated by a homogeneous background charge) keeping the cell shape and volume fixed to that of the initial cell.

Since the calculations of proton migration barriers are computationally more demanding, we concentrate in the present work on Ba₈Fe₈O₂₄H₁ and two of the low-energy oxygen vacancy arrangements of Ba₈Fe₈O₂₂H₁. Within these configurations, we systematically investigate proton migration barriers for characteristic initial and final configurations that are expected to yield a representative overall picture. This means in particular that we probe different proton migration paths relative to the Jahn–Teller lattice distortion pattern, and relative to the positions of the oxygen vacancies. The proton is attached to a host oxygen, forming one short O–H covalent bond and two weaker and longer O⋯H hydrogen bonds with neighboring oxygen atoms. The proton migrates to the closest oxygen (direction of the shorter hydrogen bond), cf.Fig. 1.

Fig. 1 Ground state geometry of a protonic defect in BaFeO₃ (left) and transition state during proton transfer (right). Hydrogen bonds are indicated with dashed lines. The transition state is characterized by the shown O–O and O–H distances.

3. Results and discussion

3.1. Protonation sites in BaFeO_3−δ

Protons in BaFeO_3−δ reside preferably on interstitial lattice sites in close proximity of ≈1 Å to an oxygen ion, forming a strong covalent O–H bond (Fig. 1). Although formally occupying an interstitial site, protonic defects are typically understood as hydroxyl groups on oxygen ion sites. The O–H axis of these groups leans towards neighboring oxygen ions, with which the proton forms hydrogen bonds. These configurations yielded the lowest total energies during structural optimization, which is in good agreement with literature data for other protonated perovskite oxides (see, e.g., ref. 56–59).

In an ideal cubic perovskite structure, oxygen ions reside on symmetrically indistinguishable lattice sites and have the same proton affinities (i.e. basicity). But if the symmetry is locally broken – e.g. by doping, Jahn–Teller distortions or the introduction of point defects – oxygen ions become chemically different and can have different proton affinities. Such effects have most extensively been studied in connection with acceptor doping of electrolyte materials (e.g. Y-doped Ba(Zr,Ce)O₃), which can lead to a trapping of protons at oxygen ions near the dopant. Proton trapping in doped BaZrO₃ occurs in zones involving the first and second coordination of oxygen ions around the dopant, indicating that not only electrostatic interactions but also lattice distortions play a role.^9,13 Proton trapping was moreover found to correlate with the O 2p band center;⁶⁰ oxygen ions coordinated to Y have higher p-band centers (i.e., p-band centers closer to VBM, and more favorable proton sites) than oxygen ions coordinated to Zr.

In BaFeO_3−δ, the presence of oxygen vacancies and Jahn–Teller distortions render the oxygen ions chemically different. The impact of such structural distortions in doped BaFeO₃ on the degree of proton uptake has been studied using a combination of EXAFS and thermogravimetry analysis. More bent Fe–O–Fe arrangements were found to correlate with more favorable enthalpies of hydration, and this was attributed to a reduced Fe–O bond covalency and an associated higher basicity (proton affinity) of the oxygen ions.⁶¹

In the present study, we use the oxygen p-band center relative to the valence band maximum (VBM) as a sensitive and reliable descriptor^60,62 to explain proton site preferences in undoped BaFeO_3−δ. The p-band center is calculated as:

where PDOS is the projected density of states as obtained by the LOBSTER calculations (see Computational details Section 2.1), with the VBM located at 0 eV. The value of the p-band center reflects the electrostatic potential at a specific oxygen site as well as covalent interactions to neighboring cations. A higher covalency generally leads to wider O 2p bands with a lower band center relative to VBM. Indeed, analysis of a Ba₈Fe₈O₂₂ supercell shows that the p-band center correlates with the energy integrated Fe–O COHP – a quantitative measure of bond covalency – such that a higher covalency leads to a deeper ε_p (see ESI S2†). Alternatively, ε_p can be aligned to vacuum (rather than VBM), which allows comparison across different materials, but requires additional slab calculations. Other oxygen ion descriptors accessible by DFT have been tested and proven less useful to distinguish chemically different oxygen ions. For example, in the Ba₈Fe₈O₂₂ supercell, Mulliken charges of oxygen ions vary by merely 0.1e, hence, are less sensitive towards structural distortions and correlate only poorly with protonation energies (Fig. S3†). Similarly, the protonation energies seem not to be correlated with the O–H covalent bond length (Fig. S4†). A discussion of the variations in Bader atomic charges and local magnetic moments can be found in ESI Sections 5 and 6.†

To demonstrate the potential of the p-band center in distinguishing chemically different oxygen ions, we analyze two different cases. Fig. 2 shows the respective PDOS curves. (i) Yttrium doped Ba₈Zr₇YO₂₄H (the proton is included for charge neutrality and is placed far from the dopant). Oxygen ions coordinated to Y have a p-band center 0.3 eV higher than oxygen ions coordinated to Zr, confirming the results by ref. 60. The total energy of the Ba₈Zr₇YO₂₄H supercell with the proton attached to the oxygen ion that is coordinated to Y (ε_p = −2.18 eV) is 0.18 eV lower than the total energy of the supercell with the proton attached to the oxygen ion coordinated to Zr (ε_p = −2.50 eV). (ii) In oxygen non-stoichiometric Ba₈Fe₈O₂₂, oxygen ions located opposite to an oxygen vacancy have a p-band center 0.4 eV lower than an oxygen ion part of an [FeO₆] octahedra. The total energy of the Ba₈Fe₈O₂₂H supercell with the proton attached to the oxygen ion located opposite an oxygen vacancy (ε_p = −2.81 eV) is 0.43 eV higher than the total energy of the supercell with the proton attached to an oxygen in a [FeO₆] octahedron (ε_p = −2.44 eV). Both cases demonstrate that, within a given supercell, the favorability for protonation correlates with the p-band center of the unprotonated oxygen ion; oxygen ions with a higher p-band center represent more favorable proton sites. Note that p-band centers of different materials cannot be compared to each other unless the Fermi levels of the materials are aligned to a common energy reference, e.g., vacuum potential.

Fig. 2 Projected density of states for (a) Ba₈Zr₇YO₂₄H and (b) Ba₈Fe₈O₂₂. The DOS curves are aligned to a common vacuum level using separate slab calculations (see ref. 63 for technical procedure). For Ba₈Zr₇YO₂₄H, the ionization potential is approximated by the value for pure BaZrO₃. The highlighted states in blue and yellow represent one specific oxygen ion as indicated in the insets, and have been multiplied by a factor of 5 for better visibility.

To further test the p-band center as a descriptor for proton site preference, we calculated the total energy for various other proton positions in the Ba₈Fe₈O₂₂ supercell. Fig. 3 shows that the energy of the protonated supercells correlates with the p-band center of the oxygen ion bound to the proton with a correlation factor of 0.71. The data points with most negative ε_p (−2.81 eV) and least favorable protonation belong to O opposite an oxygen vacancy. The correlation emphasizes that the protonation preference is not simply dominated by electrostatic arguments (according to electrostatics, a proton position closer to the oxygen vacancy should be least favorable) but by the fact that the local electronic structure has a decisive role. A closer inspection of the local geometries reveals that cases with very strong (i.e. short) or very weak (i.e. long) hydrogen bonds (dashed lines in the inset in Fig. 3b) cause deviations from the trend. Consequently, a better correlation is found upon combining the p-band center with the sum of the two hydrogen bond lengths (Fig. 3c), resulting in a correlation factor of 0.82. This summation uses a scaling factor of 0.1 eV/0.1 Å to convert differences in hydrogen bond lengths into energy differences. This value of the scaling factor ensures a good correlation. Furthermore, it is in agreement with the slope of total energy as a function of hydrogen bond lengths extracted from NEB calculations (Fig. S9†). The correlation between relative total energy and the oxygen p-band center is also observed in calculations with the hybrid HSE06 functional (see Fig. S17†).

Fig. 3 Correlation of protonation site preference (relative to most stable site) in an exemplary Ba₈Fe₈O₂₂ supercell with (a) p-band center ε_p, (b) sum of short and long hydrogen bond (if only one hydrogen bond is present due to a neighboring oxygen vacancy, a value of 2.5 Å is used for the missing bond), and (c) sum of both descriptors. For this summation, a scaling factor of 0.1 eV/0.1 Å to convert differences in hydrogen bond lengths into energy differences is used. The Pearson's correlation factor R is also indicated.

In conclusion, the favorability for protonation of an oxygen ion is found to primarily depend on the p-band center in the unprotonated state (reflecting the electrostatic potential at the oxygen ion site and covalent interactions to neighboring cations), and to a lesser extent on the strength of hydrogen bonding. The large variability of p-band centers in oxygen non-stoichiometric BaFeO_3−δ, in turn, has a direct impact on proton diffusion, with restricted proton migration via unfavorable oxygen ions that are located opposite to oxygen vacancies (however, these sites can easily be circumvented by the transferring proton).

When an oxygen ion is protonated, its p-band center is subject to a significant downward shift by virtue of O–H bond formation.³² In the Ba₈Fe₈O₂₂ supercell the downward shift of ε_p is on average 1.9 eV for the different proton positions (see ESI Fig. S7†). In fact, O–H bond formation has a tremendous effect on the p-band center. It outweighs a parallel weakening of the Fe–O bond of the protonated oxygen ion – evidenced by a decreases of approximately 43% of the Fe–O ICOHP (Fig. S8†) – which would otherwise lead to an upward shift of ε_p according to the trend in Fig. S2.† In ref. 63, it was observed for large bandgap oxides ranging from basic Cs₂O to acidic SiO₂ that the extent of the downward shift depends on the position of the unprotonated ε_p relative to vacuum level (the higher ε_p, the greater the downward shift upon protonation). However, within the Ba₈Fe₈O₂₂ supercell this correlation is less clear, and the data for O opposite an oxygen vacancy appear as outliers (ESI Fig. S7†).

3.2. Proton migration barriers in BaFeO₃

The diffusion of protons in perovskite oxides occurs by intraoctahedral proton transfer (Fig. 4a), rotational diffusion of the proton around an oxygen ion (Fig. 4b), and proton reorientation from one octahedron to a neighboring one (Fig. 4c).³⁰ From the elementary proton diffusion modes shown in Fig. 4, rotation and reorientation are characterized by low activation energies. On the other hand, proton transfer, which requires breaking the covalent O–H bond, has higher energy barriers and thus represents the rate-limiting step in long-range proton transport for perovskites with large lattice parameter.³⁰ The energy barriers for the elementary steps in BaFeO₃ shown in Fig. 4 yield the same trend as observed for electrolyte materials (e.g. BaZrO₃, see ref. 30 and references therein), with the proton transfer having the highest barrier. Consequently, in the present study, we focus on calculating the proton transfer barrier in BaFeO_3−δ, the proton rotation and reorientation barriers were only exemplarily probed in Ba₈Fe₈O₂₄H.

Fig. 4 (a–c) Elementary modes of proton diffusion in distorted perovskite oxides. The approximate activation energies are given for BaFeO_3−δ as obtained in this study.

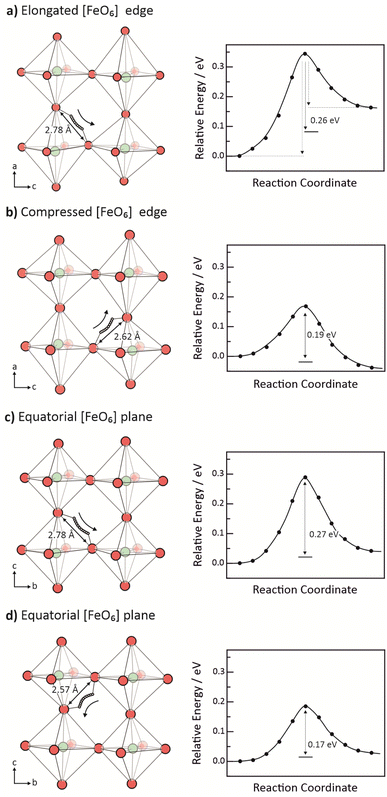
Jahn–Teller distortions in BaFeO₃ are partially quenched due to the dominating d⁵L̲ configuration, rendering the Fe-ions Jahn–Teller inactive.^40,64 However, a Jahn–Teller distortion still leads to a slightly lower total energy, giving rise to alternating elongated and compressed [FeO₆] octahedra. For a supercell containing an additional proton (Ba₈Fe₈O₂₄H), the energetically most stable structure has a columnar ordering of distorted [FeO₆] octahedra with intraoctahedral oxygen–oxygen distances, ranging from 2.8 Å in an elongated to 2.6 Å in a compressed octahedron. Based on the structural oxygen separation and analysis of corresponding barriers, we identified four different cases of proton transfer in BaFeO₃, shown in Fig. 5.

Fig. 5 (a–d) Different proton transfer trajectories and energy profiles in Jahn–Teller distorted Ba₈Fe₈O₂₄H. The migration barriers are given as average of forward and backward migration (illustrated in (a)). Ba cations not shown for simplicity.

The calculated migration barrier for proton transfer in BaFeO₃ range between 0.17 and 0.28 eV, which is similar to values calculated for the prototypical electrolyte material BaZrO₃ of 0.1 and 0.41 eV.^{9,13,15,16,18–20} This means that proton transfer barriers in cathode materials such as BaFeO₃ seem not to differ fundamentally from those in electrolyte materials. The energy profiles in Fig. 5 are partially asymmetric (especially in Fig. 5a), reflecting the different proton affinities of donor and acceptor oxygen ion. Different Fe–O bond lengths in the distorted [FeO₆] octahedra are expected to cause different p-band centers of the oxygen ions and, as such, different proton affinities, cf. Section 3.1. To nonetheless obtain a direction independent migration barrier we use the averaging (KRA barrier) as suggested by ref. 48 and illustrated in Fig. 5a.

Analysis of the structural deformation during proton transfer in BaFeO₃ shows that the O–H bond is hardly stretched in the early stages of the transfer, while the structural separation of donor and acceptor oxygen ion is already reduced considerably. Fig. 6a shows the change in O–H and O–O distance during the proton transfer illustrated in Fig. 5c. The O–H bond lengthens by merely 0.05 Å during the first 4 images, while at the same time the O–O distance is strongly reduced by 0.22 Å. Shorter O–O distances, in turn, lead to a stronger hydrogen bond to the receiving oxygen. A significant elongation of the O–H bond (and corresponding further shortening of the hydrogen bond to the receiving O) occurs only for O–O distances below approx. 2.5 Å. In fact, a correlation of total energy with O–O distance indicates that proton transfer actually comprises two stages; for O–O distances longer than 2.5 Å the energy increases with a slope of 0.5 eV Å⁻¹ while for shorter distances the energy increases with 1.9 eV Å⁻¹ (Fig. 6b).

Fig. 6 (a) Evolution of O–H (donating oxygen ion) and O–O distance during proton transfer. (b) Correlation of relative total energy with O–O distance. (c) Sum of donating and receiving O–H ICOHP during proton transfer. Data corresponds to proton transfer displayed in Fig. 5c. Relative total energies as a function of O–O distance (like (b)) corresponding to the proton trajectories in Fig. 5a, b and d are shown in Fig. S9.†

A similar conclusion was drawn in ref. 65, where for proton transfer in Y-doped BaZrO₃ the two components, O–H and O–O distance, were decomposed by fixing the position of certain atoms. It was found that the O–O approach constitutes 63% of the total migration barrier. Similarly, molecular dynamics simulations in CaZrO₃ and BaCeO₃ have shown that proton transfer occurs in situations where lattice vibrations produce shorter O–O distances, thus facilitating proton transfer.^8,66,67 The separation of proton transfer into two sub-steps is also supported by analysis of the energy integrated COHP of the O–H bond – a measure of how much energy originates from the covalent O–H interaction (Fig. 6c). In the early and late stages of proton transfer, the sum of donating and receiving O–H ICOHP becomes more negative, reflecting the approach of the acceptor oxygen ion and a corresponding shorter hydrogen bond. In the realm of the transition state, however, the sum of O–H ICOHP is significantly less negative representing a higher contribution to the overall change in total energy. This could explain the steeper slope in Fig. 6b.

3.3. Proton migration barriers in BaFeO_3−δ

Since the configuration space with coexisting oxygen vacancies and protons is very large, we limit ourselves to the analysis of prototypical [FeO₅] and [FeO₆] octahedra, cf. Section 2.2. Fig. 7 shows different scenarios of proton transfer in Ba₈Fe₈O₂₂H supercells, featuring proton transfers within [FeO₆] octahedra (Fig. 7a and b) and along the edge of square-pyramidal [FeO₅] (Fig. 7c and d). In oxygen non-stoichiometric BaFeO_3−δ there exist both symmetric (Fig. 7a and d), and asymmetric (Fig. 7b and c) energy profiles, the latter involving oxygen ions with different proton affinities. In particular, proton transfers involving oxygen ions opposite to oxygen vacancies exhibit strongly asymmetric energy profiles (Fig. 7c), reflecting the reluctance of these oxygen ions to be protonated (see Section 3.1). It is anticipated that these oxygen ions will be largely excluded in the long-range diffusion of protons. The concentration of these oxygen ions (equal to twice the oxygen vacancy concentration) is at maximum 1/3 of all oxygen ions in case of full reduction, i.e. there are still enough possibilities for migrating protons to avoid these unfavorable bonding sites. Thus, these barriers should not significantly contribute to the long-range activation energy. Nevertheless, Fig. 7 demonstrates that the migration barrier for proton transfer is very sensitive towards structural and electronic perturbation by oxygen vacancies, even if oxygen ions opposite to vacancies are not directly involved, as shown in Fig. 7b.

Fig. 7 (a–d) Different proton transfer trajectories and energy profiles in oxygen non-stoichiometric Ba₈Fe₈O₂₂H. The migration barriers are given as average of forward and backward migration (illustrated in Fig. 5a). Ba cations not shown for simplicity.

Introducing oxygen deficiency into the material can affect proton transfer barriers by several ways: by increasing local distortions, expanding the lattice parameter, and by modification of Fe and O electronic properties such as charges and the p-band center. Here we discuss the overall effect of increased oxygen deficiency, Section 3.4 then attempts to further isolate the effects of lattice parameter and oxidation state. Fig. 8 shows the statistical distribution of all calculated proton migration barriers, visualizing the key differences between the fully oxidized Ba₈Fe₈O₂₄H and oxygen non-stoichiometric Ba₈Fe₈O₂₂H systems. The Jahn–Teller distortion in Ba₈Fe₈O₂₄H with its discrete set of O–O distances translates into two distinct peaks in the migration barrier distribution at ≈0.25 and ≈0.17 eV (blue curve). Although the symmetry of Ba₈Fe₈O₂₄H supercell formally corresponds to point group C₁, characteristic distortion pattern originating from the Jahn–Teller distortion are seemingly preserved in the defective supercell. The bimodal distribution in proton migration barriers is smeared out in the Ba₈Fe₈O₂₂H system where oxygen vacancies introduce additional lattice distortion that result in a more continuous set of O–O distances and thus migration barriers (yellow curve). The spread of migration barriers is larger in oxygen non-stoichiometric Ba₈Fe₈O₂₂H ranging between 0.10 and 0.26 eV (excluding here the very asymmetric barriers involving oxygen ions opposite to oxygen vacancies) than in fully oxidized Ba₈Fe₈O₂₄H ranging between 0.17 and 0.28 eV. The average proton migration barrier, on the other hand, decreases with increasing oxygen deficiency from 0.22 eV in Ba₈Fe₈O₂₄H eV to 0.18 eV in Ba₈Fe₈O₂₂H. The latter constitutes an interesting result since the formation of oxygen vacancies is generally accompanied by an expansion of the crystal lattice (see ref. 32) and as such longer O–O distances on average. However, more pronounced lattice distortions and changes in electronic structure (increased occupation of antibonding states) seem to give rise to lower proton migration barriers. These effects will be discussed in more detail in Section 3.4.

Fig. 8 Statistical distribution of all calculated proton migration barriers (KRA average of forward and backward barrier) in Ba₈Fe₈O₂₄H and Ba₈Fe₈O₂₂H.

The height of all calculated proton migration barriers – including both Ba₈Fe₈O₂₄H and Ba₈Fe₈O₂₂H systems – was found to correlate very well with the change in O–O distance between initial and transition state, see Fig. 9a. In addition, the barriers also exhibit a robust correlation with the change in O–H bond length between initial and transition state, see Fig. 9b. Both correlations yield high correlation factors (>0.9), which again emphasizes the two-step nature of proton transfer that involves the approach of donor and acceptor oxygen in the early stage and O–H bond breaking close to the transition state. The co-dependence of the proton migration barrier on both O–O and O–H distances is visualized in Fig. 9c as a three-dimensional representation. Consequently, the lowest migration barriers are achieved in situations where donor and acceptor oxygen need to be displaced only a little, and the O–H bond needs least stretching for the actual proton transfer.

Fig. 9 Correlation of proton migration barrier with the change in O–O distance (a), change in O–H bond length (b), and both structural parameters in a three-dimensional graph (c). Blue = Ba₈Fe₈O₂₄H cells, yellow = Ba₈Fe₈O₂₂H cells, red: Ba₈Zr₈O₂₄H, discussion in Section 3.5.

Interestingly, the transition states of all calculated proton transfer events are structurally very similar with a characteristic O–O distance of ≈2.4 Å. Hence, regardless of whether the initial O–O distance is 2.9 Å (Fig. 7a and b) or 2.7 Å (Fig. 7c), in the transition state the system acquires a very similar O–O distance of ≈2.4 Å, see Fig. S12.† This explains why already the initial O–O distance correlates linearly with the migration barrier with a correlation factor of 0.85 (Fig. S11a†) such that smaller O–O distances favor proton transfer – simply because then only minimum displacement of donor and acceptor oxygen is needed to achieve the transition state geometry. Furthermore, the O–H bond lengths involving both donor and acceptor oxygen in the transition state are very similar such that the initial O–H bond length already correlates with the migration barrier with a correlation factor of −0.76 (Fig. S11b†), as a longer O–H distance typically implies weaker O–H bond strength. These trends remain valid also when the hybrid HSE06 functional is used (ESI Section S17†).

The literature available so far on DFT-based proton migration barriers in triple conducting perovskites shows that proton migration is very sensitive towards the crystallographic structure (layers in Ruddlesden–Popper²⁶ or Brownmillerite²⁷ phases) as well as the cation composition^22–25,28 of the perovskite. The barriers in the literature span a wide range of 0.2 to 0.6 eV for various perovskites^22–25,28 (excluding outliers of 0.03 (ref. 22) and 1.52 eV (ref. 24) corresponding to specific chemical environments). In ref. 28, a migration barrier for BaFeO₃ of 0.21 eV was calculated, which is virtually the same as the average value of 0.22 eV obtained in the present study for BaFeO₃. The range of available literature values strongly overlaps with the values obtained for BaFeO_3−δ in the present study (0.10–0.28 eV) although some of the reported values are higher (e.g. 0.63 eV in BaZr_0.75Co_0.25O₃ (ref. 22)). While most previous investigations focus on very few barriers in a given material, the present article provides detailed insight into the nature of proton migration in triple conducting oxides by systematically elucidating how local lattice distortions give rise to a wide range of migration barriers, and that the O–O distance is a crucial parameter in determining the height of the barrier.

3.4. Separation of isotropic strain and Fe oxidation state effects

While Fig. 7 demonstrates the effect of increasing oxygen deficiency on the proton migration barrier, in this section we strive to separate the effects of changes in supercell volume and formal Fe oxidation state. While for the migration of large ions a volume expansion typically decreases the migration barrier, the situation may differ for proton transfer. Since the proton itself is formally only a point charge, the migration barrier rather depends on the availability of a suitable arrangement of bonding partners for the proton than on available free volume.

To explore the strain effect, we stepwise increased the volume of the supercell from 1% to 4% for Ba₈Fe₈O₂₄H and Ba₈Fe₈O₂₂H cells, choosing rather symmetric (Fig. 5b and 7d) and also more asymmetric profiles (Fig. 5a and 7c) to cover all relevant cases. Fig. 10a shows that the resulting proton migration barriers depend only very slightly on this isotropic volume expansion. From this we conclude that the decrease of the average barrier in Fig. 8 from 0.22 eV to 0.18 eV for Ba₈Fe₈O₂₄H compared to Ba₈Fe₈O₂₂H is not caused by the moderate volume expansion of the supercells of ≈0.9% upon increasing the O deficiency.

Fig. 10 Proton migration barriers for exemplary Ba₈Fe₈O₂₄H (blue squares) and Ba₈Fe₈O₂₂H (yellow circles) cells as a function of isotropic volume expansion (a) and of formal Fe oxidation state (b). Variation of oxidation state is achieved by adding electrons to supercells at fixed volume. Symmetric energy profiles are marked with solid lines, asymmetric ones with dashed lines. Energy profiles of proton trajectories in Ba₈Fe₈O₂₂H with constrained increased volume and added electrons can be found in Fig. S13 and S14,† respectively.

To further explore the reasons of average barrier decrease, we analyzed the effects due to changes of the formal Fe oxidation state using charged supercells with compensating background charge. The calculations include (i) 3 electrons added to the Ba₈Fe₈O₂₂H supercell for one symmetric (Fig. 7d) and one asymmetric migration profile (Fig. 7b), (ii) 2,4,6 electrons added to Ba₈Fe₈O₂₄H for the asymmetric migration profile (Fig. 5a), (iii) 4 electrons added to Ba₈Fe₈O₂₄H for the symmetric profile (Fig. 5b). The migration barrier decreases upon decreasing formal Fe oxidation state for the O24H as well as O22H supercells (Fig. 10b). Only for the very asymmetric Ba₈Fe₈O₂₂H profile (cf.Fig. 7c) the addition of electrons increases the barrier (Fig. S15†).

A closer inspection of the supercell geometries elucidates the reasons for the barrier decrease upon electron addition. The O⋯O distance around the proton decreases by 0.06–0.08 Å when 3 or 4 electrons are added to the supercell, and the O–H length increases by 0.006–0.018 Å. This shortening of the O⋯O distance can be related to the fact that the added electrons occupy antibonding Fe–O states (cf.Fig. 2b and ref. 40) which is expected to facilitate the appearance of local lattice distortions. The decreased O⋯O distance as well as the increased O–H length both contribute to the observed lowering of the barriers in Fig. 10. The barrier for O24H with four added electrons nicely follows the correlation of the migration barrier with initial O⋯O and O–H distance (Fig. S11c†).

3.5. Proton migration barriers in BaZrO₃

To address the question of a fundamental difference between proton migration barriers in electrolyte and triple-conducting cathode materials, we calculated proton transfer in BaZrO₃ as archetypal electrolyte material. Similar to our BaFeO₃ calculations, we used a 2 × 2 × 2 supercell with a PBE functional (here without an additional Hubbard U-term) and the same electronic and structural convergence criteria. As usual for large band-gap materials, the correct charge state of the proton (H⁺) in BaZrO₃ can be achieved by either using a charged supercell (with a compensating background charge) or by acceptor doping with, e.g., Sc³⁺. Here we use a charged supercell to exclude proton trapping effects near the acceptor dopant (e.g. ref. 9), which are not of primary interest in this study.

The calculated proton migration barrier in BaZrO₃ is 0.26 eV (the proton trajectory and energy profile can be found in Fig. S16†), being slightly higher than the average migration barrier in Ba₈Fe₈O₂₄ (0.22 eV). This indicates that proton migration barriers in electrolytes and triple conducting cathode materials do not fundamentally differ in their magnitudes (the ESI† also compares the PBE+U and HSE06 functional for both BaFeO_3−δ and BaZrO₃). Furthermore, the proton barrier in BaZrO₃ follows the trend of O–O and O–H distances as shown in Fig. 9, highlighting the importance of the identified structural parameters also for other barium-based cubic perovskites. Along these lines, the higher migration barrier of 0.26 eV in BaZrO₃ compared to 0.22 eV in BaFeO₃ is mainly due to the larger O–O distance (2.84 Å) as a result of the larger lattice constant of 4.22 Å in BaZrO₃ compared to 4.06 Å in BaFeO₃. The proton migration barrier of 0.26 eV in BaZrO₃ calculated here is in agreement with literature data of DFT-based migration barriers, ranging between 0.1 and 0.4 eV.^{9,13,15,16,18–20} The disparity in the reported values, however, shows that migration barriers depend sensitively on the employed computational parameters, and that a direct comparison of absolute values should be made only when the same method and parameters are used.

4. Conclusions

In the present article, we investigated proton migration in oxygen-deficient BaFeO_3−δ using first-principles DFT calculations and identified key structural parameters that govern the height of the proton migration barrier. The systematic analysis of different protonation sites in BaFeO_3−δ, demonstrates that the O 2p-band center of a particular oxygen ion before protonation correlates with the energy change upon protonating that oxygen ion, with higher p-band centers giving more negative proton affinities. Oxygen ions opposite to oxygen vacancies have substantially lower p-band centers and, as such, much lower proton affinities.

The proton migration barrier in Jahn–Teller distorted BaFeO₃ ranges between 0.17 and 0.28 eV, with an average barrier of 0.22 eV. The analysis of geometrical changes and O–H chemical bonding during individual proton transfer events indicated that the proton transfer is a two-step process: in the early stage the energy change is mainly governed by the mutual approach of donor and acceptor oxygen ions (the O–H bond is hardly stretched), and in the second stage near the transition state the O–H bond is broken, further increasing the energy. The proton migration barrier in oxygen-deficient BaFeO_3−δ ranges between 0.10 and 0.26 eV, with an average barrier of 0.18 eV. The decrease in migration barrier with increasing oxygen deficiency is attributed to the annihilation of oxygen (ligand) holes rather than volume expansion upon reduction. Such barrier changes can appear only in redox-active mixed protonic–electronic conductors.

A very good correlation is found between the height of all calculated migration barriers in BaFeO₃ and BaFeO_2.75 with the change in O–O and O–H distances between initial and transition states. Since the transition states of all calculated proton transfer events are structurally very similar with O–O distances of ≈2.4 Å, already the initial O–O distance yields a decent correlation with the migration barriers. The latter correlation allows one to estimate the migration barrier even without an actual NEB calculation.

For comparison, we also calculated the proton migration barrier in BaZrO₃ as the archetypical electrolyte material within the same computational framework. Despite major differences in the electronic structure, the calculated barrier is 0.26 eV, being only slightly higher than the barrier of 0.22 eV in fully oxidized BaFeO₃.

From the results of this article, we can derive design guidelines for the development of triple-conducting cathode materials. To achieve low migration barriers for proton transfer, the structural O–O separation (edge of [BO₆] octahedra) must be short. However, short O–O distance should not be achieved simply by decreasing the lattice parameter, which often entails increased B–O bond covalency and thus decreased oxygen ion basicity, both disfavoring the hydration reaction. Rather, the system should be characterized by moderate B–O–B tilting, or exhibit at a certain structural flexibility (soft modes) in this direction, which allows for shorter O–O distances around a proton while maintaining the basic character of the oxygen ions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. C. and D. G. thank the Latvian Council of Science (project no. lzp-2021/1-0203) for financial support. Christina Ertural (RWTH Aachen) is thanked for assistance with LOBSTER technical questions. Yuri Mastrikov (University of Latvia) is thanked for discussions of technical details in NEB calculations at initial stages of present study. Calculations were performed at the HLRS, University of Stuttgart, within the project 12939 DEFTD. The Institute of Solid State Physics, University of Latvia, as the Centre of Excellence has received funding from the European Union's Horizon 2020 Frame-work Programme H2020-WIDESPREAD-01-2016–2017-Teaming Phase2 under grant agreement No. 739508, Project CAMART². Open Access funding provided by the Max Planck Society.

References

1. M. Papac, V. Stevanovic, A. Zakutayev and R. O'Hayre, Triple ionic-electronic conducting oxides for next-generation electrochemical devices, Nat. Mater., 2021, 20, 301–313.
2. R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Oxides with Mixed Protonic and Electronic Conductivity, Annu. Rev. Mater. Res., 2021, 51, 461–493.
3. I. Zvonareva, X.-Z. Fu, D. Medvedev and Z. Shao, Electrochemistry and energy conversion features of protonic ceramic cells with mixed ionic-electronic electrolytes, Energy Environ. Sci., 2022, 15, 439–465.
4. G. Chen, A. Feldhoff, A. Weidenkaff, C. Li, S. Liu, X. Zhu, J. Sunarso, K. Huang, X. Y. Wu, A. F. Ghoniem, W. Yang, J. Xue, H. Wang, Z. P. Shao, J. H. Duffy, K. S. Brinkman, X. Tan, Y. Zhang, H. Jiang, R. Costa, K. A. Friedrich and R. Kriegel, Roadmap for Sustainable Mixed Ionic-Electronic Conducting Membranes, Adv. Funct. Mater., 2022, 32, 2105702.
5. N. Hayashi, T. Yamamoto, H. Kageyama, M. Nishi, Y. Watanabe, T. Kawakami, Y. Matsushita, A. Fujimori and M. Takano, BaFeO₃: a ferromagnetic iron oxide, Angew. Chem., 2011, 123, 12755–12758.
6. D. Poetzsch, R. Merkle and J. Maier, Proton uptake in the H⁺-SOFC cathode material Ba_0.5Sr_0.5Fe_0.8Zn_0.2O_3-δ: transition from hydration to hydrogenation with increasing oxygen partial pressure, Faraday Discuss., 2015, 182, 129–143.
7. D. Poetzsch, R. Merkle and J. Maier, Stoichiometry Variation in Materials with Three Mobile Carriers-Thermodynamics and Transport Kinetics Exemplified for Protons, Oxygen Vacancies, and Holes, Adv. Funct. Mater., 2015, 25, 1542–1557.
8. W. Muench, G. Seifert, K. D. Kreuer and J. Maier, A quantum molecular dynamics study of proton conduction phenomena in BaCeO₃, Solid State Ionics, 1996, 86, 647–652.
9. M. E. Björketun, P. G. Sundell and G. Wahnström, Effect of acceptor dopants on the proton mobility in BaZrO₃: A density functional investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054307.
10. L. Buannic, F. Blanc, I. Hung, Z. Gan and C. P. Grey, Probing the local structures and protonic conduction pathways in scandium substituted BaZrO₃ by multinuclear solid-state NMR spectroscopy, J. Mater. Chem., 2010, 20, 6322–6332.
11. M. Karlsson, Proton dynamics in oxides: insight into the mechanics of proton conduction from quasielastic neutron scattering, Phys. Chem. Chem. Phys., 2015, 17, 26–38.
12. Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Proton trapping in yttrium-doped barium zirconate, Nat. Mater., 2013, 12, 647–651.
13. F. M. Draber, C. Ader, J. P. Arnold, S. Eisele, S. Grieshammer, S. Yamaguchi and M. Martin, Nanoscale percolation in doped BaZrO₃ for high proton mobility, Nat. Mater., 2020, 19, 338–346.
14. G. Geneste, Two-lattice-vibration theory for proton transfer in cubic perovskites: Barium zirconate versus potassium tantalate, Solid State Ionics, 2020, 358, 115493.
15. M. A. Gomez, M. A. Griffin, S. Jindal, K. D. Rule and V. R. Cooper, The effect of octahedral tilting on proton binding sites and transition states in pseudo-cubic perovskite oxides, J. Chem. Phys., 2005, 123, 094703.
16. M. E. Björketun, P. G. Sundell, G. Wahnström and D. Engberg, A kinetic Monte Carlo study of proton diffusion in disordered perovskite structured lattices based on first-principles calculations, Solid State Ionics, 2005, 176, 3035–3040.
17. P. G. Sundell, M. E. Björketun and G. Wahnström, Density-functional calculations of prefactors and activation energies for H diffusion in BaZrO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 094301.
18. B. Merinov and W. Goddard III, Proton diffusion pathways and rates in Y-doped BaZrO₃ solid oxide electrolyte from quantum mechanics, J. Chem. Phys., 2009, 130, 194707.
19. N. Bork, N. Bonanos, J. Rossmeisl and T. Vegge, Simple descriptors for proton-conducting perovskites from density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014103.
20. M. A. Gomez and F. J. Liu, Protons in Al doped BaZrO₃ escape dopant traps to access long range proton conduction highways, Solid State Ionics, 2013, 252, 40–47.
21. H. Tellez Lonzano, J. Druce, S. J. Cooper and J. A. Kilner, Double perovskite cathodes for proton-conducting ceramic fuel cells: are they triple mixed ionic electronic conductors?, Sci. Technol. Adv. Mater., 2017, 18, 977–986.
22. Z. Wang, W. Yang, Z. Zhu, R. R. Peng, X. Wu, C. Xi and Y. Lu, First-principles study of O₂ reduction on BaZr_1-xCo_xO₃ cathodes in protonic-solid oxide fuel cells, J. Mater. Chem. A, 2014, 2, 16707–16714.
23. A. B. Munoz-Garcia and M. Pavone, First-principles design of new electrodes for proton-conducting solid-oxide electrochemical cells: A-site doped Sr₂Fe_1.5Mo_0.5O_6-δ perovskite, Chem. Mater., 2016, 28, 490–500.
24. X. Xu, H. Wang, J. Ma, W. Liu, M. Fronzi and L. Bi, Impressive performance of proton-conducting solid oxide fuel cell using a first-generation cathode with tailored cations, J. Mater. Chem. A, 2019, 7, 18792–18798.
25. H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang, Y. Zhang and D. Ding, Self-sustainable protonic ceramic electrochemical cells using a triple conducting electrode for hydrogen and power production, Nat. Commun., 2020, 11, 1907.
26. M. Chen, Y. Xuan, F. Zhang, L. He, X. Wang, H. Pan, J. Ren and Z. Lin, Atomistic insight into the hydration and proton conducting mechanisms of the cobalt doped Ruddlesden-Popper structure Sr₃Fe₂O₇, Int. J. Hydrogen Energy, 2020, 45, 14964–14971.
27. M. S. Islam, A. M. Nolan, S. Wang, Q. Bai and Y. Mo, A computational study of fast proton diffusion in Brownmillerite Sr₂Co₂O₅, Chem. Mater., 2020, 32, 5028–5035.
28. Z. Wang, Y. Wang, J. Wang, Y. Song, M. J. Robson, A. Seong, M. Yang, Z. Zhang, A. Belotti, J. Liu, G. Kim, J. Lim, Z. Shao and F. Ciucci, Rational design of perovskite ferrites as high-performance proton-conducting fuel cell cathodes, Nat. Catal., 2022, 5, 777–787.
29. K. D. Kreuer, Proton Conductivity: Materials and Applications, Chem. Rev., 1996, 8, 610–641.
30. K. D. Kreuer, Proton-conducting oxides, Annu. Rev. Mater. Sci., 2003, 33, 333–3359.
31. K. D. Kreuer, On the complexity of proton conduction phenomena, Solid State Ionics, 2000, 136, 149–160.
32. M. F. Hoedl, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, Interdependence of Oxygenation and Hydration in Mixed-Conducting (Ba,Sr)FeO_3−δ Perovskites Studied by Density Functional Theory, J. Phys. Chem. C, 2020, 124, 11780–11789.
33. G. Kresse and J. Hafner, Ab-initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
34. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
35. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab-initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
40. M. F. Hoedl, C. Ertural, R. Merkle, R. Dronskowski and J. Maier, The Orbital Nature of Electron Holes in BaFeO₃ and Implications for Defect Chemistry, J. Phys. Chem. C, 2022, 126, 12809–12819.
41. B. Ribeiro, M. Godinho, C. Cardoso, R. Borges and T. Gasche, Self-doping and the role of oxygen vacancies in the magnetic properties of cubic BaFeO_3-δ, J. Appl. Phys., 2013, 113, 083906.
42. Y. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Ab initio energetics of LaBO₃ (001) (B= Mn, Fe, Co, and Ni) for solid oxide fuel cell cathodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101.
43. Z. Baiyee, C. Chen and F. Ciucci, A DFT+U study of A-site and B-site substitution in BaFeO_3-δ, Phys. Chem. Chem. Phys., 2015, 17, 23511–23520.
44. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
45. J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum:“Hybrid functionals based on a screened Coulomb potential”[J. Chem. Phys. 118, 8207 (2003)], J. Chem. Phys., 2006, 124, 219906.
46. H. Jónsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Singapore, 1998, p. 385.
47. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
48. A. Van der Ven, G. Ceder, M. Asta and P. D. Tepesch, First-principles theory of ionic diffusion with nondilute carriers, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184307.
49. R. Dronskowski and P. Blöchl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97, 8617–8624.
50. V. Deringer, A. Tchougréeff and R. Dronskowski, Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets, J. Phys. Chem. A, 2011, 115, 5461–5466.
51. S. Maintz, V. Deringer, A. Tchougréeff and R. Dronskowski, Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34, 2557–2567.
52. S. Maintz, V. Deringer, A. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035.
53. C. Ertural, S. Steinberg and R. Dronskowski, Development of a robust tool to extract Mulliken and Löwdin charges from plane waves and its application to solid-state materials, RSC Adv., 2019, 9, 29821–29830.
54. R. Nelson, C. Ertural, J. George, V. Deringer, G. Hautier and R. Dronskowski, LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory, J. Comput. Chem., 2020, 41, 1931–1940.
55. C. Ertural, R. Stoffel, P. Müller, C. Vogt and R. Dronskowski, First-Principles Plane-Wave-Based Exploration of Cathode and Anode Materials for Li-and Na-Ion Batteries Involving Complex Nitrogen-Based Anions, Chem. Mater., 2022, 34, 652–668.
56. R. A. Davies, M. S. Islam and J. D. Gale, Dopant and proton incorporation in perovskite-type zirconates, Solid State Ionics, 1999, 126, 323–335.
57. D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, Ab initio modelling of oxygen vacancies and protonic defects in La_1-xSr_xFeO_3-δ perovskite solid solutions, J. Mater. Chem. A, 2016, 4, 13093–13104.
58. M. E. Björketun, P. G. Sundell and G. Wahnström, Structure and thermodynamic stability of hydrogen interstitials in BaZrO₃ perovskite oxide from density functional calculations, Faraday Discuss., 2007, 134, 247–265.
59. W. Münch, K. D. Kreuer, G. Seifert and J. Maier, A quantum molecular dynamics study of proton diffusion in SrTiO₃ and CaTiO₃, Solid State Ionics, 1999, 125, 39–45.
60. T. Tauer, R. O'Hayre and J. W. Medlin, An ab initio Investigation of Proton Stability at BaZrO₃ Interfaces, Chem. Mater., 2014, 26, 4915–4924.
61. G. Raimondi, F. Giannici, A. Longo, R. Merkle, A. Chiara, M. F. Hoedl, A. Martorana and J. Maier, X-ray Spectroscopy of (Ba,Sr,La)(Fe,Zn,Y)O_3-δ Identifies Structural and Electronic Features Favoring Proton Uptake, Chem. Mater., 2020, 32, 8502–8511.
62. Y. L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. Morgan, Prediction of solid oxide fuel cell cathode activity with first-principles descriptors, Energy Environ. Sci., 2011, 4, 3966–3970.
63. T. S. Bjørheim, M. F. Hoedl, R. Merkle, E. A. Kotomin and J. Maier, Proton, hydroxide ion, and oxide ion affinities of closed-shell oxides: importance for the hydration reaction and correlation to electronic structure, J. Phys. Chem. C, 2019, 124, 1277–1284.
64. M. F. Hoedl, Electronic Structure and Defect Chemistry in Iron Perovskites, PhD thesis, Univ. Stuttgart, 2021.
65. Y. Jing and N. R. Aluru, The role of A-site ion on proton diffusion in perovskite oxides (ABO₃), J. Power Sources, 2020, 445, 227327.
66. M. S. Islam, R. A. Davies and J. D. Gale, Proton migration and defect interactions in the CaZrO₃ orthorhombic perovskite: A quantum mechanical study, Chem. Mater., 2001, 13, 2049–2055.
67. K. D. Kreuer, A. Fuchs and J. Maier, HD isotope effect of proton conductivity and proton conduction mechanism in oxides, Solid State Ionics, 1995, 77, 157–162.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta08664f

‡ These authors contributed equally.

---