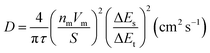Prussian blue analogues for potassium-ion batteries: insights into the electrochemical mechanisms

Abstract

A comprehensive description of the electrochemical mechanisms of the Prussian Blue Analogue (PBA) K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O is obtained by combining several complementary ex situ and operando physico-chemical characterisation techniques. This particular PBA, which shows very good electrochemical performance as a cathode material in potassium-ion batteries (PIBs), undergoes three successive redox reactions during the (de-)potassiation that are hereby identified by ex situ⁵⁷Fe Mössbauer spectroscopy and operando Mn and Fe K-edge X-ray absorption spectroscopy. These reactions come along with notable modifications of the crystal structure, which are followed in real time by operando X-ray diffraction. The correlation of these results, interpreted with the support of chemometric methods, also reveals the limitations of this PBA, probably related to the deactivation of the Mn undergoing extensive reversible Jahn–Teller distortion during cycling as well as possible dissolution in the electrolyte. These results underline that optimisation of the chemical composition of PBAs is a crucial step towards the preparation of reliable and stable PBA-based cathodes for PIBs.

---

1 Introduction

Rechargeable batteries represent one of the energy storage systems of choice in the on-going energy transition. Lithium-ion batteries (LIBs) have been playing an important role in supplying power to different systems, from portable devices to electric vehicles.¹ Their dependence on non-eco-friendly elements such as Ni or Co, however, and the inadequacy of Li resources may limit their penetration in the energy market for some applications.² In the last decade, research on new battery technologies has increased rapidly, in order to find suitable alternatives to LIBs. Amongst the next-generation battery (NGB) technologies proposed up to now, potassium-ion batteries (PIBs) are considered as promising candidates for large-scale energy storage. Besides the widespread availability of the raw materials, PIBs possess attractive merits such as fast ionic diffusion kinetics of K⁺ ions in the electrolyte, comparable energy density to LIBs, and a large choice of potential electrode materials.³

Compared to other cathode materials for PIBs, Prussian Blue Analogues (PBAs) have gained great interest due to their cost effectiveness, facile synthesis and excellent electrochemical properties.^4–10 PBAs have a general chemical formula A_xM1[M2(CN)₆]_y (x ≤ 2), in which A is an alkali cation, M1 and M2 are (TMs). M1 is usually high-spin (HS) while M2 is low-spin (LS) since they are respectively bonded to the nitrogen and carbon ends of the cyanide ligands, i.e., to weak and strong field ligands.¹¹ The TMs located in M1N₆ or M2C₆ octahedra are linked via the cyanides, forming a three-dimensional cage-like structure with open channels, which facilitates the insertion of various guest cations.¹² Among them, K⁺ is known to have a relatively high affinity to the PBA framework.^13–16 The redox mechanism of PBAs resides in the redox couples of both TMs, and it is strongly dependent on the composition as well as on the battery chemistry.^17,18 In some cases, only one of the two metals is redox active, which negatively affects the overall capacity of the material. To this regard, manganese (Mn) and iron (Fe) are commonly chosen TMs for PBAs, because they are both low-cost non-toxic elements and are redox active, thereby leading to high practical capacities, close to 150 mA h g⁻¹.^19–21 The promising electrochemical properties of Mn- and Fe-based PBAs have been reported for both aqueous and organic sodium-ion batteries (SIBs)^{17,18,22–27} and PIBs.^7,28–35 Nevertheless, the order of the redox reactions at the two Mn and Fe sites is still a matter of debate: on the one hand, by comparing the signals of the TMs in the cyclic voltammetry (CV) signatures of different PBA compositions, the redox potentials of the TMs were found in the order of HS Fe³⁺/HS Fe²⁺ < LS Fe³⁺/LS Fe²⁺ < HS Mn³⁺/HS Mn²⁺.^32,33,36,37 On the other hand, from soft X-ray absorption spectroscopy (sXAS), Pasta and co-workers proposed that the oxidation of LS Fe²⁺ and HS Mn²⁺ occurs simultaneously, yet the LS Fe³⁺/LS Fe²⁺ couple was assigned at lower potential.³⁸ The sXAS spectra at the Mn L-edge showed insignificant modifications during the anodic scan, which made the assessment difficult and ambiguous. In addition to these uncertainties, the structural evolution of these materials needs to be studied more thoroughly. In fact, operando X-ray diffraction (XRD) showed that such PBAs undergo several reversible phase transitions and volume expansion/shrinkage during the K⁺ (de)insertion, which is mainly related to the Jahn–Teller (JT) effect at the Mn³⁺ centres.³² Such structural evolution, however, might be triggered by both (1) the variation of oxidation states of the TMs (and in particular for Mn) and (2) the simultaneous (de)insertion of the cations within the cage structure, both phenomena contributing to the modification of electronic properties and local structures. As the electrochemical properties of electrode materials have a strong correlation with their structural evolution, which, in turn, affects their battery performance in terms of reversibility and cyclability, it is necessary to have a clear view of these phenomena in manganese hexacyanoferrate PBAs.

In this work, the PBA with the chemical formula K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O is chosen as a cathode material for PIBs as partial Fe substitution at the HS metal site can diminish the impact of JT effect on the Mn³⁺ centres formed upon oxidation.³⁹ The electrochemical mechanism of this PBA was investigated by employing complementary ex situ and operando characterization approaches. Ex situ⁵⁷Fe Mössbauer spectroscopy provides information about the local environment of Fe centres, while operando X-ray diffraction (XRD) allow us to follow the evolution of the global structure of the PBA. These approaches are complemented by operando X-ray absorption spectroscopy (XAS), a powerful synchrotron technique that helps acquiring local structural information of electrode materials containing TMs. While X-ray absorption near-edge structure (XANES) provides information about the oxidation states and coordination geometry of the TMs, the analysis of extended X-ray absorption fine structure (EXAFS) portion gives details about short-range distances around the metal centres.^40,41 This has already been shown to be efficient in studies of the electrochemical mechanisms of PBAs.^42–45 The analysis of the operando datasets was performed using a chemometric approach including principal component analysis (PCA) and multivariate curve resolution-alternating least squares (MCR-ALS) methods, allowing detailed descriptions of the structural evolution and local environment of the TMs.⁴⁶ These complementary findings are combined to understand in detail the influence of structural modification on the electrochemical behaviour of the investigated PBA.

2 Experimental section

2.1 Synthesis of the PBA

K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O (MF21) was synthesized by a simple co-precipitation method. Two solutions A and B were prepared at 60 °C. Solution A was obtained by dissolving 8 mmol of K₄[Fe(CN)₆]·3H₂O in 100 mL of saturated KCl solution; solution B was a mixture of 5.2 mmol and 2.8 mmol of, respectively, MnSO₄·H₂O and FeSO₄·7H₂O in 80 mL of saturated KCl solution. Solution B was poured rapidly into solution A under intense stirring. The temperature was kept at 60 °C for 24 hours of agitation. The obtained suspension was washed five times with deionized water and then two times with ethanol, and centrifuged at 20 000 rpm before being dried under vacuum. An additional drying step at 100 °C overnight was applied before the characterizations and electrode formulation to ensure that the interstitial water was removed completely. The choice of drying temperature was decided based on thermogravimetric analysis results, as explained in the ESI.†

2.2 Materials characterization and data analysis

Powder XRD patterns of the synthetized materials were collected on a Bruker Advance D8 diffractometer with a Cu Kα radiation source (λ = 1.5418 Å) and a step size of 0.02° in the range of 10–100°. Lattice parameters were obtained from profile matching method using Fullprof package.⁴⁷

Transmission ⁵⁷Fe Mössbauer spectra were collected at room temperature with a triangular velocity waveform. A Kr gas-filled proportional counter was used for the detection of γ-rays produced by a 0.5 GBq ⁵⁷Co:Rh source, kept at room temperature. Velocity calibration was performed with an α-Fe foil at room temperature. Absorbers containing 5 to 25 mg cm⁻² were protected from air using thermally sealed coffee-bags. The Mössbauer spectra were fitted by using the PC-Mos II computer program with appropriate superpositions of Lorentzian lines. In this way, hyperfine parameters such as the isomer shift (δ), the electric quadrupole splitting (Δ), the full line width at half maximum (Γ) and the relative resonance areas (Area) of the different components of the absorption patterns were determined. The isomer shift scale is referred to α-Fe at room temperature.

Thermogravimetric analysis (TGA) was performed to determine the amount of interstitial water of MF21. Measurements were carried out on a simultaneous thermal analyser STA 449 F1 Jupiter® (NETZSCH) from room temperature to 450 °C under argon atmosphere with a thermal step of 5 °C min⁻¹. The amount of interstitial water was calculated based on the mass loss at 100 °C.

Transmission electron microscopy (TEM) images of the as-prepared MF21 were taken at the “Microscopie Électronique et Analytique” platform of the University of Montpellier. The observations were carried out on a LaB₆ JEOL 1400 Plus at 120 kV. Sample preparation was performed by depositing a drop of a suspension of the studied material in ultra-pure water on a copper grid. The drop was dried in air, covered from external contaminations.

Chemical composition analysis of the as-prepared MF21 was performed on a scanning electron microscope (SEM) FEI Quanta 200 Hitachi S-2600N equipped with a silicon drift detector for Energy Dispersive X-ray (EDX) analysis (Oxford Instruments X-Max 50 mm²). The MF21 powder was deposited onto a carbon-based adhesive tape followed by an air blow to remove the excess powder. The measurement was carried out under vacuum; the quantification was performed via the INCA software with a 3 s dwell time and an acquisition time of 30 s.

X-ray absorption spectroscopy (XAS) experiments were carried out at ELETTRA Sincrotrone Trieste, Basovizza–Trieste (Italy), at the XAFS beamline.⁴⁴ The storage ring was operated at 2.0 GeV in top-up mode with a typical current of 300 mA. Data were recorded at Mn and Fe K edges in transmission mode using ionization chambers filled with a mixture of Ar, N₂, and He to have 10, 70, and 95% of absorption in the I₀, I₁, and I₂ chambers, respectively. An internal reference of Mn and Fe foils located between the I₁ and I₂ chambers was used for energy calibration at each scan. This allowed a continuous monitoring of the energy during consecutive scans. Spectra were collected with a constant k-step of 0.03 Å⁻¹ from 6300 to 8000 eV gathering both Mn and Fe. The energies were calibrated by assigning the first inflection point of the spectra of the Mn and Fe metal to 6539 and 7112 eV, respectively. The white beam was monochromated using a fixed exit monochromator equipped with a pair of Si(111) crystals. High-order harmonics were rejected by detuning the second crystal of the monochromator by 30% of the maximum. XAS spectra were analysed using the Artemis software.⁴⁸ Fourier transforms (FT) of the EXAFS data were performed in the 3–10.5 Å⁻¹k range, and the fitting was done in the R-space up to 5 Å. All FT of the EXAFS data are shown without phase correction.

For the ordinary electrochemical tests, electrode films were prepared by tape-casting on aluminium foil (18 μm, GoodFellow), a slurry obtained by mixing MF21 with Super P carbon (Alfa Aesar) and poly(vinylidene fluoride) (PVdF, Solef® 5130) as conductive additive and binder, respectively, with a mass ratio of 60/30/10 in N-methyl-2-pyrrolidone (NMP, Sigma Aldrich) in a planetary ball mill. The cast film was dried in air before punching out round-shaped electrodes with a diameter of 1.27 cm, which were then further dried under vacuum at 80 °C overnight. Coin cells (CR2032) of MF21 and K metal were assembled in an Ar-filled glovebox (O₂ < 0.5 ppm, H₂O < 0.5 ppm) using 5 M KTFSI in DME as the electrolyte, a Whatman glass fibre and a tri-layer polypropylene polyethylene membrane (Celgard 2325) as separators.

Galvanostatic cycling was carried out at a current density of 25 mA g⁻¹ for normal cycling tests, and from 15 to 500 mA g⁻¹ for the rate capability test. The galvanostatic intermittent titration technique (GITT) was applied using a current rate of 5 mA g⁻¹ with an acquisition time of 30 minutes, followed by a relaxation of 3 hours, with dE_WE/dt = 0.1 mV h⁻¹. The diffusion coefficient at each x value (x: the amount of inserted K⁺ at each pulse) was calculated as:

Here, τ (s) is the duration of the current pulse; n_m (mol) is the number of moles; V_m (cm³ mol⁻¹) is the molar volume of MF21; S (cm²) is the electrode area (1.27 cm²); ΔE_s (V) is the steady-state voltage change, due to the current pulse, and ΔE_t (V) is the voltage change during the constant current pulse, eliminating the iR drop.

For the ex situ and operando analyses, the electrodes were prepared by thoroughly mixing MF21 with Super P carbon and PTFE (poly(tetrafluoroethylene)) at a weight ratio of 60/30/10 to form a homogeneous film. The film was cut into round electrodes with the diameter of 11 mm (operando XRD and XAS) or 14 mm (ex situ Mössbauer spectroscopy). Operando XRD and XAS experiments were carried out using a special electrochemical cell equipped with a Be window.⁴⁹ A thin Al foil (thickness = 2 μm) was put between the working electrode and the Be window and used as the positive current collector. The mass loading of the electrodes used for the ex situ Mössbauer spectroscopy was ca. 25 mg cm⁻², whereas it was ≤10 mg cm⁻² for the operando XRD and operando XAS measurements. A common chemometric approach based on principal component analysis (PCA) and multivariate curve resolution-alternating least squares (MCR-ALS) analysis, described in detail elsewhere,⁴⁶ was applied to analyse the full operando XRD patterns and XAS spectra datasets. In short, PCA is used here to determine the number of independent components contributing to the whole series of collected patterns/spectra during electrochemical cycling. The number of principal components determined in this way is used as the basis for MCR-ALS analysis, which allows the stepwise reconstruction of the “pure” spectral components which are necessary for interpreting the whole multiset of operando spectra. The MCR-ALS analysis was performed with the following constraints: (i) non-negativity of the intensity of the components, (ii) unimodality for the evolution of all components along a single process and (iii) closure (the sum of all components always equal to 100 of the intensity). The pure XRD and XAS components obtained from MCR-ALS analysis are then analysed as normal XRD patterns and XAS spectra, respectively.

3 Results and discussion

3.1 Structure, composition, and morphology of the as-prepared MF21

The XRD pattern of dried MF21 and the corresponding profile matching are shown in Fig. 1a. The unit cell can be indexed as monoclinic structure (space group P2₁/n) with a, b, c, and β equal to 10.009(2) Å, 7.228(1) Å, 6.921(1) Å, and 90.38(1)°, respectively. The crystal lattice of the MF21 is slightly smaller and more tilted than other reported isostructural PBAs containing Mn and/or Fe as HS TMs,^32,50,51 probably due to the formation, during the synthesis and/or the drying processes, of small portions of oxidised Mn³⁺ or Fe³⁺ at the M1 site. The TEM image in the inset of Fig. 1a shows that MF21 consists of nanoparticles with sizes between 30 and 50 nm with a uniform cubic morphology. EDX and TGA analyses allow establishing the chemical formula K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O for the dried MF21 (cf. Fig. S1 and Table S1†) by considering only divalent M1 sites. The room temperature ⁵⁷Fe Mössbauer spectrum of dried MF21 (Fig. 1b) can be fitted with a singlet and two quadrupole split doublets. The corresponding hyperfine parameters (Table 1) provide information about oxidation states, compositions, and local geometries of the Fe centres: the isomer shift (δ = −0.10 mm s⁻¹) of the singlet, counting for 70% of the global spectral area, can be attributed to LS Fe²⁺. The lack of quadrupole splitting (Δ = 0.00 mm s⁻¹) indicates that the Fe²⁺ centres are surrounded by a centrosymmetric electron distribution, as expected for a LS d⁶ electron configuration and a symmetric octahedral coordination.⁵² The doublet with the highest isomer shift (δ = 1.02 mm s⁻¹) can be attributed to HS Fe²⁺. The larger values of quadrupoles splitting (Δ = 1.50 mm s⁻¹) for this component compared to other Na-based pure-Fe PBAs²⁷ (Δ ∼ 1.1 mm s⁻¹) suggests a more regular octahedral coordination between HS Fe²⁺ and N atoms. The third component with intermediate isomer shift (δ = 0.28 mm s⁻¹) can be attributed to HS Fe³⁺, indicating that about half of the HS Fe²⁺ was oxidized during the synthesis. This oxidation seems to occur during the synthesis, since the spectra of MF21 before and after vacuum drying are virtually identical (Fig. S3 and Table S2†), implying that no oxidation happened during drying. The surface area of the LS Fe²⁺ is ¾ of the total spectral area, as expected from the stoichiometric ratio used for the synthesis. Balancing the oxidation of half of divalent iron ions would only require a slight increase (about 0.04) of the hexacyanoferrate moieties with respect to the previously established formula. Thus, we will still use the K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O formula.

Fig. 1 (a) XRD pattern of MF21 dried at 100 °C with Rietveld refinement and TEM image (inset) and (b) Mössbauer spectrum of dried MF21.

Table 1 Refined room-temperature ⁵⁷Fe Mössbauer hyperfine parameters for dried MF21, (Δ is the quadrupole splitting, δ the isomer shift with respect to α-Fe, and Γ the Lorentzian linewidth)

Δ (mm s^−1)	δ (mm s^−1)	Γ (mm s^−1)	Area (%)	Site
0.00	−0.10(0)	0.31(−)	70(2)	LS Fe^2+
1.50(2)	1.13(1)	0.34(2)	15(1)	HS Fe^2+
0.64(7)	0.39(5)	0.46(8)	15(2)	HS Fe^3+

---

3.2 Electrochemical performance of MF21 in PIB half-cells

The electrochemical performance of MF21 in PIB half-cells as obtained from long-term galvanostatic cycling at various current densities is shown in Fig. 2. The galvanostatic profile of MF21 half-cell contains at least two plateaus in each charge/discharge process (Fig. 2a and c). During discharge, two medium-length plateaus at ca. 3.8–4.1 V and a short one at ca. 3.6 V are observed, which well correspond to the reduction of three TM sites in the material. The short plateau remains during the following charge with similar capacity contribution as in the discharge, while at high potential only one plateau is observed at ca. 4 V. The initial discharge capacity of MF21 obtained at I = 25 mA g⁻¹ is 134 mA h g⁻¹ which is equivalent to the insertion of 1.7 K⁺ ions with a high coulombic efficiency (CE) of 93% (Fig. 2a). Despite the good performance in the first cycle, a gradual capacity degradation, with CE < 99%, is observed during long-term cycling (Fig. 2b). Although the 5.0 M KTFSI in DME electrolyte has been reported to be stable towards K metal at high voltages,⁵³ this electrolyte might anyhow decompose on the cathode to form a cathode-electrolyte interphase (CEI), leading to poor cycling retention. As shown in Fig. 2c and d, MF21 can deliver 104 mA h g⁻¹ at the current density of 100 mA g⁻¹. While the discharge capacity decreases when increasing the current density, the CE approaches 99%, implying less electrolyte decomposition at high potentials. Moreover, large polarizations are observed in the cycling profile at high current rates. This phenomenon as well as the capacity loss at E < 3.9 V probably result from sluggish mass transfer and deactivation of some TM sites. Since the electrochemical performance of MF21 derives from its electronic and structural properties, it is important to dwell in-depth into the mechanism and the evolution of those properties.

Fig. 2 (a and b) Galvanostatic profile and cyclability of MF21 at a constant current of 25 mA g⁻¹, respectively; (c) cycling profiles and (d) rate capability of MF21 at currents varying between 15 and 500 mA g⁻¹.

3.3 Electrochemical mechanism of MF21

Ex situ ⁵⁷Fe Mössbauer spectroscopy measurements were carried out at different states of charge (SOC) to determine the involvement of the Fe centres in the redox reaction(s) of MF21 occurring at each plateau (Fig. 3 and Table S3†). The SOC at which the Mössbauer spectra were recorded are detailed in Fig. S4.†

Fig. 3 Room temperature ex situ Mössbauer spectra of MF21 recorded at different states: (a) 4.3 V – end of charge (EOC), (b) 3.90 V (end of plateau 1 in the discharge), (c) 3.65 V (end of plateau 2 in the discharge), (d) 3.0 V – end of discharge (EOD), and (e) 3.80 V (end of plateau 3 in the charge).

At end of charge (EOC, Fig. 3a), no contribution from HS Fe²⁺ is observed in the Mössbauer spectrum. Instead, the percentage of HS Fe³⁺ increases up to 31%. The best fit for this spectrum requires an additional quadrupole doublet characterised by an isomer shift in the typical range of octahedral LS Fe³⁺ and LS Fe²⁺. The non-zero value of the quadrupole splitting for this doublet (Δ = 0.75 mm s⁻¹), however, indicates a deviation from a centrosymmetric electron distribution, as expected for the LS d⁵ electron configuration of LS Fe³⁺. Such large values of Δ were already reported for LS Fe³⁺ in Cu^IIFe^III PBAs.^54,55 Relatively large linewidths are observed for all spectral components, indicating a certain distribution of similar coordination environments for all Fe species. About 11% of the total resonance area corresponds to LS Fe²⁺, which accounts for 16% of the amount of LS Fe species (70%) according to the Mössbauer spectrum of dried MF21 (Fig. 1b). Assuming that all the Mn²⁺ is oxidized to Mn³⁺ at the end of charge, which is equivalent to the extraction of 0.65 K⁺, and based on the amount of reacted Fe²⁺ that can be calculated from the EOC Mössbauer spectrum (0.18 HS Fe²⁺ and 0.77 LS Fe²⁺), the amount of extracted K⁺ can be estimated at ∼1.6 per unit formula, in good agreement with the observed capacity in oxidation.

As mentioned in the introduction (vide supra), the assignments in the literature of the plateaus observed in the electrochemical curves to the specific reactions of LS Fe³⁺/LS Fe²⁺ and HS Mn³⁺/HS Mn²⁺ were based on the comparison of CV peaks of the PBAs containing different M1 TM cations.^32,33,36,37 In particular, the first reduction (higher potential) was assigned to the reaction of Mn³⁺/Mn²⁺, and the second one was attributed to the redox couple LS Fe³⁺/Fe²⁺. However, the results of ex situ Mössbauer spectroscopy indicate that the opposite occurs. The spectra recorded at the end of the two high-potential plateaus in the discharge, corresponding to the cut-off voltages of 3.90 V and 3.65 V, respectively (Fig. 3b and c) show the same compositions of LS Fe²⁺ and HS Fe³⁺, with their area ratio is around 70/30. Therefore, the redox reactions at the two plateaus at 4.1 and 3.9 V can be assigned to the redox reaction LS Fe³⁺ → LS Fe²⁺ and Mn³⁺ → Mn²⁺, respectively. In addition to the identical area ratio of the iron species, the resolved spectra at these states of charge have a small difference in the quadrupole splitting of the LS Fe²⁺. After the second plateau, the simultaneous presence of the unequally charged Mn²⁺ and HS Fe³⁺ at the M1 sites would lead to a distortion of the local structure, resulting in a slightly distorted octahedral coordination of the LS Fe²⁺ sites, which results in small but observable quadrupole splitting (Δ = 0.14 mm s⁻¹, Table S2†). This spectrum is identical to that obtained after the short plateau in the charge (3.80 V, Fig. 3e), indicating that this process is well reversible and can be attributed to the redox reaction of the couple HS Fe³⁺/Fe²⁺. At the end of discharge (Fig. 3d), the HS Fe²⁺ appears again in the Mössbauer spectrum, with almost identical hyperfine parameters as the pristine material. The HS Fe³⁺ is still present in the resolved spectrum with a similar amount as before cycling, indicating that the HS Fe³⁺ formed in the synthesis is electrochemically inactive.

The relationship between the structural transformation and the redox reactions of the TMs of MF21 can be revealed by operando XRD combined with chemometric analysis. The evolution of the main peaks of the diffraction patterns (Fig. 4) shows a reversible structural transformation during the first K extraction–insertion. All of them shift to lower angles during oxidation, when K⁺ ions are extracted from the host, and then return to the pristine position in the opposite process. A profile matching refinement of the ex situ XRD pattern of charged MF21 (Fig. S5†) shows that the depotassiated PBA has a cubic structure (SG: Fm3̄m) with a = 10.3478(3) Å.

Fig. 4 Operando XRD contour map for three selected 2θ regions of MF21 recorded at the current density of 5 mA g⁻¹, in the voltage range of 3–4.3 V (vs. K⁺/K) using the 5 M KTFSI in DME electrolyte.

PCA applied on the operando XRD data (Fig. S6†) shows that at least three independent components are necessary to describe the whole dataset including the charge (depotassiation) and the discharge (potassiation). Therefore, MCR-ALS was employed separately on each process with the constraint of unimodality for all components. This chemometric approach allows us to follow the evolution of the three components (Fig. 5), and concurrently, reconstructs the patterns corresponding to the three “pure” reference components (Fig. 6), which show a shift to lower angles on going from Component 1 to 3, in line with the evolution of the operando data (Fig. 4). During the (de)potassiation, there are at least two components co-existing in the patterns (Fig. 5). Since these components correspond to different crystal structures (vide infra), it implies that the electrochemical mechanism of MF21 can be described with two consecutive steps, from component 1 to component 2, and then from component 2 to component 3. Component 1 represents the pristine monoclinic phase, being the only component at the beginning of the reaction, while component 3 corresponds to the final cubic phase, and reaches its maximum concentration at the end of charge. The intermediate component 2 reaches its maximum at x ∼ 1 (x: moles of K⁺ per mole of MF21), and totally disappears at the end of charge. In the following discharge, component 2 reappears and is maintained during the second plateau, corresponding to the reduction of Mn³⁺, then decreases but remains at ca. 10% at the end of the potassiation.

Fig. 5 Evolution of the relative contributions of the three pure components (component 1: blue, component 2: red, component 3: green) obtained from the PCA and MCR-ALS treatment of the operando XRD in the first cycle (top) and the corresponded cycling profile at 5 mA g⁻¹ (bottom).

Fig. 6 Computed XRD patterns of the three MCR-ALS components.

The profile matching refinement of the patterns of the three components (Fig. S7†) provides their space groups and lattice parameters, which are gathered in Table S4.† Component 1 has lattice parameters virtually identical to those of the pristine phase, while those of the cubic component 3 is slightly smaller than those obtained from ex situ XRD. Component 2 is also cubic (SG: Fm3̄m), but is characterised by a smaller lattice size than that of component 3. By combining the concentration evolution of the components and their lattice parameters, the mechanism can be straightforwardly described with two processes occurring sequentially. First, a bi-phasic transformation from monoclinic MF21 to cubic K_1.0MF21 occurs during the oxidation of the HS Fe²⁺ and the beginning of the long plateau. At lower K⁺ contents, the cubic phase expands until all the cations have been extracted. The whole mechanism is reversible: in the discharge, the bi-phasic process occurs in the plateau corresponding to the reduction of Mn³⁺ → Mn²⁺. However, the mechanism of the depotassiation is not yet clear, hence more details about the redox evolution and local structure of the TMs are essential.

Details about the local geometry of the TMs were acquired by operando XAS. The Fe and Mn K-edge XANES spectra (Fig. 7) recorded during the first charge show a clear shift towards higher energies, in line with the expected increases in the oxidation states of the two TMs. In previous studies of iron hexacyanocobaltate (FeHCCo) by Giorgetti and coworkers,^56,57 a large modification in the Fe K-edge was observed, whereas the Co K-edge varied only very slightly. In this case, indeed, the iron is the HS state, coordinated to six cyanides via the nitrogen atom, whereas the Co is in the LS state, coordinated to the carbon ends. Similarly, in the case of copper hexacyanoferrate (CuHCFe),⁴⁵ only the edge of the metal in the HS state coordinated through the nitrogen varies substantially, whereas that of the LS TM, e.g., Fe in this case, shows a negligible shift during charge/discharge. In both cases, however, the LS TM was supposedly not participating to the redox mechanism. In the specific case of LS Fe²⁺ and Fe³⁺, however, previous studies on K₄[Fe(CN)₆] and K₃[Fe(CN)₆] showed the occurring of only a slight edge shift between the two oxidation states, the largest modification being observed in the shape of the pre-edge peaks.⁴³ The small differences between the spectra of cyanide-coordinated LS Fe²⁺ and Fe³⁺ can be attributed to the intense π-acceptor properties of cyanide ligands, which buffer the change in the positive charge, maintaining the local environment of the Fe virtually unchanged, resulting in stable Fe–C bond lengths.⁴³ In the case of the HS Fe coordinated to the nitrogen ends of the cyanides, however, π back-donation is much weaker,^58,59 and hence the change in the oxidation state has a stronger influence on the local environment, leading to large shifts on the K-edge XAS spectra.

Fig. 7 Operando XANES at the Fe (a) and Mn (b) K edges in the MF21|K PIB in situ half-cells during the first charge (depotassiation).

Now, considering that MF21 contains 72% of LS Fe and 28% of HS Fe, and as some HS Fe³⁺ is present already in the pristine material, the slight but significant observed shift of the absorption edge (Fig. 7a) during the charge process can be attributed principally to the oxidation of the residual HS Fe²⁺. For the Mn K-edge spectrum, in contrast, a large modification of the absorption edge is observed during the depotassiation, corresponding to the oxidation of Mn²⁺ to Mn³⁺ (Fig. 7b). Such a modification, however, does not occur during the whole charge process, but only starting from the beginning of the second plateau at ∼4.0 V. Noticeably, during the oxidation, the intensity of the main edge peak decreases, a new one rises simultaneously at higher energies. The gradual modification of the spectrum lets one identify two isosbestic points at about 6555 and 6585 eV (Fig. 7b), suggesting that two species are probably sufficient to explain the evolution of the XANES spectra.

The evolution of the FT of the EXAFS spectra (Fig. 8) shows interesting modification in the coordination spheres of both Fe and Mn centres. The first part of the FT of the Fe spectra (R < 2 Å) corresponds to the first coordination shell of Fe, consisting of a weighed combination of the contributions of Fe–C and Fe–N bonds. In the FT of spectrum #1 in Fig. 8a, the main peak at ∼1.4 Å corresponds to the contribution of Fe–C. This peak exhibit a less intense shoulder at higher R, which might account for the contribution of Fe–N, given the molar ratio of these Fe species. When the depotassiation starts, the shoulder decreases in intensity, while the position of the first peak remains almost unchanged during the whole charge. When the reaction approaches the end of charge, the intensity of this main peak strongly decreases. These observations correlate with (i) a decrease in the bond length of Fe–N, due to the oxidation of HS Fe²⁺ to Fe³⁺, and (ii) the local coordination of LS Fe, which does not change with the oxidation states of the iron, in a good agreement with the XANES results discussed above. The decrease of the peak intensity might be related to a sudden increase of the Debye–Waller factor, related to the presence of several iron sites with slightly different bond lengths leading to a destructive interference of their EXAFS contributions at high k values. The second peak of Fe spectra (2 Å < R < 3.2 Å), corresponding mainly to Fe–C≡N and Fe–N≡C shells, shows almost no significant modification in the peak position, but a significant increase in intensity at the end of the process, possibly due to the same reason as that observed in the first peak. The region between 3 and 5 Å mainly corresponds to the Fe–K, Fe–M (M = Fe, Mn) shells, starts modifying after a certain number of spectra particularly in the intensity, indicating a significant change in the coordination sphere of the Fe centres due to the loss of K⁺ ions and the oxidation of the TMs.

Fig. 8 Evolution of the FT of the EXAFS of Fe (a) and Mn (b) during the first charge (depotassiation) of MF21.

The operando Mn K-edge EXAFS spectra illustrate the oxidation of HS Mn²⁺ to Mn³⁺. The same redox couple was previously investigated in olivine-based cathode materials⁶⁰ as well as in PBAs,⁶¹ where the occurring of a JT distortion of the Mn centres could be followed during oxidation. A similar evolution of the first coordination shell of Mn is observed also in the FT of the spectra of MF21 during oxidation (Fig. 8b): an intensive peak splitting into two distinct peaks of lower intensity highlights once again the distortion of the regular octahedral coordination of Mn with six homogenous bond lengths into two groups of short and long bond lengths, as expected when the JT effect sets in (vide infra).

In order to simultaneously follow both the redox reactions at the Fe and Mn sites, and to establish a clear correlation between the different reaction steps with specific redox couples, the two Mn and Fe K-edge XAS datasets were analysed independently. PCA was first applied to determine the number of principal components that can express the variance contained in each series of spectra. The results of such analysis showed that the Fe dataset can be described using three principal components (Fig. S8†), while two components are necessary for Mn series of spectra (Fig. S9†). MCR-ALS analysis was then carried out for each dataset with the number of principal components obtained from PCA, and unimodality was applied for all components for the charge process. The graphical results of two MCR-ALS analyses are combined in Fig. 9.

Fig. 9 (a) Computed concentration profiles obtained from MCR-ALS data treatment of the operando XAS data at the Fe (top) and Mn (middle) K-edge with the corresponding charge profile recorded at 7.5 mA g⁻¹, and XANES portion of the Fe (b) and Mn (c) MCR-ALS pure components.

The concentration profiles of the Fe K-edge XAS spectra (Fig. 9a) shows the simultaneous presence, at the beginning of the reaction, of a non-negligible fraction of component 2 together with the dominant component 1. The concentration of component 1 decreases rapidly during the first oxidation plateau at ∼3.6 V up to an extraction of 0.3 K⁺, and almost disappears at the beginning of the second plateau at ∼4.0 V, when component 2 becomes dominant. During the first half of this second plateau, the concentration of component 2 decreases only slightly, leaving the place to component 3. The latter increases steadily in concentration only in the second half of the plateau at ∼4.0 V, starting from about 0.9 K⁺ extracted. Concerning the Mn K-edge XAS spectra, component 1 corresponds to the pristine MF21 and remains almost unchanged in concentration up to ∼0.4 extracted K⁺, corresponding to the beginning of the second plateau. Component 2 is then rapidly replaced by component 1 during the first half of the second plateau up to about 0.9 extracted K⁺, when the reaction at the Mn site stops, and is completed only at the very end of the charge.

The pure Fe K-edge components reconstructed by MCR-ALS show a clear edge shift from component 1 to 2, while the edge of component 3 is only slightly shifted to higher energies compared to that of component 2 (Fig. 9b). Considering also the Mössbauer spectroscopy results (vide supra), component 1 can be safely attributed to the combined signals of LS and HS Fe²⁺. Component 2 then represents the signals of LS Fe²⁺ and HS Fe³⁺, and finally component 3 can be explained by the combination of LS and HS Fe³⁺. Since components 1 and 3 display the signals of either pure Fe²⁺ or pure Fe³⁺, their edges are slightly different from those of the first and the last spectra of Fe dataset, which contain a mixture of Fe at both oxidation states and spin states (Fig. S10a†). Spectrum #1, representing the pristine phase containing a small amount of HS Fe³⁺, the edge of which lies at a slightly higher energy than that of component 1. The XANES parts of component 3 and spectrum #20 (corresponding to the EOC phase) are almost identical due to insignificant edge shift when LS Fe²⁺ is oxidized (vide supra), despite the presence of this species at the EOC state. For the Mn K-edge spectra, instead, the two components 1 and 2, which perfectly match the first and the last spectra of Mn dataset (Fig. S10b†), represent HS Mn²⁺ and Mn³⁺, respectively (Fig. 9c).

It is possible to compare the evolution of the concentration of the final components of Fe and Mn, i.e., component 3 for the Fe K-edge XAS dataset and component 2 for the Mn K-edge XAS dataset, by representing the smoothed derivative of their concentration vs. potential (Fig. 10). From this graph, it is possible to appreciate that the oxidation of Mn²⁺ is centred at a lower average potential than that of LS Fe²⁺. The oxidation of Mn²⁺ therefore starts slightly earlier than that of LS Fe²⁺ and, apart from a small fraction of Mn that oxidises only in the final part of the reaction, is more rapid and is terminated at a lower potential. In the middle of the plateau, however, both reactions occur simultaneously given the slight difference in voltage between the HS Mn³⁺/Mn²⁺ and LS Fe³⁺/Fe²⁺ redox couples in K-containing PBAs.³³

Fig. 10 Smoothed derivatives of the concentration of the MCR-ALS pure component 3 of the Fe K-edge dataset and of component 2 of the Mn K-edge dataset (cf.Fig. 9).

The results of the fit in the R space and k space of the MCR-ALS pure components of Fe and Mn K-edge EXAFS spectra are shown in Fig. 11, and the corresponding fitting parameters gathered in Tables S5 and S6.† In the case of the three Fe K-edge components, the Fe–C bond length is almost identical in components 1 and 2, while the Fe–N bond is shortened by 0.15 Å in component 2 with respect to component 1. This reduction in the Fe–N bond length confirms the oxidation of the HS Fe site. Only a very slight increase in the Fe–C length is observed, in the case of component 3, as expected given the strong π-acceptor properties of C-coordinated cyanide ligands which act as a “bonding buffer” making Fe–C bonds covalent in nature and maintain the same bond length in spite of the oxidation state of the Fe. However, as one electron is removed from the LS Fe, there is slightly less electron backdonation from this Fe might weaken the π donation from the CN to the HS Fe³⁺,⁶² resulting in a small increase in HS Fe–N bond length (Table S5†). Since the lengths of Fe–N bonds in components 2 and 3 are very similar to those of Fe–C bonds, a single peak is visible in the FT of the EXAFS signal. Relatively large Debye–Waller factors were obtained for component 1 at the long-distance shells, e.g., Fe–K and Fe–C≡N–M, indicating a certain disordering in the structure of the PBA. In component 2, higher Debye–Waller factors were obtained for the Fe–C≡N–M paths, which might result from the monoclinic → cubic transformation. When the formation of the cubic phase is complete, the structure becomes more ordered, as evidenced by a decrease of the small Debye–Waller factors in component 3. The length of C–N bonds in all components, calculated by subtracting the M–C from M–C–N distances obtained from the EXAFS fitting, varies between 1.11 Å to 1.20 Å and remains almost unchanged despite the oxidation of the metal sites.

Fig. 11 Fit of the modulus of the k²-weighted χ(R) of the Fe (a) and Mn (c) K-edge MCR-ALS pure components performed in the R-range 1.0–5.5 Å. The χ(R) were extracted from the corresponding EXAFS signals using the k-ranges 3–11.5 Å⁻¹ and 3–9.855 Å⁻¹ for the Fe and Mn K-edge, respectively, using a sine window. (b) and (d) are the corresponding fits of the real part of χ(q) corresponding to the backward FT of χ(R) in the R-range of 1.0–5.5 Å. The circles represent the experimental data, and the solid lines represent the fits.

Concerning the two Fe K-edge components, the Mn–N coordination shells are very different between them, in line with the expected JT distortion around Mn³⁺. For the pristine material, represented by component 1, a single Mn–N bond length of 2.24 Å is observed, very similar to the HS Fe–N one (2.21 Å). In component 2, however, the first coordination shell contains 2 different bond lengths, a short one regrouping 4 ligands at 1.93 Å, and a longer one concerning a second group of 2 ligands at 2.4 Å. The local symmetry of Mn changes from O_h to D_4h, which apparently somehow influences the order of the local structure, as reflected by the very large Debye–Waller factors in Mn component 2.

3.4 Phase transition and K⁺ migration

The correlation between redox reactions, structural transformation, and bonding information of the TMs is illustrated in Fig. 12. The pristine structure, almost fully K⁺ occupied cavities, contains the LS Fe²⁺, HS Mn²⁺, HS Fe²⁺ and HS Fe³⁺ with their ratio obtained from Mössbauer spectroscopy and XAS analysis. The average M–N bond length equals to the value of HS Fe²⁺–N and is not very far from Mn²⁺–N one, indicating that the amount Fe³⁺ at this site has minor influence on the M–N bonding. The distances between the neighbouring TMs are diminished due to octahedral tilts herein probably caused by a large internal pressure from K⁺ ions onto the cyanide groups.^63,64 The extraction of the 0.7 K⁺ ion together with the consecutive oxidation of HS Fe and HS Mn causing two modifications: de-tilting the framework and reducing the M–N average bond length. As the content of K⁺ ions in the PBA decreases, the transformation from monoclinic to cubic occurs. This phase transition comes along with a lattice increase despite the shorter M–N bonds. As expected, the oxidation of HS Fe²⁺ shortens the Fe–N bond length (Table S5†). Besides, this cubic phase grows and reaches its maximum during the oxidation of Mn²⁺ (Fig. 5), thus, Mn³⁺ exists herein, and indeed, its local geometry alters due to the JT effect. Since its axial bonds become longer, and the equatorial ones are shorter (Table S6†), the average Mn–N bond length is 2.09 Å. Apparently, the oxidation of both HS Fe and Mn reduces the average length of M–N bonds. However, as these reactions happen simultaneously with the depotassiation, which reduces the K⁺ content in the structure, hence the internal pressure from the alkali onto the cyanide bridges decreases to some extent, and de-tilts the framework (Fig. 12). At the end of depotassiation, apart from a small fraction of unreacted LS Fe²⁺, all the TMs stay at +3 oxidation state, and since the bond lengths of LS Fe–C and HS Fe–N slightly increase, the unit cell expands.

Fig. 12 Schematic phase transition occurring in the depotassiation by combining operando XRD and XAS analysis. The M–N (M = Fe, Mn) bond lengths are the mean values calculated from EXAFS fits of pure components. The Fe–C–N–M distances are deduced from mean values of EXAFS fit data (orange) and lattice parameters of XRD pure components (dark teal).

Comparing with other reports on the JT effect at the Mn³⁺ observed at the EOC of other battery materials, this effect appears stronger than those in the literature.^65,66 The two long axial Mn–N bonds (2.42 Å) can be weakened during the continuous lattice expansion/compression, possibly inducing the creation of inactive Mn sites by the dissolution of Mn ions in the electrolyte, as already widely reported in the literature for Mn-containing PBAs.^67–71 This observation might explain the modification of the mechanism and thus of the performance of MF21 during cycling, which becomes evident by looking at the derivative of the capacity of MF21 in half-cell after 1, 2, and 50 cycles (Fig. S11†). In the first cycle, all the three processes are reversible with very similar capacity contributions from HS Mn and LS Fe. However, in the second charge, the contribution of HS Mn decreases, and after 50 cycles, most of the capacity fading can be attributed to the decline of the Mn³⁺/Mn²⁺ reaction.

To better understand how the structural transformation may affect the K⁺ migration, GITT was conducted for the first discharge (Fig. 13). In general, the open framework of MF21 facilitates the migration of K⁺ ions, which is deduced from the high diffusion coefficients (10⁻¹¹–10⁻¹⁰ cm² s⁻¹) calculated from the GITT signal, which is comparable with the transport kinetics of Na⁺ into the PB hosts.^65,66 However, a slightly decreased diffusion coefficient is observed in the plateau corresponding to the reduction of HS Mn³⁺. In this process, two long axial bonds of Mn³⁺ shorten, leading to the shrinkage of the lattice observed in the operando XRD. This structural rearrangement could influence the insertion and re-ordering of K⁺.

Fig. 13 Evolution of diffusion coefficients of K⁺ in the first discharge (blue diamonds) with the first charge (black line) and GITT curve (red line) of the discharge.

4 Conclusions

Complementary electrochemical and material characterizations give us a comprehensive view on the mechanisms of the PBA K_1.67Mn_0.65Fe_0.35[Fe(CN)₆]_0.92·0.45H₂O, which shows a very good electrochemical performance with three redox reactions that can be well distinguished by combining ⁵⁷Fe Mössbauer and X-ray absorption spectroscopy. The local geometry on Fe and Mn sites provides valuable information on the structural evolution of the PBA, with the oxidation of Mn²⁺ taking place before that of LS Fe²⁺ with the involvement of a coordination distortion due to a JT effect, which results in monoclinic-to-cubic crystal structure modification. This phase transition slows down the insertion of K⁺, and the continuous bond breathing of Mn, together with its likely slow partial dissolution in the electrolyte, might lead to an unrecoverable structure and deactivated Mn sites. Although PBAs are a promising family of cathode materials for PIBs, it is essential to optimize the chemical composition, for instance, slightly decreasing the Mn content to reduce the impact of the Jahn–Teller effect, in order to minimize the battery failure due to significant structural global and local modification.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was part of the TROPIC project supported by Agence Nationale de la Recherche (ANR, grant ANR-19-CE05-0026). ANR is also acknowledged for additional funding through the projects Labex STORE-EX (Grant ANR-10-LABX-76-01) and NANOBLUE (Grant ANR-18-CE09-0012). The Alistore-European Research Institute (ALISTORE-ERI) is warmly thanked for funding the PhD Grant of P. N. L. P. The authors acknowledge the CERIC-ERIC Consortium for access to experimental facilities at Elettra synchrotron and financial support through project 20207080. Access to several analytical methods available at the Analysis and Characterization Platform of “Pôle Chimie Montpellier” (PAC-Balard) is gratefully acknowledged. We thank Luca Olivi (Elettra) for expert advice on beamline operation. Finally, Jérôme Long, Joulia Larionova and Yannick Guari (ICGM) are warmly thanked for their help in the synthesis of the PBA used in this work, as well as for fruitful discussion and advice on the final version of this manuscript.

References

1. M. Fichtner, Batteries Supercaps, 2022, 5, 1–10.
2. H. Au, M. Crespo-Ribadeneyra and M.-M. Titirici, One Earth, 2022, 5, 207–211.
3. V. Anoopkumar, J. Bibin and T. D. Mercy, ACS Appl. Energy Mater., 2020, 3, 9478–9492.
4. Y. Yang, J. Zhou, L. Wang, Z. Jiao, M. Xiao, Q. Huang, M. Liu, Q. Shao, X. Sun and J. Zhang, Nano Energy, 2022, 99, 107424.
5. K. Hurlbutt, S. Wheeler, I. Capone and M. Pasta, Joule, 2018, 2, 1950–1960.
6. A. Zhou, W. Cheng, W. Wang, Q. Zhao, J. Xie, W. Zhang, H. Gao, L. Xue and J. Li, Adv. Energy Mater., 2021, 11, 2000943.
7. L. Deng, J. Qu, X. Niu, J. Liu, J. Zhang, Y. Hong, M. Feng, J. Wang, M. Hu, L. Zeng, Q. Zhang, L. Guo and Y. Zhu, Nat. Commun., 2021, 12, 2167.
8. A. Paolella, C. Faure, V. Timoshevskii, S. Marras, G. Bertoni, A. Guerfi, A. Vijh, M. Armand and K. Zaghib, J. Mater. Chem. A, 2017, 5, 18919–18932.
9. J. Chen, L. Wei, A. Mahmood, Z. Pei, Z. Zhou, X. Chen and Y. Chen, Energy Storage Mater., 2020, 25, 585–612.
10. G. Du and H. Pang, Energy Storage Mater., 2021, 36, 387–408.
11. M. B. Robin, Inorg. Chem., 1962, 1, 337–342.
12. L. Ma, H. Cui, S. Chen, X. Li, B. Dong and C. Zhi, Nano Energy, 2021, 81, 105632.
13. W. Shi, P. Nie, X. Shang, J. Yang, Z. Xie, R. Xu and J. Liu, Electrochim. Acta, 2019, 310, 104–112.
14. X. Wu, M. Shao, C. Wu, J. Qian, Y. Cao, X. Ai and H. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 23706–23712.
15. A. L. Crumbliss, P. S. Lugg and N. Morosoff, Inorg. Chem., 1984, 23, 4701–4708.
16. K. Itaya, I. Uchida and V. D. Neff, Acc. Chem. Res., 1986, 19, 162–168.
17. Y. Moritomo, S. Urase and T. Shibata, Electrochim. Acta, 2016, 210, 963–969.
18. A. Zhou, Z. Xu, H. Gao, L. Xue, J. Li and J. B. Goodenough, Small, 2019, 15, 1902420.
19. X. Bie, K. Kubota, T. Hosaka, K. Chihara and S. Komaba, J. Mater. Chem. A, 2017, 5, 4325–4330.
20. L. Xue, Y. Li, H. Gao, W. Zhou, X. Lü, W. Kaveevivitchai, A. Manthiram and J. B. Goodenough, J. Am. Chem. Soc., 2017, 139, 2164–2167.
21. L. Deng, J. Qu, X. Niu, J. Liu, J. Zhang, Y. Hong, M. Feng, J. Wang, M. Hu, L. Zeng, Q. Zhang, L. Guo and Y. Zhu, Nat. Commun., 2021, 12, 2167.
22. A. Mullaliu, J. Asenbauer, G. Aquilanti, S. Passerini and M. Giorgetti, Small Methods, 2020, 4, 1900529.
23. Y. Li, K. H. Lam and X. Hou, ACS Appl. Energy Mater., 2021, 4, 13098–13109.
24. J. Li, X. He, S. Ostendorp, L. Zhang, X. Hou, D. Zhou, B. Yan, D. M. Meira, Y. Yang, H. Jia, G. Schumacher, J. Wang, E. Paillard, G. Wilde, M. Winter and J. Li, Electrochim. Acta, 2020, 342, 135928.
25. T. Matsuda, M. Takachi and Y. Moritomo, Chem. Commun., 2013, 49, 2750.
26. I.-H. Jo, S.-M. Lee, H.-S. Kim and B.-S. Jin, J. Alloys Compd., 2017, 729, 590–596.
27. P. S. Camacho, R. Wernert, M. Duttine, A. Wattiaux, A. Rudola, P. Balaya, F. Fauth, R. Berthelot, L. Monconduit, D. Carlier and L. Croguennec, ACS Appl. Mater. Interfaces, 2021, 13, 42682–42692.
28. P. A. Morozova, I. A. Trussov, D. P. Rupasov, V. A. Nikitina, A. M. Abakumov and S. S. Fedotov, Crystals, 2021, 11, 895.
29. Y. Sun, C. Liu, J. Xie, D. Zhuang, W. Zheng and X. Zhao, New J. Chem., 2019, 43, 11618–11625.
30. M. Jiang, Z. Hou, L. Ren, Y. Zhang and J.-G. Wang, Energy Storage Mater., 2022, 50, 618–640.
31. H. Onuma, K. Kubota, S. Muratsubaki, T. Hosaka, R. Tatara, T. Yamamoto, K. Matsumoto, T. Nohira, R. Hagiwara, H. Oji, S. Yasuno and S. Komaba, ACS Energy Lett., 2020, 5, 2849–2857.
32. X. Bie, K. Kubota, T. Hosaka, K. Chihara and S. Komaba, J. Mater. Chem. A, 2017, 5, 4325–4330.
33. L. Xue, Y. Li, H. Gao, W. Zhou, X. Lü, W. Kaveevivitchai, A. Manthiram and J. B. Goodenough, J. Am. Chem. Soc., 2017, 139, 2164–2167.
34. E. J. Canto-Aguilar, M. A. Oliver-Tolentino, G. Ramos-Sánchez and I. González, Electrochim. Acta, 2021, 371, 137828.
35. A. Li, L. Duan, J. Liao, J. Sun, Y. Man and X. Zhou, ACS Appl. Mater. Interfaces, 2022, 5, 11789–11796.
36. Y. Lu, L. Wang, J. Cheng and J. B. Goodenough, Chem. Commun., 2012, 48, 6544–6546.
37. L. Wang, J. Song, R. Qiao, L. A. Wray, M. A. Hossain, Y.-D. Chuang, W. Yang, Y. Lu, D. Evans, J.-J. Lee, S. Vail, X. Zhao, M. Nishijima, S. Kakimoto and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2548–2554.
38. M. Pasta, R. Y. Wang, R. Ruffo, R. Qiao, H. W. Lee, B. Shyam, M. Guo, Y. Wang, L. A. Wray, W. Yang, M. F. Toney and Y. Cui, J. Mater. Chem. A, 2016, 4, 4211–4223.
39. B. Liu, Q. Zhang, U. Ali, Y. Li, Y. Hao, L. Zhang, Z. Su, L. Li and C. Wang, Chem. Sci., 2022, 13, 10846–10855.
40. M. Giorgetti and L. Stievano, in X-Ray Characterization of Nanostructured Energy Materials by Synchrotron Radiation, ed. M. Khodaei and L. Petaccia, InTech, Rijeka, 1st edn, 2017, pp. 51–75.
41. M. Fehse, A. Iadecola, L. Simonelli, A. Longo and L. Stievano, Phys. Chem. Chem. Phys., 2021, 23, 23445–23465.
42. A. Mullaliu, P. Conti, G. Aquilanti, J. Plaisier, L. Stievano and M. Giorgetti, Condens. Matter, 2018, 3, 36.
43. K. Hayakawa, K. Hatada, P. D'Angelo, S. Della Longa, C. R. Natoli and M. Benfatto, J. Am. Chem. Soc., 2004, 126, 15618–15623.
44. G. Aquilanti, M. Giorgetti, R. Dominko, L. Stievano, I. Arčon, N. Novello and L. Olivi, J. Phys. D: Appl. Phys., 2017, 50, 074001.
45. A. Mullaliu, G. Aquilanti, P. Conti, J. R. Plaisier, M. Fehse, L. Stievano and M. Giorgetti, J. Phys. Chem. C, 2018, 122, 15868–15877.
46. M. Fehse, A. Iadecola, M. T. Sougrati, P. Conti, M. Giorgetti and L. Stievano, Energy Storage Mater., 2019, 18, 328–337.
47. J. Rodríguez-Carvajal, Comm. powder Diffr. (IUCr), Newsl., 2001, vol. 26, pp. 12–19.
48. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
49. M. Morcrette, Y. Chabre, G. B. M. Vaughan, G. G. Amatucci, J.-B. Leriche, S. Patoux, C. Masquelier and J.-M. Tarascon, Electrochim. Acta, 2002, 47, 3137–3149.
50. X. Jiang, T. Zhang, L. Yang, G. Li and J. Y. Lee, ChemElectroChem, 2017, 4, 2237–2242.
51. L. Jiang, Y. Lu, C. Zhao, L. Liu, J. Zhang, Q. Zhang, X. Shen, J. Zhao, X. Yu, H. Li, X. Huang, L. Chen and Y.-S. Hu, Nat. Energy, 2019, 4, 495–503.
52. L. Samain, B. Gilbert, F. Grandjean, G. J. Long and D. Strivay, J. Anal. At. Spectrom., 2013, 28, 524.
53. J. Touja, P. N. Le Pham, N. Louvain, L. Monconduit and L. Stievano, Chem. Commun., 2020, 56, 14673–14676.
54. M. Okubo, D. Asakura, Y. Mizuno, T. Kudo, H. Zhou, A. Okazawa, N. Kojima, K. Ikedo, T. Mizokawa and I. Honma, Angew. Chem., Int. Ed., 2011, 50, 6269–6273.
55. D. O. Ojwang, J. Grins, D. Wardecki, M. Valvo, V. Renman, L. Häggström, T. Ericsson, T. Gustafsson, A. Mahmoud, R. P. Hermann and G. Svensson, Inorg. Chem., 2016, 55, 5924–5934.
56. M. Giorgetti, A. Mignani, G. Aquilanti, P. Conti, M. Fehse and L. Stievano, J. Phys.: Conf. Ser., 2016, 712, 012127.
57. A. Mullaliu, P. Conti, G. Aquilanti, J. R. Plaisier, L. Stievano and M. Giorgetti, Condens. Matter, 2018, 3, 36.
58. G. L. Miessler, Inorganic Chemistry, Pearson Education India, 2008.
59. C. Tian, E. Kan, C. Lee and M.-H. Whangbo, Inorg. Chem., 2010, 49, 3086–3088.
60. A. Iadecola, A. Perea, L. Aldon, G. Aquilanti and L. Stievano, J. Phys. D: Appl. Phys., 2017, 50, 144004.
61. A. Mullaliu, G. Aquilanti, P. Conti, M. Giorgetti and S. Passerini, ChemSusChem, 2020, 13, 608–615.
62. J.-H. Lee, J.-G. Bae, H. J. Lee and J. H. Lee, J. Energy Chem., 2022, 70, 121–128.
63. J. Cattermull, M. Pasta and A. L. Goodwin, Mater. Horiz., 2021, 8, 3178–3186.
64. M. Sugimoto, S. Yamashita, H. Akutsu, Y. Nakazawa, J. G. DaSilva, C. M. Kareis and J. S. Miller, Inorg. Chem., 2017, 56, 10452–10457.
65. Y. Zhu, B. Wang, Q. Gan, Y. Wang, Z. Wang, J. Xie, S. Gu, Z. Li, Y. Li, Z. W. Ji, H. Cheng and Z. Lu, Inorg. Chem. Front., 2019, 6, 1361–1366.
66. W. Wang, Y. Gang, Z. Hu, Z. Yan, W. Li, Y. Li, Q.-F. Gu, Z. Wang, S.-L. Chou, H.-K. Liu and S.-X. Dou, Nat. Commun., 2020, 11, 980.
67. Y. Tang, W. Li, P. Feng, M. Zhou, K. Wang, Y. Wang, K. Zaghib and K. Jiang, Adv. Funct. Mater., 2020, 30, 1908754.
68. C. Gao, Y. Lei, Y. Wei, H. Wang, F. Yuan, F. Kang and D. Zhai, Chem. Eng. J., 2022, 431, 133926.
69. Q. Ren, Y. Yuan and S. Wang, ACS Appl. Mater. Interfaces, 2022, 14, 23022–23032.
70. A. Li, L. Duan, J. Liao, J. Sun, Y. Man and X. Zhou, ACS Appl. Energy Mater., 2022, 5, 11789–11796.
71. F. Peng, L. Yu, S. Yuan, X.-Z. Liao, J. Wen, G. Tan, F. Feng and Z.-F. Ma, ACS Appl. Mater. Interfaces, 2019, 11, 37685–37692.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta08439b

---