Catalytic active centers beyond transition metals: atomically dispersed alkaline-earth metals for the electroreduction of nitrate to ammonia

Abstract

Alkaline-earth (AE) metals have rarely been reported to be the active centers in heterogeneous catalysis. However, in nature, Mg cofactors in enzymes exhibit super activity for biochemical reactions. Herein, taking the AE metal single-atom catalyst (AE-SAC) supported on graphene as a representative, we theoretically explore the feasibility of AE metals as active centers in heterogeneous catalysis for the electrocatalytic nitrate (NO₃⁻) reduction reaction (eNO₃RR) to produce NH₃. Intriguingly, the AE metal active centers could strongly adsorb and effectively activate NO₃⁻, and catalyze eNO₃RR efficiently, similar to that of the transition-metal active centers. In particular, Ba and Sr SACs coordinated with three nitrogen and one carbon atoms exhibited super eNO₃RR activity with an ultralow limiting potential of −0.05 V, which also showed desirable selectivity and good stability. Mechanistic investigations indicated that, although AE metal elements are highly ionic, they function as transmitters to assist the charge transfer between the catalyst support and NO₃⁻ as well as effective intermediates, which enables the effective activation of NO₃⁻, via the “donation-back donation” mechanism, and further completes the catalytic cycle. Our work could broaden the ideas and lay a theoretical foundation for the development of heterogeneous catalysts with AE metals as active centers.

---

1. Introduction

Heterogenous catalysis, mainly based on metal and metal-oxides, plays an important role in modern industries and emerging renewable energy conversion and storage technology.^1–3 Active centers of the vast majority of heterogeneous catalysts consist of d-block transition metals (TMs). The underlying physical mechanism can be traced back to the partially filled d orbitals, which enables the electron “donation-back donation” process for the molecule adsorption and activation, as described in the Blyholder model⁴ and the d-band center theory.⁵ Conversely, s-block metals, alkali, and alkaline-earth (AE) metals are generally thought to be chemically inert due to the lack of combined empty and occupied orbitals.⁶ It is known that they are generally prone to lose s valence electrons and form the cations in the compounds, which are hard to change the oxidation state rapidly and reversibly involved in elementary steps of a catalytic cycle. Thus, s-block metals are often considered to be catalytic inactive.⁷

Nevertheless, nature has given us some inspiration.^8–12 To be specific, magnesium (Mg), as a cofactor in enzymes, has been revealed to play key roles in the photosynthesis system and nucleic acid biochemistry.^9,10 Mg²⁺ in a cofactor has a proper binding affinity for the oxygenated species, and thus, the cofactor can serve as a Lewis acid for the transfer of a phosphate intermediate from one compound to another or the activation of Mg-bound water molecules to a hydroxide ion.⁸ For example, due to the particularly right affinity of the O atom, Mg²⁺-bound DNA and RNA polymerases can participate in the neutralization of the polyanionic charge of the nucleic acid, so they work efficiently.^9,10 Despite their unique and critical biochemical activities and even the widely used molecular catalysis,¹³ AE metals acting as active centers of the heterogeneous catalyst have been reported rarely.^14–17 For instance, in 2020, Chen et al. first showed that the Mg atom coordinated with N and C atoms embedded in graphene exhibits an excellent four-electron oxygen reduction reaction activity.¹⁴ We found that Mg²⁺ in two-dimensionally layered Mg₃(hexaiminotriphenylene)₂ electrocatalyst serves as the active center to selectively produce H₂O₂ by electroreduction of O₂.¹⁶

It is known that ammonia (NH₃) is one of the most important chemicals in modern life, which has also been regarded as a potential clean energy carrier.¹⁸ In recent years, the electrocatalytic nitrogen reduction reaction (NRR) to synthesize NH₃ under ambient conditions, driven by renewable energy, has gained considerable attention as an alternative to the traditional Haber–Bosch procedure.^19–23 However, the low solubility and chemical inertness of N₂ molecules lead to an unsatisfactory NH₃ production rate and Faraday efficiency.^24–26 In this case, very recently nitrate (NO₃⁻), having a much weaker intramolecular chemical bond (176 KJ mol⁻¹) than N₂ (941 KJ mol⁻¹), is emerging as a novel nitrogen resource for NH₃ synthesis.²⁷ Considering the ever-increasing concentration of NO₃⁻ can severely destroy ecological balance and threaten human health,¹⁹ electrocatalytic nitrate reduction reaction (eNO₃RR) could be considered as a “one stone two bird” strategy for simultaneous nitrate pollution treatment and NH₃ production.^28,29 Therefore, it is full of importance and challenge to design efficient electrocatalysts with high stability for direct electroreduction of NO₃⁻ into NH₃.^30–32

Encouragingly, diverse catalysts, such as molecular solids,³³ metallic alloys,²⁹ metallic compounds,^34,35 pure metals,^36,37 and atomic catalysts^38,39 have been proven to be efficient for eNO₃RR, and all the reported catalysts have the TM atoms as active centers. On the other hand, single-atom catalysts (SACs) have gained significant attention in electrocatalysis due to their high efficiency and simple active sites, which makes SAC an ideal platform for studying catalysis mechanisms through theoretical calculations.^40–42 For eNO₃RR, several SACs have been reported experimentally^32,38,43,44 or theoretically.^45–52 Interestingly, for these SACs, it is predicted that the binding strength of NO₃⁻ could serve as a descriptor to predict the activity trend, and the active center with the adsorption-free energy for NO₃⁻ (ΔG(*NO₃)) of around −2.0 eV exhibiting a high eNO₃RR activity. Considering that AE ions have a unique affinity for the oxygenated species,^14,16 the catalysts with AE ions as active sites may be able to bind NO₃⁻ effectively; moreover, by tuning the coordination environment or the metal center identities (Mg, Ca, Sr, and Ba), a suitable binding strength of NO₃⁻ and nice eNO₃RR activity could be achieved.^53,54 However, the direct electroreduction of NO₃⁻ into NH₃ by the AE metal active centers in the electrocatalysts has not been explored and remains an open challenge.

In this work, taking AE metal single atom incorporated graphene as representatives, we comprehensively explored the feasibility of AE metals as active centers for eNO₃RR based on the first-principles calculations. Interestingly, the AE metal active centers in the built AE metal single-atom catalyst (AE-SAC) can strongly adsorb and effectively activate NO₃⁻ ions, similar to the cases of the TM active centers. Intriguingly, by changing the active center identities and their coordination environment, the binding strength of NO₃⁻ can be tuned properly to realize high eNO₃RR activity. Especially, Ba and Sr SACs coordinated with one C and three N atoms exhibit ultrahigh eNO₃RR activity with near-zero limiting potential (U_L) of −0.05 V, together with desirable selectivity and good stability, comparable or even better than the TM-based SACs reported so far. Furthermore, the underlying mechanism for the effective NO₃⁻ activation and the excellent eNO₃RR activity on the AE metal active centers were explored.

2. Computational methods

All the spin-polarized density functional theory (DFT) calculations were performed based on the projector augmented wave (PAW)⁵⁵ method as implemented in the Vienna ab initio simulation package (VASP).⁵⁶ Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) was employed to treat the exchange-correlation effect.⁵⁷ The plane-wave cutoff energy was 450 eV. The van der Waals correction was performed using the DFT-D3 method.⁵⁸ The energy and force convergence criteria for the structural optimization were set as 10⁻⁵ eV and 0.02 eV Å⁻¹, respectively. The AE-SAC was built based on the 5 × 5 × 1 graphene supercell. The effect of relaxing lattice parameters on the adsorption stability was tested, and it was found that thanks to the large supercells, relaxing the lattice parameters has negligible influence on the adsorption energy (Fig. S1†). The Monkhorst–Pack scheme was used to sample the first Brillouin zone,⁵⁹ and the k-points grids were 3 × 3 × 1 and 6 × 6 × 1 for the structural optimization and densities of states (DOS) calculation, respectively. We also tested the DOS calculated with the hybrid functional of Heyd–Scuseria–Ernzerhof (HSE06),⁶⁰ and results indicate that the distributions of electronic states were very similar for PBE and HSE06 functionals (Fig. S2†). Given that all the AE-SACs studied in this work exhibited obviously metallic features without a band gap, thus the DOS calculated with the PBE functional was qualified. To avoid the interaction between the periodic units, a vacuum layer of ∼20 Å was added along the z direction. Ab initio molecular dynamics (AIMD) simulation was carried out to estimate the thermal stability with a time step of 2 fs.⁶¹

To explore the accessibility of the experimental synthesis, the formation energy (E_f) was calculated using the following formula:^62,63

E_f = E_total − E_G + ∑n_iμ_i (1)

in which, E_total and E_G are the total energies of AE-SAC and 5 × 5 graphene supercell, respectively. μ_i represents the chemical potential of the i species. n_i is the number of the removed and added i species, where the positive and negative values are referred to the removed and added species, respectively. The chemical potentials of the involved species, μ_C, μ_N, and μ_AE were calculated using a pristine graphene unit cell, N₂ free molecule, and AE metal bulk, respectively. It should be mentioned that the E_f is closely related to the chemical potentials of the referred species, which is in turn dependent on the experimental conditions.

To estimate the binding strength between AE metal and the N-doped graphene substrate, the binding energy (E_b) is expressed as:

E_b = E_total − E_substrate − E_AE (2)

where E_total and E_substrate represent the total energies of N-doped graphene substrate with and without anchored AE metals, E_AE is the total energy of isolated AE metal atoms. The more negative E_b implies higher stability of AE-SACs.

In addition, to further verify the thermodynamical stability of the AE-SAC systems, the energy difference (ΔE_b) between E_b and E_coh was calculated.⁶⁴ In which, E_coh is the cohesive energy of AE metal bulk and can be calculated using the formula of E_coh = (E_bulk – nE_AE)/n, where E_bulk is the total energy of the AE metal crystal and n is the number of metal atoms in the crystal. A negative ΔE_b indicates that the AE metal single atom tends to remain isolated on the substrate rather than agglomerate, and a more negative ΔE_b means higher thermodynamical stability.

The computational hydrogen electrode (CHE) mode⁶⁵ was adopted to calculate the Gibbs free energy change (ΔG) for each elementary step as follows

ΔG = ΔE +ΔE_ZPE − TΔS (3)

In the equation, ΔE is the electronic energy contribution directly obtained from DFT calculations. ΔE_ZPE and TΔS are the contributions of zero-point energy and entropy (at 298.15 K), respectively, which could be acquired by computing the vibrational frequency for intermediates and from the NIST database⁶⁶ for free molecules (tabulated in Tables S1 and S2†). The limiting potential (U_L) was formalized with U_L = –ΔG_max/e, where ΔG_max is the maximum free energy change among all elementary steps along the lowest-energy pathway, i.e., the potential-determining step (PDS).⁶⁷ In light of the difficulty of directly calculating the energy of charged NO₃⁻, the adsorption free energy of NO₃⁻ (ΔG(*NO₃)) was calculated with the assistance of the gaseous HNO₃ (ref. 36 and 68) as follows

ΔG(*NO₃) = G(*NO₃) − G(*) − [G(HNO₃) − 0.5 × G(H₂)] + ΔG_correct (4)

Here, G(*) and G(*NO₃) are the Gibbs free energies of the bare catalyst and that with the adsorbed NO₃⁻, respectively. G(HNO₃) and G(H₂) represent the Gibbs free energies of the HNO₃ and H₂ molecules, respectively. The solvation correction was carried out with an implicit solvation model as implemented in VASPsol.⁶⁹ It is worth mentioning that we have studied the eNO₃RR process on an experimentally reported DV-FeN₄ system.³⁸ As seen in Fig. S3,† good consistency between the theoretical limiting potential (−0.38 V) and experimental on-set potential (∼−0.4 V) indicates the reliability of our computational settings.

3. Results and discussion

3.1. The properties of AE-SACs

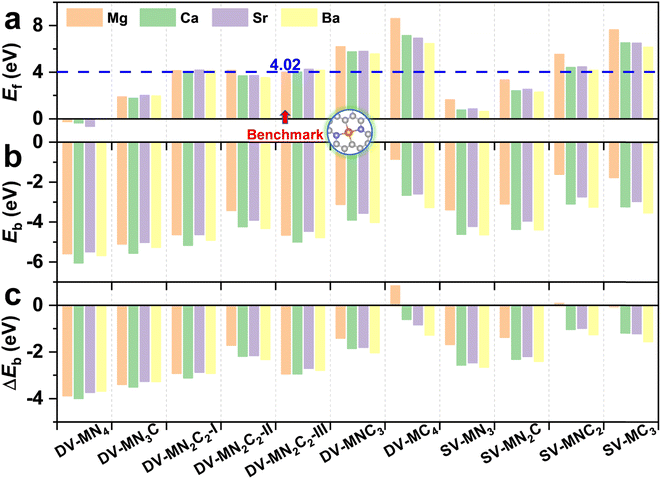
With various merits, such as facile fabrication, excellent stability, and easily tunable electronic structure, graphene-based SACs have received considerable attention for various electrocatalytic reactions.⁷⁰ Moreover, regulating the coordination environment of the active center can greatly affect its catalytic activity and selectivity.^53,54 Herein, we constructed a series of AE-SACs, where the AE metal (Mg, Ca, Sr, Ba) single-atoms are embedded into graphene with single vacancy or double vacancy decorated by certain numbers of N atoms, as illustrated in Fig. 1. Considering that Be is extremely toxic⁷¹ and Ra is a typical radioactive element,⁷² they are not involved in this work. By adjusting the number of coordinated N atoms, seven DV-MN_xC_4–x and four SV-MN_xC_3–x configurations were established for each AE metal single atom, producing 44 SAC candidates. The key parameters of these systems are listed in Table S3,† including bond length, charge transfer, spin magnetic moment, formation energy, and binding energy.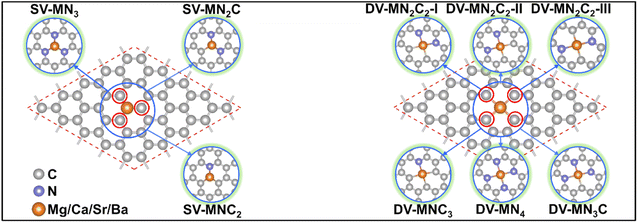

Fig. 1 Schematic illustrations of the AE-SAC systems with single Mg/Ca/Sr/Ba atom anchoring on the graphene support with different coordination environments.

The experimentally synthetic feasibility of the proposed AE-SACs can be estimated theoretically from the formation energy.^62,63 Since MgN₂C₂-III was synthesized experimentally,¹⁴ was selected as a benchmark. It can be seen from Fig. 2a that the lower the number of coordinated N atoms, the higher the formation energy. More importantly, except DV-MNC₃, DV-MC₄, SV-MNC₂, and SV-MC₃, all the AE-SACs have lower or comparable formation energies compared with MgN₂C₂-III, strongly suggesting that they are able to be synthesized experimentally too. Furthermore, as shown in Fig. 2b, the significantly negative binding energies for all the AE-SACs (except DV-MgC₄) indicate that there are strong chemical bonds between AE metals and their neighboring C or N atoms. Clearly, for all AE-SACs (except DV-MgC₄ and SV-MgNC₂), the energy differences (ΔE_b) between E_b and E_coh are less than zero (Fig. 2c), suggesting that when the AE-SACs are synthesized, the AE metals prefer to be dispersed on the supports instead of agglomerating into nanoparticles, which further demonstrates their high thermodynamical stability. Finally, the Bader charge analysis⁷³ shows that the AE metals lose most of their valence electrons (∼1.5e) to graphene and form AE cations, similar to the AE elements in other compounds. Therefore, it is expected that the AE-SACs could bind NO₃⁻ effectively. In addition, the total DOS of all the AE-SAC systems (Fig. S4–S7†) indicate their metallic characteristics, which facilitate the charge transfer during eNO₃RR.⁷⁴

Fig. 2 The calculated formation energy, E_f (a), binding energy, E_b (b), and the energy difference between E_b and E_coh, ΔE_b (c) for the AE-SAC systems. DV-MgN₂C₂-III is adopted as a reference for the formation energy.

3.2. Adsorption of NO₃⁻ on AE-SACs

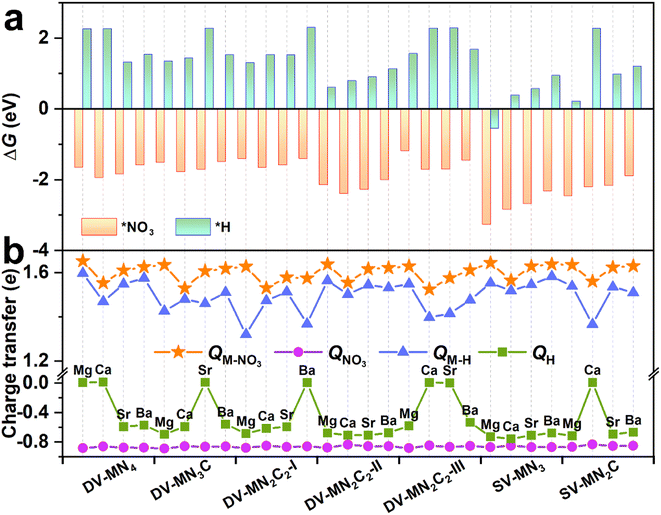
As an initial and pivotal step for the eNO₃RR process, NO₃⁻ should be adsorbed on the active center effectively. As illustrated in Fig. S8a,† all the possible NO₃⁻ adsorption configurations have been taken into account, including those with one O atom or two O atoms binding, and the parallel pattern. In addition, we have also considered several possible adsorption positions around the AE metal active centers for *NO₃ and the other key reaction intermediates (Fig. S8b†). The most stable adsorption configurations for *NO₃ are shown in Fig. S9,† meanwhile, some important parameters (bond length, charge transfer, and ΔG(*NO₃)) are displayed in Table S4.† We can see that for all the cases the configuration with two O atoms binding with the AE metal atom is the most stable. Intriguingly, the values of ΔG(*NO₃) are all less than −1.0 eV (ranging from −1.18 to −3.26 eV), indicating that the active site consisting of AE metal can strongly adsorb NO₃⁻, similar to the TM active site.^33,45 However, contrary to TM active sites, for all the systems, a considerable amount of charge transfers (∼1.6e) from the catalysts to NO₃⁻ can be observed, suggesting that the binding of NO₃⁻ mainly relied on the ionic bond interaction, for which the detailed analysis will be presented below.

It is known that hydrogen evolution reaction (HER) is the main competing reaction against eNO₃RR mainly because protons can also bind with the active sites.³³ To effectively inhibit this disadvantage, active sites should be preferentially occupied by NO₃⁻ instead of H atoms, which requires strong adsorption of NO₃⁻ compared with H.^45,51 The adsorption configurations for *H are displayed in Fig. S10,† meanwhile, some important parameters (bond length, charge transfer, and ΔG(*H)) are compiled in Table S5.† As shown in Fig. 3a, for all the systems, ΔG(*NO₃) is negative, while ΔG(*H) is positive (except SV-MgN₃), indicating that the adsorption of NO₃⁻ is much stronger than that of H atoms. Therefore, eNO₃RR will dominate and the HER can be effectively inhibited on these SACs. By analyzing the charge transfer (Fig. 3b), it is found that, for all the cases, NO₃⁻ gains more electrons from SACs than H atoms, and the NO₃⁻ bonded AE metal atoms carry more positive charges than the H-bonded ones, which could be responsible for the much stronger binding of NO₃⁻.

Fig. 3 Adsorption free energy (ΔG) (a) and charge transfer (Q) (b) for NO₃⁻ and H adsorption on the considered AE-SAC systems. Q_M–NO3 and Q_M–H denote the charge transfer of AE metals, and Q_NO3 and Q_H are the charge transfer of *NO₃ and *H, respectively. The positive and negative values represent the electron loss and electron gain, respectively.

3.3. Mechanism of eNO₃RR on AE-SACs

From the previously reported results, the binding strength of NO₃⁻ can serve as the activity descriptor for eNO₃RR, and for various kinds of SACs, the active sites with ΔG(*NO₃) of around −2 eV show high eNO₃RR activity.^45–48 Above results show that by changing the AE metal active center and its coordination environment, ΔG(*NO₃) values can be adjusted from −1.18 to −3.26 eV. Therefore, it is expected that the AE-SACs can achieve high catalytic activity for eNO₃RR. Despite the complex eNO₃RR process with multiple products, according to the Pourbaix diagram of nitrogen species, NH₃/NH₄⁺ has been identified as the most stable product in thermodynamics under negative electrode potential.^45,75 Therefore, it is essential to make a thorough investigation of the reaction mechanism of the selective electroreduction of NO₃⁻ to NH₃. Fig. 4a displays the exhaustive reaction pathways of eNO₃RR, where all the possible configurations of *HNO₃, *NO₂, and *HNO₂ have been considered. Given the multiple configurations and hydrogenation positions of intermediates during the eNO₃RR process, to economically and effectively obtain the optimal pathway, only the most stable structure in each elementary step is chosen to further study the subsequent reaction. Generally, U_L has been used to evaluate the catalytic activity of an electrocatalytic reaction,⁶⁵ and the calculated U_L for these AE-SACs are shown in Fig. 4b and tabulated in Table S6.† Surprisingly, in contrast with the traditional view that the AE metal active centers are catalytically inactive, most of the AE-SACs exhibit a high eNO₃RR activity with U_L lower than −0.6 V. Especially, DV-SrN₃C and DV-BaN₃C possess the highest eNO₃RR activity with an ultralow U_L of −0.05 V. This value is much lower than those of the previous predicted TM-based SACs. For example, U_L of Ti/g-CN,⁴⁵ Hf/g-C₃N₄,⁴⁶ Ru/g-C₃N₄,⁴⁷ V/g-C₃N₄,⁴⁸ Os/GDY,⁴⁹ V/h-BP,⁵¹ and Fe/NG⁵² are −0.39, −0.11, −0.34, −0.25, −0.37, −0.22, and −0.38 V, respectively. Therefore, the catalysts with active sites consisting of AE metal could be even superior to those consisting of TM.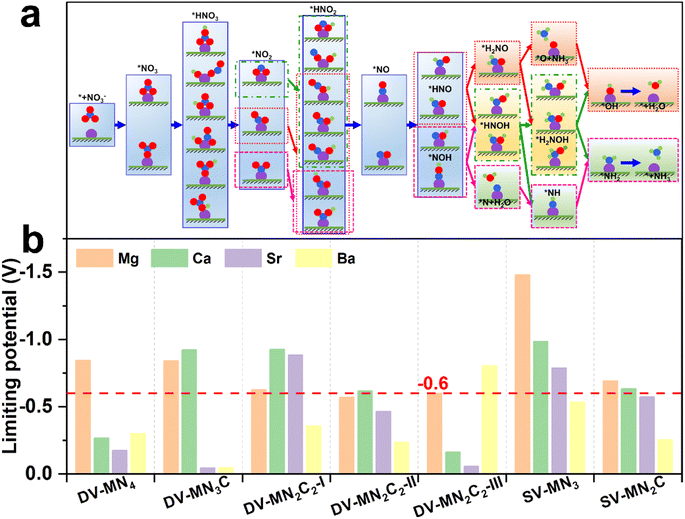

Fig. 4 (a) Schematic diagram of possible eNO₃RR pathways. (b) Summary of the limiting potential of the AE-SACs for eNO₃RR through the minimum energy pathway.

The calculated U_L as a function of ΔG(*NO₃) is presented in Fig. 5, interestingly, which also exhibits a prototypical volcano-shaped correlation, similar to the case of SACs with TM as the active center.^{45,47–49,52} One can see that, on the left branch of the volcano diagram, too strong adsorption of NO₃⁻ often leads to the last hydrogenation step (*OH → * + H₂O) as PDS, while the relatively weak adsorption of NO₃⁻ results in the early hydrogenation step (*NO₃ → *OH + *NO₂/*NO₂ → *OH + *NO) as PDS. Note that the optimal systems herein, DV-SrN₃C and DV-BaN₃C are exactly located around the peak of the volcano diagram with ΔG(*NO₃) of −1.71 and −1.48 eV, respectively. In addition to DV-SrN₃C and DV-BaN₃C, there are also a large number of other AE-SAC systems (highlighted by the green background in Fig. 5) possessing acceptable U_L, which are comparable to the reported TM catalysts, marked by the purple circle in Fig. 5.^45–50 Furthermore, it is noted that ΔG(*NO₃) of the above AE-SACs stand in the range from −1.3 to −2.5 eV, similar to the systems with TM active centers.^45–50

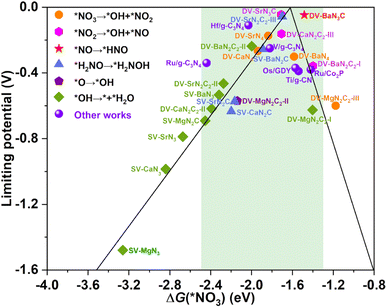Fig. 5 The eNO₃RR volcano diagram of the considered AE-SACs with the descriptor of ΔG(*NO₃). The purple spheres denote other works for comparison^45–50 The green background encloses those AE-SACs with acceptable limiting potentials.

To get more insight into the reaction mechanism, the eNO₃RR pathways on DV-BaN₃C and DV-SrN₃C are plotted in Fig. 6, and those for other systems are depicted in Fig. S11–S16.† Interestingly, on DV-BaN₃C, the first hydrogenation step of *NO₃ occurs at the O site bonded to the Ba atom, generating the co-adsorbed *OH and *NO₂ with a free energy downhill of 0.40 eV (Fig. 6a), which is completely different from previous works that the proton–electron (H⁺ + e⁻) pair firstly attacks the terminal O of *NO₃.^45,51 The second hydrogenation step results in the release of the first H₂O molecule with the free energy downhill of 0.87 eV, leaving the NO₂ asymmetric adsorption on DV-BaN₃C via one Ba–O bond and one Ba–N bond. Similar to the first hydrogenation step, the third H⁺ + e⁻ pair also prefers to attack the proximal O atom (bonded to Ba) of *NO₂, breaking another N–O bond to form *OH + *NO with the free energy uphill of only 0.02 eV. Then, the second water molecule is formed exothermically. The *NO trends to adopt the end-on pattern with the N atom bonding to the Ba atom, similar to the cases of TM active centers.^45,51 Then, the fifth H⁺ + e⁻ pair prefers to be added on the N atom of *NO, turning the end-on adsorption pattern to a side-on adsorption pattern, which is also identified as the PDS with a free energy uphill of 0.05 eV. The subsequent electroreduction processes are all exothermic. In detail, the hydrogenation of *HNO follows the pathway, *HNO → *H₂NO → *O + NH₃ (g) → OH* → * + H₂O (l), to recover the active center.

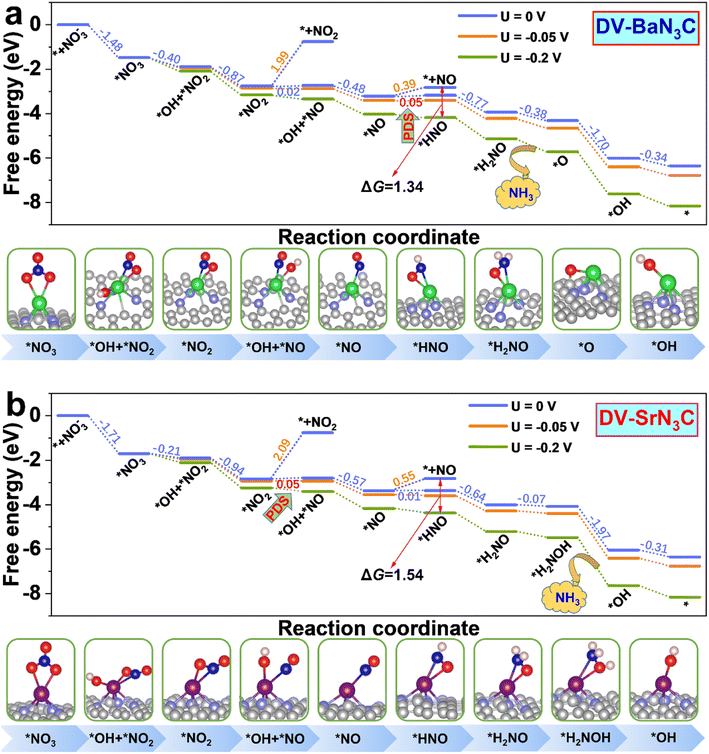Fig. 6 Free energy diagrams together with corresponding intermediate configurations for eNO₃RR on DV-BaN₃C (a) and DV-SrN₃C (b) under the potentials of 0, –0.05, and −0.2 V.

Overall, the eNO₃RR pathway on DV-SrN₃C (Fig. 6b) is almost the same as that on DV-BaN₃C, and the only difference is that the seventh hydrogenation step occurs on the O atom to form *H₂NOH, and NH₃ is released after the eighth hydrogenation step (*H₂NOH → *OH + NH₃ (g)). It is noted that all the reaction steps are exothermic on DV-SrN₃C, except the third (*NO₂ → *OH + *NO) and fifth (*NO → *HNO) hydrogenation steps with the free energy uphill of 0.05 and 0.01 eV, respectively.

Moreover, we also calculated the adsorption-free energy of *H₂O (ΔG_*H2O), and the reaction-free energy of the hydrogenation of *OH to *H₂O (ΔG_*OH→*H2O) for the studied AE-SAC systems. As seen in Table S7,† the negative ΔG_*OH→*H2O for most of the AE-SAC systems indicate that the hydrogenation of *OH to form *H₂O is spontaneous and quite easy, thereby, avoiding the *OH poisoning. It is worth mentioning that the SV-MgN₃, SV-CaN₃, and SV-SrN₃ systems with large ΔG_*OH→*H2O exhibit poor catalytic activity, which requires a high potential to remove *OH. Moreover, the ΔG_*H2O values for all AE-SAC systems are larger than −0.6 eV, indicating the weak adsorption of H₂O in the AE-SAC systems. Combining the aforementioned stronger adsorption of *NO₃ than *H, it can be concluded that the *H, *OH, and *H₂O will not poison the proposed catalysts (except SV-MgN₃, SV-CaN₃, and SV-SrN₃).

For the reaction selectivity, besides the aforementioned HER, other byproducts, mainly NO₂, NO, N₂O, and N₂, during eNO₃RR may be produced. It can be seen from Fig. 6 that direct desorption of *NO₂ from DV-BaN₃C and DV-SrN₃C is extremely difficult because large energy barriers as high as ∼2 eV are needed to overcome. Although the desorption energy barriers of *NO are not particularly high as NO₂ (0.39 and 0.55 eV), they are much higher than those for further hydrogenation (0.05 and 0.01 eV). Especially, when a tiny potential was applied, the further hydrogenation of *NO would be much more favorable thermodynamically. For instance, with an applied potential of −0.2 V, the free energy difference between the NO desorption and hydrogenation will exceed 1.3 eV. Therefore, *NO will further undergo electrochemical hydrogenation on DV-BaN₃C and DV-SrN₃C. On the other side, the NO dimer (N₂O₂) with cis O=N–N=O structure is the vital precursor to form N₂O and N₂, which could be formed by the coupling of two NO.^49,76,77 Obviously, the isolated single-atom active site cannot accommodate two NO₃⁻ simultaneously, and thus Langmuir–Hinshelwood mechanism for the formation of NO dimer can be excluded.⁷⁸ For the Eley–Rideal mechanism, the *NO needs to combine with a solvated NO molecule to form a NO dimer.⁷⁹ However, due to that *NO will be further hydrogenated rather than desorbed, the Eley–Rideal mechanism for NO dimer formation is also infeasible. Hence, the formation of NO₂, NO, N₂O, and N₂ will be effectively inhibited. Moreover, the desorption of the target product NH₃ is exothermic and spontaneous, further confirming high eNO₃RR selectivity toward NH₃ on DV-BaN₃C and DV-SrN₃C.

The electrode potential could significantly affect the selectivity of eNO₃RR against HER.³⁶ To be specific, the more negative electrode potential can bring more positive ΔG(*NO₃) but more negative ΔG(*H), so the adsorption of NO₃⁻ will become less favorable, whereas, the adsorption of the H atom may be dominant, exacerbating the selectivity problem. As shown in Fig. S17,† the adsorption of NO₃⁻ is still stronger than that of H on DV-BaN₃C and DV-SrN₃C even after applying a potential as large as −1.0 V. Therefore, the robust adsorption of NO₃⁻ could completely suppress the HER under the limiting potential, again affirming the high eNO₃RR selectivities of DV-BaN₃C and DV-SrN₃C.

Finally, the effect of the solvation on eNO₃RR was investigated for DV-BaN₃C and DV-SrN₃C. One can see from the free energy diagrams in Fig. S18† that the overall reaction pathway and PDS were unchanged when considering the solvation correction. In addition, U_L values are slightly decreased by 0.05 and 0.06 V for DV-BaN₃C and DV-SrN₃C with solvation correction, respectively, similar to other works.^39,48,49

3.4. Activity origin of eNO₃RR on AE-SACs

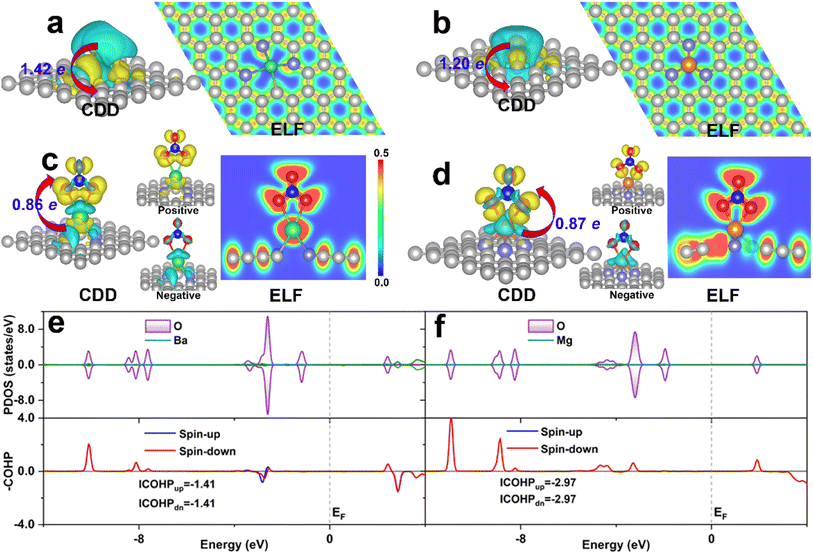
As the binding strength of NO₃⁻ can well predict the activity trend of eNO₃RR, the investigation of its activation mechanism and binding strength change, based on the electronic structure analysis, could give us insight into the activity origin. For comparison, DV-BaN₃C and SV-MgN₃ were considered, and they exhibited the highest (U_L = −0.05 V) and lowest (U_L = −1.48 V) eNO₃RR activity, respectively. Firstly, the charge density difference (CDD) is displayed in Fig. 7a and b show that considerable electrons are transferred from the embedded AE metals to the graphene support, and the AE metal atoms should be significantly positively charged, which is in agreement with the Bader charge analysis (1.42e for Ba and 1.20e for Mg). Consequently, the AE metals are stabilized by mainly ionic bond interaction, as verified by electron localization function (ELF) analysis. The positively-charged AE metals are responsible for the stable adsorption of the oxygenated species. For the adsorption of NO₃⁻ on DV-BaN₃C and SV-MgN₃, Bader charge analysis gives that *NO₃ gains 0.86 and 0.87e from the support, respectively. NO₃⁻ adsorbed Ba and Mg were positively charged by 1.62 and 1.64, respectively. Therefore, the adsorption of NO₃⁻ is mainly through the ionic bond interaction. However, from Fig. 7c and d, ELF results show that there is a certain charge overlap between *NO₃ and its bonded AE metal atoms, and especially, more electrons are located between *NO₃ and Mg than *NO₃ and Ba, indicating stronger covalent interaction between *NO₃ and Mg. It is worth noting that the charge enclosed on the Ba atom of the DV-BaN₃C system is an indicator of its lone-pair electrons. Importantly, CDD for NO₃ adsorbed systems indicates that charge accumulation and depletion occur simultaneously on *NO₃. Especially, the electrons obtained by *NO₃ mainly occupy its antibonding orbitals (positive section around the periphery of O atoms of *NO₃, as shown in Fig. 7c and d), while *NO₃ also loses some charges from its bonding orbitals (negative section on the N–O bonds of *NO₃, as shown in Fig. 7c and d). Therefore, NO₃⁻ can be effectively activated by the AE metal active center, through the “donation-back donation” mechanism, similar to the cases of TM active center,^51,52 the reason for which will be discussed later.

Fig. 7 The charge density difference (CDD) and electron localization function (ELF) for the bare DV-BaN₃C (a), bare SV-MgN₃ (b), NO₃ adsorbed DV-BaN₃C (c) and NO₃ adsorbed SV-MgN₃ (d). Projected densities of states (PDOS) and COHP for the NO₃ adsorbed DV-BaN₃C (e) and NO₃ adsorbed SV-MgN₃ (f). For CDD, the yellow and cyan regions denote electron accumulation and depletion, respectively, and the isosurface value was set to 0.002 e/bohr⁻³. In PDOS and COHP, the Fermi level (E_F) is labeled by a vertical dash line and set to 0 eV. COHP was calculated for the interaction between NO₃⁻ and Ba (Mg).

The above picture of NO₃⁻ adsorption can be supported by the DOS analysis. From Fig. 7e and f, we can see that a large number of electronic states of the O atoms in *NO₃, which are bonded with the AE metal atom, are located below the Fermi level, while the electronic states of the Ba and Mg atoms are very few. This result is in line with the ionic bond nature discussed above. Furthermore, crystal orbital Hamilton population (COHP)⁸⁰ analyses are shown in Fig. 7e and f indicate that there are more bonding states (positive value) between *NO₃ and Mg than those between *NO₃ and Ba. In addition, there are also some antibonding states occupied between *NO₃ and Ba (negative value). Integrated COHP (ICOHP) can quantitatively characterize the covalent interaction strength, that is, a more negative ICOHP signifies a stronger chemical bond interaction. The ICOHP (−5.94 eV) for the Mg–O bond is much more negative than that for the Ba–O bond (−2.82 eV). This verifies the stronger covalent interaction between *NO₃ and Mg than *NO₃ and Ba. Indeed, ΔG(*NO₃) was as high as −3.26 eV, for SV-MgN₃, which resulted in a large energy barrier (1.48 eV) in the last step of *OH → * + H₂O (Fig. S11c†). In contrast, the moderate chemical activity of the Ba active center in DV-BaN₃C endows it with ultrahigh eNO₃RR activity.

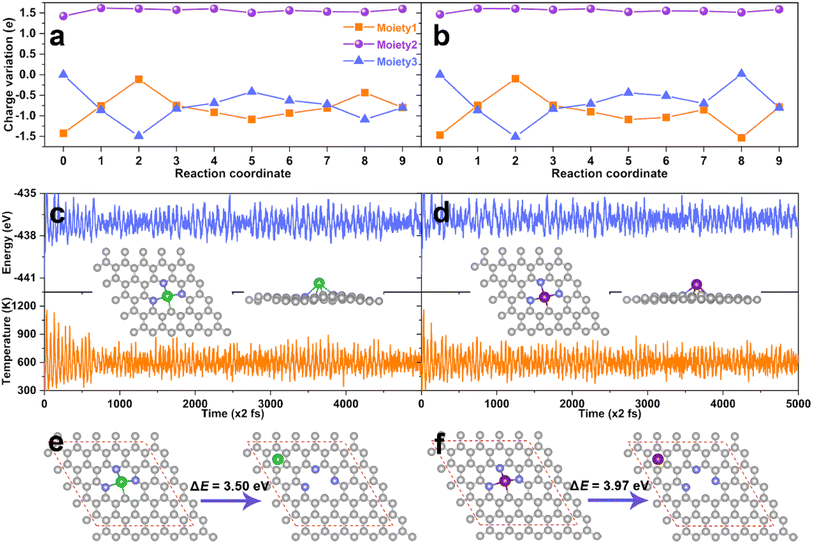
In order to further understand the excellent catalytic activity of the AE active center for eNO₃RR, the charge variations along with the reaction pathway for DV-BaN₃C and DV-SrN₃C were analyzed by subdividing the systems into three moieties, i.e., the N-doped graphene (moiety1), AE metal atom (moiety2), and adsorbate (moiety3), as illustrated in Fig. S19.† The detailed charge variations of the three moieties are presented in Fig. 8a and b, where steps 0 and 1 represent the charge distribution of the bare support and the NO₃⁻ adsorbed support, and steps 2–9 are the subsequent hydrogenation steps. Concretely, during the eNO₃RR reaction processes, the net charge of the Ba and Sr atoms remains almost unchanged (∼1.50e), and the charge change trends are similar for DV-BaN₃C and DV-SrN₃C. Meanwhile, the charges of the support (moiety1) dynamically change, which exchange charges with the intermediates indirectly with the AE ion as transmitters. Especially, the electron reservoir nature of the support enables the activation of NO₃⁻ following the charge “donation-back donation” mechanism, mimicking the behavior of TM active centers.^51,52

Fig. 8 The charge variation during the eNO₃RR process on DV-BaN₃C (a) and DV-SrN₃C (b). Energy and temperature evolution during the AIMD simulation for DV-BaN₃C (c) and DV-SrN₃C (d). Insets are the top and side views of the snapshots after 10 ps. The most stable configuration and second stable one with the Ba (e) and Sr (f) near the hollow sites, where ΔE is their energy difference.

As discussed above, the thermodynamic stability of DV-BaN₃C and DV-SrN₃C was confirmed. Next, the thermal stability was further checked through AIMD simulation. As plotted in Fig. 8c and d, the temperature and energy curves oscillate near the equilibrium states, and the DV-BaN₃C and DV-SrN₃C almost retain their intact geometric structures after 10 ps AIMD simulations under 600 K, implying their high thermal stability. Kinetically, Fig. 8e and f show that the energy differences between the most stable configuration and the second stable one with the Ba and Sr near the hollow sites are as large as 3.50 and 3.97 eV, respectively. Such high energy barriers mean that the diffusion of Ba or Sr atoms is unlikely on the graphene support, confirming the kinetic stability. Finally, the electrochemical stability was also evaluated by calculating the dissolution potential (U_diss).⁶⁷ The obtained U_diss are −0.90, −1.26, and −1.27 V for DV-MgN₂C₂-III, DV-SrN₃C, and DV-BaN₃C systems, respectively. Considering that DV-MgN₂C₂-III SAC was experimentally synthesized and used in the oxygen reduction reaction,¹⁴ DV-SrN₃C and DV-BaN₃C SACs are also stable enough under the electrochemical conditions due to their comparable U_diss values compared with the experimentally synthesized MgN₂C₂-III system.

4. Conclusions

In summary, based on the first-principles calculations, the feasibility of AE metals as active centers for eNO₃RR to produce NH₃ was systematically investigated by taking a series of AE-SACs as representatives, which were constructed by embedding AE metal (Mg, Ca, Sr, Ba) single atom into the N-doped graphene. Surprisingly, similar to the TM active sites, it was found that the AE metal active centers could also strongly adsorb and effectively activate NO₃⁻, to achieve excellent eNO₃RR activity. By thoroughly investigating the possible reaction pathways, a volcano diagram was established with ΔG(*NO₃) as the descriptor. The DV-BaN₃C and DV-SrN₃C systems were exactly located around the peak of the volcano diagram, exhibiting the highest activity for eNO₃RR to produce NH₃ with near-zero U_L of −0.05 V, comparable and even better than the TM-based SACs. With good stability, both systems also exhibited excellent selectivity against the generation of the byproducts, including H₂, NO₂, NO, N₂O, and N₂. Moreover, the electronic structure analysis indicates that although AE metal elements are highly ionic during the reaction, the support can indirectly exchange charge via the AE cations with NO₃⁻ and intermediates effectively, which enables the effective activation of NO₃⁻, via the charge “donation-back donation” mechanism, and further completes the catalytic cycle. On the one hand, these findings propose a novel kind of electrocatalyst for eNO₃RR, which may be also suitable for other reactions. Moreover, this work lays a theoretical foundation for the development of heterogeneous catalysts with AE metal as active centers, and emphasizes the great potential of AE metals, beyond transition metals, as active centers in heterogeneous catalysis.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 12074099) and the Program for Science & Technology Innovation Talents in Universities of Henan Province (Grant No. 20HASTIT028).

References

1. R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465–3520.
2. A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
3. B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048.
4. G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777.
5. B. Hammer, Y. Morikawa and J. K. Nørskov, Phys. Rev. Lett., 1996, 76, 2141–2144.
6. M.-A. Légaré, G. Bélanger-Chabot, D. Dewhurst Rian, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900.
7. B. Rösch, T. X. Gentner, J. Langer, C. Färber, J. Eyselein, L. Zhao, C. Ding, G. Frenking and S. Harder, Science, 2021, 371, 1125–1128.
8. J. A. Cowan, BioMetals, 2002, 15, 225–235.
9. C. Sissi and M. Palumbo, Nucleic Acids Res., 2009, 37, 702–711.
10. S.-L. Yean, G. Wuenschell, J. Termini and R.-J. Lin, Nature, 2000, 408, 881–884.
11. M. F. Dunn, J. A. Ramírez-Trujillo and I. Hernández-Lucas, Microbiology, 2009, 155, 3166–3175.
12. W. Guo, H. Nazim, Z. Liang and D. Yang, Crop J., 2016, 4, 83–91.
13. M. S. Hill, D. J. Liptrot and C. Weetman, Chem. Soc. Rev., 2016, 45, 972–988.
14. S. Liu, Z. Li, C. Wang, W. Tao, M. Huang, M. Zuo, Y. Yang, K. Yang, L. Zhang, S. Chen, P. Xu and Q. Chen, Nat. Commun., 2020, 11, 938.
15. Z. Lin, H. Huang, L. Cheng, W. Hu, P. Xu, Y. Yang, J. Li, F. Gao, K. Yang, S. Liu, P. Jiang, W. Yan, S. Chen, C. Wang, H. Tong, M. Huang, W. Zheng, H. Wang and Q. Chen, Adv. Mater., 2021, 33, 2107103.
16. K. Dong, J. Liang, Y. Wang, L. Zhang, Z. Xu, S. Sun, Y. Luo, T. Li, Q. Liu, N. Li, B. Tang, A. A. Alshehri, Q. Li, D. Ma and X. Sun, ACS Catal., 2022, 12, 6092–6099.
17. Q. Wang, K. Liu, J. Fu, C. Cai, H. Li, Y. Long, S. Chen, B. Liu, H. Li, W. Li, X. Qiu, N. Zhang, J. Hu, H. Pan and M. Liu, Angew. Chem., Int. Ed., 2021, 60, 25241–25245.
18. D. Bao, Q. Zhang, F.-L. Meng, H.-X. Zhong, M.-M. Shi, Y. Zhang, J.-M. Yan, Q. Jiang and X.-B. Zhang, Adv. Mater., 2017, 29, 1604799.
19. N. Lehnert, H. T. Dong, J. B. Harland, A. P. Hunt and C. J. White, Nat. Rev. Chem., 2018, 2, 278–289.
20. K. Chu, Y. Luo, P. Shen, X. Li, Q. Li and Y. Guo, Adv. Energy Mater., 2022, 12, 2103022.
21. X. Li, P. Shen, Y. Luo, Y. Li, Y. Guo, H. Zhang and K. Chu, Angew. Chem., Int. Ed., 2022, 61, e202205923.
22. J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 139, 12480–12487.
23. C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2019, 3, 1800376.
24. B. H. R. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Nat. Catal., 2019, 2, 290–296.
25. P. Shen, X. Li, Y. Luo, Y. Guo, X. Zhao and K. Chu, ACS Nano, 2022, 16, 7915–7925.
26. Y. Luo, Q. Li, Y. Tian, Y. Liu and K. Chu, J. Mater. Chem. A, 2022, 10, 1742–1749.
27. P. H. van Langevelde, I. Katsounaros and M. T. M. Koper, Joule, 2021, 5, 290–294.
28. X. Lu, H. Song, J. Cai and S. Lu, Electrochem. Commun., 2021, 129, 107094.
29. Y. Wang, A. Xu, Z. Wang, L. Huang, J. Li, F. Li, J. Wicks, M. Luo, D.-H. Nam, C.-S. Tan, Y. Ding, J. Wu, Y. Lum, C.-T. Dinh, D. Sinton, G. Zheng and E. H. Sargent, J. Am. Chem. Soc., 2020, 142, 5702–5708.
30. R. Jia, Y. Wang, C. Wang, Y. Ling, Y. Yu and B. Zhang, ACS Catal., 2020, 10, 3533–3540.
31. X. Zhang, Y. Wang, C. Liu, Y. Yu, S. Lu and B. Zhang, Chem. Eng. J., 2021, 403, 126269.
32. F.-Y. Chen, Z.-Y. Wu, S. Gupta, D. J. Rivera, S. V. Lambeets, S. Pecaut, J. Y. T. Kim, P. Zhu, Y. Z. Finfrock, D. M. Meira, G. King, G. Gao, W. Xu, D. A. Cullen, H. Zhou, Y. Han, D. E. Perea, C. L. Muhich and H. Wang, Nat. Nanotechnol., 2022, 17, 759–767.
33. G.-F. Chen, Y. Yuan, H. Jiang, S.-Y. Ren, L.-X. Ding, L. Ma, T. Wu, J. Lu and H. Wang, Nat. Energy, 2020, 5, 605–613.
34. J. Liang, B. Deng, Q. Liu, G. Wen, Q. Liu, T. Li, Y. Luo, A. A. Alshehri, K. A. Alzahrani, D. Ma and X. Sun, Green Chem., 2021, 23, 5487–5493.
35. T. Mou, J. Liang, Z. Ma, L. Zhang, Y. Lin, T. Li, Q. Liu, Y. Luo, Y. Liu, S. Gao, H. Zhao, A. M. Asiri, D. Ma and X. Sun, J. Mater. Chem. A, 2021, 9, 24268–24275.
36. J.-X. Liu, D. Richards, N. Singh and B. R. Goldsmith, ACS Catal., 2019, 9, 7052–7064.
37. Y. Lin, J. Liang, H. Li, L. Zhang, T. Mou, T. Li, L. Yue, Y. Ji, Q. Liu, Y. Luo, N. Li, B. Tang, Q. Wu, M. S. Hamdy, D. Ma and X. Sun, Mater. Today Phys., 2022, 22, 100611.
38. Z.-Y. Wu, M. Karamad, X. Yong, Q. Huang, D. A. Cullen, P. Zhu, C. Xia, Q. Xiao, M. Shakouri, F.-Y. Chen, J. Y. Kim, Y. Xia, K. Heck, Y. Hu, M. S. Wong, Q. Li, I. Gates, S. Siahrostami and H. Wang, Nat. Commun., 2021, 12, 2870.
39. P. Lv, D. Wu, B. He, X. Li, R. Zhu, G. Tang, Z. Lu, D. Ma and Y. Jia, J. Mater. Chem. A, 2022, 10, 9707–9716.
40. H.-Y. Zhuo, X. Zhang, J.-X. Liang, Q. Yu, H. Xiao and J. Li, Chem. Rev., 2020, 120, 12315–12341.
41. Y. Wang, M. Wang, Z. Lu, D. Ma and Y. Jia, Nanoscale, 2021, 13, 13390–13400.
42. J. Zhang, H. Zhang, Y. Wu, C. Liu, Y. Huang, W. Zhou and B. Zhang, J. Mater. Chem. A, 2022, 10, 5743–5757.
43. P. Li, Z. Jin, Z. Fang and G. Yu, Energy Environ. Sci., 2021, 14, 3522–3531.
44. J. Li, Y. Zhang, C. Liu, L. Zheng, E. Petit, K. Qi, Y. Zhang, H. Wu, W. Wang, A. Tiberj, X. Wang, M. Chhowalla, L. Lajaunie, R. Yu and D. Voiry, Adv. Funct. Mater., 2022, 32, 2108316.
45. H. Niu, Z. Zhang, X. Wang, X. Wan, C. Shao and Y. Guo, Adv. Funct. Mater., 2021, 31, 2008533.
46. L. Yang, S. Feng and W. Zhu, J. Phys. Chem. Lett., 2022, 13, 1726–1733.
47. L. Lv, Y. Shen, J. Liu, X. Meng, X. Gao, M. Zhou, Y. Zhang, D. Gong, Y. Zheng and Z. Zhou, J. Phys. Chem. Lett., 2021, 12, 11143–11150.
48. N. Sathishkumar, S.-Y. Wu and H.-T. Chen, Appl. Surf. Sci., 2022, 598, 153829.
49. M. Yang, Z. Wang, D. Jiao, G. Li, Q. Cai and J. Zhao, Appl. Surf. Sci., 2022, 592, 153213.
50. J. Wu and Y.-X. Yu, Catal. Sci. Technol., 2021, 11, 7160–7170.
51. J. Wu, J.-H. Li and Y.-X. Yu, J. Phys. Chem. Lett., 2021, 12, 3968–3975.
52. Y. Wang, D. Wu, P. Lv, B. He, X. Li, D. Ma and Y. Jia, Nanoscale, 2022, 14, 10862–10872.
53. X. Li, H. Rong, J. Zhang, D. Wang and Y. Li, Nano Res., 2020, 13, 1842–1855.
54. J. Zhang, H. Yang and B. Liu, Adv. Energy Mater., 2021, 11, 2002473.
55. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
56. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
57. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
58. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
59. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
60. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
61. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
62. D. Ma, Y. Wang, L. Liu and Y. Jia, Phys. Chem. Chem. Phys., 2021, 23, 4018–4029.
63. C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168.
64. S. Ghoshal, A. Ghosh, P. Roy, B. Ball, A. Pramanik and P. Sarkar, ACS Catal., 2022, 12, 15541–15575.
65. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
66. http://webbook.nist.gov/chemistry/ .
67. X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721.
68. F. Calle-Vallejo, M. Huang, J. B. Henry, M. T. M. Koper and A. S. Bandarenka, Phys. Chem. Chem. Phys., 2013, 15, 3196–3202.
69. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
70. Y. Peng, B. Lu and S. Chen, Adv. Mater., 2018, 30, 1801995.
71. C. Strupp, Ann. Occup. Hyg., 2010, 55, 43–56.
72. Y.-J. Shi and W. J. Swiatecki, Phys. Rev. Lett., 1985, 54, 300–301.
73. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
74. D. Wu, B. He, Y. Wang, P. Lv, D. Ma and Y. Jia, J. Phys. D: Appl. Phys., 2022, 55, 203001.
75. S. Garcia-Segura, M. Lanzarini-Lopes, K. Hristovski and P. Westerhoff, Appl. Catal., B, 2018, 236, 546–568.
76. Z. Wang, J. Zhao, J. Wang, C. R. Cabrera and Z. Chen, J. Mater. Chem. A, 2018, 6, 7547–7556.
77. H. Niu, Z. Zhang, X. Wang, X. Wan, C. Kuai and Y. Guo, Small, 2021, 17, 2102396.
78. R. J. Baxter and P. Hu, J. Chem. Phys., 2002, 116, 4379–4381.
79. Y. Wang and M. Shao, ACS Catal., 2022, 12, 5407–5415.
80. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.

---

Footnote

† Electronic supplementary information (ESI) available: TDOS of AE-SACs; possible adsorption configurations of *NO₃ on AE-SACs; most stable configurations and corresponding adsorption-free energies of *NO₃ and *H on AE-SACs; free energy diagrams and corresponding intermediate configurations on other AE-SAC systems; adsorption free energies of *NO₃ and *H versus electrode potential on DV-BaN₃C and DV-SrN₃C; free energy diagrams and corresponding intermediate configurations on DV-BaN₃C and DV-SrN₃C with consideration of the solvation effect; schematic diagram of three moieties; the key parameters of the AE-SAC systems; the key parameters of *NO₃ and *H adsorption on the AE-SAC systems; the PDS and corresponding U_L on the AE-SAC systems; the ΔE_ZPE and TΔS for intermediates and free molecules. See DOI: https://doi.org/10.1039/d2ta08027c

---