Open Access Article
Open Access ArticleA and B site Co-doping of CaMnO3: a route to enhanced heat storage properties†
Emanuela
Mastronardo
 *ab,
Xin
Qian
*ab,
Xin
Qian
 c,
Juan M.
Coronado
c,
Juan M.
Coronado
 b and
Sossina M.
Haile
b and
Sossina M.
Haile
 *c
*c
aEngineering Department, University of Messina, C.da di Dio, 98126, Messina, Italy. E-mail: emastronardo@unime.it
bInstituto de Catálisis y Petroleoquímica, CSIC, C/Marie Curie, 2, E-28049, Madrid, Spain
cMaterials Science and Engineering, Northwestern University, 2220 Campus Drive Cook Hall, 60208 Evanston, IL, USA
First published on 4th April 2023
Abstract
The successful commercialization of concentrating solar power (CSP) plants requires effective energy storage for the supply of power on demand during solar transients. High-temperature thermal energy storage (≥700 °C up to 1200 °C) has the potential to address storage needs and power capacity owing to the efficiency gains from a high-temperature operation. Recently, doped CaMnO3 has been identified as a promising candidate for thermochemical heat storage in CSP plants. Herein, we aim at tuning the CaMnO3 heat storage temperature window and enhancing the heat storage properties beyond that of singly doped compositions by co-doping with equal amounts of La and Fe on the A and B sites, respectively, ((LaxCa1−x)(FexMn1−x)O3). Two doping levels are investigated (x = 0.05 and 0.10). X-ray absorption spectroscopy and diffraction studies revealed that in both materials, Fe and Mn adopt, respectively, the 3+ and 4+ oxidation states under ambient conditions and the dopants are incorporated into the intended sites. Interestingly, the heat storage capacity did not vary monotonically with dopant content. The highest heat storage capacity was attained from La0.05Ca0.95Fe0.05M0.95O3−δ. This surprising result is a consequence of the substantial large extent of reduction enabled by the slightly lower enthalpy than that of La0.1Ca0.9Fe0.1Mn0.9O3−δ. Under technologically relevant conditions, operating over a temperature window value ranging from 700 to 1200 °C and under an oxygen partial pressure of about 10−3 atm, the thermochemical heat storage capacities of La0.05Ca0.95Fe0.05Mn0.95O3δ and La0.1Ca0.9Fe0.1Mn0.9O3−δ are 378.5 ± 1.0 kJ kgABO3−1 and 282.3 ± 1.5 kJ kgABO3−1, respectively, and exceed the values not only of the undoped material but also of other singly doped analogs for the first material. Furthermore, with respect to the singly Fe-doped CaMnO3, we narrowed the operating temperature range from 400–1200 °C to 700–1200 °C, which is the target temperature for the CSP plants. Hence, we demonstrated that by co-doping, it is possible to tailor reduction enthalpy and extent together with the operating temperature range.
Introduction
In setting the world's sustainable development priorities enshrined in the Sustainable Development Goals (SDG), the United Nations (UN) has included in N.7 access to affordable, reliable, and sustainable energy for all.1 Among the targets to be achieved by 2030 is a substantial increase in the share of renewable energy in the global energy mix. Solar-driven power generation has the potential to substantially contribute to this goal because of its vast solar resources. Amongst the approaches for generating electricity from sunlight, concentrated solar power (CSP), in which solar energy is concentrated to generate high temperatures that, in turn, drive a heat engine, has garnered significant interest in recent years, with an increasing number of CSP plants currently under construction or planned.2 This reflects the overall state of technological readiness of the CSP approach.Key to the efficiency and hence economic competitiveness of CSP plants is operated at high temperatures (≥700 °C up to 1200 °C),3,4 along with the storage of the high-temperature heat for on-demand power generation.5 Accordingly, about half of all CSP plants (∼47%) currently in operation globally incorporate a Thermal Energy Storage (TES) system, and even a greater proportion of plants under construction (∼72%) and planned (∼77%) do so.6,7 Most operational TES systems are based on sensible heat storage. The technology is reliable and relatively inexpensive. However, sensible heat storage suffers from low energy density. Thermochemical heat storage (TCS) technologies store heat in the form of reversible chemical reactions and have a significantly higher energy density and longer-term storage duration than sensible heat storage, which explains the growing interest in such systems. A range of reactive materials (e.g. carbonates8 to hydroxides9,10 and hydrides11 to oxides12,13) have been investigated for TCS systems. None of the materials evaluated to date achieve both the cost and efficiency targets for a CSP plant.14
A promising class of materials under examination for TCS systems are non-stoichiometric perovskite-structured oxides, AMO3−δ, in which the oxygen content can vary continuously with temperature and oxygen partial pressure.15–18 Heat is released upon the oxidation of these materials according to the following reaction:
 | (1) |
The amount of chemical heat stored per mole of material (H), or chemical heat storage capacity, is the difference in the heat content of the oxide in the two states, Hinitial and Hfinal. In nonstoichiometric oxides, ΔH depends on the net change in oxygen content through the redox cycle as well as the partial molar enthalpy of oxygen in the oxide, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) O (sometimes denoted by hO), and is given by
O (sometimes denoted by hO), and is given by
 | (2) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O, the relative partial molar enthalpy of oxygen in the oxide (
0O, the relative partial molar enthalpy of oxygen in the oxide (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) O −
O − ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O), denotes the redox thermodynamics of eqn (1),21 and the superscript 0 denotes the reference state. Thus, the two metrics that define the heat storage capacity of a nonstoichiometric oxide are thus Δ
0O), denotes the redox thermodynamics of eqn (1),21 and the superscript 0 denotes the reference state. Thus, the two metrics that define the heat storage capacity of a nonstoichiometric oxide are thus Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O, a fundamental property of the material, and the extent of stoichiometry change (Δδ = δf − δi), which depends on both the material properties and the operating conditions. The larger the magnitudes of these two parameters, the larger the heat storage capacity. The mass-normalized heat storage capacity is defined as QM = ΔH/MABO3, where MABO3 is the molar mass of the oxide.
0O, a fundamental property of the material, and the extent of stoichiometry change (Δδ = δf − δi), which depends on both the material properties and the operating conditions. The larger the magnitudes of these two parameters, the larger the heat storage capacity. The mass-normalized heat storage capacity is defined as QM = ΔH/MABO3, where MABO3 is the molar mass of the oxide.
Among the perovskites investigated for TCS systems, CaMnO3 (CM) has attracted interest owing to its cost-effectiveness and the high abundance of its constituent elements.22–24 The pristine (undoped) material suffers from ready decomposition into spinel (CaMn2O4) and Ruddlesden–Popper (Ca2MnO4) phases at temperatures above 900 °C and pO2 ≤ 0.004 atm,18,23 limiting its maximum operating temperature. The magnitude of the molar enthalpy term of CaMnO3, Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O, is also relatively small, implying a relatively small heat storage capacity. Accordingly, chemical modifications by doping were pursued to enhance stability and increase the enthalpy associated with the redox reaction (eqn (1)).
0O, is also relatively small, implying a relatively small heat storage capacity. Accordingly, chemical modifications by doping were pursued to enhance stability and increase the enthalpy associated with the redox reaction (eqn (1)).
The introduction of La on the A-site in CaMnO3-based and SrMnO3-based perovskites has been shown, both experimentally and computationally, to increase monotonically the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O.25–30 This behavior reflects the easier reduction of Mn from the fully 4+ oxidation state in the end-member A2+Mn4+O3 compounds than when Mn is already partially reduced to 3+ in (A2+, La3+)(Mn4+, Mn3+)O3. Related to this result is the frequent (but not universal) observation that the magnitude of Δ
0O.25–30 This behavior reflects the easier reduction of Mn from the fully 4+ oxidation state in the end-member A2+Mn4+O3 compounds than when Mn is already partially reduced to 3+ in (A2+, La3+)(Mn4+, Mn3+)O3. Related to this result is the frequent (but not universal) observation that the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O increases as the oxygen nonstoichiometry increases in Mn bearings and even other perovskites.26,27,29–33 These trends have been explained in terms of the perovskite electronic structure. The removal of oxygen requires the redistribution of O 2p electrons associated with the formerly occupied oxygen site to the lowest unoccupied state at the Fermi energy (EF).30,34 Thus, the greater the energy difference between the oxygen 2p band center and EF, the greater the energetic penalty of creating oxygen vacancies. The position of EF increases as the electron count increases. Hence, Sr2+ is replaced with La3+ as the reduction proceeds, causing the observed increase in oxygen formation energy, which is the dominant term in Δ
0O increases as the oxygen nonstoichiometry increases in Mn bearings and even other perovskites.26,27,29–33 These trends have been explained in terms of the perovskite electronic structure. The removal of oxygen requires the redistribution of O 2p electrons associated with the formerly occupied oxygen site to the lowest unoccupied state at the Fermi energy (EF).30,34 Thus, the greater the energy difference between the oxygen 2p band center and EF, the greater the energetic penalty of creating oxygen vacancies. The position of EF increases as the electron count increases. Hence, Sr2+ is replaced with La3+ as the reduction proceeds, causing the observed increase in oxygen formation energy, which is the dominant term in Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O. The influence of La doping has equivalently been explained in terms of a decrease in the overlap of the eg orbital of the Mn ions and the 2pσ orbital of the oxygen ions with increasing La content, again increasing the energetic penalty of adding electrons into the available electronic states upon oxygen removal.35
0O. The influence of La doping has equivalently been explained in terms of a decrease in the overlap of the eg orbital of the Mn ions and the 2pσ orbital of the oxygen ions with increasing La content, again increasing the energetic penalty of adding electrons into the available electronic states upon oxygen removal.35
The influence of B-site doping is less clear, particularly because various approaches are available: the dopant may be redox inert, with an oxidation state of either 3+ (e.g., Al36) or 4+ (e.g., Ti31,32), or it may be redox active (e.g., Co37). It has been suggested that across the SrMO3 series of perovskites, where the M-site element can adopt the 4+ oxidation state, the effective band gap decreases with the increasing electronegativity of the M species. Consequently, a decrease in the effective band gap can result in a decrease in the energetic penalty of oxygen vacancy formation.30 However, it is unknown whether an analogous trend holds upon doping, that is, when more than one species resides on the M site. In the few studies aimed at quantifying the impact of M-site doping on the thermodynamics of oxygen vacancy formation energy in CaMnO3, it has been observed that doping with Al,22 Ti22 and Fe24 at moderate levels increases the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O in all cases, suggesting that the introduction of less reducible species renders the entire material less reducible. Moreover, these dopants have been found to enhance the thermal stability of the material against decomposition into the spinel and Ruddlesden–Popper phases. Thus, although the fundamental electronic origins of these effects are unclear, B-site doping can provide significant benefits to the properties of CaMnO3.
0O in all cases, suggesting that the introduction of less reducible species renders the entire material less reducible. Moreover, these dopants have been found to enhance the thermal stability of the material against decomposition into the spinel and Ruddlesden–Popper phases. Thus, although the fundamental electronic origins of these effects are unclear, B-site doping can provide significant benefits to the properties of CaMnO3.
This study examines the behavior of La and Fe co-doped CaMnO3, ((LaxCa1−x)(FexMn1−x)O3,x = 0.05 and 0.10). In our earlier study on Fe-doped CaMnO3, we observed not only enhanced thermal stability and increased heat storage capacity compared to the undoped system but also, surprisingly, that Fe remained in the 3+ oxidation state under all conditions explored.24 Thus, the material with 10 at% Fe on the B site was most appropriately described as CaMn0.9Fe0.1O2.95−δ, reflecting the resistance of Fe towards the adoption of the 4+ oxidation state. Although light doping enhanced the heat storage capacity, compositions with Fe content beyond 10 at% displayed a low value of the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O, and thus the opportunities for enhancing the properties using Fe alone are limited. Co-doping with La is attractive because of the well-known increase La induces in the magnitude of Δ
0O, and thus the opportunities for enhancing the properties using Fe alone are limited. Co-doping with La is attractive because of the well-known increase La induces in the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O, as already described. Our previous studies of La-doped CaMnO3 generated results similar to those of Fe-doping, with the dopant increasing the thermal stability and the heat storage capacity provided that the concentration did not exceed 10 at%.38 Beyond this concentration, (La,Ca)MnO3−δ adopts the orthorhombic (rather than cubic) structure over a wide T-pO2 space with a small entropy of reduction, causing the extent of stoichiometry change between charge and discharge conditions, Δδ, to become small. Thus, again, opportunities for enhancing heat storage using just La are limited. Herein, we aimed to combine the benefits of both Fe and La. Furthermore, by introducing these elements in equal concentrations, i.e., the preparation of (LaxCa1−x)(FexMn1−x)O3 compositions, we aimed to design a material capable of attaining an oxygen stoichiometry of 3 under technologically relevant conditions. A large initial oxygen content is desirable because the contribution to the configurational entropy from oxygen vacancies scales with ln(δ/(3 − δ))39 and is thus large in the small δ region. A large entropy, in turn, encourages a large change in δ with temperature. Because of the detrimental impact of high levels of Fe and La doping, we examine the specific compositions of x = 0.05 and 0.10. We establish the thermodynamic properties by thermogravimetric analysis and characterize the crystallographic properties by in situ high-temperature diffraction to ascertain the conditions of stability and gain insight into the atomistics of the reduction behavior. The latter objective is further supported by X-ray absorption studies. Using thermodynamic data, we provide an assessment of the heat storage capacity.
0O, as already described. Our previous studies of La-doped CaMnO3 generated results similar to those of Fe-doping, with the dopant increasing the thermal stability and the heat storage capacity provided that the concentration did not exceed 10 at%.38 Beyond this concentration, (La,Ca)MnO3−δ adopts the orthorhombic (rather than cubic) structure over a wide T-pO2 space with a small entropy of reduction, causing the extent of stoichiometry change between charge and discharge conditions, Δδ, to become small. Thus, again, opportunities for enhancing heat storage using just La are limited. Herein, we aimed to combine the benefits of both Fe and La. Furthermore, by introducing these elements in equal concentrations, i.e., the preparation of (LaxCa1−x)(FexMn1−x)O3 compositions, we aimed to design a material capable of attaining an oxygen stoichiometry of 3 under technologically relevant conditions. A large initial oxygen content is desirable because the contribution to the configurational entropy from oxygen vacancies scales with ln(δ/(3 − δ))39 and is thus large in the small δ region. A large entropy, in turn, encourages a large change in δ with temperature. Because of the detrimental impact of high levels of Fe and La doping, we examine the specific compositions of x = 0.05 and 0.10. We establish the thermodynamic properties by thermogravimetric analysis and characterize the crystallographic properties by in situ high-temperature diffraction to ascertain the conditions of stability and gain insight into the atomistics of the reduction behavior. The latter objective is further supported by X-ray absorption studies. Using thermodynamic data, we provide an assessment of the heat storage capacity.
Methods
Material synthesis
(La0.05Ca0.95)(Fe0.05Mn0.95)O3 and (La0.10Ca0.90)(Fe0.10Mn0.90)O3 materials, hereinafter, LCFM5 and LCFM10, respectively, were prepared according to a modified Pechini method:39 stoichiometric amounts of the nitrate salt precursors, Ca(NO3)2·4H2O (Sigma-Aldrich, 99.0% purity), La(NO3)3·6H2O (Sigma-Aldrich, ≥99.9% purity), Mn(NO3)2·4H2O (Sigma-Aldrich, ≥97.0% purity), Fe(NO3)3·9H2O (Sigma-Aldrich, ≥98% purity), and citric acid (in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of CA
1 molar ratio of CA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal) were dissolved in distilled water. The mixture was stirred at 70 °C for 3 h. Ethylene glycol (EG) was then added in a 3
metal) were dissolved in distilled water. The mixture was stirred at 70 °C for 3 h. Ethylene glycol (EG) was then added in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of CA
2 ratio of CA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EG and stirred again at 90 °C for 45 minutes, at which point a gel was obtained. The gel was dried at 200 °C for 12 h, transformed into a brittle char, which was then ground and subsequently calcined at 1100 °C for 24 h under static air. Two additional 12 h firing steps at 1300 °C under flowing oxygen (50 ml min−1), with intermediate grinding, were required to obtain single-phase products. Cylindrical porous monoliths were obtained in the second firing step, in which a loosely formed green body was sintered lightly. The self-supporting structure was prepared by moistening ∼500 mg of the powder with isopropyl alcohol, lightly pressing it in a cylindrical alumina die (internal diameter 10 mm), and allowing the alcohol to evaporate.
EG and stirred again at 90 °C for 45 minutes, at which point a gel was obtained. The gel was dried at 200 °C for 12 h, transformed into a brittle char, which was then ground and subsequently calcined at 1100 °C for 24 h under static air. Two additional 12 h firing steps at 1300 °C under flowing oxygen (50 ml min−1), with intermediate grinding, were required to obtain single-phase products. Cylindrical porous monoliths were obtained in the second firing step, in which a loosely formed green body was sintered lightly. The self-supporting structure was prepared by moistening ∼500 mg of the powder with isopropyl alcohol, lightly pressing it in a cylindrical alumina die (internal diameter 10 mm), and allowing the alcohol to evaporate.
Chemical and morphological characterization
Chemical analysis of the products was performed by inductively coupled plasma-optical emission spectrometry (ICP-OES, iCAP7000 ThermoFisher Scientific in axial configuration) for the simultaneous detection of La, Ca, Mn, and Fe. Samples were dissolved by digestion in a solution of HNO3 and H2O2 for 12 h at 60 °C.The morphological features of the porous monoliths were characterized using scanning electron microscopy (SEM, Hitachi SU8030). Additional chemical analysis was performed alongside the morphological studies by energy dispersive X-ray spectroscopy (EDX, Oxford X-max 80 SDD) at an acceleration voltage of 20 kV. The EDX composition mapping (Fig. S1†) revealed that the cations were uniformly distributed across the materials.
Crystal–chemical properties at ambient temperature
Formation of single-phase perovskite products was established by X-ray powder diffraction (XRD, Rigaku Ultima IV, Cu Kα, 40 V, 44 mA, 0.05° s−1 scan rate) performed on ground powders obtained from sintered porous monoliths (Fig. S1a†). Rietveld refinement against the diffraction data was performed using the GSAS package40,41 to determine the average long-range crystallographic properties (Fig. S2b and c†). The orthorhombic structure of CaMnO3 (ref. 24) was used as the starting point for the refinements.X-ray Absorption Near Edge Structure (XANES) and Extended X-ray Absorption Fine Structure (EXAFS) measurements were performed to gain insight into the local structure of the materials and clarify the redox chemistry. Powders (again obtained from the sintered monoliths) were dispersed homogeneously over the adhesive tape. Data were collected at the La L-III edge, Mn K-edge and Fe K-edge in transmission mode at room temperature under synthetic air using the facilities at Sector 5 (5BM-D) of the Advanced Photon Source (APS) at Argonne National Laboratory. The transmission emissions were measured using a four-element Si-drifted detector (SII) with the incident X-ray angle θ at about 45° with respect to the sample surface.
The XAS data were analyzed using the Demeter software package.41 The oxidation state of cations was determined using the position of the adsorption edge energy (E0), the energy at which a sharp change in adsorption occurs in the XANES region, in turn identified by finding the maximum of the derivative of the normalized absorption function μ(E). Spectra of standard materials (La2O3, Fe2O3, Fe3O4, FeO, MnO, Mn2O3, and MnO2) available in the database of the International X-ray Absorption Society (https://www.i-x-s.org/)42 were used to establish calibration lines (Fig. S4†) to convert the measured edge energies to the oxidation state. LaFeO3 and CaMnO3 were prepared and used as standard materials for the comparison of XANES features. For local structure analysis, the data in the EXAFS region, spanning the k range of 2.0–9.8 Å−1, were weighted based on k3 and Fourier transformed with a Hanning window. Fitting was carried out in R space from R = 0.7 to 3.8 Å using a three-shell model with paths for the first (Mn–O and Fe–O for Mn and Fe K-edge spectra, respectively), second (Mn–Ca/La and Fe–Ca/La), and third (Mn–Mn and Fe–Mn) nearest neighbor shells.
Phase evolution and thermal analysis
Phase evolution was tracked in situ by high-temperature XRD (Rigaku Ultima IV, Cu Kα, 40 V, 44 mA, 0.05° s−1 scan rate). Data were collected at temperatures between ambient and 1200 °C in 50–100 °C increments (HTK 1200 heating chamber) under 30 ml min−1 of N2 (pO2 ∼ 10−3 atm). After each heating interval (10 °C min−1), the sample was equilibrated for 20 min before the diffraction pattern was collected. Diffraction data were collected upon the completion of the selected thermal analysis experiments. Phase formation and evolution were analyzed using whole pattern fitting (or the Pawley method), as implemented in the commercial software package Materials Data by Jade, Inc. The XRD measurements were performed under more reducing conditions than those of the thermal analysis experiments, thus revealing the suitability of the thermal data for thermodynamic characterization.Thermal analysis, in which mass and thermal events were measured as a function of temperature, was performed using a simultaneous thermal analyzer (STA449 F5 Jupiter Netzsch) coupled with an inline pO2 sensor (MicroPoas, Setnag) to measure the oxygen partial pressure of the exhaust gas. One set of measurements was made by assessing overall phase transition behavior and thermal stability, with both mass (TG, thermogravimetric) and thermal (DSC, differential scanning calorimetry) signals recorded. The sample mass was set to 80–100 mg, and data were collected at a heating rate of 10 °C min−1 under gas conditions of pO2 = 0.18 atm and 5.1 × 10−4 atm, corresponding to the most oxidizing and most reducing conditions considered for subsequent TG measurements. Each measurement was initiated with a 1 h hold at 200C under pO2 = 0.18 atm to remove surface species. Both heating and cooling profiles were recorded, and data were collected up to a temperature of 1100C. A second set of measurements was made with the objective of accurately recording mass change upon oxygen loss or uptake. For these experiments, large samples, 200–500 mg, were employed. The heating rate decreased to 5 °C min−1, and only the mass signal was recorded. Each experiment (Fig. S5†) was again initiated with a 1 h hold under pO2 = 0.18 atm to remove possible surface adsorbed species. Data were recorded at seven pO2 values: 0.18, 0.09, 0.07, 0.04, 0.02, 0.008, and 0.004 atm. Measurements were made again on both heating and cooling, with a maximum temperature of 1200 °C. For both sets of experiments, the target gas composition was achieved by mixing dry synthetic air and Ar, and the total gas flow rate was fixed at 250 ml min−1.
The change in oxygen non-stoichiometry (Δδ(molO/molABO3)) from the reference condition (200 °C and pO2 = 0.18 atm) was computed using the following equation:
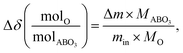 | (3) |
Results and analysis
Chemical, morphological and structural characterization
The results of the chemical analysis, Table 1, indicated that the compositions were all within 3 at% of the target Mn/Ca (nMn/nCa), Fe/Mn (nFe/nMn) and La/Ca (nLa/nCa) values. Hereinafter, the ideal cation stoichiometries are quoted. The structures displayed large porosities, with feature sizes at the tens of micrometer length-scale (Fig. 1), indicating the suitability of the samples for thermogravimetric analysis due to easy gas access to the entirety of the material.| Code | Target compositiona | n Mn/nCa (mol mol−1) | n Fe/nCa (mol mol−1) | n La/nCa (mol mol−1) | Implied stoichiometrya |
|---|---|---|---|---|---|
| a Taking Fe to be Fe3+ and Mn to be Mn4+. | |||||
| LCFM5 | La0.05Ca0.95Fe0.05Mn0.95O3 | 1.031 (3) | 0.0533 (10) | 0.0527 (10) | La0.049Ca0.922Fe0.049Mn0.951O2.97 |
| LCFM10 | La0.10Ca0.90Fe0.10Mn0.90O3 | 1.026 (9) | 0.1142 (11) | 0.1148 (14) | La0.101Ca0.877Fe0.100Mn0.900O2.98 |
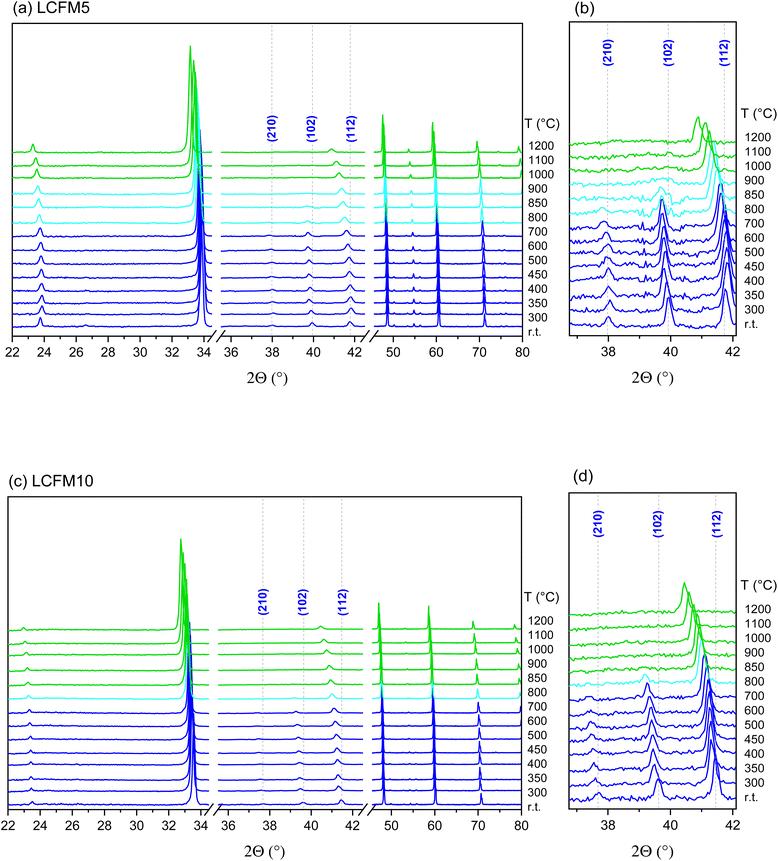
At ambient temperature, both LCFM5 and LCFM10 crystallize in the orthorhombic (Pnma) GdFeO3-type structure (Fig. 2a), as do the end-member materials CaMnO3 and LaFeO3. Because the lattice dimensions b/2 and c/√2 are metrically identical in LCFM10, the nonzero intensity of the (210) peak indicates that the cell is not tetragonal (Fig. S1a,† see also Fig. 5d below). A shift toward lower 2Θ angles (Fig. 2a) relative to CaMnO3 signifies a slight increase in the lattice parameters (and the unit cell volume) in response to the La and Fe doping (Fig. 2b). A slight broadening of the peaks as the La and Fe concentrations increase is also a reflection of the incorporation of the dopants, which induce strain gradients into the structure. The refined parameters are reported in Table 2, along with those of the singly doped compositions, for comparison. The extent of the orthorhombic distortion, defined based on the orthorhombicity,  (being α1 = a, α2 = b/√2, α3 = c and
(being α1 = a, α2 = b/√2, α3 = c and ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) = (abc/√2)1/3) and also reported in Table 2, remains relatively constant across the series.
= (abc/√2)1/3) and also reported in Table 2, remains relatively constant across the series.
 | ||
| Fig. 2 Diffraction analysis of (LaxCa1−x)(FexMn1−x)O3: (a) details of the most intense peaks of (LaxCa1−x)(FexMn1−x)O3 XRD patterns and (b) structural parameters as a function of x. | ||
| Material | Lattice parameters | ||||||
|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | V cell (Å3) | ρ (kg m−3) | O 10−2% | Source | |
| a Crystallographic density. | |||||||
| CaMnO3−δ | 5.2785 (4) | 7.4564 (5) | 5.2664 (2) | 207.27 (4) | 4820 | 7.7 (2) | Mastronardo et al.24 |
| LCFM5 | 5.2987 (7) | 7.4836 (5) | 5.2885 (5) | 209.71 (3) | 4688 | 6.9 (1) | This work |
| LCFM10 | 5.3257 (7) | 7.5199 (4) | 5.3176 (6) | 212.96 (3) | 4772 | 6.9 (1) | This work |
| CaFe0.1Mn0.9O2.95−δ | 5.2906 (5) | 7.4737 (4) | 5.2804 (7) | 208.79 (6) | 4814 | 6.8 (1) | Mastronardo et al.24 |
| La0.1Ca0.9MnO3−δ | 5.3110 (9) | 7.4988 (13) | 5.3036 (9) | 211.22 (7) | 4826 | 6.7 (1) | Mastronardo et al.24 |
The XANES study revealed that the Mn and Fe oxidation states in the as-prepared materials are, respectively, 4+ and 3+, in both LCFM5 and LCFM10 (Fig. 3), which agrees with our earlier studies of singly Fe-doped CaMnO3.24 Unsurprisingly, La is found in the 3+ oxidation state (Fig. S3†). Thus, the introduction of La at an equal concentration as Fe enables access to the crystallographic state in which all oxygen sites are fully occupied, as desired. The XAS study further revealed that doping has a negligible effect on the Mn environment, as would be expected given the minimal impact of the introduction of La and Fe on the lattice parameters and the fact that only a small fraction of the next nearest neighbours of Mn are changed between the compositions CaMnO3 and La0.1Ca0.9Fe0.1Mn0.9O3. This result is evident in both the XANES (Fig. 3a) and EXAFS (Fig. 4a) analyses. Quantitative treatment of the EXAFS data (Fig. S7 and S8†) showed that the Mn–O distance remained close to the mean value of 1.901(4) Å of undoped CaMnO3 (ref. 44) in both LCFM5 (1.918 Å) and LCFM10 (1.897 Å) (Tables S2 and S3).† In contrast, there are relatively strong changes in the X-ray absorption spectra at the Fe K edge between LaFeO3, LCFM5, and LCFM10 (Fig. 3b). Because the three materials are globally isostructural and the Fe and Mn oxidation states remain unchanged, the differences reflect changes in the local chemical environment of Fe, resulting from large differences in the concentrations of Ca and Mn between the LaFeO3 and LCFM compounds. The pre-edge feature reflects the formally forbidden 1s → 3d transition45,46 and is known to increase in intensity with Sr content in doped LaFeO3.47 This is consistent with the present observation. Significant herein is the high level of similarity in the EXAFS of the Mn and Fe species (Fig. 4), reflecting the incorporation of Fe on the B-site. The Fe–O distances of 1.94 Å in both LCFM5 and LCFM10 (Tables S4 and S5†) are almost identical to the Mn–O distances and shorter than the mean Fe–O distance of 2.03(10) Å in LaFeO3.48
 | ||
| Fig. 4 Fourier transforms (FT), with modulus (∣χ(R)∣) and imaginary part (Im[χ(R)]) of (a) Mn and (b) Fe EXAFS spectra of LCFM5 and LCFM10. | ||
Phase evolution and thermal analysis
The in situ XRD study, Fig. 5, revealed that both LCMF5 and LCMF10 were transformed upon heating from the as-prepared orthorhombic phase to a cubic phase, with a transformation temperature that slightly decreased as the dopant content increased. Additionally, both materials were stable against any sort of decomposition up to the maximum temperature of 1200 °C. The temperature dependent cell parameters, obtained by Rietveld refinement and shown in Fig. 6 (and also in Tables S7 and S8 as ESI),† revealed rather similar thermal expansion behavior. A slight decrease in the anisotropy as the dopant concentration increased was observed. Moreover, the apparent thermal expansion of both materials notably increased upon transformation to the cubic phase. As shown below, the cubic phase undergoes a reduction more readily than the lower symmetry phases. The enhanced expansion of this phase presumably reflects the contribution of chemical expansion. | ||
| Fig. 6 Temperature dependence of the lattice parameters of (a) LCFM5 and (b) LCFM10 under an inert atmosphere (30 ml min−1 N2 and pO2 ∼ 0.001 atm). | ||
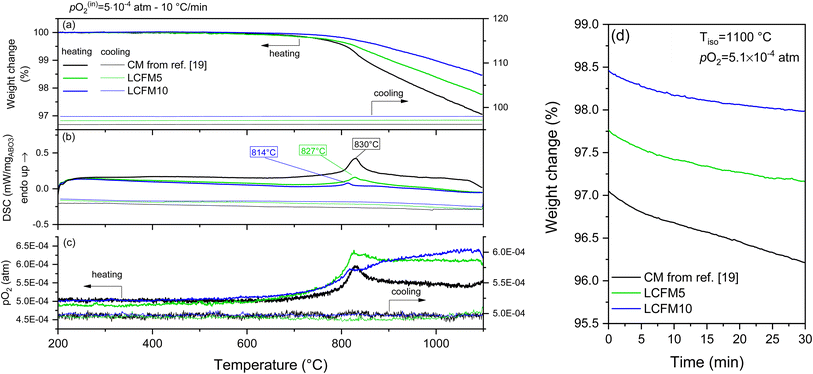
Reported in Fig. 7 and 8 are the simultaneous thermal analysis profiles for the (LaxCa1−x)(FexMn1−x)O3 materials. As indicated above, these were performed at a relatively high ramp rate (10 °C min−1) and under the most oxidizing and most reducing conditions considered in this study, pO2 = 0.18 and 5.1 × 10−4 atm, respectively. To highlight the role of the dopants, the profiles measured for CaMnO3 (CM) from our previous study24 are included in the figures.
 | ||
| Fig. 7 TGA/DSC profiles of CM,24 LCMF5, and LCMF10 on heating and cooling to 1100 °C at a ramp rate of 10 °C min−1 under a pO2 of 0.18 atm: (a) mass, (b) DSC, and (c) pO2 profiles as functions of temperature. (d) Mass evolution during 2 h isothermal hold at 1100 °C applied between heating and cooling steps. | ||
 | ||
| Fig. 8 TGA/DSC profiles of CM,24 LCMF5, and LCMF10 on heating and cooling to 1100 °C at a ramp rate of 10 °C min−1 under a pO2 of 5.1 × 10−4 atm: (a) mass, (b) DSC, and (c) pO2 profiles as functions of temperature. (d) Mass evolution during 30 min isothermal hold at 1100 °C applied between heating and cooling steps. | ||
The thermal profiles reveal anomalies that agree with the phase transitions recorded by XRD. Specifically, transformations from the low-temperature orthorhombic distortion to the cubic aristotype are observed. A tetragonal distortion appears at intermediate temperatures depending on composition and oxygen partial pressure.49 In general, the same behavior is observed by decreasing the oxygen partial pressure or introducing the dopants. Namely, the transition temperatures shift downwards, the heat of the transition decreases, and the thermal window of the intermediate tetragonal phase is narrowed (Fig. S9 and Table S6 in the ESI†). The absence of the tetragonal phase in the XRD results (Fig. 5) is related to the lower oxygen partial pressure condition of the diffraction study.
Under pO2 = 0.18 atm, as shown in Fig. 7 (the higher oxygen partial pressure conditions), the phase transformations were reversible, with only a slight hysteresis for the reverse transformation temperature evident for the doped compositions. Moreover, no change in mass was recorded during the isothermal hold at the highest measurement temperature of 1100 °C, and the mass profiles obtained on cooling exactly overlapped those recorded on heating. This behavior indicates that the materials remained in equilibrium throughout the experiment. In contrast, in the measurement at lower oxygen partial pressure (pO2 = 5.1 × 10−4 atm, Fig. 8), mass loss occurred during the isothermal hold at 1000 °C, and the masses did not return to their initial values upon cooling. These features, along with the absence of the thermal signatures of the reverse transitions, indicate that equilibrium was not maintained over the course of the measurement. The out-of-equilibrium behavior is likely a reflection of insufficient gas flow to remove evolved oxygen on heating and provide oxygen on cooling, as discussed elsewhere,50 rather than slow surface reaction kinetics or oxygen diffusion. Additional notable features of the thermal behavior are as follows: (i) a decline in high-temperature mass loss as the dopant concentration increases and (ii) an increase in mass loss upon transformation to the cubic phase. In undoped CaMnO3, the transition to the cubic phase occurs with a detectable step change in oxygen content under both measurement conditions. The transition is furthermore accompanied by a transient increase in oxygen partial pressure in the experiment performed under an inlet oxygen partial pressure of pO2 = 5.1 × 10−4 atm (Fig. 8), with similar but less pronounced effects evident for both LCMF5 and LCMF10. The absence of a similar feature in the oxygen partial pressure profiles under the higher pO2 condition (Fig. 7) indicates a marginal increase in oxygen content in the gas phase because the release from the solid is small relative to the oxygen content in the inlet gas supply.
Thermodynamic evaluation
The oxygen non-stoichiometry (δ) profiles obtained from the thermogravimetric analysis experiments with pO2 ≥ 0.008 atm are summarized in Fig. 9. At each pO2 shown, the heating (solid lines) and cooling (dashed lines) curves almost perfectly overlap, indicating that equilibrium behavior was recorded at a moderate heating/cooling rate of 5 °C min−1 used in these experiments. Moreover, the oxygen sensor recorded negligible variations of pO2 during the experiments (Fig. S10 in ESI†). In contrast, at pO2 = 0.004 atm, the heating and cooling profiles showed detectable disagreement (Fig. S11 in ESI†), indicating non-equilibrium behavior. Accordingly, this profile was omitted from the subsequent thermodynamic analysis. To permit experimental assessment of the mass loss behavior under this low oxygen partial pressure condition, additional measurements were performed in which the LCMF5 and LCMF10 samples were allowed to equilibrate at 1200 °C under a pO2 of 0.004 atm for 1 h (the single-filled symbol in each panel). A significant feature of all the mass loss (and hence non-stoichiometry) profiles is the evidence of discontinuity at the crystallographic phase transition(s). This effect, which is particularly pronounced in undoped CaMnO3,24 reflects the difference between the maximum δ in the orthorhombic phase and the minimum δ in the higher temperature phase (either tetragonal or cubic) at the pO2 of the measurement. | ||
Fig. 9 Absolute oxygen non-stoichiometry as a function of the temperature of (a) LCFM5 and (b) LCFM10 measured under six oxygen partial pressures. Solid (heating) and dashed (cooling) lines and filled symbol ( ) are measured values of δ data. Open symbols are calculated from the thermodynamic functions shown in Fig. 11. ) are measured values of δ data. Open symbols are calculated from the thermodynamic functions shown in Fig. 11. | ||
The temperature span over which the discontinuity appears reflects finite kinetics and precludes access to material nonstoichiometry over a small temperature window following the transition. Stability (pO2 − 1/T) and schematic phase (T − δ) diagrams generated from the analysis of the thermogravimetric profiles are presented in the ESI (Fig. S12 and S13†). Overall, high temperature and low oxygen partial pressure conditions favor the cubic phase. The orthorhombic phase is favored at low temperatures and high oxygen partial pressures. Moreover, the influence of co-doping CaMnO3 with Fe and La resembles that observed upon doping with either species independently. For example, the tetragonal perovskite phase is absent in both LCMF10 and 10% Fe-doped CaMnO3. The fundamental reasons that La and Fe doping shift the stability regions of the various crystallographic phases are yet unknown.
The non-stoichiometry profiles, δ(T), obtained from the thermogravimetry experiments, were used to determine the relative partial molar enthalpy and relative partial molar entropy of oxygen in the solid as a function of δ based on the van't Hoff approach,51 where the enthalpy term is required for computing the heat storage capacity based on eqn (2). In brief, at the limit of an infinitesimal extent of oxidation, δi → δf, the chemical activities of ABO3−δi and ABO3−δf become equal, and the equilibrium constant for this infinitesimal oxidation is
Koxd = ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) O2−1/2 = e−ΔoxdḠ0/RT, O2−1/2 = e−ΔoxdḠ0/RT, | (4) |
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) O2 is the oxygen pressure relative to the reference state of 1 atm (numerically identical to the oxygen partial pressure, pO2) and ΔoxdḠ0 is the standard Gibbs energy of oxidation per mole O. The latter is exactly equal to the relative oxygen chemical potential, implying that
O2 is the oxygen pressure relative to the reference state of 1 atm (numerically identical to the oxygen partial pressure, pO2) and ΔoxdḠ0 is the standard Gibbs energy of oxidation per mole O. The latter is exactly equal to the relative oxygen chemical potential, implying thatΔoxdḠ0(δ) = Δ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0O(δ) = Δ 0O(δ) = Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) − TΔ 0O(δ) − TΔ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 0O(δ) 0O(δ) | (5) |
and that the relative partial molar enthalpy and entropy of oxygen are respectively equivalent to the enthalpy and entropy of the oxidation reaction given in eqn (1), which is, in turn, equal to the negatives of the respective reduction terms. Eqn (4) can be written in Arrhenius form:
 | (6) |
Thus, from the slopes and intercepts of plots of ln(pO2) vs. 1/T for each δ, the relative partial molar enthalpy (Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O (kJ molO−1)) and relative partial molar entropy (Δ
0O (kJ molO−1)) and relative partial molar entropy (Δ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 0O (J molO K−1)) of oxygen can be extracted, respectively, as functions of δ.
0O (J molO K−1)) of oxygen can be extracted, respectively, as functions of δ.
The iso-stoichiometric data of the (LaxCa1−x)(FexMn1−x)O3 materials, along with the linear fits (R2 > 0.99), are presented in Arrhenius form, as illustrated in Fig. 10. Because of the continuous nature of the measured δ(T) profiles, it was possible to determine the temperature at which any given δ is adopted by the material under peach pO2 condition. Hence, a set of six (pO2, T) pairs are available for each arbitrarily selected δ within the measurement range and single phase region. Furthermore, the data summary presented in Fig. 10 emphasizes that the phase boundaries do not occur at fixed δ but rather at δ values that vary with and are determined by T and pO2, as shown in Fig. S13.† To avoid the influence of experimental artifacts at large δ at which fewer data are available, the enthalpy in the large δ region was fixed at the value obtained from the analysis of the Arrhenius line at the largest δ with five (pO2, T) pairs.
Extracted enthalpy (Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) (kJ molO−1)) and entropy (TΔ
0O(δ) (kJ molO−1)) and entropy (TΔ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) 0O(δ) (J molO K−1)) functions of the (LaxCa1−x)(FexMn1−x)O3 materials are depicted in Fig. 11, along with those of undoped CaMnO3.24 The insensitivity of Δ
0O(δ) (J molO K−1)) functions of the (LaxCa1−x)(FexMn1−x)O3 materials are depicted in Fig. 11, along with those of undoped CaMnO3.24 The insensitivity of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) to δ beyond δ ≈ 0.08 is immediately evident, justifying the use of a fixed Δ
0O(δ) to δ beyond δ ≈ 0.08 is immediately evident, justifying the use of a fixed Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O in the high δ region of ≥0.13. Overall, the data reveal that simultaneous doping by La and Fe increases the magnitude of the enthalpy in both the orthorhombic and cubic phases, albeit to a moderate extent, while expanding the compositional window of the cubic phase. Similar behavior was observed for singly doped materials.24,38 The results agree with the literature observations that La doping increases the enthalpy in variable valence perovskites. Somewhat surprisingly, co-doping with 10% of the dopants on both the A and B sites results in an enthalpy that is intermediate between that obtained by doping at the 10% level on either site alone. This is evident from the comparison of Δ
0O in the high δ region of ≥0.13. Overall, the data reveal that simultaneous doping by La and Fe increases the magnitude of the enthalpy in both the orthorhombic and cubic phases, albeit to a moderate extent, while expanding the compositional window of the cubic phase. Similar behavior was observed for singly doped materials.24,38 The results agree with the literature observations that La doping increases the enthalpy in variable valence perovskites. Somewhat surprisingly, co-doping with 10% of the dopants on both the A and B sites results in an enthalpy that is intermediate between that obtained by doping at the 10% level on either site alone. This is evident from the comparison of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ = 0.10) presented in Fig. 11c. Thus, the impacts of doping on the energetics are not additive, and for the materials compared, the highest enthalpy is obtained from 10% La-doped CaMnO3. The differences in the entropies of the materials are significantly smaller (Fig. S14†), indicating that the co-doping strategy with equal A and B site dopant concentrations was successful in retaining a large magnitude of Δ
0O(δ = 0.10) presented in Fig. 11c. Thus, the impacts of doping on the energetics are not additive, and for the materials compared, the highest enthalpy is obtained from 10% La-doped CaMnO3. The differences in the entropies of the materials are significantly smaller (Fig. S14†), indicating that the co-doping strategy with equal A and B site dopant concentrations was successful in retaining a large magnitude of Δ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 0O. At δ = 0.10, the values for the undoped and doubly doped materials range from 123 to 129 J molO K−1. The increasing magnitude of enthalpy with increasing co-doping levels largely explains the monotonic decrease in reducibility from CaMnO3 to LCFM5 to LCFM10 (Fig. 7 and 8). The slightly enhanced magnitude of the entropy of LCFM5 also contributes to the reducibility of this material.
0O. At δ = 0.10, the values for the undoped and doubly doped materials range from 123 to 129 J molO K−1. The increasing magnitude of enthalpy with increasing co-doping levels largely explains the monotonic decrease in reducibility from CaMnO3 to LCFM5 to LCFM10 (Fig. 7 and 8). The slightly enhanced magnitude of the entropy of LCFM5 also contributes to the reducibility of this material.
 | ||
| Fig. 11 Thermodynamic properties of CM,24 LCFM5, and LCFM10: (a) relative partial molar enthalpy and (b) relative partial molar entropy of oxygen as functions of δ; and (c) comparison of relative partial molar enthalpy of oxygen in selected doped compositions at δ = 0.10, where CFM10 (ref. 24) is CaFe0.10Mn0.90O2.95−δ, and LCM10 (ref. 38) is La0.1Ca0.9MnO3−δ. | ||
Discussion: heat storage capacity
The calculation of the heat storage capacity according to eqn (2) requires the knowledge of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) over the δ range spanning from δi (charged state) to δf (discharged state). From the XRD study, it was shown that LCFM5 and LCFM10 are both stable at T = 1200 °C and pO2 = 0.001 atm (Fig. 5), a more reducing condition than included in the TGA studies. To enable the estimation of the heat storage capacity for charging under these technologically viable and attractive conditions, the Δ
0O(δ) over the δ range spanning from δi (charged state) to δf (discharged state). From the XRD study, it was shown that LCFM5 and LCFM10 are both stable at T = 1200 °C and pO2 = 0.001 atm (Fig. 5), a more reducing condition than included in the TGA studies. To enable the estimation of the heat storage capacity for charging under these technologically viable and attractive conditions, the Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) and Δ
0O(δ) and Δ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) 0O(δ) functions were extrapolated to large δ assuming fixed values for the enthalpy and linear behavior in the entropy beyond δ = 0.1959 for LCFM5 and beyond δ = 0.1482 for LCFM10. Using these expanded functions, respective δi values of 0.291 and 0.228 were computed (for the charging conditions, T = 1200 °C and pO2 = 0.001 atm). The validity of these extrapolations to larger δ is supported by the agreement of the computed and measured (equilibrium) nonstoichometry at pO2 = 0.004 and T = 1200 °C in Fig. 9, where the predicted curves based on both pO2 = 0.004 and 0.001 atm are shown in their entirety. Additionally, for both materials, the calculated δ(T) profiles at 0.004 atm almost perfectly overlap with the experimental curves (Fig. S11 in ESI†), which show only slight disagreement between the heating and cooling regimes.
0O(δ) functions were extrapolated to large δ assuming fixed values for the enthalpy and linear behavior in the entropy beyond δ = 0.1959 for LCFM5 and beyond δ = 0.1482 for LCFM10. Using these expanded functions, respective δi values of 0.291 and 0.228 were computed (for the charging conditions, T = 1200 °C and pO2 = 0.001 atm). The validity of these extrapolations to larger δ is supported by the agreement of the computed and measured (equilibrium) nonstoichometry at pO2 = 0.004 and T = 1200 °C in Fig. 9, where the predicted curves based on both pO2 = 0.004 and 0.001 atm are shown in their entirety. Additionally, for both materials, the calculated δ(T) profiles at 0.004 atm almost perfectly overlap with the experimental curves (Fig. S11 in ESI†), which show only slight disagreement between the heating and cooling regimes.
Integration of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) was performed by assuming linear interpolation between measured data points, including across the phase transition, and by assuming linear extrapolation in the orthorhombic regime to zero δ. This conservative approach ignores the contributions to heat storage resulting from the phase transition. Fig. 12 depicts the resulting mass-normalized heat storage capacity (QM) curves:
0O(δ) was performed by assuming linear interpolation between measured data points, including across the phase transition, and by assuming linear extrapolation in the orthorhombic regime to zero δ. This conservative approach ignores the contributions to heat storage resulting from the phase transition. Fig. 12 depicts the resulting mass-normalized heat storage capacity (QM) curves:
 | (7) |
| QV(δi) = QM·ρ. | (8) |
The data illustrated in Fig. 12 reveal that, for a given Δδ, LCFM5 and LCFM10 provide similar chemical heat storage capacity. This is because the higher enthalpy of LCFM10 at high and very low δ is compensated for by the lower enthalpy at intermediate δ. The maximum attainable heat storage capacity, however, is higher for LCFM5 (378.5 ± 1.0 kJ kgABO3−1) than for LCFM10 (282.3 ± 1.5). This occurs because the latter has slightly higher entropy and slightly lower enthalpy in the high δ region, which translates into a substantially larger extent of reduction.
Heat storage in TES reactors is controlled by adjusting the temperature and gas conditions of the heat storage steps rather than controlling the nonstoichiometry values adopted by a material. Accordingly, Fig. 13 illustrates the heat storage capacities of LMFC5 and LMFC10 as functions of temperature at given pO2 values. Thus, QM is computed by integration based on eqn (2) using integration limits implied by δi = δ (T, pO2 = pO2fixed) and δf = δ (T = 700 °C and pO2 = pO2fixed), where pO2fixed is the same on charging and discharging. The representation here highlights the advantages offered by LMFC5 over LMFC10 already noted above, with the energy storage capacity of LMFC5 being greater than that of LMFC10 at all charging temperatures.
The impacts of doping by the co-doping single-site doping strategies on the heat storage capacity of lightly doped CaMnO3 materials are summarized in Fig. 14 and Table S9† for the operating conditions pO2 = 0.008 atm and Tdis = 700 °C. Undoped CaMnO3 is inherently attractive for heat storage, but as already noted, its poor high-temperature stability limits its capacity. Of the doped compositions, the previously developed material CaMn0.9Fe0.1O2.95−δ (CMF10)24 and the new material La0.05Ca0.95Fe0.05Mn0.95O3−δ (LCFM5), which displays similar relative partial molar enthalpies (Fig. 11c), attain the highest (and comparable) heat storage capacities. Significantly, the materials with the largest relative partial molar enthalpy amongst this group, LCM10 (ref. 38) and LCFM10 (Fig. 11c), exhibit diminished heat storage capacities. As discussed above, in the context of LCFM10, the large enthalpy value diminishes the extent of reduction under the charge condition. Thus, the chemical heat storage capacity does not simply scale with the enthalpy of the oxidation reaction. Design strategies that focus solely on increasing the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) in variable valence oxides is unlikely to achieve materials with a high heat storage capacity. Furthermore, co-doping has produced materials with properties comparable to those of the singly doped analogs. In both cases, doping increases the thermal stability and the enthalpy without a negative impact on the entropy, with light doping providing an optimal, intermediate value of enthalpy.
0O(δ) in variable valence oxides is unlikely to achieve materials with a high heat storage capacity. Furthermore, co-doping has produced materials with properties comparable to those of the singly doped analogs. In both cases, doping increases the thermal stability and the enthalpy without a negative impact on the entropy, with light doping providing an optimal, intermediate value of enthalpy.
 | ||
| Fig. 14 Comparison of LCFM5 and LCFM10 with previously investigated compositions CM, CMF10 and LCM10 under similar operating conditions (pO2 = 0.008 atm, Tdis = 700 °C, and Tch = 1200 °C). | ||
Overall, the properties of LCMF5 (and CMF10) are very attractive for incorporation into CSP plants. Owing to favorable operating conditions and the earth's abundance of constituent elements, the implementation of heat storage using these materials can be expected to lower the cost of CSP operation. In comparison to other CaMnO3-derived materials, including those doped with Al, Ti, Co and Sr,22,23,37,52 these compounds enable operation at higher temperatures and more moderate pO2 for a comparable, and in some cases higher, level of heat storage. The SrMO3−δ (M = Co, Fe, and Mn)53 series of perovskites have also been evaluated for chemical heat storage but can only operate in a limited temperature range of 500–1000 °C. Other investigated doped redox systems, namely LaxSr1−x(Mn,Fe,Co)O3−δ,54 and BaySr1−yCoO3−δ,54 show lower heat storage capacity than LCFM5 (and CMF10). Stoichiometric metal oxides,55 such as Co3O4/CoO (844 kJ kg−1),56 BaO2/BaO (474 kJ kg−1)57 and Mn2O3/Mn3O4 (202 kJ kg−1),58 offer higher gravimetric energy storage capacity, but as noted above, the redox reactions of these materials are discrete. Consequently, heat release is limited to the specific temperature of the reaction, which in many instances is lower than desirable. The perovskites investigated herein offer greater flexibility and access to higher temperatures of heat storage.
The volumetric heat storage density achieved by chemical redox with LCFM5 (under a pO2 of 0.001 atm) reaches ∼500 kW h m3 (Fig. 13). Such a storage capacity, which does not include the additional sensible heat storage capacity of the perovskite, exceeds that of several TES technologies employed in CSP plants for heat storage at high temperatures. For example, sensible heat storage systems offer only 70–210 kW h m−3 storage capacity and are further limited by low thermal conductivity.59 Molten salts, though somewhat higher in storage capacity (∼400 kW h m−3), still do not achieve the capacity of LCFM5 and further suffer from operability in a limited temperature range (between their melting point and decomposition temperature) and the severe risk of loss of material due to leakage.59
Conclusions
In this study, La and Fe co-doped CaMnO3 (x = 0.05 and 0.10 in compositions (LaxCa1−x)(FexMn1−x)O3) indicate that many of the features of the co-doped materials are similar to those of the singly doped materials. The structures of the co-doped materials are orthorhombic under ambient conditions, crystallizing in the GdFeO3-type perovskite distortion, with Fe entirely in the 3+ oxidation state and Mn entirely in the 4+ state. Co-doping shifts the orthorhombic to cubic transition to a lower temperature, narrows the stability range of the intermediate tetragonal phase, and stabilizes the perovskite against decomposition into spinel and Ruddlesden–Popper phases to at least 1200 °C. XANES studies confirm that Fe and Mn are always found in the +3 and +4 oxidation states, respectively, under as-synthesized conditions, whereas EXAFS reveals the insertion of these cations in octahedral B sites. The enthalpy of reduction generally increases with the co-doping level in both the orthorhombic and cubic phases, albeit to a moderate extent, and not at all values of δ. The tetragonal phase, which exists only over a very narrow window, could not be fully characterized. For a given change in non-stoichiometry, Δδ, LCFM5 [(La0.05Ca0.95)(Fe0.05Mn0.95)O3−δ] and LCFM10 [(La0.1Ca0.9)(Fe0.1Mn0.9)O3−δ] provide similar chemical heat storage capacities. This is because the higher enthalpy of LCFM10 at high and very low δ is compensated for by a lower enthalpy at intermediate δ. The maximum attainable heat storage capacity, however, is substantially higher for LCFM5 (378.5 ± 1.0 kJ kgABO3−1) compared to 282.3 ± 1.5 for LCFM10. This apparent contradiction arises because the slightly higher entropy and slightly lower enthalpy of LCFM5 in the high δ region translate into a substantially larger extent of reduction. This observation indicates that design strategies focus solely on increasing the magnitude of Δ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0O(δ) in variable valence oxides, without considering the impacts on the extent of reduction, is unlikely to produce materials with a high heat storage capacity. The intermediate value of the reduction enthalpy of LCFM5, along with its high stability, and earth-abundant constituent elements, render it an attractive material for further evaluation in TCS applications.
0O(δ) in variable valence oxides, without considering the impacts on the extent of reduction, is unlikely to produce materials with a high heat storage capacity. The intermediate value of the reduction enthalpy of LCFM5, along with its high stability, and earth-abundant constituent elements, render it an attractive material for further evaluation in TCS applications.
Author contributions
Emanuela Mastronardo: conceptualization, investigation, writing-review & editing, funding acquisition. Xin Qian: investigation. Juan M. Coronado: supervision, writing-review & editing, funding acquisition. Sossina M. Haile: supervision, writing-review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement No. 74616. Support of the US Department of Energy, Office of Energy Efficiency and Renewable Energy, Award DE-EE0008089.0000, and ACES2030 from “Comunidad de Madrid” and European Structural Funds to (P2018/EMT-4319) are also fully acknowledged. This work made use of the Jerome B. Cohen X-Ray Diffraction Facility at the Materials Research Center at Northwestern University supported by the National Science Foundation MRSEC program (DMR-1720139) and the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205). Metal analysis was performed at the Northwestern University Quantitative Bio-element Imaging Center (QBIC). This work additionally made use of the DuPont-Northwestern-Dow Collaborative Access Team (DND-CAT) located at Sector 5 of the Advanced Photon Source (APS) supported by Northwestern University, The Dow Chemical Company, and DuPont de Nemours, Inc. The APS is a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The authors acknowledge Jerrold A. Carsello, Manager of X-Ray Diffraction Facilities at the Materials Research Center at Northwestern University, for his assistance on XRD analysis, Rebecca A. Sponenburg, Assistant Core Scientist at the Northwestern University Quantitative Bio-element Imaging Center (QBIC), for her support on ICP-OES analysis, Dr Qing Ma, Research Scientist at Advanced Photon Source (APS), for his assistance in XAS analysis, Dr Ana Iglesias-Juez, Researcher at the Institute of Catalysis and Petrochemistry of CSIC, for fruitful discussions of the XAS data. Dr Weizi Yuan and graduate student Elise Goldfine are also gratefully acknowledged for their support on XAS data analysis software.References
- United Nations – Sustainable Development, https://sdgs.un.org/ Search PubMed.
- A. Boretti, S. Castelletto and S. Al-Zubaidy, Nonlinear Eng., 2019, 8, 10–31 Search PubMed.
- L. A. Weinstein, J. Loomis, B. Bhatia, D. M. Bierman, E. N. Wang and G. Chen, Chem. Rev., 2015, 115, 12797–12838 CrossRef CAS PubMed.
- A. Javanshir, N. Sarunac and Z. Razzaghpanah, Energy Convers. Manage., 2018, 163, 428–443 CrossRef CAS.
- U. Pelay, L. Luo, Y. Fan, D. Stitou and M. Rood, Renewable Sustainable Energy Rev., 2017, 79, 82–100 CrossRef.
- Global Energy Observatory: Information on Global Energy Systems and Infrastructure, https://globalenergyobservatory.org/docs/AboutUs.php Search PubMed.
- U. Pelay, L. Luo, Y. Fan, D. Stitou and M. Rood, Data Brief, 2017, 13, 597–599 CrossRef.
- C. Li, Q. Li and Y. Ding, Renewable Energy, 2019, 140, 140–151 CrossRef CAS.
- J. Yan, C. Y. Zhao, B. Q. Xia and T. Wang, Energy, 2019, 186, 115837 CrossRef CAS.
- E. Piperopoulos, E. Mastronardo, M. Fazio, M. Lanza, S. Galvagno and C. Milone, Appl. Energy, 2018, 215, 512–522 CrossRef CAS.
- P. Feng, Y. Liu, I. Ayub, Z. Wu, F. Yang and Z. Zhang, Energy Convers. Manage., 2018, 174, 239–247 CrossRef CAS.
- C. Agrafiotis, T. Block, M. Senholdt, S. Tescari, M. Roeb and C. Sattler, Solar Energy, 2017, 149, 227–244 CrossRef CAS.
- A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, AIP Conf. Proc., 2016, 1734, 3–11 CrossRef.
- C. Prieto, P. Cooper, A. I. Fernández and L. F. Cabeza, Renewable Sustainable Energy Rev., 2016, 60, 909–929 CrossRef CAS.
- C. K. Yang, Y. Yamazaki, A. Aydin and S. M. Haile, J. Mater. Chem. A, 2014, 2, 13612–13623 RSC.
- M. Ezbiri, K. M. Allen, M. E. Gàlvez, R. Michalsky and A. Steinfeld, ChemSusChem, 2015, 8, 1966–1971 CrossRef CAS PubMed.
- A. H. McDaniel, E. C. Miller, D. Arifin, A. Ambrosini, E. N. Coker, R. O'Hayre, W. C. Chueh and J. Tong, Energy Environ. Sci., 2013, 6, 2424–2428 RSC.
- B. Bulfin, J. Vieten, D. E. Starr, A. Azarpira, C. Zachäus, M. Hävecker, K. Skorupska, M. Schmücker, M. Roeb and C. Sattler, J. Mater. Chem. A, 2017, 5, 7912–7919 RSC.
- J. Vieten, B. Bulfin, M. Senholdt, M. Roeb, C. Sattler and M. Schmücker, Solid State Ionics, 2017, 308, 149–155 CrossRef CAS.
- M. T. Azcondo, M. Orfila, M. Linares, R. Molina, J. Marugán, U. Amador, K. Boulahya, J. Á. Botas and R. Sanz, ACS Appl. Energy Mater., 2021, 4, 7870–7881 CrossRef CAS.
- X. Qian, S. M. Haile, T. C. Davenport and E. Mastronardo, J. Am. Ceram. Soc., 2022, 105, 4375–4386 CrossRef CAS.
- S. M. Babiniec, E. N. Coker, J. E. Miller and A. Ambrosini, Int. J. Energy Res., 2015, 6–10 Search PubMed.
- L. Imponenti, K. J. Albrecht, J. W. Wands, M. D. Sanders and G. S. Jackson, Solar Energy, 2017, 151, 1–13 CrossRef CAS.
- E. Mastronardo, X. Qian, J. M. Coronado and S. M. Haile, J. Mater. Chem. A, 2020, 8, 8503–8517 RSC.
- A. M. Deml, V. Stevanović, A. M. Holder, M. Sanders, R. Ohayre and C. B. Musgrave, Chem. Mater., 2014, 26, 6595–6602 CrossRef CAS.
- J. Nowotny and M. Rekas, J. Am. Ceram. Soc., 1998, 81, 67–80 CrossRef CAS.
- C. Yang, J. Shen, C. Wang, H. Fei, H. Bao and G. Wang, J. Mater. Chem. A, 2014, 2, 1458–1464 RSC.
- M. Pavone, A. B. Muñoz-García, A. M. Ritzmann and E. A. Carter, J. Phys. Chem. C, 2014, 118, 13346–13356 CrossRef CAS.
- M. J. Ignatowich, A. H. Bork, T. C. Davenport, J. L. M. Rupp, C. K. Yang, Y. Yamazaki and S. M. Haile, MRS Commun., 2017, 7, 873–878 CrossRef CAS.
- C. Yang and A. Grimaud, Catalysts, 2017, 7, 149 CrossRef.
- X. Qian, J. He, E. Mastronardo, B. Baldassarri, W. Yuan, C. Wolverton and S. M. Haile, Matter, 2021, 4, 688–708 CrossRef CAS.
- X. Qian, J. He, E. Mastronardo, B. Baldassarri, C. Wolverton and S. M. Haile, Chem. Mater., 2020, 32, 9335–9346 CrossRef CAS.
- D. Maiti, Y. A. Daza, M. M. Yung, J. N. Kuhn and V. R. Bhethanabotla, J. Mater. Chem. A, 2016, 4, 5137–5148 RSC.
- A. M. Deml, V. Stevanović, A. M. Holder, M. Sanders, R. Ohayre and C. B. Musgrave, Chem. Mater., 2014, 26, 6595–6602 CrossRef CAS.
- Q. Ji, L. Bi, J. Zhang, H. Cao and X. S. Zhao, Energy Environ. Sci., 2020, 13, 1408–1428 RSC.
- M. Ezbiri, M. Takacs, D. Theiler, R. Michalsky and A. Steinfeld, J. Mater. Chem. A, 2017, 5, 4172–4182 RSC.
- F. Jin, C. Xu, H. Yu, X. Xia, F. Ye, X. Li, X. Du and Y. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 3856–3866 CrossRef CAS PubMed.
- E. Mastronardo, X. Qian, J. M. Coronado and S. M. Haile, J. Energy Storage, 2021, 40, 102793 CrossRef.
- J. Mizusaki, H. Tagawa, K. Naraya and T. Sasamoto, Solid State Ionics, 1991, 49, 111–118 CrossRef CAS.
- B. H. Toby and R. B. von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- International X-ray Absorption Society – XAFS database, https://ixs.iit.edu/database/ Search PubMed.
- D. N. Mueller, R. A. de Souza, H. I. Yoo and M. Martin, Chem. Mater., 2012, 24, 269–274 CrossRef CAS.
- E. S. Božin, A. Sartbaeva, H. Zheng, S. A. Wells, J. F. Mitchell, T. Proffen, M. F. Thorpe and S. J. L. Billinge, J. Phys. Chem. Solids, 2008, 69, 2146–2150 CrossRef.
- T. Yamamoto, X-Ray Spectrom., 2008, 37, 572–584 CrossRef CAS.
- B. Ravel, E. A. Stern, R. I. Vedrinskii and V. Kraizman, Ferroelectrics, 1998, 206–207, 407–430 CrossRef CAS.
- O. Haas, U. F. Vogt, C. Soltmann, A. Braun, W. S. Yoon, X. Q. Yang and T. Graule, Mater. Res. Bull., 2009, 44, 1397–1404 CrossRef CAS.
- C. Gökhan Ünlü, M. Burak Kaynar, T. Şimşek, A. Tekgül, B. Kalkan and Ş. Özcan, J. Alloys Compd., 2019, 784, 1198–1204 CrossRef.
- E. I. Leonidova, I. A. Leonidov, M. v Patrakeev and V. L. Kozhevnikov, J. Solid State Electrochem., 2011, 1071–1075 CrossRef CAS.
- T. C. Davenport, M. Kemei, M. J. Ignatowich and S. M. Haile, Int. J. Hydrogen Energy, 2017, 42, 16932–16945 CrossRef CAS.
- Y. Hao, C. K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- L. Imponenti, K. J. Albrecht, R. Kharait, M. D. Sanders and G. S. Jackson, Appl. Energy, 2018, 230, 1–18 CrossRef CAS.
- X. Chen, M. Kubota, S. Yamashita and H. Kita, J. Energy Storage, 2021, 38, 102501 CrossRef.
- N. Gokon, T. Yawata, S. Bellan, T. Kodama and H. S. Cho, Energy, 2019, 171, 971–980 CrossRef CAS.
- A. Bayón, A. J. Carrillo, E. Mastronardo and J. M. Coronado, in Advances in Chemical Engineering, ed. W. Lipiński, Elsevier Inc., 2021, vol. 58, pp. 247–295 Search PubMed.
- C. Agrafiotis, M. Roeb and C. Sattler, Solar Energy, 2016, 139, 695–710 CrossRef CAS.
- A. J. Carrillo, D. Sastre, D. P. Serrano, P. Pizarro and J. M. Coronado, Phys. Chem. Chem. Phys., 2016, 18, 8039–8048 RSC.
- A. J. Carrillo, D. P. Serrano, P. Pizarro and J. M. Coronado, J. Mater. Chem. A, 2014, 2, 19435–19443 RSC.
- A. K. Ray, D. Rakshit and K. Ravikumar, Cleaner Engineering and Technology, 2021, 4, 100155 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta07779e |
| This journal is © The Royal Society of Chemistry 2023 |