 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Water uptake kinetics and electrical transport in BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Tb, Pr, Fe) protonic conductors
Jagoda
Budnik
*,
Aleksandra
Mielewczyk-Gryń
,
Maria
Gazda
and
Tadeusz
Miruszewski
*
Institute of Nanotechnology and Materials Engineering and Advanced Materials Centre Gdańsk University of Technology, Narutowicza 11/12, 80-233, Gdańsk, Poland. E-mail: jagoda.budnik@pg.edu.pl; tadeusz.miruszewski1@pg.edu.pl
First published on 24th April 2023
Abstract
BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Fe, Pr, Tb) is a mixed conducting oxide in which three mobile charge carriers – oxygen ion, electron/hole, and protonic defects – are present. These types of materials have gained much interest as electrode materials for protonic ceramic fuel cells (PCFCs) and protonic ceramic electrolysis cells (PCECs). In this study, the water uptake and oxygen transport properties of different BaCe0.6Zr0.2Y0.1M0.1O3−δ samples were investigated at different pH2O using Thermogravimetry (TG) and Electrical Conductivity Relaxation (ECR) methods at various temperatures. TG results showed that in all samples the mass increases during the switch from dry to wet atmospheres, which indicates proton incorporation into the materials. The kinetics of the water uptake process differed depending on the type of substituent used. The studies of pO2 dependence of total conductivity allowed for the determination of partial conductivities in BaCe0.6Zr0.2Y0.1Tb0.1O3−δ (BCZYTb), which shows a predominant p-type conduction mechanism above 600 °C. The electrical conductivity relaxation (ECR) studies performed for a chosen BCZYTb sample have shown that the hydration/dehydration processes were asymmetric two-fold, whereas the oxidation/reduction processes had typical single-fold kinetics. Furthermore, a significant influence of pH2O on the oxidation and reduction kinetics was observed.
Introduction
Proton-conducting materials have been the subject of intense research because of their potential application in electrochemical devices. In particular, triple conducting oxides (TCOs) have gained much interest in the field of solid-state ionics, as they can conduct three types of charge carriers, i.e. oxygen ions, electrons/holes, and protons, making them ideal candidates for a positrode material for protonic ceramic fuel cells (PCFCs).1 The complex nature of the diffusion and electrical transport mechanisms involved in the proton conductivity in TCOs is still unclear and requires a comprehensive description, which may enable the proper design of new electroceramic materials with suitable properties.2–7 One of the representative groups in the TCO family is BaCe0.6Zr0.2Y0.1M0.1O3−δ (BCZYM), where M is a mixed-valence metal. This group is based on acceptor-doped barium cerate–zirconate solid solution, which is a well-known mixed oxygen ionic-protonic conductor,8 commonly applied as an electrolyte for PCFCs.9,10 Substituting cerium/zirconium with a mixed-valence cation, e.g. cobalt,11,12 praseodymium,13 and ruthenium,14 leads to enhancing the electronic conductivity of the material.The oxygen surface exchange coefficient kchem is an important parameter in the analysis of processes like hydration or oxidation in mixed-conducting materials. Knowledge of the rate of surface exchange of oxygen gas or water molecules with mixed-conducting materials is an important factor in the understanding of many electrochemical phenomena. The kinetics of the oxygen reduction reaction (ORR) was previously studied in the case of long-term degradation in IT-SOFC cathode materials.15–17 However, the rate of oxygen exchange on the surface of mixed-conducting materials in the presence of water vapor and protonic defects needs a great deal of attention and is not yet particularly well understood.
Only a few studies in the literature have reported on the effect of a water-vapor-rich atmosphere on the surface exchange of oxygen. For example, Bucher et al.18 studied the oxygen exchange kinetics of the La0.58Sr0.4Co0.2Fe0.8O3−δ mixed conductor in dry and wet atmospheres. They performed ECR studies and found that oxygen exchange kinetics and the kchem parameter are significantly affected by water-containing atmospheres at a temperature between 600 and 700 °C, mainly due to a severe modification of the surface chemical composition (Sr-rich degraded surface shows a pronounced Si accumulation, which affected kchem). On the other hand, Solis et al.19 studied the transport properties of tungsten lanthanide LaxWO12−δ by the means of conductivity relaxation measurements and stated that oxygen diffusion is not affected by the presence of protonic defects under the studied conditions. As can be seen in the literature, different and sometimes conflicting conclusions can be found.
In this article, we study water uptake in BaCe0.6Zr0.2Y0.1M0.1O3−δ (BCZYM, where M = Fe, Pr, Tb) perovskite-based materials. Knowledge about the influence of water in the atmosphere on oxygen surface exchange in proton conducting systems is highly demanded in the scientific community. The influence of water vapor on oxidation and reduction kinetics in TCOs is still unexplored and needs to be considered in future research concerning this group of materials. The analysis of the kinetics of oxygen and water transport in oxides based on barium cerate–zirconate containing a cation substituent with variable valency has not been discussed in the literature. We have shown and described for the first time the influence of proton defects on the surface exchange of water and oxygen in BaCe0.6Zr0.2Y0.1Tb0.1O3−δ (BCZYTb). Since water vapor is always present in the atmosphere, understanding of processes occurring in oxides in the presence of water is of great importance not only for such electrochemical applications like protonic ceramic fuel cells but also in the field of photoelectrochemical CO2 reduction, water-splitting technologies, catalysis, and others. Our results obtained for BCZYTb showed the highest proton defect concentration in this compound. The transport phenomena during the hydration and dehydration processes in this family of materials were also discussed. Furthermore, the analysis of chemical surface reactions of the oxygen reduction reaction as a function of water vapor pressure in BCZYTb allowed for a better understanding of the influence of protonic defects in the structure on the oxidation/reduction reaction.
Experimental
Materials synthesis
Single-phase polycrystalline samples of BaCe0.6Zr0.2Y0.1M0.1O3−δ (BCZYM), where M = Tb, Pr, Fe, were synthesized using a two-step solid-state reaction method. Stoichiometric amounts of BaCO3, CeO2, ZrO2, Y2O3, Fe2O3, Pr6O11, and Tb4O7 were ball-milled for 12 h (450 rpm) and calcined at 950 °C for 24 h. The resulting powder was then milled again, uniaxially pressed (250 MPa) and sintered at 1300 °C for 10 h. To ensure a high density of samples, which is required for the diffusion experiments, 1 wt% NiO was added as a sintering additive in the second step of the synthesis.Since the solid-state reaction route did not allow obtaining a single-phase sample of BaCe0.6Zr0.2Y0.2O3−δ (BCZY622) reference material, a wet chemistry method was employed. The BCZY622 sample was synthesized using the coprecipitation technique. A suitable amount of (NH3)2CO3 was dissolved in water and the solution was heated to 60 °C, while being mixed by using a magnetic stirrer. Stoichiometric amounts of Ba(NO3)2, Ce(NO3)3·6H2O, Y(NO3)3·6H2O, and ZrO(NO3)2·2H2O were dissolved in water in order to obtain a solution. The concentration of nitrates and carbonate solutions was 1 mol dm−3. Then, the solution of nitrates was gradually added to the carbonate solution, until a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 volume ratio was reached. The solid product was filtered and dried at 80 °C for 24 h. The obtained material was ground in a mortar and calcined at 1000 °C for 3 h. The resulting powder was then reground with the addition of 1 wt% PVB and 1 wt% NiO and uniaxially pressed with a load of 300 MPa. The pellet was sintered at 1450 °C for 4 h.
5 volume ratio was reached. The solid product was filtered and dried at 80 °C for 24 h. The obtained material was ground in a mortar and calcined at 1000 °C for 3 h. The resulting powder was then reground with the addition of 1 wt% PVB and 1 wt% NiO and uniaxially pressed with a load of 300 MPa. The pellet was sintered at 1450 °C for 4 h.
Structural characterization
The crystal structure and phase composition of the samples were verified by X-ray diffraction (XRD) using a Phillips X'Pert Pro diffractometer. The XRD patterns were analysed using HighScore Plus XRD Analysis Software. The density of the samples was determined using the Archimedes method. All studied materials exhibited >90% of theoretical density (Table 1).| a = b = c (Å) | GOF | Relative density (%) | [OH˙] (mol mol−1) | |
|---|---|---|---|---|
| BCZY622 | 4.3522(1) | 1.94 | 97.5 | 0.095 |
| BCZYFe | 4.3205(2) | 2.33 | 90.2 | 0.007 |
| BCZYPr | 4.3517(2) | 1.81 | 94.5 | 0.010 |
| BCZYTb | 4.3379(2) | 1.88 | 99.9 | 0.028 |
Thermogravimetry analysis
To investigate the water incorporation processes in the synthesized materials, thermogravimetric (TG) experiments were conducted on a Netzsch STA 449. The sintered pellets were crushed and the resulting powders were analysed. The powders were annealed at 800 °C for 5 h in dry air (pH2O ∼ 10−5 atm) to remove water and surface carbon dioxide. The powders were then cooled to 300 °C and kept at this temperature for 2 h. After that, the dried gas (flow ≈ 30 ml min−1) was switched to humidified air (pH2O ≈ 2.3 × 10−2 atm). Each sample remained in the wet atmosphere for ≈2 h and then the gas was switched back to dry air for approximately 1 h. An analogous procedure was used in a nitrogen atmosphere. The difference between the mass recorded in the dry and wet atmospheres allowed for estimating the relative mass change.Electrical measurements
Temperature dependence of total conductivity and electrical conductivity relaxation (ECR) measurements were performed for dense samples of the material, which exhibited the highest concentration of protons (BCZYTb). Studies of the total electrical conductivity in dry and humidified air (pH2O ≈ 10−5 atm and pH2O ≈ 2.3 × 10−2 atm, respectively) were carried out using electrochemical impedance spectroscopy (EIS). For this purpose, a galvanic cell Pt/BCZYTb/Pt was studied in the temperature range of 300–800 °C.Electrical conductivity relaxation measurements
To investigate the kinetics of hydration/dehydration and oxidation/reduction, the electrical conductivity relaxation method was applied. For ECR measurements, platinum reversible electrodes were applied in a four-probe arrangement (1.9 × 14.1 × 8.2 mm3) and the sample was measured using a ProboStat™ measurement system (NorECs product, Norway). Oxygen diffusion studies were carried out in a continuous flow of gas after switching oxygen partial pressure between pO2 = 0.1 atm and pO2 = 10−3 atm both in a dry and humidified gas mixture in the temperature range of 500–800 °C. Water diffusion studies were carried out in the temperature range of 450–800 °C in synthetic air (pO2 ≈ 0.2 atm) by switching gas between dry (pH2O ≈ 10−5 atm) and wet air (pH2O ≈ 0.023 atm). We assumed that the oxygen and water concentration step time (dozens of seconds) is negligible with respect to the conductivity relaxation time within the studied temperature range.During oxygen/water incorporation and release, the conductivity changes as a result of the establishment of a new equilibrium, which affects the concentrations of charge carriers in the material. The rate of those changes differs depending on the diffusion coefficient and surface exchange coefficient of oxygen or water, respectively. Conductivity as a function of time was fitted to eqn (1) and (2), which are the solutions of Fick's 2nd law with suitable boundary conditions.20
 | (1) |
 | (2) |
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = L, β = L, | (3) |
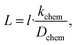 | (4) |
Results and discussion
XRD analysis
XRD data recorded at room temperature for BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Fe, Pr, Tb) samples are presented in Fig. 1. The observed diffraction reflections correspond to the perovskite phase and, in the case of the BCZYPr and BCZYTb diffraction patterns, to the nickel oxide phase (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) used for the densification of each sample. The pseudocubic unit cell parameters of the synthesized compounds refined with the Rietveld method with the corresponding GOF parameters are listed in Table 1. The Rietveld refinement was performed with the use of the crystallographic data for the cubic unit cell (Pm
m) used for the densification of each sample. The pseudocubic unit cell parameters of the synthesized compounds refined with the Rietveld method with the corresponding GOF parameters are listed in Table 1. The Rietveld refinement was performed with the use of the crystallographic data for the cubic unit cell (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) for all materials. The increasing values of unit cell parameters are consistent with the increasing ionic radii of M in that series of compounds (Fe < Tb < Pr). The unit cell parameter of BCZY622 was 4.3522(1) Å.26 It should be mentioned that the symmetry and space group of these family of materials cannot be accurately determined using the XRD method. The different symmetries in such perovskites result from minor (Ce,Zr,Y)O6 octahedral tilting, which are not readily detected by XRD. Similar phases, such as Fe-doped BCZY, Pr-doped BCZY, and Pr-doped BCY (barium cerate doped with yttrium and praseodymium), were reported in the literature to be non-cubic at room temperature.23–25
m) for all materials. The increasing values of unit cell parameters are consistent with the increasing ionic radii of M in that series of compounds (Fe < Tb < Pr). The unit cell parameter of BCZY622 was 4.3522(1) Å.26 It should be mentioned that the symmetry and space group of these family of materials cannot be accurately determined using the XRD method. The different symmetries in such perovskites result from minor (Ce,Zr,Y)O6 octahedral tilting, which are not readily detected by XRD. Similar phases, such as Fe-doped BCZY, Pr-doped BCZY, and Pr-doped BCY (barium cerate doped with yttrium and praseodymium), were reported in the literature to be non-cubic at room temperature.23–25
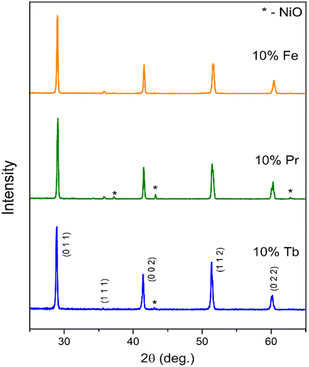 | ||
| Fig. 1 X-ray diffraction patterns recorded for BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Tb, Pr, Fe) at room temperature. | ||
Thermogravimetric analysis
Relative mass change recorded after the switch between dry and humidified air and nitrogen collected for BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Tb, Pr, Fe) and BaCe0.6Zr0.2Y0.2O3−δ at 300 °C is shown in Fig. 2. Introducing the water vapor into the atmosphere resulted in an increase in the mass of the samples. The relative mass changes in air were approximately 0.02% for the sample with Fe, 0.03% for the sample doped with Pr, and 0.08% for the sample with Tb. Thus, the highest value of proton concentration among BaCe0.6Zr0.2Y0.1M0.1O3−δ samples was obtained for the sample containing Tb; however, it was significantly lower than that of the reference BCZY622 material. It can be assumed that the only process responsible for water uptake in BCZY622 is hydration. However, in the case of the samples containing Pr, Fe, and Tb, water uptake in the air could also be realized via hydrogenation due to the possibly high concentration of electron holes in high pO2 atmospheres, such as air. In order to determine the predominant proton uptake process in those samples, additional TG measurements in nitrogen were performed. In a nitrogen atmosphere, the concentration of electron holes in investigated materials is much lower, and hence, the process of water uptake proceeds via hydration. However, although the values of mass increase were different in the two atmospheres, the shapes of the mass relaxation curves are similar. The mass increase in nitrogen was higher in the case of all samples compared to air, due to a higher concentration of oxygen vacancies filled during the hydration reaction. However, that change is not as prominent in the case of BCZYPr. It can be assumed that the nature of water uptake in both atmospheres does not change and that the protons incorporate the materials probably via the hydration process. Assuming that the only process of water uptake is hydration, the proton concentration for all samples could be determined. The calculated proton concentrations are shown in Table 1. Interestingly, after the switch from wet to dry atmospheres, the mass does not decrease notably in the case of BCZYPr and BCZYTb samples, which might indicate that the protons are stabilized inside the crystal structure and do not leave the materials during the significant decrease of pH2O. | ||
| Fig. 2 Relative mass change recorded after isothermal switch at 300 °C between dry and humidified air or nitrogen collected for BaCe0.6Zr0.2Y0.1M0.1O3−δ (M = Tb, Pr, Fe) and BaCe0.6Zr0.2Y0.2O3−δ. | ||
The time derivative of the TG signal collected in air is presented in Fig. 3. As can be noticed, the mass increase after the switch from a dry to a H2O-containing atmosphere occurs in two stages with different kinetics in all samples. The mass increase in the first stage, probably related to the proton uptake process, is rapid and then gradually flattens out. Following this abrupt change, the time derivative does not diminish to zero, but remains at approximately 10−4% min−1, indicating a slow yet progressive change. This slow increase in the recorded mass might be related to a second process competing with the hydration or hydrogenation reaction. The behaviour of proton incorporation followed by a second process (oxidation reaction) was observed in the case of TG studies of mixed conductors, i.a. in double perovskite cobaltite or doped Sr(Ti,Fe)O3 solid solutions with a higher iron content.27–29Fig. 2 and 3 also show that after the switch from humidified to dry air, mass changes are much slower than those that occur after the switch from dry to humidified air.
Electrical conductivity studies
Since the BaCe0.6Zr0.2Y0.1Tb0.1O3−δ sample showed the highest water uptake, that is, the highest proton concentration, it was chosen for further investigation.Fig. 4 presents the temperature dependence of the total electrical conductivity of BCZYTb and BCZY622 (ref. 26) in dry and wet air. It can be seen that the conduction occurs through thermally activated processes. In the BCZY622 and BCZYTb materials, the total electrical conductivity in the wet atmosphere is higher than in the dry environment, and the observed difference between the values of conductivity under dry and wet conditions increases as the temperature decreases.
 | ||
| Fig. 4 Temperature dependence of total electrical conductivity, shown in Arrhenius-type coordinates, for BCZYTb and BCZY622 (ref. 26) samples measured in dry and wet air. | ||
At higher temperatures (>750 °C), this effect is merely noticeable, whereas at lower temperatures the difference is visible due to the higher concentration of protons and may indicate that the hydration process is the predominant proton uptake mechanism.
The influence of Tb-substitution at the yttrium site on the total electrical conductivity can be examined by comparing the total electrical conductivity in the chosen atmosphere and temperature range. The conductivity values obtained for the wet atmosphere at 600 °C are 1.1 × 10−2 S cm−1 for BCZY622 and 1.6 × 10−2 S cm−1 for BCZYTb. The apparent activation energies of the electrical conduction for BCZY622 and BCZYTb in dry and wet air are presented in Table 2. The values of Ea obtained in wet air below 500 °C are: (0.50 ± 0.02) eV and (0.42 ± 0.01) eV for BCZY622 and BCZYTb, respectively. The results show that the presence of Tb in the BCZY622 structure leads to an increase in total electrical conductivity in the studied temperature range, regardless of pH2O. This is probably due to the presence of metal cations with variable valency in the Ce/Zr/Y sublattice, which might increase the concentration of electron holes.
| Activation energy (eV) | ||||
|---|---|---|---|---|
| Dry air | Wet air | |||
| 300–500 °C | 500–800 °C | 300–500 °C | 500–800 °C | |
| BCZY622 | 0.69 ± 0.02 | 0.54 ± 0.01 | 0.50 ± 0.02 | 0.43 ± 0.02 |
| BCZYTb | 0.54 ± 0.01 | 0.42 ± 0.01 | ||
Ionic transport studies
To evaluate the partial electrical conductivities in BCZYTb in dry atmospheres, the total conductivity of the material was measured as a function of pO2 at 800 and 600 °C. The results are shown in Fig. 5 and are compared to those obtained for BCZY622.26 The values of total conductivity of BCZYTb and BCZY622 are comparable in the studied pO2 range. Furthermore, two characteristic pO2 ranges were observed at both temperatures. The first region for pO2 ≤ 10−3 atm can be ascribed to the partial oxygen ionic conductivity (σO), which is known to be independent of pO2. At higher oxygen partial pressures, pO2-dependent p-type electronic conductivity (σh) is dominating. In mixed ionic-electronic conductors, the total electrical conductivity in dry atmospheres can be written as a function of pO2:| σtotal = σO + σh = σO + σh0·pO21/4 | (5) |
 | ||
| Fig. 5 Total electrical conductivity of BCZY622 (ref. 26) and BCZYTb as a function of oxygen partial pressure measured in dry air at: (a) 800 °C and (b) 600 °C. | ||
The data were fitted with eqn (5), which allowed us to obtain the partial electrical conductivities of oxygen ions and electron holes at both temperatures. The calculated values of partial conductivities with the corresponding transference number of holes (th˙) estimated for dry air (pO2 = 0.2, pH2O ≈ 10−5) are shown in Table 3. The contribution of electron holes to the total conductivity is higher at 800 °C compared to 600 °C. This results from the higher concentration of electron holes at higher temperatures. Furthermore, the values of the transference number of holes indicate that the predominant contribution to the total conductivity is electronic under the considered conditions. However, taking into consideration the two orders of magnitude difference between the mobility of oxygen vacancies and the mobility of holes, the concentration of oxygen vacancies in this system is prevailing under these conditions. This is consistent with TG analysis of the water uptake process identified as hydration.
| T (°C) | σ total (S cm−1) | σ O (S cm−1) | σ h (S cm−1) | t h˙ |
|---|---|---|---|---|
| 800 | 3.7 × 10−2 | 1.3 × 10−2 | 2.3 × 10−2 | 0.63 |
| 600 | 8.9 × 10−3 | 3.8 × 10−3 | 7.4 × 10−3 | 0.55 |
Chemical surface exchange coefficients were studied by electrical conductivity relaxation measurements following the re-equilibration of the sample after a sudden change in the atmosphere humidity. Fig. 6a shows the typical relaxation patterns of hydration and dehydration obtained during the switch from dry to wet air and from wet to dry air at 500 °C. The diffusion of H2O during the hydration/dehydration is driven by the chemical potential gradient of water and can be single-fold or two-fold. If hydration occurs as a result of chemical diffusion of water, the total electrical conductivity should relax in a single-fold curve, with one relaxation time. This is a behaviour similar to that in the case of oxidation/reduction, where the ambipolar motion of oxygen ions and electron holes occurs. Conventional charge transport theory based on the chemical diffusion of water in a proton conductor as an ambipolar diffusion of proton and oxygen vacancies has been intensively studied i.a. by Yoo and Kreuer et al.30,31 In the case of single-fold relaxation, which occurs in materials with small values of the transference number of holes (th˙), the chemical diffusion of water occurs in the material through ambipolar diffusion of hydrogen and oxygen, whereas, if th˙ is high, the presence of mobile electron holes enables the independent chemical diffusion of hydrogen and oxygen species.2 The motion of both protons and oxygen vacancies is accompanied by the transport of electronic charge carriers, leading to a proton and oxygen vacancy decoupled motion. This so-called two-fold diffusion was first interpreted by Yoo et al.32 H2O initially decomposes on the surface of the material into H and O:
| H2O → 2Hads + Oads,and | (6) |
| Hads + OxO + ḣ ↔ OHO˙ | (7) |
 | ||
| Fig. 6 (a) Typical relaxation curves observed at 500 °C upon hydration and dehydration; (b) temperature dependence of the chemical surface exchange coefficient of water for BaCe0.6Zr0.2Y0.1Tb0.1O3−δ. | ||
Therefore, proton defect formation and its diffusion result in a decrease in conductivity and (2) adsorbed oxygen fills an oxygen vacancy site, which is compensated for by generating two electron holes (eqn (8)). In this process, the filling of the oxygen vacancies by the diffusing oxygen increases the conductivity.
Therefore, the conductivity relaxation characteristics are a consequence of two diffusion processes, which occur at different rates. The first process reduces the concentration of electron holes, according to the equation while the second has the opposite effect and oxidation occurs with the creation of electron holes, which is presented in eqn (8):
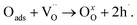 | (8) |
During the hydration process, protonic defects are incorporated into the structure, and the BCZYTb sample achieves a new equilibrium at a given temperature and pH2O. As can be seen in Fig. 6a, both hydration and dehydration proceed with two-fold non-monotonic kinetics, indicating a higher contribution of electron holes to the conductivity compared to oxygen ions in the studied temperature range, which is consistent with high calculated values of the transference number of electron holes (see Table 3). The conductivity response was found to depend on the direction of change in pH2O. When the gas was switched from wet air to dry air, the electrical conductivity did not return to the level before the hydration process started (t = 0 s).
The temperature dependence of chemical surface exchange coefficients kchem calculated for each species (protons and oxygen vacancies) during hydration and dehydration is shown in Fig. 6b. The change of pH2O during the gas switch from wet to dry does not imply any significant change in pO2. Therefore, the change in the conductivity of the material is due to the incorporation of water in the oxide (hydration process). Accordingly, the calculated surface exchange coefficients describe the steps of water adsorption, dissociation of adsorbed water molecules, and incorporation of O2− and H+ into the structure, described by eqn (7) and (8). It can be observed in Fig. 6b that the kchem of H between 450 and 700 °C is in the range of 1.2 × 10−4 to 4.9 × 10−4 cm s−1 and 4.0 × 10−5 to 2.4 × 10−4 cm s−1 in the hydration and dehydration processes, respectively. The kchem coefficients of oxygen incorporation in the same temperature range are between 1.0 × 10−5 and 6.6 × 10−5 cm s−1 in hydration and between 7.9 × 10−6 and 2.5 × 10−5 cm s−1 in dehydration, which are significantly lower than the kchem of H in both processes. In the case of both directions of pH2O change, the rate of H surface reaction is faster than that of O. The H and O chemical surface exchange coefficients were higher in the hydration step in comparison to the dehydration, indicating that water adsorption on the surface has faster kinetics than that of desorption. However, this effect may also originate from a relatively large pH2O step, affecting the bulk defect concentrations, which influence the rates of those processes. The activation energies of the surface exchange of hydrogen and oxygen for the hydration and dehydration processes are presented in Table 4. The activation energies for hydrogen are (0.39 ± 0.03) eV and (0.50 ± 0.05) eV in the hydration and dehydration processes, respectively, which are comparable to those reported for other protonic conductors.33–35 For instance, Hancke et al. found the activation energy of hydrogen surface exchange of BaCe0.9Y0.1O3−δ equal to (0.29 ± 0.03) eV.33 The activation energies of the surface exchange for protonic defect incorporation and release (hydration and dehydration) were comparable. On the other hand, in the case of oxygen ions, a noticeable difference was observed between Ea values for those processes (0.44 eV in the hydration and 0.26 eV in the dehydration step). This suggests that the presence of proton defects influences the process of oxygen chemisorption on the surface of the material.
| Activation energy (eV) | ||
|---|---|---|
| Hydrogen | Oxygen | |
| Hydration | 0.39 ± 0.05 | 0.44 ± 0.05 |
| Dehydration | 0.50 ± 0.05 | 0.26 ± 0.05 |
To investigate the reduction and oxidation kinetics, electrical conductivity relaxation measurements after an oxygen partial pressure change either from pO2 = 0.1 atm to pO2 = 10−3 atm or from pO2 = 10−3 atm to pO2 = 0.1 atm, respectively, were performed. The measurements were done both in a dry and a humidified atmosphere. The diffusion of oxygen is driven by the chemical potential gradient. The process of oxygen incorporation into oxide materials is complex and can be described as a sequence of several most probable steps.36 The incorporation of molecular oxygen into the crystal lattice of the oxide is a multistep reaction in which chemisorption, electron transfer, oxygen bond dissociation, and incorporation of atomic oxygen species into the structure take place. First, the oxygen molecule in the gas phase O2(g) is adsorbed by chemisorption on a vacant adsorption site on the surface of the material in a form O2(ads):
| O2(g) → O2(ads). | (9) |
Next, the adsorbed molecule diffuses on the surface of the material and is reduced in two steps:
| (1) O2(ads) → O2(ads)− + h˙, | (10a) |
| (2) O2(ads)− → O2(ads)2− + h˙, | (10b) |
O2(ads)− denotes an adsorbed superoxide molecular species, O2(ads)2− is a peroxide species and h˙ is an electron hole. The process described in eqn (10) is relatively fast, whereas the electron transfer between superoxide and peroxide species is much slower and generally is a rate-determining process.37–39 In the next step, the peroxide molecule is split into two single-ionized oxygen atoms O(ads)−:
| O2(ads)2− → 2O(ads)−. | (11) |
In the final reaction, oxygen is incorporated into the structure of the material:
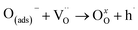 | (12) |
 is an oxygen vacancy and OxO is an oxygen atom in an oxygen lattice site in the bulk material. The summarized oxidation reaction can then be written as:
is an oxygen vacancy and OxO is an oxygen atom in an oxygen lattice site in the bulk material. The summarized oxidation reaction can then be written as: | (13) |
The introduced oxygen ion migrates in the direction according to the concentration gradient of this charge carrier. These processes influence the shape of the diffusion relaxation curve and should be monotonic in both directions, oxidation and reduction.40,41 When the curve is fitted with an adequate formula related to Fick's 2nd law,20 the chemical diffusivity Dchem and/or chemical surface exchange coefficient kchem of oxygen can be determined. Typical relaxation curves for the oxidation and reduction steps are shown in Fig. 7. As can be noticed, both oxidation and reduction are single-fold, regardless of pH2O. The conductivity changes are related to the ambipolar diffusion of oxygen ions and electron holes. This is an expected behavior reported in the literature, i.a. by Yoo et al.42 for BaZr0.8Y0.2O3−δ. Since the kinetics in the oxidation step in dry and wet atmospheres differ substantially, it can be considered that the surface exchange process of oxygen in the presence of protons is different from that in a dry atmosphere, where the concentration of protonic defects in the structure is negligible.
 | ||
| Fig. 7 Typical conductivity relaxation curves observed upon oxidation/reduction for (a) dry gas and (b) wet gas. | ||
The temperature dependence of the chemical surface exchange coefficient of oxygen for the oxidation and reduction steps in dry and humidified air is presented in Fig. 8. The activation energies of the surface exchange of oxygen for oxidation and reduction in the dry and wet atmospheres are displayed in Table 5. The kchem values in the studied temperature range common for all the samples (550–700 °C) is between 2 × 10−5 and 2 × 10−3 cm s−1. Moreover, the activation energy of the surface exchange of oxygen depends on pH2O, being lower in wet atmospheres. The highest difference between the activation energy in the dry and wet atmospheres was observed in the case of reduction (1.63 and 1.13 eV, respectively). Therefore, the presence of proton defects affects the oxidation and reduction kinetics in this material.
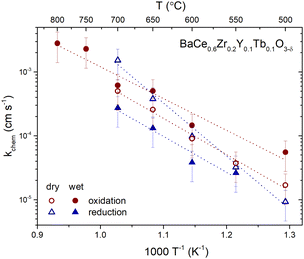 | ||
| Fig. 8 Temperature dependence of the chemical surface exchange coefficient of oxygen for the oxidation and reduction steps in dry and humidified air of BCZYTb. | ||
| Activation energy (eV) | ||
|---|---|---|
| Dry | Wet | |
| Oxidation | 1.13 ± 0.06 | 0.98 ± 0.11 |
| Reduction | 1.63 ± 0.10 | 1.13 ± 0.18 |
Conclusions
Single-phase polycrystalline BaCe0.6Zr0.2Y0.1M0.1O3−δ, where M was a multivalent constituent, i.e. Tb, Pr, and Fe, were synthesized and studied.Thermogravimetric analysis of the water uptake showed that the highest relative mass change, that is the highest content of protonic defects, occurred in BaCe0.6Zr0.2Y0.1Tb0.1O3−δ. Regardless of differences in the values of water uptake, in all the studied oxides, the mass increase takes place in two stages proceeding with different kinetics. It was proposed that the first stage is the proton uptake process (hydration), whereas the second one was considered to be related to oxidation.
The higher total electrical conductivity of BaCe0.6Zr0.2Y0.1Tb0.1O3−δ in comparison to that of BaCe0.6Zr0.2Y0.2O3−δ showed that the presence of terbium which is a multivalent cation leads to an increase in the concentration of electron holes.
The total electrical conductivity dependence on pO2 enabled the calculation of the partial conductivities of oxygen ions and electron holes at 800 °C and 600 °C and the determination of the transference number of holes in BaCe0.6Zr0.2Y0.1Tb0.1O3−δ. In the atmosphere of air (pO2 ≈ 0.2 atm), the material exhibits a predominant p-type electronic conduction mechanism, despite the prevailing concentration of oxygen vacancies compared to the concentration of electron holes.
The electrical conductivity relaxation studies of hydration/dehydration processes in the BaCe0.6Zr0.2Y0.1Tb0.1O3−δ material showed two-fold asymmetric hydration/dehydration kinetics, with the rate of the hydration process significantly higher than that of the dehydration. What is very important, the kinetics of oxidation/reduction vary substantially in humidified air. The oxidation reaction becomes considerably faster under wet conditions. It was proposed that similarly to the diffusion, also surface exchange of oxygen may be enhanced in the humidified atmosphere since oxide ions might be accelerated by protons to maintain charge neutrality. The results of this study show that the influence of water in the atmosphere on the kinetics of oxidation and reduction should be taken into account in the research concerning the transport thermodynamics of different charge carriers in materials containing three mobile charge carriers.
Author contributions
Jagoda Budnik: investigation, visualisation, funding acquisition, formal analysis, project administration, and writing – original draft. Aleksandra Mielewczyk-Gryń: investigation and writing – review & editing. Maria Gazda: conceptualization, resources, supervision, and writing – review & editing. Tadeusz Miruszewski: conceptualization, project administration, and writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was supported by the National Science Centre Poland (2021/41/N/ST5/03437).Notes and references
- J. Kim, S. Sengodan, G. Kwon, D. Ding, J. Shin, M. Liu and G. Kim, ChemSusChem, 2014, 7, 2811–2815 CrossRef CAS PubMed.
- D. Poetzsch, R. Merkle and J. Maier, Adv. Funct. Mater., 2015, 25, 1542–1557 CrossRef CAS.
- R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Adv. Funct. Mater., 2018, 28, 1–10 CrossRef.
- A. v. Kasyanova, L. R. Tarutina, A. O. Rudenko, J. G. Lyagaeva and D. A. Medvedev, Russ. Chem. Rev., 2020, 89, 667–692 CrossRef CAS.
- Y. Xu, F. Hu, Y. Guo, J. Zhang, Y. Huang, W. Zhou and J. Sun, Sep. Purif. Technol., 2022, 297, 121482 CrossRef CAS.
- D. Poetzsch, R. Merkle and J. Maier, Faraday Discuss., 2015, 182, 129–143 RSC.
- D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453 RSC.
- M. Dippon, S. M. Babiniec, H. Ding, S. Ricote and N. P. Sullivan, Solid State Ionics, 2016, 286, 117–121 CrossRef CAS.
- P. Sawant, S. Varma, B. N. Wani and S. R. Bharadwaj, Int. J. Hydrogen Energy, 2012, 37, 3848–3856 CrossRef CAS.
- T. L. Simonenko, M. v. Kalinina, N. P. Simonenko, E. P. Simonenko, O. v. Glumov, N. A. Mel’nikova, I. v. Murin, O. O. Shichalin, E. K. Papynov, O. A. Shilova, V. G. Sevastyanov and N. T. Kuznetsov, Int. J. Hydrogen Energy, 2019, 44, 20345–20354 CrossRef CAS.
- T. Shimura, H. Tanaka, H. Matsumoto and T. Yogo, Solid State Ionics, 2005, 176, 2945–2950 CrossRef CAS.
- M. A. Azimova and S. McIntosh, Solid State Ionics, 2009, 180, 160–167 CrossRef CAS.
- J. Melnik, J. Luo, K. T. Chuang and A. R. Sanger, Open Fuels Energy Sci. J., 2008, 1, 7–10 CAS.
- H. Matsumoto, T. Shimura, T. Higuchi, H. Tanaka, K. Katahira, T. Otake, T. Kudo, K. Yashiro, A. Kaimai, T. Kawada and J. Mizusaki, J. Electrochem. Soc., 2005, 152, A488 CrossRef CAS.
- H. Yokokawa, H. Tu, B. Iwanschitz and A. Mai, J. Power Sources, 2008, 182, 400–412 CrossRef CAS.
- M. Backhaus-Ricoult, Solid State Sci., 2008, 10, 670–688 CrossRef CAS.
- S. P. Simner, M. D. Anderson, M. H. Engelhard and J. W. Stevenson, Electrochem. Solid-State Lett., 2006, 9, 478–481 CrossRef.
- E. Bucher and W. Sitte, Solid State Ionics, 2011, 192, 480–482 CrossRef CAS.
- C. Solís, S. Escolastico, R. Haugsrud and J. M. Serra, J. Phys. Chem. C, 2011, 115, 11124–11131 CrossRef.
- J. Crank, The Mathematics of Diffusion, 2nd edn, 1975 Search PubMed.
- C. J. Shin and H. I. Yoo, Solid State Ionics, 2007, 178, 1089–1094 CrossRef CAS.
- F. Ciucci, Solid State Ionics, 2013, 239, 28–40 CrossRef CAS.
- B. Mirfakhraei, F. Ramezanipour, S. Paulson, V. Birss and V. Thangadurai, Front. Energy Res., 2014, 2, 1–10 Search PubMed.
- G. Heras-Juaristi, U. Amador, R. O. Fuentes, A. L. Chinelatto, J. Romero De Paz, C. Ritter, D. P. Fagg, D. Pérez-Coll and G. C. Mather, J. Mater. Chem. A, 2018, 6, 5324–5334 RSC.
- C. T. G. Petit and S. Tao, Solid State Sci., 2013, 17, 115–121 CrossRef CAS.
- T. Miruszewski, K. Dzierzgowski, P. Winiarz, S. Wachowski, A. Mielewczyk-Gryń and M. Gazda, J. Mater. Chem. A, 2022, 10, 7218–7227 RSC.
- S. L. Wachowski, I. Szpunar, M. H. Sørby, A. Mielewczyk-Gryń, M. Balaguer, C. Ghica, M. C. Istrate, M. Gazda, A. E. Gunnæs, J. M. Serra, T. Norby and R. Strandbakke, Acta Mater., 2020, 199, 297–310 CrossRef CAS.
- T. Miruszewski, K. Dzierzgowski, P. Winiarz, S. Wachowski, A. Mielewczyk-Gryń and M. Gazda, Materials, 2020, 13, 1–16 CrossRef PubMed.
- T. Miruszewski, K. Dzierzgowski, P. Winiarz, D. Jaworski, K. Wiciak-Pawłowska, W. Skubida, S. Wachowski, A. Mielewczyk-Gryń and M. Gazda, RSC Adv., 2021, 11, 19570–19578 RSC.
- H.-I. Yoo, J.-K. Kim and C.-E. Lee, J. Electrochem. Soc., 2009, 156, B66 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- H. I. Yoo, J. Y. Yoon, J. S. Ha and C. E. Lee, Phys. Chem. Chem. Phys., 2008, 10, 974–982 RSC.
- R. Hancke, Z. Li and R. Haugsrud, J. Electrochem. Soc., 2013, 160, F757–F763 CrossRef CAS.
- K. D. Kreuer, T. Dippel, Y. M. Baikov and J. Maier, Solid State Ionics, 1996, 86–88, 613–620 CrossRef CAS.
- C. Solís, S. Escolastico, R. Haugsrud and J. M. Serra, J. Phys. Chem. C, 2011, 115, 11124–11131 CrossRef.
- I. Riess, Solid State Ionics, 2019, 329, 95–109 CrossRef CAS.
- R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2002, 4, 4140–4148 RSC.
- J. Maier, Solid State Ionics, 2000, 135, 575–588 CrossRef CAS.
- R. Merkle and J. Maier, Angew. Chem., Int. Ed., 2008, 47, 3874–3894 CrossRef CAS PubMed.
- H. I. Yoo and C. E. Lee, J. Am. Ceram. Soc., 2005, 88, 617–623 CrossRef CAS.
- D. K. Lim, H. N. Im, S. Y. Jeon, J. Y. Park and S. J. Song, Acta Mater., 2013, 61, 1274–1283 CrossRef CAS.
- E. Kim and H. I. Yoo, Solid State Ionics, 2013, 252, 132–139 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |

