Short range order in disordered spinels and the impact on cation vacancy transport

Abstract

Spinels are important complex oxides for use in radiation damage environments and result from the corrosion of steel. It is known that, in these environments, normal spinels exist with some concentration of antisite cation pairs known as inversion. In this work we show that even in highly disordered states characterized by high levels of inversion, spinels still show some short range order (SRO) that manifests itself in antisite chains. The propensity to form these antisite chains is confirmed through Monte Carlo simulations which find that the length of chains which can form depends on the spinel chemistry. We also consider the effect of antisite chains on the diffusivity of cation vacancies and find that the effect strongly depends on the spinel chemistry. Two examples illustrate the range of chemistry dependance on cation vacancy diffusivity, chains in FeCr₂O₄ significantly increase vacancy transport but in MgAl₂O₄, they have the inverse effect of drastically reducing vacancy mobility. The explanation of these dramatically different effects results from the assessment of the thermodynamic stability of the antisite chains and contrasting attractive/repulsive interactions of vacancies with the chains.

---

1 Introduction

Spinels are a large family of naturally occurring complex oxides with the general formula AB₂O₄. The most common form of this structure is known as a ‘normal’ spinel where A cations occupy tetrahedral sites and B cations occupy octahedral sites with an fcc oxygen sublattice. There are also spinels which have an ‘inverse’ structure meaning B cations occupy tetrahedral sites whereas both B and A cations occupy octahedral sites; this type of spinel is rarer and will not be discussed in this work.¹ The ground state of all spinels is either fully normal or fully inverse depending on the choice of cations. Real spinels always exhibit some deviation from the ideal fully normal or fully inverse configurations. However, when spinels form from the corrosion of steels or are in environments where radiation damage effects are present, coupled with the high temperature environments of, for example, nuclear reactors, even greater mixing of species and sites can occur. In the context of a normal spinel, this process can be thought of as partial inversion in which some A cations occupy octahedral sites and a corresponding number of B cations occupy tetrahedral sites. This level of inversion can be viewed as a variable where an inversion of 0 corresponds to a normal spinel and a value of 1 is a fully inverse spinel. A spinel's ability to withstand these inversion processes is a key component of its resilience in radiation damage environments as it has a mechanical robustness due to its ability to accommodate these point defects.^2–4 A comprehensive description of the spinel structure and the concept of cation disorder in spinels is provided by Sickafus et al.¹

A schematic explanation of the process of inversion in a spinel is given in Fig. 1(a) where O has been removed for visibility. As discussed, radiation damage can take a spinel from a nominally normal structure (I) to having some level of inversion with the creation of antisite pairs (II). There is some indirect experimental evidence that inversion results in SRO in a spinel, showing that in Mg_1−xNi_xAl₂O₄, cation inversion creates a local tetragonal symmetry as determined by neutron total scattering experiments.⁵ In this work we show that cation antisites can form A_B antisite chains, hence producing short-ranged order (SRO) in the disordered spinel (III), with some evidence also presented in the literature for this type of B-site short range ordering in the NiFe₂O₄ spinel.⁶

Fig. 1 (a) Schematic of radiation damage leading to antisite pair creation leading to the formation of an A_B antisite chain. (b) Schematic of a cation vacancy moving along an antisite chain.

The use of spinel structures as prospective battery materials,^7,8 where defect transport is of paramount importance, motivates the study of the impact of the disorder in our spinels on defect migration. The hypothesis is that cation vacancies may use the antisite chains as fast pathways for migration; a schematic of this proposed migration behavior can be seen in Fig. 1(b). Moreover, SRO has been found in disordered oxides used as battery materials to form percolation pathways which increase cation transport.^9,10 To this end, we also assess the importance of the antisite chains which form percolating pathways of SRO and how that further impacts defect transport.

In this work, we use molecular dynamics (MD) methods to understand the impact of SRO in spinels as a function of inversion using FeCr₂O₄, NiCr₂O₄ and MgAl₂O₄ as example spinel chemistries. The SRO structure is examined through the use of high temperature Monte Carlo simulations, inducing varied levels of inversion in the material. The thermodynamic stability of antisite chains is evaluated and the implications of this antisite chain-based SRO on cation vacancy transport is then considered using static thermodynamic considerations and MD simulations, resulting in a complex but complete picture of the role of SRO on cation vacancy properties in these spinels.

2 Methodology

The atomistic simulation package LAMMPS¹¹ has been used throughout this work. In particular, LAMMPS is used within the integrated development environment (IDE) for computational materials science Pyiron¹² to simulate, manage, and analyze the data generated in this work.

Atomic interactions for the (Fe/Ni)Cr₂O₄ spinel are described by using a Buckingham–Coulomb potential plus a Morse potential form by Chartier et al.¹³ while a Buckingham–Coulomb potential form by Smith et al.¹⁴ is used for MgAl₂O₄. These models have a fixed charge meaning they do not allow for charge transfer; in particular, (Fe/Ni)Cr₂O₄ spinels use partial charges, i.e., Fe/Ni: 1.2+, Cr: 1.8+ and O: 1.2 – while MgAl₂O₄ uses the full formal charges of Mg: 2+, Cr: 3+ and O: 2−. This difference is a reflection of the differing degrees of ionic behavior in the materials themselves. Furthermore, the potential used for (Fe/Ni)Cr₂O₄ was assessed against experimental values of structural, elastic and thermal expansion properties.¹³ While these potential models do not allow for charge transfer, they have had success in capturing cation disordering effects in other studies^15–17 and since the cation disorder is fundamentally connected to the electrostatics of the material,¹⁸ this implies that there are relatively weak charge transfer effects on cation disorder. Furthermore, since the Néel temperature of these materials is generally <100 K^19,20 we expect no impact caused by magnetism at the temperatures of our simulations or experimental/real applications.

Simulation cells were based on a spinel unit cell of size 8.37 × 8.37 × 8.37 ų for the FeCr₂O₄ spinel. The volume was relaxed for other spinel chemistries causing a slight difference in the unit cells used. Generally a supercell of 3 unit cells in each direction was used for calculations and, unless otherwise stated, these supercells contained 1512 atoms. For the sake of brevity, we use FCO, NCO, and MAO to denote the FeCr₂O₄, NiCr₂O₄ and MgAl₂O₄ structures, respectively.

A metropolis-based Monte Carlo (MC) algorithm^21,22 was employed on the spinel structures to generate a catalogue of disordered structures with a defined level of inversion. Cation positions are swapped and the energy change (ΔE) was calculated; the swap is accepted if ΔE < 0 or if the Metropolis condition is satisfied, that is, , for some random number, r, between 0 and 1, where the simulation is conducted at a given temperature, T₀;^21,23k_B is the Boltzmann constant. This was performed for a total of 75 000–100 000 accepted swaps where a sample structure was taken every 216 accepted swaps, equal to the number of A cations in the structure, referred to as an MC cycle.^11,23 We note that the temperatures needed to reach high levels of inversion are unphysical, in the order of 10⁴ K for the largest inversion cases, emphasizing that these materials do not naturally accommodate much inversion. The temperature in these simulations is only used to calculate the Metropolis condition with no dynamics being run, and they are performed at the 0 K lattice constant. We are simply using the MC simulations to generate representative structures with varying levels of inversion. In reality, radiation may supply the energy needed to reach the level of inversion represented by these structures.²

Upon analysis of the structures resulting from the MC simulations, we found the preferential development of antisite cation chains in which A_B cations were coordinated to each other with a distance of ≃2.85 Å, depending on the spinel chemistry and associated lattice constant. This allowed us to use Ovito's cluster analysis algorithms²⁴ to classify and count each chain by setting the cutoff of the cluster to a value below the A_A–A_A bond length (≃3.6 Å) and the A_A–A_B bonds (≃3.4 Å) but above the A_B–A_B bond length (≃2.85 Å). In general, an ≃3 Å cutoff was used for the cluster analysis resulting in finding A_B cations coordinated as chains while neglecting atoms on their normal lattice sites. When discussing the length of chains we define the chain length as N_A − 1, where N_A is the number of atoms that are part of the chain, so that a single A_B antisite is considered as a 0-chain.

Simulation cells resulting from the MC simulations had multiple chains of varied length within them. To isolate these chains and more methodically analyze their properties, a script was written which generated isolated chains of the types we had observed from the MC procedure. This script takes a normal spinel structure and artificially creates antisites in the structure, randomly growing a chain to a predefined length. This procedure was conducted as follows. A random B cation was chosen as the starting point. The nearest A cation neighbour was randomly selected and the two atoms were swapped to create an antisite pair. From this initial A_B starting position, a B cation nearest neighbour (NN) was chosen as the next position along the chain and the antisite pair creation was then conducted again. From this new A_B antisite the process was repeated until the required length had been reached. We note that this procedure results in A_B chains with random internal topology and random decoration of B_A cations to maintain local charge neutrality.

We classified the topology of the chains which we have built by borrowing a definition from polymer physics for the radius of gyration,²⁵ or, the gyradius. The gyradius quantifies the deviation of atoms as part of a chain from the center of mass of the chain by using the equation,

where r_i is the coordinate of chain atom i and r_cm is the center of mass of the chain. The mass term has been neglected due to each atom in our chain being of the same mass.

Finally, MD simulations were used to find the diffusivity of cations in a normal spinel compared to a spinel with some antisite chains present. Structures were first relaxed at 0 K and then a 300 K initialization run was conducted for 10 ps, and the temperature was then ramped to the required temperature. At this temperature the simulation box size was allowed to change during an NPT run and the average box size over this 20 ps run was calculated and then fixed at that size for the remainder of the run. The mean-squared displacement (MSD) of cations was then tracked through a 10 ns NVT run and the diffusivity extracted from the MSD once a linear regime was reached, after the transient phase of the dynamic evolution.

3 Results and discussion

3.1 Short-ranged order in disordered FeCr₂O₄ spinels

We first aim to assess the SRO of the FCO spinel as a function of inversion parameter, i, by quantifying the length and distribution of the FCO Fe_Cr antisite chains that form. Since in this spinel Fe is the A cation and Cr is the B cation, i is calculated as the number of Fe_Cr divided by the total number of Fe sites and is sometimes referred to as a percentage of inversion.

Fig. 2(a) shows a box plot of the distribution of Fe_Cr chain lengths as a function of inversion level which developed during an MC procedure at a given temperature. A steady increase in the length of chains can be seen with the maximum chain length found to be a 52-chain at the highest inversion level of 64.1%. Two representative example structures of the chains are shown in Fig. 2(b and c) which were found in the i = 16.2% and i = 64.1% simulations; color is used to distinguish between the different chains and the 5 longest chains from that simulation are shown in each box. Only the Fe_Cr antisites, which are at the core of the chain, are shown here; however, decorating these chains are a corresponding number of Cr_Fe antisites which do not form any distinguishable structure. Note also that each structure generated via MC contained a range of different chain lengths, all of which are included in Fig. 2(a).

Fig. 2 (a) Box plot of lengths of chains which developed through the MC simulations at the resulting inversion level. Red lines are median chain lengths resulting from a random placement of antisites. (b and c) Example Fe_Cr antisite chains from the output of the MC showing the 5 longest chains in the simulation box, colored to distinguish individual chains, in the (b) 16.2% inversion and (c) 64.1% inversion case.

We also find that chains of length 20 and higher grown during the MC are able to percolate the system, spanning the length of our simulation box. This was determined again using Ovito's cluster analysis tool.²⁴ If the length of a chain doubled when the simulation box was replicated rather than the frequency of that chain length doubling then the chain spans the simulation box and is therefore considered a percolating chain.

For comparison, the red lines show the median value of chain lengths if the antisites are instead placed randomly through the structure. We find that at i ≤ 41.0% there is a significant increase in chain length statistics from the MC compared to the random placement. At i ≥ 47.9% the median chains are comparable between MC and random. We conclude this is due to the high concentration of antisites not able to ‘spread-out’ at large values of inversion, resulting in the unavoidable formation of chains. However, the fact we see a significant increase in chain lengths at moderate inversion values implies that antisite chains in FCO could be energetically favorable compared to isolated antisite chains.

To study these chains more systematically, we manually grew isolated antisite chains with a range of topologies and lengths. These chains had a range of lengths and topologies, distinguished by the gyradius, that was consistent with those produced during the MC procedure. We assess the stability of these chains by calculating their binding energy compared to that of isolated antisite pairs with the equation E_B = E_C + NE_b − (N + 1)E₀, where E_C is the energy of the system containing the chain, E_b is the energy of a normal spinel, N is the length of the chain (recalling that a chain of length N contains (N + 1) Fe_Cr antisites) and E₀ is the energy of a cell containing a single antisite pair as NN, referred to as a 0-chain. A schematic of this calculation can be found in Fig. 3(b).

Fig. 3 (a) Binding energy of chains of a given length colored by the chain gyradius. (b) Schematic defining the energy represented in (a). (c) Vacancy binding energy to the highest and lowest energy sites in each chain with lines of best fit for the weakest and strongest bound sites. (d) Schematic defining the energy represented in (c).

The results are presented in Fig. 3(a) and show that the formation of Fe_Cr antisite chains decorated by a corresponding amount of Cr_Fe antisites is energetically preferred compared to isolated antisite pairs in a linear fashion with increasing chain length. This explains the high concentration and length of chains discovered through the MC simulations. Clearly, the binding energy at a given chain length varies with some spread and was first assumed to be based on the topology of the chain. Thus the gyradius, which quantifies the topology of a given chain was calculated and chains are colored by the gyradius as shown in Fig. 3(a). There is no clear correlation between the topology of the chain as described by the gyradius and its binding energy, implying that the energy of a chain is not controlled by its topology; rather it seems agnostic to the topological structure of the chain.

The magnitude of the spread depends linearly on chain length implying that the origin is the same in 1-chains as in 54-chains but that the magnitude of the deviation is larger in longer chains. The only degree of freedom in the formation of 1-chains is the placement of the Cr_Fe antisites, i.e., how the Cr_Fe antisites decorate the central Fe_Cr chain which are placed at NN sites for which there are multiple choices. We find that the placement of these antisites has a strong effect on the binding energy of the chain which implies that two chains with the same length and topology can have different binding energies depending on how the Cr_Fe sites are dispersed around that chain. Since the generation of the inverted regions is driven by radiation damage we would not expect these chains to be driven to exist in their lowest energy environment, rather we would expect to see chains with a range of distributions and binding energies.

With the formation of SRO and long antisite chains, some of which percolate through the system, it seems plausible that these could provide fast pathways for migration of cation vacancies. In order for this to be the case, we must see a thermodynamic driving force attracting cation vacancies to chains or at least find that chains do not repel cation vacancies. In an attempt to quantify this effect, we calculate the binding energy of an Fe vacancy on a chain as compared to that of an isolated Fe vacancy in an otherwise undefected normal spinel, , where is the energy of a vacancy at some site along a chain, and E_C is the energy of the structure with that chain present. E_b is the energy of a normal spinel structure and 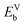is the energy of a normal spinel structure with a vacancy. This is schematically described in Fig. 3(d). We perform this calculation for all sites on each chain and the results are illustrated in Fig. 3(c). This shows, for a given chain, the binding energy of a vacancy to the highest energy (weakest bound) site and the lowest energy (strongest bound) site along that chain. We find that the majority of sites along our chains would attract vacancies. There is only a small percentage of chains which have sites that would repel vacancies. Furthermore, except for the very largest chains, there are chains where all sites are attractive (where the weakest bound site has a negative binding energy), indicating that the vacancy would be attracted to all sites on the chain and the entire length of the chain could act, in principle, as a percolating pathway. Note that since we are only plotting the weakest and strongest bound sites, other sites along a specific chain will have vacancy binding energies between the two extremes. The dashed lines show lines of best fit through the two sets of points. The overall attractive nature of these antisite chains implies that there would be a strong effect of antisite chains on migrating vacancies.

Intuition may suggest that cation vacancy defects will always be repelled from A_B antisites in spinels due to both having negative charges. However, the story is more complex since, for every A_B antisite, there is a corresponding B_A antisite which has an effective charge of +1. These antisite pairs are typically bound due to their charge difference, leading to a local environment that is electrostatically neutral. This means the cation vacancy may be attracted to the positively charged B_A antisites which often decorate the A_B antisite chain. Furthermore, for FCO, there is also a covalent interaction represented by the Morse term that can also facilitate this interaction. These competing effects result in a more complex picture of how cation vacancies will interact with the antisite chains.

3.2 Short-ranged order in other disordered spinel chemistries

To understand how universal this antisite chain structure is in the spinel structure, we have performed a similar but terser analysis for NiCr₂O₄ (NCO) and MgAl₂O₄ (MAO) spinels. The MC simulations were repeated for these two spinels but only for a few specific inversions. While in NCO we find the development of antisite chains of analogous lengths and frequencies as in FCO, in MAO, we find the length of chains to be on average around half the length of chains in FCO, and in fact shorter than that if the antisites were placed randomly, indicating that chains in MAO are potentially not energetically stable in MAO.

A catalogue of isolated chains was again generated using the previously described approach but this time using the normal NCO and MAO spinels as starting structures. Fig. 4(a) shows the combined chain binding energies for both NCO and MAO against the chain length, analogous to the data shown in Fig. 3(b) for FCO. For the NCO spinel, a similar trend is seen between chain length and chain binding energy as for FCO, implying again that chains are energetically favourable compared to isolated antisite pairs. However, in the MAO spinel, the trend is not as clear. Some chains have a negative binding energy but the majority are positive. This points to chains having qualitatively different behaviour in MAO spinels. These findings are consistent with the MC simulations which found less frequent and shorter chains in MAO.

Fig. 4 (a) Binding energy of antisite chains in NCO and MAO. (b) Lines of best fit of vacancy binding energy to the highest and lowest energy sites in each chain in NCO and MAO.

Fig. 4(b) shows the results of the vacancy binding energy to chains in NCO and MAO, calculated in the same way as described in Fig. 3(d). In this case, however, only the lines of best fit are shown for clarity. In contrast to FCO, we find that in NCO there is an equal split between attractive and repulsive sites for vacancies along the chains. This indicates that NCO may not be able to provide fast pathways for vacancies due to the repulsive nature of a large portion of the sites along these chains. For MAO, the story is similar to FCO indicating that vacancies are almost always attracted to chains and that, while chains in MAO are generally not favorable, they could provide a fast pathway for vacancies due to their strong attraction to chains if they were to form.

3.3 Kinetics of vacancy defects in SRO inverted spinels

We now examine more directly the impact of antisite chains on transport of cation vacancies in each of our example spinel chemistries. A detailed study of vacancy migration in spinels is given by Murphy et al.²⁶ which outlines vacancy pathways and barriers in a normal MAO spinel system. As a first approximation, cation vacancies in a normal spinel can be considered to migrate through their respective sublattices. However, depending on the spinel chemistry and the relative stability of cation vacancies on each sublattice the vacancy can ‘swap’ sites, this process induces a cation antisite so the ability for a vacancy to do this is also related to the energy required for antisite formation in a particular spinel chemistry. This process becomes increasingly complex when there is already cation disorder present in the system. Due to this added complexity in our systems, we do not seek the migration pathways and barriers explicitly but rather quantify the diffusivity of cations using MD to understand the overall effect of SRO on cation vacancy transport.

In particular, we compare the diffusivity of cations in the normal spinel structure to one of our maximum inversion structures from MC which contains percolating antisite chains. To do this, 0.5% cation vacancies were randomly created in each structure, split between A and B cations in a 1 : 2 ratio corresponding to the stoichiometry of the normal spinels. The creation of cation vacancy defects induced a large negative total charge in the system which was compensated by altering the charge on each O by ≃0.5%, a common strategy in other similar studies.^27–29 This is similar to adding a charge compensating background but different since the charge compensation only acts on the O. In addition, in order to separate the effects of inversion from the SRO represented by the chains, we attempted to assess the vacancy transport in a structure with no chains, ensuring that antisites were maximally separated. However, with this distribution of antisites, the system was unstable and effectively amorphized during the 10 ps 300 K MD initialization run. This implies that the formation of chains is key in the inversion process and stabilizes the inverted/disordered spinel structure. As a compromise, we used a different structure with i = 64.1% inversion where the maximum chain length was 12, a minimum for those discovered through the MC at this level of inversion. These structures were simulated using MD at temperatures between 1800 K and 2200 K for 10 ns each and the mean squared displacement (MSD) of every atom in the system was calculated from these trajectories.

It first must be acknowledged that the mechanisms available for defect migration in a spinel are extremely complex, especially when some percentage of inversion is present and the resulting potential energy landscape is rather rough. We calculate the energy barrier of some of these mechanisms using nudged elastic band (NEB) calculations³⁰ and present them in Table 1, with more detail available in previous work.^14,26,31 This is by no means an exhaustive list of mechanisms or barriers, but will be used to help interpret the vacancy diffusion simulations.

Table 1 Forward and reverse barriers for A & B cation vacancy migration mechanisms in FCO, NCO and MAO

Number	Spinel	Equation	Forward barrier (eV)	Reverse barrier (eV)
1	FCO	Cr + VFe → VCr + CrFe	2.39	2.14
2	FCO	Fe + VCr → VFe + FeCr	2.60	0.80
3	NCO	Cr + VNi → VCr + CrNi	2.40	2.27
4	NCO	Ni + VCr → VNi + NiCr	2.97	1.84
5	MAO	Al + VMg → VAl + AlMg	2.80	3.92
6	MAO	Mg + VAl → VMg + MgAl	3.35	1.16

---

Fig. 5(a and b) show the diffusivity of A and B cations, respectively, in the three spinels. We compare the diffusivity of both cations independently and assess the effect that the chains have on the diffusivity of each. During the MD of the vacancies in FCO normal spinel, we found that a significant portion of the Fe vacancies transpose to Cr vacancies through mechanism 1 in Table 1. While these defects are attractive due to their opposite charges, the subsequently created V_Cr can migrate away from the Cr_Fe with a barrier of 2.0 eV. This barrier is lower than the reverse barrier in mechanism 1, possibly leading to isolated and frozen Cr_Fe. Fe vacancies are then not replenished in significant quantity because of the larger barrier and significantly smaller reverse barrier of mechanism 2 in Table 1, which could in principle lead to more Fe vacancies. This resulted in an inconsistent MSD as a function of temperature, shown in Fig. 5(c), from which we could not extract a reliable fit for the diffusivity calculation. To provide an estimate of how this diffusivity may look, we have generated an approximate diffusivity by fitting to the final 1 ns of data in this case, and these are provided as dashed lines and labeled as “approx.” in Fig. 5(a). We stress that these are not meant to be reliable values for diffusivity, but are provided to understand qualitative trends in how inversion and SRO impact transport.

Fig. 5 (a and b) Diffusivity of (a) A cations and (b) B cations in FCO, NCO and MAO spinels comparing vacancy diffusion in a normal spinel to a spinel with SRO, in the form of antisite chains. (c–e) Mean squared displacement of Fe in an FCO (c) normal spinel, (d) inverse spinel and (e) inverse spinel with a percolating chain.

That being said, we see that the presence of inversion in FCO increases the diffusivity of both Fe (A cation) and Cr (B cation) vacancies and this effect is amplified when that inversion is structured as percolating SRO chains, while some mobility will be derived from the mechanisms outlined in Table 1 mechanism 1 & 2, shifting the defect content of each cation. Since we see an increase in the diffusivity of both cations this is not the driver for mobility change, rather we conclude that the percolating SRO chain provides fast pathways for vacancies, therefore increasing mobility. In Fig. 5(a and b) this can be seen as an increase in the diffusivity when we go from a normal spinel to a spinel structure with inversion to one with percolating chains. The increase in Fe diffusivity can be seen directly from the MSDs in Fig. 5(c–e). Generally the diffusivity is extracted from the MSD (in d and e) at times after 4 ns (before this, transient mechanisms dominate resulting in an unreliable fit). Note that the MSD is averaged over all the atoms of that type in the simulation cell, resulting in diffusivity values which may appear small given the large number of cations that do not participate in transport at all.

Conversely, we see that the effect of the chains in the MAO spinel significantly hinders the vacancy transport as evidenced by the large decrease in Mg diffusivity as SRO is introduced. Furthermore, Al diffusivity is relatively unaffected by the inversion. This implies that the migration of vacancies along that chain must be considerably slower than the migration of vacancies through the normal MAO structure. Note that due to higher barriers for Mg vacancies to transpose to Al vacancies and vice versa (mechanisms 5 and 6 in Table 1) there is no significant change in the concentration of each vacancy type during the course of the simulations and there are no issues with obtaining reliable MSDs.

As with FCO, no reliable MSD could be generated for Ni in a normal NCO spinel, again due to comparable barriers for the conversion of one type of vacancy to the other. Therefore another approximate line has been plotted in Fig. 5(a). In this case, we see that there is a decrease in diffusivity due to the chains in A cation diffusivity. However, for B cation diffusivity (Fig. 5(b)), there is a slight increase in diffusivity, particularly at lower temperatures. Therefore, in NCO, the SRO chains have contrasting effects on diffusivity depending on the nature of the cation in question.

3.4 Discussion

It is clear that, regardless of the spinel chemistries we have discussed in this work, some short-ranged ordered regions form in disordered spinels which have the form of A_B antisite chains that are decorated by B_A antisites. We have found that the degree to which these antisite chains are thermodynamically favourable depends on the spinel chemistry. However, high levels of inversion, at least in these spinel chemistries, is driven by non-equilibrium processes such as irradiation, so the extent to which the SRO chains form is unclear. In reality, some level of chain formation likely occurs as the disorder induced by irradiation locally relaxes, particularly since these chains are critical for stabilizing the inverted structure.

The impact of this SRO on the transport of defects is an important consideration for their relevancy in spinels, and vacancies are a representative defect used in this work to determine this impact. We have found that, perhaps counter-intuitively, cation vacancies are thermodynamically attracted to antisite chains; again the degree of this attraction strongly depends on the spinel chemistry but, in the spinels investigated, there were always sites on the chain which attracted the vacancy. However, the diffusivity of vacancy defects in SRO and normal spinel environments is a complex phenomenon thanks to many migration mechanisms available to vacancies in these structures. The conclusions of this diffusivity assessment are no simpler. The findings strongly depend on the spinel chemistry. We see a significant increase in diffusivity for vacancies in FCO. However, cation vacancy motion in MAO is significantly decreased with the presence of chains. This is in contrast to the thermodynamics which shows strong attraction of vacancies and antisite chains. This implies that while vacancies are attracted to chains in MAO, the chains do not provide a faster migration pathway than the bulk, meaning that in MAO antisite chains, they act as a trap for cation vacancies. NCO seems to sit between these two extreme cases, decreasing diffusivity of A cation vacancies but increasing diffusivity in B cation vacancies.

This difference in the behaviour between the vacancy in the MAO spinel and the FCO/NCO spinel could be due to the stronger electrostatic contribution to the atomic interactions in the MAO spinel. This effect is manifested in the interatomic potential by the use of full formal charges for the MAO species but only partial charges in the FCO/NCO potential. We do not consider this effect an artifact of the potential parameters but is rather a realistic representation of the difference in the strength of ionic interactions in these different spinels. Furthermore, FCO and NCO have a stronger covalency in the interatomic interactions as embodied by the Morse potential, suggesting more complex bonding than expected simply from electrostatic considerations. Furthermore, the large difference in ionic radii between, for example, Mg and Al compared with the negligible atomic radii difference between Fe and Cr could also impact the ability for different chemistries to accommodate coordinated chains of antisites where the strain caused by the antisites will be different and possibly lead to different behaviors.

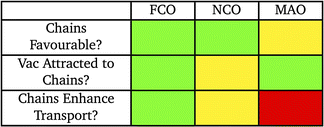
Table 2 summarises the main results of this work and provides some insight as to the behavior of vacancies in the SRO-structure spinel. In FCO, the story is clear: chains are energetically favourable to form, vacancies are almost always strongly attracted to sites along these chains, and the chains act as fast pathways for vacancies. In NCO, while forming the chains is favourable, there is a seemingly an even number of repulsive and attractive sites for cation vacancies along the chains and as a result the effect on vacancy transport is less straightforward. While chains in NCO could be fast pathways for vacancies, if vacancies are repelled from chains, this will limit their ability to facilitate vacancy transport. Finally, we found the majority of chains to be energetically unfavorable in MAO but that vacancies are strongly attracted to them. However, pathways for vacancies to move along chains are much slower than in the bulk, resulting in decreased transport when antisite chains are present in this material.

Table 2 Summary of salient SRO findings for FCO, NCO and MAO derived from calculations throughout this work

---

While the potentials used in this work have been benchmarked during their production and subsequent studies and are believed to be accurate enough to capture the dominant trends present in these materials, no potential can capture the subtle effects neglected by the classical MD framework. Thus, this work is presented to indicate the qualitative trends of SRO as a function of inversion rather than the quantitative nature of the SRO and its interaction with defects in particular chemistries. Therefore, we only indicate the range of possible effects that this SRO may have on different spinel chemistries.

However, the finding of SRO in spinels and the impact of inversion on defect transport is perhaps not surprising since analogous findings have been made for similarly structured compounds. For example, other complex oxides can also go through a process of chemical disorder leading to an effect akin to inversion.³² Disorder has been studied in pyrochlore and the enhancement of cation transport^33,34 and anion mobility^35,36 resulting from this disorder has been found. While there is experimental evidence for SRO in pyrochlore,^37,38 only random disorder has been considered computationally so far, not any SRO structured disorder. Anion transport in disordered systems has also been considered in other compounds, finding that disorder decreases anion vacancy transport due to trap sites in disordered regions in the double perovskite GdBaCo₂O_5+σ (ref. 39) and Mg(Al/Ga/In)₂O₄ spinels.⁴⁰ Again, SRO was not considered in these cases.

Some evidence that disorder in high entropy rocksalt compounds resulting in SRO and percolating networks positively affects transport has been seen in the battery field.^9,10 Since controlling the transport of ions in battery materials is key and spinel structured materials are being considered for use in this field,^7,8 it may be possible to allow for the tuning of transport properties in spinels by choosing spinel chemistries which lead to natural levels of inversion. Furthermore, the finer control of transport in these materials could be accessed by controlling the inversion and therefore, the concentration of percolating networks which work to alter the defect transport environment alongside the choice of the correct spinel chemistry.

4 Conclusion

We have given computational evidence that spinels with some natural level of inversion or in environments where inversion processes can occur due to damage can exhibit short ranged order which manifests as A_B antisite chains. The energetic favorability of this SRO as well as the impact of the antisite chains on cation vacancy migration depend strongly on the spinel chemistry, ranging from significant enhancement to significant impedance of vacancy diffusivity. Some indicators for predicting the impact of SRO and antisite chains on vacancy transport are suggested but more work on other spinels is needed to fully classify this behavior. In any case, we conclude that the qualitative trends identified in this work indicate that SRO in spinels must be accounted for when considering inversion/disorder, though the direction and magnitude of the trends of SRO depend greatly on spinel chemistry. In particular, mass transport is strongly dependent on the antisite structure, and reliable assessment of transport in these materials, and we suspect in complex oxides more generally, requires understanding of the SRO in these compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Jan Janssen, lead developer of pyiron, for his help in developing of an efficient pyiron script to develop and analyze these data. We also acknowledge the support of Enrique Martinez when using his Monte Carlo simulation code. This research used resources of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This work was supported as part of FUTURE (Fundamental Understanding of Transport Under Reactor Extremes), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (Contract No. 89233218CNA000001).

Notes and references

1. K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82, 3279–3292.
2. K. Sickafus, A. Larson, N. Yu, M. Nastasi, G. Hollenberg, F. Garner and R. Bradt, J. Nucl. Mater., 1995, 219, 128–134.
3. K. Sickafus, L. Minervini, R. Grimes, J. Valdez, M. Ishimaru, F. Li, K. McClellan and T. Hartmann, Science, 2000, 289, 748–751.
4. B. P. Uberuaga, M. Tang, C. Jiang, J. A. Valdez, R. Smith, Y. Wang and K. E. Sickafus, Nat. Commun., 2015, 6, 1–8.
5. E. C. O'Quinn, J. Shamblin, B. Perlov, R. C. Ewing, J. Neuefeind, M. Feygenson, I. Gussev and M. Lang, J. Am. Chem. Soc., 2017, 139, 10395–10402.
6. V. Ivanov, M. Abrashev, M. Iliev, M. Gospodinov, J. Meen and M. Aroyo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 024104.
7. K. Shimokawa, T. Atsumi, M. Harada, R. E. Ward, M. Nakayama, Y. Kumagai, F. Oba, N. L. Okamoto, K. Kanamura and T. Ichitsubo, J. Mater. Chem. A, 2019, 7, 12225–12235.
8. D. K. Kim, P. Muralidharan, H.-W. Lee, R. Ruffo, Y. Yang, C. K. Chan, H. Peng, R. A. Huggins and Y. Cui, Nano Lett., 2008, 8, 3948–3952.
9. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Science, 2014, 343, 519–522.
10. J. Lee, D.-H. Seo, M. Balasubramanian, N. Twu, X. Li and G. Ceder, Energy Environ. Sci., 2015, 8, 3255–3265.
11. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
12. J. Janssen, S. Surendralal, Y. Lysogorskiy, M. Todorova, T. Hickel, R. Drautz and J. Neugebauer, Comput. Mater. Sci., 2019, 163, 24–36.
13. A. Chartier, B. Golovchuk, S. Gossé and L. Van Brutzel, J. Chem. Phys., 2013, 139, 134702.
14. R. Smith, D. Bacorisen, B. Uberuaga, K. Sickafus, J. Ball and R. Grimes, J. Phys.: Condens. Matter, 2005, 17, 875.
15. T. Yamamoto, A. Chartier, K. Yasuda, C. Meis, K. Shiiyama and S. Matsumura, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 2676–2682.
16. A. Chartier, T. Yamamoto, K. Yasuda, C. Meis and S. Matsumura, J. Nucl. Mater., 2008, 378, 188–192.
17. L. Van Brutzel, A. Chartier, B. Sicaud and M. Sauzay, J. Chem. Phys., 2019, 151, 014701.
18. V. Stevanović, M. d'Avezac and A. Zunger, Phys. Rev. Lett., 2010, 105, 075501.
19. G. Shirane, D. Cox and S. Pickart, J. Appl. Phys., 1964, 35, 954–955.
20. R. Batulin, M. Cherosov, A. Kiiamov, A. Zinnatullin, F. Vagizov, D. Tayurskii and R. Yusupov, Magnetochemistry, 2022, 8, 86.
21. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092.
22. E. Martínez and A. Caro, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214109.
23. D. Frenkel, B. Smit and M. A. Ratner, Understanding Molecular Simulation: from Algorithms to Applications, Academic press San Diego, 1996, vol. 2.
24. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
25. R. Stepto, T. Chang, P. Kratochvíl, M. Hess, K. Horie, T. Sato and J. Vohlídal, Pure Appl. Chem., 2015, 87, 71–120.
26. S. Murphy, B. Uberuaga, J. Ball, A. Cleave, K. Sickafus, R. Smith and R. Grimes, Solid State Ionics, 2009, 180, 1–8.
27. T. Heisig, J. Kler, H. Du, C. Baeumer, F. Hensling, M. Glöβ, M. Moors, A. Locatelli, T. O. Menteş and F. Genuzio, et al. , Adv. Funct. Mater., 2020, 30, 2004118.
28. H. Zhang, A. H. Ramadan and R. A. De Souza, J. Mater. Chem. A, 2018, 6, 9116–9123.
29. H. Zhang and R. A. De Souza, J. Mater. Chem. A, 2019, 7, 25274–25278.
30. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
31. J. Ball, S. Murphy, R. Grimes, D. Bacorisen, R. Smith, B. Uberuaga and K. Sickafus, Solid State Sci., 2008, 10, 717–724.
32. C. R. Kreller, J. A. Valdez, T. G. Holesinger, J. Morgan, Y. Wang, M. Tang, F. H. Garzon, R. Mukundan, E. L. Brosha and B. P. Uberuaga, J. Mater. Chem. A, 2019, 7, 3917–3923.
33. R. Perriot, B. P. Uberuaga, R. J. Zamora, D. Perez and A. F. Voter, Nat. Commun., 2017, 8, 1–8.
34. V. Kocevski, G. Pilania and B. P. Uberuaga, Front. Chem., 2021, 9, 712543.
35. P. Wilde and C. Catlow, Solid State Ionics, 1998, 112, 173–183.
36. R. Perriot and B. P. Uberuaga, J. Mater. Chem. A, 2015, 3, 11554–11565.
37. J. Shamblin, M. Feygenson, J. Neuefeind, C. L. Tracy, F. Zhang, S. Finkeldei, D. Bosbach, H. Zhou, R. C. Ewing and M. Lang, Nat. Mater., 2016, 15, 507–511.
38. D. Drey, E. O'Quinn, S. Finkeldei, J. Neuefeind and M. Lang, Acta Mater., 2022, 225, 117590.
39. D. Parfitt, A. Chroneos, A. Tarancón and J. A. Kilner, J. Mater. Chem., 2011, 21, 2183–2186.
40. B. Uberuaga, D. Bacorisen, R. Smith, J. Ball, R. Grimes, A. Voter and K. Sickafus, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104116.

---