Dynamics of non-spherical particles in viscoelastic fluids flowing in a microchannel

Abstract

The migration and orientation dynamics of prolate spheroidal particles suspended in a viscoelastic liquid flowing in a square microchannel is experimentally investigated under inertialess flow conditions. The suspending fluid is an aqueous solution of PolyEthylene Oxyde at relatively high concentration characterized by a high level of elasticity and shear-thinning. Fluid viscoelasticity drives the spheroids towards the channel central region at relatively low flow rates when the particles explore the constant viscosity region of the fluid, without showing a preferential orientation. As the flow rate increases and the fluid enters in the shear-thinning region, a smaller fraction of particles migrates at the central channel region, reducing the focusing efficiency. The focused spheroids rotate sufficiently fast to attain a stable orientation with major axis aligned along the flow direction.

---

1. Introduction

Particle manipulation through viscoelastic liquids in microfluidics is a well-established technique to achieve focusing, separation, and ordering in geometrically simple channels.^1–5

Since the first application of the viscoelasticity-driven lateral displacement of particles in microfluidics,⁶ several works have been carried out clarifying the effect of fluid rheology, flow conditions, channel geometry, particle properties on the efficiency of focusing, i.e., the capability to obtain a single plane (2D) or line (3D) of particles. More recently, the formation of equally-spaced aligned particles, referred as “particle ordering”, induced by fluid elasticity has been investigated^7,8 and applied to encapsulation processes.⁹

Most of the available works deal with spherical particle suspensions. However, in real situations, the shape of the suspended particles may be different from the sphere, especially in biological applications, e.g., the biconcave discoid of healthy red blood cells¹⁰ and platelets,¹¹ sickle-like infected red blood cells,¹² germ-tube structure of Candida albicans,^13,14 rod-like shape of Escherichia coli,^15,16 cell spheroids.¹⁷ Needless to say, the dynamics of non-spherical particles in flow may strongly differ from the spherical ones, especially when suspended in non-Newtonian liquids.^18–25

The first experiments of a viscoelastic suspension of non-spherical particles in a microchannel are carried out by Lu and Xuan²⁶ and Lu et al.²⁷ The flow conditions are such that both inertia and elasticity are important (inertio-elastic regime). It has been shown that spheres and peanuts particles follow different trajectories, allowing separation by shape. Peanuts particles migrate slower than spheres and orient along the flow direction in a viscoelastic fluid, in contrast with the Newtonian case where a tumbling motion is observed. Inertio-elastic separation by shape has been also exploited in biological applications.^{14,16,28–31}

All these works highlight the importance of the particle shape on the cross-stream migration. However, the separation mechanism involves both inertia and viscoelasticity so that it is not easy to single out the role of elastic effects. In addition, the shapes of the particles are rather complex, and simple model shapes would be desirable to understand the interplay between particle shape, fluid rheology, and confinement.³²

In this regard, an important step forward is the very recent experimental paper by Tai and Narsimhan³³ that follows a series of theoretical works from the same authors.^34–36 Both the experimental conditions and the theory assumptions are such that the Deborah number (denoted by De and defined as the ratio between the fluid and flow characteristic times) is very small. Specifically, experiments are carried out for spheres, prolate and oblate spheroids with aspect ratio of about 3 suspended in an 8% polyvinylpyrrolidone (PVP) solution with constant viscosity flowing in an 8 cm long straight glass capillary tube. The distributions taken at different distances from the channel inlet show a faster lateral motion for spheres as compared to spheroids. The evolution of the distributions along the channel is fairly predicted by using the particle mobilities evaluated in their previous theoretical works.^35,36 The theoretical results also show that a prolate particle first undergoes a log-rolling motion and then slowly aligns along the flow in a circular tube, whereas no flow alignment is found in a wide-slit channel. An oblate spheroid, instead, initially tumbles and then aligns with its longer axis along the flow in both circular and slit channel. The theory is developed considering a second order fluid model which is valid for slow and slowly varying flows. The experiments are carried in the same weak viscoelastic limit (De = 0.043) as the primary purpose is to validate the theoretical predictions.

Recent numerical simulations investigate the dynamics of a prolate spheroidal particle with aspect ratio 2 in a viscoelastic liquid flowing in a wide-slit channel at moderate Deborah numbers (De = 0.5 and De = 1).²² The results show that the spheroid migrates transversally to the flow direction and, as for spheres, the migration can be towards the channel centerplane or the closest wall. However, wall migration occurs for a narrow set of initial orientations, i.e., for particles near the wall and with major axis close to the neutral direction. Furthermore, for all the investigated parameters, the particle always tends to align along the flow direction, with the alignment process much slower than migration. The discrepancy with the previously mentioned theoretical works on the long-time stable orientation attained by a prolate spheroid in a wide-slit channel might be attributed to the vanishing Deborah number assumption adopted in the theoretical analysis.

In summary, experimental evidences on the effect of fluid elasticity on the dynamics of non-spherical particles in microchannels have been reported for complex shapes in inertio-elastic regime or under conditions of weak elasticity.

In this work, we carry out experiments on the dynamics of a dilute suspension of prolate spheroidal particles in a water solution of polyethylene oxide (PEO) flowing in a square-shaped microchannel. The PEO concentration is chosen in order to explore both the constant viscosity case and the shear-thinning regime by properly selecting the flow rate. The experimental conditions are such that viscoelastic effects are relevant whereas inertia is negligible. The experimental apparatus allows a direct visualization of the particles so that both their lateral position and orientation can be measured. The paper is organized as follows: in Section 2 the relevant dimensionless parameters are presented. Section 3 discusses the preparation procedure of the fluid and the particles, the fluid rheology, the experimental setup, and the particle detection procedure. The results are presented in Section 4 in terms of distributions of the lateral position, tilt angle, and angular velocity. In the same section, the results are discussed and rationalized through a comparison with previous experiments for spheres and theoretical/numerical predictions for spheroids. Finally, conclusions are drawn in Section 5.

2. Dimensionless parameters

It is useful to define some dimensionless parameters to be used in the following sections.

When dealing with viscoelastic fluids, the most important dimensionless parameter is the Deborah number defined for a square-shaped channel, as:

where λ is the fluid relaxation time, Q is the volumetric flow rate, and H is the side of the channel cross section. The Deborah number represents the ratio between the fluid relaxation time and the flow characteristic time t_f = H³/Q. When De = 0, the fluid is Newtonian (because λ = 0), whereas increasing De corresponds to more pronounced viscoelastic effects.

To evaluate the importance of inertial effects, we define the Reynolds number:

with ρ and η the suspending fluid density and viscosity, respectively. The Reynolds number represents the ratio between inertial and viscous forces.

The ratio between the Deborah and Reynolds numbers defines the Elasticity number:

According to the value of El, different situation can be encountered. For El ≫ 1, viscoelastic forces are dominant, inertial ones are prevalent when El ≪ 1, whereas, for El ∼ 1, the viscoelastic forces are comparable with the inertial ones. It is worthwhile to notice that, once selected the fluid and the channel geometry, the Elasticity number is a flow rate independent parameter, since it only depends on the fluid properties and the characteristic channel dimension.

3. Materials and methods

3.1. Suspending fluid and particles

The suspending fluid used in the experiments is a water solution of polyethylene oxide (PEO), with average molecular weight M_w = 4000 kDa (Sigma-Aldrich), at 1.5% wt obtained by dissolving 0.15 g of PEO in 9.85 g of water. The fluid rheological properties are measured by a stress-controlled rheometer (HAAKE MARS III), with cone and plate geometry with diameters of 60 mm and with a solvent trap to avoid fluid evaporation.

Fig. 1a reports the linear viscoelastic response of the fluid for an imposed stress τ = 1 Pa. The typical slopes of 2 and 1 for G′ and G′′ at low frequencies can be observed. Fig. 1b reports the steady-shear viscosity as a function of the shear rate. It can be observed that the zero-shear viscosity is η₀ = 0.40 Pa s, with a shear thinning behavior starting at a shear rate around 3 s⁻¹. The fluid relaxation time is estimated by fitting the flow curve in Fig. 1b with the Carreau model through a standard non-linear regression technique, giving an estimate of the relaxation time λ ≈ 0.18 s.

Fig. 1 (a) Measured elastic modulus G′ (black circles) and loss modulus G′′ (white circles) for the aqueous PEO 1.5% wt as a function of the frequency. The slopes of the low frequency data are 2 and 1 for G′ and G′′, respectively, and denote the expected frequency dependence in the terminal region of a viscoelastic fluid. (b) Measured steady shear viscosity for the aqueous PEO 1.5% wt as a function of the shear rate.

Concerning the particles, starting from polystyrene (PS) spheres (molecular probes), the procedure reported by Champion et al.³⁷ was followed to get ellipsoidal particles. Briefly, polyvinyl alcohol (PVA) with average molecular weight M_w = 89 000–98 000, 99% hydrolyzed (Sigma-Aldrich) is dissolved in water at 85 °C at a 10% wt vol⁻¹ concentration. Then, PS spherical particles (average diameter 9 μm), are dispersed in the solution at a concentration of 0.04% wt vol⁻¹ and the dispersion is poured into some plastic containers and it is dried for 20 hours up to a thickness of about 70 μm.

After the drying, the films are cut into rectangular sections and inserted between the clamps of the stretching device. In order to obtain the non-spherical particles, it is necessary to liquefy the particles by reaching a temperature higher than the glass transition temperature of PS (around 100 °C) and then to stretch the film. For this reason, the stretching system is inserted inside a climate chamber to heat the system up to 120 °C. Once a uniform temperature is reached in the chamber, the film is stretched with a rate of 0.5 mm s⁻¹. To separate the particles from the PVA, the film is dissolved in an isopropanol–water solution (30% vol) at 65 °C. Then, the solution is centrifugated for 5 minutes at 5400 rpm, separating the particles at the bottom and the solution at the top. Subsequently, the particles are added to the water solution of PEO 1.5% wt in order to obtain a dilute suspension with a volume fraction ϕ = 0.003%.

The aspect ratio (AR) of the obtained non-spherical particles is evaluated by observing them at the outlet of the channel. Fig. 2 reports the distribution of the aspect ratio showing that most of the particles have an AR between 2.5 and 5, and only few particles present a lower or higher AR.

Fig. 2 Aspect ratio distribution for polystyrene spheroidal particles measured at the channel outlet.

3.2. Experimental setup

The experimental setup is shown in Fig. 3 and consists of: (a) a 5 cm long microchannel with a square cross-section with side 100 μm, (b) a syringe pump (KDS 200P Legacy) to impose the flow rate, (c) a light source to illuminate the region of interest, (d) a system of optical lenses with a 20× objective to get clearer and magnified images, (e) a high-speed CMOS area scan camera (Flare 4M180-CL) to observe the particles moving in the microchannel, working at a variable frame rate between 75 and 150 according to the fluid flow rate.

Fig. 3 Experimental setup: (a) 5 cm long microchannel, (b) syringe pump, (c) light source, (d) optical lenses, (e) high-speed CMOS area scan camera.

All the experiments are carried out at room temperature. To check if a proper focusing is present along the entire length of the channel, the observation is performed just after the inlet (1 mm) and in correspondence of the outlet (49 mm).

Two flow rates are considered: Q = 20 μL h⁻¹ and Q = 100 μL h⁻¹. As will be discussed later, the flow rate values are chosen to investigate the effect of both the constant viscosity rheology (low flow rate) and of the shear-thinning regime (high flow rate) on the particle dynamics. The dimensionless numbers corresponding to the low flow rate are De ∼ 1, Re = 1.37 × 10⁻⁴. At high flow rate, we obtain De ∼ 5, Re = 7 × 10⁻⁴. In both cases, the Elasticity number is El ≫ 1, hence elastic effects are relevant whereas inertia is negligible.

3.3. Particle tracking and distributions

To visualize and detect the particle motion, an in-house routine in MATLAB was developed. First, the background was removed by image subtraction to get clean image sequence (Fig. 4A). Then, an image thresholding process has been applied to all the frames of each recorded video to get binary images that allow to better distinguish the particle from the background, as shown in Fig. 4B. The MATLAB app “Image Region Analyzer” has been then used, which is able to analyze a binary image, detect all the white pixels, and consider the adjacent ones as a single object, providing in output information such as the particle major axis and the orientation with respect to the horizontal direction. After that, to evaluate the particle position in the channel, a recursive function has been used. Starting from an initial white pixel, its coordinates are saved in a variable, then the pixel is blackened, and the adjacent ones are checked to verify if they are white or not. If one of them is white, the coordinates of the white pixel are added to the variable used before and this pixel is chosen as a new starting one. Hence, the coordinates of all the white pixels forming the particle are contained in a single variable, and the barycenter can be obtained. At the end, the barycenter distance from the centerline could be computed by knowing the coordinates of the centerline.

Fig. 4 (A) Cleaned frame, (B) frame after image thresholding. In panel (A), the indication of the tilt angle is shown.

The particle motion is recorded within an observation window of 563 μm and, from the resulting videos, we measure the barycenter position of the particle with respect to the channel centerline. We also measure the orientation of the particles. In this regard, an accurate evaluation of the particle orientation would require two orthogonal cameras as the particles are generally oriented with major axis out of the observation plane. The main purpose of tracking the orientation is to assess whether the particle achieves a stable orientation. We anticipate that two kinds of orientational dynamics are observed: tumbling and flow alignment. An example of tumbling particles is shown in Fig. 5A and B. The sequence of superimposed frames in Fig. 5A shows that the particle is rotating around the axis orthogonal to the observation plane. However, the last frames show a blurred and shorter shape, suggesting that the particle is also rotating around the flow axis. The sequence of frames in Fig. 5B shows tumbling as well but apparently in the opposite direction as one would expect. This is likely due to the fact that the particle is travelling near the top or bottom walls so that its tumbling motion is affected by two orthogonal walls. Fig. 5C displays a sequence of frames where the spheroid is oriented along the flow. We, then, define the “tilt angle”, depicted in Fig. 4A, as the angle between the flow direction and the direction obtained by connecting the two extrema of the observed particle shape (that can be seen as the projection of the particle over the observation plane). For a tumbling motion as in Fig. 5A and B, the tilt angle continuously changes during the frame sequence, whereas it is nearly constant and close to 0° for the images in Fig. 5C. As said before, our interest is to investigate the orientation of the particles once, eventually, they have reached the channel central region. Hence, the evaluation of the tilt angle is limited to these particles only.

Fig. 5 Typical sequences of images obtained by our observations. Panels (A) and (B) display a spheroid undergoing tumbling motion, panel (C) shows the alignment of the particle along the flow direction. The images have been obtained by superimposing successive frames.

The results will be presented in terms of distributions. To this aim, the channel height is divided in 7 bins, each one of width equal to 14 μm, ranging from −49, the lower wall, to 49, the upper wall, and it is counted how many particles belong to each bin. From the obtained data, a distribution function, normalized with respect to the total population of particles, is obtained.

We verified the capability of our setup to detect particles at different depth. To this aim, we changed the focusing of the microscope verifying that the particles passing in the channel are always detectable. Hence, the number of particles in each bin includes all particles passing through the selected height, independently from their position along the depth.

4. Results and discussion

Fig. 6 reports the distributions of the particle position at a flow rate of Q = 20 μL h⁻¹ close to the inlet (blue bars) and the outlet (cyan bars) of the microchannel. The diagram shows an almost uniform distribution at the inlet, without the presence of a prevailing peak; on the contrary, the distribution in correspondence of the outlet results much more peaked around the channel central region, with almost 70% of the total particles included in the region between −7 and 7 μm after 5 cm from the channel inlet, confirming that fluid viscoelasticity induces a lateral migration of spheroids towards the channel center. It is interesting to note that almost no particle flows near the walls. In a longer channel, we expect that the particles belonging to the bins adjacent to the central one migrate there, obtaining the formation of a single line of particles.

Fig. 6 Distributions of the lateral position of spheroidal particles in the PEO 1.5% wt at the inlet (blue bars) and outlet (cyan bars) of the square microchannel at a flow rate of Q = 20 μL h⁻¹.

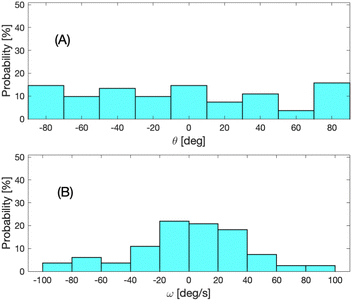
In Fig. 7A, the distribution of the tilt angle (see Section 3.3 for the definition) for spheroidal particles passing in the central bin is reported. The data clearly show that a preferential angle is not observed, suggesting that the particles are mainly tumbling, as displayed in Fig. 5B. For the central bin, we have also evaluated the rotational velocities of the particles, i.e., the angular velocity component over the observation plane, as the average of Δθ/Δt over all the frames of the acquired videos, with Δt the interval time between two consecutive frames. As shown in Fig. 7B, most of the particles have a small angular velocity. However, the tails of the distribution extend up to rotational velocities of about 100 deg s⁻¹, denoting a faster tumbling motion. We did not find a correlation between the particle angular velocity and their transversal position. Indeed, the relatively high angular velocity is observed both for particles that are at the boundaries of the central bin and for those that travel at the channel centerline. As discussed later, we conclude that a distance of 5 cm of the channel inlet is insufficient to fully align the particles at a flow rate of Q = 20 μL h⁻¹.

Fig. 7 Distribution of the tilt angle (A) and of the angular velocity (B) of spheroidal particles in the PEO 1.5% wt at the outlet of the square microchannel at a flow rate of Q = 20 μL h⁻¹ for the particles passing in the central bin.

Let us now consider the high flow rate case Q = 100 μL h⁻¹. The inlet and outlet distributions are reported in Fig. 8. In this case, the particle migration appears to be much less effective since the distribution is less peaked around the channel central region. Indeed, only about 30% of the total particles is included in the region between −7 and 7 μm and much more particles are found in the regions close to the walls. Nevertheless, the central bar in outlet is notably higher than the same bar in inlet, denoting that an inward lateral migration is taking place. Also in this case, the tilt angle is investigated for the particles included in the central bin region in correspondence of the outlet.

Fig. 8 Distributions of the lateral position of spheroidal particles in the PEO 1.5% wt at the inlet (blue bars) and outlet (cyan bars) of the square microchannel at a flow rate of Q = 100 μL h⁻¹.

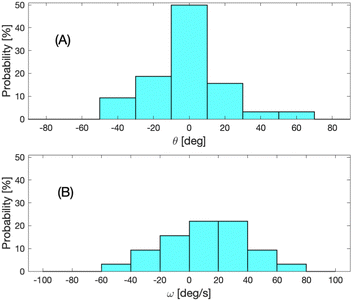
Conversely to the previous case, the data in Fig. 9A highlight a preferential angle between −10° and 10°, meaning that most of the particles result aligned along the flow direction as displayed in Fig. 5C. The rotational velocity distribution reported in Fig. 9B shows that most of the particles travelling in the central bin have a very small angular velocity. Some of these particles are those with tilt angle in the range −10° and 10 that have almost reached flow alignment. The (few) other particles slowly tumble, likely reaching an orientation towards the flow at larger distances. Notice that the distribution is slightly asymmetric towards positive angular velocity values, denoting a larger number of particles in the upper half of the channel. This agrees with the outlet distribution in Fig. 8.

Fig. 9 Distribution of the tilt angle (A) and of the angular velocity (B) of spheroidal particles in the PEO 1.5% wt at the outlet of the square microchannel at a flow rate of Q = 100 μL h⁻¹ for the particles passing in the central bin.

The experimental results just presented show that spheroidal particles can be focused at the central region of a square channel filled by a viscoelastic fluid, in agreement with recent theoretical predictions^34–36 and numerical simulations.²² The flow rate plays a crucial role on the migration direction and focusing rate. At low flow rate (Q = 20 μL h⁻¹), about 70% of the particles have been focused around the channel centerline after 5 cm from the inlet (Fig. 6). No particle flowing at the wall is observed. These results agree with those reported in Del Giudice et al.³⁸ for 10 μm spherical particles in a square channel with side 100 μm filled with a PEO 1.6% having a similar rheology of the fluid employed in the present work. The measurements taken at 8 cm from the channel inlet showed a migration towards the channel centerline at low flow rate (Q = 6 μL h⁻¹).

As the flow rate is increased to Q = 100 μL h⁻¹, our results show a central peak in the lateral particle position distribution, which is higher than the corresponding bar measured in inlet, denoting a migration of particles towards the channel central region. However, particles are also observed to flow in other lateral positions up to the walls. The reduced focusing efficiency at high flow rates is due to the shear-thinning of the fluid. As previously reported,³⁸ a spherical particle in a viscoelastic, shear-thinning fluid migrates towards the channel centerline or the corners depending on its initial position. The two migration directions are separated by a separatrix that approaches the channel centerline as the Deborah number increases, resulting in a wider wall-attraction region. To quantify the entity of the viscosity thinning in our experiments, we have evaluated the shear rate distribution in the microchannel in absence of particles by numerical simulations. Since we are interested in the order of magnitude, we have employed the (inelastic) Carreau constitutive equation to model the PEO solution with parameters obtained by fitting the viscosity curve in Fig. 1. At the low flow rate of Q = 20 μL h⁻¹, the average shear rate is about 30 s⁻¹, with a maximum value of about 60 s⁻¹ at the middle of the channel sides. As shown in Fig. 1, the shear rate window in the channel corresponds to the onset of the shear-thinning. On the contrary, at Q = 100 μL h⁻¹, the average shear rate is 130 s⁻¹, with a shear rate between 10 s⁻¹ and 300 s⁻¹ in almost the whole channel (except a very narrow region around the centerline and the corners), corresponding to a significant viscosity variation. Hence, the low flow rate value selected in this work corresponds to a case where the viscosity is nearly constant, whereas the high value to a regime where the shear-thinning is relevant.

Our measurements at high flow rate differ from those reported by Del Giudice et al.³⁸ for spheres under similar conditions (the flow rate was set to Q = 180 μL h⁻¹) where an accumulation of the particles near the corners was observed with no particle at the central channel region. Although in our experiments the flow rate is lower and the observations are taken closer to the inlet (5 cm vs. 8 cm), Del Giudice et al.³⁸ reported the same scenario for a flow rate of 60 μL h⁻¹. Hence, the lower flow rate and the shorter focusing length do not seem to justify the different particle distributions. Concerning the effect of fluid rheology, the PEO solution used in this work is slightly less concentrated than the one used in Del Giudice et al.³⁸ (1.5% vs. 1.6%) resulting in a lower zero-shear viscosity. The viscosity curve, however, shows comparable features with the onset of the shear-thinning at around 5 s⁻¹ and a similar slope in the thinning region. The shape of the particles might be responsible for the different migration mechanism. D’Avino et al.²² showed by numerical simulations that the migration direction for non-spherical particles in a wide-slit channel depends on their orientation. Particles oriented with major axis close to the vorticity direction migrate towards the centerplane or the closest wall depending on their position along the channel gap like spheres. On the contrary, wall-attraction is suppressed for particles aligned along the flow, even if initially released very close to the wall, due to the high normal stress region between the particle tip and the wall, pushing the spheroid away from the wall.²² Hence, the lateral motion towards the wall of spheroids is possible, but it is restricted to a narrow set of initial orientations. Although the channel employed in the present work is not a wide-slit geometry, we expect an effect of the particle orientation on the migration direction as well which could be even enhanced by the presence of four confining walls (instead of two as in the slit channel). In addition, steric effects due to the elongated shape should facilitate the particles to fall within the center-attractive region during tumbling, further enhancing the focusing mechanism of spheroids as compared to spheres.

As a final comment, we would like to emphasize that shear-thinning still works against the focusing mechanism, slowing down the migration velocity, especially for the particles near the separatrix. Likely, the distribution at 5 cm in Fig. 8 is not steady and continues evolving as the particles flow along the channel. At larger distances from the channel inlet, we expect a central peak due to the focused particles and two lateral peaks with particles tumbling (or rolling) near the walls.

Concerning the particle orientation, the measurements reported in Fig. 7A show that, at low flow rate (Q = 20 μL h⁻¹), the spheroids flowing around the channel central region do not show a clear preferential orientation. This observation once again agrees with previous numerical results²² reporting that the migration mechanism is much faster than the attainment of a stable orientation, i.e., the spheroids are first focused and then slowly change their orientation. This is due to the fact that the spheroids feel a weak velocity gradient when flowing in a region around the channel centerline (the velocity gradient is zero if the particle has the barycenter on the centerline and is aligned with the major axis along or perpendicular to the flow). The simulation results showed that the characteristic rotation time depends on the particle orientation and can be even one order magnitude higher than the migration time,²²i.e., a channel ten times longer is needed to observe a stable orientation along the flow. The tilt angle distribution displayed in Fig. 7A suggests that a channel of 5 cm is insufficient to align all the focused particles at low flow rate. In contrast, at the high flow rate, the tilt angle distribution of the focused particles shows a clear peak in the range [−10°,10°] (Fig. 9A), denoting that the spheroids are almost completely aligned with major axis along the flow direction. In this case, indeed, the particles experience a larger velocity gradient (due to the high flow rate) that speeds up the rotation rate and the achievement of the stable orientation.

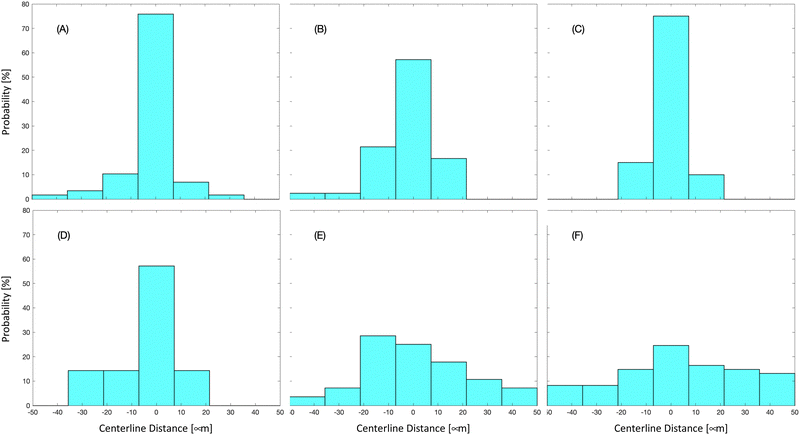
The distributions reported in the previous figures consider all the particles passing through the observation window. To investigate the effect of the aspect ratio on the lateral migration phenomenon, we have evaluated the distributions of the lateral position of the particles for different aspect ratios. The results are displayed in Fig. 10 for the low (top row) and high (bottom row) flow rate. We have divided the aspect ratio range in three sets. The leftmost distributions in Fig. 10 refer to particles with aspect ratio lower than 2.9, the rightmost panels to aspect ratio higher than 3.5, and the middle plots to aspect ratio in between these two values. The results clearly show that, at low flow rate, the particles migrate towards the channel central region regardless of the aspect ratio, i.e., a distance from the channel inlet of 5 cm is sufficient to observe the migration of all the particles. On the contrary, at high flow rate, a clear central peak is observed only for particles with small aspect ratio, whereas the distributions are flatter as the aspect ratio increases. Hence, in this case, a channel of 5 cm is sufficient to focus only the particles with aspect ratio relatively low, and a longer channel is required for more elongated particles. These results agree with what reported in Tai and Narsimhan³³ where the fastest migration was found for spheres.

Fig. 10 Distributions of the lateral position of spheroidal particles in the PEO 1.5% wt at the outlet of the square microchannel at a flow rate of Q = 20 μL h⁻¹ (top row) and Q = 100 μL h⁻¹ (bottom row) for particle aspect ratios lower than 2.9 (A) and (D), between 2.9 and 3.5 (B) and (E), and higher than 3.5 (C) and (F).

5. Conclusions

In this work, the lateral migration and orientation of spheroidal particles in a viscoelastic fluid in a square-shaped microchannel is experimentally investigated. The liquid is an aqueous solution of PEO at mass concentration 1.5% wt, showing a relatively high level of elasticity and shear-thinning. Experiments are carried at two flow rates. At the lowest one, the viscosity of the fluid is nearly constant, while the highest flow rate corresponds to a shear rate region where the shear-thinning is relevant. In all experiments, inertial effects are irrelevant.

Our results show that fluid viscoelasticity drives the spheroids towards the channel central region as the shear rate distribution in the channel is such that the viscosity is nearly constant (low flow rate). At the channel outlet, the focused particles do not show a preferential orientation due to the low angular velocity experienced around the channel centerline. As the flow rate increases and the fluid enters in the shear-thinning region, the focusing efficiency reduces. However, at variance with a suspension of spheres in the same fluid and under similar flow conditions, the migration of spheroids towards the channel center is still observed along with particles tumbling near the walls. At high flow rate, the spheroids that reach the central channel region rotate sufficiently fast to attain a stable orientation with major axis aligned along the flow direction.

In summary, spheroidal particles are less likely to migrate towards the wall as compared to spheres, even in a shear-thinning fluid. This is due to the high normal stress region between the particle tip and the wall that pushes the particle away from the wall.²² This effect is more pronounced as the particle aspect ratio increases. However, more elongated particles migrate slowly, and longer channels are required to get a 3D focusing with all the particles aligned at the channel centerline and with major axis along the flow direction. This has a relevant impact on the ordering mechanism⁷ as the focused particles have different orientations resulting in complex hydrodynamic interactions.

Finally, although the in-plane tilt angle and angular velocity give information about the capability of fluid elasticity to align the particles along the flow direction, the 3D orientational dynamics of elongated objects is rather complex and a full characterization would require two orthogonal points of view. The ordering mechanism of non-spherical particles along with their detailed orientational dynamics will be part of future research.

Author contributions

AL: data curation, formal analysis, investigation, software, visualization, writing (original draft). FG: data curation, visualization. PLM: conceptualization, formal analysis, investigation, writing (review and editing). DL and GDA: conceptualization, funding acquisition, formal analysis, investigation, supervision, writing (original draft), writing (review and editing).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Mr F. Docimo for the technical support in the development of the setup.

Notes and references

1. G. D’Avino, F. Greco and P. L. Maffettone, Annu. Rev. Fluid Mech., 2017, 49, 341–360.
2. X. Lu, C. Liu, G. Hu and X. Xuan, J. Colloid Interface Sci., 2017, 500, 182–201.
3. D. Yuan, Q. Zhao, S. Yan, S.-Y. Tang, G. Alici, J. Zhang and W. Li, Lab Chip, 2018, 18, 551–567.
4. J. Zhou and I. Papautsky, Microsyst. Nanoeng., 2020, 6, 113.
5. M. K. D. Manshadi, M. Mohammadi, L. K. Monfared and A. Sanati-Nezhad, Biotechnol. Bioeng., 2020, 117, 580–592.
6. A. M. Leshansky, A. Bransky, N. Korin and U. Dinnar, Phys. Rev. Lett., 2007, 98, 234501.
7. F. Del Giudice, G. D’Avino, F. Greco, P. L. Maffettone and A. Q. Shen, Phys. Rev. Appl., 2018, 10, 064058.
8. L. Liu, H. Xu, H. Xiu, N. Xiang and Z. Ni, Analyst, 2020, 145, 5128–5133.
9. K. Shahrivar and F. Del Giudice, Soft Matter, 2022, 18, 5928–5933.
10. K. Khairy, J. Foo and J. Howard, Cell. Mol. Bioeng., 2008, 1, 173–181.
11. N. C. Jain, Thromb. Haemostasis, 1975, 33, 501–507.
12. A. Aich, Y. Lamarre, D. P. Sacomani, S. Kashima, D. T. Covas and L. G. de la Torre, Front. Mol. Biosci., 2021, 7, 1–17.
13. D. W. R. Mackenzie, J. Clin. Pathol., 1962, 15, 563–565.
14. J. Nam, H. Jee, W. S. Jang, J. Yoon, B. G. Park, S. J. Lee and C. S. Lim, Micromachines, 2019, 10, 817.
15. X. Chen, L. Zhou, K. Tian, A. Kumar, S. Singh, B. A. Prior and Z. Wang, Biotechnol. Adv., 2013, 31, 1200–1223.
16. T. Zhang, H. Liu, K. Okano, T. Tang, K. Inoue, Y. Yamazaki, H. Kamikubo, A. K. Cain, Y. Tanaka, D. W. Inglis, Y. Hosokawa, Y. Yaxiaer and M. Li, Lab Chip, 2022, 22, 2801–2809.
17. K. Białkowska, P. Komorowski, M. Bryszewska and K. Miłowska, Int. J. Mol. Sci., 2020, 21, 6225.
18. L. G. Leal, J. Fluid Mech., 1975, 69, 305–337.
19. D. Z. Gunes, R. Scirocco, J. Mewis and J. Vermant, J. Non-Newtonian Fluid Mech., 2008, 155, 39–50.
20. G. D’Avino, M. A. Hulsen, F. Greco and P. L. Maffettone, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 43006.
21. V. Dabade, N. K. Marath and G. Subramanian, J. Fluid Mech., 2015, 778, 133–188.
22. G. D’Avino, M. A. Hulsen, F. Greco and P. L. Maffettone, J. Non-Newtonian Fluid Mech., 2019, 263, 33–41.
23. Y. Wang, Z. Yu and J. Lin, Microfluid. Nanofluid., 2019, 23, 89.
24. B. Liu, J. Lin, X. Ku and Z. Yu, Rheol. J., 2021, 33, 343–355.
25. G. D’Avino, J. Non-Newtonian Fluid Mech., 2022, 310, 104947.
26. X. Lu and X. Xuan, Anal. Chem., 2015, 87, 11523–11530.
27. X. Lu, L. Zhu, R. Hua and X. Xuan, Appl. Phys. Lett., 2015, 107, 264102.
28. D. Yuan, S. Yan, J. Zhang, R. M. Guijt, Q. Zhao and W. Li, Anal. Chem., 2021, 93, 12648–12654.
29. P. Liu, H. Liu, L. Semenec, D. Yuan, S. Yan, A. K. Cain and M. Li, Microsyst. Nanoeng., 2022, 8, 7.
30. H. Lim, J. Y. Kim, S. Choo, C. Lee, B. J. Han, C. S. Lim and J. Nam, Micromachines, 2023, 14, 712.
31. P. Liu, H. Liu, D. Yuan, D. Jang, S. Yan and M. Li, Anal. Chem., 2021, 93, 1586–1595.
32. D. Jiang, S. Liu and W. Tang, Micromachines, 2022, 13, 1659.
33. C.-W. Tai and V. Narsimhan, Soft Matter, 2022, 18, 4613–4624.
34. C. Tai, S. Wang and V. Narsimhan, AIChE J., 2020, 66, 1–14.
35. S. Wang, C.-W. Tai and V. Narsimhan, Phys. Fluids, 2020, 32, 120–124.
36. C.-W. Tai, S. Wang and V. Narsimhan, J. Fluid Mech., 2020, 895, A6.
37. J. A. Champion, Y. K. Katare and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11901–11904.
38. F. Del Giudice, G. D’Avino, F. Greco, P. A. Netti and P. L. Maffettone, Microfluid. Nanofluid., 2015, 19, 95–104.

---