Droplet detachment force and its relation to Young–Dupre adhesion

Abstract

Droplets adhere to surfaces due to their surface tension γ and understanding the vertical force F_d required to detach the droplet is key to many technologies (e.g., inkjet printing, optimal paint formulations). Here, we predicted F_d on different surfaces by numerically solving the Young–Laplace equation. Our numerical results are consistent with previously reported results for a wide range of experimental conditions: droplets subjected to surface vs. body forces with |F_d| ranging from nano- to milli-newtons, droplet radii R ranging from tens of microns to several millimetres, and for various surfaces (micro-/nano-structured superhydrophobic vs. lubricated surfaces). Finally, we derive an analytic solution for F_d on highly hydrophobic surfaces and further show that for receding contact angle θ_r > 140°, the normalized F_d/πR is equivalent to the Young–Dupre work of adhesion γ(1 + cos θ_r).

---

We encounter the effects of droplet adhesion every day: dew of droplets can be seen clinging to blades of grass in early morning, and droplets stuck to camera lenses affect image clarity on rainy/misty days.^1,2 Despite the prevalence of the phenomenon and clear importance in various technologies (from inkjet printing³ to agricultural technologies^4,5), there is still no consensus on how to link the vertical force F_d required to detach a droplet from a surface to its wetting properties.^6–9 For example, Tadmor et al. (2017) proposed that F_d/2πr (where r is the contact radius) is equivalent to the Young–Dupre work of adhesion γ(1 + cos θ_r) where γ is the surface tension and θ_r is the receding contact angle,¹⁰ but others disagreed.^11–13

Extensive experimental data for droplet detachment exist in the literature,^10,13–17 but their interpretation is complicated by the fact that various groups use very different methods to measure F_d (Fig. 1) with very different droplet volumes (V = 5 pL–10 μL) and detachment speeds (U = 10⁻⁶–10⁻³ m s⁻¹). As a result, different groups reported force magnitudes that vary considerably from 38 nN (as measured using atomic force microscopy or AFM) to 1.8 μN (force microbalance),⁷ and 0.36 mN (centrifugal adhesion balance or CAB).¹⁰ We will show later that the various datasets are in broad agreement with one another once F_d is normalized by the droplet radius R. The various approaches described in the literature can be broadly categorized into surface vs. body force methods—an important distinction that is often ignored. Methods such as AFM and microbalance force sensor (Fig. 1A and B) apply a pulling force only at the top surface of the droplet, i.e., surface force. In contrast, in CAB (and other methods¹⁸), the centrifugal pulling force is applied to the entire droplet, i.e., body force.

Fig. 1 Different methods to measure droplet detachment force F_d using (A) atomic force microscope (volume V = 65 pL, U = 2 μm s⁻¹, superhydrophobic surface), (B) microbalance force sensor (V = 5 μL, U = 5 μm s⁻¹, superhydrophobic surface), and (C) centrifugal adhesion balance (V = 10 μL, hydrophobic). A is original unpublished data, while B and C are taken from Daniel et al. (2023)⁷ and Tadmor et al. (2017),¹⁰ respectively.

In this paper, we show that the quasi-static approximation applies during the retraction process for slow detachment speeds, and that F_d can be predicted by numerically solving the Young–Laplace equation.¹⁹ Our numerical results are consistent with the experimental data collected independently by various research groups. We derive an analytic solution for F_d and further show that for a droplet of radius R the normalized F_d/πR (as opposed to F_d/2πr) is equivalent to the Young–Dupre work of adhesion γ(1 + cos θ_r) for highly hydrophobic surfaces with θ_r > 140°. In contrast, for less hydrophobic surfaces with θ_r < 140° there is no simple way to relate F_d to the Young–Dupre work of adhesion.

Our analysis is general and applies for a wide range of experimental conditions (including those in Fig. 1) and different surfaces (flat, micro-/nano-structured superhydrophobic,²⁰ and lubricated surfaces^21,22).

1 Methods

1.1 Surface preparation

To make the superhydrophobic surface in Fig. 5A, we started with a 3 mm thick Sylgard 184 polydimethylsiloxane (PDMS) slab. We used a 10 : 1 monomer to linker ratio which was cured by heating the mixture at 70 °C for 3 hours. We then spraycoated the cured PDMS slab with a layer of hydrophobic nanoparticles (Glaco Mirror Coat Zero, Soft 99 Co.) before placing it vertically to dry for one hour before use. Note that the wetting properties of the resulting surface is dominated by the structured nanoparticles. We chose to use a PDMS slab as the base so that we can easily puncture the surface with a 34 Gauge needle (see Section 1.1.1). Scanning electron micrograph of the resulting nanostructures can be found in Fig. 1 of our previous publication.²³

To make the lubricated surface in Fig. 5B, we coated a thin layer of fluorinated oil (GPL Krytox 101, ∼3 μm thick, viscosity η = 30 mPa s⁻¹) onto the nanostructured PDMS slab.

1.1.1 Measuring detachment force. To measure the detachment force using AFM, please see our previous publications.^14,24 We also measure detachment force due to gravity by first puncturing the PDMS slab with a 34 Gauge needle (outer diameter of 0.16 mm), placing the surface upside down, and using a syringe pump to slowly increase the droplet volume until the droplet detaches (due to gravity).

1.1.2 Numerical simulations. To solve the axi-symmetric Young–Laplace equation, we use the shooting method implemented in the Python programming language. We have described the method at length in our previous publication.¹⁴ Python codes used here are provided in github repositories.^25,26 Since we are solving for an axi-symmetric system, the contact angle value we use is necessarily a radially averaged value.

2 Results and discussions

Previously, different groups have suggested (implicitly⁶ or explicitly^13,19) that detachment results when the droplet is so stretched that it can no longer be described by the Young–Laplace equation. In contrast, Tadmor et al. (2017) suggest that the detachment force should be related to the Young–Dupre work of adhesion,¹⁰ while others disagreed.^11–13 In this paper, we aim to reconcile these different views.

We start by numerically solving the axisymmetric Young–Laplace equation for a droplet subjected to either a surface force (Fig. 2) or a body force (Fig. 3). We can recast the Young–Laplace equation into its non-dimensional form by normalizing the various quantities with V^1/3 and surface tension γ (e.g., ũ = u/V^1/3, ΔP̃ = ΔPV^1/3/γ) to give

where r is the droplet's contact radius and we assume that the droplet retracts with a constant receding contact angle θ_r.

Fig. 2 (A) Schematic of a droplet attached to a disc of radius a and retracting from the surface. (B) Numerical solutions to Young–Laplace equation showing the non-dimensional force F/γV^1/3 as a function of increasing h/V^1/3 for different contact angles θ_r = 40–160°. Inset shows the magnified plot for θ_r = 160°. (C)–(E) Droplet geometries at the point of detachment for different θ_r.

Fig. 3 (A) Schematic of a droplet of volume V and density ρ subjected to a body force F = Vρg_eff where g_eff is the effective acceleration. (B) Numerical solutions to Young–Laplace equation showing the non-dimensional contact radius r/V^1/3 as a function of increasing F/γV^1/3 for different contact angles θ_r = 2–160°. Inset shows the magnified plot for θ_r = 160°. (C)–(E) Droplet geometries at the point of detachment for different θ_r. Scale bar in C is the non-dimensional capillary length for θ_r = 2°.

For the surface force method, we can approximate the droplet geometry as being held by a circular disc with radius a at the top and further impose the boundary condition ũ(0) = ã (Fig. 2A) and assume that the Laplace pressure ΔP̃ = ΔP̃₀ is constant (i.e., we neglect the effects of gravity since the droplets are typically smaller than the capillary length). We performed numerical simulations for different θ_r = 40–160° and fixed ã = 0.45 (which approximates well the geometries used in various papers^14,15 including in Fig. 1A and B) and plotted the force acting on the droplet

F̃ = −2πr̃ sin θ + πr̃²ΔP̃₀ (2)

(in its non-dimensional form) as we progressively stretched the droplet (Fig. 2B).

We terminate the simulations when we can no longer achieve numerical convergence; this is the point of droplet detachment and we can define the corresponding detachment force F̃_d which strongly depends on θ_r, i.e., the surface wetting properties. For hydrophilic surfaces, the detachment force is high (F̃_d = 1.6 for θ_r = 40°) but can become negligible for superhydrophobic surfaces (F̃_d = 0.1 for θ_r = 160°). For hydrophilic surfaces, the droplet is highly stretched at the point of detachment and resembles more of a capillary bridge (Fig. 2C). In contrast, the droplet retains its spherical cap shape till the point of detachment for highly hydrophobic surfaces (Fig. 2D and E).

Interestingly, the droplet experiences a maximum force F̃_max > F̃_d before detaching. For hydrophilic surfaces, the two force quantities can be quite different, with F̃_max/F̃_d = 2.2 for θ_r = 40° (Fig. 2B). In contrast, F̃_max/F̃_d = 1.1 for θ_r = 160° (inset in Fig. 2B)

We now repeat the numerical simulations for a droplet subjected to an effective acceleration g_eff and an equivalent non-dimensional body force.

F̃ = V^2/3ρg_eff/γ. (3)

The droplet geometry still obeys the Young–Laplace equation in eqn (1), except with different boundary conditions ũ(0) = ũ′(0) = 0 and with the Laplace pressure ΔP̃ = ΔP̃₀ − F̃z̃ that varies with position z̃ (Fig. 3A).

We progressively stretch the droplets by increasing F̃ and noted the decrease in base radius r̃ for different θ_r = 2–160° (Fig. 3B). Note that F̃; is the input variable here, whereas it is the output variable in Fig. 2B. As is before, we terminate the simulations when there is no longer numerical convergence, and we can define the corresponding detachment force F̃_d (but no F̃_max). For hydrophilic surfaces, the droplet resembles a spherical cap whose base is surrounded by a wetting skirt/meniscus of size the non-dimensional capillary length (see scale bar in Fig. 3C). The wetting skirt is a low pressure region and provides the suction required to hold onto the droplet. In contrast, for highly hydrophobic surfaces, the droplet retains its spherical cap geometry (Fig. 3D and E).

We can check the validity of our simulation results by superimposing experimental data collected independently by five different research groups using different methodologies ranging from AFM,¹⁴ microbalance force sensors,^15,16 and CAB.^10,13 When the normalized detachment force F_d/γV^1/3 is plotted against ε = 1 + cos θ_r, all the experimental data are consistent with results from our numerical simulations for both surface and body forces (blue and red curves in Fig. 4A, respectively). We have also included results collected by us (open symbols in Fig. 4A), including previously unpublished results in Fig. 1A and 5.

Fig. 4 (A) Plot of F_d/γV^1/3 as a function of (1 + cos θ_r). Unfilled data points are our experimental results corresponding to Fig. 1A and 5A, B and from our previous paper,¹⁴ while filled data points are results from various groups.^10,13,15,16 (B) Droplet geometry during the detachment process for high θ_r. Raw dataset can be found in ref. 27.

Fig. 5 Droplet detachment due to gravity. Water droplets at the point of detachment for (A) superhydrophobic and (B) lubricated surfaces. Raw dataset can be found in ref. 27.

Interestingly, the two master curves approach each other in the limit of θ_r > 140°. In other words, F_d measurement is independent of the method chosen for highly hydrophobic surfaces with θ_r > 140°. In contrast, for less hydrophobic surfaces with θ_r < 140°, F_d measurement values depend strongly on the method chosen (surface vs. body forces), a point that is not well appreciated in the literature.

We have tabulated the simulation results in Table S1 (ESI†): we found that F̃_d values for body and surface forces differ by 10% or less for θ_r > 140°. For convenience, the numerical solutions of F̃_d for surface and body force methods can be fitted globally with the polynomial functions

Note however that there are significant local deviation of the actual simulation results from the fitted polynomials in eqn (4). If we perform regression analysis only for θ > 140° (equivalently for ε < 0.2), we found that F̃_d = 1.95ε for both body and surface forces. The slope of 1.95 has a simple physical interpretation which we will explore in the next section.

Relation of F_d to Young–Dupre work of adhesion

We can derive an analytic expression for F_d in terms of ε = 1 + cos θ_r for ε ≪ 1, i.e., in the limit of θ_r → 180°. According to Young–Dupre, the energy required to detach the droplet is given by ΔE_γ = πr²γε, which assumes that the droplet retains its spherical cap geometry after detachment. This is a reasonable assumption for a frozen water droplet detaching from a cold surface,²⁸ but not for liquid droplets at room temperature. In reality, the detached droplet adopts a spherical shape (Fig. 4B); using simple geometrical arguments and power series expression, we can show that ΔE_γ ≈ πR²γε². At the same time, the droplet's centroid is raised by an amount δz = z′ − z ≈ Rε (See full derivation in Fig. S1, ESI†).

Since the work done by the detachment force F_dδz must be equal to ΔE_γ,

using the fact that V = 4/3πR³ (Compare eqn (5) and (4)). The analytic expression in eqn (5) (gray curve in Fig. 4) agrees well with the experimental data and the two numerical solutions to Young–Laplace equation for ε < 0.2 or equivalently θ_r > 140°. This is not surprising since for high θ_r, the droplet geometry is well approximated by a sphere (see Fig. 2D, E and 3D, E). See also Table S1 (ESI†).

For highly hydrophobic surface, the detachment force F_d when normalized by πR is therefore equivalent to γ(1 + cos θ_r) the Young–Dupre work of adhesion (per unit area). This result is different from the scaling proposed by Tadmor et al. (2017) where the authors suggested that F_d/2πr = γ(1 + cos θ_r).¹⁰ For hydrophilic surfaces, there is no simple way to relate F_d to cos θ_r since the droplet is highly deformed and its geometry depends on the choice of experimental method (compare Fig. 2C and 3C).

The results presented here are general and apply for a wide range of experimental conditions and surface types from superhydrophobic (Fig. 5A) to lubricated surfaces (Fig. 5B). In Fig. 5, we slowly increase the droplet volume until gravity (another example of body force) causes the droplet to detach from the surface. Eqn (5) correctly predicts the droplet weight F_d = Vρg at the point of detachment for both surfaces (see red open circles in Fig. 4). Note that there is a wrapping layer of the fluorinated oil for the droplet on lubricated surface (Fig. 5B),^29,30 and we used an effective surface tension γ = 69 mN m⁻¹ when calkculating F_d/γV^1/3. Strictly speaking, our approach is true only for lubricated surfaces with vanishingly small wetting ridge and when viscous dissipation due to the wetting ridge can be ignored. These two conditions were met in our experiment since we used a relatively thin lubricant layer of about 3 μm and relatively non-viscous lubricant of viscosity η = 30 mPa s.

Validity of quasi-static approximation

In our analysis so far, we have used the quasi-static approximation and assumed that the body force applied or the gap h is increased gradually such that F_d is dominated by surface wetting properties (in particular θ_r) and not by dynamic effects (e.g., viscous dissipation). This is true for the cases described above and also explains why different groups reported that F_d is independent of U (at least for superhydrophobic surfaces).^14,15

There are however cases where this assumption is not valid. For example, viscous dissipation can dominate for highly viscous or non-Newtonian liquids.³¹ If the speed of detachment is faster than the speed at which the contact-line can recede, dynamical effects such as pinch-off instability can occur. Some underwater superoleophobic surface also exhibits θ_r = 180° (i.e., no contact line pinning) and F_d is always dominated by viscous dissipation even at low U ∼ μm s⁻¹. Previously, we showed that F_d ∝ U^3/5 for an oil droplet detaching from such a surface.^24,32

Maximum vs. detachment force

As discussed previously, for surface force method (but not for body force), the droplet experiences a maximum force F_max > F_d. There is much less data available for F_max in the literature. Nevertheless, the experimental results from Samuel et al. (2011)¹⁶ and Zhu et al. (2022)¹⁷ are consistent with our numerical results (Fig. 6).

Fig. 6 Comparison between numerical results for F̃_max (dashed blue line) and experimental results from Samuel et al. (2011)¹⁶ and Zhu et al. (2022).¹⁷ Results in Fig. 4 are also superimposed (in faint) for easy comparison.

Our numerical simulations indicate that F_max is linearly proportional to ε, i.e.,

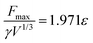(dashed blue line, Fig. 6). Our numerical results therefore suggest that F_max (unlike F_d) can be related to γ(1 + cos θ_r) even for hydrophilic surfaces, though more experimental data is required to confirm this.

Detachment vs. friction force

It is important to recognize that the lateral F_fric acting on a droplet can be very different in magnitude from the vertical F_d discussed in this paper. Furmidge proposed that the lateral friction force acting on the droplet is given by the relation

F_fric = πrγ(cos θ_r − cos θ_a) (7)

where θ_a is the advancing contact angle. For superhydrophobic surfaces which have θ_a ≈ 180°, F_fric ≈ πrγ(1 + cos θ_r).³³ Hence, F_d/F_fric = R/r ∼ 10, i.e., it is easier to move a droplet on a superhydrophobic surface by applying a lateral force as compared to a vertical force.

More recently developed surfaces, such as lubricated^21,22 and slippery covalently-attached liquid (SCAL) surfaces,³⁴ typically exhibit θ_r ∼ 90°, r ∼ R, and 1 + cos θ_r ∼ 1, cos θ_r − cos θ_a ∼ 10⁻³.^35–37 Hence, F_d/F_fric ∼ 10³.

3 Conclusions

Using a combination of numerical simulations and simple geometrical arguments, we were able to explain the observed detachment forces reported by various research groups spanning over a wide range of experimental parameters from micron- to millimetric-sized droplets and force magnitudes ranging from nano- to millinewtons. We also showed that for highly hydrophobic surfaces with θ_r > 140°, the normalized detachment force F_d/πR is equivalent to the Young–Dupre adhesion γ(1 + cos θ_r).

Author contributions

X. Q. K. performed the experiments here. D. D. conceptualized the project, performed numerical and theoretical analysis, supervised the research, and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Sadullah and co-workers for sharing their data with us and for their valuable comments.

Notes and references

1. P.-G. Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer, 2004.
2. D. Beysens, The physics of dew, breath figures and dropwise condensation, Springer, 2022, vol. 994.
3. B. Derby, Annu. Rev. Mater. Res., 2010, 40, 395–414.
4. C. Furmidge, J. Colloid Sci., 1962, 17, 309–324.
5. C. Cao, Y.-Y. Song, Z.-L. Zhou, L.-D. Cao, F.-M. Li and Q.-L. Huang, Soft Matter, 2018, 14, 8030–8035.
6. H.-J. Butt, I. V. Roisman, M. Brinkmann, P. Papadopoulos, D. Vollmer and C. Semprebon, Curr. Opin. Colloid Interface Sci., 2014, 19, 343–354.
7. D. Daniel, M. Vuckovac, M. Backholm, M. Latikka, R. Karyappa, X. Q. Koh, J. V. I. Timonen, N. Tomczak and R. H. A. Ras, Commun. Phys., 2023, 6, 152.
8. Y. Jiang and C.-H. Choi, Adv. Mater. Interfaces, 2021, 8, 2001205.
9. M. E. Schrader, Langmuir, 1995, 11, 3585–3589.
10. R. Tadmor, R. Das, S. Gulec, J. Liu, H. E. N’guessan, M. Shah, P. S. Wasnik and S. B. Yadav, Langmuir, 2017, 33, 3594–3600.
11. C. W. Extrand, Langmuir, 2017, 33, 9241–9242.
12. S. Gulec, S. Yadav, R. Das and R. Tadmor, Langmuir, 2017, 33, 13899–13901.
13. M. S. Sadullah, Y. Xu, S. Arunachalam and H. Mishra, arXiv, 2023, preprint, arXiv:2307.12527 DOI:10.48550/arXiv.2307.12527.
14. D. Daniel, C. L. Lay, A. Sng, C. J. J. Lee, D. C. J. Neo, X. Y. Ling and N. Tomczak, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25008–25012.
15. V. Liimatainen, M. Vuckovac, V. Jokinen, V. Sariola, M. J. Hokkanen, Q. Zhou and R. H. A. Ras, Nat. Commun., 2017, 8, 1798.
16. B. Samuel, H. Zhao and K.-Y. Law, J. Phys. Chem. C, 2011, 115, 14852–14861.
17. Z. Zhu, Y. Jiang and J. W. Drelich, Langmuir, 2022, 38, 8456–8461.
18. M. Jamali, A. Moghadam, H. V. Tafreshi and B. Pourdeyhimi, Appl. Surface Sci., 2018, 456, 626–636.
19. J. F. Padday and A. R. Pitt, Philos. Trans. R. Soc., A, 1973, 275, 489–528.
20. D. Quéré, Phys. A: Stat., 2002, 313, 32–46.
21. T.-S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447.
22. A. Lafuma and D. Quéré, Europhys. Lett., 2011, 96, 56001.
23. C. Thenarianto, X. Q. Koh, M. Lin, V. Jokinen and D. Daniel, Langmuir, 2023, 39, 3162–3167.
24. D. Daniel, S. S. Goh, T. N. B. Truong, X. Q. Koh and N. Tomczak, Adv. Mater. Interfaces, 2021, 8, 2001203.
25. D. Daniel, Codes for Solving Young–Laplace Equation, 2019, accessed: 2018-08-16, https://github.com/ddaniel331/laplace_solver.
26. D. Daniel, Codes for Solving Young–Laplace Equation (Body force), 2023, accessed: 2023-08-18, https://github.com/ddaniel331/laplace_pendant.
27. D. Daniel, Replication Data for: Droplet detachment force and its relation to Young–Dupre adhesion, 2023, accessed: 2023-08-16, https://doi.org/10.7910/DVN/3M6VQX.
28. A. J. Meuler, J. D. Smith, K. K. Varanasi, J. M. Mabry, G. H. McKinley and R. E. Cohen, ACS Appl. Mater. Interfaces, 2010, 2, 3100–3110.
29. J. D. Smith, R. Dhiman, S. Anand, E. Reza-Garduno, R. E. Cohen, G. H. McKinley and K. K. Varanasi, Soft Matter, 2013, 9, 1772–1780.
30. M. J. Kreder, D. Daniel, A. Tetreault, Z. Cao, B. Lemaire, J. V. I. Timonen and J. Aizenberg, Phys. Rev. X, 2018, 8, 031053.
31. G. H. McKinley, HML Report No. 05-P-04, 2005.
32. D. Daniel, A. Y. T. Chia, L. C. H. Moh, R. Liu, X. Q. Koh, X. Zhang and N. Tomczak, Commun. Phys., 2019, 2, 105.
33. F. Schellenberger, N. Encinas, D. Vollmer and H.-J. Butt, Phys. Rev. Lett., 2016, 116, 096101.
34. I. J. Gresham and C. Neto, Adv. Colloid Interface Sci., 2023, 102906.
35. D. Daniel, J. V. I. Timonen, R. Li, S. J. Velling and J. Aizenberg, Nat. Phys., 2017, 13, 1020–1025.
36. D. Daniel, J. V. I. Timonen, R. Li, S. J. Velling, M. J. Kreder, A. Tetreault and J. Aizenberg, Phys. Rev. Lett., 2018, 120, 244503.
37. A. Keiser, P. Baumli, D. Vollmer and D. Quéré, Phys. Rev. Fluids, 2020, 5, 014005.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01178j

---