Transition from scattering to orbiting upon increasing the fuel concentration for an active Janus colloid moving at an obstacle–decorated interface

Abstract

Efficient exploration of space is a paramount motive for active colloids in practical applications. Yet, introducing activity may lead to surface-bound states, hindering efficient space exploration. Here, we show that the interplay between self-motility and fuel-dependent affinity for surfaces affects how efficiently catalytically-active Janus microswimmers explore both liquid–solid and liquid–fluid interfaces decorated with arrays of similarly-sized obstacles. In a regime of constant velocity vs. fuel concentration, we find that microswimmer–obstacle interactions strongly depend on fuel concentration, leading to a counter-intuitive decrease in space exploration efficiency with increased available fuel for all interfaces. Using experiments and theoretical predictions, we attribute this phenomenon to a largely overlooked change in the surface properties of the microswimmers' catalytic cap upon H₂O₂ exposure. Our findings have implications in the interpretation of experimental studies of catalytically active colloids, as well as in providing new handles to control their dynamics in complex environments.

---

1 Introduction

In distinction from matter at thermal equilibrium, active systems feature the capability to take up energy from their local environment and convert it into directed motion. In the biological purview,^1–3 motion, i.e., self-motility, is a natural feature that enables enhanced exploration of space in search for nutrients and to escape from external threats.⁴ Inspired by such biological systems at a small scale, substantial efforts from combined research fields have led to the development of a wide range of artificial agents that feature self-motility, a.k.a. microswimmers, as useful agents for new approaches in, e.g., healthcare and environmental remediation, as well as invaluable models to uncover new aspects of out-of-equilibrium physics. In fact, the inherent autonomy of the constituents comprising active matter systems confers a wealth of out-of-equilibrium behaviours, such as collective self-organization,^5,6 new forms of phase separation^7,8 and the capability of “sensing” boundaries and obstacles.^9,10 The latter capability has been identified as a promising feature to endow microswimmers with steering and guidance in practical applications.¹¹ However, attraction towards boundaries, and the tendency to be trapped into steady state motion along them,^9–14 may turn into a bottleneck when the microswimmer needs to efficiently explore the whole available space.

Therefore, to date, an increasing number of studies have emerged to explore the complexity of microswimmer–boundary interactions. First of all, it should not be forgotten that microswimmers in typical experimental setups move near the surface of their confinement (e.g., above a microscopy glass) due to density mismatch and sedimentation. Moreover, theoretical, as well as experimental studies have shown that long-range hydrodynamic interactions between a microswimmer and a nearby surface may result in certain surface-bound states, such as trapping,¹⁵ 2D quenching,¹⁶ and circling.¹⁷ Finally, the characteristics of the underlying substrate may even affect the microswimmer speed.¹⁸ When adding other geometric confinements or obstacles to the substrate, the phenomenology becomes even richer.¹⁰ Mathematically, it has been shown that, depending on the flow field generated by the swimmer (i.e., pusher or puller type), it may be either captured or scattered by stationary obstacles.¹⁹ Experiments with pusher-type bacteria have shown forward scattering²⁰ as well as hydrodynamic capture²¹ by microfabricated posts, depending on the confinement geometry. Turning to the paradigmatic case of model synthetic microswimmers that self-propel by catalyzing the decomposition of H₂O₂ on a Pt-coated hemisphere, it has been shown that activity–sourced interactions, which include both hydrodynamics and the occurrence of chemical gradients, lead to surface-bound states of hovering and sliding.²² Moreover, geometric features in the form of step-like topographies and planar walls have been shown to function as docking and guiding platforms for chemically-active Janus colloids.^11,13 Beside flat walls, the capture of chemically-active microswimmers has been reported alongside curved obstacles, including cylindrical^11,23 and teardrop-shaped posts,¹² as well as spheres.^24,25 Interestingly, several of the latter works hint at an additional role of H₂O₂ concentration, other than just fuelling self-motility. It has in fact been repeatedly observed that the H₂O₂ concentration dictates the degree of surface–bounding and interaction with obstacles,^11,13,16,26 sometimes even in the absence of a changing propulsion speed.²⁵ However, a rationalization of this effect and of its consequences on the dynamics of chemical microswimmers in patterned environments is currently lacking.

Here, we study how the interplay between self-motility and fuel-dependent affinity for boundaries affects the efficiency of a catalytically-active microswimmer to explore the quasi two-dimensional space of an interface decorated with regularly-spaced obstacles with a size comparable to the one of the microswimmer. In particular, our microswimmers are Pt-capped polystyrene Janus particles that self-propel by catalyzing the decomposition of H₂O₂ in their surrounding. The microswimmers slide either above a glass substrate with micro-fabricated obstacle arrays or below a water–hexadecane interface populated by self-assembled lattices of polystyrene spheres. At the H₂O₂ fuel concentrations used in our study, the sliding velocity of the swimmers along the interface in the absence of obstacles is independent of the fuel concentration. Nevertheless, we find that, surprisingly, the interaction between the microswimmers and the obstacles clearly depends on fuel concentration. At the lower fuel concentrations, the obstacles marginally affect the swimming dynamics by weakly scattering the microswimmers upon a collision event; in contrast, at higher concentrations of fuel, we observe a transition from a scattering state to a situation in which the microswimmers exhibit marked orbiting around the obstacles. The consequence, at first counter-intuitively, is that an increase in the fuel concentration leads to a decrease in the efficiency of exploring the space of the interface due to trapping around obstacles. This scenario is robust relative to the nature of the supporting interface, with the only noticeable difference being the threshold in fuel concentration at which the transition from scattering to orbiting occurs. The emergence of stable steady states of orbiting around obstacles is captured by a simple theoretical model of a self-phoretic swimmer near a patterned surface. In good agreement with the experimental evidence, our model predicts that a particle approaching an obstacle can be scattered away from it, or be trapped around it in an orbit, depending on the substrate boundary conditions and on the microswimmer surface mobilities. Finally, we show by experiments, as well as via theoretical predictions, that the puzzling transition from scattering to orbiting with increasing fuel concentrations (while the velocity remains practically independent of the fuel concentration) is most likely the result of a change in the surface properties of the particle when exposed to the fuel. This so far little-explored effect may have interesting consequences concerning both the interpretation of previous experimental studies, in particular systems involving Pt catalytic particles and H₂O₂, as well as the practical applications of such particles.

2 Results

2.1 Dynamics of catalytic microswimmers at different fuel concentrations

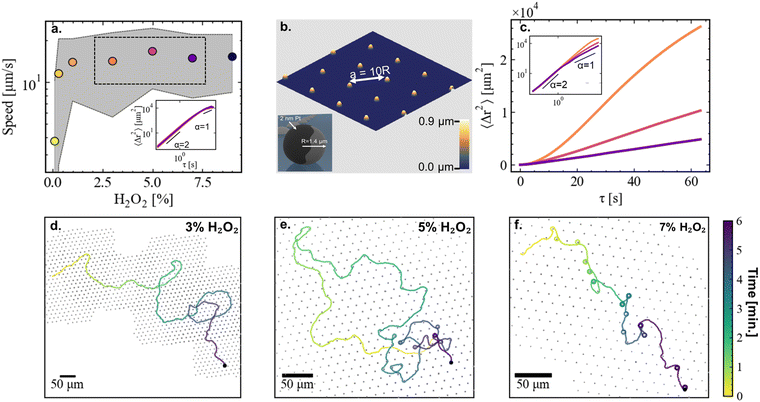
Janus microswimmers are fabricated by sputtering a thin layer (2 nm) of Pt on one hemisphere of polystyrene particles with a radius R = 1.4 μm (see inset Fig. 1(b)). The microswimmers are suspended in an H₂O₂-enriched aqueous solution and reside above a fused SiO₂ substrate. We first investigate the microswimmer speed as a function of fuel (i.e., H₂O₂) concentration in the absence of any obstacles. To limit the effects of possible fuel depletion over time, we only introduce a very small number of particles (<100) into the suspension, and limit the duration of each experiment to a maximum of 10 minutes. Over the course of the experiments we observed no significant time-dependent changes in the sliding velocity of the Janus colloids. In agreement with previous works,^27–29 we find that the mean instantaneous velocity of the microswimmers steeply increases at low H₂O₂ concentrations, and levels off at a certain H₂O₂ concentration, in our case ∼1% H₂O₂ (Fig. 1(a)).

Fig. 1 Experimental system and corresponding trajectories at different fuel concentrations. (a) Free swimming velocities of the Janus particles as a function of fuel concentration. Averages and 95% Confidence Interval (CI) of the instantaneous velocities are taken from at least 80 trajectories. The inset shows the corresponding Mean Squared Displacements (MSDs) at 3, 5, an 7% H₂O₂. (b) AFM height image of the solid substrate containing hemispherical obstacles over which the microswimmers navigate. The inset shows a schematic of the microswimmers used for the experiments. (c) MSDs of Janus particles at different fuel concentrations in an obstacle array. The decrease in the MSD with increasing fuel concentration is related to the nature of the interactions between the swimmer and the obstacles at the different fuel concentrations. The bottom (d)–(f) row shows typical experimental trajectories (6 min long) of the microswimmers at different fuel (H₂O₂) concentrations.

2.2 Effect of fuel concentration in the presence of obstacles

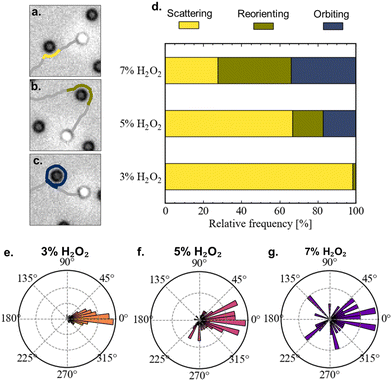
Having benchmarked the velocity-fuel dependence of our system, we proceed to operate in a constant velocity regime (3–7% H₂O₂, black rectangular box in Fig. 1(a), corresponding Mean Squared Displacements (MSDs) shown in the inset), and study the effect of introducing obstacles. We micro-fabricate arrays of small hemispherical bumps with a maximum height of 0.9 μm using two-photon-nanolithography. An AFM height image of the resulting substrate with obstacles is shown in Fig. 1(b). Constructing the mean squared displacements (MSDs) of microswimmers propelling in a constant velocity regime at 3, 5, and 7% H₂O₂ above the obstacle-patterned substrate (Fig. 1(c)) yields a counter-intuitive observation. Increasing the H₂O₂ concentration leads to a reduced MSD, i.e., the efficiency to explore space goes down when the amount of available fuel is increased. The reason behind this observation becomes clearer when looking in more detail at typical, 6 minute-long microswimmer trajectories through the arrays of hemispheres (Fig. 1(d)–(f)). Starting with 3% H₂O₂ (Fig. 1(d)), we observe that the swimmer navigates through the array of obstacles while being minimally affected by them. Interestingly, at 5% H₂O₂ (Fig. 1(e)), we observe that the way the swimmer interacts with the obstacles depends on time. At short times, the trajectory is marginally affected by the presence of the obstacles, similar to the 3% H₂O₂ case. However, at longer timescales we observe that the swimmer occasionally gets strongly reoriented by an obstacle, or even gets temporarily captured in an orbit around it. In particular, we observe orbiting events starting to appear at 4–5 min after the start of the experiment, and after 6–7 min the frequency of orbiting events reaches a steady-state (see ESI,† Fig. S1). When increasing the H₂O₂ concentration even further to 7% (Fig. 1(d)), we observe that strong reorientations and orbiting caused by obstacles occur from the start of the experiment. We note that the MSDs at 5 and 7% H₂O₂ show signatures of orbital motion at timescales beyond the ones displayed in Fig. 1(c). However, despite the constant speed and fixed obstacle size, the time between orbiting events is not constant, thereby limiting the presence of a distinct oscillatory pattern.

We investigate the resulting dynamics in more detail by identifying the approach of a microswimmer to an obstacle as a collision event. We distinguish three different types of collision events. Events where the change in the direction of the velocity vector of the swimmer before and after the interaction with the obstacle remains within the range expected from pure rotational diffusion are identified as scattering (Fig. 2(a)), changes beyond that are identified as reorienting (Fig. 2(b)). Finally, events where the swimmer orbits at least one full circle around an obstacle are identified as orbiting (Fig. 2(c)). The relative frequency of the different types of collision events occurring at different H₂O₂ concentrations are shown in Fig. 2(d). At 3% H₂O₂, collisions are almost exclusively scattering events. At 5% H₂O₂, a fraction of the collision events include reorientations and orbiting. When increasing the H₂O₂ concentration to 7%, reorientation and orbiting events dominate. As mentioned above, at 5% H₂O₂ the frequency of the different collision events displays a time dependency, implying that the data represents an average over a non-steady state and therefore depends on the time span over which the data is taken. Overall, the collision events contribute to changes in the orientation of the velocity vector, implying that the velocity vector of the swimmer going into the collision event may differ from its orientation coming out of the collision. These changes of direction due to the collision events are quantified in Fig. 2(e)–(g). Note that the figure displays the overall clockwise change in the direction velocity vector before and after a collision event, and does not consider the nature of the event (i.e. amount of full circles included in case of orbiting). It can be observed that at 3% H₂O₂ the changes in the orientation of the swimmer are mostly distributed around 0° (Fig. 2(e)). When increasing the H₂O₂ concentration (Fig. 2(f) and (g)), the orientation of the swimmer gets increasingly randomized, thereby impeding its efficiency to explore space and effectively reducing the persistence of its motion.

Fig. 2 Effect of different fuel concentrations on the dynamics of the Janus particles in the presence of obstacles. Different types of collision events: (a) scattering, (b) reorienting, (c) orbiting. (d) Relative frequency of the occurrence of the different types of collision events. (e)–(g) Distributions of the overall angular deflections (computed clockwise) of the swimmer velocity vector caused by the collision events at different fuel concentrations. Distributions are determined from at least 50 collision events per fuel concentration.

2.3 Role of the interface

To investigate the role of the substrate, i.e. the planar interface close to the swimmer, we exchange the solid substrate below the swimmer for a liquid–fluid interface above it. We create a hexadecane–water interface, and inject polystyrene spheres (R = 1.4 μm) at this interface, yielding loosely packed colloidal arrays confined at the liquid–fluid interface.^30,31 We thus obtain a liquid–fluid interface that is geometrically similar to the patterned solid substrate described before.³² We subsequently look at the dynamics of our microswimmers when sliding below the oil–water interface and interacting with the hemispheres of the colloids confined at the oil–water interface (the inset of Fig. 3 shows an AFM height image of a replica of the interface). We observe that, at this interfacial coverage, the microswimmers do not significantly displace the PS spheres at the liquid–fluid interface, and interact with them in a similar fashion as compared to the hemispheres printed on the solid substrate. The relative frequencies of the different types of collision events occurring at the liquid–fluid interface at different H₂O₂ concentrations are shown in Fig. 3(a). The microswimmers show qualitatively similar dynamics to the ones at the solid–liquid interface, with an increasing H₂O₂ concentration leading to more frequently occurring reorientation and orbiting events. However, it should be noted that the H₂O₂ concentration required to transition towards orbiting events is higher compared to the solid–fluid interface case. We quantify the efficiency of the microswimmers to explore space at the different interfaces at different H₂O₂ concentrations by extracting the long-time effective diffusion coefficients (D_eff) of the microswimmers. As shown in Fig. 3(b), a large drop in D_eff is observed at the fluid–solid interface from 3 to 5% H₂O₂, followed by a continuing gradual decrease. At the liquid–fluid interface a sharp drop in D_eff is observed from 7 to 9% H₂O₂.

Fig. 3 Dynamics of a microswimmer sliding below a liquid–fluid interface with obstacles. (a) Schematic of the experiment at the liquid–fluid interface. The microswimmer is sliding below the oil–water interface. Polystyrene (PS) spheres confined at the interface after self-assembly act as arrays of hemispherical obstacles. The inset shows an AFM height image of a replica of the interface made using the Gel Trapping Technique. (b) Relative frequencies of the occurrence of the different types of collision events for a microswimmer sliding below the liquid–fluid interface. Distributions are determined from at least 50 collision events per fuel concentration. (c) Comparison of the effective diffusion coefficients extracted from long-time MSDs of the microswimmers at the fluid–solid and liquid–fluid interface in the presence of obstacles.

2.4 Theoretical model and results for a catalytic swimmer interacting with obstacles

To gain insight in the phenomenology underlying the transition from microswimmers getting scattered away from obstacles to being captured in an orbit by obstacles, we describe our system with a coarse-grained model of a self-phoretic swimmer near a patterned surface. We consider a single Janus particle interacting with a hemispherical obstacle embedded in a planar surface (Fig. 4(a)). As detailed in Methods, the Janus particle interacts with the planar surface and obstacle through self-generated concentration and flow fields (Fig. 4(b)). We assume that the obstacle is solid: it is impenetrable to the reaction product (i.e., imposes a no-flux boundary condition on the concentration), and imposes a no-slip boundary condition on the hydrodynamic flow. Concerning the planar surface, it is considered to be either solid (no-flux and no-slip) or an ideal liquid–fluid interface (constant concentration and stress-free). The latter set of boundary conditions assumes that the non-aqueous phase has negligible viscosity and perfectly absorbs solute, reminiscent of a gaseous phase. (We note that the actual boundary conditions presented by the water/hexadecane interface are intermediate between these two cases.) The surface chemistry of the inert and catalytic face of the particle is characterized by the respective so-called surface mobilities b_i and b_c, which represent the effective attractive or repulsive character of the molecular interaction between the reaction product and the surface. Here, the surface mobility has a constant value b_i·b₀ on the inert face, and a constant value b_c·b₀ on the catalytic face. Here, b₀ > 0 is a characteristic surface mobility, a dimensional quantity, while b_i and b_c are dimensionless. Throughout the following, we choose these parameters such that the particle tends to move away from its catalytic cap, i.e., b_i + b_c < 0.

Fig. 4 Numerical model. (a) Schematic of the geometry considered in the numerical modeling. The hemispherical obstacle (light grey) is solid: it is impenetrable to the reaction product, and imposes a no-slip boundary condition on the hydrodynamic flow. Various boundary conditions are considered for the planar surface (dark grey). The hydrodynamic flow is considered to be either solid (no-slip) or a liquid–fluid interface (stress-free). Correspondingly, the boundary for the concentration field is considered to be either solid and impenetrable (no-flux), or absorbing (constant concentration). The inset illustrates the definition of the tilt angle θ between the particle's axis of symmetry and the planar surface, which is assumed to be fixed. (b) Representative surface concentration (background color) and streamlines of the flow (red lines) obtained from numerical modeling. The thick black line on the sphere indicates the boundary between the inert and catalytic regions of the Janus particle. In this case, the particle axis is oriented perpendicular to the sphere-to-obstacle vector (φ = 90°), and the two sides of the particle have identical surface mobility (b_i = b_c < 0). The planar substrate is a solid wall. The direction of motion of the particle is indicated by the arrow. It can be seen that the presence of the obstacle affects both the solute concentration and the flow streamlines. (c) Phase portrait for reorienting behavior. Here, b_i = −1 and b_c = 0.7, θ = 135°, and the substrate is solid. (d) Scattering trajectory for the particle in (c). (e) Phase portrait for orbiting. The surface chemistry parameters b_i and b_c and tilt angle θ are the same as in (c) and (d), but the planar boundary is a liquid–fluid interface. The dark blue dot indicates a dynamical attractor. (f) An orbiting trajectory for the particle in (e).

We assume the particle has fixed height z = h above the planar surface, and that the tilt angle θ of the catalytic cap with respect to the surface is fixed. Physically, these assumptions are motivated by the observation that catalytic Janus particles tend to “lock” into a fixed height and orientation with respect to a nearby planar surface.^11,27,29 Interaction with a more distant hemispherical obstacle is unlikely to significantly affect the steady height and tilt angle; this is consistent with the experimental observations in this study showing no noticeable changes in its tilt angle in the vicinity of an obstacle. Furthermore, the experiments display no visible influence on the lateral (in-plane) microswimmer dynamics for obstacles located further than approximately three particle diameters. With these assumptions, and due to the rotational symmetry of the system, there are two degrees of freedom: the radial position r of the particle (Fig. 4(a)), and the angle φ between the particle axis and the obstacle-to-particle vector (Fig. 4(d)). We study the dynamical system defined by ṙ and [small phi (variant), Greek, dot above]. The dynamics depend on the character of the planar surface (solid vs. liquid–fluid interface), as well as on the surface chemistry of the particle (b_i and b_c). For instance, in Fig. 4(c), we show a phase portrait for reorienting behavior: for nearly all initial φ and r, the particle eventually rotates its inert face away from the obstacle (i.e., φ increases), and swims away from the obstacle (r increases). Depending on initial orientation and position, it may approach the obstacle (r decreases) before eventually moving away. A top-down view of one reorienting trajectory is shown in Fig. 4(d). (Note that the calculations do not incorporate the effect of thermal noise. Thus, we make no distinction between scattering and reorienting behaviors.) Here, the particle surface chemistry is characterized by b_i = −1 and b_c = 0.7, the tilt angle is θ = 135°, and the substrate is “solid,” i.e., imposes no-flux and no-slip boundary conditions on the chemical and hydrodynamic fields. Significantly, by changing the character of the planar boundary, we can obtain the different behavior for the same particle surface chemistry. In Fig. 4(e) and (f), θ = 135°, b_i = −1 and b_c = 0.7, as before, and the planar boundary is a liquid–fluid interface that imposes absorbing and stress-free conditions on the chemical and hydrodynamic fields, respectively, for which we observe orbiting behavior. For orbiting, the particle is attracted to a bound state (r_o,φ_o), for which ṙ = 0 and [small phi (variant), Greek, dot above] = 0. In other words, the particle maintains a constant angle φ between its inert face and the obstacle-to-particle vector, and continuously moves around the obstacle (Fig. 4(f)). In Fig. 4(e), it is clear that for most initial configurations in which the particle is initially facing the obstacle (φ < π/2), the particle is attracted to an orbiting state (dark blue circle). We also note that, more rarely, we can obtain a motionless “hovering” state in which either the inert or catalytic face of the particle is directly oriented towards the obstacle, i.e., φ = 0 or φ = π. This is a specialized case of the orbiting state without particle motion. In the case of hovering, there is actually an entire circular “ring” of degenerate hovering configurations around the obstacle, due to rotational symmetry. Therefore, in experiments, due to thermal motion of the particle, the hovering state would most likely be observed as weak orbiting, with some tendency to intermittently change the clockwise or counterclockwise character of motion.

In the example given in Fig. 4(c)–(e), the scattering-to-orbiting transition is induced by a change of substrate boundary condition from solid to liquid–fluid. We note that a change of the substrate from liquid–fluid to solid can also induce this transition. An example of a parameter set for which this occurs is b_c = −1, b_i = 0.85, and θ = 90°.

2.5 Role of the particle history

The results discussed in the previous sections consistently argue for a qualitative change in the dynamics of collisions between the catalytic swimmer and the obstacle as the concentration of fuel increases. This happens irrespective of the support of the obstacles being provided by a solid wall or a liquid–fluid interface. The puzzling detail, though, is that the dynamics of the particle outside the collision with the obstacles seems to not be dependent on the fuel concentration: neither the sliding velocity of the swimmer (see Fig. 1(a)), nor the orientation of the particle relative to the interface (the angle θ, see the supporting Videos, ESI†), show any noticeable changes upon increasing the concentration of fuel. These features, which seem to have been also noticed in previous experiments,³³ led us to consider the so far unexplored possibility that the fuel changes the surface properties, i.e., the mobilities b, of the particle. This hypothesis is also supported by the observation that the trajectories in the case of the wall–liquid interface and 5% H₂O₂ show a qualitative change from “mainly scattering” to “frequent orbiting” as time progresses (see Fig. 1(e)).

Accordingly, we carried out an investigation into the role of the history of the particle by pre-exposing it to a high concentration of H₂O₂, and then bringing it back into a 3% H₂O₂ environment. The effect of this pre-treatment on the dynamics of the microswimmers is represented in Fig. 5. Pre-exposing the microswimmers to a H₂O₂ concentration at which frequent orbiting is observed, followed by bringing them back into a H₂O₂ concentration where orbiting is typically absent, yields microswimmers that orbit. The latter indicates that the history of the Janus particle, i.e., the surface state of the Pt cap, matters in the way the microswimmer interacts with boundaries.

Fig. 5 Effect of the history of the microswimmer. (a) Typical 2 min trajectories of swimmers at the solid–fluid interface in the presence of obstacles and 3% H₂O₂, and corresponding relative frequency of the occurrence of the different types of collision events. (b) Same as (a), but in this experiment the microswimmers are pre-exposed to 9% H₂O₂ and then brought back to the same 3% H₂O₂ environment. Distributions are determined from at least 50 collision events per fuel concentration. (c) Dynamical behavior in the numerical calculations for b_c = −1 and varying b_i and tilt angle θ. The planar boundary is no-flux and no-slip. A change in surface chemistry b_i can lead to transition from orbiting to scattering/orienting and vice versa. This transition is robust against changes in tilt angle. (d) Same as (c), but for b_i = −1 and varying b_c and θ.

In the model, the observed dynamical behavior depends on the surface chemistry parameters b_i and b_c (Fig. 5(c) and (d)). Change in these properties can induce a transition from scattering/reorienting to orbiting, and vice versa. These transitions occur for a wide range of tilt angles θ. We also obtain the same phenomenology for a liquid–fluid boundary condition on the substrate. Therefore, the experimentally observed history dependence is consistent with the model: changes in surface chemistry can induce dynamical transitions.

3 Discussion

In summary, we have probed the dynamics of Pt-capped polystyrene catalytic microswimmers sliding along interfaces presenting regular arrays of obstacles of comparable size at varying concentrations of H₂O₂ fuel. The study involved Janus particles sliding either above a glass substrate patterned with micro-fabricated obstacles or below a water–hexadecane interface with trapped polystyrene spheres. In a regime in which the speed of the particles is independent of the fuel concentration, we observed a change in the swimmer–obstacle interactions upon increasing the fuel concentration. This change manifests in the form of a transition in the outcome of swimmer–obstacle collisions from that of microswimmers being weakly scattered by obstacles to the one of being captured into orbits around the obstacle, the latter leading to a decreased efficiency of exploring space at high fuel concentrations. Noteworthy, increasing or decreasing the lattice spacing between the obstacles at such high fuel concentrations is expected to respectively diminish or enhance the confinement of the Janus colloid, corresponding to delaying or advancing the transition from the ballistic to the diffusive regime. The experimentally observed phenomenology is well captured by a minimal model of a self-phoretic Janus particle near a patterned surface, which predicts that either scattering or orbiting states can occur, depending on the boundary conditions at the interface, as well as on the surface mobilities of the particle.

We note that small changes in the experimental free propulsion velocity may be present, but not resolvable in the experiment due to the error bars. In the framework of the model, the propulsion speed is proportional to b₀(b_i + b_c). As shown in Fig. 5(c) and (d), for many orientations θ the model predicts a change from scattering to orbiting upon a minimal change in b_i or b_c. For instance, at θ = 110°, the model predicts a transition upon changing from b_i = 0.35 to b_i = 0.40, roughly corresponding to a change in velocity of Δb_i/(b_i + b_c) ≈ 10%, which is within the experimental error (Fig. 1(a)).

The key insight into the cause of that unexpected behavior is provided by the behavior exhibited by the trajectories above the solid substrate at 5% H₂O₂ (Fig. 1(e)), where a transition from scattering to orbiting states is observed as a time-dependent process. At 3% H₂O₂ only scattering is observed on the time scale of the experiment (up to 10 min), while at 7% H₂O₂ only orbiting states are observed from the very beginning of the experiment. These observations suggested the hypothesis that exposure to H₂O₂ above a certain concentration changes the properties of the surface of the particle, with a rate that might be dependent on the concentration of H₂O₂. We note that the observation of orbiting states only occurring at high fuel concentrations leads us to exclude depletion of H₂O₂ to be a possible leading cause of the scattering to orbiting transition. If fuel depletion (i.e. a decrease in H₂O₂) were the leading cause of the scattering-to-orbiting transition, one would expect orbiting to occur at lower fuel concentrations, which is opposite to our observations (see Fig. 1(e) and (f)). This is consistent with the fact that pre-exposing the microswimmers to a high H₂O₂ concentration is sufficient for subsequently observing them exhibiting orbiting states while suspended in freshly prepared solutions of H₂O₂ concentrations where scattering would have been otherwise observed (Fig. 5(a) and (b)). Further investigations showed that the zeta potential of the bare PS particles in different H₂O₂ solutions is essentially independent of the H₂O₂ concentration. This then leaves only changes in the state of the Pt cap as a plausible explanation; although we cannot yet pinpoint a specific change of the surface chemistry, we note that it is known that the catalytic decomposition of H₂O₂ on Pt surfaces may involve several degradation pathways, as well as intermediate states of the Pt, such as Pt(O), formed by chemisorption of oxygen onto the Pt surface.^34,35

In addition, we have tested Janus particles with a 10 nm Pt cap at the solid substrate, for which we found the transition from scattering to orbiting to occur already at lower H₂O₂ concentrations. It is, however, difficult to directly compare the results from Janus colloids with different cap thicknesses, since the cap thickness may change several factors such as the roughness of the Pt cap, the O₂ production rate, the speed of the Janus particle,³⁶ as well as its chirality.

Changing the supporting interface near the swimmers (i.e. solid–fluid or liquid–fluid) yielded a qualitatively analogous behaviour, with the most discernible difference being the threshold in H₂O₂ concentration required to observe the transition from scattering to orbiting. (This aligns with previous reports that the propulsion behavior of catalytic microswimmers at the oil–water and glass–water interfaces is qualitatively and quantitatively similar.³⁷) While it can be argued that the presence of Marangoni flows at the liquid–fluid interfaces may contribute to the shift in behavior we see compared to the solid–fluid interface.³⁸ Nevertheless, we find that our minimalistic theoretical model recovers the experimentally observed transition without requiring the inclusion of such additional effects.

From a theoretical perspective, we note some additional interesting features of Fig. 5(c) and (d). The transition between reorienting and bound states (orbiting and hovering) is re-entrant. Taking the case of θ = 110° in Fig. 5(c) as an example, the left edge of the band of bound states is a bifurcation in which a saddle point and an attractor separate in the phase plane as b_i increases. Concerning the right edge of the band, the hovering attractor distance r_h → ∞ as b_i increases. Since we truncate the numerical domain to r/R ≤ 5, this limit is registered as a transition to scattering. (We note that a distant “hovering” state of a fluctuating active colloid would be only very weakly stable, and would hence be overwhelmed by thermal noise.) Future work could systematically characterize these bifurcations and analyze how they arise from the interplay of hydrodynamic and phoretic interactions with the obstacle.

Finally, although the current work focuses on catalytically active Janus particles, we envisage similar types of studies exploiting different active matter systems to provide substantial insights. In particular, it could be interesting to contrast the current study to the behaviour of Janus particle driven by Induced Charge Electrophoresis (ICEP), where the experimental conditions (i.e. material properties, field strength, and AC frequency) allow for tunability of the sign and magnitude of inter-particle interactions.^39–42

4 Conclusion

In conclusion, we have shown by experiments, as well as via theoretical predictions, that a transition from scattering by to orbiting around the small-sized obstacles occurs with increasing fuel concentrations in a practically constant propulsion speed regime. This observation is most likely the result of a change in the surface properties of the particle, and in particular of the Pt catalyst side, when exposed to H₂O₂ above a threshold concentration. A scenario where the fuel is not solely causing propulsion, but also changes the swimmer's properties has been so far overlooked, but provides new insights into the nature of the propulsion mechanism, which is still under debate. Our findings have far-reaching consequences concerning both the interpretation of experimental studies involving catalytic particles as well as the practical applications of such microswimmers, in particular those involving efficient transport through complex topographical landscapes. Finally, these insights also provide new handles to steer and control the dynamics of active particles in practical applications.

5 Materials and methods

5.1 Sample preparation

Janus microswimmers were fabricated using a metal deposition technique. First, 60 μL of a 5 mg mL⁻¹ commercial particle solution (MicroParticle GmbH, PS-FluoGreen-Fi135) was spread on a plasma-cleaned microscopy slide. Upon evaporation of the water phase, the particles form monolayers on which a 2 nm layer of Pt was deposited using a sputter-coating machine (Safematic, CCU-010), yielding particles with half of their surfaces coated with metal. The resulting Janus particles were subsequently sonicated for 2 minutes into 50 mL miliQ water, followed by three times washing by centrifugation, solvent exchange and redispersion, and finally concentrated into a volume of 0.5 mL.

Patterned substrates were prepared by 3D printing hexagonally-arranged hemispheres on top of a plasma-cleaned fused SiO₂ substrate using a photosensitive resin (Nanoscribe Photonic Professional GT2, IP-Dip). After developing the printed structures, the substrates were rinsed with excess of EtOH and mQ water and dried with a pure nitrogen stream.

For the experiments at the solid–fluid interface, a flat glass ring (inner diameter 6 mm, height 3 mm) was placed on top of the (patterned) substrate, creating a circular chamber. Subsequently, the chamber was filled with 1 μL microswimmer suspension and 100 μL H₂O₂ enriched mQ water. For the pre-exposure, microswimmers were exposed to 9% H₂O₂ for 5 min, diluted to 3% H₂O₂, concentrated by centrifugation and immediately redispersed in a fresh 3% H₂O₂ solution.

For the experiments at the liquid–fluid interface, a custom cell was made to hold a hexadecane–water interface. The cell was composed of two concentric glass rings (inner diameters of 14 and 6 mm) glued on glass cover slip with a minimal amount of UV curable glue (NOA 81 Optical Adhesive). The inner and an outer glass ring had a height of respectively 3 and 5 mm. Just before starting the experiment, the inner glass ring was filled with H₂O₂ enriched mQ water until the surface was pinned to the edge (84 μL). Hexadecane (Acros Organics) was then poured on top to fill up the outer glass ring. We note that the hexadecane was preventatively purified by three times extracting through an alumina (EcoChromTM, MPAluminaB Act.1) and silica gel 60 (Merck) column. Spherical obstacles are introduced at the interface using a solvent-assisted spreading technique. A 0.5 μL drop of a 1 : 1 particle suspension (MicroParticle GmbH, PS-FluoGreen-Fi135)-isopropanol mixture was spread at the water–hexadecane interface via injection with a pre-cleaned micro syringe pipette with a flat PFTE tip (Hamilton, 701 N Micro SYR Pipette). Janus particles were released into the water phase close to the liquid–fluid interface. There, the active particles typically have the tendency to slide along the interface.^43,44

A replica of the liquid–fluid interface decorated with spherical particles (inset Fig. 3(a)) was obtained using the Gel Trapping Technique.⁴⁵ In brief, using the solvent-assisted spreading technique described above, particles were introduced at an interface between an aqueous solution of gellan gum (2 wt%) and hexadecane at 80 °C. The sample was then cooled down to room temperature, causing the aqueous gel phase to set and immobilize the particle–decorated interface. The hexadecane was then carefully removed and replaced with UV curable glue (NOA 63 Optical Adhesive). After 10 min exposure to UV light, the solidified glue with the particles embedded was peeled off from the gel surface. The particle–decorated interface replica was then imaged using atomic force microscopy (AFM, Bruker Icon Dimension) in tapping mode.

5.2 Data acquisition and particle tracking

Videos of moving microswimmers were recorded for up to 10 min (starting 1 min after preparing the experimental cell) using an inverted microscope (Nikon, ECLIPSE Ti2) equipped with a 20× air objective. We apply real-time tracking and following of individual microswimmers using the NIS-Elements Object Tracker function, allowing us to record the swimmers over long timescales. For statistical reasons, MSDs of the microswimmers are calculated for up to 1 min, corresponding to up to 10 data points for the maximum lag time. In addition, we record large field-of-view (900 × 900 μm) videos to obtain more statistically relevant data. In the latter case, particles are tracked using python's library Trackpy.⁴⁶ Data analysis was done with custom codes written in python.

5.3 Theoretical model

The experimental system is relatively simple, in that: it is set-up with “obstacles” that are regularly spaced and widely separated; it involves flat (to a good approximation) interfaces on which the obstacles are placed; and the density of active particles is adjusted to sufficiently small values, such that single active particle-single obstacle collisions are practically the only events observed. Nevertheless, even in this case it remains an extremely difficult task to develop an in-detail, and yet tractable, model for the dynamics of a chemically active particle which moves near a structured interface within a fluid solution driven out-of-equilibrium by the (intrinsically complex) chemical reaction of hydrogen peroxide decomposition promoted by the platinum catalyst.

Accordingly, we focus solely on qualitatively capturing and interpreting the experimental observations of steady states of bounded motion, i.e., orbiting around the obstacle, which are exhibited by the chemically active Janus particles at both types (wall–solution and liquid–solution) of interfaces. For this aim, we use a previously employed simple model that accounts for the chemical activity and the generation of hydrodynamic flow, involves only a few adjustable parameters, and yet still captures the main qualitative features observed in the experiments.^11,22,47,48 In a succinct description: the decomposition of the “fuel” molecules at the catalytic cap of the particle is modeled as a current of solute molecules (i.e., oxygen) being released in the solution. We describe this current by the simple choice that the catalytic cap of the particle emits the solute at a constant and uniform rate κ and the solute diffuses in the surrounding solution with diffusion coefficient D. This leads to spatial inhomogeneities in the chemical composition of the solution. The gradients of the solute number density c(r) (chemical field), where r is a position in the solution, source the hydrodynamic flow u(r) of the solution by inducing an actuation of the fluid at the surface of the particle via a “slip'” velocity v_s(r_p) = −b∇_||c(r_p) (r_p denotes a position at the surface of the particle, ∇_|| the surface gradient, and b the so-called phoretic mobility) as in the classical theory of neutral diffusiophoresis.^49,50 Thus, the Janus particle is characterized by the rate κ of solute release and by two phoretic mobility coefficients, b_c·b₀ at the catalytic (Pt) cap and b_i·b₀ at the chemically inactive (PS) part of the Janus particle, that encode the material-dependent interactions between the solid surfaces and the molecules in the solution. Here, b₀ > 0 is a characteristic surface mobility, with dimensions of m⁵ s⁻¹, and the quantities b_c and b_i are dimensionless.

In order to determine the chemical field c(r), one makes the further assumptions that it can be treated as an ideal gas, that it relaxes very fast (quasi steady state), and that its convective transport by the flow u(r) is negligible compared to the diffusion currents. (The latter condition is expressed in terms of the Péclet number as Pe ≡ U₀R/D ≪ 1, where R is the radius of the particle and U₀ is a characteristic particle velocity.) Under these assumptions, c(r) is governed by the Laplace equation ∇²c = 0, subject to the boundary conditions of a source current −D[∇c·n̂] = κ on the catalytic cap and −D[∇c·n̂] = 0 on the inert face of particle (impenetrable surface). Here and in the following, the surface normal n̂ is defined to point into the liquid solution. This boundary value problem is supplemented by boundary conditions at the surface of the obstacle and at that of the planar interface. The obstacle is also catalytically inert and impenetrable to the solute, thus the impenetrable surface boundary condition −D[∇c·n̂] = 0 at the obstacle. At the planar interface, the boundary condition depends on the type of interface. For a wall, the impenetrable surface condition of zero normal current, as above, applies. For a liquid–fluid interface, the suitable boundary condition depends on whether or not the solute can diffuse from the liquid solution to the other fluid and on the Donnan potential at the interface.⁵¹ For simplicity, here we consider just the case of a perfectly adsorbing interface (i.e., the solute can pass unhindered to the fluid phase, corresponding to a vanishing Donnan potential, and the diffusion within the fluid is much faster than the one within the liquid solution), which implies c(r) = 0 at the interface.

We turn now to the hydrodynamics of the solution. The surface flows represent an active actuation, localized at the surface of the particle, that drives flow of the bulk solution. Assuming that the Reynolds number Re ≡ ρU₀R/μ ≪ 1, where μ is the viscosity of the solution and ρ is the fluid density, we take the fluid velocity u(r) to be governed by the incompressible Stokes equation −∇P + μ∇²u = 0, ∇·u = 0, where P(r) is the fluid pressure. The fluid velocity, u(r), is subject to the boundary conditions u = v_s(r_p) at the surface of the particle. At the surface of the obstacle a no-slip boundary condition u = 0 is imposed. As for the chemical field, the boundary condition imposed on u at the flat interface depends on the interface being a wall–liquid or a liquid–fluid one. For the case of the wall, the no-slip boundary condition is imposed on u, while for the liquid–fluid interface we require zero shear stress, (I − n̂n̂)·σ = 0. In other words, the fluid phase (i.e., the phase not containing the Janus particle) is assumed to have negligible viscosity, as for a liquid–gas interface. Here, the stress tensor is Newtonian, i.e., σ = −PI + μ[∇u + (∇u)^T], and the projector (I − n̂n̂) extracts the components tangential to the surface of the tensor on which it is applied. Finally, the model is closed by the condition that the motion of the particle is in the overdamped regime, thus the particle translates and rotates with velocities V and Ω, respectively, while the net force and torque on the particle are zero.

The Laplace and Stokes equations, in conjunction with their respective boundary conditions and the vanishing net force and torque conditions on the particle, are solved numerically via the Boundary Element Method.^52,53 The geometry of the system is as follows. The obstacle is assumed to be a hemispherical cap with the same radius R as the Janus particle. The center of the base of the cap is at the origin of a stationary Cartesian reference frame. The normal to the planar surface defines the ẑ direction. The Janus particle position is (x,y,z). For simplicity, we assume a fixed vertical position z = h, where h/R = 1.05. The orientation of the particle is defined by a unit vector d̂ that points from the catalytic “pole” of the particle to the inert “pole.” It can also be specified using two angles, θ and φ. The angle θ is the angle between d̂ and ẑ. For simplicity, we assume that θ is fixed, and consider various values θ ∈ [0,π]. The angle φ is defined as the angle between the vector (x,y,0) (i.e., the obstacle to particle vector, projected onto the xy plane) and the orientation vector d̂. Thus, when φ = 0°, the inert face of the particle is directly facing the obstacle, and when φ = 180°, the catalytic face of the particle is directly facing the obstacle.

For the numerical solution, the particle and obstacle are both meshed, while the boundary conditions on the planar surface are imposed by using appropriate Green's functions. For each instantaneous configuration r and φ, the governing equations are solved for V and Ω. Given the rotational symmetry of the system, and the assumptions that the particle height and angle θ are fixed, there are two degrees of freedom: the angle φ and the radial position . Thus, the dynamics are captured by a two-dimensional dynamical system: [small phi (variant), Greek, dot above] = [small phi (variant), Greek, dot above] (r,φ), and ṙ = ṙ (r,φ). The angle φ evolves according to [small phi (variant), Greek, dot above] =Ω_z + (r̂ × ẑ)·V/r. Likewise, the radial position evolves according to ṙ = V·r̂.

The assumptions of fixed θ and h, aside from simplifying the dynamics, have an additional motivation. Particles moving near a bounding surface tend to assume a constant tilt angle and height via chemical and hydrodynamic interactions with the surface. Gravitational effects and electrostatic interactions often have an additional role in determining θ and h. For a particle moving close to a planar surface (h/R ≲ 1.1) in the vicinity of a hemispherical obstacle, the particle/surface interaction will play the dominant role in determining θ and h. Thus, these quantities can be approximated as quasi-steady in our study. We note that variations in h/R ≲ 1.1 will not have a significant effect on particle/obstacle interactions. Concerning θ, we vary the fixed value of θ and show that orbiting and scattering/reorienting behavior, and transitions between the two behaviors, occur over a broad range of θ.

In order to prevent the Janus particle from “crashing” into the obstacle, where “crashing” is defined as approaching within r/R ≲ 1.02, we also include a short-ranged repulsive force in the r̂ direction, F_R = F₀ exp(−kδ) r̂, where δ is the dimensionless gap width δ ≡ (r − 2R)/R, k⁻¹ is the (dimensionless) length scale of the repulsive interaction, and F₀ is the magnitude of the repulsive force. Defining the characteristic velocity as U₀ ≡ |b₀κ/D|, we non-dimensionalize F₀ as F̃₀ ≡ F₀/μU₀R. Generally, we choose F̃₀ = 2 and k = 10. The results shown here are robust against other choices for these parameters. For instance, for F̃₀ = 50 and k = 20, we obtain similar results, with some slight shifts in the phase boundaries. The contribution of the force to the particle velocity V_R follows straightforwardly from the linearity of the Stokes equation: , where is the hydrodynamic resistance matrix.

Finally, we note that the possibility that at the surface of the obstacle and of the wall osmotic flows are induced, as well as that of Marangoni stresses occurring at the liquid–fluid interface, is disregarded in the model. This is not to say that such effects cannot occur, or that they are in general unimportant, but that the minimalist model we discussed already contains the ingredients capturing the phenomenology. Additional effects, as noted above, bring more complexity, but also additional flexibility in the number of parameters and their values, in the model; accordingly, the expectation is that such more complex models would include the phenomenology we discussed, eventually as a subset of a richer behavior, but at the expense of a much more demanding computational work to explore an extensive parameter space.

Author contributions

Author contributions are defined based on the CRediT (Contributor Roles Taxonomy) and listed alphabetically. Conceptualization: C. v. B. and L. I. Formal Analysis: C. v. B. and W. E. U. Funding acquisition: L. I. Investigation: C. v. B. and W. E. U. Methodology: C. v. B. and W. E. U. Project Administration: L. I. Software: C. v. B. and W. E. U. Supervision: L. I. Validation: C. v. B., L. I., M. N. P. and W. E. U. Visualization: C. v. B and W. E. U. Writing – original draft: C. v. B., L. I., M. N. P., W. E. U. Writing – review and editing: C. v. B., L. I., M. N. P. and W. E. U.

Conflicts of interest

The authors declare that they have no conflicts of interests.

Acknowledgements

The authors acknowledge Jacopo Vialetto, Nuno Araújo, and Danne van Roon for fruitful discussions. C. v. B. acknowledges funding from the European Unions Horizon 2020 MSCA-ITN-ETN, project number 812780. The technical support and advanced computing resources from University of Hawaii Information Technology Services – Cyberinfrastructure, funded in part by the National Science Foundation CC* awards #2201428 and #2232862 are gratefully acknowledged. W. E. U. gratefully acknowledges support from the Army Research Office under Grant Number W911NF-23-1-0190. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. M. N. P. gratefully acknowledges the support by ProyExcel-00505 funded by Junta de Andalucía, PID2021-126348N funded by MCIN/AEI/10.13039/501100011033, and a María Zambrano fellowship funded by the Spanish Ministerio de Universidades (all grants partially financed also by the European Regional Development Fund and the NextGenerationEU funds). L. I. acknowledges funding from the European Research Council (ERC) under the European Unions Horizon 2020 Research and innovation program grant agreement no. 101001514.

References

1. E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601.
2. M. E. Cates, Rep. Prog. Phys., 2012, 75, 042601.
3. W. Poon, Proc. Int. Sch. Phys. “Enrico Fermi”, 2013, 184, 317–386.
4. G. M. Viswanathan, M. G. Da Luz, E. P. Raposo and H. E. Stanley, The physics of foraging: an introduction to random searches and biological encounters, Cambridge University Press, 2011.
5. J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001.
6. I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301.
7. I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303.
8. J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940.
9. L. Rothschild, Nature, 1963, 198, 1221.
10. G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810.
11. J. Simmchen, J. Katuri, W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Sánchez, Nat. Commun., 2016, 7, 10598.
12. M. S. D. Wykes, X. Zhong, J. Tong, T. Adachi, Y. Liu, L. Ristroph, M. D. Ward, M. J. Shelley and J. Zhang, Soft Matter, 2017, 13, 4681–4688.
13. S. Das, A. Garg, A. I. Campbell, J. Howse, A. Sen, D. Velegol, R. Golestanian and S. J. Ebbens, Nat. Commun., 2015, 6, 8999.
14. J. Elgeti and G. Gompper, Eur. Phys. J.-Spec. Top., 2016, 225, 2333–2352.
15. S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147.
16. X. Zheng, B. ten Hagen, A. Kaiser, M. Wu, H. Cui, Z. Silber-Li and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032304.
17. E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412.
18. S. Ketzetzi, J. de Graaf, R. P. Doherty and D. J. Kraft, Phys. Rev. Lett., 2020, 124, 048002.
19. S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411.
20. K. Hoeger and T. Ursell, Soft Matter, 2021, 17, 2479–2489.
21. Y. Takaha and D. Nishiguchi, Phys. Rev. E, 2023, 107, 014602.
22. W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438.
23. S. Ketzetzi, M. Rinaldin, P. Dröge, J. de Graaf and D. J. Kraft, Nat. Commun., 2022, 13, 1772.
24. D. Takagi, J. Palacci, A. B. Braunschweig, M. J. Shelley and J. Zhang, Soft Matter, 2014, 10, 1784.
25. A. T. Brown, I. D. Vladescu, A. Dawson, T. Vissers, J. Schwarz-linek, S. Lintuvuori and W. C. K. Poon, Soft Matter, 2016, 12, 131.
26. J. Katuri, W. E. Uspal, M. N. Popescu and S. Sánchez, Sci. Adv., 2021, 7, 719.
27. K. Dietrich, D. Renggli, M. Zanini, G. Volpe, I. Buttinoni and L. Isa, New J. Phys., 2017, 19, 065008.
28. J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102.
29. S. Ketzetzi, J. de Graaf and D. J. Kraft, Phys. Rev. Lett., 2020, 125, 238001.
30. A. J. Hurd, J. Phys. A: Math. Gen., 1985, 18, L1055–L1060.
31. P. Pieranski, Phys. Rev. Lett., 1980, 45, 569–572.
32. K. Dietrich, G. Volpe, M. N. Sulaiman, D. Renggli, I. Buttinoni and L. Isa, Phys. Rev. Lett., 2018, 120, 268004.
33. A. T. Brown, I. D. Vladescu, A. Dawson, T. Vissers, J. Schwarz-Linek, J. S. Lintuvuori and W. C. K. Poon, Soft Matter, 2016, 12, 131–140.
34. R. Serra-Maia, M. Bellier, S. Chastka, K. Tranhuu, A. Subowo, J. D. Rimstidt, P. M. Usov, A. J. Morris and F. M. Michel, ACS Appl. Mater. Interfaces, 2018, 10, 21224–21234.
35. R. Serra-Maia, S. Chastka, M. Bellier, T. Douglas, J. D. Rimstidt and F. M. Michel, J. Catal., 2019, 373, 58–66.
36. X. Lyu, X. Liu, C. Zhou, S. Duan, P. Xu, J. Dai, X. Chen, Y. Peng, D. Cui, J. Tang, X. Ma and W. Wang, J. Am. Chem. Soc., 2021, 143, 12154–12164.
37. P. Sharan, W. Postek, T. Gemming, P. Garstecki and J. Simmchen, Langmuir, 2021, 37, 204–210.
38. P. Malgaretti and J. Harting, ChemNanoMat, 2021, 7, 1073–1081.
39. J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095–1099.
40. J. Zhang and S. Granick, Faraday Discuss., 2016, 191, 35–46.
41. J. Zhang, J. Yan and S. Granick, Angew. Chem., Int. Ed., 2016, 128, 5252–5255.
42. A. M. Boymelgreen, T. Balli, T. Miloh and G. Yossifon, Nat. Commun., 2018, 9, 760.
43. S. Das, Z. Jalilvand, M. N. Popescu, W. E. Uspal, S. Dietrich and I. Kretzschmar, Langmuir, 2020, 36, 7133–7147.
44. A. Brown and W. C. K. Poon, Soft Matter, 2014, 10, 4016–4027.
45. V. N. Paunov, Langmuir, 2003, 19, 7970–7976.
46. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
47. W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Phys. Rev. Lett., 2016, 117, 048002.
48. W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Dietrich, New J. Phys., 2018, 20, 015013.
49. J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99.
50. R. Golestanian, T. B. Liverpool and A. Ajdari, New J. Phys., 2007, 9, 126.
51. A. Domínguez, P. Malgaretti, M. N. Popescu and S. Dietrich, Phys. Rev. Lett., 2016, 116, 078301.
52. C. Pozrikidis, A Practical Guide to Boundary Element Methods with the Software Library BEMLIB, CRC Press, Boca Raton, 2002.
53. C. Pozrikidis, J. Eng. Math., 1997, 31, 29–42.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental viedoes and corresponding description. See DOI: https://doi.org/10.1039/d3sm01079a

---