Shear wave generation from non-spherical bubble collapse in a tissue phantom

Abstract

Elastography is a non-invasive technique to detect tissue anomalies via the local elastic modulus using shear waves. Commonly shear waves are produced via acoustic focusing or the use of mechanical external sources, shear waves may result also naturally from cavitation bubbles during medical intervention, for example from thermal ablation. Here, we measure the shear wave emitted from a well-controlled single laser-induced cavitation bubble oscillating near a rigid boundary. The bubbles are generated in a transparent tissue-mimicking hydrogel embedded with tracer particles. High-speed imaging of the tracer particles and the bubble shape allow quantifying the shear wave and relate it to the bubble dynamics. It is found that different stages of the bubble dynamics contribute to the shear wave generation and the mechanism of shear wave emission, its direction and the efficiency of energy converted into the shear wave depend crucially on the bubble to wall stand-off distance.

---

1 Introduction

Elastography is a non-invasive imaging technique to determine solid tumours, fibrosis, and cirrhosis associated with chronic liver diseases, by taking advantage of the change in the visco-elasticity of tissues resulting from specific pathological or physiological processes.¹ Since its invention in the early 1990s,² different qualitative and quantitative elastography approaches have been proposed which can be divided into these four types: Compression sonoelastography, transient elastography, tension elastography, and shear-wave elastography.³ The last is one of the most successful quantitative techniques, which has gained large attentions since it was proposed by Sarvazyan.⁴ With this technique, a spatial elasticity map of the tissue is created using the dependence of the shear wave propagation velocity V_s on the elasticity modulus E:

E = 2ρV_s²(1 + ν). (1)

Here, ρ, and ν are mass density and Poissons ratio, respectively.⁵ Compound plane wave ultrasound imaging may be used to track the shear front from the speckle motion.⁶ Higher elasticity modulus, i.e., stiffer tissue and larger shear propagation velocities, usually indicates abnormal parts of the tissue.

A crucial step in shear wave elastography concerns the generation of the shear waves in tissue. A very elegant technique that is widely used is the acoustic radiation force impulse technique.⁷ There, focused ultrasound push beams is used to create local displacement in the tissue from which a shear wave emerges. Other techniques are external mechanical vibrations,⁸ in conductive media Lorentz forces,⁹ and nucleation of bubbles from electrolysis.¹⁰ Also, cavitation bubble collapses near a tissue-air boundary have been shown to generate shear waves.¹¹

In the current work, we show that the non-spherical dynamics of a cavitation bubble near a rigid boundary with is expected to occur at a hard tissue or near a bone, also generates shear waves. These cavitation-generated shear waves are measured with high-speed optical imaging of the motion from tracer particles. We then correlate this motion to the bubble dynamics using high-speed imaging. Single bubbles are conveniently generated at a variable distance from a rigid boundary through a pulsed and focused laser beam.

Our interest on the possibility that cavitation bubbles may excite shear waves is motivated by the rather common occurrence of bubble nucleation in a variety of medical procedures such as high intensity focused ultrasound (HIFU),^12,13 histotripsy,^14,15 laser lithotripsy^16,17 and thermal ablation of tumours,^18,19 to name a few. Also, cavitation has been reported to occur within the brain following the impact of the skull,²⁰ as well as in synovial fluid during joint cracking.^21,22

2 Experiments

Gelatin samples are prepared and embedded with graphite powder particles for use as optical tracers. Gelatin is a hydrogel that is commonly used as a Tissue Mimicking Material (TMM). Its elastic properties can be adjusted by changing the gelatin concentration. In the first step, powdered gelatin (Gelatin 250 bloom, Yasin Gelatin Co., Ltd) is mixed with deionized water at a mass ratio of 4% (gelatin to water) and is dissolved in a flask on a hot plate with a magnetic stirrer similar to a previously described procedure.²³ The mixture is poured into a home build cuvette (dimensions 20 × 20 × 10 mm³), which provides optical access from three sides through glass windows for accurate laser focusing, observation with a high-speed camera, and illumination. Here, shear wave propagation is measured through the shear-induced displacement of graphite tracer particles using a particle image velocimetry (PIV) technique. While the common technique for displacement field measurements employ volumetric particle seeding within a fluid domain and light sheet illumination of the plane of interest, here we seed the particles in a plane and illuminate the whole volume. This is beneficial, as the laser pulse to generate the cavitation bubble would be absorbed and multiple bubbles may be generated along the path of the laser beam. To seed tracer particles in a plane, a 3D-printed spacer with a thickness of 1 mm is embedded from above into the uncured gelatin. Then the samples are stored in a fridge for gelation. After curing, the spacer is carefully removed, and the resulting gap is filled with uncured gelatin-graphite particle mixture. The mixture is obtained by adding graphite particles (Fluka 231-153-3, diameter distribution 5–20 μm) at a mass ratio of 0.1% to the previously described gelatin solution. Again, the samples are stored in a fridge for gelation. Before use, we ensure that the samples have reached room temperature. The tracer particles follow well the shear motion in the gelatin. This can be seen in the Appendix B.

A sketch of the experimental setup is shown in Fig. 1. A single laser-induced cavitation bubble is created by focusing a collimated laser pulse (Litron Nano series, Q-switched Nd:YAG, 6 ns, wavelength 532 nm) with a microscope objective (Mitutoyo 50×, NA = 0.42, nominal working distance 20.5 mm) through the bottom of the cuvette into the thin, about 1 mm thick, layer of graphite particles. For optical index matching, the microscope objective output aperture and the cuvette are submerged in water for optical index matching. In the focal region of the objective, the bubble is generated through optical breakdown, i.e. by plasma generation.

Fig. 1 Experimental setup for measurements of the shear waves generated by the non-spherical collapse of a laser-induced cavitation bubble in a tissue-mimicking material. (a) Side view: The bubble is generated by focusing a collimated laser pulse at a specific distance d from the lower cuvette wall into gelatin seeded with tracer particles. The origin of the coordinate system is chosen such that the wall is located at z = 0 and the plasma and the bubble center are situated on the axis of symmetry at r = 0. (b) Example high-speed image of the bubble during maximum expansion. The shear field is symmetric with respect to the red axis, and the blue box indicates the quadrant of the shear wave measurements presented here. Here, the entire plane was seeded with particles, which was used to confirm the symmetry of shear emission. (c) Top view of the setup, with the bubble being generated in the thin layer of graphite particles (layer thickness ≈1 mm).

An important quantity for characterizing the bubble dynamics is the distance of the bubble from the boundary. Here, we normalize this stand-off distance with γ = d/R_max, where d is the distance of centre of plasma to the solid boundary and R_max is the bubble radius at maximum expansion. R_max is measured in the direction perpendicular to the solid, as discussed in ref. 24. The bubble dynamics and the particle motion are recorded with a high-speed camera (Photron, FASTCAM Mini, AX200) equipped with a macro lens (Canon MP-E 65 mm f/2.8 1 − 5× Macro) with a pixel resolution of 6.6 μm per pixel. Additionally, to resolve the much faster bubble dynamics, a Shimadzu HPV-X2 high-speed camera is used at 500 000 frames per second. Again, it is equipped with the same macro lens resulting at a pixel resolution of 6.5 μm per pixel. The timing of the laser and the high-speed camera is controlled with a digital delay generator (BNC 525, Berkeley Nucleonics).

Fig. 1b presents a selected image of a cavitation bubble with the axis of symmetry at r = 0. The shear wave generation can be considered symmetric, as shown in Appendix A, thus, here we record and process the shear wave only within the blue window. This allows for camera recordings at higher resolutions to obtain more accurate measurements of the of displacement. The displacement field is obtained using PIVlab which is an open source MATLAB toolbox to perform PIV with image data.²⁵ We use FFT window deformation algorithm with three passes and deforming windows with 64, 24 and 16 interrogation areas with 50% overlap for each window. Sub-pixel estimation is performed using a Gauss 2 × 3 point sub-pixel estimator, which fits a Gaussian function to the integer intensity distribution.²⁶ Prior PIV analysis, the images are inverted and background subtracted with a rolling ball background subtraction (radius of 20 pixels). Once the particle velocity is extracted from the images, we can estimate the kinetic energy density of the propagating shear wave. For this, we have to assume a cylinder symmetry of the displacement field around the axis of symmetry, i.e. r = 0. Then the energy density per cross-sectional area e at point (r, z) is calculated as where ρ = 1000 kg m⁻³ is the mass density, and V_r and V_z are the horizontal and vertical components of the speed at point (r, z). This way, the entire cylindrical volume is considered.

3 Results and discussions

The bubble dynamics in the vicinity of a solid depends crucially on the stand-off distance. Therefore, in the following, we first present and discuss the bubble dynamics for three representative stand-off cases, and then we will discuss the resulting shear waves. The bubble dynamics for the three stand-offs are depicted with selected frames from a high-speed recording in Fig. 2.

Fig. 2 Dynamics of laser-induced cavitation bubbles in a tissue-mimicking material for three different stand-off distances γ, recorded at 500 000 frames per s and exposure time of 2 μs. The laser pulse was focused from below, and the solid boundary interface is shown with a dashed line below each frame. During bubble collapse, a shock wave is emitted. High-speed movies of these time series can be found in the ESI† as Movies M1–M3. Approximate locations of the centroids of shear generation are, extracted from Fig. 4 and indicated in the respective frames here.

The location of the solid boundary of the experiment is indicated with a dashed line at the bottom of each frame, which restricts the deformation of the gelatin sample around the bubble. Each bubble is nucleated at time t = 0. For γ = 1.85 shown in Fig. 2a, the bubble expands spherically to a maximum radius of R_max = 566 ± 6 μm at t ≈ 47 μs. As the bubble shrinks, its shape becomes increasingly non-spherical and an axial jet towards the solid boundary develops during the collapse. This jet results in the bubble indentation in the axial direction, visible for example in the frame just before the bubble collapse (t = 99 μs). This jetting phenomenon is commonly observed for bubbles collapsing in liquids close to solids.²⁷

Reducing the stand-off distance to γ = 0.97, see Fig. 2b, the bubble expansion is not spherical anymore. The bubble reaches a maximum radius R_max = 555 ± 6 μm, and collapses at t ≈ 108 μs. The instance of collapse can be determined with a higher precision than the interframe time of 2 μs via backtracking of the shockwave emitted during collapse. The shockwave is clearly imaged with the very short illumination using shadowgraphy. As a result, the collapse occurred at t = 108 μs. Looking at the frame just before the collapse, the bubble indentation in the axial direction is wider than the previous case, suggesting a wider jet flow.

At the smallest stand-off, i.e. γ = 0.11, the bubble reaches a maximum radius of R_max = 720 ± 6 μm and collapses at t ≈ 116 μs (see the shockwave Schlieren), see Fig. 2c. In this stand-off regime, a considerably different bubble dynamics develops. It results in the formation of a so-called needle jet, as shown for the case of water.^28,29 It results from a planar, and initially boundary-parallel jetting flow, see the kink at t = 108 μs. In contrary to the previous cases, the bubble indentation during collapse is not in axial but in the radial direction now, as clearly visible at time t = 110 μs. Once this radial jet impacts on the axis of symmetry, a high speed needle-like jet forms and impacts axially onto the boundary. This is not resolved in Fig. 2c and occurs between t = 110 μs and t = 116 μs.

We have now a look at the shear waves generated from these three cases of far, intermediate and short stand-off distance. Therefore, the graphite particles were added to the samples as described in the experimental section. Fig. 3 depicts the propagation of the energy density associated with the shear wave for the three different stand-off cases. Please note that the stand-offs slightly differ from the previous figure but the dynamics is still representative to the respective cases. The time t = 0 refers to the instance of bubble generation, and we only show frames for t > 474 μs for the first two cases and t > 148 μs for the third case, thus after the bubble collapse. From these times onward, the shear field has propagated sufficiently, such that it can be well-resolved with the present setup. The shock wave is not visible in these series as the speed of sound is about 1483 m s⁻¹, thus much larger than the shear velocity, such that the shock wave has already propagated out of the imaging frame 1.1 μs after its generation at the instance of collapse.

Fig. 3 Temporal evolution of areal energy density of the shear wave for three different stand-off distances γ, corresponding animations are provided in the ESI† as Movies M4–M6. For each stand-off distance, the location of the shear measurements with respect to the bubble is shown on the left. The bubble is depicted just prior collapse, and the stand-off distance d is indicated. The shear maps are analysed in the blue box, see also Fig. 1b. The Poynting vector of the shear wave indicates the direction of energy flux, and its direction is shown on the first frame of each case. The directions of the Poynting vectors are obtained from the linear motion of the shear wave fronts, see for example the slopes of the dashed lines in Fig. 4b and c. For the large stand-off case, γ = 1.75, the shear wave propagates mostly parallel to the boundary, while for the small stand-off case (γ = 0.15) it propagates mostly in the vertical direction, i.e. perpendicular to the boundary. For the intermediate case, γ = 0.97, a superposition of a boundary-perpendicular and a boundary-parallel wave is observed. We show the vertically propagating shear with “VS” and the horizontally propagating shear wave with “HS” at t = 563 μs.

For γ = 1.75, a shear wave is emitted in horizontal direction. Its propagation velocity is V_s = 1.84 ± 0.12 m s⁻¹. For the estimation of the uncertainty in the magnitude, we assume that the position of the shear wave front is detected with an uncertainty of 1/3 PIV window size. This velocity is in agreement with previous works using a similar gelatin recipe by Rapet et al.¹¹ who found V_s = 1.8 m s⁻¹. From the propagation velocity, we calculate an elastic modulus of 9.8 kPa for our gelatin sample, using eqn (1) with ρ = 1000 kg m⁻³ and ν = 0.45.¹¹

Before studying the intermediate distance, we look at the closest distance γ = 0.15 (bottom graph). Here, unlike in the previous case, the shear wave is propagating approximately in the vertical direction and this shear pulse is much more energetic. The total energy amounts for 0.4 μJ in one quadrant, which is 7 times higher than in the γ = 1.75 case. Also, the wave geometries are disparate. While the γ = 0.15 case appears to produce a plane wave, the γ = 1.75 case emits a wave that is partially spherically shaped.

For the intermediate stand-off distance, γ = 0.97, a more complex pattern is found. It can be unraveled as a superposition of two shear waves, namely, one that propagates about parallel to the boundary (HS) and one that propagates about perpendicular to the boundary (VS). This suggests that in the intermediate case both shear wave generation mechanisms occur. Here, they produce shear waves of approximately equal energy. The total shear energy in one quadrant is about 3 times larger than for the γ = 1.75 case.

To further elucidate the origin of the shear wave, we correlate the shear wave emission with the bubble dynamics. First, we track the shear front in space and time. Linear extrapolation of the shear wave trajectory allows following the shear wave back in space and time and localize its origin. Fig. 4 illustrates the propagation of shear waves in space and time for the large (γ = 1.75) and small (γ = 0.15) stand-offs in black and blue, respectively. The time t = 0 denotes the bubble generation, and the coordinate z = 0 denotes the position of the solid wall.

Fig. 4 Shear wave trajectories in space and time for two stand-offs, the large stand-off γ = 1.75 shown in black and the small stand-off with γ = 0.15 in blue. Linear fits (dashed lines) allow to back-propagate the shear wave both in time and space to their approximate origin of generation. The solid is located at z = 0 and T_C denotes the instance of collapse. (a) Shear wave trajectories and bubble contours at their respective maximum expansion. The bubbles were initiated at (r = 0, z = 1098) μm and (r = 0, z = 99) μm, respectively. The shear waves originate from some point along the dashed lines which are shown extrapolated from t = 0 to t = 1000 μs. (b) and (c) Depict the shear front trajectories for the z and r coordinate separately, for the two stand-off cases. They allow to further restrict the shear source locations. The shear in the large stand-off case (b) was mainly generated at the instance of collapse, as can be seen by the r(t) line which crosses the axis of symmetry around T_C. For the small stand-off case where the shear wave travel in z-direction, the z(t) time plot contains the most relevant information. It suggests that the shear was generated rather close to the solid at either the collapse or the generation.

Fig. 4a plots the shear wave trajectories along with the respective bubble shapes at maximum expansion. As the centroid of shear generation must coincide with the linear extrapolations, it follows that in the large stand-off case the shear wave was generated close to the bubble generation region, i.e., the centre of the expanded bubble, while in the small stand-off case the shear was generated much closer to the solid wall and outside the maximum bubble expansion region.

Further insight is provided by Fig. 4b, where the positions z(t) and r(t) are plotted for the large stand-off case. They denote the coordinates of the shear wave trajectory. Again, the centroid of shear wave generation must coincide with the dashed lines. The r(t) trajectory is the more relevant one here, as the shear wave propagates in r-direction. The curve implies that the shear was generated at about the instance of collapse T_C = 109 μs, because at this time the trajectory intersects the t-axis and due to the symmetry considerations, negative r coordinates are forbidden. Then, the centroid of shear emission can be read as (r(T_C), z(T_C)) = (r = 0, z = 1126) μm which is close to the point of bubble generation (r = 0, z = 1098) μm.

This position coincides with the region where the jet forms and penetrates the bubble. The jetting into the bubble is visible from its deformation, see Fig. 2γ = 1.85 and 99 μs ≤ t ≤ 103 μs. Always connected with the jetting is a motion of the bubble towards the rigid wall. The origin of the shear generations suggests that it is the formation of the jet on the upper part of the bubble that launches the shear wave.

The small stand-off case shown in Fig. 4c is more involved. The shear can either be generated at around T_C, implying z ≈ 205 μm, or at about the time of bubble generation, t = 0 at z ≈ 0 μm or at both times. To unravel this shear generation dynamics, in Fig. 5 we plot the time evolution of the particles in the potential shear generation region (blue box) in time. One particle is tracked using the dashed line. Sudden changes in the slope of the dashed line indicate shear generation. Thus, shear is mainly generated at the wall and during early expansion already. In addition, some shear seems to be generated during the late collapse stage and after jet impact. Thus, both expansion and collapse contribute to the shear wave.

Fig. 5 Study of origin of shear wave generation for the small stand-off case γ = 0.15. The temporal development of a selected region indicated with a blue box is shown, and a selected particle is tracked in time with the dashed line. The sudden changes in the slope of the dashed line at early expansion and late collapse stage indicate shear generation.

Thus, the shear wave can be generated during bubble collapse in the jet region for larger γ or during expansion and collapse at the wall for smaller stand-offs and accordingly the shear wave travels either in horizontal or vertical direction, respectively, i.e., the Poynting vector has an angle with respect to the wall that is ideally 0° or 90°, respectively. In Fig. 6 we show the angle of the Poynting vector as function of the γ. To estimate the uncertainty we first take the standard error of the slope³⁰ of the fitted shear wave trajectories. From that, we derive the propagation angle error using error estimation of derived quantities.³¹ It can be seen that for γ < 0.5 the shear wave is generated in the wall-near generation and for γ > 1 around the jet. The stand-offs between γ = 0.5 and γ = 1.0 represent an intermediate regime where both shear waves are generated. It should be noted, though, that the shear wave that is generated in the wall near region may be underestimated in our measurements because the shear measurement window is in the upper quadrant, which implies a certain propagation distance of the shear wave into the measurement window with respective attenuation.

Fig. 6 Angle of shear wave Poynting vector with respect to the axis of symmetry. For γ < 0.5, the shear wave propagates almost parallel to the axis of symmetry. For γ > 1 it propagates at an angle of about 75° with respect to the axis of symmetry. In the transition regime (0.5 ≤ γ ≤ 1) both shear waves are generated with similar amplitude.

In the above shear maps of Fig. 3 it was shown that for the smallest stand-off the shear wave energy is largest. Now, we systematically study the efficiency of the shear generation η and plot the ratio of shear energy to bubble energy as function of the stand-off in Fig. 7, i.e., η = U_SW/U_bubble = p₀V. The shear wave energy is obtained from the area integral where u is the shear wave energy density shown in Fig. 3 and Ω is the measurement area. The vertically propagating shear wave, once it reaches the quadrant of evaluation, is completely in the measurement window, the horizontal wave, however, needs a special treatment. As it is symmetric with respect to the bottom axis of the evaluation window, we multiply the associated energy by a factor of two for γ > 0.5 cases. The bubble energy is approximated as U_bubble = p₀V, where p₀ = 1 bar is the atmospheric pressure, and V is the maximum bubble volume. To estimate the volume of the non-spherical bubble we use 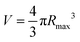for γ > 1, for stand-offs smaller than 1, we chose as discussed by Bußmann et al.³² with R_max standing for bubble radius in its maximum expansion and d for the bubble seeding distance.

Fig. 7 Efficiency of the shear generation as a function of stand-off distance. Fitting an exponential curve as η = a exp(bγ), we show shear efficiency reduces exponentially with γ as η = a exp(bγ) with a = 1.22 and b = −1.87 (RMSE = 0.1241).

The shear energy fluctuates in time, and we chose to take the energy maximum. To estimate the uncertainty we assume a spatial uncertainty of 1/3 PIV window size for the detection of the shear front.

It can be seen that the shear generation indeed has a maximum for γ → 0 and approaches zero as the bubble dynamics become spherical, i.e., η(γ → ∞) = 0, which is what we expect for spherically oscillating bubbles. We make a phenomenological fit of the shear generation efficiency using the following function: η = ae^bγ with a = 1.22 and b = −1.87. Extrapolation of the fit suggests that in this configuration, at most η(γ = 0) = 1.22% of the bubble energy can be converted into shear energy for the given material.

Finally, we would like to discuss the condition for shear wave excitation and make a connection with the acoustic emission from laser light absorption, i.e. photoacoustics. There, for the emission of acoustic waves from impulsive laser-induced heating, the heating duration must be shorter than the stress confinement time, i.e. the time for the stress to travel across the heating region as an acoustic pulse.³³ Then, stresses can be built up and are released by a strong acoustic emission. This condition is commonly termed as stress confinement. In analogy, if the duration of shear generation is shorter than the transport of the shear out of the volume, shear stress will be confined. Let us quantify this argument in very simple terms. The duration of shear stress generation is of the order of the Rayleigh collapse time, while the shear wave propagates out of this volume of stress generation within a time . Shear stress confinement is then reached once T_C < T_SW or . At maximum expansion the pressure in the bubble is typically almost zero, thus the pressure difference can be estimated as the atmospheric pressure: ΔP = 100 kPa. For the present material of about E ≈ 10 kPa, we obtain a value of T_C/T_SW ≈ 0.1. Following this argument, shear stress confinement is more difficult to obtain in stiffer materials. Thus, if a tissue becomes stiffer during therapy, e.g. in thermal ablation, the strength of the shear wave should reduce. It may be possible to monitor the strength of the emitted shear waves in thermal procedures and use that value to evaluate the thermal dose of the tissue it has received. For that, it may also be important looking into the shear wave generation as function of tissue properties, in particular the elastic modulus in future works.

Conflicts of interest

There are no conflicts to declare.

Appendices

A Symmetry of shear wave generation

We aim for a precise shear measurement, which requires a high pixel resolution. As in turn only a smaller geometric section can be imaged, we make use of the symmetric shear wave emission and image only one quadrant. The symmetry was confirmed at different stand-offs by imaging the entire geometry around the bubble. An example for γ = 0.48 is shown in Fig. 8. In the left image section the wave propagates at an angle of 8° and in the right wave at 10°. The shear wave propagation speeds on the left and right quadrants are of the same value 1.8 ± 0.12 m s⁻¹.

Fig. 8 Shear measured in the left and right quadrant generated here by a cavitation bubble with γ = 0.48. The solid boundary is shown with a dashed line below the frame.

B Assessing tracer particle behavior: following the shear

To make sure that the particles follow the shear motion with gelatin,we compare the spatial distribution of particles before and after the cavitation event. Particles that elastically return to their initial position have moved with the gelatin, while particles detached from the gelatin would be found at different positions. Fig. 9 shows an overlay of initial distribution of the particles in purple with the particle image in green from after the shear wave has passed using the Matlab function imshowpair. This way differences in the particle distribution before and after the cavitation event and shear propagation are visualized. Particles that elastically return to their initial position appear black. Small deviations from the initial particle position result in green and purple coronas around the tracer particles, while entirely green or purple particles would indicate a particle motion larger than the particle length. Almost all particle positions align well with their initial positions, i.e., particles appear black. Only in the lower left corner where the violent part of the bubble dynamics took place, small colored coronas appear around the particles and a larger green region occurs which is an artefact from the residual bubble. For the data evaluation only regions where the particles elastically follow the shear are taken into account and the lower left region is not evaluated.

Fig. 9 Overlay of initial particle distribution in purple color at t < 0 μs and long after the shear wave has passed the imaging frame in green at t = +4300 μs for the case γ = 0.15. The bubble is generated at t = 0. The black color in the image indicates that particles elastically returned to their initial position. This is the case for most of the image section, i.e., the tracers follow the shear. The bubble contours is shown at its respective maximum expansion. Only in a very small region where the violent bubble dynamics took place the tracer behave significantly non-ideal. Scale bar in the image represents 500 μm.

Acknowledgements

This project has partially received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 813766. It was also partly funded by the Federal Ministry of Education and Research in Germany within the Research Campus STIMULATE under Grant no. 13GW0473A and the DFG (German Research Association) under Grant no. ME 1645/12-1.

References

1. R. M. Sigrist, J. Liau, A. El Kaffas, M. C. Chammas and J. K. Willmann, Theranostics, 2017, 7, 1303.
2. J. Ophir, I. Cespedes, H. Ponnekanti, Y. Yazdi and X. Li, Ultrason. Imaging, 1991, 13, 111–134.
3. M. S. Taljanovic, L. H. Gimber, G. W. Becker, L. D. Latt, A. S. Klauser, D. M. Melville, L. Gao and R. S. Witte, Radiographics, 2017, 37, 855.
4. A. P. Sarvazyan, O. V. Rudenko, S. D. Swanson, J. B. Fowlkes and S. Y. Emelianov, Ultrasound Med. Biol., 1998, 24, 1419–1435.
5. R. M. Sigrist, J. Liau, A. E. Kaffas, M. C. Chammas and J. K. Willmann, Theranostics, 2017, 7, 1303–1329.
6. M. Tanter and M. Fink, IEEE Trans. Ultrason. Eng., 2014, 61, 102–119.
7. K. Nightingale, Curr. Med. Imaging, 2011, 7, 328–339.
8. H. Zhao, P. Song, D. D. Meixner, R. R. Kinnick, M. R. Callstrom, W. Sanchez, M. W. Urban, A. Manduca, J. F. Greenleaf and S. Chen, IEEE Trans. Med. Imaging, 2014, 33, 2140–2148.
9. A. T. Basford, J. R. Basford, J. Kugel and R. L. Ehman, Magn. Reson. Imaging, 2005, 23, 647–651.
10. S. Montalescot, B. Roger, A. Zorgani, R. Souchon, P. Grasland-Mongrain, R. Ben Haj Slama, J.-C. Bera and S. Catheline, Appl. Phys. Lett., 2016, 108, 094105.
11. J. Rapet, Y. Tagawa and C.-D. Ohl, Appl. Phys. Lett., 2019, 114, 123702.
12. C. E. Brennen, Interface Focus, 2015, 5, 20150022.
13. E.-A. Brujan, T. Ikeda and Y. Matsumoto, Soft Matter, 2012, 8, 5777–5783.
14. K. B. Bader, K. J. Haworth, A. D. Maxwell and C. K. Holland, IEEE Trans. Med. Imaging, 2017, 37, 106–115.
15. Y. Zhou and Y. Lei, Eng. Res. Express, 2020, 2, 025015.
16. S. Tiwari, A. Kazemi-Moridani, Y. Zheng, C. W. Barney, K. R. McLeod, C. E. Dougan, A. J. Crosby, G. N. Tew, S. R. Peyton and S. Cai, et al. , Soft Matter, 2020, 16, 9006–9013.
17. M. Li, B. Lan, G. Sankin, Y. Zhou, W. Liu, J. Xia, D. Wang, G. Trahey, P. Zhong and J. Yao, IEEE Trans. Med. Imaging, 2019, 39, 468–477.
18. N. Chang, S. Lu, D. Qin, T. Xu, M. Han, S. Wang and M. Wan, Ultrason. Sonochem., 2018, 45, 57–64.
19. M. O. Steinhauser and M. Schmidt, Soft Matter, 2014, 10, 4778–4788.
20. J. Lang, R. Nathan, D. Zhou, X. Zhang, B. Li and Q. Wu, Phys. Fluids, 2021, 33, 031908.
21. G. N. Kawchuk, J. Fryer, J. L. Jaremko, H. Zeng, L. Rowe and R. Thompson, PLoS One, 2015, 10, e0119470.
22. D. P. Chang, N. I. Abu-Lail, J. M. Coles, F. Guilak, G. D. Jay and S. Zauscher, Soft Matter, 2009, 5, 3438–3445.
23. S. Izak Ghasemian, F. Reuter and C. Ohl, Appl. Phys. Lett., 2021, 119, 114101.
24. F. Reuter, Q. Zeng and C.-D. Ohl, J. Fluid Mech., 2022, 944, A11.
25. W. Thielicke and R. Sonntag, J. Open Res. Softw., 2021, 9, 12.
26. W. Thielicke and E. J. Stamhuis, J. Open Res. Softw., 2014, 2, 30.
27. B. Dollet, P. Marmottant and V. Garbin, Annu. Rev. Fluid Mech., 2019, 51, 331–355.
28. F. Reuter and C.-D. Ohl, Appl. Phys. Lett., 2021, 118, 134103.
29. C. Lechner, W. Lauterborn, M. Koch and R. Mettin, Phys. Rev. Fluids, 2019, 4, 021601.
30. A. F. Siegel and M. R. Wagner, in Practical Business Statistics (Eighth Edition), ed. A. F. Siegel and M. R. Wagner, Academic Press, Eighth Edition edn, 2022, pp. 313–370.
31. A. Clifford, Multivariate Error Analysis: A Handbook of Error Propagation and Calculation in Many-parameter Systems, Applied Science Publishers, 1973.
32. A. Bußmann, F. Riahi, B. Gökce, S. Adami, S. Barcikowski and N. A. Adams, Phys. Fluids, 2023, 35, 016115.
33. B. Choi, E. D. Jansen and A. J. Welch, J. Appl. Phys., 2003, 94, 7826–7831.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01077e

---