Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From angular to round: in depth interfacial analysis of binary phosphatidylethanolamine mixtures in the inverse hexagonal phase†
Gerome
Vancuylenberg
,
Amin
Sadeghpour
 ,
Arwen I. I.
Tyler
,
Arwen I. I.
Tyler
 and
Michael
Rappolt
and
Michael
Rappolt
 *
*
School of Food Science and Nutrition, University of Leeds, Leeds LS2 9JT, UK. E-mail: m.rappolt@leeds.ac.uk
First published on 25th October 2023
Abstract
Packing stress in the lipidic inverse hexagonal HII phase arises from the necessity of the ideally cylinder-shaped micelles to fill out the hexagonally-shaped Wigner–Seitz unit cell. Thus, hydrocarbon chains stretch towards the corners and compress in the direction of the flat side of the hexagonal unit cell. Additionally, the lipid/water interface deviates from being perfectly circular. To study this packing frustration in greater detail, we have doped 1-palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE) with increasing molar concentrations of 1,2-palmitoyl-sn-phosphatidylethanolamine (DPPE: 0 to 15 mol%). Due to its effectively longer hydrophobic tails, DPPE tends to aggregate in the corner regions of the unit cell, and thus, increases the circularity of the lipid/water interface. From small angle X-ray diffraction (SAXD) we determined electron density maps. Using those, we analysed the size, shape and homogeneity of the lipid/water interface as well as that of the methyl trough region. At 6 and 9 mol% DPPE the nanotubular water core most closely resembles a circle; further to this, in comparison to its neighbouring concentrations, the 9 mol% DPPE sample has the smallest water core area and smallest number of lipids per circumference, best alleviating the packing stress. Finally, a three-water layer model was applied, discerning headgroup, perturbed and free water, demonstrating that the hexagonal phase is most stable in the direction of the flat faces (compression zones) and least stable towards the vertices of the unit cell (decompression zones).
1. Introduction
Hexagons represent an omnipresent class of polygons throughout nature: on the nanoscale, hexagonal close packed crystal structures are present for many different elements with Mg and Co coming the closest to the ideal cell axial ratio c/a of 1.633.1 On a slightly larger scale, lipid self-assemblies display various pathways for formation of hexagonally closest packed cylindrical micelles,2–4 on the macroscale it has been the shape of choice in the construction of beehives. Larger still are the rock formations, which adopt hexagonal columns at the Giants Causeway, and even larger, is the hexagonal storm situated at Saturn's north pole.5,6 The major intrinsic property of regular hexagons, which allows them to be used so seamlessly and efficiently throughout the natural world, is the hexagons’ proclivity for closest packing in two dimensions. Already two millenniums ago, Pappus of Alexandria (∼290 to 350 A.D.), a Greek mathematician, expressed this in the honeycomb conjecture that ‘any partition of the plane into regions of equal area has a perimeter at least of that of a regular hexagonal grid’, but it took until 2001 until this conjecture could be finally proved.7Focussing on self-assembled lipid aggregates, particularly phospholipid-based membranes, the fluid lamellar Lα phase is the biologically most relevant for modelling and understanding the behaviour of the cell wall.8,9 Nonetheless, non-lamellar phases are of interest due to the formation of cubic membranes in biological systems, which can develop under protein alterations, drug intervention or stress,10,11 and due to their importance in fusion-related processes (for a review see ref. 12). Cylindrical-shaped membranes play a crucial role in local and transient steps of membrane fusion.13,14 It has been proposed that cylindrical-shaped micelles form within the Lα phase, either by fusion of inverted spherical micellar intermediates (IMI),15 or alternatively, apposing IMIs may seed line-defects,16 inducing the formation of inverted micellar rods (for a review see ref. 12). Furthermore, tubular intercellular connections could be identified in cell-to-cell communication.17
Aside from possible biological implications this system delivers, e.g., using lipid extracts,18 the inverted hexagonal phase is widely studied for drug delivery of antivirals and other bioactives.19–24 Practical use has been made from the inverted hexagonal phase for the determination of the spontaneous monolayer curvature of various amphiphilic molecules25 as well as a detailed structural model now allows for the global fitting of small angle scattering patterns of the HII phase.26
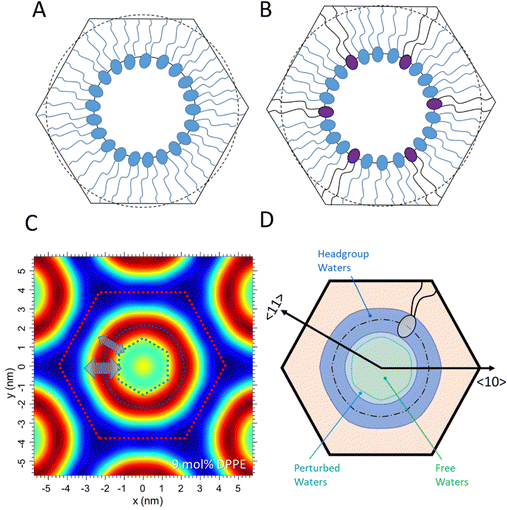
The inverted hexagonal HII phase as a model system has been widely studied,13,27–31 and is characterised by a high lipid/water interfacial curvature perpendicular to the long axis of the cylinder-shaped micelles arranged on a hexagonal lattice (Fig. 1A). Non-lamellar lipids with relatively small interfacial head-group areas (Fig. 1B), such as phosphatidylethanolamines (PE) with a non-zero spontaneous curvature, induce membrane curvature towards the water phase, which constitutes the driving force for the Lα to HII transition. Comparing the critical packing parameters at a given temperature of various PEs,3,29,32 demonstrates that the formation temperature, TH, for the inverse hexagonal phase decreases linearly with the degree of chain splay (Fig. 1C). Furthermore, the packing of the lipid nanotubes on a hexagonal grid allows for the closest packing of the inverse lipid cylindrical micelles. Considering the crystallographically used oblique unit cell description for the hexagonal lattice (a = b and γ = 120°), it is helpful to also employ the hexagonal Wigner–Seitz unit cell, when describing the packing frustration within the HII phase (Fig. 1A). As can be easily demonstrated,33 an inscribed circle to the Wigner Seitz cell only covers 91% of the area, that is, 9% of interstitial area is unaccounted for. Thus filling out the hexagon with inverted columnar micelles is accomplished firstly by a deformation of the ideally circular lipid/water interface, and secondly, the lipid chains must stretch and compress around the quasi-circular water core in order to fill the unit cell, leaving no void space in the interstitial regions (decompression regions). Note, the radius defining the position of the phosphates, RP, is the longest, when pointing towards the vertices of the hexagon and the shortest, when oriented perpendicular to the flat side. This stretching and compression of the hydrocarbon chains (Fig. 1A, top right), as well as the deformation of the lipid/water interface, comes at an energetic cost known as the ‘packing frustration’.34–36 Interestingly, only when lipid-shape anisotropy is taken into account (Fig. 1B), the overall correct interfacial shape can be simulated, hereby determining the appropriate relationship between the bending deformation and stretching of hydrocarbon chains.30,37,38
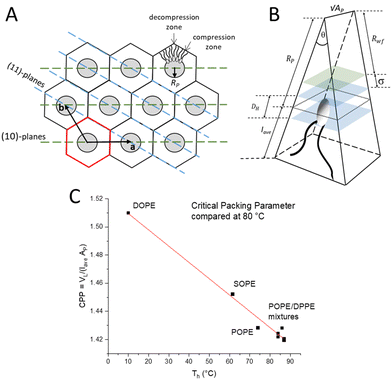 | ||
| Fig. 1 (A) Illustration of the hexagonal lattice with unit vectors a and b. The Wigner Seitz cell is shown in red. Monolayers of lipids align around the water cores (grey circles). The lattice planes in the 〈1 0〉 direction (green) and in the 〈1 1〉 direction (blue) are shown. (B) A schematic of a single lipid encased in a wedge geometry. The black dotted line indicates Ap. The volume encased by the two blue planes depicts the headgroup region. The green plane indicates the fluctuation distance, σ. Rwf is the radius related to the free water region. Note, the wedge has a depth of √AP. (C) Critical packing parameter (CPP) compared for different PEs (data retrieved from the references3,29,32 are compared to this study on POPE/DPPE mixtures). | ||
The alleviation of packing frustration is achievable with the addition of host molecules. Here, alkanes such as tetradecane are well-studied, aggregating within the hydrophobic region and essentially filling the interstitial void spaces.39 Reducing the packing stress in this way has been shown to lower the transition temperature at which the HII phase occurs. This additional ‘padding’ along the methyl trough region allows the packing stress to relax and the water core interface to become more circular. Dodecane has also been studied, similarly demonstrated to aggregate within the hydrophobic regions, i.e., mainly in the corners of the Wigner–Seitz cell,40 reducing the need for lipid-chain compression towards short length (flat side) and increasing the effective maximum lipid length, lmax. Overall, alkanes not only relieve the extension stress but concomitantly relax the compression stress at the flat sides of the hexagon. Conversely, alpha-tocopherol (vitamin E) aggregates within the short lipid-length regions, allowing the lipids to stretch to their natural length in the corner regions,41 leading to a reduction in lmax. Any stress reducing additives serve to lower the free energy of the HII phase, as much of the energetic cost arises from the distortion of the cylindrical water core into a quasi-cylindrical shape. This energy cost is intrinsically linked to the stretching and compression of the lipid chains.
In this study, we scrutinised the shape of the water core by how closely it resembles a perfect circle after adding a host lipid akin to the main building block. That is, SAXD measurements were performed on 1-palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE) with increasing molar concentrations of 1,2-palmitoyl-sn-phosphatidylethanolamine (DPPE). DPPE is a phospholipid with two fully saturated C16 hydrocarbon tails, whereas POPE has one monounsaturated C18 hydrocarbon tail. Due to its effective longer chain length (note, at 75 °C the steric membrane thickness of DPPE is 4.6 nm compared to 4.3 nm of POPE42), DPPE is thought to aggregate orientated towards the vertices of the Wigner–Seitz cell, while POPE will aggregate mainly in the flat side regions. In this way, packing stress is released as each lipid will tend to locate where it can assume its natural length. Therefore, the energy loss associated with the interstitial void regions is accounted for by the longer-chained DPPE lipids. Our aim of this study was to find the critical DPPE concentration at which the packing stress is minimised and the water core will adapt a nearly perfect circle in order to understand the interplay of packing and curvature frustration within the inverse hexagonal unit cell. Furthermore, we are presenting the local membrane hydration differences in the flat and corner zones of the hexagonal unit cell and demonstrated how the lipid compression and decompression alter the hydration properties locally.
2. Materials and methods
2.1 Materials and sample preparation
1-Palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE) and 1,2-palmitoyl-sn-phosphatidylethanolamine (DPPE) were used as supplied from Avanti Polar Lipids, Alabaster, AL (purity >99%). Lipid stock solutions were prepared by dissolving weighted amounts of dry POPE or DPPE powder in chloroform. DPPE concentrations of 3, 6, 9, 12 and 15 mol% within the lipid bilayer were obtained by mixing appropriate amounts of the stock-solutions. The organic POPE/DPPE mixture was vortexed for 2 min and the solvent was evaporated in a vacuum oven for 24 h at 30 °C at 2 · 10−3 mbar to secure that all traces of chloroform were removed. The thin lipid films on the bottom of the glass vials were subsequently suspended in 18 MΩ cm water (MilliQ). To ensure complete hydration, the lipid dispersions were shock-frozen in liquid nitrogen, thereafter thawed for 15 min, reaching a final temperature of 75 °C (about 15 °C above the main transition of DPPE), and finally vigorously vortexed for 2 min. For further annealing of the multilamellar vesicles, the above procedure was repeated six times. For the X-ray scattering experiments a final lipid concentration of 20 wt% was used.2.2 X-ray scattering measurements and analysis
Diffraction patterns of multilamellar vesicles were recorded on the Austrian SAXS beamline at the Synchrotron of Trieste,43,44 using a one-dimensional Gabriel detector45 covering the corresponding q-range (q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)/λ) of interest from about 2π/450 to 2π/12 Å−1. The angular calibration of the detector was performed with silver-behenate.46 The lipid dispersions were measured in a thin-walled, 1 mm diameter quartz capillary in a steel cuvette (Anton Paar, Graz, Austria), which was inserted into a brass block, being in thermal contact with a water bath circuit (Unistat CC, Huber, Offenburg, Germany). The entrance and exit windows of the sample cell have been covered with a thin polymer film in order to avoid air convection at the capillary. The temperature was measured in the vicinity of the capillary in the sample holder block with a Pt-element (100 Ω). Before exposure, the sample was equilibrated for a period of 10 min for any given temperature. Exposure times was set to 30 s.
sin(θ)/λ) of interest from about 2π/450 to 2π/12 Å−1. The angular calibration of the detector was performed with silver-behenate.46 The lipid dispersions were measured in a thin-walled, 1 mm diameter quartz capillary in a steel cuvette (Anton Paar, Graz, Austria), which was inserted into a brass block, being in thermal contact with a water bath circuit (Unistat CC, Huber, Offenburg, Germany). The entrance and exit windows of the sample cell have been covered with a thin polymer film in order to avoid air convection at the capillary. The temperature was measured in the vicinity of the capillary in the sample holder block with a Pt-element (100 Ω). Before exposure, the sample was equilibrated for a period of 10 min for any given temperature. Exposure times was set to 30 s.
The electron density maps of the HII phase were derived from the small-angle X-ray diffraction pattern by standard procedures.3,32 Briefly, after the raw data had been corrected for detector efficiency and the background scattering arising from the water and the capillary had been subtracted, all Bragg peaks were fitted by Lorentzian distributions (see fitting examples in Fig. S1 in the ESI†). The fittings were carried out with the software package Origin Pro 9.0 (OriginLab Corporation, Northampton, MA). Second, the intensities were normalised for their multiplicity. Thereafter, a Lorentz correction was applied by multiplying each peak intensity (peak area) by its corresponding squared wave vector modulus, q2. Finally, the square root of the corrected peak intensity was used to determine the form factor F of each respective reflection (for details see ref. 47). The electron density contrast relative to water was calculated by the Fourier analysis:
 | (1) |
After Fourier analysis, the real space electron density map can be plotted for each molar fraction of DPPE defined as f = DPPE/(POPE + DPPE). Using a MatLab programme, 2D images of the electron density map were plotted (x, y), where the height in the z-axis represents the electron density contrast, Δρ. The centre of the nanotube, which resides in the water core, rests on the origin (see Fig. 1 and 4A). Thus, the nanotube long-axis is parallel to the z-axis. The lattice parameter, a, is the distance from the centre of one nanotube to the centre of an adjacent nanotube.
The y-axis passes through the origin and intersects with the centre of the flat side of the Wigner–Seitz cell, which is referred to as the zero position, denoted by an orientation angle γ = 0°. An electron density profile (EDP) along y(0°) (the short length) was determined. Using the MatLab programme, the line y(0°) is rotated by γ =30° to create an EDP, which intersects with the corner of the Wigner–Seitz cell, the longest distance that the lipids need to fill (Fig. 1 and 4A). Further, EDPs along two interfacial lines were calculated, i.e., concerning the maximum density at the position of the phosphate group and the minimum density in the methyl-trough region as a function of the rotation angle γ (Fig. 4A). Finally, using these two orientation angles, the radial position, RP, of the phosphate group can be determined as a function of γ using the electron density profiles along the two interfacial lines. However, in this study, we solely report on Rmax and Rmin.
To calculate the circularity of the water core, it is necessary to first calculate its circumference and area. Starting from the zero position, Rp as a function of γ was calculated. The angle, y, was varied in steps of 1°, leading to two subsequent radii, which we shall refer to as Rn and Rn+1. The corresponding points of the phosphate group positions are defined as Hn(x,y) and Hn+1(x,y), respectively. These two positions are observable from the maximum in electron density. The distance,  , between these two consecutive points, was then calculated using Pythagoras’ theorem. By rotating y in 1° steps within a 30° segment, the arc length around the water core was then calculated from the summation of 30 segments:
, between these two consecutive points, was then calculated using Pythagoras’ theorem. By rotating y in 1° steps within a 30° segment, the arc length around the water core was then calculated from the summation of 30 segments:  . The arc length of one 30° segment multiplied by 12 results in the water core circumference (Fig. S3 in the ESI†). The area of the water core was calculated from the summation of each of the small triangles enclosed by the lengths of Rn, Rn+1 and the distance
. The arc length of one 30° segment multiplied by 12 results in the water core circumference (Fig. S3 in the ESI†). The area of the water core was calculated from the summation of each of the small triangles enclosed by the lengths of Rn, Rn+1 and the distance 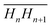 . The lengths of Rn and Rn+1 were calculated from the distance of their respective phosphate group positions from the origin. The area of a single triangle was given by the formula:
. The lengths of Rn and Rn+1 were calculated from the distance of their respective phosphate group positions from the origin. The area of a single triangle was given by the formula:
 | (2) |
 | (3) |
Calculation of the maximum and minimum lipid length requires the average water core radius Rave. For this study we have averaged the radius from each measurement within the 30° segment. The minimum, maximum and average lipid length can then be calculated from:
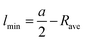 | (4) |
 | (5) |
 | (6) |
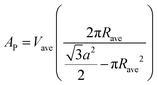 | (7) |
 | (8) |
Further, the number per lipids along the circumference, nL, the area per lipid at the steric lipid/water interface, AW (see Fig. 1), and the molecular wedge angle, θ (see Fig. 3) were determined according to ref. 32
 | (9) |
 | (10) |
 | (11) |
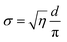 | (12) |
Following the recently published three-water layer model,52 and having estimated the membrane-fluctuation distance, σ, allows us to divide the water core into three distinct regions: (i) the “headgroup region” associated with the water volume around the headgroup, (ii) the “perturbed region” defined by the fluctuation distance σ, and (iii), the “free water region”, which is unperturbed by the fluctuating lipid monolayer. For the calculation of the total water volume, we used the approximation:32
 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53). The headgroup extension, DH, in radial direction was taken from literature to be 1.1 nm;29 accordingly Rp = Rwf + σ + 0.55 nm.
53). The headgroup extension, DH, in radial direction was taken from literature to be 1.1 nm;29 accordingly Rp = Rwf + σ + 0.55 nm.
All errors given in the Results and discussion section are referring to standard deviation for directly-retrieved parameters, e.g., d-spacings that were determined by fitting their corresponding diffraction peak positions. All other derived parameters errors were determined by standard error propagation.
3. Results and discussion
3.1 Fluid lamellar to inverse hexagonal phase transition
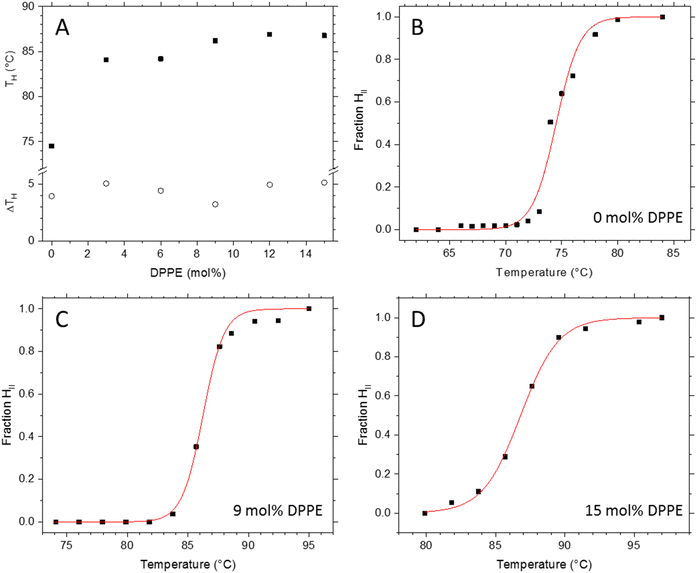
Transition temperatures were obtained from the fractional formation plots of the HII phase, f(HII), which were derived from the fitted total intensities of the first order diffraction peaks of the Lα and HII phase with f(HII) = I(HII)/[I(HII) + I(Lα)] (Fig. 2B–D; see Fig. S5 in the ESI,† for an overview of all transition plots). The inflection point determines the transition temperature, TH (Fig. 2A). The data were fitted with a logistic function, setting f(HII) at the beginning and the end of the transition to 0 and 1, respectively. For the best comparison, all inverse hexagonal phases were analysed in this study 5 °C above TH, ensuring the systems had developed a fully stable HII phase. We note that this choice meant that traces of the Lα phase are coexisting with HII phase, but even so, avoiding the onset of dispersion instabilities that we observed closer to the boiling point of water.The observed increase in TH (Fig. 2A) is in agreement with the linear relationship of the critical packing parameter (the CPP) with TH (Fig. 1C). The addition of DPPE causes the overall degree of chain splay to decrease which leads to an increase of TH of about 11 °C. Interestingly, we observe a local minimum in the transition width at 9 mol% DPPE, which means that this particular sample displays the highest transition cooperativity. Generally, the cooperativity in a given transition increases with its crystallinity, or in other words, with the degree of structural order. The following section on the fine structural analysis of the different POPE/DPPE mixtures will explain the exceptional good degree of order for the 9 mol% DPPE sample in more detail.
The stack plot of the small angle X-ray diffraction patterns (SAXD) displays Lα to HII phase transition of the POPE/DPPE mixture with 3 mol% DPPE (Fig. 3). The temperature-range spans from 78 to 95 °C with TH = 84 °C. From the Lα phase, the first three diffraction orders were recorded, while the (31)-reflection was the highest recorded diffraction peak for the HII phase. In order to analyse the effect of the host molecule concentration of DPPE on the packing frustration within the HII phase, electron density maps of all mixtures with DPPE concentrations of 0, 3, 6, 9, 12 and 15 mol% were determined at T = TH + 5 °C. This included all recorded reflections from (10) to (31). For an overview on the experimental conditions and the determined intensities Ih,k and amplitudes Fh,k of all experiments refer to Table S1 in the ESI.† Further note, given the similar molecular volumes of POPE and DPPE, the corresponding vol% values at TH + 5 °C are close to the mol% values, i.e., 2.9, 5.8, 8.8, 11.7 and 14.6 vol%.
3.2 Fine-structural analysis of the inverse hexagonal phases
Nanostructural analysis conducted on the electron density maps is shown in Fig. 4 (see also the overview graph Fig. S6 in the ESI†). In panel A, two key orientations within the Wigner–Seitz unit cell (red dotted line) are shown, concerning γ = 0° being congruent with the y-axis (red dashed line), as well as the orientation for γ = 30° (blue dashed line). The first orientation shows the shortest radial distance in the Wigner–Seitz cell, whilst the second orientation shows the longest radial distance. Thus, these are the two orientations of the maximum hydrocarbon chain compression (γ = 0°) and decompression (γ = 30°), respectively (see also Fig. 1A). The HII phase structure has a 6-fold symmetry, therefore the lipid compression and decompression is the same in the orientation of any corner or flat side, meaning that it is sufficient to analyse all structural details over a 30° segment as pictured in Fig. 4A. Maximum electron density is colour-coded with dark-red and minimum electron density with dark blue; correspondingly, the red-dotted line indicates the methyl trough region of the lipid matrix, and the blue-dotted line indicates the apparent position of the phosphate groups. The radial position of the phosphate group, RP, as a function of γ was calculated as the distance from the origin to the maximum density. Whilst some structural differences are already seen by the naked eye in the electron density maps (Fig. 4 and Fig. S6, ESI†), finer details are revealed through investigation of the different structural parameters as a function of the rotational angle, γ. A first overview of the structural results is given in Table 1.| DPPE (mol%) @ T (°C) | a (nm) | R P ave (nm) | Water core area (nm2) | l ave (nm) | V ave (10−3 nm3) | A P (nm2) | n L | Wedge angle (°) |
|---|---|---|---|---|---|---|---|---|
| 0 @ 80.0 | 7.12 ± 0.007 | 1.98 ± 0.01 | 12.4 ± 0.02 | 1.77 ± 0.01 | 1215 ± 5 | 0.48 ± 0.1 | 18.0 ± 0.2 | 19.9 ± 0.2 |
| 3 @ 89.5 | 7.66 ± 0.008 | 2.13 ± 0.01 | 14.2 ± 0.02 | 1.91 ± 0.01 | 1222 ± 5 | 0.45 ± 0.1 | 20.0 ± 0.2 | 17.8 ± 0.2 |
| 6 @ 89.5 | 7.73 ± 0.008 | 2.17 ± 0.01 | 14.8 ± 0.02 | 1.90 ± 0.01 | 1221 ± 5 | 0.45 ± 0.1 | 20.3 ± 0.2 | 17.6 ± 0.2 |
| 9 @ 90.5 | 7.66 ± 0.008 | 2.14 ± 0.01 | 14.4 ± 0.02 | 1.90 ± 0.01 | 1221 ± 5 | 0.45 ± 0.1 | 20.0 ± 0.2 | 17.8 ± 0.2 |
| 12 @91.5 | 7.72 ± 0.008 | 2.16 ± 0.01 | 14.7 ± 0.02 | 1.91 ± 0.01 | 1221 ± 5 | 0.45 ± 0.1 | 20.2 ± 0.2 | 17.7 ± 0.2 |
| 15@ 91.5 | 7.70 ± 0.008 | 2.15 ± 0.01 | 14.6 ± 0.02 | 1.91 ± 0.01 | 1220 ± 5 | 0.45 ± 0.1 | 20.2 ± 0.2 | 17.7 ± 0.2 |
From Table 1 it can be seen that the averaged radius, RP ave, increases after the addition of DPPE, gradually at first, but it appears to plateau after 6 mol%. This is to be expected since the addition of fully saturated DPPE lipids reduces the effective chain splay. This is best observed in the averaged molecular shape: the molecular wedge-angle (see Fig. 1B) drops from initially 19.9° to 17.8° (Table 1; eqn (11)). As this occurs, the added DPPE reduces the need for stretching and compression of lipids around the water core, since both POPE and DPPE are allowed to reside in regions where they can best adopt their natural length. This is confirmed by the local minima of the lattice spacing, a, at 9 mol% DPPE, which is dominated by the phosphate position radius RP ave. We also observe for 9 mol% the smallest water core area (πRp2) and lowest number of lipids around its circumference with respect to its neighbouring DPPE concentrations. Note, the average lipid length, the headgroup area and the chain splay change significantly only once DPPE is added, but these parameters remain within errors constant from 3 to 15 mol% DPPE (Table 1). Since the interstitial regions in the inverse hexagonal phase account for about 9 vol%,33 it is plausible that 3 mol% DPPE (equal to 2.9 vol% DPPE) is not sufficient to fill out the corners of the unit cell. Beyond the ideal concentration of 9 vol%, it is plausible that DPPE again starts to inhibit the ideal packing of POPE, causing the lipid chains to stretch/compress beyond their natural state. Interestingly, for 9 mol% DPPE the water core area is the smallest compared to adjacent concentrations; although the headgroup area per lipid remains, within errors, the same. Indeed, the number of lipids per water core circumference, nL, also displays accordingly, a local minimum. This means, adding too little DPPE most probably leads to an accumulation of relatively more POPE in the vertices (decompression zones) to overcome the packing frustration, whereas adding too much DPPE leads to packing stress in the compression zones of the hexagon. This is then compensated by accumulating relatively more POPE in the compression zones. Last, we note that average chain splay – which is directly observed in the wedge angle – increases linearly with temperature for pure lipid/water systems.32 However, the wedge angle in our study does actually decrease when DPPE is added, although the mixtures are analysed at slightly increasing temperatures. This is understandable, due to the lower chain splay caused by the added DPPE lipids. Concluding, the lowest water core area and smallest number of lipids per circumference imply that the packing stress is the lowest at 9 mol% DPPE; further to this, the 9 mol% mixture displays the best circularity of the water/lipid interface (Table 2), which is discussed in more details in the next paragraphs.
| DPPE (mol%) | l min (nm) | l max (nm) | R min (nm) | R max (nm) | Circularity |
|---|---|---|---|---|---|
| 0 | 1.58 ± 0.01 | 2.12 ± 0.01 | 1.97 ± 0.01 | 2.00 ± 0.01 | 0.993 ± 0.005 |
| 3 | 1.70 ± 0.01 | 2.30 ± 0.01 | 2.11 ± 0.01 | 2.14 ± 0.01 | 0.982 ± 0.005 |
| 6 | 1.69 ± 0.01 | 2.29 ± 0.01 | 2.16 ± 0.01 | 2.18 ± 0.02 | 0.997 ± 0.005 |
| 9 | 1.69 ± 0.01 | 2.28 ± 0.01 | 2.13 ± 0.01 | 2.15 ± 0.01 | 0.997 ± 0.005 |
| 12 | 1.70 ± 0.01 | 2.29 ± 0.01 | 2.15 ± 0.01 | 2.18 ± 0.01 | 0.994 ± 0.005 |
| 15 | 1.70 ± 0.01 | 2.29 ± 0.01 | 2.13 ± 0.01 | 2.17 ± 0.01 | 0.994 ± 0.005 |
As seen in Fig. 5A, the EDP curves as a function of γ smoothen out at 9 mol% DPPE in the head group region. In the methyl trough region (Fig. 5B), it is the 15 mol% DPPE sample instead, which shows the least disparity between its minimum and maximum electron density values. Nonetheless, 9 mol% DPPE promotes the greatest homogeneity of the lipid packing around the water core itself. From Fig. 5C–E comparing the EDPs along Rmin and Rmax, it is shown that the electron density is closest to uniformity at 9 mol% DPPE, as opposed to the two extremes of 0 and 15 mol% DPPE. Similarly low are the electron density fluctuations for the 6 mol% (see Fig. S8 in ESI†). This interpretation is further illustrated in Fig. 6C, where the ratio of the phosphate electron density values given for the 〈10〉 and 〈11〉 direction, is close to unity at 9 mol% due to a more even distribution of the lipid headgroups around at the water/lipid interface. Conversely for the 0 and 15 mol%, which display about 8% lower ρmin/ρmax values (Fig. 6C), where the phosphate electron density ratio is much lower, it suggests lipid headgroups are not homogenously spread out at this interface compared to 9 mol%.
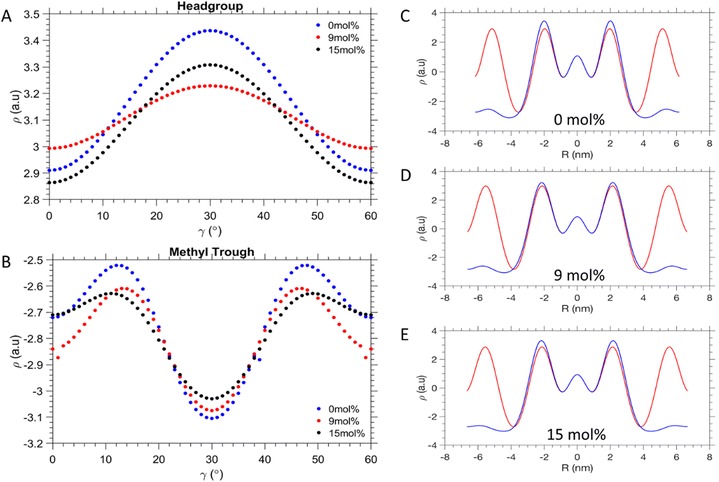 | ||
| Fig. 5 Electron density profiles. (A) Electron density fluctuation along in the head-group regions and (B) the methyl trough interfaces. (C)–(E) Radial electron density profiles with orientation of γ = 0° (red) and γ = 30° (blue). The interfaces and γ orientations are defined in Fig. 4A. Comparisons of all concentration are shown in Fig S7 and S8 in the ESI.† | ||
Table 2 summarises the characteristics of the phosphate interface and its circularity. The data show that the system is at near equilibrium at 9 mol%, because the values for Rmax and Rmin are not only the lowest (Fig. 6A), but display the smallest deviation from each other (Fig. 6B). This is plausible from the alleviation of packing stress, meaning the lipids do not have to compress/decompress as much as compared to the neighbouring concentrations of DPPE. This is further supported by the value of the circularity being closest to 1 at this concentration. For pure POPE we observe the smallest lmax and lmin values due to the strongest chain splay given (Table 1). This is also reflected in the fact that POPE lipids in the fluid state are about 0.15 nm shorter than DPPE lipids42 (see also lave in Table 1). Furthermore, for pure POPE the circularity is relatively low, clearly displaying non-ideal lipid packing. The same is true of 3 mol% DPPE, which in fact has the lowest circularity all around. It can be inferred that after the introduction of 3 mol% of DPPE, the packing efficiency may have worsened in this respect. The DPPE is therefore acting here essentially as an impurity, not yet at the threshold concentration to provide packing frustration relief. The 6 and 9 mol% DPPE mixtures appear to be the most homogenously packed aggregations, given their values for circularity. At the highest DPPE concentrations, a subsequent decrease of the circularity is observed. This is reflected in the increase of differing Rmin and Rmax values, mirroring the behaviour at 0 and 3 mol% of DPPE (Fig. 6B). The notion that the 9 mol% DPPE sample is reducing packing frustration the best, is further illustrated in Fig. 6C. The ratio of the phosphate electron densities given for γ = 0° and 30°comes close to unity. In contrast, the 0 and 15 mol% DPPE mixtures display a significantly lower the electron density ratio, which suggests that lipid headgroups are less homogeneously packed. However, the 6 and 9 mol% DPPE samples display a slightly bigger chain packing frustration as compared to 12 and 15 mol% DPPE, with their ρmax/ρmin values being about 2% smaller (Fig. 6D). These subtle homogeneity improvements in the methyl trough region are most likely caused by a smoother and broader distribution of DPPE around the vertices as can be seen in the EDPs in Fig. 5B. Summarising, while 3 mol% of DPPE does not induce any apparent chain packing frustration release (ρmax/ρmin = 0.81), a sudden improvement in the chain packing order is achieved for concentration for 6 mol% and greater (0.85–0.87).
Overall, the 9 mol% DPPE sample parameters confirm close to ideal lipid packing within the hexagon. From the geometric considerations of the Wigner–Seitz cell, the interstitial void regions constitute 9% of the overall area, so it is volumetrically plausible that 9 mol% DPPE (8.8 vol%) best accounts for this interstitial region to be occupied with the lowest packing frustration, and hence leading to a minimum in hydrocarbon chain compression/decompression within the vertex and flat areas. Predominant locations of DPPE in corner zones and POPE in the flat zones of the Wigner–Seitz cell, are therefore likely to be driven by releases in chain stretching energy.30,31,37 Indeed, free energy model calculations based on the theory of Iglič and colleagues,30 display a shallow local minimum in the free energy around 6–9 mol% DPPE with a value of about −0.06 kT per lipid, in which the bending energy accounts for −0.47 kT per lipid and the stretching energy with 0.41 kT per lipid (Fig. S9 in the ESI†).
Fig. 7A and B display schematic models of the POPE-only and POPE/DPPE 9 mol% mixture. Note, the Wigner Seitz cells are drawn in scale, refering in their heights to the lattice parameters, a, equal to 7.12 and 7.66 nm, respectively. Further, the circles with the radius RP plus lave of the POPE-only case are shown in both models with a dashed line, indicating that the average lipid length in the pure POPE sample comes closer to the minimum length, lmin, of the 9 mol% DPPE sample. These models confirm the notion that the POPE lipids are dominating the flat side locations, while the relatively longer DPPE lipids concentrate in the vertices of the hexagon.
3.3 Anisotropy of disorder – thermal versus disorder of second kind
Finally, we have analysed the dynamic behaviour of the inverse hexagonal phase for 3, 9 and 15 mol% of DPPE samples. Of special interest is the local membrane fluctuation behaviour of the inverse hexagonal phases in the 〈10〉 and 〈11〉 directions (Fig. 1 and 7), which refer to the direction of Rmax (towards the vertices) and Rmin (towards the flat sides) within the hexagonal unit cell. As clearly demonstrated in the Fig. S4 (ESI†), the peak shape progression in the 〈10〉 direction shows an increase in width as function of the diffraction order, which reveals disorder of 2nd kind with strong undulations within this set of planes. In contrast, the peak shape progression in the 〈11〉 direction displays a constant width as function of the diffraction order, which demonstrates dominating thermal disorder instead. Thus, there is a clear anisotropy of disorder given in the inverse hexagonal phase. At this point, we have to stress once more that the MCT analysis that we applied to the (10), (20), (30) peaks (Fig. S4, ESI†) can strictly only be applied to smectic liquid crystals in the fluid phase;54 however, the purpose here is to gain an approximate value of the local layer fluctuations in this direction. The value of the fluctuation distance, σ, being in the order of 0.3 nm compares very well to the σ published for 1,2-dimyristoyl-sn-glycero-3-phospho-ethanolamine (DMPE) in the smectic phase at 80 °C.42,55Given the fact that the disorder in the 〈11〉 direction is dominated by thermal disorder (Fig. S4B, ESI†), we interpret the (10) planes to fluctuate more than the (11) planes at all concentrations of DPPE. Interestingly, this mechanical behaviour of the hexagonal aggregate being more compressible in the 〈10〉 directions, is also reflected in the electron density maps (Fig. 4 and 7C). The headgroup thickness apparently stretches over a wider region in the 〈10〉, and subsequently the inner water core reduces in diameter in this direction. Thus, the water core can roughly be described as a rounded hexagon, but rotated by 30° relative to the hexagonal Wigner–Seitz unit cell (Fig. 7C). While no clear DPPE concentration-dependent trend was observed in the fluctuation parameter, we deduce the compressed lipid zones (flat sides) are mechanically more stable than the decompressed lipid zones around the vertices (see Fig. S4, ESI†).
3.4 Hydration properties of the inverse hexagonal phase
Concerning the number of water molecules in each defined water region, the headgroup waters are constant within errors for all mixtures (Table 3), which aligns with the small changes in the area per lipid, Ap. Indeed, Ap does not vary more than 1% from 3 to 15 mol% DPPE (Table 1). For our DPPE/POPE mixtures, we find 8 water for the headgroup region, which compares to 7 waters per headgroup found in 1-stearoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (SOPE).32 Also the total numbers of about 17 waters per lipid are within error margins constant and compare well to the 16 waters per lipids found in SOPE. Second, the number of perturbed waters per lipid is expected to be larger in the 〈10〉 direction as mediated by the larger fluctuation distance, σ. This consequently leads to a relatively smaller number of free waters per lipid in the vertices regions, when compared to the flat regions. In Fig. 7D, we have graphically summarised our model for the extension of the headgroup water region, the perturbed water layer and the free water core.| DPPE (mol%) | σ (nm) 〈10〉 | Total waters (averaged) | Headgroup waters | Core waters | Perturbed waters 〈10〉 | Free waters 〈10〉 |
|---|---|---|---|---|---|---|
| 3 | 0.26 ± 0.05 | 16.7 ± 0.8 | 8.0 ± 0.6 | 8.7 ± 0.7 | 2.6 ± 0.3 | 6.1 ± 0.5 |
| 9 | 0.30 ± 0.06 | 17.0 ± 0.9 | 8.1 ± 0.6 | 8.9 ± 0.7 | 3.0 ± 0.3 | 5.9 ± 0.5 |
| 15 | 0.28 ± 0.06 | 16.9 ± 0.9 | 8.0 ± 0.6 | 8.9 ± 0.7 | 2.9 ± 0.3 | 6.2 ± 0.5 |
Comparing the water distribution in the inverse hexagonal phase to the three-water layer model applied to the fluid lamellar phase of PEs,52 some remarkable differences become clear: First, the fluid lamellar phase of PEs has no free waters per lipid, while the inverse hexagonal phase displays 6.5 free waters per lipid in the 〈10〉 direction and most probably displaying an even greater number in the 〈11〉 direction (Table 3). Second, while the perturbed water layer thickness is constant along the lipid/water interface (σ = 0.3 nm for DMPE at 80 °C52), the membrane undulations in the inverse hexagonal phase differ in the vertices (σ ≈ 0.3 nm) from those in the flat regions (disorder of 2nd kind versus thermal disorder). Third, the number of waters in the headgroup region are slightly smaller in the inverse hexagonal phase. Here 8 waters compare to 8.5 waters in the lamellar phase of DMPE at 80 °C.52 The same accounts for number of perturbed waters per lipid (about 3 waters compare to 6 waters in DMPE at 80 °C52). The latter differences are explained by the smaller area per lipid in the inverse hexagonal phase (Ap = 0.45 nm2 in the HII-phase compares to Ap = 0.64 nm2 in DMPE at 80 °C52) and its molecular wedge shape (Fig. 1B).
The observed anisotropy in the mechanical behaviour of the inverse hexagonal phase, and concomitantly, the change of local hydration properties has implications that go beyond this study. It can indeed be expected that any curved membrane contains a curvature-dependent mechanical stress distribution,56 which in turn will lead to local variations in hydration properties of lipid/water interface. Noteworthy, local variations in hydration properties go hand in hand with changes in repulsive undulation and attractive van der Waals forces,55 and hence might be decisive for a deeper understanding of biomembrane interactions with its extracellular world.57
Conclusion
In this study, POPE was investigated in the HII phase with increasing molar concentration of DPPE. The circularity as a function of DPPE concentration was determined to illustrate the alleviation of packing stress around the quasi-cylindrical outline of the phosphate positions. It was found that adding 6 and 9 mol% DPPE produced polar/apolar interfaces, which most closely resembled a perfect circle. Most likely, the longer hydrophobic chains of DPPE lead to its aggregation in the corner areas of the hexagonal Wigner–Seitz cell, and thereby reducing packing frustration in these interstitial regions. In particular, at 9 mol% of DPPE the smallest water core area and lowest number of lipids per circumference is given with respect to its neighbouring concentrations of 6 and 12 mol%, supporting the hypothesis that DPPE allows the lipids to aggregate more homogenously around the water core and ultimately reducing the energetic cost of chain stretching. Finally, we have shown that the local variations in interfacial fluctuations are not significantly influenced the addition of DPPE, but we have shown that the inverse hexagonal phase is mechanically most stable in the 〈11〉 direction (thermal disorder), and least stable in the 〈10〉 direction (disorder of 2nd kind). The compression and decompression zones within the lipid monolayer also lead to a variation of hydration behaviour along the membrane/water interface.Author contributions
Conceptualisation, data interpretation and revising drafts: G. V., A. S., A. T. and M. R.; data analysis and writing: G. V. and M. R.; carrying out experiments: M. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the EPSRC scholarship grant (EP/S023631/1) of Gerome Vancuylenberg. Gerome is part of the 6th cohort of the EPSRC Centre for Doctoral Training in Soft Matter for Formulation and Industrial Innovation (SOFI2).References
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Elsevier, 1997 Search PubMed.
- A. Yaghmur, L. Paasonen, M. Yliperttula, A. Urtti and M. Rappolt, J. Phys. Chem. Lett., 2010, 1, 962–966 CrossRef CAS.
- M. Rappolt, A. Hickel, F. Bringezu and K. Lohner, Biophys. J., 2003, 84, 3111–3122 CrossRef CAS PubMed.
- M. Rappolt, in Advances in Planar Lipid Bilayers and Liposomes, ed. I. Aleš and G. Julia, Academic Press, 2013, vol. 17, pp. 29–54 Search PubMed.
- A. Sánchez-Lavega, A. García-Muñoz, T. del Río-Gaztelurrutia, S. Pérez-Hoyos, J. F. Sanz-Requena, R. Hueso, S. Guerlet and J. Peralta, Nat. Commun., 2020, 11, 2281 CrossRef PubMed.
- D. A. Godfrey, Icarus, 1988, 76, 335–356 CrossRef.
- T. C. Hales, Discrete Comput. Geom., 2001, 25, 1–22 CrossRef.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS PubMed.
- M. Rappolt, in Advances in Biomembranes and Lipid Self-Assembly, ed. A. Iglic, M. Rappolt and A. J. Garcia-Saez, Elsevier B.V., 2019, vol. 29, pp. 1–21 Search PubMed.
- Z. A. Almsherqi, S. D. Kohlwein and Y. Deng, J. Cell Biol., 2006, 173, 839–844 CrossRef CAS PubMed.
- Y. Deng and A. Angelova, Front. Cell Dev. Biol., 2021, 9, 617984 CrossRef PubMed.
- M. Rappolt, Journal, 2013, 17, 29–54 CAS.
- J. M. Seddon, Biochim. Biophys. Acta, 1990, 1031, 1–69 CrossRef CAS PubMed.
- M. Rappolt, A. Hodzic, B. Sartori, M. Ollivon and P. Laggner, Chem. Phys. Lipids, 2008, 154, 46–55 CrossRef CAS PubMed.
- R. Van Venetie and A. J. Verkleij, Biochim. Biophys. Acta, Biomembr., 1981, 645, 262–269 CrossRef CAS PubMed.
- D. P. Siegel, Biophys. J., 1986, 49, 1155–1170 CrossRef CAS PubMed.
- P. Veranic, M. Lokar, G. J. Schütz, J. Weghuber, S. Wieser, H. Hägerstrand, V. Kralj-Iglic and A. Iglic, Biophys. J., 2008, 95, 4416–4425 CrossRef CAS PubMed.
- V. Luzzati, F. Reiss-Husson, E. Rivas and T. Gulik-Krzywicki, Journal, 1966, 137, 409–413 CAS.
- Y. D. Dong, A. J. Tilley, I. Larson, M. Jayne Lawrence, H. Amenitsch, M. Rappolt, T. Hanley and B. J. Boyd, Langmuir, 2010, 26, 9000–9010 CrossRef CAS PubMed.
- A. Yaghmur, P. Laggner, B. Sartori and M. Rappolt, PLoS One, 2008, 3, e2072 CrossRef PubMed.
- A. Yaghmur, P. Laggner, S. Zhang and M. Rappolt, PLoS One, 2007, 2, e479 CrossRef PubMed.
- G. C. Shearman, A. I. I. Tyler, N. J. Brooks, R. H. Templer, O. Ces, R. V. Law and J. M. Seddon, Liq. Cryst., 2010, 37, 679–694 CrossRef CAS.
- W. K. Fong, A. Sánchez-Ferrer, M. Rappolt, B. J. Boyd and R. Mezzenga, Langmuir, 2019, 35, 14949–14958 CrossRef CAS PubMed.
- A. Hickel, S. Danner-Pongratz, H. Amenitsch, G. Degovics, M. Rappolt, K. Lohner and G. Pabst, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 2325–2333 CrossRef CAS PubMed.
- B. Kollmitzer, P. Heftberger, M. Rappolt and G. Pabst, Soft Matter, 2013, 9, 10877–10884 RSC.
- M. P. K. Frewein, M. Rumetshofer and G. Pabst, J. Appl. Crystallogr., 2019, 52, 403–414 CrossRef CAS PubMed.
- P. E. Harper and S. M. Gruner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 2, 217–228 CrossRef CAS.
- M. W. Tate and S. M. Gruner, Biochemistry, 1989, 28, 4245–4253 CrossRef CAS PubMed.
- D. C. Turner and S. M. Gruner, Biochemistry, 1992, 31, 1340–1355 CrossRef CAS PubMed.
- S. Perutkova, M. Daniel, G. Dolinar, M. Rappolt, V. Kralj-Iglic and A. Iglic, in Advances in Planar Lipid Bilayers and Liposomes, ed. A. Leitmannova-Liu and H. T. Tien, Elsvier, Academic Press, Burlington, 2009, vol. 9, pp. 238–278 Search PubMed.
- S. Perutkova, M. Daniel, M. Rappolt, G. Pabst, G. Dolinar, V. Kralj-Iglic and A. Iglic, Phys. Chem. Chem. Phys., 2011, 13, 3100–3107 RSC.
- M. Rappolt, A. Hodzic, B. Sartori, M. Ollivon and P. Laggner, Chem. Phys. Lipids, 2008, 154, 46–55 CrossRef CAS PubMed.
- M. Rappolt, F. Cacho-Nerin, C. Morello and A. Yaghmur, Soft Matter, 2013, 9, 6291–6300 RSC.
- M. M. Kozlov, S. Leikin and R. P. Rand, Biophys. J., 1994, 67, 1603–1611 CrossRef CAS PubMed.
- P. M. Duesing, R. H. Templer and J. M. Seddon, Langmuir, 1997, 13, 351–359 CrossRef CAS.
- G. C. Shearman, O. Ces and R. H. Templer, Soft Matter, 2010, 6, 256–262 RSC.
- T. Mareš, M. Daniel, Š. Perutkova, A. Perne, G. Dolinar, A. Iglič, M. Rappolt and V. Kralj-Iglič, J. Phys. Chem. B, 2008, 112, 16575–16584 CrossRef PubMed.
- A. Perutková, M. Daniel, M. Rappolt, G. Pabst, G. Dolinar, V. Kralj-Igli and A. Igli, Phys. Chem. Chem. Phys., 2011, 13, 3100–3107 RSC.
- A. Yaghmur, M. Kriechbaum, H. Amenitsch, M. Steinhart, P. Laggner and M. Rappolt, Langmuir, 2010, 26, 1177–1185 CrossRef CAS PubMed.
- D. C. Turner, J. S. Huang and S. M. Gruner, Biochemistry, 1992, 31, 1356–1363 CrossRef CAS PubMed.
- P. E. Harper, A. T. Cavazos, J. J. Kinnun, H. I. Petrache and S. R. Wassall, Langmuir, 2020, 36, 4908–4916 CrossRef CAS PubMed.
- M. Rappolt, P. Laggner and G. Pabst, in Recent Research Developments in Biophysics, ed. S. G. Pandalai, Transworld Research Network, Trivandrum, 2004, vol. 3, Part II, ch. 20, pp. 365–394 Search PubMed.
- H. Amenitsch, S. Bernstorff, M. Kriechbaum, D. Lombardo, H. Mio, G. Pabst, M. Rappolt and P. Laggner, Il Nuovo Cimento D, 1998, 20, 9 Search PubMed.
- S. Bernstorff, H. Amenitsch and P. Laggner, J. Synchrotron Radiat., 1998, 5, 1215–1221 CrossRef CAS PubMed.
- A. M. Petrascu, M. H. J. Koch and A. Gabriel, J. Macromol. Sci. Phys., 1998, B37, 463–483 CrossRef CAS.
- T. C. Huang, H. Toraya, T. N. Blanton and Y. Wu, J. Appl. Crystallogr., 1993, 26, 180–184 CrossRef CAS.
- N. Y. D. Li, Š. Perutková, A. Iglič and M. Rappolt, Elektrotehniski Vestnik/Electrotechnical Review, 2017, 84, 69–75 Search PubMed.
- P. E. Harper, D. A. Mannock, R. N. Lewis, R. N. McElhaney and S. M. Gruner, Biophys. J., 2001, 81, 2693–2706 CrossRef CAS PubMed.
- B. Tenchov, M. Rappolt, R. Koynova and G. Rapp, Biochim. Biophys. Acta, Biomembr., 1996, 1285, 109–122 CrossRef PubMed.
- R. T. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 5047–5060 CrossRef CAS PubMed.
- H. I. Petrache, S. Tristram-Nagle and J. F. Nagle, Chem. Phys. Lipids, 1998, 95, 83–94 CrossRef CAS PubMed.
- G. Vancuylenberg, A. Sadeghpour, A. I. I. Tyler and M. Rappolt, Journal, 2023, 27, DOI:10.26434/chemrxiv-2023-wdjqm-v2.
- M. Gerstein and C. Chothia, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 10167–10172 CrossRef CAS PubMed.
- R. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 5047–5060 CrossRef CAS PubMed.
- G. Vancuylenberg, A. Sadeghpour, A. I. I. Tyler and M. Rappolt, Soft Matter, 2023, 19, 5179–5192 RSC.
- S. Aeffner, T. Reusch, B. Weinhausen and T. Salditt, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1609–E1618 CrossRef CAS PubMed.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev., 2006, 7, 9–19 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01029e |
| This journal is © The Royal Society of Chemistry 2023 |