Open Access Article
Open Access ArticleSelf-propulsion of a calcium alginate surfer†
Réka
Zahorán
a,
Pawan
Kumar‡
a,
Dezső
Horváth
 b and
Ágota
Tóth
b and
Ágota
Tóth
 *a
*a
aDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary. E-mail: atoth@chem.u-szeged.hu
bDepartment of Applied and Environmental Chemistry, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary
First published on 10th October 2023
Abstract
A droplet of sodium alginate dripped into calcium chloride solution results in plate or boat shaped hydrogels. Both exhibit several minute-long self-propelled motion on the liquid surface without any extra fuel added, offering a new method to making active materials. By changing the initial concentrations, we are able to tune the transient dynamic activities from translational to rotational or stop-and-run motion. Dynamics are governed by osmotic pressure induced Marangoni effect, depending on the density difference and initial concentrations.
1 Introduction
Most living organisms move by self-propulsion, which is an essential tool for their survival.1 The locomotion is prerequisite for doing tasks and therefore scientists are highly interested in designing inanimate active matter, that can move itself in a pre-planned manner.2,3 Several techniques are available to generate autonomous activities by consuming chemical energy4 or exploiting physical phenomena (electromagnetic,5 electrical energy,6 light7,8). Further mechanisms have been proposed as well, such as Marangoni effect,9 electroosmosis,6 bubble ejection10 and dielectrophoresis.11 Different names also distinguish artificial active objects depending on their characteristics. In general, active matter is called either motor12 or machine13 reflecting on that the object powers itself by converting some kind of energy into kinetic energy. Gear14 and droplet15 are also used to mirror the physical design. Moreover, a surfer7 propels along the interface, whilst a swimmer16,17 moves in the bulk phase.18Marangoni effect is an interfacial phenomenon, where thermal or chemical gradients cause surface tension gradient, which induces mass transport. A well-known example of this is simply based on the dissolution of camphor in water.19–22 In literature, reactive self-propulsion considered as a chemical reaction induced motion, but an extra component (usually a surfactant or an organic solvent) always implemented in the reaction to create the surface tension gradient.23–25 In addition to the camphor dissolution, only a recent article reports on tension-lowering polyelectrolyte reactants, which self-generate motion without an additive.26 In a different way, the concept of exclusively one chemical reaction is responsible for the motion was also imagined earlier by van’t Hoff, by generating osmotic pressure gradient as the concept of truly exploiting “chemomechanical” forces.27 The idea to convert chemical energy into mechanical motion in a form of an osmotic motor is supported by computational results.28 Our purpose is to demonstrate experimentally that a simple reaction without additives can induce self-propulsion by exploiting osmotic pressure gradient through gelation.
In designing synthetic motile objects, their physical and chemical constructions are very important, because they affect the dynamics differently, resulting in translational, rotational, spinning or even oscillatory motions. This could mean applying liquids in the form of oil droplets,24,29 solid materials, like in the case of strings of camphor disks30 or gel-based structures like enzyme-programmed alginate objects.31 Gel-based systems25,32–34 are especially favorable in technology-development due to their soft matter properties. Besides that, various applications are being explored, such as developing bio-actuators,35 drug delivery carriers,17,36 sensors for toxicity detection37 and environmental remediation of chemical spills.38 More control can be achieved with the help of studying interactions between the self-propelled objects.39
In this work, we introduce a new type of active material exploiting osmosis. We use the simple reaction between calcium and alginate ions without any additives.40 While the gelation takes place, different types of motions are observed. We demonstrate, how the initial concentrations influence the dynamics along with the hydrogel shape.
2 Experimental
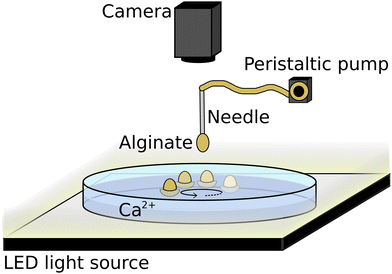
Fig. 1 illustrates the experimental system. Self-propelled hydrogels were made in a glass Petri dish (i.d. = 6 cm) filled with 15 mL, 2–6 M calcium chloride solution. To make the surfer, one droplet of 0.3–1.5% w/V sodium alginate (ALG) solution was dripped (0.38 mL min−1) into the electrolyte from 5 mm above, aiming for the center of the Petri dish. The dripping was implemented by using a peristaltic pump (Ismatec Reglo) installed with a Tygon tube (i.d. = 0.76 mm) ending in a scalp vein needle (i.d. = 0.4 mm). In order to minimize geometrical effects, we kept all experimental conditions constant. Trajectories of the hydrogel surfers were recorded from above and sidewise by taking images with 5 fps using a digital camera (Unibrain Fire-i 630c) equipped with a 24 mm focal length lens (Vivitar). For shadowgraph imaging, a 12 mm extension tube (Vivitar) was inserted between the lens and the camera. The Petri dish was placed above an LED light source and 0.1 mL of 0.4% congo red dye was added to the alginate solution to enhance the visibility.Analytical grade CaCl2·2H2O (99–105%) and technical grade sodium alginate reagents from VWR International were used. Chemicals were dissolved in deionized water (Purite RO100). Alginate solution was first stirred overnight to properly dissolve the polysaccharide, and then kept in a fridge for a maximum usage of one week. Experiments were repeated at least three times at 23 ± 2 °C. Images were analyzed using Fiji or Wolfram Mathematica, and edited in Inkscape. Viscosity, density, droplet weight, surface tension and nuclear magnetic resonance (NMR) measurements are added in Tables S1–S3 in the ESI.†
3 Results and discussion
Phenomenon
When the dripped alginate droplet comes into contact with the calcium chloride solution, crosslinking occurs immediately. During the gelation, the guluronate block of the alginate chains crosslinks with calcium ions diffusing inward from the surrounding solution. As soon as gelation begins on the outside, the self-propulsion of the droplet starts because of the minute asymmetry in the shape and gel structure (Movie S1 in ESI†). Initially the floating droplet spreads out on the surface and takes up the shape of a plate. For smaller alginate concentrations (0.3 or 0.5% w/V), the droplet maintains this shape (see Fig. 2b). However, at greater alginate content (1 or 1.5% w/V), it transforms into a boat (see Fig. 2a). This transition is shown in Fig. 2c–h), where the entire droplet, both under and above the liquid surface, shrinks till it reaches the boat form. The bottom part of the droplet crosslinks immediately after contacting the CaCl2 solution (Fig. 2c), while the upper part remains initially in a solution form and bulges higher (Fig. 2d–f). Later, it stops rising and shrinks as gelation also takes place inside (Fig. 2g and h). In contrast, plates (at lower alginate concentration) crosslink in a different way resulting in thin and flexible structures due to slower gelation. After contacting with the calcium chloride solution, the surfer only shrinks and becomes thinner. Along with the drastic shape transformations, particle image velocimetry (PIV) reveals that strong fluid flow evolves (see Fig. S3, S4 and Movies S2 and S3 in ESI†) in the calcium solution. These observations are inevitably the results of the arising osmotic pressure,41 whilst gelation also supports the shrinkage.42With shadowgraph imaging, we detect that the refractive-index changes in the immediate vicinity of the surfer when it moves (see Fig. 3). The only chemical that can be exerted out from the hydrogel, which is detected as it dilutes the surrounding calcium solution, is water.43 The arising osmotic pressure exerts the water out which decreases the surface tension around (see Table S2 for the surface tension values, ESI†). The surfer appears symmetric, however, around its perimeter small fluctuations in the surface tension (δγ) exist. The magnitude can be estimated from the velocity on the surface (u) and the liquid viscosity (η) as δγ ≈ uη = 0.02 − 0.7 mN m−1. This yields an upper limit on the Marangoni number as Ma = δγl/(ηD) ≈ 105 where l is the liquid depth. Hence, motion is driven by surface tension gradient.
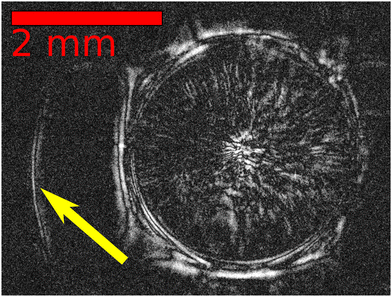 | ||
| Fig. 3 Top view of a surfer (1.5% w/V ALG) after exerting water to the surrounding 4 M CaCl2 solution using shadowgraph imaging. The yellow arrow points to the boundary of the diluted area. | ||
Our system does not include any additional “fuel” unlike in other published cases,24,25,30,34 only the gelation of two reactants is responsible for the self-propulsion as osmosis takes place.
Dynamics
The surfer position in the xy-plane of the Petri dish was gathered by an in-house imaging script using built-in macros in Fiji. First, the contour of the surfer was determined using Canny Edge Detector, then a circle with the corresponding radius was fitted and its center position (X, Y coordinates) was exported through Hough Circle Transform. Knowing the time delay (Δt) between two images, the instantaneous speed (v) of the object, defined as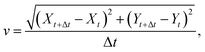 | (1) |
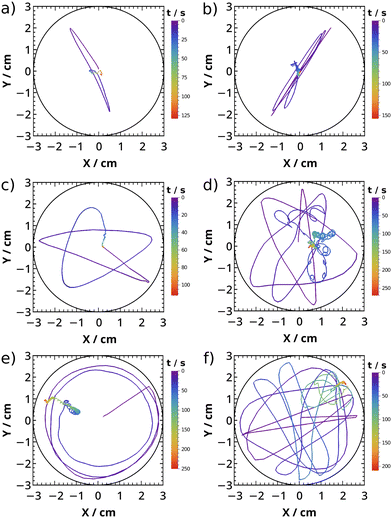
With different initial concentrations, we created different dynamic behavior (see Fig. 5). We see trajectories rather moving linearly at 1–1.5% w/V alginate concentrations (Fig. 5a and b and Fig. S7 in ESI†). Nonetheless, parallel experiments show that trajectories stochastically located in the Petri dish in all of the different concentrations (see Fig. S7 in ESI†). Increasing the CaCl2 concentration creates higher surface tension gradient (see Table S2 in ESI†), hence gives more energy to the surfer (see Fig. 5a and b). However the linear motion of period I does not change due to the similar repulsive force between the wall and the surfer caused by the similar boat shape. We also see in Fig. 5b that turning points move further away from the wall over time, because the surface tension gradient (thus repulsion) changes along the crosslinking. At 0.5% w/V alginate concentration, repulsion decreases between the plate and the wall. The surfer manages to approach the wall for a longer time, yet soon diverts its direction and therefore the traveled route in period I resembles a star-shape (Fig. 5c and d). The repulsion between the wall and the surfer changes and proceeds similarly to the above mentioned alginate composition in a single experiment. At 0.3% w/V alginate, the surfer can touch the wall due to the small repulsion, so it can even follow the Petri dish boundaries (Fig. 5e). If we use high CaCl2 concentration at this alginate amount, more repulsion exerted yields the turnings of the surfer (Fig. 5f).
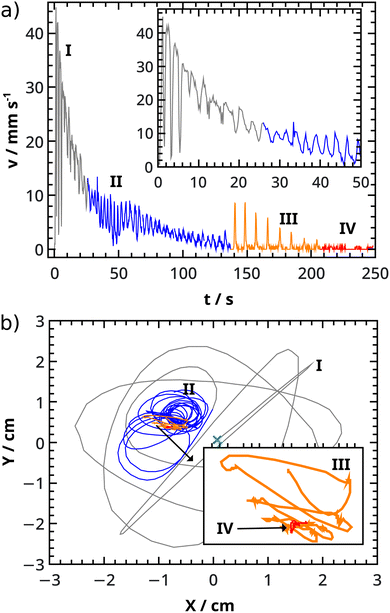
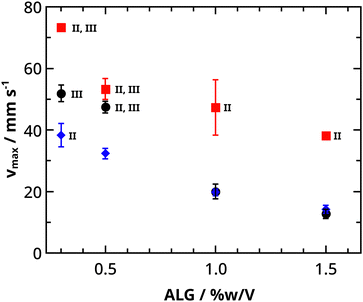
The surfer accelerates the most in period I. It reaches its maximum velocity (vmax) in this phase, where different maximum velocities are measured depending on the initial concentrations (see Fig. 6a). By increasing the alginate concentration, the maximum velocity decreases. The alginate concentration regulates the amount of exerted water, which sets the extent of the Marangoni effect (and thus the velocities). We observe this (Fig. 2c–h) when the surfer is distorted upwards into a boat at higher alginate concentrations, while it retains water unlike plates, which only releases water. It is also important to note, that plates (lower alginate concentrations) are more likely to approach the wall boundaries closer because of the smaller repulsion, which slows down the plates less.
We have found that the highest maximum velocities are reached in 4 M CaCl2 solutions. To understand this, we discuss the increase and decrease in maximum velocity separately, along with the CaCl2 concentration. At 2 M CaCl2, the density difference significantly decreases, which influences the surfer's depth of immersion. This affects the speed, which was already published about camphor boats: deeper immersion decreases velocity.46 We have also observed, that fully immersed surfers do not move. At 6 M CaCl2, we suggest that the gelation is faster due to the high concentration, which restricts the exertion of water. For example, at 6 M CaCl2 and 0.3% w/V alginate, dominantly stop-and-run motion is observed (see Fig. 7d), which indicates water regulation in a short period of time due to the high-rate gelation.
 | ||
| Fig. 7 Different velocity profiles of (a) 2 M CaCl2 + 1% w/V ALG, (b) 4 M CaCl2 + 0.5% w/V ALG, (c) 2 M CaCl2 + 0.3% w/V ALG and (d) 6 M CaCl2 + 0.3% w/V ALG. | ||
Occasionally the kinetic energy of period I is transformed into period II and/or III motions as indicated in Fig. 6. This transformation can occur by changing both CaCl2 and alginate concentration, but randomly based on the durations of period I (see Fig. S8 in ESI†). From Fig. 6 we can also see that there are concentrations where only period I exists besides period IV (an example in Fig. 7a). When surfers have more energy, which is indicated by a higher maximum velocity value, they are able to make rotational motions (II). With even more energy, they are also able to make stop-and-run motion (III) in addition to period II (see Fig. 7b). Increasing the CaCl2 concentration can make a complete transformation from period II to III (illustrated in Fig. 7c and d) through a transition state (see Fig. S9 in ESI†), where both types exist while the frequency of period II is altered with the changing spatial extent of the rotational motion (larger or smaller circles). If the alginate concentration is reduced, period III is more strongly present than period II (see Fig. 4a and 7d). By changing the initial concentrations, we are able to dissipate chemical energy in the four characteristic periods and observe different dynamical behavior.
4 Conclusions
We have created an active material exploiting osmosis in the gelling reaction of alginate and calcium ions. The appearing osmotic pressure during the crosslinking exerts water from the surfer, which changes the surface tension around the surfer and thus forcing it to move due to Marangoni effect. We have not used any extra chemical to provide “fuel” for the motion, which offers a new method for transient self-propulsion based on hydrogels.Two types of surfer shapes have been observed after complete crosslinking, where plates considered more active than boats. We have observed the complete dynamical transition from harmonic to relaxation-like motion with the more active surfers. Consecutively four periods (translational, rotational, stop-and-run, quasi-equilibrium) have been distinguished and different trajectories have been observed according to the initial concentrations. The occurrence of these motions (from linear to curvilinear to rotational) is also influenced by the shape of the surfer.
We have found that maximum velocities increase with decreasing alginate concentration, which depends on the water retention ability set by the alginate concentration. It also increases with the CaCl2 concentration to a certain extent, because the density difference increases, which decreases the depth of immersion. Further increase in the CaCl2 concentration results in smaller maximum velocities because of the greater gelation rate. We have also explained that the duration of the observed periods can be tuned by the initial concentrations. The study presented here advances energy-based motors and suggests a new way on how to design soft self-propelled surfers based on osmosis.
Data availability
Original data are available from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research, Development and Innovation Office (K138844) and by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund (TKP2021-NVA-19). We also thank Cintia Hajdu for the NMR measurements. The authors are grateful to the University of Szeged OpenAccess Fund (6593) for support.References
- M. T. Rosing, Thermodynamics of life on the planetary scale, Int. J. Astrobiology, 2005, 4, 9–11 CrossRef CAS.
- A. A. Solovev, S. Sanchez, M. Pumera, Y. F. Mei and O. G. Schmidt, Magnetic control of tubular catalytic microbots for the transport, assembly, and delivery of micro-objects, Adv. Funct. Mater., 2010, 20, 2430–2435 CrossRef CAS.
- T.-Y. Huang, M. S. Sakar, A. Mao, A. J. Petruska, F. Qiu, X.-B. Chen, S. Kennedy, D. Mooney and B. J. Nelson, 3D printed microtransporters: Compound micromachines for spatiotemporally controlled delivery of therapeutic agents, Adv. Mater., 2015, 27, 6644–6650 CrossRef CAS PubMed.
- M. Cheng, G. Ju, Y. Zhang, M. Song, Y. Zhang and F. Shi, Supramolecular Assembly of Macroscopic Building Blocks Through Self-Propelled Locomotion by Dissipating Chemical Energy, Small, 2014, 10, 3907–3911 CrossRef CAS.
- M. C. Hoang, K. T. Nguyen, V. H. Le, J. Kim, E. Choi, B. Kang, J.-O. Park and C.-S. Kim, Independent electromagnetic field control for practical approach to actively locomotive wireless capsule endoscope, IEEE Trans. Syst. Man Cybern. Syst., 2019, 51, 3040–3052 Search PubMed.
- T. Yamanaka and F. Arai, Miniaturization effect of electroosmotic self-propulsive microswimmer powered by biofuel cell, ROBOMECH J., 2019, 6, 1–9 CrossRef.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Living crystals of light-activated colloidal surfers, Science, 2013, 339, 936–940 CrossRef CAS.
- A. Yucknovsky, B. B. Rich, A. Westfried, B. Pokroy and N. Amdursky, Self-Propulsion of Droplets via Light-Stimuli Rapid Control of Their Surface Tension, Adv. Mater. Interfaces, 2021, 8, 2100751 CrossRef CAS.
- J. Chen, C. Yang and Z.-S. Mao, The interphase mass transfer in liquid-liquid systems with Marangoni effect, Eur. Phys. J.: Spec. Top., 2015, 224, 389–399 CAS.
- P. Kumar, Q. Wang, D. Horváth, Á. Tóth and O. Steinbock, Collective motion of self-propelled chemical garden tubes, Soft Matter, 2022, 18, 4389–4395 RSC.
- S. Gangwal, O. J. Cayre and O. D. Velev, Dielectrophoretic assembly of metallodielectric Janus particles in AC electric fields, Langmuir, 2008, 24, 13312–13320 CrossRef CAS PubMed.
- M. Guix, S. M. Weiz, O. G. Schmidt and M. Medina-Sánchez, Self-propelled micro/nanoparticle motors, Part. Part. Syst. Charact., 2018, 35, 1700382 CrossRef.
- B. Khezri and M. Pumera, Metal-Organic Frameworks Based Nano/Micro/Millimeter-Sized Self-Propelled Autonomous Machines, Adv. Mater., 2019, 31, 1806530 CrossRef.
- M. Yang and M. Ripoll, A self-propelled thermophoretic microgear, Soft Matter, 2014, 10, 1006–1011 RSC.
- G. Launay, M. S. Sadullah, G. McHale, R. Ledesma-Aguilar, H. Kusumaatmaja and G. G. Wells, Self-propelled droplet transport on shaped-liquid surfaces, Sci. Rep., 2020, 10, 14987 CrossRef.
- B. Dai, J. Wang, Z. Xiong, X. Zhan, W. Dai, C.-C. Li, S.-P. Feng and J. Tang, Programmable artificial phototactic microswimmer, Nat. Nanotechnol., 2016, 11, 1087–1092 CrossRef CAS PubMed.
- H. Ceylan, I. C. Yasa, O. Yasa, A. F. Tabak, J. Giltinan and M. Sitti, 3D-printed biodegradable microswimmer for theranostic cargo delivery and release, ACS Nano, 2019, 13, 3353–3362 CrossRef CAS PubMed.
- P. Dwivedi, D. Pillai and R. Mangal, Self-propelled swimming droplets, Curr. Opin. Colloid Interface Sci., 2022, 101614 CrossRef CAS.
- C. Tomlinson II, On the motions of camphor on the surface of water, Proc. R. Soc. London, 1862, 575–577 Search PubMed.
- S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Self-rotation of a camphor scraping on water: New insight into the old problem, Langmuir, 1997, 13, 4454–4458 CrossRef CAS.
- Y. Hayashima, M. Nagayama and S. Nakata, A camphor grain oscillates while breaking symmetry, J. Phys. Chem. B, 2001, 105, 5353–5357 CrossRef CAS.
- I. Tiwari, S. Upadhye, V. S. Akella and P. Parmananda, Revealing the deterministic components in active avalanche-like dynamics, Soft Matter, 2021, 17, 2865–2871 RSC.
- T. Mitsumata, J. P. Gong and Y. Osada, Shape memory functions and motility of amphiphilic polymer gels, Polym. Adv. Technol., 2001, 12, 136–150 CrossRef CAS.
- T. Ban, T. Yamagami, H. Nakata and Y. Okano, pH-dependent motion of self-propelled droplets due to Marangoni effect at neutral pH, Langmuir, 2013, 29, 2554–2561 CrossRef CAS.
- P. Kumar, D. Horváth and Á. Tóth, Sol-gel transition programmed self-propulsion of chitosan hydrogel, Chaos, 2022, 32, 063120 CrossRef CAS.
- K. Feng, J. C. U. Marcos, A. K. Mukhopadhyay, R. Niu, Q. Zhao, J. Qu and B. Liebchen, Self-solidifying active droplets showing memory-induced chirality, Adv. Sci., 2023, 10, 2300866 CrossRef CAS.
- Y. Osada, J. Gong, M. Uchida and N. I. N. Isogai, Spontaneous motion of amphoteric polymer gels on water, Jpn. J. Appl. Phys., 1995, 34, L511 CrossRef CAS.
- U. M. Córdova-Figueroa and J. F. Brady, Osmotic propulsion: the osmotic motor, Phys. Rev. Lett., 2008, 100, 158303 CrossRef.
- C. Watanabe, S. Tanaka, R. J. Löffler, M. M. Hanczyc and J. Górecki, Dynamic ordering caused by a source-sink relation between two droplets, Soft Matter, 2022, 18, 6465–6474 RSC.
- I. Tiwari, P. Parmananda and R. Chelakkot, Periodic oscillations in a string of camphor infused disks, Soft Matter, 2020, 16, 10334–10344 RSC.
- R. W. Jaggers and S. A. Bon, Independent responsive behaviour and communication in hydrogel objects, Mater. Horiz., 2017, 4, 402–407 RSC.
- N. Bassik, B. T. Abebe and D. H. Gracias, Solvent driven motion of lithographically fabricated gels, Langmuir, 2008, 24, 12158–12163 CrossRef CAS.
- R. Sharma, S. T. Chang and O. D. Velev, Gel-based self-propelling particles get programmed to dance, Langmuir, 2012, 28, 10128–10135 CrossRef CAS PubMed.
- V. Pimienta and C. Antoine, Self-propulsion on liquid surfaces, Curr. Opin. Colloid Interface Sci., 2014, 19, 290–299 CrossRef CAS.
- V. Chan, H. H. Asada and R. Bashir, Utilization and control of bioactuators across multiple length scales, Lab Chip, 2014, 14, 653–670 RSC.
- Z. Sun and Y. Hou, Micro/Nanorobots as Active Delivery Systems for Biomedicine: From Self-Propulsion to Controllable Navigation, Adv. Ther., 2022, 5, 2100228 CrossRef CAS.
- Y. Zhang, K. Yuan and L. Zhang, Micro/nanomachines: from functionalization to sensing and removal, Adv. Mater. Technol., 2019, 4, 1800636 CrossRef.
- J. Wang, J. Si, Y. Hao, J. Li, P. Zhang, C. Zuo, B. Jin, Y. Wang, W. Zhang and W. Li, et al., Halloysite-Based Nanorockets with Light-Enhanced Self-Propulsion for Efficient Water Remediation, Langmuir, 2022, 38, 1231–1242 CrossRef CAS.
- R. W. Jaggers and S. A. Bon, Communication between hydrogel beads via chemical signalling, J. Mater. Chem. B, 2017, 5, 8681–8685 RSC.
- R. Zahorán, P. Kumar, Á. Juhász, D. Horváth and Á. Tóth, Flow-driven synthesis of calcium phosphate-calcium alginate hybrid chemical gardens, Soft Matter, 2022, 18, 8157–8164 RSC.
- K. Wiese, Osmotically induced tissue expansion with hydrogels: a new dimension in tissue expansion? A preliminary report, J. Craniomaxillofac. Surg., 1993, 21, 309–313 CrossRef CAS PubMed.
- B. H. Rehm, Alginates: biology and applications, Springer, 2009, vol. 13 Search PubMed.
- J. M. C. Puguan, X. Yu and H. Kim, Characterization of structure, physico-chemical properties and diffusion behavior of Ca-Alginate gel beads prepared by different gelation methods, J. Colloid Interface Sci., 2014, 432, 109–116 CrossRef CAS.
- V. Akella, D. K. Singh, S. Mandre and M. Bandi, Dynamics of a camphoric acid boat at the air-water interface, Phys. Lett. A, 2018, 382, 1176–1180 CrossRef CAS.
- P. Kumar, D. Horváth and Á. Tóth, Self-assembly to synchrony of active gels, Soft Matter, 2023, 19, 4137–4143 RSC.
- Y. Matsuda, N. J. Suematsu, H. Kitahata, Y. S. Ikura and S. Nakata, Acceleration or deceleration of self-motion by the Marangoni effect, Chem. Phys. Lett., 2016, 654, 92–96 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Physico-chemical properties of the solutions, details of particle image velocimetry, further figures depicting trajectories, information on the supporting movies. See DOI: https://doi.org/10.1039/d3sm01026k |
| ‡ Current address: Department of Chemical Engineering, Indian Institute of Technology Kanpur, Uttar Pradesh-208016, India. |
| This journal is © The Royal Society of Chemistry 2023 |