DOI:
10.1039/D3SM00951C
(Paper)
Soft Matter, 2023,
19, 8988-8996
Static wetting of a barrel-shaped droplet on a soft-layer-coated fiber
Received
20th July 2023
, Accepted 11th October 2023
First published on 11th October 2023
Abstract
A droplet can deform a soft substrate due to capillary forces when they are in contact. We study the static deformation of a soft solid layer coated on a rigid cylindrical fiber when an axisymmetric barrel-shaped droplet is embracing it. We found that elastic deformation increases with a decreasing rigid fiber radius. Significant disparities of deformation between the solid–liquid side and the solid–gas side are found when their solid surface tensions are different. When the coated layer is soft enough and the rigid fiber radius is less than the thickness of the coated layer, pronounced displacement oscillations are observed. Such slow decay of deformation with distances from the contact line position suggests a possible long-range interaction between droplets on a soft-layer-coated fiber.
1. Introduction
A layer of a soft solid material such as gels and elastomers coated on rigid solid substrates can be significantly deformed by capillary forces, when a droplet is in contact with it.1,2 The shape of deformation has been explored extensively in the last few decades; however, those studies have mainly focussed on situations of a droplet on a planar substrate.1–25 Although there have been numerous studies of droplets on rigid fibers,26–31 wetting on a rigid fiber coated with a soft layer has been far less investigated.32 How this geometry modifies the deformation of the coated elastic layer remains unclear, which is the focus of this study.
The wetting of droplets on fibers is ubiquitous in both industrial and natural phenomena, and examples range from the modulation of the mechanical properties of spider silk,33 to the droplet transport on spines of cacti,34 to water collection by fog nets. Compared to a planar surface, the slender geometry of fibers modifies the droplet shape,27,31 and could induce directional motion of droplets.26,35–37 When it comes to droplet wetting on soft fibers, most studies have focused on the bending and buckling of flexible fibers which result in, for instance, the winding around a droplet,38 the coiling inside a droplet39 or the modification of droplet morphology by multiple fibers.40 On the other hand, a soft fiber with a rigid core, i.e. a soft-layer-coated fiber, can hardly bend. Hence, the interaction of droplets with a soft-layer-coated fiber is expected to be different from that of a totally soft fiber.
Unlike droplets on planar surfaces, which appear in a spherical-cap shape given that the Laplace pressure is the dominant force (e.g. effects of gravity are neglected), the shape of a droplet on a fiber is far more complex. Extensive studies in the literature31,41,42 have shown that stable droplets can appear in an axisymmetric barrel-shape or a non-axisymmetric clam-shell shape. For small equilibrium contact angles θ and large droplet sizes relative to the fiber radius, axisymmetric barrel-shaped droplets tend to be more stable. When the droplet size (V1/3, here V is the droplet volume) is smaller than the fiber radius, barrel-shaped droplets exist only for θ ≲ 10°.31
In this study, we investigate the axisymmetric deformation of a soft solid layer coated on a rigid cylindrical fiber when a barrel-shaped droplet is embracing it. Previous studies of elastic deformation by wetting often assume that θ = 90°, and thus the solid surface tension of the soft-solid/liquid interface γsg is the same as that of the soft-solid/gas interface γsl.12,14 For stable barrel-shaped droplets on a fiber, the contact angle has to be smaller than 90°. We hence consider generic situations where the two solid surface tensions can be different, i.e. γsg ≠ γsl. Moreover, it is known that the solid surface tensions not only determine the contact angle at the contact line, but also play a crucial role in suppressing the deformation of a planar soft solid layer.8,12 How the solid surface tensions affect the soft solid deformation in fiber geometries is studied in detail below.
2. Formulation
A schematic of a droplet of volume V resting on a soft-layer-coated fiber is shown in Fig. 1. We consider the droplet bond number Bo ≡ ρgV2/3/γ ≪ 1, where ρ is the liquid density, g is the gravitational acceleration and γ is the liquid–air surface tension. Hence, the effects of gravity on the droplet shape are negligible. The rigid fiber has a radius r0. A soft solid layer of uniform thickness H at an undeformed state is coated on the surface of the rigid fiber. Due to the axisymmetry of the problem, we will use the cylindrical coordinate system (r, ϕ, and z) and the corresponding unit vectors are denoted as ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) and
and ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) , ẑ. The center of mass of the droplet is at the origin, i.e. r = 0 and z = 0. The soft layer is deformed by the droplet. The displacement of the material of the soft layer is denoted as U(r, z) = Ur
, ẑ. The center of mass of the droplet is at the origin, i.e. r = 0 and z = 0. The soft layer is deformed by the droplet. The displacement of the material of the soft layer is denoted as U(r, z) = Ur![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) + Uϕ
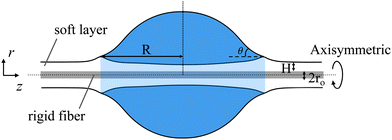
+ Uϕ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) + Uzẑ. Due to symmetry, the displacement has a property that U(r, z) = U(r, −z). Hence, we consider only z ≥ 0 in the following. The equilibrium contact angle θ is defined as the angle of the droplet liquid–air interface at the contact line position z = R with respect to the z-axis as shown in Fig. 1. In this study, we assume that θ is determined by Young's law,14 which reads
+ Uzẑ. Due to symmetry, the displacement has a property that U(r, z) = U(r, −z). Hence, we consider only z ≥ 0 in the following. The equilibrium contact angle θ is defined as the angle of the droplet liquid–air interface at the contact line position z = R with respect to the z-axis as shown in Fig. 1. In this study, we assume that θ is determined by Young's law,14 which reads| | γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = γsg − γsl. θ = γsg − γsl. | (1) |
Denoting the elastic stress tensor as σ, the deformation of the soft layer is governed by the force balance equation:As we only consider small slopes of the deformed soft-solid/fluid interface, we employ a linear elastic constitutive model for determining the relationship between the stress tensor and the displacement, for which the tensor components are as follows:| | 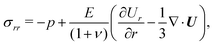 | (3) |
| | 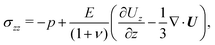 | (4) |
| |  | (5) |
| | 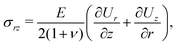 | (6) |
where the isotropic part of the stress tensor (or the pressure) is:| | 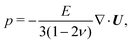 | (7) |
where E is the Young modulus and ν is the Poisson ratio. Note that Uϕ = 0 due to axisymmetry.
 |
| | Fig. 1 Schematic diagram of an axisymmetric barrel-shaped droplet embracing a rigid cylindrical fiber of radius r0 coated with a soft (elastic) solid layer of thickness H. The droplet makes an equilibrium contact angle θ with the fiber. The soft solid layer is deformed by the droplet due to capillary forces. | |
The boundary conditions for governing eqn (2) are as follows. Consider that the length of the fiber 2L is much larger than the droplet radius R, we impose the condition
Due to symmetry, at
z = 0, we have
and
| | 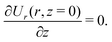 | (10) |
At the interface where the soft layer is in contact with the rigid solid,
i.e. r =
r0, the soft material is undeformed, so we have
For the soft-solid/fluid boundary,
i.e. r =
r0 +
H, we impose a force balance condition. Here, we introduce all the tractions (force per unit area) acting on the interface as the following. At the contact line, the localized capillary traction
fl =
γδ(
R −
z)(sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
− cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θẑ
θẑ) is pulling the soft layer,
9,16 where
δ(
z) is the Dirac delta function. Second, the Laplace pressure inside the droplet can also deform the soft layer. The traction
fLa due to the Laplace pressure is given as
fLa = −
γκlHs(
R −
z)
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
, where
κl is the curvature of the droplet's liquid–air interface and
Hs(
z) is the Heaviside step function. Third, the elastic traction due to soft solid deformation is
fel = −(
σrr![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
+
σrzẑ)|
r=r0+H. Fourth, the contribution from the soft solid surface tension gives a traction
fs = −
γsκs![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
+ ∂
γs/∂
zẑ, where
γs is the soft solid surface tension and
κs is the curvature of the deformed soft-solid/fluid interface. We assume that the solid surface stress is the same as the solid surface energy, and call them the solid surface tension. In other words, we neglect the Shutter worth effect.
21,43,44 Note that the assumption of a small soft-solid/fluid interface slope has been used to obtain the expression of
fs. For small interface slopes, the curvature can be simplified as
κs = [1/(
r0 +
H +
Ur) − ∂
2Ur/∂
z2]|
r=r0+H. For the soft solid surface tension, there is a jump across the contact line, meaning that
γs =
γsl + (
γsg −
γsl)
Hs(
R −
z). Thus,
fs = −
γsκs![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
+ (
γsg −
γsl)
δ(
R −
z)
ẑ. Balancing all the tractions we have the following boundary conditions at
r =
r0 +
H,
| | | fl + fLa + fel + fs = 0. | (12) |
Regarding the shape of the droplet's liquid–air interface, described by
r =
g(
z), the profile is obtained by solving the equation of uniform Laplace pressure, which implies
κl has a constant value,
i.e. κl =
kc. We describe the details of the governing equation and the corresponding boundary conditions at the later part of this section.
Next, we non-dimensionalize the variables as the following. We rescale the coordinates and displacements by H and the pressure by E, namely
| | 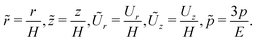 | (13) |
For the elastic deformation, the dimensionless forms of the governing
eqn (2) written in vector components are
| | 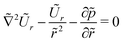 | (14) |
in the
r-direction and
| |  | (15) |
in the
z-direction. The dimensionless forms of the boundary conditions
(8)–(11) are
| | Ũz(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) , , ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0) = 0, = 0) = 0, | (17) |
| | 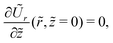 | (18) |
and
respectively, where
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0
0 =
r0/
H and
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif)
=
L/
H. In this study, we consider
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif)
≫ 1.
For the soft-solid/fluid interface, we first define ũr ≡ Ũr(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 +
0 + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) and ũz ≡ Ũz(
) and ũz ≡ Ũz(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 +
0 + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ). The dimensionless form of the force balance condition (12), written in vector components, is given as follows. For r-components, we obtain
). The dimensionless form of the force balance condition (12), written in vector components, is given as follows. For r-components, we obtain
| |  | (20) |
where the dimensionless parameters are defined as
| |  | (21) |
For the
z-components of the force balance
(12), after using Young's law (1), −
γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θδ
θδ(
R −
z) cancels out (
γsg −
γsl)
δ(
R −
z); hence, we obtain the vanishing elastic shear stress condition
| |  | (22) |
For the droplet profile, the dimensionless form of the uniform curvature equation is
| |  | (23) |
where
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif)
=
g/
H. The boundary conditions at the contact line are as follows:
| | ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ( (![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = = ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ) = ) = ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr( 0 + 1 + ũr(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) = = ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1, 0 + 1, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = = ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ) ) | (24) |
and
| | 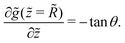 | (25) |
The droplet volume is given by:
| | 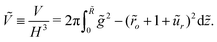 | (26) |
In this study, we consider the soft material to be incompressible, which means
ν = 0.5. The incompressibility condition implies
| |  | (27) |
The governing
eqn (14), (15), (23) and (27) are solved together with the conditions
(16)–(20), (22), (24)–(26) using the finite element method for which the details are given in the Appendix. The dimensionless control parameters are
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0
0,
Ẽ,
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl
sl,
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg
sg and
Ṽ.
3. Results
3.1 Large droplet limit
First we look at situations in which the droplet length scale (R) is much larger than the other length scales: H, r0, γ/E, γsl/E and γsg/E. The Laplace pressure fLa is neglected in this limit, and thus, the only external capillary force acting on the soft solid is the localized force fl at the contact line. We will demonstrate how the solid deformation varies with the change of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, Ẽ and
0, Ẽ and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg for both cases of γsg = γsl (i.e. θ = 90°) and γsg ≠ γsl (i.e. θ ≠ 90°).
sg for both cases of γsg = γsl (i.e. θ = 90°) and γsg ≠ γsl (i.e. θ ≠ 90°).
3.1.1 Cases of γsg = γsl (i.e. θ = 90°).
We look at two different cases of softness, namely Ẽ = 1 and Ẽ = 10. In Fig. 2, the displacements at the soft-solid/fluid interface ũr and ũz are plotted as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of
for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. To validate our computations, we first compare our results for a large rigid fiber radius
0. To validate our computations, we first compare our results for a large rigid fiber radius ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 10 with the analytical solution of the 2D plain strain case.12 In the insets of Fig. 2, we show that our numerical results collapse with the analytical 2D solutions. Next, we look at how the rigid fiber radius modifies the deformation. When the layer is stiff (Ẽ = 10), as shown in Fig. 2(a), the out-of-plane displacement ũr is insensitive to the value of
0 = 10 with the analytical solution of the 2D plain strain case.12 In the insets of Fig. 2, we show that our numerical results collapse with the analytical 2D solutions. Next, we look at how the rigid fiber radius modifies the deformation. When the layer is stiff (Ẽ = 10), as shown in Fig. 2(a), the out-of-plane displacement ũr is insensitive to the value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. Relatively, there is a stronger dependence of the in-plane displacement ũz on
0. Relatively, there is a stronger dependence of the in-plane displacement ũz on ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 as shown in Fig. 2(b). In contrast, for the softer case of Ẽ = 1 shown in Fig. 2(c) and (d), the magnitude of displacements increases significantly with decreasing
0 as shown in Fig. 2(b). In contrast, for the softer case of Ẽ = 1 shown in Fig. 2(c) and (d), the magnitude of displacements increases significantly with decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 when
0 when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≤ 1. Moreover, unlike the stiff or large rigid fiber radius cases, in which the magnitude of displacement decays quickly with distances from the contact line, the oscillations are significant for the case of Ẽ = 1 when
0 ≤ 1. Moreover, unlike the stiff or large rigid fiber radius cases, in which the magnitude of displacement decays quickly with distances from the contact line, the oscillations are significant for the case of Ẽ = 1 when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≪ 1.
0 ≪ 1.
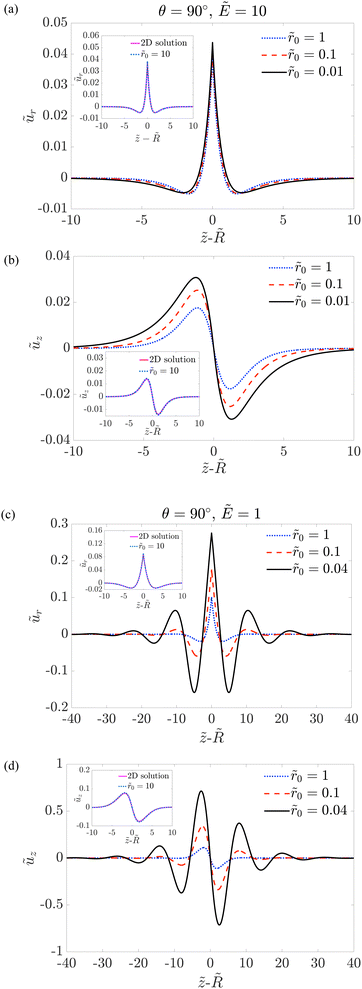 |
| | Fig. 2 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − − ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Insets: The analytical solutions of the 2D plain strain case (solid lines)12 and our numerical results for 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Insets: The analytical solutions of the 2D plain strain case (solid lines)12 and our numerical results for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 10 (dotted lines). Other parameters are as follows: 0 = 10 (dotted lines). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = sl = ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5. sg = 5. | |
How do we understand the results? For ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≫ 1, the deformation behaves the same as the 2D solution as one might expect. The more interesting regime is when
0 ≫ 1, the deformation behaves the same as the 2D solution as one might expect. The more interesting regime is when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1. When the material is stiff, namely Ẽ ≫ 1 (i.e. γ/E ≪ H), the dimensional out-of-plane displacement ur scales as/E and weakly depends on H,7,12 meaning that the deformation is small compared to the thickness of the soft layer. The displacements vanish at a short distance from the soft-solid/fluid interface. Hence, the no-displacement condition at
0 ≲ 1. When the material is stiff, namely Ẽ ≫ 1 (i.e. γ/E ≪ H), the dimensional out-of-plane displacement ur scales as/E and weakly depends on H,7,12 meaning that the deformation is small compared to the thickness of the soft layer. The displacements vanish at a short distance from the soft-solid/fluid interface. Hence, the no-displacement condition at ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 only plays as a small correction to the displacements. On the other hand, when Ẽ ≲ 1, the bulk material deforms more significantly; hence, the boundary conditions at
0 only plays as a small correction to the displacements. On the other hand, when Ẽ ≲ 1, the bulk material deforms more significantly; hence, the boundary conditions at ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 have a stronger effect. Furthermore, not only do the bulk elastic stresses play a significant role, but also the traction fs involving the azimuthal curvature of the soft solid interface, i.e. 1/(
0 have a stronger effect. Furthermore, not only do the bulk elastic stresses play a significant role, but also the traction fs involving the azimuthal curvature of the soft solid interface, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), is crucial for inducing strong displacement oscillations. We found that removing the azimuthal curvature term in eqn (20) results in the disappearance of displacement oscillations. In Section 3.1.4, we will look at how the displacement oscillations depend on the solid surface tension.
0 + 1 + ũr), is crucial for inducing strong displacement oscillations. We found that removing the azimuthal curvature term in eqn (20) results in the disappearance of displacement oscillations. In Section 3.1.4, we will look at how the displacement oscillations depend on the solid surface tension.
3.1.2 Cases of γsg ≠ γsl (i.e. θ ≠ 90°).
We take ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4.13,
sl = 4.13, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5, and thus θ = 30° using Young's law (1). In Fig. 3, we plot the displacements ũr and ũz as a function of
sg = 5, and thus θ = 30° using Young's law (1). In Fig. 3, we plot the displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) . For Ẽ = 10, although the maximum of ũr is almost independent of
. For Ẽ = 10, although the maximum of ũr is almost independent of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, the dimple (minimum) depends significantly on
0, the dimple (minimum) depends significantly on ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 as shown in Fig. 3(a). When the rigid fiber radius is large, for example, for
0 as shown in Fig. 3(a). When the rigid fiber radius is large, for example, for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 1000, the dimple on the solid–liquid side (left) is slightly larger than the solid–gas side (right). This is consistent with the finding of previous studies for plate cases that the solid surface tension suppresses deformation.8 Note that
0 = 1000, the dimple on the solid–liquid side (left) is slightly larger than the solid–gas side (right). This is consistent with the finding of previous studies for plate cases that the solid surface tension suppresses deformation.8 Note that ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl <
sl < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg. However, when decreasing
sg. However, when decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, ũr increases on the solid/liquid side and decreases on the solid/gas side. Hence, the dimple of the solid/liquid interface decreases and disappears. On the other hand, the dimple of the solid/gas interface becomes larger. This disparity can be observed clearly for
0, ũr increases on the solid/liquid side and decreases on the solid/gas side. Hence, the dimple of the solid/liquid interface decreases and disappears. On the other hand, the dimple of the solid/gas interface becomes larger. This disparity can be observed clearly for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1 in Fig. 3(a).
0 = 0.1 in Fig. 3(a).
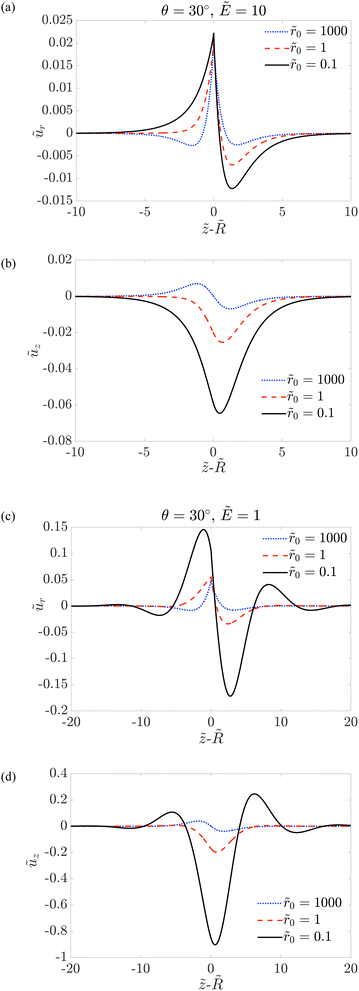 |
| | Fig. 3 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − −![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4.13 and sl = 4.13 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5. sg = 5. | |
The in-plane displacement ũz shown in Fig. 3(b) also demonstrates specific features when varying ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. For large
0. For large ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, the material around the contact line at the interface displaces towards the contact line for both sides. When decreasing
0, the material around the contact line at the interface displaces towards the contact line for both sides. When decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, ũz decreases. For
0, ũz decreases. For ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1, ũz is negative for the whole interface, meaning that all the material at the interface displaces towards the side of interface with a smaller solid surface tension (left).
0 ≲ 1, ũz is negative for the whole interface, meaning that all the material at the interface displaces towards the side of interface with a smaller solid surface tension (left).
For a softer material (Ẽ = 1) shown in Fig. 3(c) and (d), the behavior of ũr and ũz when decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 is similar to that of Ẽ = 10. Remarkably, when
0 is similar to that of Ẽ = 10. Remarkably, when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 is reduced to
0 is reduced to ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1, ũr around the contact line on the solid–liquid side increases to values larger than ũr at the contact line. Hence, the maximum of ũr is not at the contact line position but shifts to the solid/liquid side as shown in Fig. 3(c). Similar to that we have seen for the case of θ = 90°, pronounced oscillations of ũr and ũz appear when
0 = 0.1, ũr around the contact line on the solid–liquid side increases to values larger than ũr at the contact line. Hence, the maximum of ũr is not at the contact line position but shifts to the solid/liquid side as shown in Fig. 3(c). Similar to that we have seen for the case of θ = 90°, pronounced oscillations of ũr and ũz appear when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≪ 1.
0 ≪ 1.
3.1.3 Dependence on the contact angle.
We look at how the features of deformation change when the contact angle is varied from θ = 90° to θ = 0° for a fixed value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. According to Young's law, changing θ also means that
0 = 0.1. According to Young's law, changing θ also means that ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg −
sg − ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl is varied. We keep
sl is varied. We keep ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 for all cases and change the value of
sg = 5 for all cases and change the value of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl. We again consider two different values of Ẽ. The displacements ũr and ũz as a function of
sl. We again consider two different values of Ẽ. The displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different θ (or
for different θ (or ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl) are plotted in Fig. 4.
sl) are plotted in Fig. 4.
 |
| | Fig. 4 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − −![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of for different values of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: sl and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 and sg = 5 and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. 0 = 0.1. | |
In Fig. 4(a), we can see that the maximum of ũr decreases when θ reduces due to the fact that the pulling contact line force scales as γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The sharp tip at the contact line disappears for θ = 0° as the pulling force vanishes. Interestingly, there is still a significant deformation for θ = 0°. The deformation then comes from the traction fs generated by the solid surface tensions. When
θ. The sharp tip at the contact line disappears for θ = 0° as the pulling force vanishes. Interestingly, there is still a significant deformation for θ = 0°. The deformation then comes from the traction fs generated by the solid surface tensions. When ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl and
sl and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg are different, the traction fs involving the azimuthal curvature, i.e. 1/(
sg are different, the traction fs involving the azimuthal curvature, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), gives different stresses at the liquid side and the gas side.
0 + 1 + ũr), gives different stresses at the liquid side and the gas side.
As θ is decreased, the asymmetry of displacements between the solid–liquid side and the solid–gas side becomes more apparent. When compared with the results in Fig. 3, we observe that the enhancement of asymmetry when reducing θ (for a fixed value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0) is similar to that of decreasing
0) is similar to that of decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 (for a fixed value of θ). In the following, we point out some of these similar trends. As shown in Fig. 3(a) or in Fig. 4(a) for Ẽ = 10, when reducing
0 (for a fixed value of θ). In the following, we point out some of these similar trends. As shown in Fig. 3(a) or in Fig. 4(a) for Ẽ = 10, when reducing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ, the dimple of ũr on the solid–liquid side (with a smaller solid surface tension) decreases and the dimple on the solid–gas side becomes larger. For Ẽ = 1, the maximum of ũr shifts from the contact line position to the solid–liquid side when
0 or θ, the dimple of ũr on the solid–liquid side (with a smaller solid surface tension) decreases and the dimple on the solid–gas side becomes larger. For Ẽ = 1, the maximum of ũr shifts from the contact line position to the solid–liquid side when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ is reduced to below a certain value as shown in Fig. 3(c) or in Fig. 4(c). For the in-plane displacement shown in Fig. 3(b) and (d) or Fig. 4(b) and (d), ũz around the contact line decreases when reducing
0 or θ is reduced to below a certain value as shown in Fig. 3(c) or in Fig. 4(c). For the in-plane displacement shown in Fig. 3(b) and (d) or Fig. 4(b) and (d), ũz around the contact line decreases when reducing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ. This means that the material at the interface displaces more to the side of the interface with a smaller solid surface tension (left).
0 or θ. This means that the material at the interface displaces more to the side of the interface with a smaller solid surface tension (left).
3.1.4 Dependence on the solid surface tension.
In Fig. 5, we plot the dimensionless displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). We see that when
for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). We see that when ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg is reduced, ũr at the contact line enhances. This is because the traction fs term involving the longitudinal curvature, i.e. ∂2ũr/∂
sg is reduced, ũr at the contact line enhances. This is because the traction fs term involving the longitudinal curvature, i.e. ∂2ũr/∂![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 2, suppresses the sharp tip deformation at the contact line.8,12 On the other hand, the displacement oscillations and the displacement disparity (for θ = 30°) become less pronounced when
2, suppresses the sharp tip deformation at the contact line.8,12 On the other hand, the displacement oscillations and the displacement disparity (for θ = 30°) become less pronounced when ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg is reduced. This can be understood as follows. Away from the contact line, the azimuthal curvature term, i.e. 1/(
sg is reduced. This can be understood as follows. Away from the contact line, the azimuthal curvature term, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), dominates over the longitudinal curvature term. The displacement oscillations and displacement disparity are due to the azimuthal curvature term in the traction fs. Decreasing
0 + 1 + ũr), dominates over the longitudinal curvature term. The displacement oscillations and displacement disparity are due to the azimuthal curvature term in the traction fs. Decreasing ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg thus reduces the effects of this traction. In Fig. 5, we also add the results for a smaller value of Ẽ. As we demonstrate previously, reducing the value of Ẽ enhances the displacement oscillations and displacement disparity.
sg thus reduces the effects of this traction. In Fig. 5, we also add the results for a smaller value of Ẽ. As we demonstrate previously, reducing the value of Ẽ enhances the displacement oscillations and displacement disparity.
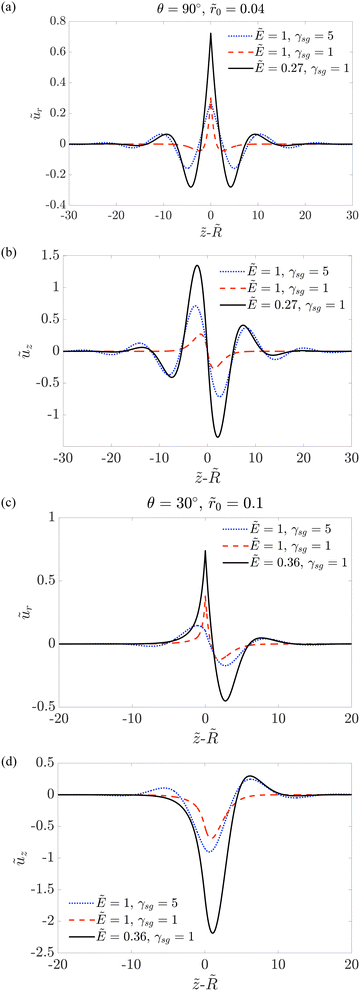 |
| | Fig. 5 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − −![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). | |
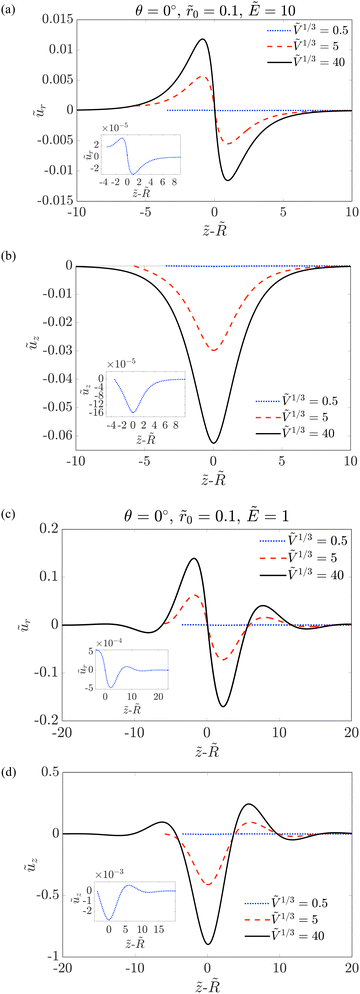
3.2 Dependence on the droplet size
For a droplet of the finite size, the traction term due to the Laplace pressure fLa is included in our computations. As small stable barrel-shaped droplets exist only when the contact angle is small, we choose two small contact angles, i.e. θ = 30° and θ = 0°, and investigate how the deformation depends on the droplet size. We fix ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. In Fig. 6 and 7, the displacements ũr and ũz are plotted as a function of
0 = 0.1. In Fig. 6 and 7, the displacements ũr and ũz are plotted as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
− ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) respectively for θ = 30° and θ = 0°. We can see that for Ṽ1/3= 40, the results are the same as those for the large droplet limit. When Ṽ1/3 decreases, ũr decreases on the liquid side and increases on the gas side. This is because the Laplace pressure pressing the soft layer on the liquid side is stronger for smaller droplets. For ũz, the Laplace pressure term reduces the magnitude of ũz on both the liquid and gas sides. The magnitude of displacement oscillation is also reduced when the droplet size decreases. Note that we assume the contact angle follows Young's relationship and is independent of the droplet size. Hence, the contact angle transition observed for small droplets on planar surfaces14,17 is not considered in our present study.
respectively for θ = 30° and θ = 0°. We can see that for Ṽ1/3= 40, the results are the same as those for the large droplet limit. When Ṽ1/3 decreases, ũr decreases on the liquid side and increases on the gas side. This is because the Laplace pressure pressing the soft layer on the liquid side is stronger for smaller droplets. For ũz, the Laplace pressure term reduces the magnitude of ũz on both the liquid and gas sides. The magnitude of displacement oscillation is also reduced when the droplet size decreases. Note that we assume the contact angle follows Young's relationship and is independent of the droplet size. Hence, the contact angle transition observed for small droplets on planar surfaces14,17 is not considered in our present study.
 |
| | Fig. 6 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − −![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of Ṽ1/3 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: for different values of Ṽ1/3 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4.13 (θ = 30°), sl = 4.13 (θ = 30°), ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 and sg = 5 and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. 0 = 0.1. | |
 |
| | Fig. 7 Rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − −![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of Ṽ1/3 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: for different values of Ṽ1/3 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4 (θ = 0°), sl = 4 (θ = 0°), ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 and sg = 5 and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. Insets: Zoom in view of Ṽ1/3 = 0.5. 0 = 0.1. Insets: Zoom in view of Ṽ1/3 = 0.5. | |
4. Conclusions
We study the elastic deformation of a soft layer coated on a rigid cylindrical fiber when an axisymmetric barrel-shaped droplet is embracing it. For a droplet contact angle of θ = 90°, and thus γsl = γsg according to Young's law, we found that the magnitudes of both displacements ũr and ũz increase with a decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. For θ ≠ 90° (i.e. γsl ≠ γsg), the deformations on the solid–liquid side and the solid–gas side are different. This disparity of deformation is enhanced when decreasing
0. For θ ≠ 90° (i.e. γsl ≠ γsg), the deformations on the solid–liquid side and the solid–gas side are different. This disparity of deformation is enhanced when decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 (for a fixed value of θ) or decreasing θ (for a fixed value of
0 (for a fixed value of θ) or decreasing θ (for a fixed value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0). The dimple of ũr on the side with a smaller solid surface tension becomes smaller while the dimple becomes larger on the other side. Interestingly, significant deformation is observed even for θ = 0° for which the pulling force at the contact line vanishes and the Laplace pressure is neglected for large droplets. The deformation is due to the part of traction fs involving the azimuthal curvature term, i.e. 1/(
0). The dimple of ũr on the side with a smaller solid surface tension becomes smaller while the dimple becomes larger on the other side. Interestingly, significant deformation is observed even for θ = 0° for which the pulling force at the contact line vanishes and the Laplace pressure is neglected for large droplets. The deformation is due to the part of traction fs involving the azimuthal curvature term, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), which generates different stresses on the liquid and the gas sides when the solid surface tensions are different.
0 + 1 + ũr), which generates different stresses on the liquid and the gas sides when the solid surface tensions are different.
Pronounced oscillations of displacements are observed for the cases of Ẽ < 1 and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1. This slow decay of deformation with distances from the contact line position suggests a relatively long-range interaction between droplets on a soft-layer-coated fiber. Hence, it is expected that droplet migration and interactions are significantly different from those observed on a planar soft substrate or a purely rigid fiber, for example, the inverted Cheerios effect45 and coalescence,37 which remain open questions to be explored.
0 ≲ 1. This slow decay of deformation with distances from the contact line position suggests a relatively long-range interaction between droplets on a soft-layer-coated fiber. Hence, it is expected that droplet migration and interactions are significantly different from those observed on a planar soft substrate or a purely rigid fiber, for example, the inverted Cheerios effect45 and coalescence,37 which remain open questions to be explored.
Conflicts of interest
There are no conflicts to declare.
Appendix: finite element method
The non-dimensional deformation of the soft layer of the fiber and the droplet profile are computed by solving the governing eqn (14), (15), (23) and (27) together with the conditions (16)–(20), (22), and (24)–(26) by using a finite element method (FEM). We discretize our non-dimensional variables with linear elements and solve the coupled equations using a Newton solver from the FEM library FEniCS.46
For the Dirac delta function, we approximate it with a Gaussian function as  , where lm can be interpreted as a microscopic length (e.g. interface thickness) such that lm ≪ H. In the limit that lm → 0, δ(R − z) = W(R − z). In this study, lm/H = 10−5 is set for all the cases. We have used the adaptive mesh sizing such that the smallest mesh size near the contact line is dx1/H = 10−7 and the largest mesh size far away from the contact line is dx0/H = 0.05.
, where lm can be interpreted as a microscopic length (e.g. interface thickness) such that lm ≪ H. In the limit that lm → 0, δ(R − z) = W(R − z). In this study, lm/H = 10−5 is set for all the cases. We have used the adaptive mesh sizing such that the smallest mesh size near the contact line is dx1/H = 10−7 and the largest mesh size far away from the contact line is dx0/H = 0.05.
The mesh convergence of the numerical solver is tested with the case of the large droplet limit and the condition of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≫ 1. In this limit, the deformation of the soft layer will converge towards the 2D soft plate case. In Fig. 8, we compare our numerical results with the analytical solution for the 2D soft plate case by plotting the deformation of the soft solid for three different mesh resolutions, namely dx0/H = 0.1, 0.05 and 0.025. For all three mesh sizes, the numerical solutions are in good agreement with the analytical solution.
0 ≫ 1. In this limit, the deformation of the soft layer will converge towards the 2D soft plate case. In Fig. 8, we compare our numerical results with the analytical solution for the 2D soft plate case by plotting the deformation of the soft solid for three different mesh resolutions, namely dx0/H = 0.1, 0.05 and 0.025. For all three mesh sizes, the numerical solutions are in good agreement with the analytical solution.
 |
| | Fig. 8 Convergence of the mesh. The rescaled displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) − − ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different mesh sizes. Other parameters are as follows: θ = 90°, for different mesh sizes. Other parameters are as follows: θ = 90°, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = sl = ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5, and sg = 5, and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 1000. 0 = 1000. | |
Acknowledgements
The authors gratefully acknowledges financial support from the Research Council of Norway (project no. 315110). BXZ thanks Stephane Poulain, Jarle Sogn and Miroslav Kuchta for the discussions of the numerical method.
Notes and references
- S. J. Park, B. M. Weon, J. S. Lee, J. Lee, J. Kim and J. H. Je, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
- G. R. Lester, J. Colloid Sci., 1961, 16, 315–326 CrossRef CAS.
- A. I. Rusanov, Colloid J., 1975, 37(4), 614–622 Search PubMed.
- R. Pericet-Cámara, A. Best, H. J. Butt and E. Bonaccurso, Langmuir, 2008, 24, 10565–10568 CrossRef PubMed.
- Y. S. Yu and Y. P. Zhao, J. Colloid Interface Sci., 2009, 339, 489–494 CrossRef CAS PubMed.
- R. Pericet-Camara, G. K. Auernhammer, K. Koynov, S. Lorenzoni, R. Raiteri and E. Bonaccurso, Soft Matter, 2009, 5, 3611–3617 RSC.
- E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 1–4 CrossRef PubMed.
- S. Das, A. Marchand, B. Andreotti and J. H. Snoeijer, Phys. Fluids, 2011, 23, 072006 CrossRef.
- L. Limat, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–13 CrossRef PubMed.
- Y. S. Yu, J. Appl. Math. Mech., 2012, 33, 1095–1114 CrossRef.
- R. W. Style and E. R. Dufresne, Soft Matter, 2012, 8, 7177–7184 RSC.
- R. W. Style, R. Boltyanskiy, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, J. Fluid Mech., 2014, 747, R1 CrossRef CAS.
- C. Y. Hui and A. Jagota, Proc. R. Soc. A, 2014, 470, 20140085 CrossRef.
- J. B. Bostwick, M. Shearer and K. E. Daniels, Soft Matter, 2014, 10, 7361–7369 RSC.
- J. Dervaux and L. Limat, Proc. R. Soc. A, 2015, 471, 20140813 CrossRef.
- R. W. Style, A. Jagota, C. Y. Hui and E. R. Dufresne, Annu. Rev. Condens. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- R. W. Style and Q. Xu, Soft Matter, 2018, 14, 4569–4576 RSC.
- M. Zhao, J. Dervaux, T. Narita, F. Lequeux, L. Limat and M. Roché, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1748–1753 CrossRef CAS PubMed.
- R. Masurel, M. Roché, L. Limat, I. Ionescu and J. Dervaux, Phys. Rev. Lett., 2019, 122, 1–6 CrossRef PubMed.
- J. W. Choi, D. Ham, S. Han, D. Y. Noh and H. C. Kang, Nanomaterials, 2021, 11, 1–10 Search PubMed.
- Y. Yang, X. Li and W. Wang, Sci. Rep., 2021, 11, 1–17 CrossRef PubMed.
- H. K. Khattak, S. Karpitschka, J. H. Snoeijer and K. Dalnoki-Veress, Nat. Commun., 2022, 13, 4436 CrossRef CAS PubMed.
- T. S. Chan, Soft Matter, 2022, 18, 7280–7290 RSC.
- É. Lorenceau and D. Quéré, J. Fluid Mech., 2004, 510, 29–45 CrossRef.
- E. Q. Li and S. T. Thoroddsen, Phys. Fluids, 2013, 25, 052105 CrossRef.
- T. S. Chan, C. Pedersen, J. Koplik and A. Carlson, J. Fluid Mech., 2021, 907, A29 CrossRef CAS.
- T. S. Chan, C. L. Lee, C. Pedersen, K. Dalnoki-Veress and A. Carlson, Phys. Rev. Fluids, 2021, 6, 1–8 Search PubMed.
- C. Fournier, C. L. Lee, R. D. Schulman, É. Raphaël and K. Dalnoki-Veress, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 36–41 CrossRef PubMed.
- C. Xu, Z. Lu and L. Li, Frontiers Energy Research, 2022, 9, 1–7 Search PubMed.
- D. Guan, E. Charlaix and P. Tong, Phys. Rev. Lett., 2020, 124, 188003 CrossRef CAS PubMed.
- F. Vollrath and D. Edmonds, Nature, 1989, 340, 305–307 CrossRef.
- C. Liu, Y. Xue, Y. Chen and Y. Zheng, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- B. J. Carroll, J. Colloid and Interface Sci., 1976, 57, 488–495 CrossRef CAS.
- T. S. Chan, F. Yang and A. Carlson, J. Fluid Mech., 2020, 894, A26 CrossRef CAS.
- C. L. Lee, T. S. Chan, A. Carlson and K. Dalnoki-Veress, Soft Matter, 2022, 18, 1364–1370 RSC.
- R. D. Schulman, A. Porat, K. Charlesworth, A. Fortais, T. Salez, E. Raphaël and K. Dalnoki-Veress, Soft Matter, 2017, 13, 720–724 RSC.
- H. Elettro, F. Vollrath, A. Antkowiak and S. Neukirch, Int. J. Non Linear Mech., 2015, 75, 59–66 CrossRef.
- C. Duprat, S. Protière, A. Y. Beebe and H. A. Stone, Nature, 2012, 482, 510–513 CrossRef CAS PubMed.
- C. Bauer and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2428–2438 CrossRef CAS PubMed.
- T. H. Chou, S. J. Hong, Y. E. Liang, H. K. Tsao and Y. J. Sheng, Langmuir, 2011, 27, 3685–3692 CrossRef CAS PubMed.
- R. Shuttleworth, Proc. Phys. Soc. A, 1950, 63, 444 CrossRef.
- B. Andreotti and J. H. Snoeijer, EPL, 2016, 113, 66001 CrossRef.
- S. Karpitschka, A. Pandey, L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7403–7407 CrossRef CAS PubMed.
-
A. Logg, K.-A. Mardal and G. Wells, Automated solution of differential equations by the finite element method: The FEniCS book, Springer Science & Business Media, 2012, vol. 84 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Christian
Pedersen
,
Christian
Pedersen
 ,
Andreas
Carlson
,
Andreas
Carlson
 and
Tak Shing
Chan
and
Tak Shing
Chan
 *
*
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) and
and ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) , ẑ. The center of mass of the droplet is at the origin, i.e. r = 0 and z = 0. The soft layer is deformed by the droplet. The displacement of the material of the soft layer is denoted as U(r, z) = Ur
, ẑ. The center of mass of the droplet is at the origin, i.e. r = 0 and z = 0. The soft layer is deformed by the droplet. The displacement of the material of the soft layer is denoted as U(r, z) = Ur![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) + Uϕ
+ Uϕ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) + Uzẑ. Due to symmetry, the displacement has a property that U(r, z) = U(r, −z). Hence, we consider only z ≥ 0 in the following. The equilibrium contact angle θ is defined as the angle of the droplet liquid–air interface at the contact line position z = R with respect to the z-axis as shown in Fig. 1. In this study, we assume that θ is determined by Young's law,14 which reads
+ Uzẑ. Due to symmetry, the displacement has a property that U(r, z) = U(r, −z). Hence, we consider only z ≥ 0 in the following. The equilibrium contact angle θ is defined as the angle of the droplet liquid–air interface at the contact line position z = R with respect to the z-axis as shown in Fig. 1. In this study, we assume that θ is determined by Young's law,14 which reads![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = γsg − γsl.
θ = γsg − γsl.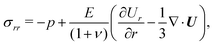
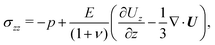

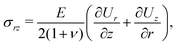
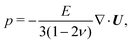
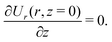
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) − cos
− cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θẑ) is pulling the soft layer,9,16 where δ(z) is the Dirac delta function. Second, the Laplace pressure inside the droplet can also deform the soft layer. The traction fLa due to the Laplace pressure is given as fLa = −γκlHs(R − z)
θẑ) is pulling the soft layer,9,16 where δ(z) is the Dirac delta function. Second, the Laplace pressure inside the droplet can also deform the soft layer. The traction fLa due to the Laplace pressure is given as fLa = −γκlHs(R − z)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) , where κl is the curvature of the droplet's liquid–air interface and Hs(z) is the Heaviside step function. Third, the elastic traction due to soft solid deformation is fel = −(σrr
, where κl is the curvature of the droplet's liquid–air interface and Hs(z) is the Heaviside step function. Third, the elastic traction due to soft solid deformation is fel = −(σrr![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) + σrzẑ)|r=r0+H. Fourth, the contribution from the soft solid surface tension gives a traction fs = −γsκs
+ σrzẑ)|r=r0+H. Fourth, the contribution from the soft solid surface tension gives a traction fs = −γsκs![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) + ∂γs/∂zẑ, where γs is the soft solid surface tension and κs is the curvature of the deformed soft-solid/fluid interface. We assume that the solid surface stress is the same as the solid surface energy, and call them the solid surface tension. In other words, we neglect the Shutter worth effect.21,43,44 Note that the assumption of a small soft-solid/fluid interface slope has been used to obtain the expression of fs. For small interface slopes, the curvature can be simplified as κs = [1/(r0 + H + Ur) − ∂2Ur/∂z2]|r=r0+H. For the soft solid surface tension, there is a jump across the contact line, meaning that γs = γsl + (γsg − γsl)Hs(R − z). Thus, fs = −γsκs
+ ∂γs/∂zẑ, where γs is the soft solid surface tension and κs is the curvature of the deformed soft-solid/fluid interface. We assume that the solid surface stress is the same as the solid surface energy, and call them the solid surface tension. In other words, we neglect the Shutter worth effect.21,43,44 Note that the assumption of a small soft-solid/fluid interface slope has been used to obtain the expression of fs. For small interface slopes, the curvature can be simplified as κs = [1/(r0 + H + Ur) − ∂2Ur/∂z2]|r=r0+H. For the soft solid surface tension, there is a jump across the contact line, meaning that γs = γsl + (γsg − γsl)Hs(R − z). Thus, fs = −γsκs![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) + (γsg − γsl)δ(R − z)ẑ. Balancing all the tractions we have the following boundary conditions at r = r0 + H,
+ (γsg − γsl)δ(R − z)ẑ. Balancing all the tractions we have the following boundary conditions at r = r0 + H,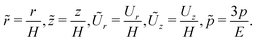
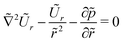

![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) =
= ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ) = 0,
) = 0,![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0) = 0,
= 0) = 0,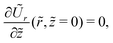
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0,
0, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) = 0,
) = 0,![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = r0/H and
0 = r0/H and ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = L/H. In this study, we consider
= L/H. In this study, we consider ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ≫ 1.
≫ 1.
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 +
0 + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) and ũz ≡ Ũz(
) and ũz ≡ Ũz(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 +
0 + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ,
, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ). The dimensionless form of the force balance condition (12), written in vector components, is given as follows. For r-components, we obtain
). The dimensionless form of the force balance condition (12), written in vector components, is given as follows. For r-components, we obtain

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θδ(R − z) cancels out (γsg − γsl)δ(R − z); hence, we obtain the vanishing elastic shear stress condition
θδ(R − z) cancels out (γsg − γsl)δ(R − z); hence, we obtain the vanishing elastic shear stress condition

![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) =g/H. The boundary conditions at the contact line are as follows:
=g/H. The boundary conditions at the contact line are as follows:![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) (
(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ) =
) = ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr(
0 + 1 + ũr(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1,
0 + 1, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) )
)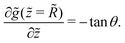
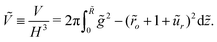

![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, Ẽ,
0, Ẽ, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl,
sl, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg and Ṽ.
sg and Ṽ.
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, Ẽ and
0, Ẽ and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg for both cases of γsg = γsl (i.e. θ = 90°) and γsg ≠ γsl (i.e. θ ≠ 90°).
sg for both cases of γsg = γsl (i.e. θ = 90°) and γsg ≠ γsl (i.e. θ ≠ 90°).
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of
for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. To validate our computations, we first compare our results for a large rigid fiber radius
0. To validate our computations, we first compare our results for a large rigid fiber radius ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 10 with the analytical solution of the 2D plain strain case.12 In the insets of Fig. 2, we show that our numerical results collapse with the analytical 2D solutions. Next, we look at how the rigid fiber radius modifies the deformation. When the layer is stiff (Ẽ = 10), as shown in Fig. 2(a), the out-of-plane displacement ũr is insensitive to the value of
0 = 10 with the analytical solution of the 2D plain strain case.12 In the insets of Fig. 2, we show that our numerical results collapse with the analytical 2D solutions. Next, we look at how the rigid fiber radius modifies the deformation. When the layer is stiff (Ẽ = 10), as shown in Fig. 2(a), the out-of-plane displacement ũr is insensitive to the value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. Relatively, there is a stronger dependence of the in-plane displacement ũz on
0. Relatively, there is a stronger dependence of the in-plane displacement ũz on ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 as shown in Fig. 2(b). In contrast, for the softer case of Ẽ = 1 shown in Fig. 2(c) and (d), the magnitude of displacements increases significantly with decreasing
0 as shown in Fig. 2(b). In contrast, for the softer case of Ẽ = 1 shown in Fig. 2(c) and (d), the magnitude of displacements increases significantly with decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 when
0 when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≤ 1. Moreover, unlike the stiff or large rigid fiber radius cases, in which the magnitude of displacement decays quickly with distances from the contact line, the oscillations are significant for the case of Ẽ = 1 when
0 ≤ 1. Moreover, unlike the stiff or large rigid fiber radius cases, in which the magnitude of displacement decays quickly with distances from the contact line, the oscillations are significant for the case of Ẽ = 1 when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≪ 1.
0 ≪ 1.

![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
− ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of
for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Insets: The analytical solutions of the 2D plain strain case (solid lines)12 and our numerical results for
0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Insets: The analytical solutions of the 2D plain strain case (solid lines)12 and our numerical results for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 10 (dotted lines). Other parameters are as follows:
0 = 10 (dotted lines). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl =
sl = ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5.
sg = 5.![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≫ 1, the deformation behaves the same as the 2D solution as one might expect. The more interesting regime is when
0 ≫ 1, the deformation behaves the same as the 2D solution as one might expect. The more interesting regime is when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1. When the material is stiff, namely Ẽ ≫ 1 (i.e. γ/E ≪ H), the dimensional out-of-plane displacement ur scales as/E and weakly depends on H,7,12 meaning that the deformation is small compared to the thickness of the soft layer. The displacements vanish at a short distance from the soft-solid/fluid interface. Hence, the no-displacement condition at
0 ≲ 1. When the material is stiff, namely Ẽ ≫ 1 (i.e. γ/E ≪ H), the dimensional out-of-plane displacement ur scales as/E and weakly depends on H,7,12 meaning that the deformation is small compared to the thickness of the soft layer. The displacements vanish at a short distance from the soft-solid/fluid interface. Hence, the no-displacement condition at ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 only plays as a small correction to the displacements. On the other hand, when Ẽ ≲ 1, the bulk material deforms more significantly; hence, the boundary conditions at
0 only plays as a small correction to the displacements. On the other hand, when Ẽ ≲ 1, the bulk material deforms more significantly; hence, the boundary conditions at ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 have a stronger effect. Furthermore, not only do the bulk elastic stresses play a significant role, but also the traction fs involving the azimuthal curvature of the soft solid interface, i.e. 1/(
0 have a stronger effect. Furthermore, not only do the bulk elastic stresses play a significant role, but also the traction fs involving the azimuthal curvature of the soft solid interface, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), is crucial for inducing strong displacement oscillations. We found that removing the azimuthal curvature term in eqn (20) results in the disappearance of displacement oscillations. In Section 3.1.4, we will look at how the displacement oscillations depend on the solid surface tension.
0 + 1 + ũr), is crucial for inducing strong displacement oscillations. We found that removing the azimuthal curvature term in eqn (20) results in the disappearance of displacement oscillations. In Section 3.1.4, we will look at how the displacement oscillations depend on the solid surface tension.![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4.13,
sl = 4.13, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5, and thus θ = 30° using Young's law (1). In Fig. 3, we plot the displacements ũr and ũz as a function of
sg = 5, and thus θ = 30° using Young's law (1). In Fig. 3, we plot the displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) . For Ẽ = 10, although the maximum of ũr is almost independent of
. For Ẽ = 10, although the maximum of ũr is almost independent of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, the dimple (minimum) depends significantly on
0, the dimple (minimum) depends significantly on ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 as shown in Fig. 3(a). When the rigid fiber radius is large, for example, for
0 as shown in Fig. 3(a). When the rigid fiber radius is large, for example, for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 1000, the dimple on the solid–liquid side (left) is slightly larger than the solid–gas side (right). This is consistent with the finding of previous studies for plate cases that the solid surface tension suppresses deformation.8 Note that
0 = 1000, the dimple on the solid–liquid side (left) is slightly larger than the solid–gas side (right). This is consistent with the finding of previous studies for plate cases that the solid surface tension suppresses deformation.8 Note that ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl <
sl < ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg. However, when decreasing
sg. However, when decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, ũr increases on the solid/liquid side and decreases on the solid/gas side. Hence, the dimple of the solid/liquid interface decreases and disappears. On the other hand, the dimple of the solid/gas interface becomes larger. This disparity can be observed clearly for
0, ũr increases on the solid/liquid side and decreases on the solid/gas side. Hence, the dimple of the solid/liquid interface decreases and disappears. On the other hand, the dimple of the solid/gas interface becomes larger. This disparity can be observed clearly for ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1 in Fig. 3(a).
0 = 0.1 in Fig. 3(a).

![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of
for different values of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows:
0 and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl = 4.13 and
sl = 4.13 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5.
sg = 5.![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. For large
0. For large ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, the material around the contact line at the interface displaces towards the contact line for both sides. When decreasing
0, the material around the contact line at the interface displaces towards the contact line for both sides. When decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0, ũz decreases. For
0, ũz decreases. For ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1, ũz is negative for the whole interface, meaning that all the material at the interface displaces towards the side of interface with a smaller solid surface tension (left).
0 ≲ 1, ũz is negative for the whole interface, meaning that all the material at the interface displaces towards the side of interface with a smaller solid surface tension (left).![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 is similar to that of Ẽ = 10. Remarkably, when
0 is similar to that of Ẽ = 10. Remarkably, when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 is reduced to
0 is reduced to ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1, ũr around the contact line on the solid–liquid side increases to values larger than ũr at the contact line. Hence, the maximum of ũr is not at the contact line position but shifts to the solid/liquid side as shown in Fig. 3(c). Similar to that we have seen for the case of θ = 90°, pronounced oscillations of ũr and ũz appear when
0 = 0.1, ũr around the contact line on the solid–liquid side increases to values larger than ũr at the contact line. Hence, the maximum of ũr is not at the contact line position but shifts to the solid/liquid side as shown in Fig. 3(c). Similar to that we have seen for the case of θ = 90°, pronounced oscillations of ũr and ũz appear when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≪ 1.
0 ≪ 1.![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. According to Young's law, changing θ also means that
0 = 0.1. According to Young's law, changing θ also means that ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg −
sg − ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl is varied. We keep
sl is varied. We keep ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 for all cases and change the value of
sg = 5 for all cases and change the value of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl. We again consider two different values of Ẽ. The displacements ũr and ũz as a function of
sl. We again consider two different values of Ẽ. The displacements ũr and ũz as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different θ (or
for different θ (or ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl) are plotted in Fig. 4.
sl) are plotted in Fig. 4.

![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different values of
for different values of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows:
sl and Ẽ = 10 in (a) and (b) and Ẽ = 1 in (c) and (d). Other parameters are as follows: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5 and
sg = 5 and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1.
0 = 0.1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The sharp tip at the contact line disappears for θ = 0° as the pulling force vanishes. Interestingly, there is still a significant deformation for θ = 0°. The deformation then comes from the traction fs generated by the solid surface tensions. When
θ. The sharp tip at the contact line disappears for θ = 0° as the pulling force vanishes. Interestingly, there is still a significant deformation for θ = 0°. The deformation then comes from the traction fs generated by the solid surface tensions. When ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl and
sl and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg are different, the traction fs involving the azimuthal curvature, i.e. 1/(
sg are different, the traction fs involving the azimuthal curvature, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), gives different stresses at the liquid side and the gas side.
0 + 1 + ũr), gives different stresses at the liquid side and the gas side.![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0) is similar to that of decreasing
0) is similar to that of decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 (for a fixed value of θ). In the following, we point out some of these similar trends. As shown in Fig. 3(a) or in Fig. 4(a) for Ẽ = 10, when reducing
0 (for a fixed value of θ). In the following, we point out some of these similar trends. As shown in Fig. 3(a) or in Fig. 4(a) for Ẽ = 10, when reducing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ, the dimple of ũr on the solid–liquid side (with a smaller solid surface tension) decreases and the dimple on the solid–gas side becomes larger. For Ẽ = 1, the maximum of ũr shifts from the contact line position to the solid–liquid side when
0 or θ, the dimple of ũr on the solid–liquid side (with a smaller solid surface tension) decreases and the dimple on the solid–gas side becomes larger. For Ẽ = 1, the maximum of ũr shifts from the contact line position to the solid–liquid side when ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ is reduced to below a certain value as shown in Fig. 3(c) or in Fig. 4(c). For the in-plane displacement shown in Fig. 3(b) and (d) or Fig. 4(b) and (d), ũz around the contact line decreases when reducing
0 or θ is reduced to below a certain value as shown in Fig. 3(c) or in Fig. 4(c). For the in-plane displacement shown in Fig. 3(b) and (d) or Fig. 4(b) and (d), ũz around the contact line decreases when reducing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 or θ. This means that the material at the interface displaces more to the side of the interface with a smaller solid surface tension (left).
0 or θ. This means that the material at the interface displaces more to the side of the interface with a smaller solid surface tension (left).![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
−![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). We see that when
for θ = 90° in (a) and (b) and θ = 30° in (c) and (d). We see that when ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg is reduced, ũr at the contact line enhances. This is because the traction fs term involving the longitudinal curvature, i.e. ∂2ũr/∂
sg is reduced, ũr at the contact line enhances. This is because the traction fs term involving the longitudinal curvature, i.e. ∂2ũr/∂![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 2, suppresses the sharp tip deformation at the contact line.8,12 On the other hand, the displacement oscillations and the displacement disparity (for θ = 30°) become less pronounced when
2, suppresses the sharp tip deformation at the contact line.8,12 On the other hand, the displacement oscillations and the displacement disparity (for θ = 30°) become less pronounced when ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg is reduced. This can be understood as follows. Away from the contact line, the azimuthal curvature term, i.e. 1/(
sg is reduced. This can be understood as follows. Away from the contact line, the azimuthal curvature term, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), dominates over the longitudinal curvature term. The displacement oscillations and displacement disparity are due to the azimuthal curvature term in the traction fs. Decreasing
0 + 1 + ũr), dominates over the longitudinal curvature term. The displacement oscillations and displacement disparity are due to the azimuthal curvature term in the traction fs. Decreasing ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg thus reduces the effects of this traction. In Fig. 5, we also add the results for a smaller value of Ẽ. As we demonstrate previously, reducing the value of Ẽ enhances the displacement oscillations and displacement disparity.
sg thus reduces the effects of this traction. In Fig. 5, we also add the results for a smaller value of Ẽ. As we demonstrate previously, reducing the value of Ẽ enhances the displacement oscillations and displacement disparity.
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 0.1. In Fig. 6 and 7, the displacements ũr and ũz are plotted as a function of
0 = 0.1. In Fig. 6 and 7, the displacements ũr and ũz are plotted as a function of ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
− ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) respectively for θ = 30° and θ = 0°. We can see that for Ṽ1/3= 40, the results are the same as those for the large droplet limit. When Ṽ1/3 decreases, ũr decreases on the liquid side and increases on the gas side. This is because the Laplace pressure pressing the soft layer on the liquid side is stronger for smaller droplets. For ũz, the Laplace pressure term reduces the magnitude of ũz on both the liquid and gas sides. The magnitude of displacement oscillation is also reduced when the droplet size decreases. Note that we assume the contact angle follows Young's relationship and is independent of the droplet size. Hence, the contact angle transition observed for small droplets on planar surfaces14,17 is not considered in our present study.
respectively for θ = 30° and θ = 0°. We can see that for Ṽ1/3= 40, the results are the same as those for the large droplet limit. When Ṽ1/3 decreases, ũr decreases on the liquid side and increases on the gas side. This is because the Laplace pressure pressing the soft layer on the liquid side is stronger for smaller droplets. For ũz, the Laplace pressure term reduces the magnitude of ũz on both the liquid and gas sides. The magnitude of displacement oscillation is also reduced when the droplet size decreases. Note that we assume the contact angle follows Young's relationship and is independent of the droplet size. Hence, the contact angle transition observed for small droplets on planar surfaces14,17 is not considered in our present study.
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0. For θ ≠ 90° (i.e. γsl ≠ γsg), the deformations on the solid–liquid side and the solid–gas side are different. This disparity of deformation is enhanced when decreasing
0. For θ ≠ 90° (i.e. γsl ≠ γsg), the deformations on the solid–liquid side and the solid–gas side are different. This disparity of deformation is enhanced when decreasing ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 (for a fixed value of θ) or decreasing θ (for a fixed value of
0 (for a fixed value of θ) or decreasing θ (for a fixed value of ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0). The dimple of ũr on the side with a smaller solid surface tension becomes smaller while the dimple becomes larger on the other side. Interestingly, significant deformation is observed even for θ = 0° for which the pulling force at the contact line vanishes and the Laplace pressure is neglected for large droplets. The deformation is due to the part of traction fs involving the azimuthal curvature term, i.e. 1/(
0). The dimple of ũr on the side with a smaller solid surface tension becomes smaller while the dimple becomes larger on the other side. Interestingly, significant deformation is observed even for θ = 0° for which the pulling force at the contact line vanishes and the Laplace pressure is neglected for large droplets. The deformation is due to the part of traction fs involving the azimuthal curvature term, i.e. 1/(![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 + 1 + ũr), which generates different stresses on the liquid and the gas sides when the solid surface tensions are different.
0 + 1 + ũr), which generates different stresses on the liquid and the gas sides when the solid surface tensions are different.
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≲ 1. This slow decay of deformation with distances from the contact line position suggests a relatively long-range interaction between droplets on a soft-layer-coated fiber. Hence, it is expected that droplet migration and interactions are significantly different from those observed on a planar soft substrate or a purely rigid fiber, for example, the inverted Cheerios effect45 and coalescence,37 which remain open questions to be explored.
0 ≲ 1. This slow decay of deformation with distances from the contact line position suggests a relatively long-range interaction between droplets on a soft-layer-coated fiber. Hence, it is expected that droplet migration and interactions are significantly different from those observed on a planar soft substrate or a purely rigid fiber, for example, the inverted Cheerios effect45 and coalescence,37 which remain open questions to be explored. , where lm can be interpreted as a microscopic length (e.g. interface thickness) such that lm ≪ H. In the limit that lm → 0, δ(R − z) = W(R − z). In this study, lm/H = 10−5 is set for all the cases. We have used the adaptive mesh sizing such that the smallest mesh size near the contact line is dx1/H = 10−7 and the largest mesh size far away from the contact line is dx0/H = 0.05.
, where lm can be interpreted as a microscopic length (e.g. interface thickness) such that lm ≪ H. In the limit that lm → 0, δ(R − z) = W(R − z). In this study, lm/H = 10−5 is set for all the cases. We have used the adaptive mesh sizing such that the smallest mesh size near the contact line is dx1/H = 10−7 and the largest mesh size far away from the contact line is dx0/H = 0.05.![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 ≫ 1. In this limit, the deformation of the soft layer will converge towards the 2D soft plate case. In Fig. 8, we compare our numerical results with the analytical solution for the 2D soft plate case by plotting the deformation of the soft solid for three different mesh resolutions, namely dx0/H = 0.1, 0.05 and 0.025. For all three mesh sizes, the numerical solutions are in good agreement with the analytical solution.
0 ≫ 1. In this limit, the deformation of the soft layer will converge towards the 2D soft plate case. In Fig. 8, we compare our numerical results with the analytical solution for the 2D soft plate case by plotting the deformation of the soft solid for three different mesh resolutions, namely dx0/H = 0.1, 0.05 and 0.025. For all three mesh sizes, the numerical solutions are in good agreement with the analytical solution.
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) −
− ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) for different mesh sizes. Other parameters are as follows: θ = 90°,
for different mesh sizes. Other parameters are as follows: θ = 90°, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sl =
sl = ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) sg = 5, and
sg = 5, and ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) 0 = 1000.
0 = 1000.



