Open Access Article
Open Access ArticleCapillary washboarding during slow drainage of a frictional fluid†
Louison
Thorens
ab,
Knut J.
Måløy
bc,
Eirik G.
Flekkøy
bd,
Bjørnar
Sandnes
e,
Mickaël
Bourgoin
a and
Stéphane
Santucci
 *a
*a
aENSL, CNRS, Laboratoire de Physique, F-69342 Lyon, France. E-mail: stephane.santucci@ens-lyon.fr
bPoreLab, The Njord Centre, Department of Physics, University of Oslo, P. O. Box 1048 Blindern, N-0316 Oslo, Norway
cPoreLab, Dep. of Geoscience and Petroleum, Norwegian University of Science and Technology, Trondheim, Norway
dPoreLab, Dep. of Chemistry, Norwegian University of Science and Technology, Trondheim, Norway
eDepartment of Chemical Engineering, Swansea University, Bay Campus, Swansea, UK
First published on 19th October 2023
Abstract
Numerous natural and industrial processes involve the mixed displacement of liquids, gases and granular materials through confining structures. However, understanding such three-phase flows remains a formidable challenge, despite their tremendous economic and environmental impact. To unveil the complex interplay of capillary and granular stresses in such flows, we consider here a model configuration where a frictional fluid (an immersed sedimented granular layer) is slowly drained out of a horizontal capillary. Analyzing how liquid/air menisci displace particles from such granular beds, we reveal various drainage patterns, notably the periodic formation of dunes, analogous to road washboard instability. Considering the competitive role of friction and capillarity, a 2D theoretical approach supported by numerical simulations of a meniscus bulldozing a front of particles provides quantitative criteria for the emergence of those dunes. A key element is the strong increase of the frictional forces, as the bulldozed particles accumulate and bend the meniscus horizontally. Interestingly, this frictional enhancement with the attack angle is also crucial in small-legged animals' locomotion over granular media.
1. Introduction
Transport processes driven by fluid flow within confined media are common in our everyday life. The functioning of most of the living organisms1 depends on the circulation of physiological fluids2–4 and the continuous supply of metabolites through vascular systems.5 Multiphase flows through porous confined geometries play also an essential role in a wide variety of engineering settings with many technological applications, such as fuel cells,6 CO2 sequestration7 and filtration.8More specifically, numerous natural and industrial processes such as the transport of sediments remodelling river beds,9 the irrigation and decontamination of soils,10 or oil recovery methods11 imply the mixed and confined displacement of three phases with liquids, gases and granular materials. Despite their importance and tremendous impact on our environment and economy—billions of litres of crude oil are extracted every minute world-wide12—, understanding such three-phase flows in confining structures remains a formidable challenge, in stark contrast now to our current knowledge and control of two-phase flows,13–17 even in heterogeneous media.18–26 Indeed, the interplay of capillary effects and granular stresses, governed by the frictional contacts between the grains and the confining walls, coupled with hydrodynamics interactions leads to an extremely complex flow dynamics.
In order to tackle this challenge and apprehend this complexity, experiments in Hele–Shaw cells and capillary tubes have been designed in the spirit of Saffman and Taylor's seminal work,13 using glass beads and water.27–31 Such model experiments allowing for a direct visualization of the multi-phasic displacement dynamics reveal a wide range of puzzling flow instabilities,28 from stick-slip bubbles32 to destabilized viscous fingers,18,33,34 and labyrinths,27,35 depending on the amount of particles present in the confining medium and the liquid flow rate. Furthermore, even for the very simple configuration involving the drainage of a mixture of water and glass beads settling in a horizontal capillary tube, the displacement of the grains by the water/air meniscus can become unstable: the particles may be pushed up to the top of the tube, clogging it. Reaching this limit, the friction force exerted by the particles on the wall grows exponentially with the length of this bulldozing front, via the Janssen effect within the granular packing.36 When the pressure necessary to push this front surpasses the capillary pressure threshold required to penetrate an interface pore, air percolates through the granular medium and a plug of grains is left behind. Imposing a constant drainage velocity, this process repeats itself, resulting in the periodic formation of granular plugs along the capillary tube. While the plug formation has already been described,30,31 the onset of the bulldozing process has never been explored so far, and the physical conditions for its triggering are unknown.
Therefore, in the present manuscript, we focus on the emergence of this capillary bulldozing mechanism. Modifying systematically the wetting properties and surface tension of the draining liquid, as well as the initial height of the granular bed, we identify the necessary physical conditions for the triggering of a capillary bulldozing process. Furthermore, we also reveal various drainage regimes (and the transitions between those), leading notably to the periodic formation of dunes, analogous to the road washboard instability,37 when the particles are only partially bulldozed by the meniscus. Those drainage regimes and corresponding final patterns (specifically, the so-called rest and dune phases) have not been observed in previous studies,30,31 using simply water as the draining liquid. A 2D theoretical analysis based on the competitive role of friction and interfacial tension and quantitatively supported by 2D numerical simulations of a meniscus displacing a granular assembly allows us to define a Capillary Bulldozing dimensionless number, and capture the essence and origin of the bulldozing process, describing all the qualitative features of the various drainage dynamics observed experimentally.
2. Results
2.1 Drainage of frictional fluids
We consider an immersed granular bed, composed of glass beads of diameter d = (127 ± 32) μm resting in a one meter long capillary tube of radius R = 1.0 mm, as shown in Fig. 1.The preparation of the initial state of this granular layer with a packing fraction of ϕ = 0.60 ± 0.05 is described in Appendix A. We specifically explain the procedure to obtain a controlled initial height of this granular bed of 2ε0R, where ε0 is the initial filling height fraction, with height fluctuations of ±1 grain diameter.
The internal surface of the capillary tube is rendered hydrophobic with a silanization solution (∼5% dimethyldichlorosilane in heptane). The efficiency of this hydrophobic coating was checked before each drainage experiments, by flowing pure water inside the tube and measuring a 90° contact angle.
In previous studies,28 the immersing liquid was simply water, of surface tension γw = 72 mN m−1. Here, in order to modify systematically the capillary effects, we use a mixture solution of water and isopropanol which has a lower surface tension than water, γ2-propanol = 22 mN m−1. We checked that self-induced Marangoni flows38 that may arise when mixing liquids due to a differential evaporation are negligible in our experiments.
Using a drop-shape analyser (Kruss DSA24E), we measured the surface tension γ of this solution as a function of the weight amount of isopropanol (2-propanol % w/w). Our measurements show a systematic decrease of the surface tension γ with the isopropanol concentration, in agreement with the literature.39 The wetting contact angle with the tube surface ξ (obtained from the shape of a sessile drop on a silanized glass plate) decreases also systematically with the isopropanol concentration. Those measurements are provided in Appendix B.
As shown in the schematic illustration of Fig. 1, a fluid-filled syringe pump is connected to one end of the tube, with no air bubbles present in the system. The pump is set to a constant withdrawal rate of I0 = 0.1 mL min−1. This imposed flow rate was chosen slow enough in order to neglect viscous effects.28 Therefore, the grains remain unperturbed by the flow, and only the water–isopropanol solution is slowly pumped out of the tube. We checked that up to 1.0 mL min−1, our measurements do not depend on this rate, while increasing it beyond this value (typically of few tens of mL min−1) results in the flushing of the suspended granular mixture,30,31 as used for the preparation of the initial state of the granular bed (explained in Appendix C). A meniscus at the liquid/air interface appears on the opposite side of the capillary tube open to the air. Interestingly, we observe very different drainage dynamics and final patterns of the granular layer of height h within the capillary tube, once the drainage was completed. Fig. 2 shows typical examples of those drainage patterns. Indeed, depending on the initial height of the granular layer, and the isopropanol concentration, which controls directly the wettability and surface tension of the solution, the liquid/air meniscus is either able to bulldoze and clog the tube leading to the formation of granular plugs (Fig. 2a), or partly bulldoze the particles resulting in the formation of periodic dunes (Fig. 2b) or finally, simply slide over the resting layer of grains (Fig. 2c).
The distinction between the different drainage patterns observed and in particular between the rest and dune phases is illustrated in Fig. 3 where we superimposed on the final drainage pattern pictures, the detected granular layer interface (in blue) with the initial one, right after its preparation (in red). When after the drainage, the granular bed presents height fluctuations similar to those observed right after its preparation, of ±1 grain diameter, the sample is considered in the rest phase. On the other hand, the dune phase is determined by measuring periodic height fluctuations larger or equal to two grain diameters, such that Δh = max(h) − min(h) ≥ 2d. Finally, the plugs are dunes that have reached the top wall of the capillary tube, clogging it.
Fig. 4 summarizes our experimental findings by providing a phase diagram of the different drainage patterns observed (plugs, dunes or undisturbed granular beds at rest) as a function of the initial height of the granular layer, and the isopropanol concentration. Those different patterns are directly related to the different shape and dynamics of the meniscus bulldozing the particles front. Typical illustrating examples are also shown in Fig. 4. Furthermore, we also provide typical video recordings of our experiments in ESI.†
For a low concentration of isopropanol, and/or high initial height of the granular layer in the tube, the meniscus can displace the grains which accumulate ahead up to clogging the capillary and finally forming plugs. For a high concentration of isopropanol and low initial height of the glass beads layer, the meniscus slides over the granular layer without displacing any particles, leaving this granular bed at rest. Finally, we also reveal an intermediate situation, with a new drainage regime, occurring essentially for a low initial height of the granular layer, when the meniscus is not able to push ahead the particles up to clogging the capillary. In this case, before reaching the top wall of the capillary tube, the meniscus passes over the bulldozed granular front, leaving a dune behind. The final drainage pattern of the granular bed is made up of a recurring series of dunes as shown in Fig. 2(b), analogous to the periodic ripples arising along sand roads with the repeated passage of vehicles, called “washboard” instability.37
2.2 A 2D model
To explain the various drainage patterns and the corresponding transitions in the phase diagrams, we reduce the complex 3D geometry of our experiments to a 2D one. Therefore, we consider an air/liquid meniscus line pushing a triangular front of particles, as represented in Fig. 5.To elucidate the washboard instability, Percier et al.40 have studied in a similar geometry (see Appendix C) the drag FD and lift FL forces acting on an inclined plate dragged over a granular bed. They showed that those forces are proportional to the weight of the steady wedge of grains plowed, with constants of proportionality, corresponding to friction coefficients μD(α) and μL(α) respectively, that increase strongly when the angle of attack α of the plow diminishes. While they did not provide any theoretical explanation for such angular dependency, they demonstrate that the triangular bulldozed front can be simply modelled as a solid block sliding over a flat surface with Coulomb friction.
In this 2D geometry, the air/liquid meniscus line can be divided in two distinct zones. First, the bottom part in contact with the particles front of height h = 2(ε − ε0)R is represented in red in Fig. 5. There, we consider a simple straight shape for this part of the meniscus line, assuming that it makes an angle α with the horizontal. Second, the upper part of the meniscus above the triangular pile of particles, shown in black in Fig. 5, is similar to a pore of radius (1 − ε)R. Such a pore imposes a pressure difference between the liquid and air phases, given by the Young–Laplace equation: ΔP = γ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ + cos
ξ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)/(2(1 − ε)R)
α)/(2(1 − ε)R)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (as explained in Appendix D). Therefore, the capillary force exerted on the meniscus (in contact with the granular pile, red line in Fig. 5) in the horizontal direction is given by Fxc = Fc
(as explained in Appendix D). Therefore, the capillary force exerted on the meniscus (in contact with the granular pile, red line in Fig. 5) in the horizontal direction is given by Fxc = Fc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = γ(cos
α = γ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ + cos
ξ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)(ε − ε0)/(1 − ε).
α)(ε − ε0)/(1 − ε).
Following the results of Percier et al.,40 we consider that the triangular granular front is opposing a drag friction force FD, in the horizontal direction, proportional to the front mass, FD = μD(α)gM where g is the acceleration of gravity, and μD a drag friction coefficient, that depends on the attack angle α, as detailed in Appendix C. The mass of this bulldozed granular front, corrected for the buoyancy, is  , with
, with 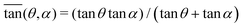 , where ϕ is the volume fraction of particles, Δρ the density difference between the particles and the fluid, θ the avalanche angle of our granular assembly. Together with the attack angle α, this angle θ sets the shape of the bulldozed granular front.
, where ϕ is the volume fraction of particles, Δρ the density difference between the particles and the fluid, θ the avalanche angle of our granular assembly. Together with the attack angle α, this angle θ sets the shape of the bulldozed granular front.
Therefore, we can define the dimensionless Capillary Bulldozing number ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) as the ratio between the meniscus drag force Fxc to the drag friction force FD:
as the ratio between the meniscus drag force Fxc to the drag friction force FD:
 | (1) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) > 1, the air/liquid meniscus is able to push forward the granular front, the capillary force overcomes the frictional force. Interestingly,
> 1, the air/liquid meniscus is able to push forward the granular front, the capillary force overcomes the frictional force. Interestingly, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) decreases with the height of the bulldozing front (given by ε) until reaching a minimum value, at ε = (ε0 + 1)/2:
decreases with the height of the bulldozing front (given by ε) until reaching a minimum value, at ε = (ε0 + 1)/2: | (2) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) min > 1, the meniscus will always be able to bulldoze the granular front until the clogging of the capillary tube, when the dune reaches its top wall (ε = 1), and the formation of a granular plug. One can notice that larger values of
min > 1, the meniscus will always be able to bulldoze the granular front until the clogging of the capillary tube, when the dune reaches its top wall (ε = 1), and the formation of a granular plug. One can notice that larger values of ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) min can be achieved by increasing the surface tension γ and/or the initial height of the granular bed, given by the filling fraction ε0, which agrees qualitatively with our experimental measurements. Otherwise, when
min can be achieved by increasing the surface tension γ and/or the initial height of the granular bed, given by the filling fraction ε0, which agrees qualitatively with our experimental measurements. Otherwise, when ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) min < 1, the bulldozing process will lead to the formation of a dune. Thus, the critical value
min < 1, the bulldozing process will lead to the formation of a dune. Thus, the critical value ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) min = 1 provides the transition between plugs and dunes for the initial height of the granular bed:
min = 1 provides the transition between plugs and dunes for the initial height of the granular bed: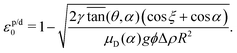 | (3) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (εdmin) = 1. Actually, this equation brings forward the transition between the formation of dunes and the rest phase, for the initial height of the granular bed:
(εdmin) = 1. Actually, this equation brings forward the transition between the formation of dunes and the rest phase, for the initial height of the granular bed: | (4) |
2.3 2D numerical simulations
We have developed simulations inspired by the approach proposed by Knudsen et al. who modelled the in-plane deformation of an air/water meniscus displacing glass beads within a Hele–Shaw cell to reproduce the formation of labyrinthine patterns during the slow drainage of frictional fluids.35,41 . Thus, one can obtain the capillary pressure acting on the meniscus given by Laplace equation: δPk = γκk, where γ is the effective liquid surface tension in contact with air. The wetting contact angle between the meniscus and the confining walls ξ is fixed during the whole simulation by forcing the meniscus local angles at the top and bottom of the tube:
. Thus, one can obtain the capillary pressure acting on the meniscus given by Laplace equation: δPk = γκk, where γ is the effective liquid surface tension in contact with air. The wetting contact angle between the meniscus and the confining walls ξ is fixed during the whole simulation by forcing the meniscus local angles at the top and bottom of the tube:  , where N is the number of points modelling the meniscus. Initially, N points are generated vertically within the capillary tube. This number is chosen accordingly to the diameters of the grains d and of the capillary tube 2R considered in our experiments, such that N = 2R/d. However, at each time step, if the distance between two points i and i + 1 is higher than d, an additional point is added between them.
, where N is the number of points modelling the meniscus. Initially, N points are generated vertically within the capillary tube. This number is chosen accordingly to the diameters of the grains d and of the capillary tube 2R considered in our experiments, such that N = 2R/d. However, at each time step, if the distance between two points i and i + 1 is higher than d, an additional point is added between them.
Concerning the granular packing, the amount of bulldozed particles ahead of the meniscus is characterized by its height h. The inward edge of bulldozed grains is forming a constant avalanche angle θ with the horizontal. For each meniscus segment in contact with the grains, we can identify four different horizontal force contributions corresponding to four different packing zones as shown in Fig. (6):
• the layer itself, of mass Mi, applying a force fi = μgMi,
• the layers above, of mass  , applying a force
, applying a force 
• the bulldozed layer, of mass Mbulli, applying a force
f
bull
i
= μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θgMbulli,
θgMbulli,
• the tilted layer in contact with the meniscus, of mass Mcontacti, applying a force fcontacti = μD(αi)gMcontacti.
We thus can compute the local granular stress σi (using the sum of all those frictional forces acting on each granular layer i).
Finally, at each time step, the local horizontal capillary action and the local granular stress are computed at each meniscus point. On the other hand, the pressure difference across the fluid air interface δPi(z) at position z decreases with the height according to: δPi(z) = δPi(z = 2R) − ρlg(2R − z). Therefore, a meniscus point may advance if δPi(z) overcomes the sum of the horizontal capillary pressure γκisinαi and granular stress term σi:
δPi(z) > γκi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi + σi. αi + σi. | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi + σi. This point advances horizontally over a distance δxi which is set to keep the withdrawing rate constant in order to match our experimental protocol. Finally, to ensure mass conservation, at each time step the bulldozed height h is updated accordingly while keeping the avalanche angle θ constant.
αi + σi. This point advances horizontally over a distance δxi which is set to keep the withdrawing rate constant in order to match our experimental protocol. Finally, to ensure mass conservation, at each time step the bulldozed height h is updated accordingly while keeping the avalanche angle θ constant.
Importantly, as already mentioned, one has to take into account that the friction force exerted by the granular front on the meniscus depends strongly on the local angle of attack αi. Actually, legged animals such as lizards take advantage of such frictional enhancement with the local angle of attack to move and even run effectively on flowing granular media.42 In practice, to compute the local frictional forces acting on the bulldozing meniscus in our numerical simulations, we use a phenomenological power-law evolution of the drag friction coefficient μD, obtained by fitting the experimental data of Percier et al.,40μD ∝ α−1.0, as shown in Section C.
Thus, during the capillary bulldozing process, as the meniscus bends horizontally, the local angles of attack αi decrease, resulting in a strong increase in the local granular stress. At this point, we observe in our experiments (see the video Movie S2, provided in ESI,† corresponding to a drainage experiment of a 50% w/w isopropanol solution with an initial height of grains given by ε0 = 0.23), that the meniscus plunges in the granular bed forming an angle θ with the horizontal, corresponding to the avalanche angle. To reproduce this behaviour in our numerical simulations, we impose the descent of the meniscus within the granular bed, when the local attack angle αi is lower than 4°.
We provide as accompanying ESI,† videos of typical numerical simulations, showing different drainage patterns, plugs, dunes or undisturbed granular beds at rest. Importantly, our numerical simulations can indeed reproduce the three different drainage patterns and dynamics observed experimentally, with in particular the emergence of a capillary washboarding instability, leading to the formation of a periodic pattern of dunes along the capillary tube.
Interestingly, in contrast to our experiments, our numerical simulations allows us to vary the surface tension γ and the wetting contact angle ξ, independently. As such, Fig. 7 provides two typical examples of the phase diagram of the different drainage patterns observed in our numerical simulations, as a function of the surface tension γ and the wetting contact angle ξ, corresponding to two different initial filling height fraction ε0 of the granular layer. It is important to notice that those numerical results appear in qualitative agreement with our experimental measurements and observations. Indeed, for a high value of surface tension γ as well as a high value of the wetting contact angle with the tube wall ξ, corresponding typically to the properties of pure water as a draining liquid, the drainage will always lead to granular plugs clogging the capillary. On the other hand, decreasing either the surface tension γ, or this wetting contact angle ξ, a transition to a dune phase and eventually to a rest phase can be observed, for both very low values of both γ and ξ, which is typically the case when using pure iso-propanol. Moreover, for a very low surface tension of γ ∼ 20 mN m−1, the dune phase is observed over a wider range of wetting contact angle when decreasing the initial height of the granular bed given by the filling height fraction ε0. In other words, increasing the initial height of the granular layer facilitates indeed the emergence of plugs clogging the capillary.
We show in Fig. 8 a typical example of a final drainage pattern, displaying a series of dunes for a numerical simulation with the following parameters, ε0 = 0.20, γ = 25 mN m−1 and ξ = 33°. In contrast to our experiments, due to the idealized 2D geometry considered, we can clearly monitor the evolution of the shape of the moving meniscus points in contact with the granular packing, as shown by the inset of Fig. 8 (see specifically, the blue points/line). Therefore, we can obtain in our numerical simulations the average angle of attack, as defined in our theoretical model (see Fig. 5), α = 〈αi〉contact, measured along the moving meniscus points in contact with the grains.
Thus, we provide in Fig. 8(b) the temporal evolution of this average angle α for the same numerical example. The initial value of α is close to the wetting contact angle ξ of the draining fluid and decreases during the bulldozing process until a minimum value αmin (blue triangle) when a dune is formed. Then, the average angle of attack increases sharply towards the value of ξ, and the process repeats itself leading to the periodic formation of dunes along the tube, as shown in Fig. 8(a).
Interestingly, we could observe for the various simulations displaying a dune phase, operating over a wide range of controlling parameters (ε0, γ and ξ) that this minimum value of α evolves as αmin ≃ ξ/2, as reported in Fig. 9.
 | ||
| Fig. 9 Evolution of the minimum average angle of attack αmin (defined in Fig. (8) as a function of the wetting contact angles ξ, well fitted by αmin ≃ ξ/2 (dashed line). | ||
Importantly, inserting in eqn (3) and (4) this value of the average angle of attack αmin allows to estimate numerically the transitions between dunes/plugs, and dunes/rest phases, respectively.
Finally, to go further in the comparison with our experimental results, we can consider among the various numerical simulations performed, the ones with the values of surface tension and wetting contact angle (γ, ξ) of the mixture solution of water and isopropanol measured at various isopropanol concentration, 2-propanol % w/w, given in Appendix B. Therefore, we can provide in Fig. 10 a phase diagram of the different drainage patterns observed in our numerical simulations, as a function of the initial filling height fraction of the granular layer, and the isopropanol concentration of the draining fluid, as for our experiments.
 | ||
| Fig. 10 (a) Phase diagram of the final drainage patterns observed in our numerical simulations as a function of the experimental control parameters, the filling height fraction ε0 and the isopropanol concentration. The two lines correspond to our predictions for the different phase transitions given by eqn (3), in blue, and (4), in black, estimated with the average angle of attack αmin, measured in our simulations. The shadows reflect a ±2° error in the measurement of this angle. (b) Snapshots of typical meniscus shape observed for the different drainage dynamics. | ||
Strikingly, this phase diagram as well as the typical meniscus shapes displayed Fig. 10 shows that our numerical results are in excellent agreement with our experimental measurements, with the observation of three different regimes of the drainage, and in particular the emergence of a capillary washboarding instability, leading to the formation of a periodic pattern of dunes along the capillary tube, as a function of the initial height of the granular bed, and the isopropanol concentration. However, this agreement can be only qualitative. Indeed, our theoretical and numerical analysis is based on an idealized 2D geometry, which doesn't take into account the complex 3D shape of the meniscus, nor the varying cross section of the capillary tube. Thus, it cannot predict the exact values of of the initial height of the granular bed, and the isopropanol concentration for the occurrence of the different drainage dynamics. With our experimental 3D geometry, we expect notably higher capillary pressure (due to the curvature of the meniscus in the third dimension that we ignore in our 2D modeling), and smaller frictional stresses (related to a larger effective cross-sectional area of the granular packing). Therefore, the bulldozing process should be facilitated (larger Capillary Bulldozing number). This may explain that for intermediate concentration of isopropanol, in our 3D experiments, the granular plug phases appear for smaller initial filling height fraction of the capillary tube than in the 2D simulations. We also observe some differences in the bulldozing dynamics itself, between our 2D simulations and our experiments, notably, the formation of well-separated dunes or not for given control parameters, as show on Fig. 2b and 8a. This is related to the conservation of the mass of the bulldozed granular front, which is different in our 2D simulations than in our experiments, because of the varying horizontal cross section of the capillary tube along the vertical direction in our 3D experiments. Nevertheless, the theoretical predictions of the transitions between the formation of dunes and plugs, and between the dunes and the granular bed at rest, given by eqn (3) and (4) respectively, estimated with the average angle of attack αmin (value measured in our simulations, when a dune is formed), are found in quantitative agreement with the phase diagrams reported in Fig. 10(a).
3 Discussion and perspectives
Combining experiments, theory and numerical simulations, we could elucidate the emergence of various drainage patterns arising when an immersed granular bed in a capillary tube is displaced by a liquid/air meniscus as the liquid is slowly drained out. Such a model system is a proxy for numerous natural and industrial processes of prime importance, with various technological applications.A first important aspect of the present work relies on the fact that we propose here a generalized theoretical framework to tackle capillary bulldozing phenomena, via the definition of a dimensionless number that compares frictional and capillary forces involved in such three-phase displacements. On one hand, this theoretical analysis allows to explain previous experimental observations, with the formation of granular plugs.30,31 Indeed, those previous drainage experiments were performed with pure water (corresponding to a particular case of our phase diagram with a zero concentration of isopropanol) for which only a plug regime was observed. By modifying systematically the wetting properties and surface tension of the draining liquid, we reveal here experimentally the emergence of various drainage regimes, with in particular a transition from a rest to a dune phase with the periodic formation of ripples. Using pure water as a draining liquid, the air/water meniscus is always able to bulldoze the glass beads. Therefore, the plug regime appears simply as a limit case of the dune phase: a granular plug being simply a dune that has reached the top wall of the capillary leading to its clogging.
More importantly, our theoretical analysis allows to explain the formation of those dunes. We coined this process capillary washboarding, by analogy with the ripples arising along sandy roads due to the repeated passage of vehicles, so-called “washboard roads”.37 The strong increase of the frictional forces as the bulldozed particles accumulate and bend the meniscus horizontally is a key element at the basis of the emergence of this pattern.
Similarly to the emergence of various patterns with well-know interfacial fluid instabilities, we can simply consider that the dunes and plugs patterns, characterized by periodic oscillations of the height of the sedimented granular layer resulting from the competition between capillary and frictional forces during the drainage are spatial instabilities of the initially flat granular bed. Thus, the order parameter of the corresponding transitions is indeed the height variation Δh of the granular layer. The dimensionless Capillary Bulldozing number C allows to define a threshold for the emergence of the bulldozing mechanism, occurring as soon as C > 1. The capillary force overcomes the frictional force, the air/liquid meniscus displaces the grains leading to variation in the height of the granular bed. In the rest phase, the meniscus simply slides over the granular bed without displacing any grains, and thus leaves behind the granular interface flat and undisturbed, Δh = 0. Therefore, this phase can be considered as a stable regime of the drainage. We could show that this regime occurs typically for a high concentration of alcohol in the draining fluid (mixture of water and isopropanol), leading to low surface tension and wetting contact angle. Decreasing the isopropanol concentration below 70% (and thus, increasing the surface tension and the wetting contact angle of the draining liquid with the capillary walls) leads to a periodic modulation of the granular interface height, and the formation of dunes along the tube, due to the capillary displacement of grains. Although we haven’t performed yet a stability analysis of such a complex three-phase situation of an air/liquid meniscus pushing a granular assembly, a full linear stability analysis has been done by Percier et al.44 for the development of ripples over granular surfaces under the action of rolling wheels. They “argued that the appearance of the ripples should be regarded as an instability of the flat road”. Thus, the analogy with our current system justifies to call the formation of dunes observed in our experiments as a capillary washboarding instablity. Finally, reducing further the isopropanol concentration leads to an increase of the dunes’ amplitude that may reach the system size (the top wall of the capillary tube), clogging it by forming granular plugs. Therefore, the granular plugs could be considered as diverging dunes.
Interestingly, a recent work has revealed an innovative strategy to control the mechanical properties of confined granular columns, using ferromagnetic particles submitted to a magnetic field, via the emergence of a “magnetic Janssen effect”.43 In the current framework, we could also take advantage of such magnetic control over frictional interactions to modify and tame the various drainage patterns observed here. Indeed, in preliminary experiments with ferromagnetic steel spheres much denser than the glass beads used in the present study, and eventually their mixture, we observe a transition between dunes and plugs at a far higher value of the initial height of the granular layer, as predicted by our Capillary bulldozing number. Furthermore, we could also remotely trigger the formation of plugs by applying an external magnetic field (in regions of the phase diagram for which C< 1). Such interesting observations highlight the robustness of our modelling and could be of of practical importance regarding the possibility to control this bulldozing instability.
Author contributions
All authors contributed to this work as a team effort. S. S., K. J. M. and M. B. designed the study. L. T. performed the experiments, wrote and ran the numerical simulations and the theoretical analysis, supervised by S. S., K. J. M., M. B. and E. F., S. S. and L. T. wrote the manuscript. All authors read critically and participate in the writing of the manuscript.Conflicts of interest
The authors declare no competing interests.Appendices
A. Preparation of the immersed granular layer
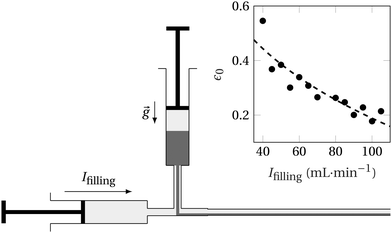
The preparation of the immersed granular bed with a controlled initial filling height fraction ε0 of the capillary tube is obtained thanks to the experimental set-up shown in Fig. (11). This setup involves two syringes: a horizontal one containing the liquid, and a vertical one filled with the grains immersed in the same liquid.Initially, the top syringe is opened, initiating a gravity-driven granular flow. Subsequently, the liquid is injected into the capillary tube at a constant flow rate Ifilling with the second syringe. The high injecting flow rate of several tens of mL min−1 allows to displace the grains, and actually governs the height of the particle layer at the bottom of the capillary tube, as shown in the inset of Fig. (11). One can predict in this specific geometry, the following dependency:  , with I* = 200 mL min−1. Following this procedure, the resulting granular layer has an initial height h = 2ε0R ± d, d being the grain diameter.
, with I* = 200 mL min−1. Following this procedure, the resulting granular layer has an initial height h = 2ε0R ± d, d being the grain diameter.
Comparing the mass of the capillary tube empty and filled with this initial layer, one can obtain a measurement of the granular packing fraction of ϕ = 0.60 ± 0.05, corresponding to a random close packing, in good agreement with ref. 30
B. Water–isopropanol solution properties
Using a drop shape analyser (Kruss DSA24E), we measured the properties (surface tension and contact wetting angle) of the water-isopropanol mixtures.For different weight concentration of isopropanol in the solution, noted 2-propanol % w/w, the shape of a pendant solution drop was fitted using Young–Laplace method. The experimental measurements are shown in Fig. (12c) and found in good agreement with ref. 39 The wetting contact angle was measured analysing the shape of a sessile drop of the solution in contact with a silanized glass plate. The experimental measurements are shown in Fig. (12d). The contact wetting angle drops from 90° for pure water (hydrophobic surface) to 0° for pure alcohol. We also notice a faster decrease of the wetting contact angle for 2-propanol % w/w ≥ 75.
C. Friction coefficient dependence on the angle of attack
As introduced by ref. 37,40,44 the drag and lift forces exerted by a pile of grains on a tilted pushing plane is strongly dependent on the angle of attack α. Both forces, represented in Fig. (13a), can be expressed as two friction forces of respective friction coefficient μD(α) and μL(α):| FD(α) = μD(α)Mg; FL(α) = μL(α)Mg, | (6) |
 . The experimental results from ref. 40 are shown in Fig. (13b). A strong increase of the friction coefficients μD(α) and μL(α) is observed when the angle of attack approaches zero. To compute the local frictional drag forces acting on the bulldozing meniscus in our numerical simulations, we extracted the evolution of μD(α) by fitting these experimental data with a power-law, giving:
. The experimental results from ref. 40 are shown in Fig. (13b). A strong increase of the friction coefficients μD(α) and μL(α) is observed when the angle of attack approaches zero. To compute the local frictional drag forces acting on the bulldozing meniscus in our numerical simulations, we extracted the evolution of μD(α) by fitting these experimental data with a power-law, giving:  .
.
 | ||
| Fig. 13 (a) Geometry of the pad pushed by a plate advancing at a constant velocity v with an angle of attack α. (b) Data from ref. 40. Friction coefficients of the drag FD and lift FL forces, fitted by two power laws (dashed lines). | ||
D. Young–Laplace relation
The pressure set by the top of the meniscus is given by the Young–Laplace relation in the considered 2D geometry shown in Fig. 14.The pressure difference on the top part of the meniscus above the advancing pile is given by ΔP = γ/r, where r is the radius of curvature of the meniscus. We assume that the meniscus is smooth (i.e. continuous derivative) at z = 2εR. This condition imposes that the local angle of the meniscus with the horizontal at this point is equal to the average angle of attack α. The top part of the meniscus however is making an angle ξ set by the wetting properties of the liquid with the surface of the capillary tube.
By simple geometry considerations, the angle β follows the relation β = π − ξ − α − β, leading to β = π/2 − (ξ + α)/2. Using the value of β, the arc length l and radius r follow the relation l = 2r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos((ξ + α)/2). The arc length is also related to the particles height following: sin(β + ξ) = cos((α − ξ)/2) = 2(1 − ε)R/l.
cos((ξ + α)/2). The arc length is also related to the particles height following: sin(β + ξ) = cos((α − ξ)/2) = 2(1 − ε)R/l.
Therefore, the radius of curvature of the meniscus is:
Acknowledgements
We thank N. Taberlet for the constructive discussion concerning the washboard instability. We thank the Research Council of Norway through its Centre of Excellence funding scheme, project no. 262644, the support of ENS de Lyon, and of the CNRS, through the French-Norwegian IRP, (D-FFRACT), and the support of the Engineering and Physical Sciences Research Council grant no. EP/S034587/1.Notes and references
- K. Alitalo, Nat. Med., 2011, 17, 1371 CrossRef CAS PubMed.
- L. E. Niklason and J. H. Lawson, Science, 2020, 370(6513), eaaw8682 CrossRef CAS PubMed.
- D. B. Camasão and D. Mantovani, Mater. Today Bio, 2021, 10, 100106 CrossRef PubMed.
- C. O’Connor, E. Brady, Y. Zheng, E. Moore and K. R. Stevens, Nat. Rev. Mater., 2022, 7, 702–716 CrossRef PubMed.
- F. J. Meigel and K. Alim, J. R. Soc., Interface, 2018, 15, 20180075 CrossRef PubMed.
- L. Ma, D. Ingham and M. Pourkashanian, Transport Phenomena in Porous Media III, Elsevier, 2005, pp. 418–440 Search PubMed.
- H. E. Huppert and J. A. Neufeld, Annu. Rev. Fluid Mech., 2014, 46, 255 CrossRef.
- T. Sparks and G. Chase, Filters and Filtration Handbook, 6th edn, Butterworth-Heinemann, 2016, ch. 4 Search PubMed.
- W. E. Dietrich and J. D. Smith, Water Resour. Res., 1984, 20, 1355 CrossRef.
- J. R. Landel and D. I. Wilson, Annu. Rev. Fluid Mech., 2021, 53, 147 CrossRef.
- P. E. Oren, J. Billiotte and W. V. Pinczewski, SPE Form. Evaluation, 1992, 7, 70 CrossRef CAS.
- U.S. Energy Information Administration, accessed: Jun. 2022.
- P. G. Saffman and G. Taylor, Proc. Math. Phys. Eng. Sci., 1958, 245, 312 CAS.
- D. Bensimon, L. Kadanoff, S. Liang, B. Shraiman and C. Tang, Rev. Mod. Phys., 1986, 58, 977 CrossRef.
- P. Garstecki, I. Gitlin, W. DiLuzio, G. M. Whitesides, E. Kumacheva and H. A. Stone, Appl. Phys. Lett., 2004, 85, 2649 CrossRef CAS.
- L. Shui, J. C. Eijkel and A. van den Berg, Adv. Colloid Interface Sci., 2007, 133, 35 CrossRef CAS PubMed.
- T. T. Al-Housseiny, P. A. Tsai and H. A. Stone, Nat. Phys., 2012, 8, 747 Search PubMed.
- K. J. Måløy, J. Feder and T. Jøssang, Phys. Rev. Lett., 1985, 55, 2688 CrossRef PubMed.
- G. M. Homsy, Annu. Rev. Fluid Mech., 1987, 19, 271 CrossRef.
- R. Lenormand, J. Condens. Matter Phys., 1990, 2, SA79 CrossRef.
- M. Sahimi, Rev. Mod. Phys., 1993, 65, 1393 CrossRef.
- E. Aker, K. J. Måløy, A. Hansen and G. G. Batrouni, Transp. Porous Media, 1997, 32, 163 CrossRef.
- M. Alava, M. Dubé and M. Rost, Adv. Phys., 2004, 53, 83 CrossRef CAS.
- S. Berg and H. Ott, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3755 CrossRef CAS PubMed.
- R. Holtzman and E. Segre, Phys. Rev. Lett., 2015, 115, 164501 CrossRef PubMed.
- J. Ortín and S. Santucci, Avalanches in Functional Materials and Geophysics, Springer, Cham, 2017, pp. 261–292 Search PubMed.
- B. Sandnes, H. A. Knudsen, K. J. Måløy and E. G. Flekkøy, Phys. Rev. Lett., 2007, 99, 038001 CrossRef CAS PubMed.
- B. Sandnes, E. G. Flekkøy, H. A. Knudsen, K. J. Måløy and H. See, Nat. Commun., 2011, 2, 038001 Search PubMed.
- B. Marks, B. Sandnes, G. Dumazer, J. A. Eriksen and K. J. Måløy, Front. Phys., 2015, 3, 1 Search PubMed.
- G. Dumazer, B. Sandnes, M. Ayaz, K. J. Måløy and E. G. Flekkøy, Phys. Rev. Lett., 2016, 117, 028002 CrossRef PubMed.
- G. Dumazer, B. Sandnes, K. J. Måløy and E. G. Flekkøy, Phys. Rev. Fluids, 2020, 5, 028002 Search PubMed.
- B. Sandnes, E. G. Flekkøy and K. J. Måløy, Eur. Phys. J.-Spec. Top., 2012, 204, 19 CrossRef CAS.
- C. Chevalier, A. Lindner and E. Clément, Phys. Rev. Lett., 2007, 99, 174501 CrossRef CAS PubMed.
- S. Li, J. S. Lowengrub, J. Fontana and P. Palffy-Muhoray, Phys. Rev. Lett., 2009, 102, 174501 CrossRef PubMed.
- H. A. Knudsen, B. Sandnes, E. G. Flekkøy and K. J. Måløy, Phys. Rev. E, 2020, 77, 021301 CrossRef.
- H. A. Janssen, Vereins Eutscher Ingenieure Zeitschrift, 1895, p. 1045 Search PubMed.
- N. Taberlet, S. W. Morris and J. N. McElwaine, Phys. Rev. Lett., 2007, 99, 068003 CrossRef PubMed.
- C. Buffone and K. Sefiane, Int. J. Multiphase Flow, 2004, 30(9), 1071–1091 CrossRef CAS.
- G. Vazquez, E. Alvarez and J. M. Navaza, J. Chem. Eng. Data, 1995, 40, 611 CrossRef CAS.
- B. Percier, S. Manneville, J. N. McElwaine, S. W. Morris and N. Taberlet, Phys. Rev. E, 2011, 84, 051302 CrossRef PubMed.
- H. A. Knudsen, B. Sandnes, E. G. Flekkøy and K. J. Måløy, AIP Conf. Proc., 2009, 1145, 1043 CrossRef.
- C. Li, T. Zhang and D. I. Goldman, Science, 2013, 339, 1408 CrossRef CAS PubMed.
- L. Thorens, K. J. Måløy, M. Bourgoin and S. Santucci, Nat. Commun., 2021, 12, 2486 CrossRef CAS PubMed.
- B. Percier, S. Manneville and N. Taberlet, Phys. Rev. E, 2013, 87, 12203 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00717k |
| This journal is © The Royal Society of Chemistry 2023 |






![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif)