Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of the heat transfer fluctuations in the Rayleigh–Bénard convection of concentrated emulsions with finite-size droplets†
Francesca
Pelusi
 *a,
Stefano
Ascione‡
b,
Mauro
Sbragaglia
c and
Massimo
Bernaschi
a
*a,
Stefano
Ascione‡
b,
Mauro
Sbragaglia
c and
Massimo
Bernaschi
a
aIstituto per le Applicazioni del Calcolo, CNR – Via dei Taurini 19, 00185 Rome, Italy. E-mail: f.pelusi@iac.cnr.it
bDepartment of Physics, Tor Vergata University of Rome – Via della Ricerca Scientifica 1, 00133 Rome, Italy
cDepartment of Physics & INFN, Tor Vergata University of Rome -, Via della Ricerca Scientifica 1, 00133 Rome, Italy
First published on 28th August 2023
Abstract
Employing numerical simulations, we provide an accurate insight into the heat transfer mechanism in the Rayleigh–Bénard convection of concentrated emulsions with finite-size droplets. We focus on the unsteady dynamics characterizing the thermal convection of these complex fluids close to the transition from conductive to convective states, where the heat transfer phenomenon, expressed in terms of the Nusselt number Nu, is characterized by pronounced fluctuations triggered by collective droplet motion [F. Pelusi et al., Soft Matter, 2021, 17(13), 3709–3721]. By systematically increasing the droplet concentration, we show how these fluctuations emerge along with the segregation of “extreme events” in the boundary layers, causing intermittent bursts in the heat flux fluctuations. Furthermore, we quantify the extension S and the duration  of the coherent droplet motion accompanying these extreme events via a suitable statistical analysis involving the droplet displacements. We show how the increase in droplet concentration results in a power-law behaviour of the probability distribution function of S and
of the coherent droplet motion accompanying these extreme events via a suitable statistical analysis involving the droplet displacements. We show how the increase in droplet concentration results in a power-law behaviour of the probability distribution function of S and  and how this outcome is robust at changing the analysis protocol. Our work offers a comprehensive picture, linking macroscopic heat transfer fluctuations with the statistics of droplets at the mesoscale.
and how this outcome is robust at changing the analysis protocol. Our work offers a comprehensive picture, linking macroscopic heat transfer fluctuations with the statistics of droplets at the mesoscale.
1. Introduction
Rayleigh–Bénard convection (RBC) is one of the most paradigmatic buoyancy-driven flows in fluid dynamics.1,2 It is observed whenever a fluid is placed between two plates under the influence of buoyancy forces, while being heated from below and cooled from above. The heat transfer properties are generally quantified in terms of the dimensionless Nusselt number Nu, expressing the importance of the convective transport in comparison to the conductive one.3–6 RBC plays an important role in a variety of fields, ranging from the atmosphere dynamics7–9 to the design of indoor environments,10,11 from the geophysical context12 to the metallurgical industry.13 From the theoretical side, RBC represents a fascinating problem that leads to the study of the instabilities and the transition from conductive to convective states, with the associated heat transfer properties, from the large scale down to the small ones. Different reviews have been written on the topic, covering experimental, numerical, and theoretical aspects.3–5,14RBC has been traditionally addressed in the context of single-phase fluids, but studies in recent years also investigated the importance of the multi-phase and/or multi-component nature of the convective fluids,15 since it can impact engineering technological applications, such as energy storage,16–18 petroleum industry,19,20 and liquid food processing.21,22 For example, RBC between two fluid layers has been studied, and numerical simulations helped in understanding the relationship between the heat transport efficiency and the properties of the two fluid layers, e.g., viscosity contrast, density contrast, and layers thickness.23–25 In the presence of multi-phase fluids, some studies also revealed enhanced heat transfer in comparison to the single-phase case, especially in proximity of the critical point, due to an increased occurrence of droplet condensation, or in the presence of the melting of a solid above a liquid melt.26,27 RBC laden with bubbles/droplets has also been numerically studied in recent works,4,28–33 showing how the heat transport properties can be affected by the presence of the dispersed phase,4,28–30 the surface wettability,32 the condensation conditions,31 and the presence of non-trivial correlations between distant droplets.33 Furthermore, experiments show that the introduction of a small percentage of a second component in a pure water solution is sufficient to affect the overall heat transfer.34,35
In the present paper, we focus on those situations where RBC laden with droplets is studied at increasing droplet concentration – i.e., concentrated emulsions – resulting in a non-Newtonian response of the fluid.36 The impact of non-Newtonian rheology itself has been studied in the framework of RBC for a while,37–48 while in a recent study33 some of the authors have highlighted the richness brought by the finite-size of the droplets, i.e., the situation where RBC takes place in a confined environment and the actual extension of the droplets cannot be neglected in comparison to the characteristic size of the confining channel (cf.Fig. 1(a)). Numerical simulations allowed tuning the droplet concentration, ranging from less concentrated Newtonian to more concentrated non-Newtonian emulsions, revealing that the increase in droplet concentration results in enhanced fluctuations in the heat transfer.33 Although these fluctuations may exhibit qualitative similarities with fluctuations triggered in homogeneous fluids under turbulent RBC,49,50 they have the peculiarity of emerging just above the transition from a conductive to a convection state, i.e., in a purely laminar regime. This evidence highlights the role played by finite-size droplets. Here we take a step forward and provide comprehensive characterization of the fluctuations. We first delve deeper into the connection between fluctuations at large scales and fluctuations at the droplet scales by systematically increasing the droplet concentration. The increase in droplet concentration reveals the emergence of “extreme” fluctuations that we characterize in terms of their spatial localization. The extreme fluctuations materialize in terms of collective droplet motion with a characteristic extension S and duration  . We therefore investigate the statistical properties of both S and
. We therefore investigate the statistical properties of both S and  following a well-established protocol based on the tracking of droplets displacement.51 This result is robust at changing analysis protocol.
following a well-established protocol based on the tracking of droplets displacement.51 This result is robust at changing analysis protocol.
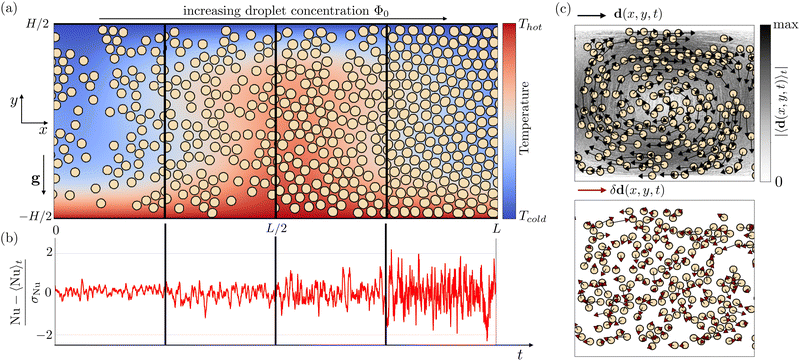 | ||
| Fig. 1 Panel (a): A sketch of the numerical setup. We investigate heat transfer fluctuations in a Rayleigh–Bénard cell with horizontal size L, where an emulsion is placed between a bottom hot and a top cold wall at a distance equal to H. In this setup, the emulsion dynamics is affected by the action of the gravity g and by the presence of a temperature field, which varies from Thot (red) to Tcold (blue), creating a temperature range ΔT = Thot − Tcold between the two walls. The numerical experiment is repeated at increasing droplet concentration Φ0, from a less concentrated (Φ0 = 0.27) to a more concentrated emulsion (Φ0 = 0.73). Panel (b): we study the heat transfer in terms of the dimensionless parameter Nu defined in eqn (1). Specifically, we are interested in fluctuations of Nu with respect to the averaged-in-time value 〈Nu〉t (here shown normalised to its standard deviation σNu), which are observed to increase at increasing Φ0. Panel (c): A sketch of the computation of the Eulerian displacement fluctuations δd(x,y,t) defined in eqn (4) (bottom panel, brown arrows) as the difference between the Eulerian droplet displacement d(x,y,t) (top panel, black arrows) and the absolute value of the averaged-in-time displacement field 〈d(x,y,t)〉t (top panel, colorbar). | ||
The rest of this paper is organized as follows: the numerical methodology along with the necessary theoretical tools of analysis are recalled in Section 2; a detailed characterization of the heat flux fluctuations, from “extreme events” localization to their statistical characterization, is provided in Section 3; conclusions will be drawn in Section 4.
2. Methods
Numerical simulations have been conducted with the open-source code TLBfind52 developed by some of the authors. TLBfind is a GPU code that implements a lattice Boltzmann model53,54 for non-ideal multi-component systems to simulate the thermal convection of a multi-component fluid made of immiscible non-coalescing droplets in a two-dimensional system. The multi-component fluid comprises two components with densities ρ1 and ρ2, respectively.§ Non-ideal interactions between the two components allow for phase separation and the formation of diffuse interfaces between regions with the majority of one of the two components, while additional competing interactions are considered to inhibit droplet coalescence. In TLBfind, the dynamics of the temperature field T(x,y,t) obeys the advection-diffusion equation,55 driven by the hydrodynamic fluid velocity. In turn, the two fluid components evolve following the Navier–Stokes equation with an additional buoyancy term introduced via the Boussinesq approximation56 implying a force term F = ραgT, where ρ = ρ1 + ρ2 is the total density, α is the thermal expansion coefficient and g is the gravity acceleration. Furthermore, TLBfind allows the choice of the system size L and H along the x- and y-directions, respectively, and the number of emulsion droplets Ndroplets (cf.Fig. 1(a)). The resulting droplet concentration Φ0 is defined as the fraction of domain size occupied by the dispersed phase, i.e., , where Θ is the Heaviside step function and ρ* is a reference density value (cf. ref. 33). Relevant equations on the employed thermal multi-component lattice Boltzmann model are provided in Section S1 of the ESI.†
, where Θ is the Heaviside step function and ρ* is a reference density value (cf. ref. 33). Relevant equations on the employed thermal multi-component lattice Boltzmann model are provided in Section S1 of the ESI.†
In this work, simulations have been performed on a domain of size H ∼ 40d and L ∼ 2H, where d is the average droplet diameter and it is fixed to 40 lattice spacing (Δx) for each simulated emulsion. Our choice of domain size allowed us to maintain consistency between simulations at different droplet concentrations. We explore emulsions with different Φ0 by varying Ndroplets, i.e., from less concentrated (Φ0 = 0.27, Ndroplets = 352) to more concentrated emulsions (Φ0 = 0.73, Ndroplets = 800). A detailed rheological characterization of the simulated emulsions is provided in Section S2 of the ESI.† In all simulations, density and viscosity ratios between dispersed and continuous phases are fixed to the unity. Furthermore, the capillary number (Ca) and Reynolds number (Re) are measured to be moderately small (Ca < 10−2, Re < 102).
We prepare monodisperse emulsions with a desired droplet concentration and we place them between two parallel plates located at y = ±H/2. In the proximity of these plates, both components feel the effect of no-slip velocity boundary conditions, while we linearly initialize the temperature field between the two walls by prescribing T(x,y = ±H/2,t) = ∓ΔT/2, resulting in a system heated from below and cooled from above.¶ Notice that, before applying the buoyancy term to the two fluid components dynamics, a “preparation” run is necessary to let the emulsion relax towards its equilibrium configuration. Intending to investigate the heat transfer properties of the emulsions in the framework described above, we introduce a macroscopic observable indicating the importance of convective transport, i.e., the dimensionless Nusselt number. This quantity is defined as3,5,57,58
 | (1) |
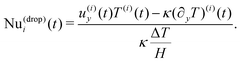 | (2) |
as the fluctuations of Nu(drop)i with respect to its averaged value 〈Nu(drop)〉 and normalized with respect to its standard deviation σNu:
 | (3) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + Yiŷ, we compute the vectorial displacement di(t). Then, starting from di(t), at any simulation time step, the corresponding Eulerian field d(x,y,t) is extracted.33 Finally, we compute the averaged-in-time displacement field 〈d(x,y,t)〉t and consider the fluctuations of d(x,y,t) with respect to it
+ Yiŷ, we compute the vectorial displacement di(t). Then, starting from di(t), at any simulation time step, the corresponding Eulerian field d(x,y,t) is extracted.33 Finally, we compute the averaged-in-time displacement field 〈d(x,y,t)〉t and consider the fluctuations of d(x,y,t) with respect to it| δd(x,y,t) = d(x,y,t) − 〈d(x,y,t)〉t. | (4) |
All the simulations have been conducted on GPUs (Tesla K80 and Quadro RTX 8000 GPUs), gathering data about tens of millions of droplets for each emulsion. In order to collect the same amount of data for all the concentrations, less concentrated emulsions require longer simulations due to the smaller number of droplets for each time step. In all cases, we exclude from the statistical analysis the initial, transient, period necessary to the development of the convective state.
3. Results and discussion
We first report on the statistical analysis of the droplet heat flux fluctuations defined in eqn (3). The aim is to extend and improve the preliminary results reported in ref. 33, which allowed to establish a link between the fluctuations on the macroscopic observable Nu shown in Fig. 1(b) and the statistics of heat transfer at the droplet scale. In ref. 33, only two “categories” of emulsions have been compared, i.e., a less concentrated Newtonian and a more concentrated non-Newtonian emulsion. Here a systematic characterization at increasing droplet concentration Φ0 is provided in order to delve deeper into the way heat flux fluctuations emerge, i.e., whether there is a sharp transition or a more continuous change. In Fig. 2, we show the probability distribution function (PDF) of the droplet-scale observable
defined in eqn (3). The aim is to extend and improve the preliminary results reported in ref. 33, which allowed to establish a link between the fluctuations on the macroscopic observable Nu shown in Fig. 1(b) and the statistics of heat transfer at the droplet scale. In ref. 33, only two “categories” of emulsions have been compared, i.e., a less concentrated Newtonian and a more concentrated non-Newtonian emulsion. Here a systematic characterization at increasing droplet concentration Φ0 is provided in order to delve deeper into the way heat flux fluctuations emerge, i.e., whether there is a sharp transition or a more continuous change. In Fig. 2, we show the probability distribution function (PDF) of the droplet-scale observable  for different droplet concentrations Φ0 (different symbols/colors). It is apparent that the larger Φ0, the more pronounced the PDF tails are. We also observe that these tails grow continuously upon increasing the droplet concentration. This trend is also confirmed by the inset of Fig. 2, reporting the values of σNu used to normalize the droplet Nusselt number fluctuations (cf.eqn (3)). It shows a non-monotonic behaviour, which may be due to statistical fluctuations, and an almost doubled standard deviation in the more concentrated case as compared to the less concentrated one. Moreover, for a more concentrated emulsion, the authors of ref. 33 showed that large fluctuations in the PDF of Nu*,(drop) are due to droplets localized in the boundary layers. Here we take a step forward in that starting from the PDF reported in Fig. 2 we report the spatial localization of the events that contribute to the PDF tails. Specifically, we compute the PDF of the y-coordinate of the droplet center-of-mass positions Y, by conditioning the statistics to a specific range of Nu*,(drop) in Fig. 2: from the entire positive (Nu*,(drop) > 0) and negative (Nu*,(drop) < 0) tails, to smaller portions of them (e.g., Nu*,(drop) > 4 and Nu*,(drop) < −2). Results are shown in Fig. 3, where an increasing Φ0 results in different line styles and colors and each panel refers to a different range of Nu*,(drop). Left panels ((a)–(c)–(e)–(g)) refer to data contributing to the negative tails, whereas right panels ((b)–(d)–(f)–(h)) refer to portions of positive tails. PDFs are close to being flat when considering all collected data (panels (a) and (b)), whereas the scenario changes when approaching the extreme tails. Any emulsion shows a common trend: droplets moving in the proximity of the center of the rolls, do not experience large velocities and follow the average-in-time flow, thus not contributing to large heat transfer fluctuations whereas only droplets which are close to the walls, and receive a boost from the upward or downward thermal plume, instantly experience a significant velocity, resulting in a shift of the peaks of PDF(Y) from the center of the Rayleigh–Bénard cell towards the boundary layers. This trend is exacerbated in the most concentrated cases, where droplets are highly packed and the free volume of each droplet, as well as their mobility, is, in general, very limited. In other words, the extreme heat transfer fluctuations observed especially in the case of more concentrated emulsions are localized close to the walls of the Rayleigh–Bénard cell. Finally, we can state that Fig. 3 is further confirmation of the continuous transition from less concentrated emulsions, exempted from heat flux fluctuations, to more concentrated emulsions, that accommodate anomalous heat flux fluctuations at the macro- as well as droplet- scales. Note that, in the case of Φ0 = 0.48, the PDF(Y) is slightly asymmetric for Nu*,(drop) > 4 because of the limited statistics. Moreover, since PDF(Nu*,(drop)) in Fig. 2 are asymmetric, then the shape of PDF(Y) for the case Nu*,(drop) < −2 is qualitatively similar to the one for Nu*,(drop) > 5 (data not shown). To enrich this result with information about the dynamics, we monitored the time evolution of
for different droplet concentrations Φ0 (different symbols/colors). It is apparent that the larger Φ0, the more pronounced the PDF tails are. We also observe that these tails grow continuously upon increasing the droplet concentration. This trend is also confirmed by the inset of Fig. 2, reporting the values of σNu used to normalize the droplet Nusselt number fluctuations (cf.eqn (3)). It shows a non-monotonic behaviour, which may be due to statistical fluctuations, and an almost doubled standard deviation in the more concentrated case as compared to the less concentrated one. Moreover, for a more concentrated emulsion, the authors of ref. 33 showed that large fluctuations in the PDF of Nu*,(drop) are due to droplets localized in the boundary layers. Here we take a step forward in that starting from the PDF reported in Fig. 2 we report the spatial localization of the events that contribute to the PDF tails. Specifically, we compute the PDF of the y-coordinate of the droplet center-of-mass positions Y, by conditioning the statistics to a specific range of Nu*,(drop) in Fig. 2: from the entire positive (Nu*,(drop) > 0) and negative (Nu*,(drop) < 0) tails, to smaller portions of them (e.g., Nu*,(drop) > 4 and Nu*,(drop) < −2). Results are shown in Fig. 3, where an increasing Φ0 results in different line styles and colors and each panel refers to a different range of Nu*,(drop). Left panels ((a)–(c)–(e)–(g)) refer to data contributing to the negative tails, whereas right panels ((b)–(d)–(f)–(h)) refer to portions of positive tails. PDFs are close to being flat when considering all collected data (panels (a) and (b)), whereas the scenario changes when approaching the extreme tails. Any emulsion shows a common trend: droplets moving in the proximity of the center of the rolls, do not experience large velocities and follow the average-in-time flow, thus not contributing to large heat transfer fluctuations whereas only droplets which are close to the walls, and receive a boost from the upward or downward thermal plume, instantly experience a significant velocity, resulting in a shift of the peaks of PDF(Y) from the center of the Rayleigh–Bénard cell towards the boundary layers. This trend is exacerbated in the most concentrated cases, where droplets are highly packed and the free volume of each droplet, as well as their mobility, is, in general, very limited. In other words, the extreme heat transfer fluctuations observed especially in the case of more concentrated emulsions are localized close to the walls of the Rayleigh–Bénard cell. Finally, we can state that Fig. 3 is further confirmation of the continuous transition from less concentrated emulsions, exempted from heat flux fluctuations, to more concentrated emulsions, that accommodate anomalous heat flux fluctuations at the macro- as well as droplet- scales. Note that, in the case of Φ0 = 0.48, the PDF(Y) is slightly asymmetric for Nu*,(drop) > 4 because of the limited statistics. Moreover, since PDF(Nu*,(drop)) in Fig. 2 are asymmetric, then the shape of PDF(Y) for the case Nu*,(drop) < −2 is qualitatively similar to the one for Nu*,(drop) > 5 (data not shown). To enrich this result with information about the dynamics, we monitored the time evolution of  and the corresponding Yi for a single droplet i randomly chosen among droplets moving closer to the walls (see Fig. 4). For the sake of readability, we show data for only three values of Φ0 (panel (a): Φ0 = 0.27, panel (b): Φ0 = 0.48, and panel (c): Φ0 = 0.73). From Fig. 4 it is clear that
and the corresponding Yi for a single droplet i randomly chosen among droplets moving closer to the walls (see Fig. 4). For the sake of readability, we show data for only three values of Φ0 (panel (a): Φ0 = 0.27, panel (b): Φ0 = 0.48, and panel (c): Φ0 = 0.73). From Fig. 4 it is clear that 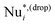 exhibits an intermittent behavior, more pronounced as the droplet concentration increases. It reveals a non-trivial correlation between “bursts” in the droplet heat transfer fluctuation and the spatial approach-to/departure-from a wall. Contrariwise, when the droplet “slips” close to the wall, i.e., in the periods where the signal of Yi is almost flat, the droplet does not contribute to an extreme event. In addition, Fig. 4 reveals that the oscillation period of Yi is dependent on the droplet concentration and it is not constant as expected for a homogeneous material. We interpret this finding as due to a droplet layer change by the drop under consideration, whose oscillation period around the center of the convective roll decreases as the droplet approaches it (see dotted lines outlining droplet layers). The droplet layer change is triggered by one or more collisions with the surrounding droplets, especially in the concentrated case where the droplet mobility is further reduced. This picture can be caught by the eye by watching the density map animations we include in Section S3 of the ESI† (Phi027.mp4, Phi048.mp4, and Phi073.mp4). Notice that in the less concentrated case the selected droplet rarely moves in the boundary layers, as already observed in Fig. 3.
exhibits an intermittent behavior, more pronounced as the droplet concentration increases. It reveals a non-trivial correlation between “bursts” in the droplet heat transfer fluctuation and the spatial approach-to/departure-from a wall. Contrariwise, when the droplet “slips” close to the wall, i.e., in the periods where the signal of Yi is almost flat, the droplet does not contribute to an extreme event. In addition, Fig. 4 reveals that the oscillation period of Yi is dependent on the droplet concentration and it is not constant as expected for a homogeneous material. We interpret this finding as due to a droplet layer change by the drop under consideration, whose oscillation period around the center of the convective roll decreases as the droplet approaches it (see dotted lines outlining droplet layers). The droplet layer change is triggered by one or more collisions with the surrounding droplets, especially in the concentrated case where the droplet mobility is further reduced. This picture can be caught by the eye by watching the density map animations we include in Section S3 of the ESI† (Phi027.mp4, Phi048.mp4, and Phi073.mp4). Notice that in the less concentrated case the selected droplet rarely moves in the boundary layers, as already observed in Fig. 3.
 | ||
Fig. 2 Probability distribution functions (PDFs) of the droplet-scale observable  , given in eqn (3). Different symbols/colors correspond to different droplet concentrations Φ0. Vertical dashed lines identify the thresholds of ranges of Nu*,(drop) considered in Fig. 3. In the inset we report the values of the standard deviation σNu of the droplet Nusselt number Nu(drop), appearing in eqn (3), as a function of Φ0. , given in eqn (3). Different symbols/colors correspond to different droplet concentrations Φ0. Vertical dashed lines identify the thresholds of ranges of Nu*,(drop) considered in Fig. 3. In the inset we report the values of the standard deviation σNu of the droplet Nusselt number Nu(drop), appearing in eqn (3), as a function of Φ0. | ||
 | ||
Fig. 4 Time evolution of  (solid red lines) and Yi (dashed black lines) of a selected droplet i, one for each considered droplet concentration Φ0 (panel (a): Φ0 = 0.27, panel (b): Φ0 = 0.48, and panel (c): Φ0 = 0.73). Time is shown in simulation units. Dotted gray lines outline the droplet layers. In Section S3 of the ESI† the reader can find the corresponding density map animations (Phi027.mp4, Phi048.mp4, and Phi073.mp4). (solid red lines) and Yi (dashed black lines) of a selected droplet i, one for each considered droplet concentration Φ0 (panel (a): Φ0 = 0.27, panel (b): Φ0 = 0.48, and panel (c): Φ0 = 0.73). Time is shown in simulation units. Dotted gray lines outline the droplet layers. In Section S3 of the ESI† the reader can find the corresponding density map animations (Phi027.mp4, Phi048.mp4, and Phi073.mp4). | ||
The observation of an intermittent behavior in the heat transfer and its fluctuations in RBC of concentrated emulsions naturally leads to asking whether these materials present a droplets collective motion in such a situation. To answer this question, we inspected the statistical properties of droplets coherent motion in terms of its spatial extension S and its temporal duration  following ref. 51. In the latter reference, the system was driven by coarsening dynamics, characterized by an averaged-in-time flow that is almost zero, and the authors employed a protocol based on the absolute value of the vectorial droplet displacement di(t) (cf.Fig. 1(c), black arrows). However, under RBC the system's dynamics exhibits an averaged-in-time flow characterized by the presence of convective rolls (cf.Fig. 1(c), colorbar), meaning that, to apply the same protocol, we need to subtract the mean flow and consider the vectorial droplet displacement fluctuation δd as the key observable (cf.eqn (4) and Fig. 1(c), brown arrows). As highlighted by Fig. 5(a), this observable exhibits a weak intensity in the less concentrated emulsion with no manifest coherence, while it is substantial in the more concentrated case, highlighting large regions of droplet coherent motion. Thus, in order to focus on extreme events, we select at any time step only the droplet with the largest absolute value of δd, obtaining an intermittent signal in the time of δdsup (cf.Fig. 5(b)). As the threshold value of δd to identify a droplets coherent motion, we take the knee value of the PDF of that observable (cf.Fig. 5(c)): whenever the signal of δdsup overcomes the threshold, we record a tstart as the beginning of the spatial coherence. Then, the first time t > tstart where δdsup returns below the threshold, we record its end (tend). We measure the spatial extension of the detected coherent motion S by summing up the area of droplets whose absolute value of δd is larger than the threshold value during its temporal duration, defined as
following ref. 51. In the latter reference, the system was driven by coarsening dynamics, characterized by an averaged-in-time flow that is almost zero, and the authors employed a protocol based on the absolute value of the vectorial droplet displacement di(t) (cf.Fig. 1(c), black arrows). However, under RBC the system's dynamics exhibits an averaged-in-time flow characterized by the presence of convective rolls (cf.Fig. 1(c), colorbar), meaning that, to apply the same protocol, we need to subtract the mean flow and consider the vectorial droplet displacement fluctuation δd as the key observable (cf.eqn (4) and Fig. 1(c), brown arrows). As highlighted by Fig. 5(a), this observable exhibits a weak intensity in the less concentrated emulsion with no manifest coherence, while it is substantial in the more concentrated case, highlighting large regions of droplet coherent motion. Thus, in order to focus on extreme events, we select at any time step only the droplet with the largest absolute value of δd, obtaining an intermittent signal in the time of δdsup (cf.Fig. 5(b)). As the threshold value of δd to identify a droplets coherent motion, we take the knee value of the PDF of that observable (cf.Fig. 5(c)): whenever the signal of δdsup overcomes the threshold, we record a tstart as the beginning of the spatial coherence. Then, the first time t > tstart where δdsup returns below the threshold, we record its end (tend). We measure the spatial extension of the detected coherent motion S by summing up the area of droplets whose absolute value of δd is larger than the threshold value during its temporal duration, defined as  . The statistics of S at varying droplet concentration Φ0 is reported in Fig. 6(a): it is evident how the extension of the PDF of S increases as the droplet concentration Φ0 increases, meaning that the spatial coherence develops in originally small regions which grow in extension with Φ0. However, only the most concentrated emulsion presents a robust power-law behavior that covers two decades, echoing observations on other systems presenting an avalanche-like behaviour.59–61 This result is further confirmed by analyzing the statistics of the temporal duration
. The statistics of S at varying droplet concentration Φ0 is reported in Fig. 6(a): it is evident how the extension of the PDF of S increases as the droplet concentration Φ0 increases, meaning that the spatial coherence develops in originally small regions which grow in extension with Φ0. However, only the most concentrated emulsion presents a robust power-law behavior that covers two decades, echoing observations on other systems presenting an avalanche-like behaviour.59–61 This result is further confirmed by analyzing the statistics of the temporal duration  (cf.Fig. 6(b)), where, once again, a power-law behavior is better visible in the case of the most concentrated emulsion. Both panels of Fig. 6 still confirm how the phenomenology changes in a continuous way from less to more concentrated emulsions. We remark that the PDF cut-off at large values of S and T arise because of system size, in agreement with ref. 51 and 62. In addition, since δd is not the only observable at the droplet-scale we can measure in our simulations, it is interesting to double-check whether the droplet-scale heat transfer fluctuation Nu*,(drop) is equally good at capturing the droplets coherent motion of emulsions under RBC. Fig. 7 provides the answer, showing the comparison of the PDF of spatial coherence S and duration
(cf.Fig. 6(b)), where, once again, a power-law behavior is better visible in the case of the most concentrated emulsion. Both panels of Fig. 6 still confirm how the phenomenology changes in a continuous way from less to more concentrated emulsions. We remark that the PDF cut-off at large values of S and T arise because of system size, in agreement with ref. 51 and 62. In addition, since δd is not the only observable at the droplet-scale we can measure in our simulations, it is interesting to double-check whether the droplet-scale heat transfer fluctuation Nu*,(drop) is equally good at capturing the droplets coherent motion of emulsions under RBC. Fig. 7 provides the answer, showing the comparison of the PDF of spatial coherence S and duration  for Φ0 = 0.73 between the protocol based on δd and the one based on
for Φ0 = 0.73 between the protocol based on δd and the one based on  , where the latter follows the same procedure mentioned for δd. The qualitative good overlap of the two PDFs is somehow expected but it contains multiple information: first, it confirms the strong correlation between bursts of heat transfer and displacement at the droplet scale; second, it also supports the idea of the emergence of “thermal avalanches” for the most packed systems and very close to the transition point between conduction and convection; then, it confirms that our analysis and simulations are realistic in reproducing the same qualitative results at changing the observable at the droplet scale.
, where the latter follows the same procedure mentioned for δd. The qualitative good overlap of the two PDFs is somehow expected but it contains multiple information: first, it confirms the strong correlation between bursts of heat transfer and displacement at the droplet scale; second, it also supports the idea of the emergence of “thermal avalanches” for the most packed systems and very close to the transition point between conduction and convection; then, it confirms that our analysis and simulations are realistic in reproducing the same qualitative results at changing the observable at the droplet scale.
4. Conclusions
We have used numerical simulations with the open source code TLBfind52 to study the statistical properties of heat flux fluctuations in concentrated emulsions under thermal convection, just above the transition from conductive to convective states. Numerical simulations have been helpful in providing a systematic analysis at varying droplet concentrations, ranging from less concentrated (showing small heat transfer fluctuations) to more concentrated emulsions (highlighting enhanced heat flux fluctuations). By systematically increasing the droplet concentration, we have observed evidence of a continuous transition that goes together with a continuous rise of the tails of the PDF of the droplet-scale observable Nu*,(drop) used to quantify the droplet heat transfer fluctuations. We have analyzed these extreme fluctuations, observing their strong correlation with the droplet spatial localization, resulting in an accumulation in the boundary layer region of droplets contributing to the extreme fluctuations. The physical effect hinges on the presence of finite-size droplets, which increase their contact as the droplet concentration increases but without merging via coalescence events. These “soft collisions” provoke the observed extreme heat transfer fluctuations and collective phenomena, such as the coherent droplets motion with a spatial extension S and with a characteristic temporal duration . A statistical analysis of both S and
. A statistical analysis of both S and 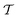 has been conducted, showing a neat power-law behavior when the emulsion is more concentrated. This result is found to be robust at changing the droplet-scale observable used to identify droplet coherent motion.
has been conducted, showing a neat power-law behavior when the emulsion is more concentrated. This result is found to be robust at changing the droplet-scale observable used to identify droplet coherent motion.
We remark that the observed findings of anomalous fluctuations have the peculiarity of emerging while the emulsion experiences a laminar regime. This is unexpected in homogeneous fluid dynamics, since they are observed appearing along with the onset of a turbulent regime.21,63–65 It is apparent that a more precise analysis would be needed for a real quantitative assessment. This prompts the need for a clearer comparison between the two dynamics (laminar emulsion vs. turbulent homogeneous fluid), which surely sets interesting future perspectives. Our findings also open new questions concerning other aspects that may affect the heat transfer properties in emulsion systems with finite-size droplets. For instance, it is not known so far if the heat flux fluctuations explored in this work can be more pronounced by changing from a two-dimensional to a three-dimensional system or by varying the number of convective rolls in the Rayleigh–Bénard cell. The role played by these fluctuations may also change as the Rayleigh number Ra = ραgΔTH3/(κη0) increases, assessing the regime that for Newtonian fluids is no longer laminar. Furthermore, an investigation into the effect of confinement may be useful to shed light on the characteristic domain size limit beyond which the observed extreme heat flux fluctuations disappear.
Author contributions
Francesca Pelusi: software, formal analysis, investigation, visualization, writing – original draft. Stefano Ascione: data curation, formal analysis, investigation, visualization, writing – reviewing and Editing. Mauro Sbragaglia: supervision, conceptualization, writing – reviewing and editing. Massimo Bernaschi: software, resources, supervision, writing – reviewing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We wish to acknowledge Fabio Bonaccorso for his support. MS and MB gratefully acknowledge CN1 – Centro Nazionale di Ricerca in High-Performance Computing Big Data and Quantum Computing – for support. This work received funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (grant agreement no. 882340).Notes and references
- H. Bénard, J. Phys. Theor. Appl., 1900, 11, 1261–1271 Search PubMed.
- L. Rayleigh, ondon, Edinburgh Dublin Philos. Mag. J. Sci., 1916, 32, 529–546 CrossRef.
- G. Ahlers, S. Grossmann and D. Lohse, Rev. Mod. Phys., 2009, 81, 503 CrossRef CAS.
- D. Lohse and K.-Q. Xia, Annu. Rev. Fluid Mech., 2010, 42, 335–364 CrossRef.
- F. Chillà and J. Schumacher, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–25 CrossRef PubMed.
- O. Shishkina, Phys. Rev. Fluids, 2021, 6, 090502 CrossRef.
- B. Stevens, Annu. Rev. Earth Planet. Sci., 2005, 33, 605–643 CrossRef CAS.
- D. Shipley, H. Weller, P. A. Clark and W. A. McIntyre, Q. J. R. Meteorol. Soc., 2022, 148, 351–377 CrossRef.
- J. Lin, T. Qian, P. Bechtold, G. Grell, G. J. Zhang, P. Zhu, S. R. Freitas, H. Barnes and J. Han, Atmos.-Ocean, 2022, 60, 422–476 CrossRef.
- D. Enescu, Renewable Sustainable Energy Rev., 2017, 79, 1353–1379 CrossRef.
- F. Xu, S. Xu, U. Passe and B. Ganapathysubramanian, Sustainable Energy Technologies and Assessments, 2021, 45, 101153 CrossRef.
- M. Le Bars and A. Davaille, J. Geophys. Res.: Solid Earth, 2004, 109, B03403 Search PubMed.
- D. M. Matson, Influence of Convection on Phase Selection, Springer, 2022, pp. 299–313 Search PubMed.
- M. Plumley and K. Julien, Earth and Space Science, 2019, 6, 1580–1592 CrossRef.
- X.-Q. Wang and A. S. Mujumdar, Int. J. Therm. Sci., 2007, 46, 1–19 CrossRef.
- A. Moradikazerouni, J. Energy Storage, 2022, 49, 104097 CrossRef.
- J. Du, Y. Gao, J. Wu, Z. Ge and X. Du, Appl. Therm. Eng., 2023, 219, 119470 CrossRef CAS.
- J. Zhang, G. Zhang, G. Cui, B. Dou, X. Yan, W. Lu and Q. Yang, Appl. Therm. Eng., 2023, 226, 120312 CrossRef CAS.
- K. Ghorayeb and A. Firoozabadi, Soc. Pet. Eng. J., 2000, 5, 158–171 Search PubMed.
- S. Gupta, R. Helmig and B. Wohlmuth, Comput. Geosci., 2015, 19, 1063–1088 CrossRef.
- J. Welti-Chanes, F. Vergara-Balderas and D. Bermúdez-Aguirre, J. Food Eng., 2005, 67, 113–128 CrossRef.
- N. Moraga, A. Torres, A. Guarda and M. J. Galotto, J. Food Process Eng., 2011, 34, 2000–2025 CrossRef.
- M. Yoshida and Y. Hamano, Phys. Fluids, 2016, 28, 116601 CrossRef.
- H.-R. Liu, K. L. Chong, Q. Wang, C. S. Ng, R. Verzicco and D. Lohse, J. Fluid Mech., 2021, 913, A9 CrossRef CAS.
- H.-R. Liu, K. L. Chong, R. Yang, R. Verzicco and D. Lohse, J. Fluid Mech., 2022, 938, A31 CrossRef CAS.
- J.-Q. Zhong, D. Funfschilling and G. Ahlers, Phys. Rev. Lett., 2009, 102, 124501 CrossRef PubMed.
- R. Yang, C. J. Howland, H.-R. Liu, R. Verzicco and D. Lohse, J. Fluid Mech., 2023, 956, A23 CrossRef CAS.
- P. Oresta, R. Verzicco, D. Lohse and A. Prosperetti, Phys. Rev. E, 2009, 80, 026304 CrossRef PubMed.
- R. Lakkaraju, R. J. A. M. Stevens, P. Oresta, R. Verzicco, D. Lohse and A. Prosperetti, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9237–9242 CrossRef CAS PubMed.
- L. Biferale, P. Perlekar, M. Sbragaglia and F. Toschi, Phys. Rev. Lett., 2012, 108, 104502 CrossRef CAS PubMed.
- M. Li, Y. Zhang, H. Liu, Y. Wang and B. Yang, Phys. Fluids, 2021, 33, 012109 CrossRef CAS.
- H.-R. Liu, K. L. Chong, C. S. Ng, R. Verzicco and D. Lohse, J. Fluid Mech., 2022, 933, R1 CrossRef CAS.
- F. Pelusi, M. Sbragaglia, R. Benzi, A. Scagliarini, M. Bernaschi and S. Succi, Soft Matter, 2021, 17, 3709–3721 RSC.
- Z. Wang, V. Mathai and C. Sun, Nat. Commun., 2019, 10, 3333 CrossRef PubMed.
- Z. Wang, V. Mathai and C. Sun, Int. J. Heat Mass Transfer, 2020, 152, 119515 CrossRef.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- J. Zhang, D. Vola and I. A. Frigaard, J. Fluid Mech., 2006, 566, 389–419 CrossRef CAS.
- N. J. Balmforth and A. C. Rust, J. Non-Newtonian Fluid Mech., 2009, 158, 36–45 CrossRef CAS.
- A. Vikhansky, Phys. Fluids, 2009, 21, 103103 CrossRef.
- A. Vikhansky, J. Non-Newtonian Fluid Mech., 2010, 165, 1713–1716 CrossRef CAS.
- B. Albaalbaki and R. E. Khayat, J. Fluid Mech., 2011, 668, 500–550 CrossRef.
- O. Turan, N. Chakraborty and R. J. Poole, J. Non-Newtonian Fluid Mech., 2012, 171–172, 83–96 CrossRef CAS.
- A. Davaille, B. Gueslin, A. Massmeyer and E. Di Giuseppe, J. Non-Newtonian Fluid Mech., 2013, 193, 144–153 CrossRef CAS.
- A. Massmeyer, E. Di Giuseppe, A. Davaille, T. Rolf and P. J. Tackley, J. Non-Newtonian Fluid Mech., 2013, 195, 32–45 CrossRef CAS.
- Z. Kebiche, C. Castelain and T. Burghelea, J. Non-Newtonian Fluid Mech., 2014, 203, 9–23 CrossRef CAS.
- N. J. Balmforth, I. A. Frigaard and G. Ovarlez, Annu. Rev. Fluid Mech., 2014, 46, 121–146 CrossRef.
- M. Hassan, M. Pathak and M. K. Khan, J. Non-Newtonian Fluid Mech., 2015, 226, 32–45 CrossRef CAS.
- I. Karimfazli, I. Frigaard and A. Wachs, J. Fluid Mech., 2016, 787, 474–507 CrossRef CAS.
- S. Aumatre and S. Fauve, Europhys. Lett., 2003, 62, 822 CrossRef.
- V. Labarre, S. Fauve and S. Chibbaro, Phys. Rev. Fluids, 2023, 8, 053501 CrossRef.
- F. Pelusi, M. Sbragaglia and R. Benzi, Soft Matter, 2019, 15, 4518–4524 RSC.
- F. Pelusi, M. Lulli, M. Sbragaglia and M. Bernaschi, Comput. Phys. Commun., 2022, 273, 108259 CrossRef CAS.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method, Springer International Publishing, 2017, vol. 10, pp. 4–15 Search PubMed.
- S. Succi, The lattice Boltzmann Equation, Oxford University Press, 2018 Search PubMed.
- S. Chandrasekhar, Hydrodynamic and hydromagnetic stability, Oxford University Press, 1961 Search PubMed.
- E. A. Spiegel and G. Veronis, Astrophys. J., 1960, 131, 442 CrossRef.
- B. I. Shraiman and E. D. Siggia, Phys. Rev. A, 1990, 42, 3650 CrossRef PubMed.
- R. J. Stevens, R. Verzicco and D. Lohse, J. Fluid Mech., 2010, 643, 495–507 CrossRef.
- H. Barkhausen, Z. Phys., 1917, 20, 401–403 Search PubMed.
- A. Ruina, J. Geophys. Res.: Solid Earth, 1983, 88, 10359–10370 CrossRef.
- D. Bonamy, S. Santucci and L. Ponson, Phys. Rev. Lett., 2008, 101, 045501 CrossRef CAS PubMed.
- P. Leishangthem, A. D. Parmar and S. Sastry, Nat. Commun., 2017, 8, 14653 CrossRef PubMed.
- X.-D. Shang, P. Tong and K.-Q. Xia, Phys. Rev. E, 2005, 72, 015301 CrossRef PubMed.
- J. D. Scheel and J. Schumacher, J. Fluid Mech., 2014, 758, 344–373 CrossRef CAS.
- F. Zonta and S. Chibbaro, Europhys. Lett., 2016, 114, 50011 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Rheological characterisation of simulated emulsions; and movies showing the time evolution of density maps of droplets shown in Fig. 4. See DOI: https://doi.org/10.1039/d3sm00716b |
| ‡ Current address: Department of Geosciences, Université de Rennes, 263 avenue Général Leclerc, 35000 Rennes, France. |
| § Note that hereafter we use the convention of considering the first component as the one associated with the dispersed phase. |
| ¶ The value of ΔT = Thot − Tcold (cf.Fig. 1(a)) is fixed in all simulations. |
| This journal is © The Royal Society of Chemistry 2023 |