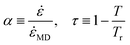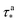Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simple and convenient mapping of molecular dynamics mechanical property predictions of bisphenol-F epoxy for strain rate, temperature, and degree of cure†
Sagar U.
Patil
 a,
Aaron S.
Krieg
a,
Aaron S.
Krieg
 a,
Leif K.
Odegard
a,
Upendra
Yadav
a,
Julia A.
King
a,
Marianna
Maiaru
b and
Gregory M.
Odegard
a,
Leif K.
Odegard
a,
Upendra
Yadav
a,
Julia A.
King
a,
Marianna
Maiaru
b and
Gregory M.
Odegard
 *a
*a
aMichigan Technological University, Houghton, MI-49931, USA. E-mail: gmodegar@mtu.edu
bUniversity of Massachusetts, Lowell, MA-01854, USA
First published on 25th August 2023
Abstract
It is well-known that all-atom molecular dynamics (MD) predictions of mechanical properties of thermoset resins suffer from multiple accuracy issues associated with their viscoelastic nature. The nanosecond simulation times of MD simulations do not allow for the direct simulation of the molecular conformational relaxations that occur under laboratory time scales. This adversely affects the prediction of mechanical properties at realistic strain rates, intermediate degrees of cure, and elevated temperatures. While some recent studies have utilized a time-temperature superposition approach to relate MD predictions to expected laboratory observations, such an approach becomes prohibitively difficult when simulating thermosets with a combination of strain rates, intermediate degrees of cure, and temperatures. In this study, a phenomenological approach is developed to map the predictions of Young's modulus and Poisson's ratio for a DGEBF/DETDA epoxy system to the corresponding laboratory-based properties for intermediate degrees of cure and temperatures above and below the glass transition temperature. The approach uses characterization data from dynamical mechanical analysis temperature sweep experiments. The mathematical formulation and experimental characterization of the mapping is described, and the resulting mapping of computationally-predicted to experimentally-observed elastic properties for various degrees of cure and temperatures are demonstrated and validated. This mapping is particularly important to mitigate the strain-rate effect associated with MD predictions, as well as to accurately predict mechanical properties at elevated temperatures and intermediate degrees of cure to facilitate accurate and efficient composite material process modeling.
1. Introduction
Thermosetting polymer composites are extensively used in the aerospace industry because of their relatively low mass density and unique combination of mechanical, thermal, and electrical properties. Computationally-driven design of new generations of thermoset composites for improved performance requires multiscale modeling techniques that are powerful and reliable. Such multiscale modeling must be able to incorporate molecular-scale structure for the prediction of structural-level properties. In particular, molecular dynamics (MD) methods need to be developed that can efficiently predict accurate properties of thermoset neat resins as input into higher-length scale modeling techniques.Thermoset neat resins consist of a complex network of covalently-linked molecular segments. Generally, for a given state of external conditions (e.g. temperature, mechanical deformation) these segments change their conformation to reach a state of lower energy (relaxation), which ultimately manifests itself as the phenomena known as physical aging and viscoelasticity.1 These relaxation processes can occur over a wide range of time periods spanning nanoseconds to years, but a significant portion of them occur over timescales associated with composite laminate processing and laboratory mechanical testing. Although all-atom MD simulations have been used over the last several decades to predict molecular structure and nano-scale properties of thermoset resins,2–16 these simulations can only capture the thermoset network response over a nanosecond time scale, creating a significant discrepancy between simulated and laboratory timescales. Although coarse-grain simulation techniques17–21 can be used to somewhat avert the time scale limitation over a broad range of frequencies, atomistic details often play a more significant role at higher frequencies.
Because of the timescale discrepancy between the conformational response on laboratory and MD-based timescales, all-atom MD predictions cannot precisely capture the relaxation processes that occur over time increments above nanoseconds. This shortcoming manifests itself in three major ways. First, MD predictions of fully crosslinked thermosets slightly overestimate the room-temperature elastic properties and yield strength.7,8,15 This is commonly referred to as the “strain rate effect”. Second, MD predictions of mechanical properties above the glass transition temperature (Tg) significantly overestimate experimental observations. Whereas the measurements indicate a multiple order-of-magnitude drop in elastic modulus relative to room temperature,22 simulations predict only about a 50% drop.22 Third, MD predictions of partially-crosslinked epoxies indicate a steady increase in elastic modulus over the entire range of degrees of cure,15 whereas experiments show a negligible modulus for all levels of crosslinking below the nearly fully-crosslinked state.15,22 These three manifestations of the viscous response have the same origin. During simulated mechanical deformations, conformational relaxation processes are not given sufficient time to occur, and thus the associated energy relaxation does not occur, resulting in a stiffer apparent structural response of the network. That is, quantities such as shear modulus and Young's modulus are overpredicted relative to their experimentally-measured values. Decreases in the degree of cure and increases in temperature exaggerate this effect, as they increase the viscous response of the material.
Multiple methods have been proposed to account for the predicted modulus discrepancy in fully crosslinked systems at room temperature.23–27 However, a convenient and comprehensive approach that accounts for the viscous response of thermosets in MD predictions of mechanical properties for various levels of strain rates, temperatures, and degrees of cure has not been established. Such a method should have three minimum requirements. First, the method should involve minimal MD simulations. One approach to capturing the viscoelastic effect of polymers in MD predictions is to use a time-temperature superposition principle.10,25–29 Approaches like this require significant computational resources to fully characterize each polymer system considered, especially for multiple degrees of cure. In a materials engineering environment where computational material design and process optimization need to be performed as efficiently as possible, a full MD-based characterization of the time-temperature superposition is not feasible and does not directly address the dependency of degree of cure on the viscous response. Also, it is important to note that the time-temperature superposition principle can sometimes fail for some polymer systems30,31 and is thus not a comprehensive solution.
Second, the method should require minimal experimental input (although no experimental input is ultimately desired). Bulk-level characterization of the material response as a function of strain rate, temperature, and degree of cure can be performed by experiment. However, such an approach is prohibitively time-consuming and expensive for most composite material development applications and does not capture molecular-scale events and the bulk behavior at relatively high strain rates. Third, the method should directly address all three of the above-mentioned manifestations of the viscous response of thermosets.
In this work, a comprehensive approach satisfying all the above-mentioned criteria to establish a phenomenological viscous response mapping factor is proposed for correlating elastic properties predicted with all-atom MD simulations to those expected at laboratory-scale timeframes. In addition, experimental characterization of thermal and mechanical properties of epoxy for different mixing ratios to efficiently emulate a range of degrees of cure32,33 is performed to inform the mapping procedure. It is important to emphasize that this approach is phenomenological and is designed to be parameterized by a convenient set of experiments to quickly map MD predictions for rapid computationally-driven thermoset material design. It is not intended to be a comprehensive viscoelastic characterization of a resin via classical viscoelastic constitutive modeling.34,35 This article is organized as follows: first the methodology to establish the viscous response mapping is introduced, followed by a description of the experimental methods used to characterize the mapping. The parameterization and optimization of the mapping is then described, and results of the modeling with the mapping technique follow. The results show that the proposed approach effectively provides an accurate mapping for MD predicted Young's moduli of thermosets to capture the effects of strain rate, temperature, and degree of cure.
The significance of this work is that, for the first time, a relatively simple and efficient modeling approach has been developed that maps elastic properties predicted from MD simulations (which are naturally over-predictive because of the simulated high strain rates) to those that would be expected if MD could be run at times scales associated with experimental measurements of elastic properties (seconds, minutes, hours, etc.). The proposed mapping approach does not require rigorous time-temperature superposition relationships (which are difficult and time-consuming to establish), and thus provides efficient corrections to MD-predicted elastic properties that can be immediately utilized in multi-scale, computationally-driven material and structural design.
2. Viscous correction
Using an approach inspired by the Buckingham π theorem,36 the viscous response can be expressed in terms of a minimal set of dimensionless parameters. It is first assumed that a laboratory-scale mechanical property (specifically, the Young's modulus in this case) can be related to its MD-predicted value by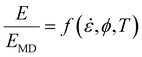 | (1) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is the strain rate, ϕ is the degree of cure, T is the temperature, E is the laboratory-scale Young's modulus, and EMD is the all-atom MD-predicted Young's modulus in the fully crosslinked system at room temperature and MD-scale strain rates. The function f is thus limited to the range of 0 ≤ f ≤ 1. The degree of cure is a dimensionless parameter valued between 0 (completely uncured) and 1 (fully cured). It is important at this point to discuss the assumptions associated with eqn (1). It is assumed that as strain rates decrease towards laboratory-based strain rates and the degree of cure approaches the maximum value of 1, the MD-predicted modulus approaches the value that is experimentally-measured at the corresponding temperature. If MD simulations could be run long enough (or fast enough), then EMD would naturally approach E, however, currently this is not feasible. Of course, for very long simulation times, EMD will only approach E if the simulation also accurately captures topological features such as porosity, chain/network morphology, etc. Additionally, EMD can only approach E if the molecular-level interactions are accurately captured with an appropriate force field. For example, the Interface Force Field (IFF)37 has been shown to accurately capture bulk physical, mechanical, and thermal properties of thermosets7,38 and thermoplastics.39
is the strain rate, ϕ is the degree of cure, T is the temperature, E is the laboratory-scale Young's modulus, and EMD is the all-atom MD-predicted Young's modulus in the fully crosslinked system at room temperature and MD-scale strain rates. The function f is thus limited to the range of 0 ≤ f ≤ 1. The degree of cure is a dimensionless parameter valued between 0 (completely uncured) and 1 (fully cured). It is important at this point to discuss the assumptions associated with eqn (1). It is assumed that as strain rates decrease towards laboratory-based strain rates and the degree of cure approaches the maximum value of 1, the MD-predicted modulus approaches the value that is experimentally-measured at the corresponding temperature. If MD simulations could be run long enough (or fast enough), then EMD would naturally approach E, however, currently this is not feasible. Of course, for very long simulation times, EMD will only approach E if the simulation also accurately captures topological features such as porosity, chain/network morphology, etc. Additionally, EMD can only approach E if the molecular-level interactions are accurately captured with an appropriate force field. For example, the Interface Force Field (IFF)37 has been shown to accurately capture bulk physical, mechanical, and thermal properties of thermosets7,38 and thermoplastics.39
Dimensionless parameters can now be introduced such that this formulation is independent of units and contains functions with direct proportionality with the dependent variable (modulus ratio). Specifically, the following dimensionless variables are defined:
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) MD is the strain rate associated with MD time scales (for example, 1 × 108 s−1); Tr is the reference temperature, which should be the highest temperature for which experimental Young's modulus data is available, and herein will be assigned as the processing temperature of the thermoset resin; and T and Tr are expressed in degrees Kelvin. Thus, α and τ are dimensionless scalars that are valued between 0 and 1. Eqn (1) can be re-written in terms of the dimensionless parameters
MD is the strain rate associated with MD time scales (for example, 1 × 108 s−1); Tr is the reference temperature, which should be the highest temperature for which experimental Young's modulus data is available, and herein will be assigned as the processing temperature of the thermoset resin; and T and Tr are expressed in degrees Kelvin. Thus, α and τ are dimensionless scalars that are valued between 0 and 1. Eqn (1) can be re-written in terms of the dimensionless parameters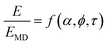 | (2) |
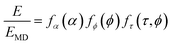 | (3) |
There is one other important point to discuss in terms of eqn (3). The intent of eqn (3) is not to reproduce the rigorous mapping associated with the time-temperature superposition principle. If the full time-temperature superposition principle was comprehensively known a priori for thermoset systems for which it is valid, then the approach discussed herein would not be necessary. For polymer systems in which the time-temperature superposition principle fails, there is no clear alternative predictive approach. Either way, eqn (3) provides an efficient means to map raw MD-predicted properties to the corresponding properties that would be expected at laboratory time scales and temperatures. This is important in computationally-driven materials discovery, developing digital twins, and integrated computational materials engineering; in which material discovery and development needs to be performed efficiently and within the context of higher-length scale modeling. It is important to note that machine learning can be utilized to characterize eqn (2) directly. However, for such analyses, abundant well-curated data is necessary, as previously shown for other computational-based composites research.41 For this study, eqn (3) was utilized because sufficient data was not available for a rigorous machine-learning parameterization.
3. Material
The chosen material for the parameterization of eqn (3) is an epoxy system consisting of a diglycidyl ether bisphenol F (DGEBF) epoxide monomer with a diethyltoluenediamine (DETDA) curing agent, as shown in Fig. 1. These materials are commonly marketed as EPON 862 and EPIKURE W, respectively. This system was chosen because it is highly benchmarked and represents a baseline high-performance thermoset.4. Experimental details
This section describes the details of the experiments performed to parameterize eqn (3). The experiments were performed on the DGEBF/DETDA epoxy system with a range of mixing ratios as proxies to various degrees of cure.32,33 The use of these proxies was necessary because of the high level of difficulty of testing thermal properties of thermoset systems as a function of degree of cure. Although it is acknowledged that the use of off-stoichiometry systems is not a direct substitute for fully stoichiometric systems with intermediate degrees of cure, the proxies provide a reasonable substitute that is relatively easy to fabricate and test. It is also important to note that the parameterization of eqn (3) is based purely on experimental data, not on MD-generated data.Epoxy samples were manufactured using a compression molding method. A total of two speedmixer cups were each charged with 50 g of DGEBF epoxy resin and an appropriate amount of DETDA curing agent to achieve systems with seven different mixing ratios of resin and hardener (Table 1). The mixing ratio is defined as the ratio of the mass of the actual DETDA hardener with respect to the mass of the DETDA hardener in the fully stoichiometric mixture. Speedmixer cups were mixed in a FlackTek Speedmixer (DAC 150.1 FVZ) at 2000 rpm for 5 minutes at 25 °C and then heated to 90 °C in a vacuum oven. The speedmixer cups were degassed in the vacuum oven at 90 °C for 30 minutes at 0.101 MPa vacuum pressure. The resin system was cast into a tooling assembly and compression molded at 121 °C for 2 hours and then ramped to 177 °C and held for 2 hours. The compression molder was cooled using air and water until the system was cooled to 150 °C and then was switched to water cooling only to continue cooling the system to 25 °C before removing the plate. The tooling assembly produced 152.4 × 152.4 mm plates with 3.2 mm thickness.
| Mixing ratio (%) | DGEBF (g) | DETDA (g) |
|---|---|---|
| 100 | 100 | 26.4 |
| 95 | 100 | 25.1 |
| 85 | 100 | 22.4 |
| 75 | 100 | 19.8 |
| 65 | 100 | 17.2 |
| 55 | 100 | 14.5 |
| 45 | 100 | 11.9 |
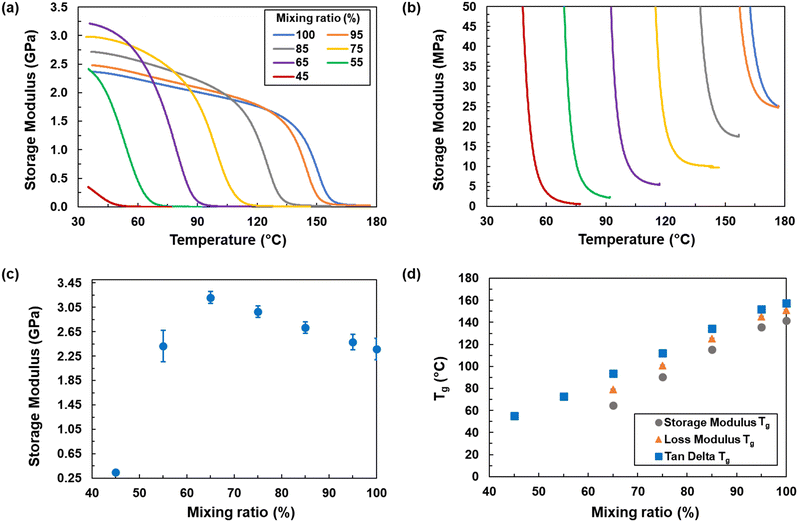
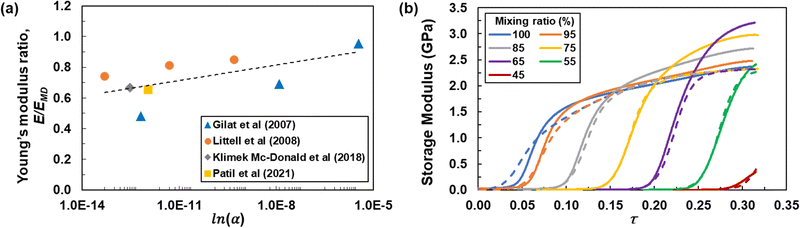
Dynamic mechanical analysis (DMA) was used to determine the thermo-mechanical response of the epoxy as a function of temperature and degree of cure. The testing was performed for all mixing ratios shown in Table 1 to approximate the corresponding degrees of cure. The DMA specimens were cut from fabricated plates using a vertical bandsaw. Three specimens were tested for each mixing ratio. The specimens were 38.1 mm long, 12.7 mm wide, and 3.2 mm thick and the tests were performed using a TA Instruments Q800 DMA in single cantilever test mode with a constant frequency of 1 Hz, an amplitude of 25 μm, and a ramp rate of 3 °C min−1. For this study, constant frequency of 1 Hz was utilized, as varying frequencies have shown no significant effect on the storage moduli measured using DMA tests of high-performance resins.42 The storage modulus, loss modulus, and tan delta values were continuously monitored during the temperature sweep. The storage modulus for all of the mixing ratios is shown in Fig. 2a for the whole range of temperatures. From this data, it is evident that the transition from glassy to rubbery states occurs at decreasing temperatures with decreasing levels of DETDA (thus degree of cure).
Fig. 2b shows the same data as Fig. 2a, but with the vertical axis scale focused on small values of storage modulus. The purpose of this graph is to show the details of the storage modulus curves above Tg for each mixing ratio. Even the post-Tg curves in Fig. 2a appear to drop to zero, Fig. 2b shows that they are not zero-valued above Tg, they are 2–3 orders of magnitude smaller than their respective values below Tg.
Fig. 2c shows the storage modulus as a function of mixing ratio at room temperature. It can be seen from the plot that the storage modulus gradually increases from the fully stoichiometric level with decreasing mixing ratios until 65%. This is likely because of increasing levels of mass density of the proxy systems as DETDA monomers are removed. Fully stoichiometric systems with intermediate degrees of cure are not expected to exhibit this behavior, and this is the primary disadvantage of using proxy systems. However, as described below, this behavior did not affect the viscous response parameterization, and the advantages of using proxy systems for the purposes of this study far outweigh this disadvantage. In Fig. 2c, it is also observed that as the mixing ratio decreases below 65%, the storage modulus drastically decreases as the sparse network can no longer sustain significant mechanical loads.
The Tg was determined using three different metrics: storage modulus, loss modulus, and tan delta. To determine the Tg using the storage modulus, the onset of the decline in storage modulus was located by finding the intersection between the baseline and the tangent at the point of the highest slope. The Tg values for the loss modulus and tan delta metrics were determined from the peak of the loss modulus and tan delta curves, respectively. Fig. 2d shows the Tg values as a function of mixing ratio using all three metrics. It is clear that the Tg trends from the three metrics are very similar with mixing ratio, with only a difference in the magnitude. From Fig. 2(c) and (d), no significant deviation in the measured storage modulus and Tg was observed between the three specimens. For storage modulus and Tg (all three metrics) the standard deviations are within 3% and 1% respectively.
5. Viscous mapping parameterization
The specific forms of functions in eqn (3) and the corresponding phenomenological parameters for the DGEBF/DETDA system were determined as described in this section. First, the specific forms of the functions and the initial guesses of the parameters are outlined, followed by a description of the parameter optimization using the Newton–Raphson43 iterative numerical technique.5.1 Functional forms, parameters, and initial guesses
It has been demonstrated6,7,9 that the DGEBF/DETDA system shows a logarithmic dependance of elastic modulus and yield strength on strain rate over a range of strain rates spanning experimental timescales (10−5 s−1) to those associated with MD simulations (109 s−1) for fully crosslinked systems at room temperature. Therefore, f(α) can be expressed asfα(α) = αa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(α) + αb ln(α) + αb | (4) |
 | ||
| Fig. 3 (a) Normalized Young's modulus of DGEBF/DETDA epoxy as a function of applied normalized strain rate determined experimentally, (b) plot of storage modulus vs. τ. Solid lines are data from the DMA experiments, and dashed lines are from eqn (3)–(8) with the optimized parameters from Table 2. | ||
As shown in Fig. 2c, the storage modulus exhibits a sigmoid-type response as a function of degree of cure. Thus, a logical choice for the fϕ(ϕ) functional form is a Fermi–Dirac function,47 whose value ranges between 0 and 1 and describes a continuous, yet step-like change from 0 to 1 centered at ϕ0 with a step change intensity described by ϕσ:
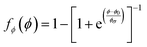 | (5) |
From the data shown in Fig. 2a, it is clear that the modulus exhibits a sigmoid-type response with respect to temperature. Furthermore, it is evident that this temperature response is dependent on the degree of cure of the thermoset. Therefore, a functional form of f(τ,ϕ) that captures this dependance is
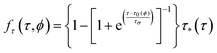 | (6) |
| τ0(ϕ) = τa0ϕ + τb0 | (7) |
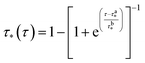 | (8) |
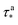 and
and 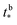 are dimensionless phenomenological parameters. The parameters in eqn (6)–(8) were determined using the DMA data shown in Fig. 2a. The same data is plotted in Fig. 3bversus τ for all mixing ratios. The parameters τa0 and τb0 were determined by locating the sigmoid centers of the data in Fig. 3b for the different degrees of cure and fitting those values to the linear function shown in eqn (7). The best-fit values were τa0 = −0.4712 and τb0 = 0.5268. It is important to note that eqn (6) predicts values that quickly approach zero as the temperature increases through Tg. Fig. 2b shows that experimental values of modulus above Tg are not zero-valued, but are 2–3 orders of magnitude smaller than the values below Tg. Thus, eqn (6) is only an approximation for temperatures above Tg, but is sufficiently accurate for the purposes of predicting the relative elastic response of the polymer over the entire temperature range.
are dimensionless phenomenological parameters. The parameters in eqn (6)–(8) were determined using the DMA data shown in Fig. 2a. The same data is plotted in Fig. 3bversus τ for all mixing ratios. The parameters τa0 and τb0 were determined by locating the sigmoid centers of the data in Fig. 3b for the different degrees of cure and fitting those values to the linear function shown in eqn (7). The best-fit values were τa0 = −0.4712 and τb0 = 0.5268. It is important to note that eqn (6) predicts values that quickly approach zero as the temperature increases through Tg. Fig. 2b shows that experimental values of modulus above Tg are not zero-valued, but are 2–3 orders of magnitude smaller than the values below Tg. Thus, eqn (6) is only an approximation for temperatures above Tg, but is sufficiently accurate for the purposes of predicting the relative elastic response of the polymer over the entire temperature range.
Close examination of Fig. 3b shows that the curves do not exactly exhibit a sigmoidal shape, that is, for higher values of τ beyond the center of the sigmoid, the storage modulus continues to increase by a steady amount (modulus is a function of temperature in the glassy regime). Therefore, the τ* multiplier in eqn (6) is used to correct the sigmoid for this discrepancy. From Fig. 3b it is also evident that the maximum value of the modulus for each degree of cure proxy follows the same trend observed in Fig. 2c, that is, the maximum value is the greatest for ϕ = 65%. Once again, the maximum value of the modulus would be expected to occur at ϕ = 100% if these curves were from epoxies with intermediate degrees of cure, instead of proxies. However, as explained above, the proxy systems were used to characterize eqn (5)–(8) because of the convenience of obtaining modulus data for a range of degrees of cure and temperature using proxy systems. The values for 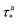 and
and 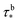 were determined by quantifying the discrepancy between the modulus values from the DMA data just above the sigmoidal jump and the modulus of the full stoichiometry system at room temperature. The relationship between these discrepancy values and their corresponding τ values were fit with the power law relationship of eqn (8). The corresponding phenomenological parameters are
were determined by quantifying the discrepancy between the modulus values from the DMA data just above the sigmoidal jump and the modulus of the full stoichiometry system at room temperature. The relationship between these discrepancy values and their corresponding τ values were fit with the power law relationship of eqn (8). The corresponding phenomenological parameters are 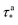 = 0.065 and
= 0.065 and 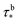 = 0.065.
= 0.065.
Finally, with the initial guess values of eight out of nine phenomenological parameters determined, the final parameter, τσ, which describes the relative steepness of the sigmoid jumps shown in Fig. 3b, was determined using a least-squares fit of eqn (3)–(8) to the DMA data shown in Fig. 3b, with a value of τσ = 0.009. The values of the initial guesses are summarized in Table 2.
5.2 Optimization of parameters
After the initial guesses of all the parameters were determined, they were used in the Newton–Raphson iterative optimization technique to determine the final optimized values of the full set of nine parameters. The optimized values are provided in Table 2. Fig. 3b shows the storage modulus calculated with eqn (3)–(8) and the optimized values plotted against the τ parameter. It is important to note that the model predicts the room temperature modulus of each system to be equal to that of the full stoichiometry system. The model parameters were fit this way to offset the effect of using a series of proxy systems instead of fully stoichiometric systems at partial degrees of cure.6. Application of mapping to MD predictions
It is uncommon for all the crosslinking reactions that can occur in a thermoset network to actually occur because of steric hindrance constrains on the motion of the reactive groups.48,49 The degree of cure is defined as the relative amount of conversion that has occurred in a thermosetting polymer system, ranging from 0 (no crosslinking reactions have occurred) to 1.0 (100% of all crosslinking reactions have occurred that can possibly occur given steric hindrance constraints). Conversely, the crosslink density, as defined above, indicates the relative number of crosslinking reactions that have occurred with respect to the total number of reactive group pairs that exist in the material. Therefore, it is typical for a crosslink density to never reach 100%, but a degree of cure can always reach 100% given a sufficiently long cure time. Because the crosslink density is a convenient metric to track with MD, but degree of cure is more convenient from a processing perspective, it is necessary to convert the crosslink densities simulated with MD to degree of cure quantified experimentally. With these definitions, the degree of cure can be determined from the crosslink density as follows:• The degree of cure is 0 when the crosslink density is 0
• The degree of cure is 1 when the crosslink density has reached its maximum value for a given material
• Intermediate values of the degree of cure are calculated using a linear scaling such that the degree of cure is the ratio of the crosslink density to the maximum crosslink density
MD simulations were reported by Patil et al.38 to predict the Young's modulus of the same DGEBF/DETDA epoxy system studied herein as a function of crosslinking density. In this study, after converting the data of Patil et al. to be a function of degree of cure, the mapping functions from eqn (3)–(8) were applied using the optimized parameters shown in Table 2. It is emphasized that the MD data of Patil et al. was not used to parameterize the mapping function, it was simply used for mapping to the corrected state given the strain rate, temperature, and degree of cure effects.
The viscous response of thermoset materials is only apparent in deformations with a finite deviatoric (shape changing) component of deformation. For hydrostatic (volume changing) deformations, the response is purely elastic.50 Therefore, it is possible to predict the viscous response of the Poisson's ratio (v) for the isotropic epoxy system as a function of degree of cure, temperature, and strain rate through the standard elasticity equation
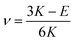 | (9) |
7. Results
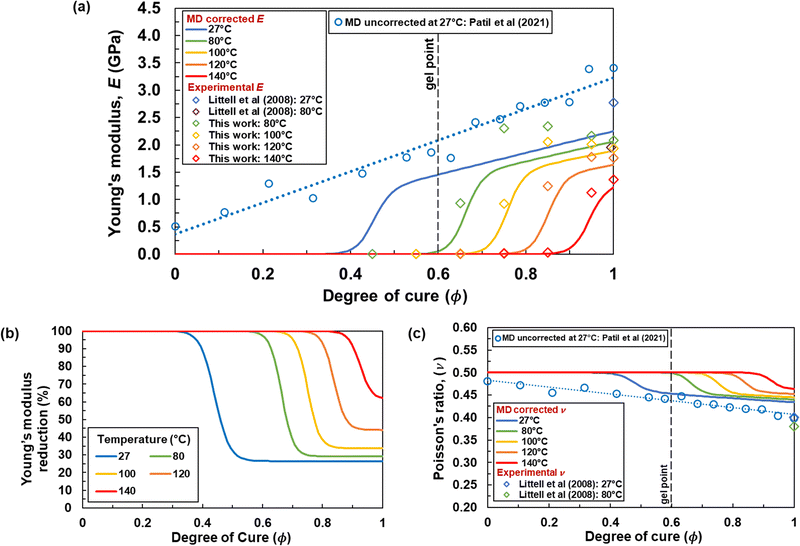
Fig. 4a shows the mapped MD-predicted Young's modulus for varying temperatures (solid lines) compared with the room temperature raw MD Young's modulus predictions (open circles) with a linear regression fit (dashed line). The experimental data points are included (open diamonds) at varying temperatures, as well as a data point from Littell et al.45 at 80 °C. As expected, the predicted and measured Young's moduli decrease with increasing temperatures and decreasing degrees of cure. At increasing temperatures, intermolecular distances increase because of increasing thermal fluctuations. As a consequence, there is a decrease in intermolecular forces and a corresponding decrease in the Young's modulus. At lower degrees of cure, the epoxy network is sparsely connected, thus there are fewer covalent bonds between the monomers. Thus, the network is unable to sustain any significant load, manifesting in a lower Young's modulus.The mapped modulus for the fully crosslinked state (ϕ = 1) at all temperatures agrees well with the experimental data, although the mapping is less accurate for room temperature relative to temperatures of 80 °C and above. The reason that the mapping at 27 °C and ϕ = 1 slightly underpredicts the experimental value involves the disagreement of the experimental data between the experiments described herein and those described by Littell et al.45 The room temperature storage modulus from Fig. 2 is about 2.4 GPa, while the value reported by Littell et al. is about 2.7 GPa. Because the parameterization was performed with the data in Fig. 2 and not with the data from Littell et al., the difference of 0.3 GPa between the two values is apparent in Fig. 4a.
The mapped modulus at 80 °C at degrees of cure above the gel point of the DGEBF/DETDA system (ϕ = 0.6)38 is slightly higher than the experimental value before it reduces to match the experimental value as the model approaches the fully crosslinked state. This discrepancy, as explained above, is due to the use of proxy materials systems as a substitute for the full stoichiometry epoxy system with intermediate degrees of cure. As the temperature increases, the mapped moduli exhibit improved agreement with the experimental data both below and above gel point. Also, as the temperature approaches 140 °C, the modulus approaches a near zero value as the material advances toward the transition from glassy to rubbery states (shown in Fig. 2c, 155 °C). At 177 °C (the processing temperature for this epoxy system), the modulus is expected to reduce to zero because the material is in the rubbery state and unable to sustain any appreciable mechanical load. This behavior is similar to that observed in Fig. 2a, where the storage modulus goes to zero at 177 °C.
Perhaps the most striking feature of Fig. 4a is the overall significance of the viscous mapping on the MD predicted modulus values. Fig. 4b shows the overall reduction in the MD predicted modulus as a function of degree of cure and temperature. It can be seen that the mapping reduction is highest for low degrees of cure and high temperatures, and lowest for high degrees of cure and low temperatures. Thus, the need for the mapping in MD predictions of thermoset properties is clearly evident for not only strain rates, but for temperatures and degrees of cure as well. Mapped mechanical properties of thermoset and thermoplastic materials can then be used in a process modeling framework to predict and optimize the processing and properties of composite laminates and structures.15,22,51–61
Fig. 4c shows the mapped MD-predicted Poisson's ratio for varying temperatures (solid lines) compared with the room temperature raw MD predicted Poisson's ratio predictions (open blue circles) with a linear regression fit (dashed line). An experimental data point from Littell et al.45 at 80 °C is also included (open diamond). The predicted Poisson's ratio increases with increasing temperatures, in agreement with experiment,62–67 because of increased molecular motion. The predicted Poisson's ratio generally decreases with increasing degrees of cure, as observed experimentally.68,69 Similar to the discussion above regarding the discrepancy between the mapped MD values and the experimental results of Littell et al.,45 it is important to note that the mapping was parameterized with the experimental data obtained herein, and not the data from Littell et al. The corresponding discrepancy in the experimental results leads to the apparent differences between the experimental and predicted Poisson's ratios at ϕ = 1.
In the fully cured state (ϕ = 1), the predicted Poisson's ratios show no significant difference with respect to temperature. Littell et al.45 also observed an insignificant difference in the experimentally measured Poisson's ratio of 0.4, 0.4 and 0.38 at temperatures of 27 °C, 50 °C and 80 °C, respectively, from tensile tests at a strain rate of 1 × 10−1 s−1.
As the temperature approaches 140 °C (near the Tg, as shown in Fig. 2c), the mapped MD Poisson's ratio approaches an asymptotic value of 0.5, similar to an incompressible liquid. For 177 °C (above the Tg), the Poisson's ratio is expected to reach 0.5 for the entire range of degree of cure. This behavior of the MD-mapped Poisson's ratio with temperature agrees well with experimental observations.65–69
8. Conclusions
An efficient phenomenological-based mapping function has been developed for correlating raw MD-predicted elastic properties of thermosets that exhibit significant viscoelastic effects, such as the DGEBF/DETDA epoxy system studied herein, to the corresponding time-dependent laboratory-based properties. This approach satisfies the three requirements articulated at the beginning of this study. First, the method requires only minimal MD simulations. Only MD predictions of the mechanical properties of the polymer at multiple degrees of cure are needed, as opposed to an ambitious program of simulations to establish the time-temperature superposition relationship. Second, the method requires minimal experimental input. Only the storage modulus from DMA temperature sweep tests on off-stoichiometry specimens are required, and not the rigorous experimental characterization of the full viscoelastic constitutive response. Third, this approach directly addresses the well-known major issues associated with the inability of all-atom MD to fully simulate conformational relaxation processes at nanosecond timescales. Specifically, the over-estimation of mechanical properties at MD-scale strain rates, at temperatures above Tg, and at intermediate degrees of cure.It's important to note that this approach is intended for efficient mapping of MD-predicted properties of viscoelastic thermosets. This level of efficiency is particularly beneficial for materials engineering environments where computational material design and process optimization need to be performed in a timely manner. This approach is not a direct substitute for comprehensive characterization of viscoelastic constitutive models or complete quantification of properties at intermediate degrees of cure. However, it does offer a simple approach to map MD simulation data for the strain-rate effect and the overestimation of properties at elevated temperatures and intermediate degrees of cure.
Although the proposed approach does require experimental input (strain-rate dependence on elastic response and DMA temperature sweep data), the effort and resources required to obtain this input is far less than that required to obtain fully-characterized time-temperature superposition data. This approach only requires some basic characterization of the viscous response of the polymer. Thus, this approach provides a means to efficiently establish a mapping function for transforming raw MD data into MD data that can be immediately used for further multi-scale analysis.
Author contributions
SUP: conceptualization, data curation, investigation, methodology, visualization, writing – original draft, writing – review & editing; ASK: investigation, formal analysis; LKO: investigation; UY: investigation; JAK: project administration; MM: funding acquisition, project administration, writing – review & editing; GMO: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.Data availability
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially supported by the NASA Space Technology Research Institute (STRI) for Ultra-Strong Composites by Computational Design (US-COMP), grant NNX17AJ32G; NASA grants 80NSSC19K1246 and 80NSSC21M0104; and NSF grant 2145387. SUPERIOR, a high-performance computing cluster at Michigan Technological University, was used in obtaining the MD simulation results presented in this publication.References
- G. M. Odegard and A. Bandyopadhyay, Physical aging of epoxy polymers and their composites, J. Polym. Sci., Part B: Polym. Phys., 2011, 49(24), 1695–1716 CrossRef CAS.
- C. E. Estridge, The effects of competitive primary and secondary amine reactivity on the structural evolution and properties of an epoxy thermoset resin during cure: a molecular dynamics study, Polymer, 2018, 141, 12–20 CrossRef CAS.
- S. V. Kallivokas, A. P. Sgouros and D. N. Theodorou, Molecular dynamics simulations of EPON-862/DETDA epoxy networks: structure, topology, elastic constants, and local dynamics, Soft Matter, 2019, 15(4), 721–733 RSC.
- C. Li and A. Strachan, Molecular dynamics predictions of thermal and mechanical properties of thermoset polymer EPON862/DETDA, Polymer, 2011, 52(13), 2920–2928 CrossRef CAS.
- C. Li and A. Strachan, Molecular scale simulations on thermoset polymers: a review, J. Polym. Sci., Part B: Polym. Phys., 2015, 53(2), 103–122 CrossRef CAS.
- G. M. Odegard, B. D. Jensen, S. Gowtham, J. Wu, J. He and Z. Zhang, Predicting mechanical response of crosslinked epoxy using ReaxFF, Chem. Phys. Lett., 2014, 591, 175–178 CrossRef CAS.
- G. M. Odegard, S. U. Patil, P. P. Deshpande, K. Kanhaiya, J. J. Winetrout, H. Heinz, S. P. Shah and M. Maiaru, Molecular Dynamics Modeling of Epoxy Resins Using the Reactive Interface Force Field, Macromolecules, 2021, 54(21), 9815–9824 CrossRef CAS.
- M. S. Radue, B. D. Jensen, S. Gowtham, D. R. Klimek-Mcdonald, J. A. King and G. M. Odegard, Comparing the Mechanical Response of Di-, Tri-, and Tetra-functional Resin Epoxies with Reactive Molecular Dynamics, J. Polym. Sci., Part B: Polym. Phys., 2018, 56(3), 255–264 CrossRef CAS PubMed.
- M. S. Radue, V. Varshney, J. W. Baur, A. K. Roy and G. M. Odegard, Molecular Modeling of Cross-Linked Polymers with Complex Cure Pathways: A Case Study of Bismaleimide Resins, Macromolecules, 2018, 51(5), 1830–1840 CrossRef CAS.
- T. W. Sirk, K. S. Khare, M. Karim, J. L. Lenhart, J. W. Andzelm, G. B. Mckenna and R. Khare, High strain rate mechanical properties of a cross-linked epoxy across the glass transition, Polymer, 2013, 54(26), 7048–7057 CrossRef CAS.
- M. Tsige, C. D. Lorenz and M. J. Stevens, Role of Network Connectivity on the Mechanical Properties of Highly Cross-Linked Polymers, Macromolecules, 2004, 37(22), 8466–8472 CrossRef CAS.
- V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties, Macromolecules, 2008, 41(18), 6837–6842 CrossRef CAS.
- A. Vashisth, C. Ashraf, W. Zhang, C. E. Bakis and A. C. T. Van Duin, Accelerated ReaxFF Simulations for Describing the Reactive Cross-Linking of Polymers, J. Phys. Chem. A, 2018, 122(32), 6633–6642 CrossRef CAS PubMed.
- G. M. Odegard, S. U. Patil, P. S. Gaikwad, P. Deshpande, A. S. Krieg, S. P. Shah, A. Reyes, T. Dickens, J. A. King and M. Maiaru, Accurate predictions of thermoset resin glass transition temperatures from all-atom molecular dynamics simulation, Soft Matter, 2022, 18(39), 7550–7558 RSC.
- S. U. Patil, S. P. Shah, M. Olaya, P. P. Deshpande, M. Maiaru and G. M. Odegard, Reactive Molecular Dynamics Simulation of Epoxy for the Full Cross-Linking Process, ACS Appl. Polym. Mater., 2021, 3(11), 5788–5797 CrossRef CAS.
- H. Al Mahmud, S. U. Patil, M. S. Radue and G. M. Odegard, Probing the Influence of Surface Chemical Functionalization on Graphene Nanoplatelets-Epoxy Interfacial Shear Strength Using Molecular Dynamics, Nanomaterials, 2023, 13(2), 287 CrossRef CAS PubMed.
- A. Aramoon, T. D. Breitzman, C. Woodward and J. A. El-Awady, Coarse-Grained Molecular Dynamics Study of the Curing and Properties of Highly Cross-Linked Epoxy Polymers, J. Phys. Chem. B, 2016, 120(35), 9495–9505 CrossRef CAS PubMed.
- S. Yang, Z. Cui and J. Qu, A Coarse-Grained Model for Epoxy Molding Compound, J. Phys. Chem. B, 2014, 118(6), 1660–1669 CrossRef CAS PubMed.
- M. Langeloth, T. Sugii, M. C. Böhm and F. Müller-Plathe, The glass transition in cured epoxy thermosets: a comparative molecular dynamics study in coarse-grained and atomistic resolution, J. Chem. Phys., 2015, 143(24), 243158 CrossRef PubMed.
- C. Li and A. Strachan, Coarse-grained molecular dynamics modeling of reaction-induced phase separation, Polymer, 2018, 149, 30–38 CrossRef CAS.
- S. Yang and J. Qu, Coarse-grained molecular dynamics simulations of the tensile behavior of a thermosetting polymer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(1), 012601 CrossRef PubMed.
- S. P. Shah, S. U. Patil, C. J. Hansen, G. M. Odegard and M. Maiarù, Process modeling and characterization of thermoset composites for residual stress prediction, Mech. Adv. Mater. Struct., 2023, 30(3), 486–497 CrossRef.
- O. G. Kravchenko, C. Li, A. Strachan, S. G. Kravchenko and R. B. Pipes, Prediction of the chemical and thermal shrinkage in a thermoset polymer, Composites, Part A, 2014, 66, 35–43 CrossRef CAS.
- H. Park, J. Choi, B. Kim, S. Yang, H. Shin and M. Cho, Toward the constitutive modeling of epoxy matrix: temperature-accelerated quasi-static molecular simulations consistent with the experimental test, Composites, Part B, 2018, 142, 131–141 CrossRef CAS.
- H. Park and M. Cho, A multiscale framework for the elasto-plastic constitutive equations of crosslinked epoxy polymers considering the effects of temperature, strain rate, hydrostatic pressure, and crosslinking density, J. Mech. Phys. Solids, 2020, 142, 103962 CrossRef CAS.
- C. Park, J. Jung and G. J. Yun, Multiscale micromorphic theory compatible with MD simulations in both time-scale and length-scale, Int. J. Plast., 2020, 129, 102680 CrossRef.
- C. Park, J. Jung, T. Park and G. Yun, Multiscale Micromorphic Theory and Simulation with Co-existing Molecular and Continuum Time Scales, in AIAA Scitech 2020 Forum.
- K. S. Khare and F. R. Phelan Jr., Integration of Atomistic Simulation with Experiment Using Time–Temperature Superposition for a Cross-Linked Epoxy Network, Macromol. Theory Simul., 2020, 29(2), 1900032 CrossRef CAS.
- K. S. Khare and F. R. Phelan, Quantitative Comparison of Atomistic Simulations with Experiment for a Cross-Linked Epoxy: A Specific Volume–Cooling Rate Analysis, Macromolecules, 2018, 51(2), 564–575 CrossRef CAS.
- A. J. Levine and S. T. Milner, Star Polymers and the Failure of Time−Temperature Superposition, Macromolecules, 1998, 31(24), 8623–8637 CrossRef CAS.
- J. Zou, F. You, L. Su, Z. Yang, G. Chen and S. Guo, Failure mechanism of time-temperature superposition for poly(vinyl chloride)/dioctylphthalate (100/70) system, J. Appl. Polym. Sci., 2012, 124(1), 452–458 CrossRef CAS.
- M. N. Olaya, G. M. Odegard and M. Maiaru, A Novel Approach to Characterization of Composite Polymer Matrix Materials for Integrated Computational Materials Engineering Approaches, in AIAA Scitech 2021 Forum.
- M. N. Olaya, S. S. Shah and M. Maiaru, Thermoset Polymers Characterization as a Function of Cure State Using Off-Stoichiometry Proxies, ChemRxiv, 2022, preprint DOI:10.26434/chemrxiv-2022-ddlc9.
- R. M. Christensen, Theory of Viscoelasticity An Introduction, Academic Press, 2nd edn, 1982 Search PubMed.
- W. N. Findley, J. S. Lai and K. Onaran, Creep and Relaxation of Nonlinear Viscoelastic Materials, Dover Publications, 2011 Search PubMed.
- E. Buckingham, On Physically Similar Systems; Illustrations of the Use of Dimensional Equations, Phys. Rev., 1914, 4(4), 345–376 CrossRef.
- J. J. Winetrout, K. Kanhaiya, G. Sachdeva, R. Pandey, B. Damirchi, D. Adri Van, G. M. Odegard and H. Heinz, Implementing Reactivity in Molecular Dynamics Simulations with the Interface Force Field (IFF-R) and Other Harmonic Force Fields, arXiv, 2021, preprint, arXiv.2107.14418 DOI:10.48550/arXiv.2107.14418.
- S. U. Patil, S. P. Shah, M. Olaya, P. P. Deshpande, M. Maiaru and G. M. Odegard, Reactive Molecular Dynamics Simulation of Epoxy for the Full Cross-Linking Process, ACS Appl. Polym. Mater., 2021, 3(11), 5788–5797 CrossRef CAS.
- W. A. Pisani, M. S. Radue, S. Chinkanjanarot, B. A. Bednarcyk, E. J. Pineda, K. Waters, R. Pandey, J. A. King and G. M. Odegard, Multiscale modeling of PEEK using reactive molecular dynamics modeling and micromechanics, Polymer, 2019, 163, 96 CrossRef CAS.
- L. Pauling, E. Bright and J. Wilson, Introduction to Quantum Mechanics: with Applications to Chemistry, Dover Publications, 1985 Search PubMed.
- A. Rahman, P. Deshpande, M. S. Radue, G. M. Odegard, S. Gowtham, S. Ghosh and A. D. Spear, A machine learning framework for predicting the shear strength of carbon nanotube-polymer interfaces based on molecular dynamics simulation data, Compos. Sci. Technol., 2021, 207, 108627 CrossRef CAS.
- G. M. Odegard, T. S. Gates and H. M. Herring, Characterization of viscoelastic properties of polymeric materials through nanoindentation, Exp. Mech., 2005, 45(2), 130–136 CrossRef.
- A. Galántai, The theory of Newton's method, J. Comput. Appl. Math., 2000, 124(1), 25–44 CrossRef.
- D. R. Klimek-Mcdonald, J. A. King, I. Miskioglu, E. J. Pineda and G. M. Odegard, Determination and Modeling of Mechanical Properties for Graphene Nanoplatelet/Epoxy Composites, Polym. Compos., 2018, 39(6), 1845–1851 CrossRef CAS.
- J. D. Littell, C. R. Ruggeri, R. K. Goldberg, G. D. Roberts, W. A. Arnold and W. K. Binienda, Measurement of Epoxy Resin Tension, Compression, and Shear Stress-Strain Curves over a Wide Range of Strain Rates Using Small Test Specimens, J. Aerosp. Eng., 2008, 21(3), 162–173 CrossRef.
- A. Gilat, R. K. Goldberg and G. D. Roberts, Strain Rate Sensitivity of Epoxy Resin in Tensile and Shear Loading, J. Aerosp. Eng., 2007, 20(2), 75–89 CrossRef.
- D. S. Sholl and J. A. Steckel, Density Functional Theory A Practicle Introduction, John Wiley & Sons, Inc., 2009 Search PubMed.
- M. S. Radue, B. D. Jensen, S. Gowtham, D. R. Klimek-Mcdonald, J. A. King and G. M. Odegard, Comparing the mechanical response of di-, tri-, and tetra-functional resin epoxies with reactive molecular dynamics, J. Polym. Sci., Part B: Polym. Phys., 2018, 56(3), 255–264 CrossRef CAS PubMed.
- C. M. Hadden, D. R. Klimek-Mcdonald, E. J. Pineda, J. A. King, A. M. Reichanadter, I. Miskioglu, S. Gowtham and G. M. Odegard, Mechanical properties of graphene nanoplatelet/carbon fiber/epoxy hybrid composites: multiscale modeling and experiments, Carbon, 2015, 95, 100–112 CrossRef CAS.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, Ithaca, 1953 Search PubMed.
- S. U. Patil, S. S. Shah, P. P. Deshpande, K. Kashmari, G. M. Odegard and M. Maiaru, Prediction Of Residual Stress Build-Up In Polymer Matrix Composite During Cure Using A Two-Scale Approach in Proceedings of the American Society for Composites—Thirty-fourth Technical Conference, 2019.
- S. U. Patil, S. S. Shah, P. P. Deshpande, K. Kashmari, M. N. Olaya, G. M. Odegard and M. Maiaru, Multi-scale Approach to Predict Cure-Induced Residual Stresses in an Epoxy System in Proceedings of the American Society for Composites—Thirty-fifth Technical Conference, 2020.
- P. P. Deshpande, S. S. Shah, S. U. Patil, K. Kashmari, M. N. Olaya, G. M. Odegard and M. Maiaru, Multiscale Modelling of the Cure Process in Thermoset Polymers using ICME in Proceedings of the American Society for Composites—Thirty-fifth Technical Conference, 2020.
- P. P. Deshpande, S. S. Shah, S. U. Patil, K. Kashmari, G. M. Odegard and M. Maiaru A Multi-Scale Approach For Modelling The Cure Of Thermoset Polymers Within ICME in Proceedings of the American Society for Composites—Thirty-fourth Technical Conference, 2019.
- S. S. Shah, S. U. Patil, P. P. Deshpande, K. Kashmari, G. M. Odegard and M. Maiaru, Multiscale modeling of thermoset composite to predict process-induced residual stresses, in ICCM22, Engineers Australia, 2019.
- S. P. Shah and M. Maiarù, Effect of Manufacturing on the Transverse Response of Polymer Matrix Composites, Polymers, 2021, 13(15), 2491 CrossRef CAS PubMed.
- M. Maiaru, Effect of uncertainty in matrix fracture properties on the transverse strength of fiber reinforced polymer matrix composites, in 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.
- R. J. D'mello, A. M. Waas, M. Maiaru and R. Koon, Integrated Computational Modeling for Efficient Material and Process Design for Composite Aerospace Structures, in AIAA Scitech 2020 Forum.
- S. Shah, S. Patil, P. Deshpande, A. Krieg, K. Kashmari, H. A. Mahmud, J. King, G. M. Odegard and M. Maiaru, Multiscale Modeling for Virtual Manufacturing of Thermoset Composites, in AIAA Scitech 2020 Forum.
- P. S. Gaikwad, A. S. Krieg, P. P. Deshpande, S. U. Patil, J. A. King, M. Maiaru and G. M. Odegard, Understanding the Origin of the Low Cure Shrinkage of Polybenzoxazine Resin by Computational Simulation, ACS Appl. Polym. Mater., 2021, 3(12), 6407–6415 CrossRef CAS.
- S. S. Shah and M. Maiaru, Microscale analysis of virtually cured polymer matrix composites accounting for uncertainty in matrix properties during manufacturing, in Proceedings of the American Society for Composites-Thirty-third Technical Conference, Seattle, USA, 2018.
- V. H. Carneiro and H. Puga, Temperature Variability of Poisson's Ratio and Its Influence on the Complex Modulus Determined by Dynamic Mechanical Analysis, Technologies, 2018, 6(3), 81 CrossRef.
- S. Pandini and A. Pegoretti, Time, temperature, and strain effects on viscoelastic Poisson's ratio of epoxy resins, Polym. Eng. Sci., 2008, 48(7), 1434–1441 CrossRef CAS.
- C. M. Migwi, M. I. Darby, G. H. Wostenholm, B. Yates, M. Moss and R. Duffy, A method of determining the shear modulus and Poisson's ratio of polymer materials, J. Mater. Sci., 1994, 29(13), 3430–3432 CrossRef CAS.
- P. H. Mott, J. R. Dorgan and C. M. Roland, The bulk modulus and Poisson's ratio of “incompressible” materials, J. Sound Vib., 2008, 312(4), 572–575 CrossRef.
- A. Tcharkhtchi, S. Faivre, L. E. Roy, J. P. Trotignon and J. Verdu, Mechanical properties of thermosets, J. Mater. Sci., 1996, 31(10), 2687–2692 CrossRef CAS.
- L. Yang, L. Yang and R. L. Lowe, A viscoelasticity model for polymers: time, temperature, and hydrostatic pressure dependent Young's modulus and Poisson's ratio across transition temperatures and pressures, Mech. Mater., 2021, 157, 103839 CrossRef.
- D. J. O’brien, N. R. Sottos and S. R. White, Cure-dependent Viscoelastic Poisson's Ratio of Epoxy, Exp. Mech., 2007, 47(2), 237–249 CrossRef.
- S. Saseendran, M. Wysocki and J. Varna, Cure-state dependent viscoelastic Poisson's ratio of LY5052 epoxy resin, Adv. Manuf.: Polym. Composites Sci., 2017, 3(3), 92–100 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Brief analysis of the effect of the scatter shown in Fig. 3a on the predicted Young's modulus. See DOI: https://doi.org/10.1039/d3sm00697b |
| This journal is © The Royal Society of Chemistry 2023 |