Thermodynamics, morphology and molecular structure of molecular compounds in trisamide triarylamine organogels and pseudo-organogels

Abstract

In this paper, potentially-gelling binary systems are investigated by DSC, X-ray and Electron microscopy in order to assess their gel status and the role of the Hansen solubility parameter. The low molecular weight organogelator is a Triarylamine Trisamide (TATA) while the solvents consist of a series of halogeno-ethanes and of toluene. Temperature–concentration phase diagrams are mapped out from DSC traces. They reveal the existence of one or more TATA/solvent molecular compounds. The X-ray data, that display different diffraction patterns depending on the solvent and the temperature, show the existence of different molecular structures, and thus confirm the outcome of the T–C phase diagram. Tentative molecular organizations are also discussed in light of previous results obtained in the solid state. The morphology by TEM on dilute systems, and TEM on more concentrated systems highlight the degree of physical cross-links, which leads one to regard some systems as pseudo-gels.

---

Introduction

The formation of gels from molecules of low molecular weight in organic solvents, designated as organogelation, has drawn continuous interest these past years, as ascertained by the growing number of publications.^1–7 This unexpected phenomenon, which was previously known only for polymers and biopolymers, is usually observed with molecules, frequently named organogelators, bearing different types of interaction sites (H-bonding, van der Waals, π–π interaction,…), hence their designation as “chimeras”.⁶

Current issues deal with the possibility of predicting whether a given molecule can produce a gel in a given solvent.^8–12 This raises two questions: how do we define a gel, and how can we select the appropriate solvent or class of solvent for producing a gel?

A gel is basically a network, whose definition in language dictionaries is “a large system of lines, tubes, wires, etc. that cross one another or are connected with one another.”.¹³ Clearly, this definition entails that the gel architecture consists of elongated objects such as fibrils. Other type of morphologies should not be considered gels (sphere packing, spherulitic assemblies for instance). This implies that molecular organization should be privileged in one direction for producing fibrillar structures,^6,14 an effect probably favoured by the “chimera” character⁶ of these molecules. A system can be, however, considered a gel if and only if these fibrils are interconnected in one way or another. This existence of physical cross-links between fibrils can be observed for example by morphological investigations.

As to the choice of the solvent, the Hansen solubility parameter (HSP) has been recently considered in an attempt to predict gel formation.^9–12,15 As discussed in previous publications,^16,17 the HSP allows one to find out whether a solvent is not too good, thus preventing the system from organizing (crystallization), nor not too bad, thus hindering the formation of a homogeneous solution prior to gelation. The use of the HSP for predicting the occurrence of organogelation meets with two pitfalls: (1) it cannot anticipate the morphology of the system, and (2) it cannot predict specific organogelator/solvent interactions. In particular, the complementary shapes of the solvent molecules and the polymer helical structure, often involved in the formation of molecular compounds in the case of crystalline polymers,^18–23 may play a role. Some authors have already contemplated the existence of molecular compounds in organogels^24–26

The most important step in the investigation of these binary systems consists in mapping out the temperature–concentration phase diagrams for elucidating their possible complex thermodynamic behaviour.^6,14 Clearly, the occurrence of organogelation cannot always be accounted for by one single parameter.²⁷ We have recently reported that the solvent shape in trisamide triarylamine (TATA) organogels impacts upon the formation of TATA/solvent molecular compounds.^16,17 This molecule is of interest as it displays conducting properties in the gel state, whose value depend upon the solvent.^28–31 The occurrence of molecular compounds is derived from the phase diagrams by applying Gibbs phase rules, and subsequently backed up by neutron diffraction experiments. Here, we present new results obtained by DSC, X-ray diffraction and electron microscopy on a series of halogeno-ethanes (1,2 dichloroethane, DCE, 1,1,2,2,-tetrachoroethane, TCE, and 1,1,2,2,-tetrabromoetane, TBE), and on toluene. The choice of these solvents arises from their differing behaviour towards the conductivity properties of TATA gels. In chlorine-containing solvents TATA molecules display an enhanced conductivity,^28,31 while this property is virtually lost in bromine-containing-solvents. A solvent free of halogen atoms is considered for comparison, namely toluene. We observe again different types of thermodynamic behaviour that are not correlated to the HS parameter, and also different type of molecular structures depending on the solvent and/or the temperature. The study of the morphology further shows that some systems are actually pseudo-gels although consisting of elongated objects, yet not interconnected.

Experimental

Materials

The triaryl trisamines²⁸ designated as TATA in what follows (see Fig. 1) were synthesised as described in ref. 28–30. As shown in these references these molecules pile up to form helical structures that further aggregate to produce fibrillar or elongated morphologies.

Fig. 1 Left: Chemical structure of TATA molecules; right: space-filling, energy-minimized chemical structure of the triaryl amine trisamide C11 in its completely extended conformation (blue: nitrogen, red: oxygen). Under this conformation it can be inscribed in a circle of radius r_out ≈ 2 nm (blue). The domain defined by the red circle of radius r_in ≈ 0.83 nm possesses a higher electron density than the outer corona does. As can be seen the phenyl rings are tilted due to steric hindrance, so that this molecule differs from its mirror image.

Due to steric hindrance the phenyl groups are tilted which entails the existence of a helical chirality when TATA moleculare are stacked.

1,1,2,2,-tetrachloroethane (TCE), 1,2-dichloroethane (DCE), 1,1,2,2-tetrabromoethane (TBE) and toluene were purchased from SigmaAldrich (purity grade 99.5%), and were used without further purification.

The TATA/solvent systems are obtained from mixtures prepared at the desired concentration, and then heated up to the appropriate temperature so as to make clear, homogeneous solutions. These solutions are then quenched at low temperature (0 °C down to −20 °C depending on the solvent) for producing the organized systems.

TATA concentrations are in the range from 0.5 × 10⁻² g cm⁻³ to 0.12 g cm⁻³ for all the solvents. These concentrations are further expressed in weigh/weight in the temperature concentration phase diagrams, and therefore the w/w concentration range depends upon the solvent's density.

Differential scanning calorimetry

The DSC 8500 from PerkinElmer has been used for determining the different first order transitions (melting, formation, transformation), as well as the corresponding enthalpies. Three heating and cooling rates were used, namely 5 °C min⁻¹, 10 °C min⁻¹ and 15 °C min⁻¹ within a temperature range in accordance with the solvent's physical property. As a rule, the results recorded at 5 °C min⁻¹ provide transition temperatures close to those derived by extrapolating to zero heating rate. Therefore, the T–C phase diagrams are mapped out from the DSC traces obtained at 5 °C min⁻¹, while the enthalpies are usually heating-rate-independent. The transition and melting temperature are taken at the maximum of the endotherm as derived from the Pyris software developed by PerkinElmer.

About 30–40 mg of materials are weighted in stainless steel pans that are hermetically sealed by means of an o-ring. This allows one to access temperature above the solvent boiling point whenever necessary. A first run is systematically performed for erasing the sample history, as well as to suppress parasitic mechanical effects at the gel melting. The weight of the sample is systematically checked after the different cycles in order to evaluate any solvent loss.

Cryoscanning electron microscopy

A piece of a material is deposited onto a cryo-holder and quickly plunged into a nitrogen slush. Once transferred into the Quorum PT3010 chamber attached to the microscope, the frozen sample is coated with a thin Pt layer by sputter deposition, and finally fractured with a razor blade. Subsequent etching is performed at T = −70 °C so as to unravel the underlying morphology. Samples are eventually transferred in the FEG-cryoSEM (Hitachi SU8010) and observed at 1 keV and at T = −150 °C. The images are taken with the SE-in lens detector.

Scanning transmission electron microscopy (STEM) and transmission electron microscopy (TEM)

Electron microscopic observations of the xerogel morphology were performed by STEM imaging on a FEG-SEM Hitachi SU8010 at room temperature at 20 kV, or by TEM on a Philips CM12 microscope operating at 120 kV. For TEM measurements, images were recorded using a MegaView III digital camera (Soft Imaging System).

Samples were prepared by direct deposition of the gels, or pseudo gels, onto a carbon-coated grid and dried under high vacuum. During the imaging process, thin regions of the xerogels were actively searched for to allow imaging of their structure. If necessary, the grids containing the gels were quickly plunged into pure solvent to remove excess material. The observations were made directly on the xerogels without the need of staining agents.

X-ray diffraction

X-ray diffraction experiments in the low-q range (MAXS) are performed by means of a diffractometer developed at the Institut Charles Sadron DiffériX platform. The instrument operates with a pinhole collimator and a hybrid photon counting detector (HPC-Dectrics Pilatus®3 R 300 K). A monochromatic beam of wavelength λ = 0.154 nm is generated by reflection of the primary beam produced by means of an X-ray generator from Rigaku (Micromax 007HF) onto a confocal mirror with multilayer coating (Confocal Max-FluxTM Optic, Rigaku). The distance sample-detector is set so as to access scattering vectors q = 4π sin(θ/2)/λ ranging from q = 0.5 to 10 nm⁻¹. Typical counting times are about 10 min.

WAXS (q = 10 to 20 nm⁻¹) are developed at the Institut Charles Sadron DiffériX platform, and there are performed by means of a diffractometer from Rigaku and a Storage Phosphor Screen from Molecular Dynamics. A monochromatic beam of wavelength λ = 0.154 nm is generated by reflection of the primary beam produced by means of an X-ray generator from Rigaku (Micromax 007HF) onto a confocal mirror with multilayer coating (Confocal Max-FluxTM Optic, Rigaku). Typical counting times are about 2 h. Calibration of the scattering vector range is performed with a silver behenate sample. The samples are introduced in home-made sealed cells of adjustable thickness.

Results and discussion

Thermodynamic: thermal behaviour and phase diagrams

The thermodynamic properties of the TATA/solvent systems, and correspondingly the temperature–concentration phase diagrams, have been obtained from typical DSC traces obtained on heating at 5 °C min⁻¹ (Fig. 2). As expected, the four systems behave differently. For TATA/TCE only a broad endotherm is observed. For TATA/TBE and TATA/DCE a sharp endotherm occurs, and then followed by a broader endotherm. TATA/Toluene systems exhibit two sharp endotherms and a broader terminal endotherm.

Fig. 2 Top: Typical DSC traces obtained at 5 °C min⁻¹ for the different TATA/solvent systems. Below: temperature–concentration phase diagrams and Tamman's diagram (ΔH vs. X); symbols together with their colours are related to the different thermal events; (a) TATA/DCE; (b) TATA/TCE; the red dotted line in the Tamman's plot stands for the variation of the enthalpy if the molecular structure were that in the solid state; (c) TATA/TBE; (d) TATA/Toluene.

The temperature–concentration phase diagrams together with the Tamman's diagram (enthalpies associated with each thermal event) are therefore differing for the four sets of systems.

For TATA/DCE, the sharp thermal event at 40 °C turns out to correspond to a non-variant event (Fig. 2a). Based on the diffraction experiment detailed below, it is assumed that it corresponds to the transformation of molecular compound C₁ into molecular compound C₂. It is worth emphasizing that the terminal melting in this system, namely the liquidus, is beyond the solvent boiling point. This makes the determination of the terminal melting enthalpy difficult. Only the enthalpy associated with the non-variant event at T = 40 °C can be straightforwardly measured.

Results for TATA/TCE have been recently published³² (Fig. 2b). Here, only a liquidus line is observed, which increases monotonously with concentration, and stands always at lower temperature than the TCE boiling point. Note that TCE and DCE have rather close solubility parameters (20.2 and 19.9). The extrapolation to X = 1 of the enthalpies associated with the liquidus line for TATA/TCE gives ΔH_X=1 = 39 J g⁻¹, which is significantly lower than the bulk melting enthalpy³³ (ΔH_s = 53 J g⁻¹). A dotted line has been added to the Tamman's plot in Fig. 2b to emphasize this point. As can be seen the experimental results are well out of this line. Again, these outcomes together with previous diffraction experiment that have demonstrated the formation of a TATA/TCE molecular compound, the domain under the liquidus line can be labelled C + Liq.

In 1,1,2,2-tetrahalogeno-ethane solvents, the replacement of chlorine atoms by bromine atoms yields a phase diagram of significantly different aspect. The liquidus line stands at much higher temperatures in TBE (Fig. 2c). This discrepancy between TCE and TBE may most probably be accounted for by considering a difference in Hansen solubility parameter (20.2 against 23.6), namely TCE is a better solvent than TBE. Yet, in TATA/TBE there is a non-variant event at T = 40 °C that is absent in TATA/TCE systems. The extrapolation to X = 1 of the enthalpies associated with the liquidus line yields ΔH_X=1 = 40 J g⁻¹, which is also significantly lower than the bulk melting enthalpy. The shape of the phase diagram, especially the occurrence of a non-variant event, together with the relatively low value of ΔH_X=1, suggest again the existence of molecular compounds. It is worth noting that the enthalpies associated with the liquidus line possess values close to those measured for the transformation at 40 °C. For experimental reasons detailed below no diffraction curve is available for confirming or disregarding this assumption.

The T–C phase diagrams for the TATA/Toluene systems reveals two non-variant events at T = 22.6 °C and T = 54 °C (Fig. 2d). As to the liquidus line, it stands in most cases in a temperature range above toluene's boiling point. This phase diagram is reminiscent of that mapped out for TATA/o-dichlorobenzene systems where several non-variant events are seen that correspond to diverse molecular compounds as ascertained by neutron diffraction investigations.^16,17 For this system ΔH_X=1 = 42 J g⁻¹, which is still significantly lower than the bulk melting enthalpy. Here, as opposed to TATA/TBE systems, the melting enthalpies associated with the liquidus line are larger than those of both transformation at 22.6 °C and 54 °C. All these outcomes are again consistent with the occurrence of molecular compounds as will be confirmed below by diffraction experiments.

This thermodynamic study highlights that the behaviour of TATA/solvent binary systems cannot be simply predicted from the knowledge of the solubility parameters. Clearly, the behaviour is further dictated by a subtle interaction between the shapes of the solvent and of the TATA helical structure, which results in the formation of molecular compounds. This effect is already well-documented for polymer/solvent systems.^18–23

Note further that the temperature–concentration phase diagrams presented here does not allow one to anticipate as to the gel status of these systems.

Molecular structure: diffraction experiments

Due to the very large absorption of X-ray photons by TBE, no diffraction experiments have been conducted on the system TATA/TBE.

Only tentative 2D lattices on how TATA helices pack are to be derived from the limited numbers of diffraction peaks. Hitherto, only one helical structure has been considered, namely a 20₁ helix,²⁹ where TATA molecules pile up onto one another while rotating by 18°. As the phenyl group are tilted due to steric hindrance (see Fig. 1), both left-handed and right-handed helices are generated. The pitch is about 10 nm and the elevation h = 0.488 nm. This helix may, however, not be appropriate in what follows, particularly in the case of TATA/Toluene gels.

Diffraction patterns obtained for TATA/TCE and TATA/DCE systems are drawn in Fig. 3a. The diffraction pattern for TATA/TCE have been obtained by neutron diffraction.¹⁶ The difference between the patterns obtained by using hydrogenous TCE and deuterated TCE demonstrates the occurrence of a TATA/TCE molecular compound. As can be seen the diffraction pattern of TATA/DCE is conspicuously at variance with its TATA/TCE counterpart, particularly only one prominent peak at q = 2.41 nm⁻¹ is seen. Two very weak peaks may possibly be observed at q = 3.749 nm⁻¹ and q = 5.403 nm⁻¹, yet they are hardly detectable from the noisy background. The lattice shown in Fig. 4 has been considered in a previous paper for the TATA/TCE systems.^16,32

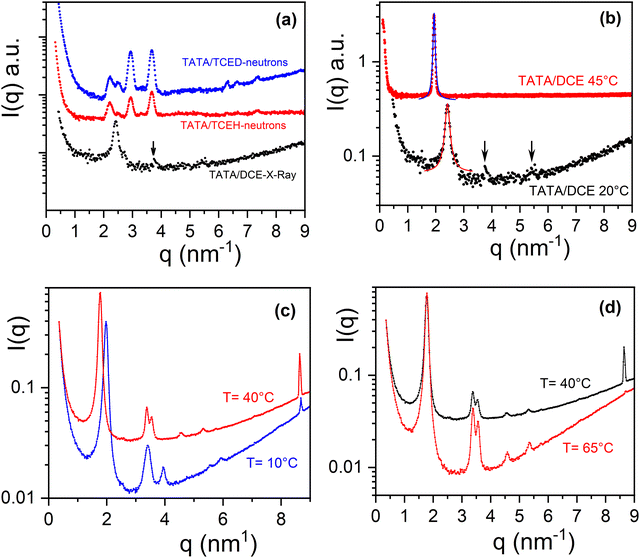Fig. 3 (a) Top left: X-ray diffraction patterns of TATA/DCE (arrows indicate possible weak reflections), and neutron diffraction patterns of TATA/TCEH and TATA/TCED from a previous publication;¹⁸ (b) top right, diffraction patterns of TATA/DCE at T = 20 °C (black) and at T = 45 °C (red), (C_TATA = 0.03 w/w), solid lines= fits with Lorentz functions; c) bottom left diffraction patterns TATA/Toluene at T = 10 °C (blue) and at T = 40 °C (red), for the sake of clarity the blue curve has been shifted downwards, (C_TATA= 0.035 w/w); (d) bottom right, diffraction patterns TATA/Toluene at T = 40 °C (black) and at T = 65 °C (red)), for the sake of clarity the red curve has been shifted downwards.

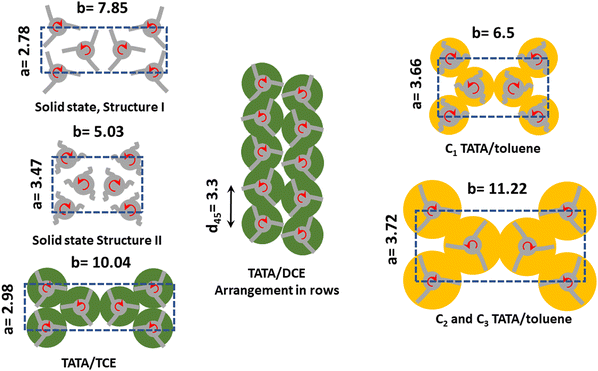Fig. 4 Schematic 2-D molecular arrangements for the various systems as seen parallel to the helical axis. Solid structures are from ref. 32, and TATA/TCE from ref. 16. Solvent shells are represented by green discs for chlorinated solvents, and yellow discs for toluene. Curly lines stand for disorganized TATA arms as opposed to straight lines that indicate extended TATA arms. Lattice parameters a and b are in nanometres. Sketches are not to scale. For further details see text and supplementary information.

It is worth emphasizing that in all the 2D lattices shown in Fig. 4 a right-handed helix is always surrounded by three left-handed helices, and vice-versa. As right-handed and left-handed helices can interpenetrate, then their spacing can be lower than their outer radius.

As was already suggested for TATA/bromobenzene systems,³³ the occurrence of only one, narrow peak can be accounted for by considering arrangements of uncorrelated, adjacent rows, wherein right-handed and left-handed helices alternate (see Fig. 4). A hexagonal arrangement can be discarded as the FWHM of the peak is too large for a low number of helices, and increasing the number of rods does not lower this parameter enough but further gives rise to additional peaks.

The diffracted intensity can be written for assemblies of TATA helices in the low-resolution diffraction range:^34–36

where A_in and A_out are the scattering amplitudes while r_in and r_out are the inner and the outer radii of the hollow cylinder, with γ = r_in/r_out, and A_m = γ²A_in + [1 − γ²]A_out, with A_in/A_out = 4.03, d_jk the distance between the axis of cylinders j and k, N the number of cylinders, and J₁ and J_o Bessel functions of first type and order 1 and 0. In the case of rows of cylinder, (1) can be rewritten (see ESI† S3):where d is the distance between two adjacent helices.

As is detailed in the ESI† the FWHM decreases drastically with increasing the number of cylinders (Fig. S3, ESI†). FWMH reaches 0.1 for N = 30, that is for a relatively low number of helices. The position of the peak at q = 2.41 nm⁻¹ can be reproduced by taking d = 2.63 nm⁻¹.

The diffraction pattern recorded above the transition seen at T = 40 °C in the phase diagram, namely taken at T = 45 °C, shows a shift of the prominent peak towards a lower q value (q = 1.98 nm⁻¹) (Fig. 3b). The change in the diffraction pattern confirms the first order character of this transformation. By considering again arrangement of TATA helices in adjacent rows, relation 2 provides d = 3.3 nm. These outcomes entail that helices are more spaced above 40 °C, which in turn suggests a higher degree of solvation. The stoichiometry of this molecular compound, namely the number of solvent molecules per TATA, has therefore increased.

This system exhibits a rare behaviour since the stoichiometry usually decreases on heating through an incongruent melting process as is well-documented for polymers.²³ Such a behaviour can be, however, encountered in some metallic alloys such as copper-tin.^37–39 Increasing the stoichiometry consequently implies that the aliphatic arms of the TATA molecules most probably take on a more extended conformation. These concomitant effects may be related to a rise in solvent quality. It is worth emphasizing that there may exist two populations of solvent: one type interacting strongly with the TATA helices, namely tightly-bound solvent, and another type that moves more or less freely inside the channels between helices, designated as loosely-bound solvent.

It is noteworthy that TATA/DCE systems at 45 °C behave the same as TATA/bromobenzene systems as reported previously,³³ although the peak is somewhat broader in the latter (FWHM = 0.12 against 0.065) (Fig. S4, ESI†). Yet, unlike TATA/DCE only one molecular compound was identified for this system.

The origin of the arrangement in uncorrelated rows of TATA helices remains presently unclear. In the ESI† (Fig. S1) is detailed a possible, simple process for transforming the monoclinic lattice of the TATA/TCE systems into uncorrelated rows made up with helices of alternate handedness.

The diffraction patterns obtained for TATA/Toluene at T = 10 °C, T = 35 °C and T = 65 °C confirm the sequence of three different molecular structure as expected from the outcomes of the temperature–concentration phase diagram (Fig. 3d). For the last two temperatures the prominent peak is shifted to lower q values (q₃₅ = q₆₅ = 1.779 nm⁻¹).

For T = 10 °C, a crystalline lattice whose diffraction peaks can be indexed on the basis of structure II reported in the solid state (Table S1, ESI†). The resulting lattice parameters are a = 3.66 nm and b = 6.5 nm, γ = 90° are, however, larger, which implies that the structure of TATA/Toluene systems at T = 10 °C is nothing but a swollen version of structure II (see Fig. 4). A small peak is seen at q = 8.68 nm⁻¹, which corresponds to d = 0.73 nm. The meaning of this peak will be discussed below.

For T = 35 °C, the peaks of the diffraction pattern can still be indexed with the same type of lattice yet with even larger a and b parameters (a = 3.72 nm and b = 11.22 nm, γ = 90°) on account of the shift of the peaks toward the lower q values (Fig. 4). This suggests a higher degree of solvation, namely a larger stoichiometry, as discussed above for TATA/DCE systems, and another rare case where the stoichiometry increases on heating.

A narrow peak is again observed at q = 8.68 nm⁻¹ as with the system at T = 10 °C. Due to its large intensity and narrowness, this peak at q = 8.68 nm⁻¹ is probably not related to the 2D lattice. At this stage, we suspect it to be possibly related to the elevation parameter h_new of a new helical structure. This value h_new= 0.73 is about 1.5 larger than that of the 20₁ helix. The “intercalation” of solvent molecules between the phenyl groups is a possible way of increasing this parameter, something already contemplated on the basis of recent neutron diffraction on benzene derivatives.^16,17 The appearance of peaks when deuterated solvent is used suggests an organization of the latter different from a simple solvation shell. This presumably intercalated solvent molecules may correspond to the tightly-bound solvent. It should be mentioned that the peak at d = 0.48 nm assigned to the N–N distance is still present in the WAXS patterns (see ESI† S5). Yet, the elevation of a helix is not necessarily the distance between the adjacent nitrogen atoms, but is related to the repeat unit of the helix (see for instance the case of the 2₁ helix of syndiotactic polystyrene^40,41 where the repeat unit consists of two monomers).

Above T = 65 °C, the diffraction pattern is essentially the same except the vanishing of the peak at q = 8.68 nm⁻¹. The 1st order transformation pointed out by DSC, namely C₂ → C₃ may then correspond to a helix-helix transition without change of the 2D lattice.

Morphology

The morphologies of the four systems have been studied by TEM for dilute dispersions dropped onto a carbon-coated grid, and cryoSEM on freeze-fractured gels or pseudo-gels. In addition to revealing the elongated aspect of the objects constituting the system, their interconnection can be further evaluated.

Here it is worth underlying that oscillatory rheology commonly used for recognizing a gel, namely G′> G′′, may be deceiving. As shown by Collin et al.,⁴² and already reported for polymer thermoreversible gels⁴³G′> G′′ can be satisfied in the usual frequency range, yet compression experiments can reveal that the system is actually characterized by very long, finite relaxation times, which implies the absence of permanent connectedness. This has been discussed in details in ref. 6 and 14, particularly the cascade of criteria that have to be considered before deciding about the gel status of a system.

The TEM pictures of TATA/DCE systems reveal an assembly of well-defined elongated, platelets, crystal-like objects. The TATA helices are within the plane.^28–30 Their extremities are generally frayed, while the sides are regular. Their typical widths stand somewhere between 0.1–0.5 μm. In view of the transparency of these crystals, their thickness is most probably well below 50 nm. These objects are essentially not connected with one another. Clearly, these systems cannot be regarded as gels. While TATA molecules are generally considered organogelators, this property does not apply to DCE. As already suggested, this emphasizes that the formation of organized structures does not necessarily entails the creation of a network. These systems are therefore pseudo-gels as they may deceivingly show apparent gel properties, such as absence of flow when submitted to the tube-tilting test. These systems would most probably display thixotropic behaviour.

Conversely, the objects generated by TATA/TCE dilute systems display curved features with a high degree of interconnection. Typically, their widths are somewhere between 0.05–0.4 μm, that is about one order of magnitude smaller than those in DCE. Yet, one can still observe a small amount of rectangular-shaped crystals of a few microns’ width. Seemingly, the curved crystals may arise from the “peeling” of the larger rectangular-shaped crystals (see ESI† Fig. S6).

The dilute TATA/TBE systems appear as dispersed “splinters” detached from bigger shapeless objects. Again, these splinters are produced by lateral aggregation of TATA helices. The cross-sections of these objects lay within 0.06–0.3 μm, while their lengths are somewhere between 0.5–2 μm. As already mentioned for the thermodynamic properties, the change from chlorine atoms to bromine atoms has also a conspicuous effect on the morphology, which is most probably related to the molecular structure.

TATA/Toluene systems do exhibit an unmistakable network structure: fibrils of various cross-sections ranging from 0.1–1.2 μm are connected with one another. Here too, the fibrils arise from lateral aggregation of the TATA helices (Fig. 5).

Fig. 5 Transmission electron micrographs from low-concentrated TATA/solvent systems as indicated. Inset in image top left highlights the frayed fibrils extremities.

The cryoSEM investigations on the concentrated systems confirm globally the conclusions drawn from TEM on dilute systems (Fig. 6). The connections are clearly absent in the case of DCE systems. In TATA/TBE systems, the objects have a more regular fibrillar shape, and are interconnected.

Fig. 6 Scanning electron microscopy images from moderately-concentrated TATA/solvent systems (0.05 g cm⁻³) as indicated.

The cross-sections possess values virtually identical to those determined in dilute systems, namely 0.1–0.5 μm in TATA/DCE, 0.05–0.2 μm in TATA/TCE, 0.05–0.5 μm in TATA/TBE, and 0.3–1.2 μm in TATA/Toluene.

Although EM pictures may not faithfully represent the actual wet gel structure, the difference between TATA/TCE, TATA/DCE, and TATA/Toluene cannot be assigned to preparation artefacts. TATA/DCE is reminiscent of assemblies of single crystals, that are not interconnected.

Concluding remarks

We again emphasize in this paper that the thermodynamic behaviour of binary systems with supposedly gelling properties cannot be described with the only Hansen solubility parameter, more specifically the occurrence of molecular compounds. All the results are consistent with the existence of at least one TATA/solvent molecular compound, and even more than one in some aromatic solvents.¹⁷ Interestingly, some compounds form or transform around room temperature, something that should be considered when determining the onset gelation concentration. Clearly, this concentration is too much dependant on many parameters that it should not be designated as “critical”.⁶

In the case of toluene another helical structure is contemplated wherein solvent molecules may be intercalated (tightly-bound solvent). This assumption meets recent neutron diffraction results that highlight some degree of organization of the solvent. Yet, the overall organization of these systems does not allow one to place the solvent molecules within the structure. From recent neutron diffraction experiments it can be stated that part of the solvent is organized as opposed to being randomly located between the TATA helices.¹⁶ Further neutron diffraction investigations on oriented samples would be necessary in an attempt to place the bound solvent molecules within the helical structure.

Finally, the morphology investigation reveals that some systems, although displaying elongated objects, such as TATA/TCE, cannot be regarded as gel due to the conspicuous lack of physical cross-linking. This is why the term pseudo-gel is used in the title as all systems cannot be a gel. Again, the Hansen parameter cannot be used for deciding whether a network will be produced or not for a specific system.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors are indebted to C. Saettel for experimental assistance in the DSC data acquisition.

References

1. P. Terech and R. G. Weiss, Low molecular mass gelators of organic liquids and the properties of their gels, Chem. Rev., 1997, 97, 3133.
2. In Molecular Gels: Materials with Self-Assembled Fibrillar Networks, ed. P. Terech, R. G. Weiss, Springer Verlag, 2006.
3. X. L. Liu and J. L. Li, Soft Fibrillar Materials: Fabrication and Applications, Wiley-VCH, 2013.
4. R. G. Weiss, The past, present and future of molecular gels. What is the status of the field, and where is it going?, J. Am. Chem. Soc., 2014, 136, 7519.
5. S. S. Babu, V. K. Praveen and A. Ajayaghosh, Functional π-Gelators and Their Applications, Chem. Rev., 2014, 114, 1973.
6. J. M. Guenet, Organogels: thermodynamics, structure, solvent role and properties, Springer International Publishing, N.Y., 2016.
7. Monograph in Supramolecular Chemistry, Molecular Gels, Structure and Dynamics, ed. Weiss, R. G., Royal Society of Chemistry, London, 2018.
8. P. Dastidar, Supramolecular gelling agents: can they be designed?, Chem. Soc. Rev., 2008, 37, 2699.
9. Y. Lan, M. G. Corradini, R. G. Weiss, S. R. Raghavan and M. A. Rogers, To gel or not to gel: correlating molecular gelation with solvent parameters, Chem. Soc. Rev., 2015, 44, 6035.
10. M. Raynal and L. Bouteiller, Organogel formation rationalized by Hansen solubility parameters, Chem. Commun., 2011, 47, 8271.
11. N. Yan, Z. Xu, K. K. Diehn, S. R. Raghavan, Y. Fang and R. G. Weiss, How do liquid mixtures solubilize insoluble gelators? Self-assembly properties of pyrenyl-glucono gelators in tetrahydrofuran-water mixtures, J. Am. Chem. Soc., 2013, 135, 8989.
12. J. Bonnet, G. Suissa, M. Raynal and L. Bouteiller, Organogel formation rationalized by Hansen solubility parameters: dos and don’ts, Soft Matter, 2014, 10, 3154.
13. A. W. Longman, Dictionary of English language and culture, Longman Group UK ltd, Harlow, 1992.
14. J. M. Guenet, Physical Aspects of Organogelation: A Point of View, Gels, 2021, 7, 65.
15. C. M. Hansen, Hansen Solubility Parameter, Users’ handbook, CRC Press, 2nd edn, 2007.
16. J.-M. Guenet, B. Demé, O. Gavat, E. Moulin and N. Giuseppone, Evidence by neutron diffraction of molecular compounds in triarylamine tris-amide organogels and in their hybrid thermoreversible gels with PVC, Soft Matter, 2022, 18, 2851.
17. X. Yao, D. Collin, O. Gavat, A. Carvalho, E. Moulin, N. Giuseppone and J.-M. Guenet, Effect of solvent isomer on the gelation properties of tri-aryl amine organogels and their hybrid thermoreversible gels with poly[vinyl chloride], Soft Matter, 2022, 18, 5575.
18. J. J. Point and C. Coutelier, Linear high polymers as host in intercalates. Introduction and example, J. Polym. Sci. Polym. Phys., 1985, 23, 231.
19. J. J. Point, C. Coutelier and D. Villers, Intercalates with linear polymer host. Part 4. Structure of p-C6H4XY-polyoxyethylene) intercalates from unit-cell determination and energy minimization, J. Phys. Chem., 1986, 90, 3277.
20. A. Chenite and F. Brisse, Structure and conformation of poly(ethylene oxide), PEO, in the trigonal form of the PEO-urea complex at 173 K, Macromolecules, 1991, 24, 2221.
21. V. Petraccone, G. Esposito, O. Tarallo and L. Caporaso, A New Clathrate Class of Syndiotactic Poly(p-methylstyrene) with a Different Chain Conformation, Macromolecules, 2005, 38, 5668.
22. V. Petraccone, O. Tarallo, V. Venditto and G. Guerra, An Intercalate Molecular Complex of Syndiotactic Polystyrene, Macromolecules, 2005, 38, 6965.
23. J. M. Guenet, Polymer-solvent molecular compounds, Elsevier, London, 2008.
24. S. J. George, Z. Tomovic, P. H. J. Albertus Schenning and E. W. Meijer, Insight into the chiralinduction in supramolecular stacks through preferential solvation, Chem. Commun., 2011, 47, 3451.
25. K. K. Kartha, S. S. Babu, S. Srinivasan and A. Ajayaghosh, Attogram Sensing of Trinitrotoluene with a Self-Assembled Molecular Gelator, J. Am. Chem. Soc., 2012, 134, 4834.
26. K. K. Kartha, A. Sandeep, V. K. Praveen and A. Ajayaghosh, Detection of Nitroaromatic Explosives with Fluorescent Molecular Assemblies and π-Gels, Chem. Rec., 2015, 15, 252.
27. L. Feng and K. A. Cavicchi, Investigation of the relationships between the thermodynamic phase behavior and gelation behavior of a series of tripodal trisamide compounds, Soft Matter, 2012, 8, 6483.
28. E. Moulin, J. J. Armao IV and N. Giuseppone, Triaryl amine-based supramolecular polymers: structure, dynamics, and functions, Acc. Chem. Res., 2019, 52, 975.
29. J. J. Armao IV, M. Maaloum, T. Ellis, G. Fuks, M. Rawiso, E. Moulin and N. Giuseppone, Healable supramolecular polymers as organic metals, J. Am. Chem. Soc., 2014, 136, 11382.
30. A. Osypenko, E. Moulin, O. Gavat, G. Fuks, M. Maaloum, A. J. Koenis Mark, W. J. Buma and N. Giuseppone, Temperature control of sequential nucleation–growth mechanisms in hierarchical supramolecular polymers, Chem. – Eur. J., 2019, 25, 13008.
31. D. Collin, G. Viswanatha-Pillai, O. Gavat, A. Vargas Jentzsch, E. Moulin, N. Giuseppone and J. M. Guenet, Some remarkable rheological and conducting properties of hybrid PVC thermoreversible gels/organogels, Gels, 2022, 8, 557.
32. P. Talebpour, B. Heinrich, O. Gavat, A. Carvalho, E. Moulin, N. Giuseppone and J. M. Guenet, Modulation of the Molecular Structure of Tri-aryl Amine Fibrils in Hybrid Poly[vinyl chloride] Gel/Organogel Systems, Macromolecules, 2021, 54, 8104.
33. B. Kiflemariam, D. Collin, O. Gavat, A. Carvalho, E. Moulin, N. Giuseppone and J. M. Guenet, Hybrid materials from tri-aryl amine organogelators and poly[vinyl chloride] networks, Polymer, 2020, 207, 122814.
34. O. A. Pringle and P. W. Schmidt, Small-Angle X-Ray Scattering from Helical Macromolecules, J. Appl. Crystallogr., 1971, 4, 290.
35. G. Oster and D. P. Riley, Scattering from Cylindrically Symmetric Systems, Acta Cryst., 1952, 5, 272.
36. P. Mittelbach and G. Porod, Zur Röntgenkleinwinkelstreuung verdünnter kolloiden Systeme, Acta Phys. Austriaca, 1961, 14, 185.
37. M. Le Chatelier, Les alliages métalliques, Rev. Gen. Sci., 1895, 6, 529.
38. C. T. Heycock and F. H. Neville, On the Constitution of the Copper Tin Series, Phil. Trans., 1903, 202, 1.
39. X. J. Liu, C. P. Wang, I. Ohnuma, R. Kainuma and K. Ishida, Experimental Investigation and Thermodynamic Calculation of the Phase Equilibria in the Cu-Sn and Cu-Sn-Mn Systems, Metallurgical, Mater. Trans. A, 2004, 35A, 1641.
40. A. Immirzi, F. de Candia, P. Ianelli, A. Zambelli and V. Vittoria, Makromol. Chem. Rapid Commun., 1988, 9, 761.
41. V. Vittoria, F. de Candia, P. Ianelli and A. Immirzi, Makromol. Chem. Rapid Commun., 1988, 9, 765.
42. D. Collin, R. Covis, F. Allix, B. Jamart-Grégoire and P. Martinoty, Jamming transition in solutions containing organogelator molecules of amino-acid type: rheological and calorimetry experiments, Soft Matter, 2013, 9, 2947.
43. C. Daniel, C. Dammer and J. M. Guenet, On the Definition of Thermoreversible Gels: Case of Syndiotactic Polystyrene, Polymer, 1994, 35, 4243.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00624g

‡ For the author biography see https://www.ics-cnrs.unistra.fr/member-141-Guenet%20Jean-Michel.html

---