Open Access Article
Open Access ArticleSpontaneous motion of a passive fluid droplet in an active microchannel†
Adriano
Tiribocchi
 *a,
Mihir
Durve
b,
Marco
Lauricella
*a,
Mihir
Durve
b,
Marco
Lauricella
 a,
Andrea
Montessori
c and
Sauro
Succi
abd
a,
Andrea
Montessori
c and
Sauro
Succi
abd
aIstituto per le Applicazioni del Calcolo CNR, via dei Taurini 19, 00185 Rome, Italy. E-mail: adriano.tiribocchi@cnr.it
bCenter for Life Nano Science@La Sapienza, Istituto Italiano di Tecnologia, 00161, Roma, Italy
cDipartimento di Ingegneria Civile, Informatica e delle Tecnologie Aeronautiche (DICITA), Università degli studi Roma Tre, Via Vito Volterra 62, 00146 Rome, Italy
dDepartment of Physics, Harvard University, Cambridge, MA 02138, USA
First published on 9th August 2023
Abstract
We numerically study the dynamics of a passive fluid droplet confined within a microchannel whose walls are covered with a thin layer of active gel. The latter represents a fluid of extensile material modelling, for example, a suspension of cytoskeletal filaments and molecular motors. Our results show that the layer is capable of producing a spontaneous flow triggering a rectilinear motion of the passive droplet. For a hybrid design (a single wall covered by the active layer), at the steady state the droplet attains an elliptical shape, resulting from an asymmetric saw-toothed structure of the velocity field. In contrast, if the active gel covers both walls, the velocity field exhibits a fully symmetric pattern considerably mitigating morphological deformations. We further show that the structure of the spontaneous flow in the microchannel can be controlled by the anchoring conditions of the active gel at the wall. These findings are also confirmed by selected 3D simulations. Our results may stimulate further research addressed to design novel microfludic devices whose functioning relies on the collective properties of active gels.
1. Introduction
The last few years have seen a rapid surge in the study of active matter, which deals with systems composed of self-driven units capable of converting stored energy into systematic movement.1 Active matter encompasses a large variety of natural and artificial instances, ranging from flocks of birds2 and school of fishes3 at the macroscopic scale to suspensions of bacteria,4 cytoskeletal proteins5 and self-propelled colloids at the microscopic one.6 Their inherent non-equilibrium nature results in a wealth of enthralling phenomena, such as spontaneous flows,7,8 active turbulence,9,10 anomalous diffusion,11 superfluid-like behavior12,13 and motility induced phase separation,14,15 to name a few.Innovative examples of autonomous systems are synthetic self-propelled droplets, i.e. spatially confined fluid suspensions whose motion is guided by sophisticated modes of propulsion mechanisms which can involve, for example, the use of an active gel confined within.16–20 Some of the best known experimental realizations of such active materials are actomyosin solutions21,22 and suspensions of microtubules and kinesin,7,23 which are soft fluids comprising force dipoles exhibiting a long range orientational order typical of liquid crystals.24–26 The former is an example of contractile material since the dipolar forces (exerted by the myosin) are directed towards the center of mass, whereas the latter pertains to extensile fluids. From a technological perspective, active gel droplets are gaining significant interest as model systems for studying the dynamics of micro-organisms, such as cells,27–31 and for designing artificial microswimmers.32–40
Alongside these objects, an alternative design is represented by the “inverted” counterpart, i.e. passive Newtonian droplets surrounded (partially or entirely) by an active (or passive) gel.41,42 A number of theoretical and experimental works have demonstrated that the inclusion of micron-sized objects in an active fluid bath often results in a persistent motion induced by a combination of mechanical energy extracted by the surrounding fluid and a careful manufacturing of the object, such as rigid structures with asymmetric boundaries43–45 or soft deformable ones, like polymeric chains.46,47 It would then be natural to ask whether similar conditions can be realized in the context of inverted liquid crystals, where a passive drop can be spontaneously set into motion using the energy provided by the external active gel. Indeed, while many efforts have been dedicated to realizing self-motile droplets containing the active material, a much less investigated system is that in which the latter is hosted in the exterior environment.
In this paper we consider a microchannel comprising a mixture of an active extensile gel and a passive isotropic fluid, where the former is confined within a thin layer attached to the wall while the latter occupies the rest of the channel and is made of a Newtonian fluid droplet immersed in a second fluid (see Fig. 1a). With respect to a typical “inverted” design where a passive drop would be fully embedded in an active medium, here the active component is distanced from the drop and occupies only a small portion of the channel. Such a system could be realized in the lab by dispersing self-attractive cytoskeletal gels in a layer of water wetting the wall (following a protocol akin to that discussed in ref. 16), while the passive mixture could be produced through usual microfluidic techniques.35,48,49
We will show below that this geometry is capable of producing a spontaneous flow triggering a unidirectional motion of the passive drop, with a speed strongly depending on the activity. We also find that, if the active layer covers a single wall, the flow propelling the drop displays an asymmetric saw-tooth profile, fostering significant morphological changes for high activities. Alternatively, if the layers cover both walls, the fluid velocity acquires a symmetric profile suppressing droplet deformations. In agreement with previous works,50 our results also suggest that controlling the orientation of the active gel at the boundaries decisively affects the emerging flow as well as the speed and shape of the droplet. These findings could be relevant for the design of autonomous microdevices able to sort and drive non-motile drops in a predictable manner, a challenging task in active matter especially if the need for keeping a certain direction of motion is required for long periods of time.51,52 In addition, they may be potentially useful for realizing energy-saving soft systems whose functioning would require a reduced amount of active material (and hence energy) with respect to a fully inverted geometry.41
The paper is structured as follows. In the next section we shortly describe the theory and some numerical details while in the following ones we illustrate the results. First we discuss the physics of a passive drop plus a single active layer in terms of the structure of the flow and droplet kinematics, and then we move on to the case with two layers. Afterwards, the effect of boundary conditions is described and, before concluding, a selection of 3D results is presented.
2. The model
Here we shortly summarize the theoretical model used in this work. Our system consists of a two dimensional microfluidic channel in which a passive fluid droplet is surrounded by a passive solvent (see Fig. 1a) while a layer of extensile material is glued at the bottom wall. Its physics is described using a combination of phase field modeling and active liquid crystal hydrodynamics, an approach already adopted in previous works.32,53–56 More specifically, we consider two scalar phase fields ϕi(r, t) (i = 1, 2) accounting for the density of the droplet and the layer, a polar field P(r, t) capturing the mesoscale orientation of the active material confined within the layer, the density ρ(r, t) of the fluid and its global velocity v(r, t). The presence of a further active component (such an extensile layer on the top wall) would require the inclusion of additional scalar and polar fields.The equilibrium features of a passive suspension are encoded in the following free energy density
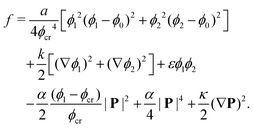 | (1) |
The fields ϕ and P generally obey advection-diffusion equations, in which the time evolution is governed by thermodynamic forces obtained by functional differentiation of the free energy 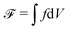 .
.
The equation of the scalar phase field ϕi is
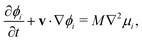 | (2) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /ϕi is the chemical potential.
/ϕi is the chemical potential.
The equation of the polar field P is given by
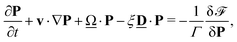 | (3) |
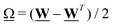 ,
, 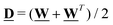 and Wαβ = ∂βvα (Greek indexes denote Cartesian components). We set ξ > 1 as usually done for flow-aligning rodlike particles. Also, Γ is the collective diffusion rotational constant multiplying the molecular field h = δ
and Wαβ = ∂βvα (Greek indexes denote Cartesian components). We set ξ > 1 as usually done for flow-aligning rodlike particles. Also, Γ is the collective diffusion rotational constant multiplying the molecular field h = δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /δP.
/δP.
The density ρ and the fluid velocity v are governed by the Navier-Stokes equations which, in the incompressible limit, are
| ∇·v = 0, | (4) |
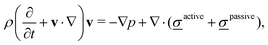 | (5) |
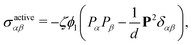 | (6) |
The passive stress consists of three further contributions, namely a viscous one given by
| σviscousαβ = η(∂ανβ + ∂βνα) | (7) |
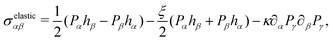 | (8) |
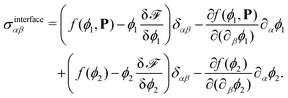 | (9) |
2.1 Numerical aspects
Eqn (2)–(5) are numerically solved by a hybrid lattice Boltzmann (LB) method,58–61 where a standard LB approach is used to integrate eqn (4) and (5) and a finite-difference scheme for eqn (2) and (3).Our 2D simulations are run on rectangular boxes of size Lz = 140 (vertical one) and Ly = 400 (horizontal one) lattice sites. Periodic boundary conditions are set along the y direction while two flat parallel walls are placed at z = 0 and z = Lz. A passive fluid droplet is placed in the middle of the microchannel and a layer of extensile fluid is glued at the bottom wall (see Fig. 1). The scalar fields are initialized as follows: ϕ1 ≃ 2 within a layer of height ranging from h = 10 to h = 30 lattice sites (thus occupying a portion from 5 to 20 percent of the channel) and zero everywhere else, while ϕ2 ≃ 2 solely within the passive droplet of radius R = 20. Also, the polar field is set uniform and parallel to the y direction (i.e.P(r, 0) = Py(r, 0) with Py = 1) within the layer and zero outside. We impose no-slip conditions at both walls for v, i.e. v|z=0,Lz = 0, tangential anchoring at the bottom wall for P, i.e. P|z=0 = Py and neutral wetting for ϕi, meaning that n·∇μi|z=0,Lz = 0 (no mass flux through the walls) and n·∇(∇2ϕi)|z=0,Lz = 0 (interfaces perpendicular to the walls), with the n unit vector normal to the boundaries. The addition of an active layer at the top wall follows an analogous prescription, i.e. a further scalar field identifying a region of thickness ranging from 10 to 30 lattice sites with a uniform and unidirectional polarization pointing towards the y-direction. Accordingly, neutral wetting and strong planar anchoring are set at the wall.
Following previous works,32,41,62 thermodynamic parameters have been chosen as follows: a = 4 × 10−2, k = 6 × 10−2, ε = 5 × 10−3, α = 10−1, κ = 4 × 10−2, ξ = 1.1, Γ = 1, M = 10−1, η = 1.67, while ζ is generally varied between ≃10−3 and ≃5 × 10−2. Parameters a and k determine the value of the surface tension σ and interface thickness λ which, for simplicity, are the same for the droplet and active layer. One has 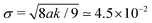 and
and 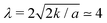 . Also, the lattice spacing and integration timestep are fixed to Δx = 1 and Δt = 1. Suitable dimensionless quantities capturing the physics at the mesoscale are the Reynolds number, the Capillary number and the Ericksen number. The first one, defined as Re = ρvdD/η (where vd is the droplet speed at the steady state and D is its diameter) ranges from ∼5 × 10−2 to ∼1, whereas the second one, defined as Ca = vdη/σ varies between ∼4 × 10−2 and ∼7 × 10−1. These values ensure that the flow is laminar and droplet breakup is a very unlikely event. Finally, the Ericksen number is defined as
. Also, the lattice spacing and integration timestep are fixed to Δx = 1 and Δt = 1. Suitable dimensionless quantities capturing the physics at the mesoscale are the Reynolds number, the Capillary number and the Ericksen number. The first one, defined as Re = ρvdD/η (where vd is the droplet speed at the steady state and D is its diameter) ranges from ∼5 × 10−2 to ∼1, whereas the second one, defined as Ca = vdη/σ varies between ∼4 × 10−2 and ∼7 × 10−1. These values ensure that the flow is laminar and droplet breakup is a very unlikely event. Finally, the Ericksen number is defined as 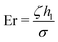 , where hl is the height of the layer. On a general basis, if this parameter is larger than 1 the active forces would overcome the resistance to deformation of the liquid crystal (controlled by the elastic constant κ), thus inducing a spontaneous flow. In our simulations, a sufficiently intense flow capable of triggering the motion of the passive droplet is found at Er ≃ 1.3, for hl ≃ 30. Note that this effect occurs only if the polarization (initially uniform everywhere in the layer, with P = Py) is destabilized by a weak perturbation, such as a change of the local orientation of the polar field, lasting for a short period of time. Otherwise, in a perfectly ordered and parallel collection of extensile units, the self-generated force dipoles would cancel and no spontaneous flows would be produced.
, where hl is the height of the layer. On a general basis, if this parameter is larger than 1 the active forces would overcome the resistance to deformation of the liquid crystal (controlled by the elastic constant κ), thus inducing a spontaneous flow. In our simulations, a sufficiently intense flow capable of triggering the motion of the passive droplet is found at Er ≃ 1.3, for hl ≃ 30. Note that this effect occurs only if the polarization (initially uniform everywhere in the layer, with P = Py) is destabilized by a weak perturbation, such as a change of the local orientation of the polar field, lasting for a short period of time. Otherwise, in a perfectly ordered and parallel collection of extensile units, the self-generated force dipoles would cancel and no spontaneous flows would be produced.
A mapping to real units can be built considering that a unit of time, length and force in our simulations are approximately equal to L = 1 μm, T = 1 ms and F = 100 nN. Thus, our numerical experiment would simulate a droplet of diameter D ≃ 40 μm with σ ≃ 4 mN m−1 moving at speed ranging from 1 to 10 μm s−1 (corresponding to values varying between 10−3 and 10−2) in a Newtonian fluid, such as water. The active layer of thickness ranging from ≃10 to ≃30 μm would consist of an extensile material (such as a bacterial suspension) with a shear viscosity η ≃ 0.1 kPa s, elastic constant κ ≃ 4 nN and activity ζ ≃ 102 Pa.
3. Results
We start off by discussing the dynamics of the passive droplet whose motion is triggered by the active layer glued at the bottom wall of a microfluidic channel. Afterwards we study the effect produced by a second active layer attached at the opposite wall and, finally, we showcase a selection of results obtained for a 3d channel. In all such cases, the drop is initially placed in the middle of the microchannel while the layers uniformly cover the walls. Once the drop and layer are relaxed towards equilibrium, the liquid crystal is activated by setting ζ to values capable of generating a sufficiently high spontaneous flow.3.1 Single active layer
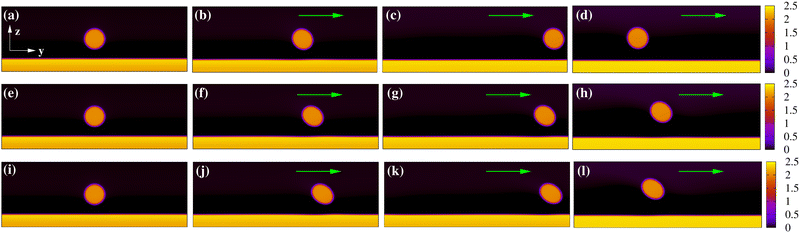
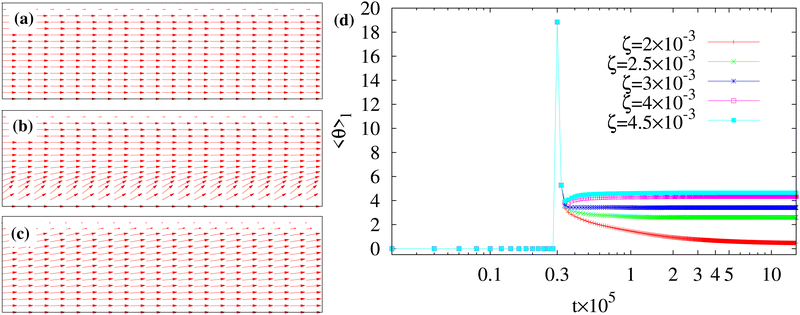
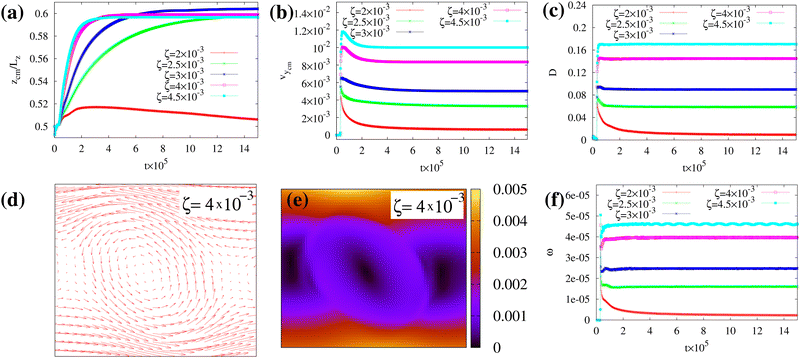
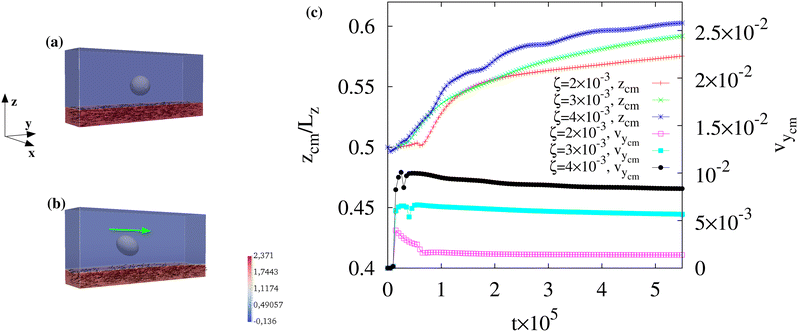
We generally identify a regime for ζ ≲ 4.5 × 10−3 where the spontaneous flow triggers a unidirectional motion, while for ζ > 4.5 × 10−3 the flow destabilizes and breaks the layer.In Fig. 1 we show a time sequence of the droplet dynamics for h/Lz ≃ 0.2, R = 20 and 2 × 10−3 ≲ ζ ≲ 4.5 × 10−3, a range of values for which a long-lasting motion can be observed (see also the ESI,† Movies M1–M3). As previously mentioned, this is sustained by the flow produced by the active liquid crystal located within the layer. Since the polar field is initially uniform (Fig. 2a), the extensile force pairs of each active unit nullify. Hence, in order to unbalance these forces and generate a spontaneous flow, the orientation of the field above the bottom wall is slightly tilted with an angle θ (with 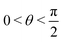 ), a process that concurrently changes the orientation of the surrounding liquid crystal except that at the walls, which remains fixed (Fig. 2b). This perturbation lasts for a period of time sufficient to destabilize the direction of the polarization, while preserving the integrity of the layer. Later on, the polar field recovers a uniform orientation albeit not parallel to the wall anymore (see Fig. 2c). A rough estimate of its slope can be evaluated by computing the time evolution of the angle 〈θ〉l averaged over a layer of thickness l < h (with l ≃ 10, see Fig. 2d), which identifies a region where a substantial change of orientation occurs. Once the field is perturbed, 〈θ〉l shows a sharp peak at approximately 20 degrees, followed by a rapid relaxation towards a steady state whose value generally increases with ζ. For activities lower than 2 × 10−3, 〈θ〉l would approach zero, thus drastically weakening the spontaneous flow.
), a process that concurrently changes the orientation of the surrounding liquid crystal except that at the walls, which remains fixed (Fig. 2b). This perturbation lasts for a period of time sufficient to destabilize the direction of the polarization, while preserving the integrity of the layer. Later on, the polar field recovers a uniform orientation albeit not parallel to the wall anymore (see Fig. 2c). A rough estimate of its slope can be evaluated by computing the time evolution of the angle 〈θ〉l averaged over a layer of thickness l < h (with l ≃ 10, see Fig. 2d), which identifies a region where a substantial change of orientation occurs. Once the field is perturbed, 〈θ〉l shows a sharp peak at approximately 20 degrees, followed by a rapid relaxation towards a steady state whose value generally increases with ζ. For activities lower than 2 × 10−3, 〈θ〉l would approach zero, thus drastically weakening the spontaneous flow.
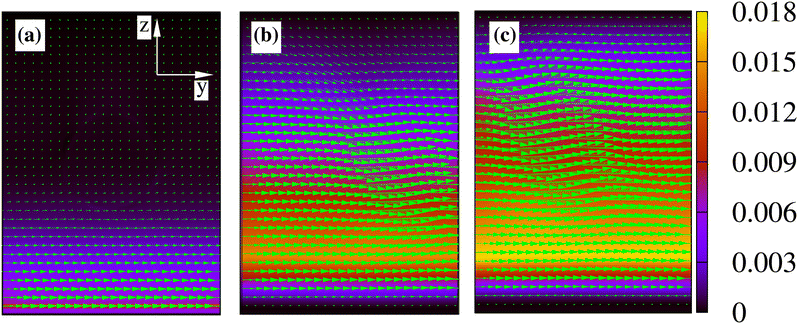
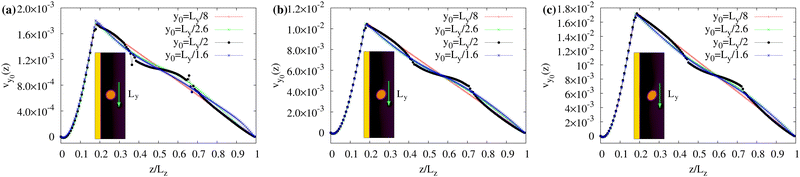
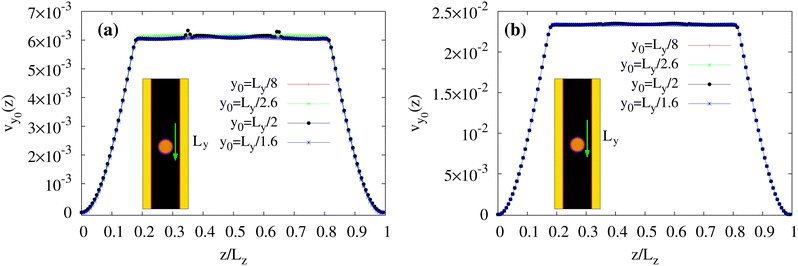
This mechanism produces a velocity field whose typical structure is shown in Fig. 3. At the onset of the instability the velocity is larger within the layer (Fig. 3a) and, afterwards, it becomes essentially unidirectional in the whole channel (except in the surrounding of the droplet where weak oscillations form, see Fig. 3b), preserving this pattern for long periods of time (Fig. 3c). Despite an apparent regularity, a more careful inspection of the velocity field unveils crucial non-uniform features. In Fig. 4a–c we plot its cross-sectional profile at different positions along the channel at the steady state, and show that the velocity generally displays a saw-toothed shape, growing linearly within the active layer (for 0 < z/Lz ≲ 0.2, with a sharp peak at z/Lz ≃ 0.2) essentially because the amount of material increases with the distance from the wall, and decreases outside towards the opposite wall. Weak undulations of the profile observed at y0 = Ly/2 are, once again, due to the presence of the droplet, which is located in the middle of the channel. Close to the wall at z/Lz ≃ 1, the slope of the curve levels out the one in the bulk whereas, near the opposite wall at z = 0, it is basically flat because the strong and parallel anchoring of the liquid crystal stabilizes a tiny stress-free region. Indeed, at the steady state one has 〈σtotyz〉s ∼ 0, where σtotyz = σactiveyz + σviscousyz + σelasticyz + σinterfaceyz, averaged over a layer of thickness s near the wall. A more detailed description of the effect produced by a change of liquid crystal orientation at the wall is given later, in the paragraph focused on the boundary conditions.
As previously discussed, this flow field induces a persistent motion of the droplet along a rectilinear trajectory and essentially at a constant speed. This is shown in Fig. 5a and b where the time evolution of the z component of the center of mass and y component of its speed are plotted for different values of ζ. Once ζ is turned on, the drop shifts towards the upper wall because of the initial asymmetry of the velocity field (larger in the active layer and weaker outside, see Fig. 3a), an effect that boosts the early time motion (see the peak of vycm). Then, the droplet stabilizes at z/Lz ≃ 0.6 for sufficiently high values of ζ and travels at a constant velocity (whose values increase with ζ). Note that the lift-like effect towards the top wall is also conditioned by the Reynolds and Capillary numbers. Indeed, while for low values of ζ (thus weak flows) the drop essentially moves along the mid-line of the channel (see Fig. 5a, ζ = 2 × 10−3), for higher values it is subject to more intense flows and large shape deformations, which favour the shift upwards (see Fig. 1h, l and 5a).
Such morphological changes are quantitatively captured by the Taylor parameter 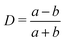 (where a and b represent the major and minor axis of the droplet), which ranges between 0 (no deformation, circular drop) to 1 (maximal deformation, needle-like shape). At early times D generally exhibits a peak becoming milder as ζ increases, an effect mirroring the one seen for vycm and indicating that the drop undergoes a quick deformation once the activity is turned on. Afterwards, D relaxes to a steady state value faster for higher ζ, since a strong flow stabilizes the shape changes easier than a weaker one (Fig. 5c).
(where a and b represent the major and minor axis of the droplet), which ranges between 0 (no deformation, circular drop) to 1 (maximal deformation, needle-like shape). At early times D generally exhibits a peak becoming milder as ζ increases, an effect mirroring the one seen for vycm and indicating that the drop undergoes a quick deformation once the activity is turned on. Afterwards, D relaxes to a steady state value faster for higher ζ, since a strong flow stabilizes the shape changes easier than a weaker one (Fig. 5c).
It is worth noting that the motion along a rectilinear trajectory is partially akin to that observed in a microchannel when the drop is subject to a Poiseuille flow (where no-slip conditions hold and the walls are at rest).63 A well-known feature of this process is that, while in the lab frame the fluid velocity displays a parabolic-like profile, in the comoving frame it would exhibit a couple of counter-rotating vortices resulting from the sheared structure of the flow. Thus, it is natural to ask whether similar structures emerge in our system. In Fig. 5d and e we show the typical steady-state velocity vs computed in the droplet frame (i.e.vs = v − vcm) for ζ = 4 × 10−3. It exhibits a well-defined counter-rotating vortex with magnitude increasing up to ≃10−3 towards the edge of the drop. As for vcm, the angular velocity is also found to gradually augment for increasing values of ζ. This is shown in Fig. 5f, where we plot the time evolution of 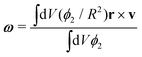 for different values of ζ. If, for example, ζ = 4 × 10−3, one has ω ≃ 4 × 10−5 and, for a droplet of radius R ≃ 20, v = ωR ≃ 10−3, thus a rolling-like condition would be satisfied. This is in contrast with the results of a spinning droplet containing an active spiral-like gel (where the rotation speed is expected to follow a logarithmic-like behavior64,65) and suggests that, although the motion is triggered by the same medium (here placed outside), the drop behaves as a fully passive object.
for different values of ζ. If, for example, ζ = 4 × 10−3, one has ω ≃ 4 × 10−5 and, for a droplet of radius R ≃ 20, v = ωR ≃ 10−3, thus a rolling-like condition would be satisfied. This is in contrast with the results of a spinning droplet containing an active spiral-like gel (where the rotation speed is expected to follow a logarithmic-like behavior64,65) and suggests that, although the motion is triggered by the same medium (here placed outside), the drop behaves as a fully passive object.
These results show that a rectilinear motion of the droplet can be generated by a properly designed layer of active material of predefined thickness. But what if the thickness decreases? In the ESI,† Movie M4 we show the dynamics in a microchannel with an active layer of thickness h = 10 lattice sites (h/Lz ≃ 0.07, three times narrower than the previous case) and ζ = 2.5 × 10−2. The motion shares features akin to the ones observed for higher values of h, although the reduced amount of active material requires higher values of ζ to set a sufficiently intense spontaneous flow.
One may finally wonder whether the shape deformations can be mitigated even for a droplet moving at high speed (such as for ζ = 4 × 10−3). This can be achieved by covering the upper wall with a further active layer, whose design follows that of the opposite one. In the next section we describe the dynamics of the drop precisely in this configuration.
3.2 Double active layer
In Fig. 6 we show a time sequence of a passive droplet moving within a microchannel with two symmetric layers for ζ = 4 × 10−3 (equal in both layers). As described in the Methods section, within the upper region one has ϕ2 ≃ ϕ0 and ϕ1 ≃ 0, while the polarization is initially parallel to the wall and points along the positive y direction. Also, the thickness of both layers is h = 30. The mechanism triggering the motion essentially mirrors the one discussed for the single layer. Once the orientation of the polar field is weakly titled of an angle θb (with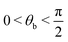 with respect to the y direction) from the bottom wall and θt from the top one (with θt = 2π − θb), the activity is turned on and a spontaneous flow emerges.
with respect to the y direction) from the bottom wall and θt from the top one (with θt = 2π − θb), the activity is turned on and a spontaneous flow emerges.
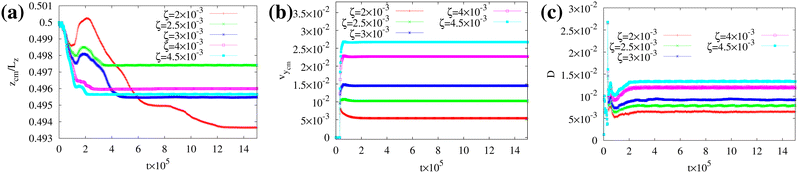
Unlike the previous case, here the fluid velocity displays a symmetric structure, uniform within the passive fluid (in the middle of the channel, the black region of Fig. 6) and growing almost linearly from the wall towards the interfaces of each layer (the yellow regions of Fig. 6) with equal slope. This is shown in Fig. 7, where we plot the steady state cross sectional profile, at different positions along the channel, for various values of ζ. For increasing activity, vy0 attains higher values and the fluctuations due to the drop interface become progressively negligible. In analogy to the single layer case, the slope of the speed near both walls is approximately flat, an effect caused by the orientation of the liquid crystal (see the section on the boundary conditions).
This flow triggers, once again, a rectilinear motion at constant speed, keeping the droplet along the mid-line of the channel, regardless of the values of ζ (see Fig. 8a and b). In addition, the flat pattern of the velocity profile in the passive fluid suppresses morphological deformations (see Fig. 8c) and stabilizes a droplet that maintains a long-lasting circular shape. Note also that the speed of the drop is approximately twice that obtained in the single layer, provided that ζ is set to equal values in both regions.
Interestingly, the flow structure closely resembles the electro-osmotic flow observed across porous materials and capillary tubes.66–68 In this case, the flow is caused by an electric field (applied, for instance, via electrodes) which induces the motion of a net charge forming two tiny layers of mobile ions, sandwiched between the wall of the microchannel and the bulk electrolyte solution. The resulting flow field is found to display a growing profile within the electrical layers (which would correspond to the yellow layers of Fig. 6) while a uniform, flat one, in the intermediate solutions (which would correspond to the black region of Fig. 6).
3.3 Shear-like dynamics
The dynamics described so far ultimately results from the orientation of the polar field which, in both layers, points towards the positive y axis forming an angle θb with the bottom wall and θt = 2π − θb with the top one. An alternative scenario emerges if the polarization is oriented along opposite directions in the layers.In Fig. 9a we show, for example, the steady state configurations of droplet and polarization under this condition for ζ = 4 × 10−3, where the liquid crystal has been initially aligned along the negative y direction in the top layer. While at late times the latter displays the usual uniform arrangement, the droplet attains a non-motile elliptical shape induced by the shear-like structure of the velocity field (shown in Fig. 9b). Indeed, the velocity exhibits a striped pattern, where an intense bidirectional flow near the fluid interfaces of the layers combine with a much weaker counterclockwise vortex within the droplet. Near both walls, the flow is once again very low. The corresponding transversal profile is shown in Fig. 9c; it is shear-like in the passive region and almost linearly growing in the active layers, with features akin to those discussed in the previous section. Also, near the top wall (z/Lz ≃ 1), vy0 has a local maximum necessary to accommodate the stress-free region due to the parallel anchoring of P.
It is worth highlighting that the stability of this configuration crucially depends on the orientation of the liquid crystal. More specifically, shear-like dynamics occurs when θt ≃ θb + π (with 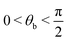 ), otherwise the droplet, still keeping an elliptical shape, would move, following a rectilinear trajectory, along the direction imposed by the larger flow, thus rightwards if π < θt < θb + π (the bottom flow dominates) or leftwards if
), otherwise the droplet, still keeping an elliptical shape, would move, following a rectilinear trajectory, along the direction imposed by the larger flow, thus rightwards if π < θt < θb + π (the bottom flow dominates) or leftwards if 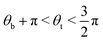 (the top one prevails).
(the top one prevails).
3.4 Boundary conditions
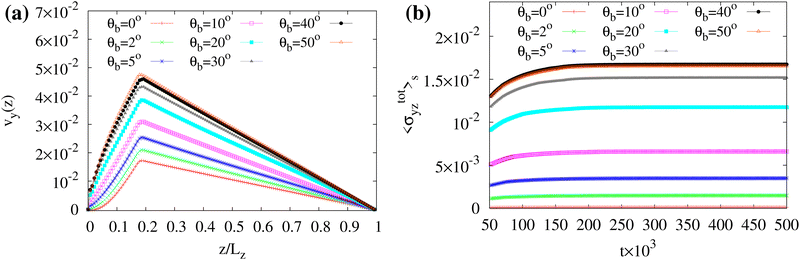
In Fig. 4, 7 and 9c we have shown that the velocity profile grows almost linearly within the active layer and is approximately flat near the wall covered by the active material. The latter crucially depends on the orientation of the liquid crystal at the wall. In Fig. 10a we plot the cross-sectional velocity profile for different anchoring angles θb at the bottom wall for ζ = 4 × 10−3. For increasing values of θb, the slope of vy sharpens (thus removing the flatness close to the wall) and the total speed concurrently grows, attaining the highest value at θb ≃ 50°. Indeed, while for θb ≃ 0 the force dipoles (aligned along the vectors P) nullify each other, for θb > 0 the balance is broken and an additional spontaneous flow is produced by the active liquid crystal anchored at the boundary. Changing of the anchoring orientation modifies the total stress too, as shown in Fig. 10b where we plot the time evolution of 〈σtotyz〉s averaged over a film of thickness s = 4 lattice sites from the bottom wall. The stress remains approximately zero for θb = 0 while it considerably augments for higher values.These results suggest that, at fixed activity, changing the tilt of the active gel at the boundary can control the structure of the spontaneous flow and, more generally, could potentially trigger the transition from a passive quiescent state towards an active one. Note that these findings extend the ones of ref. 50, which describe the formation of spontaneous flows in one dimensional liquid crystal cells only for two different anchoring conditions (perpendicular and conflicting).
3.5 Extension to 3D systems
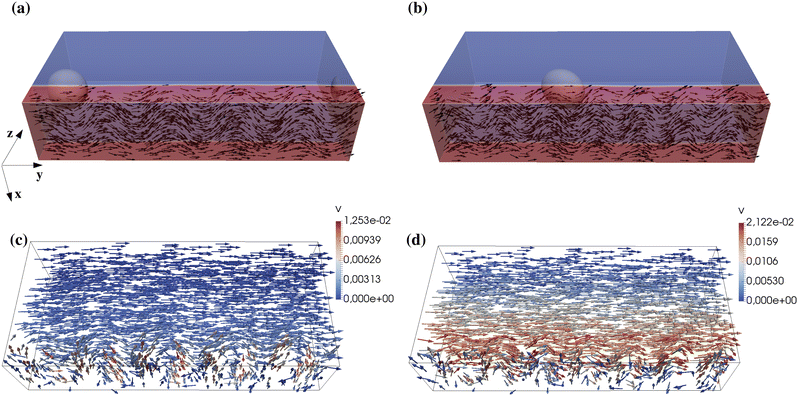
The dynamics found in 2D can be observed in a 3D microfludics channel as well. For simplicity, we consider the case where a single active layer covers the bottom wall and the polarization is initially uniform and parallel to the y axis (see Fig. 11a). The system consists of a passive fluid droplet of radius R = 20 sandwiched between two flat parallel walls placed at Lz = 0 and Lz = 140. Along the x and y directions, periodic boundary conditions are set with Lx = 70 and Ly = 300. Once the droplet is equilibrated, the activity is turned on and, following the mechanism discussed for the 2D system, a spontaneous flow is produced within the channel. This one, in turn, triggers a rectilinear motion of the droplet which, at the steady state, attains a permanent elliptical shape (Fig. 11b, c and the ESI,† Movie M5).Although these results are overall akin to the 2D system, crucial differences emerge in the polarization and velocity field within the layer. Indeed, the liquid crystal exhibits stable bend deformations mostly in the xy plane, an effect stemming from the hydrodynamic instability produced by dipolar forces of extensile materials made of rod-shaped particles (Fig. 12a and b), while the velocity field displays two distinct patterns: a unidirectional flow within the passive fluid and an undulating motif, with vectors (once again mostly in the xy plane) pointing perpendicularly to the liquid crystal orientation, in the layer (Fig. 12c and d), a result in agreement with the typical flow structure observed in extensile gels.24 It is interesting to highlight that, despite the higher complex pattern of the velocity with respect to the 2D device, the unidirectional motion of the droplet is preserved in 3D (see Fig. 11c). This is precisely because the distortions of the polar field are confined within the layer (thus the spontaneous flow displays the undulations only within this region) while out of it the fluid is passive and isotropic, and the velocity follows the direction imposed by the one in the layer for continuity. However, at high ζ (such as ζ = 4 × 10−3), the droplet trajectory and the fluid interface are found to exhibit weak oscillations, caused by temporary out-of-plane components (along z) of the polar field and of the fluid velocity (see Fig. 11c and the ESI,† Movie M5).
4. Conclusions
To summarize, we have theoretically studied the dynamics of a passive fluid droplet confined within a microfluidic channel whose walls are covered with a layer of an extensile active gel. The physics is mostly controlled by the activity and the orientation of the liquid crystal both in the layer and at the walls. Our results show that, for sufficiently high values of activity, the passive droplet acquires a rectilinear motion lasting over long periods of time caused by the spontaneous flow produced by the active material. If the active gel covers only one wall, at the steady state the droplet attains an ellipsoidal shape, whose rate of deformation increases with the activity. This is due to the asymmetric structure of the spontaneous flow, which exhibits a saw-toothed pattern with a maximum at the interface of the layer. If, in contrast, the active material covers both walls, the flow displays a trapezoidal-like symmetric structure and shape deformations turn negligible. In addition, if the liquid crystal points along opposite directions in the layers, a shear-like profile of the flow is found. These behaviors are also affected by the orientation of the liquid crystal at the wall. Indeed, our simulations suggest that, for a fixed value of activity, the magnitude of the flow (and thus the speed of the drop) increases when the anchoring angle at the wall augments. These findings are confirmed by 3D simulations, although the liquid crystal and velocity field display a more complex structure especially within the active layer, where an undulating flow favours the formation of well-defined bend distortions.In this paper we devise a strategy to control and rectify the trajectory of passive fluid drops confined in an “active” microchannel, in which the necessary work to sustain the motion is extracted from a layer of active material. This result could be in principle extended to active droplets, where maintaining a certain direction of motion remains challenging. Indeed, although an enhanced Brownian motion has been observed in drops containing either a dispersion of bacteria69,70 or a suspension of motorized microtubules,16 only recently a controllable propulsion has been realized in active droplets hosted in a nematic environment52 or activated through a Marangoni-like effect.35
Our device could be concretely realized by dispersing an extensile fluid (such as microtubule bundles and kinesin or bacterial suspensions) into a water–oil solution, in which the aqueous medium containing the active material wets the walls. To enforce a specific anchoring, the active fluid could be pinned following the protocols adopted for passive liquid crystals, i.e. through mechanical or chemical treatment of the surface.57,71 Although not discussed in the present study, it would be relevant to investigate how a predetermined anchoring at the fluid interface (where the active gel may either orient tangentially72,73 or perpendicularly74) would affect the motion of the droplet and the structure of the flow.
Finally, it is interesting to discuss some directions of future works. Releasing, for example, the approximation of single viscosity of both fluid components could be a further route to control shape deformations as well as simulate highly viscous drops closely behaving as rigid particles. In this context, the system studied in this work would partially capture the dynamics of a spherical non-deformable particle when the activity is low (as in Fig. 1a–d) whereas for non-spherical solid objects, such as elliptical ones, the dynamics is expected be more complex since in-plane or out-of-plane rotations could be observed.75 Likewise, abandoning the restriction of small Capillary numbers would be useful to explore regimes in which breakup events are more likely. While this physics is well understood in passive systems (such as a droplet subject to shear flows76,77), less is known when the rupture would be determined by a spontaneous flow, as well as to what extent this kind of flow would impact on critical Capillary numbers, beyond which no-steady state droplet exists. Our device would also be highly suitable for exploring more complex designs, such as those in which the activity is spatially dependent. One may envisage, for example, a microfluidic channel in which the wall is patterned with separated holes (realized using static phase fields32) containing an active gel which could trigger a hop-like motion of a drop dispersed in the surrounding passive fluid. This may hold an interest for the manufacturing of active energy-saving devices whose functioning relies on reduced amounts of active material.
Author contributions
A. Tiribocchi: conceptualization; data curation; formal analysis; investigation; methodology; validation; visualization; writing – original draft; writing – review & editing. M. Durve: investigation; writing – review & editing. M. Lauricella: investigation; funding acquisition; writing – review & editing. A. Montessori: investigation; writing – review & editing. S. Succi: investigation; funding acquisition; writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the European Research Council under the European Union's Horizon 2020 Framework Program (no. FP/2014-2020) ERC grant agreement no. 739964 (COPMAT) and ERC-PoC2 grant no. 101081171 (DropTrack). The authors also warmly thank Prof. Ramin Golestanian for useful discussions.Notes and references
- M. C. Marchetti, J. F. Joanny, T. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- A. Cavagna, A. Cimarelli, I. Giardina, G. Parisi, R. Santagati, F. Stefanini and V. Viale, Proc. Natl. Acad. Sci., U. S. A., 2010, 107, 11865–11870 CrossRef CAS PubMed.
- A. Okubo, Adv. Biophys., 1986, 22, 1–94 CrossRef CAS PubMed.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- J. Prost, F. Jülicher and J. F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- F. J. Surrey, T. Nédélec, S. Leibler and E. Karsenti, Science, 2001, 292, 1167 CrossRef PubMed.
- N. Uchida and R. Golestanian, Phys. Rev. Lett., 2010, 104, 178103 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, H. Lowen, R. E. Goldstein and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bär and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 CrossRef PubMed.
- R. Golestanian, Phys. Rev. Lett., 2009, 102, 188305 CrossRef PubMed.
- H. M. López, J. Gachelin, C. Douarche, H. Auradou and E. Clément, Phys. Rev. Lett., 2015, 115, 028301 CrossRef PubMed.
- D. Saintillan, Annu. Rev. Fluid Mech., 2018, 50, 563–592 CrossRef.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- G. Gonnella, D. Marenduzzo, A. Suma and A. Tiribocchi, C. R. Phys., 2015, 16, 316–331 CrossRef CAS.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- P. Guillamat, Z. Kos, J. Hardoüin, J. Ignés-Mullol, M. Ravnik and F. Sagués, Sci. Adv., 2018, 4, eaao1470 CrossRef PubMed.
- J. Ignés-Mullol and F. Sagués, Curr. Opin. Colloid Interface Sci., 2020, 49, 16–26 CrossRef.
- S. Saha, A. Das, C. Patra, A. A. Anilkumar, P. Sil, S. Mayor and M. Rao, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2123056119 CrossRef CAS PubMed.
- R. Sakamoto, Z. Izri, Y. Shimamoto and Y. T. Maeda, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2121147119 CrossRef CAS PubMed.
- S. Köhler, V. Schaller and A. R. Bausch, Nat. Mater., 2011, 10, 462–468 CrossRef PubMed.
- T. Loisel, R. Boujemaa, D. Pantaloni and M. F. Carlier, Nature, 1999, 401, 603–616 CrossRef PubMed.
- Y. Sumino, K. H. Nagai, Y. Shitaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 493, 448–452 CrossRef PubMed.
- S. Ramaswamy, Annu. Rev. Cond. Mat. Phys., 2010, 1, 323–345 CrossRef.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- T. Kozhukhov and T. N. Shendruk, Sci. Adv., 2022, 8, 34 Search PubMed.
- E. Tjhung, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci., U. S. A., 2012, 109, 12381–12386 CrossRef CAS PubMed.
- L. Giomi and A. DeSimone, Phys. Rev. Lett., 2014, 112, 147802 CrossRef PubMed.
- D. Khoromskaia and G. P. Alexander, Phys. Rev. E, 2015, 92, 062311 CrossRef PubMed.
- D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Julicher, Nat. Phys., 2017, 13, 408–413 Search PubMed.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi, Y. Toyama, P. Marcq, C. T. Lim, J. M. Yeomans and B. Ladoux, Nature, 2017, 544, 212–216 CrossRef CAS PubMed.
- A. Tiribocchi, M. Durve, M. Lauricella, A. Montessori, D. Marenduzzo and S. Succi, Nat. Commun., 2023, 14, 1096 CrossRef CAS PubMed.
- L. N. Carenza, G. Gonnella, D. Marenduzzo and G. Negro, Proc. Natl. Acad. Sci., U. S. A., 2019, 116, 22065–22070 CrossRef CAS PubMed.
- A. Loisy, J. Eggers and T. B. Liverpool, Phys. Rev. Lett., 2019, 123, 248006 CrossRef CAS PubMed.
- B. V. Hokmabad, K. A. Baldwin, C. Krüger, C. Bahr and C. C. Maass, Phys. Rev. Lett., 2019, 123, 178003 CrossRef CAS PubMed.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2015, 7, 171–193 CrossRef.
- F. Ziebert, S. Swaminathan and I. S. Aranson, J. R. Soc., Interface, 2012, 9, 1084–1092 CrossRef PubMed.
- J. Löber, F. Ziebert and I. S. Aranson, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- F. Ziebert and I. S. Aranson, npj Comput. Mater., 2016, 2, 16019 CrossRef.
- L. J. Ruske and J. M. Yeomans, Phys. Rev. X, 2021, 11, 021001 CAS.
- G. De Magistris, A. Tiribocchi, C. A. Whithfield, R. J. Hawkins, M. E. Cates and D. Marenduzzo, Soft Matter, 2014, 10, 7826–7837 RSC.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770–1773 CrossRef CAS PubMed.
- L. Angelani and R. Di Leonardo, New J. Phys., 2010, 12, 113017 CrossRef.
- R. Di Leonardo, L. Angelani, D. Dell’aArciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis and F. Di Fabrizio, Proc. Natl. Acad. Sci., U. S. A., 2010, 107, 9541–9545 CrossRef CAS PubMed.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. D. Aranson, Proc. Natl. Acad. Sci., U. S. A., 2009, 107, 969–974 CrossRef PubMed.
- N. Nikola, A. P. Solon, M. Kafri, Y. Kardar, J. Tailleur and R. Voituriez, Phys. Rev. Lett., 2016, 117, 098001 CrossRef PubMed.
- M. S. Aporvari, M. Utkur, E. U. Saritas, G. Volpe and J. Stenhammar, Soft Matter, 2020, 16, 5609–5614 RSC.
- J. Petit, I. Polenz, J. C. Baret, S. Herminghaus and O. Bäumchen, Eur. Phys. J. E, 2016, 39, 59 CrossRef PubMed.
- F. Diotallevi, L. Biferale, S. Chibbaro, A. Lamura, G. Pontrelli, M. Sbragaglia, S. Succi and F. Toschi, Eur. Phys. J.-Spec. Top., 2009, 166, 111–116 CrossRef.
- D. Marenduzzo, E. Orlandini, M. E. Cates and J. M. Yeomans, J. Non-Newt. Fluid Mech., 2008, 149, 56–62 CrossRef CAS.
- M. C. Marchetti, Nature, 2012, 491, 340–341 CrossRef CAS PubMed.
- M. Rajabi, H. Baza, T. Turiv and O. D. Lavrentovich, Nat. Phys., 2021, 17, 260–266 Search PubMed.
- A. Tiribocchi, A. Montessori, M. Lauricella, F. Bonaccorso, S. Succi, S. Aime, M. Milani and D. Weitz, Nat. Commun., 2021, 12, 82 Search PubMed.
- A. Tiribocchi, A. Montessori, M. Durve, F. Bonaccorso, M. Lauricella and S. Succi, Phys. Rev. E, 2021, 104, 065112 CrossRef CAS PubMed.
- A. Tiribocchi, A. Montessori, S. Aime, S. Milani, M. Lauricella, S. Succi and D. A. Weitz, Phys. Fluids, 2020, 32, 017102 CrossRef CAS.
- A. Tiribocchi, A. Montessori, S. Bonaccorso, M. Lauricella and S. Succi, Phys. Fluids, 2021, 33, 047105 CrossRef CAS.
- P. G. de Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 2nd edn, 1993, ISBN: 9780198517856 Search PubMed.
- S. Succi, The Lattice Boltzmann equation: For complex states of flowing matter, Oxford University Press, 2018 Search PubMed.
- R. Benzi, S. Succi and M. Vergassola, Phys. Rep., 1992, 222, 145–197 CrossRef.
- F. J. Higuera, S. Succi and R. Benzi, Europhys. Lett., 1989, 9, 345 CrossRef.
- D. Marenduzzo, E. Orlandini, M. E. Cates and J. M. Yeomans, Phys. Rev. E, 2007, 76, 031921 CrossRef CAS PubMed.
- E. Tjhung, A. Tiribocchi, D. Marenduzzo and M. E. Cates, Nat. Commun., 2015, 6, 5420 CrossRef CAS PubMed.
- G. Coupier, A. Farutin, C. Minetti, T. Podgorski and C. Misbah, Phys. Rev. Lett., 2012, 108, 178106 CrossRef PubMed.
- K. Kruse, J.-F. Joanny, F. Jülicher, J. Prost and K. Sekimoto, Phys. Rev. Lett., 2004, 92, 078101 CrossRef CAS PubMed.
- F. Jülicher, K. Kruse, J. Prost and J.-F. Joanny, Phys. Rep., 2007, 449, 3–28 CrossRef.
- R. J. Yang, L. M. Fu and Y. C. Lin, J. Colloid Interface Sci., 2001, 239, 98–105 CrossRef CAS PubMed.
- G. H. Tang, X. F. Li, Y. L. He and W. Q. Tao, J. Non-Newt. Fluid Mech., 2009, 157, 133–137 CrossRef CAS.
- G. C. Shit, A. Mondal, A. Sinha and P. K. Kundu, Colloids Surf., A, 2016, 506, 535–549 CrossRef CAS.
- G. Ramos, M. L. Cordero and R. Soto, Soft Matter, 2020, 16, 1359–1365 RSC.
- G. Miño, T. E. Mallouk, T. Darnige, M. Hoyos, J. Dauchet, J. Dunstan, R. Soto, Y. Wang, A. Rousselet and E. Clement, Phys. Rev. Lett., 2011, 106, 048102 CrossRef PubMed.
- D. S. Miller, R. J. Carlton, P. C. Mushenheim and N. L. Abbott, Langmuir, 2013, 29, 3154–3169 CrossRef CAS PubMed.
- J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. E. Cates, D. Marenduzzo, A. N. Morozov and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057 CrossRef CAS PubMed.
- L. Guanglai, J. Bensson, L. Nisomova, D. Munger, P. Mahatumr, J. X. Tang, M. R. Maxey and Y. V. Brun, Phys. Rev. E, 2011, 84, 041932 CrossRef PubMed.
- F. Bonelli, L. N. Carenza, G. Gonnella, D. Marenduzzo, E. Orlanini and A. Tiribocchi, Sci. Rep., 2019, 9, 2801 CrossRef CAS PubMed.
- M. Masaeli, E. Sollier, H. Amini, W. Mao, K. Camacho, N. Doshi, S. Mitragotri, A. Alexeev and D. Di Carlo, Phys. Rev. X, 2012, 2, 031017 Search PubMed.
- H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65 CrossRef.
- B. J. Bentley and L. G. Leal, J. Fluid Mech., 1986, 167, 241 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00561e |
| This journal is © The Royal Society of Chemistry 2023 |