 Open Access Article
Open Access ArticleStrain stiffening elastomers with swelling inclusions†
Stefanie
Heyden
*,
Robert W.
Style
 and
Eric R.
Dufresne
and
Eric R.
Dufresne
Department of Materials, ETH Zürich, 8093 Zürich, Switzerland. E-mail: stefanie.heyden@mat.ethz.ch
First published on 5th June 2023
Abstract
Inhomogeneously swollen elastomers are an emergent class of materials, comprising elastic matrices with inclusion phases in the form of microgel particles or osmolytes. Inclusion phases can undergo osmotically driven swelling and deswelling over orders of magnitude. In the swollen state, the inclusions typically have negligible Young's modulus, and the matrix is strongly deformed. In that regime, the effective mechanical properties of the composite are governed by the matrix. Laying the groundwork for a generic analysis of inhomogeneously swollen elastomers, we develop a model based on incremental mean-field homogenization of a hyperelastic matrix. The framework allows for the computation of the macroscopic effective stiffness for arbitrary hyperelastic matrix materials. For an in-depth quantification of the local effective stiffness, we extend the concept of elastic stiffness maps to incompressible materials. For strain-stiffening materials, stiffness maps in the swollen state highlight pronounced radial stiffening with a non-monotonic change in stiffness in the hoop direction. Stiffening characteristics are sensitive to the form of constitutive models, which may be exploited in the design of hydrated actuators, soft composites and metamaterials. For validation, we apply this framework to a Yeoh material, and compare to recently published data. Model predictions agree well with experimental data on elastomers with highly swollen embedded microgel particles. We identify three distinct regimes related to an increasing degree of particle swelling: first, an initial decrease in composite stiffness is attributed to particle softening upon liquid intake. Second, dilute particle swelling leads to matrix stiffening dominating over particle softening, resulting in an increase in composite stiffness. Third, for swelling degrees beyond the dilute limit, particle interactions dominate further matrix stiffening.
I. Introduction
Plants lacking water are wilted and limp. This familiar sight highlights an interesting interplay of physical phenomena, where osmotically driven fluid flow and turgor pressure within cell walls compete to determine the mechanical strength and shape.1–3 Recently, several approaches to synthetic materials mimicking this concept have emerged. They comprise either encapsulated osmolytes4 or highly swelling hydrogel particles embedded in soft5 or tough6 matrices. Establishing continuity with recent experimental work,4 we refer to these hydrated elastomers as the class of hydroelastomers. Inhomogeneously swollen elastomers gained interest as a means of enhancing composite properties,7,8 providing mechanically responsive actuators,4,9 and enabling shape morphing.5 Applications typically share three common features: spheroidal inclusion shape, attendant large deformations, and negligible Young's moduli of the inclusion phase. Effective composite properties in the deformed state could hence be dominated by nonlinear properties of the matrix material. In this setting, the pressure within droplets in equilibrium is assumed to have a negligible influence on composite stiffness.A large body of literature has evolved in the realm of computing effective properties of composites with spherical inclusions, starting from Eshelby's pioneering single inclusion solution,10 which was later extended to account for multiple inclusions interacting in an average fashion (cf., e.g.,11–13). The introduction of a linear comparison composite further allowed to take into account nonlinearities in material behavior.14–16 In this approach, the nonlinear elastic behavior of constituents is linearized at given strain levels. Afterwards, higher level homogenization schemes are applied to derive the effective response of the composite. As the simplest and computationally most efficient method, Mean-Field Homogenization computes homogenized stress- and strain fields as volume averages over composite constituents. More complex homogenization methods involve numerical and semi-analytical schemes, as well as extensions to elasto-visco-plastic materials (see ref. 17–21 and references therein).
Here, we develop a model based on incremental mean-field homogenization, laying the groundwork in characterizing generic inhomogeneously swollen elastomers. The model is applicable for any hyperelastic matrix. We derive the macroscopic mechanical properties of the dominant matrix phase in the dilute swelling regime. Scaled by the matrix volume fraction, this corresponds to the upper bound on composite properties with inclusions of negligible Young's modulus. Exploiting the fully analytical solutions, we furthermore provide an in-depth quantification of the local stiffness at the material point level prior to homogenization. To this end, we extend the concept of elastic stiffness maps to incompressible materials. To illustrate the characterization of swelling regimes, the model is tailored to a Yeoh material up to second order. By comparison to experimental data, the model characterizes three distinct stiffness regimes of highly swollen elastomers.
II. Theory
A. Deformation and force balance
We consider a spherical particle of initial radius R0 embedded in an elastic incompressible matrix of radius R1 (see Fig. 1). Upon swelling, the particle undergoes a spherically symmetric growth to its deformed radius r0.Kinematics governing the deformation follow from the incompressibility constraint
 | (1) |
 | (2) |
For a generic hyperelastic material, we have
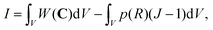 | (3) |
 | (4) |
For subsequent computations within the framework of linearized elasticity, the elastic modulus  is moved to the spatial configuration as22
is moved to the spatial configuration as22
 | (5) |
B. Homogenized matrix stiffness
The deformation upon swelling derived in Section IIA induces a continuous stiffening of the elastic matrix. To compute the incremental effective matrix stiffness as a function of pre-stretch λR, Cijkl from eqn (5) is written in a Cartesian coordinate frame as![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) abcd = ΨiaΨjbΨkcΨldCijkl, abcd = ΨiaΨjbΨkcΨldCijkl, | (6) |
An upper bound on the effective matrix stiffness (also denoted as the Voigt bound) is calculated by assuming a homogeneous state of strain within the material.23 Starting from the equations of equilibrium in spatial form within the framework of linearized elasticity with internal constraints, we have
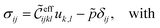 | (7) |
 | (8) |
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) is a second Lagrange multiplier, which enforces that also the linearized material behaves as an incompressible solid. Component-wise integration of the elastic modulus specified in eqn (8) is performed numerically using global adaptive methods. Note that the volume integral in eqn (8) may also be thought of as the 'mean spherical approximation' of the Wigner–Seitz cell.24
is a second Lagrange multiplier, which enforces that also the linearized material behaves as an incompressible solid. Component-wise integration of the elastic modulus specified in eqn (8) is performed numerically using global adaptive methods. Note that the volume integral in eqn (8) may also be thought of as the 'mean spherical approximation' of the Wigner–Seitz cell.24
We are now in place to calculate the effective stiffness EeffM(F) of the matrix material. Note that  constitutes a homogeneous and isotropic elastic modulus, such that EeffM(F) is unique. Under uniaxial stretch conditions, we have σij = ((σxx,0,0), (0,0,0), (0,0,0)) and
constitutes a homogeneous and isotropic elastic modulus, such that EeffM(F) is unique. Under uniaxial stretch conditions, we have σij = ((σxx,0,0), (0,0,0), (0,0,0)) and  . Eqn (7) may thus be solved for both
. Eqn (7) may thus be solved for both ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) as well as EeffM(F), which is the pre-factor relating σxx and εxx.
as well as EeffM(F), which is the pre-factor relating σxx and εxx.
So far, we have computed the macroscopic effective stiffness EeffM(F). Since we know the closed-form solution of 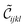 at each material point (prior to integration), we are furthermore interested in the local unidirectional stiffness EM(F,ζ). Here, ζ ∈ S(ζ) is any direction on the unit sphere S(ζ). EM(F,ζ) thus denotes the local stiffness into the direction ζ at a material point.
at each material point (prior to integration), we are furthermore interested in the local unidirectional stiffness EM(F,ζ). Here, ζ ∈ S(ζ) is any direction on the unit sphere S(ζ). EM(F,ζ) thus denotes the local stiffness into the direction ζ at a material point.
The local unidirectional Young's modulus E(ζ) in compressible materials is computed as25
EM(F,ζ) = (![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) ijklζiζjζkζl)−1, ijklζiζjζkζl)−1, | (9) |
 . We extend this concept to incompressible materials starting from eqn (7) and enforcing that tr(ε) = 0, which gives
. We extend this concept to incompressible materials starting from eqn (7) and enforcing that tr(ε) = 0, which gives | (10) |
III. Results
Exploiting the fully analytical solution for the local unidirectional Young's modulus, we compute 3D stiffness maps (also denoted as elastic surfaces) for materials exhibiting different degrees of strain stiffening. For these purposes, the generic model outlined in the previous section is tailored to a Neo-Hookean material, as well as a Yeoh material up to second order. Elastic surfaces of strain stiffening materials highlight both anisotropy and inhomogeneity. We quantify the degree of strain stiffening necessary for an increase of incremental stiffness. Furthermore, we show how elastic surfaces provide a graphical interpretation relating to the homogenized matrix response.To validate the outlined generic framework, the homogenized matrix response is compared to experimental data.5 Inhomogeneous Lagrange multipliers, as well as the incremental stiffness are derived in closed form. Finally, we exemplify how the upper bound construction derived in the foregoing allows for a characterization of distinct swelling regimes.
A. Characteristics governing effective matrix stiffness
In Section IIB, we developed a closed-form analytical solution for the local stiffness around an isolated droplet, shown in eqn (10). We exploit this solution to explore unidirectional Young's moduli of the anisotropic, inhomogeneous matrix at the material point level for materials exhibiting different degrees of strain stiffening. To this end, the generic model outlined in Section IIB needs to be tailored to a specific material model. Here, we choose to model the elastic matrix as a Yeoh material with strain energy density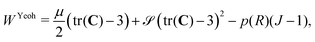 | (11) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is the strain stiffening parameter. Application of linear momentum balance (4) gives
is the strain stiffening parameter. Application of linear momentum balance (4) gives | (12) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) = r03 − R03 + R13. Fig. S7 in the ESI† illustrates p(R) for varying inflation levels r0/R0.
= r03 − R03 + R13. Fig. S7 in the ESI† illustrates p(R) for varying inflation levels r0/R0.
Even though the matrix is originally isotropic, swelling creates an anisotropic incremental stiffness. The degree of elastic anisotropy increases with swelling. Fig. 2a shows 3D polar plots of the incremental stiffness, which are known as elastic surfaces. These elastic surfaces highlight pronounced radial stiffening with a non-monotonic change in stiffness in the hoop direction. Starting from the isotropic state at r0 = R0, the elastic surface at fixed position (R = R0, θ = 0, φ = 0) gradually evolves into a rhomboidal shape at a low swelling value of r0 = 1.15R0. The anisotropy in stiffness is markedly pronounced with increasing swelling. While radial stiffening dominates at all swelling levels, elastic surfaces develop a pronounced neck in higher swelling regimes. We find that the softest material response is attained at θmin ∼ 54° (eqn (10) can be utilized to analytically solve for θ minimizing unidirectional Young's modulus EM). Fig. 2 furthermore highlights isotropy within the azimuthal direction φ.
Swelling also induces inhomogeneity within the matrix material, as illustrated in Fig. 2b, as well as Fig. S8 in the ESI.† Anisotropy is most pronounced at the matrix/inclusion interface (R = R0) and rapidly decreases with increasing R, which is a common feature at all strain levels. This is in agreement with a fast decay in stretches, see Fig. S6 in the ESI.†
Fig. 2c shows the incremental stiffness under the angle θmin of softest material response as a function of swelling level s for materials exhibiting different degrees of strain stiffening. For ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0, the Yeoh-model reduces to a Neo–Hookean solid. In this limit, the incremental stiffness EM(θmin) is decreasing. We calculate a limiting value of
= 0, the Yeoh-model reduces to a Neo–Hookean solid. In this limit, the incremental stiffness EM(θmin) is decreasing. We calculate a limiting value of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = μ/1000 for an increasing incremental stiffness.
= μ/1000 for an increasing incremental stiffness.
Elastic surfaces allow for an intuitive illustration of the homogenized matrix stiffness at the material point level. The integral over (θ,φ) in eqn (8) may be illustrated as the volume enclosed within elastic surfaces. A continuous increase of homogenized matrix stiffness is thus equivalent to a continuously increasing enclosed volume within elastic surfaces. At the continuum level, this homogenized matrix stiffness allows for validation with experimental data, as outlined in the following section.
B. Comparison to experiments
To illustrate the characterization of swelling regimes, we compare the homogenized matrix model outlined in Section IIB to recent experimental data on hydroelastomers.5 In experiments, sodium polyacrylate (NaPAA) microgels of varying mass fractions are embedded in an elastomeric matrix. For validation purposes, we focus on the case R1 = 2.3R0 (which corresponds to 10 wt% NaPAA). As shown in Fig. 3, the composite stiffness E shows distinct swelling regimes, which are governed by an interplay between softening of the particle and stiffening of the elastic matrix. The initial decrease in composite stiffness is attributed to a steep drop in particle stiffness upon swelling (see blue shaded area in Fig. 3). | ||
| Fig. 3 Experimentally measured composite stiffness E for 10 wt% NaPAA particles embedded in smooth-on Dragonskin 30 (Sil-DS).5 Initial Young's moduli of the particle- and matrix material are EP0 = 13 MPa and EM0 = 1.12 MPa, respectively. s gives the scaling parameter r0 = sR0. The inset highlights a separate measurement of particle's Young's modulus EP upon swelling.5 | ||
The inset in Fig. 3 illustrates the stiffness of the pure particle material upon swelling,5 which monotonously decreases from the initial value of EP0 for dry NaPAA). Subsequently, matrix stiffening starts to dominate over particle softening, resulting in an increase in composite stiffness (see yellow shaded area in Fig. 3).
Mean-field homogenization as introduced in Section IIB furnishes an upper bound on material properties. Here, we employ the corresponding upper (Voigt) bound to extract the incremental matrix stiffness from experimental data. In addition to the hyperelastic matrix material, this construction allows for generic inclusion phases. Exploiting a negligible particle stiffness at swelling values beyond 50 wt%, an upper-bound for Young's modulus of the matrix material is inferred from the Voigt bound as EM = E/(1 − φh),23 with φh the volume fraction of microgel particles. While the hyperelastic matrix is modeled as incompressible, employing a Voigt bound prescribes inclusions to change in volume by the amount of added liquid. This is in keeping with classical mixture theories such as Flory–Huggins solution theory. As shown in Fig. 4, the matrix material undergoes a continuous increase in stiffness. This stiffening is captured well by the homogenized matrix model outlined in Section IIB, which agrees with measurements within experimental error bounds. Our prediction has no free parameters, we used the experimental values ρP = 1220 kg m−3, ρM = 1000 kg m−3, μ = 0.37 MPa and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0.02 MPa.
= 0.02 MPa.
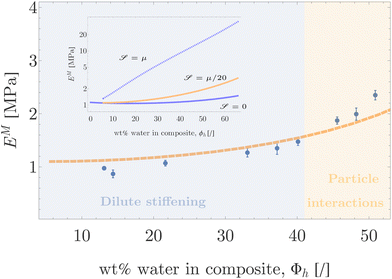 | ||
Fig. 4 Matrix stiffness EM inferred from experimental data (10 wt% NaPAA particles embedded in Sil-DS5) in comparison to the theoretical model of homogenized matrix stiffness. The inset illustrates different degrees of strain stiffening ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) , with , with ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ∼ μ/20 highlighting the prediction from fitting to the pure Sil-DS matrix. ∼ μ/20 highlighting the prediction from fitting to the pure Sil-DS matrix. | ||
Note that the chosen Yeoh strain energy density given in eqn (11) allows for a continuous change between a classical Neo–Hookean model (![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0) and a material exhibiting strain stiffening, where the degree of strain stiffening is controlled by the magnitude of
= 0) and a material exhibiting strain stiffening, where the degree of strain stiffening is controlled by the magnitude of ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) . Fig. 4 (inset) illustrates the transition from a Neo–Hookean model to a material with
. Fig. 4 (inset) illustrates the transition from a Neo–Hookean model to a material with ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = μ, the shear modulus of the matrix. Material parameters μ and
= μ, the shear modulus of the matrix. Material parameters μ and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) are obtained from comparing to the pure, dry Sil-DS matrix when stretched uniaxially5 (see orange curve in the inset in Fig. 4).
are obtained from comparing to the pure, dry Sil-DS matrix when stretched uniaxially5 (see orange curve in the inset in Fig. 4).
In combination, Fig. 3 and 4 allow for the characterization of three distinct swelling regimes: First, the initial drop in composite stiffness is solely governed by particle softening (see blue shaded area in Fig. 3). We refer to this as the particle softening regime. At higher swelling values, matrix stiffening starts to dominate the composite response (see yellow shaded area in Fig. 3). We can differentiate the regime of matrix stiffening according to the degree of swelling (see Fig. 4). In the beginning, elastic matrix stiffening is solely governed by the growth of isolated particles. We refer to this as the dilute stiffening regime. This regime corresponds to the theoretical model presented in Section IIA. At higher swelling ratios, stress fields induced by previously isolated growing particles start to overlap, such that particle–particle interactions influence the resultant matrix stiffening. We refer to this as the particle interactions regime.
While the theoretical model is targeted towards capturing the dilute swelling regime, we can exploit its set-up in order to identify the transition to a particle interactions regime in experimental data sets. As the homogenized matrix model is based on a mean field approach, it furnishes an upper bound on the homogenized matrix stiffness. Any measurements above model predictions must hence be governed by stiffening mechanisms beyond the dilute setting. At swelling values up to ∼50 wt% water within the composite, the matrix is therefore strain stiffening in the dilute limit, whereas particle interactions dominate the behavior at larger swelling values (see shaded areas in Fig. 4).
IV. Discussion and outlook
We have developed a generic model to predict the incremental stiffness of inhomogeneously swollen elastomers incorporating growing spherical inclusions of negligible Young's modulus. The outlined model is applicable to a large class materials, which includes systems incorporating both encapsulated osmolytes and microgels. At the material point level, the incremental stiffness is derived in closed form, which allows to quantify shapes of elastic surfaces. The stiffest material response will be attained for radial loadings initiating at the matrix/inclusion interface, while the material is most compliant at θmin∼ 54°. Zooming out to the homogenized material response, our results suggest that a simple model based on incremental mean field homogenization agrees well with experimental data in the dilute swelling regime. The upper bound construction furthermore allows to distinguish three distinct swelling regimes.Future studies on a detailed model of higher swelling regimes, in which particle–particle interactions dominate the matrix behavior, could aid in predicting optimal initial mass fractions of inclusions and upper swelling limits. Recently developed numerical frameworks could readily be tailored to this purpose.26 In addition, solutions to the exact boundary value problem without homogenization could aid in elucidating additional stiffening effects, such as the pressure acting at the inclusion/matrix interface. These further routes could facilitate to not only qualitatively, but also quantitatively identify different swelling regimes. The outlined framework furthermore lends itself to a straightforward extension to anisotropic inclusion growth/stiffening, which is solely based on the specific strain energy density chosen in eqn (11).
Characteristics of the anisotropic and inhomogeneous matrix may be exploited in the design of novel synthetic hydrated composites and metamaterials. Future experiments could highlight the swelling induced anisotropy by tracking particle shapes in the swollen state upon uniaxial stretch. As an example of exploiting matrix anisotropy, the matrix/microgel system might act as a mechanical resonator, capable of reducing vibrational amplitudes induced by environmental changes (such as humidity when using hydrogel inclusions). Moreover, the angle of softest response at θmin is close to the direction of maximum shear stresses in simple tension, which could be utilized in the design of materials actively tuning shear compliance according to changes in, e.g., humidity. For design goals of maximizing composite stiffness, target ‘sweet spots’ are regimes in which strain stiffening dominates over composite softening due to higher water contents.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
SH gratefully acknowledges funding via the SNF Ambizione grant PZ00P2186041.References
- P. T. Martone, M. Boller, I. Bungert, J. Dumais, J. Edwards and K. Mach, et al., Mechanics without muscle: biomechanical inspiration from the plant world, Integr Comp Biol., 2010, 50, 888–907 CrossRef PubMed.
- Y. Forterre, Slow, fast and furious: understanding the physics of plant movements, J. Exp. Bot., 2013, 64, 4745–4760 CrossRef CAS PubMed.
- E. Sinibaldi, A. Argiolas, G. L. Puleo and B. Mazzolai, Another Lesson from Plants: The Forward Osmosis-Based Actuator, PLoS One, 2014, 9(7), e102461 CrossRef PubMed.
- A. Kataruka and S. B. Hutchens, Swelling of a non-vascularplant- inspired soft composite, Matter, 2021, 4, 3991–4005 CrossRef CAS.
- S. Moser, Y. Feng, O. Yasa, S. Heyden, M. Kessler, E. Amstad, et al. Hydroelastomers: soft, tough, highly swelling composites, ArXiv, 2022, preprint, ArXiv:2203.17131.
- F. Horkay and P. J. Basser, Hydrogel composite mimics biological tissues, Soft Matter, 2022, 18, 4414–4426 RSC.
- J. Hu, K. Hiwatashi, T. Kurokawa, S. M. Liang, Z. L. Wu and J. P. Gong, Microgel-reinforced hydrogel films with high mechanical strength and their visible mesoscale fracture structure, Macromolecules, 2011, 44(19), 7775–7781 CrossRef CAS.
- R. W. Style, R. Tutika, J. Y. Kim and M. D. Bartlett, Solid–liquid composites for soft multifunctional materials, Adv. Funct. Mater., 2021, 31(1), 2005804 CrossRef CAS.
- M. C. Koetting, J. T. Peters, S. D. Steichen and N. A. Peppas, Stimulus-responsive hydrogels: Theory, modern advances, and applications, Mater. Sci. Eng., R, 2015, 93, 1–49 CrossRef PubMed.
- J. D. Eshelby, The determination of the elastic eld of an ellipsoidal inclusion, and related problems, PRSA, 1957, 241, 376–396 Search PubMed.
- T. Mori and K. Tanaka, Average stress in matrix and average elastic energy of materials with misfi tting inclusions, Acta Metall., 1957, 21, 571–574 CrossRef.
- E. Kröner, Berechnung der elastischen konstanten des Vielkristalls aus den konstanten des Einkristalls, Z. Phys., 1958, 151, 504–518 CrossRef.
- R. Hill, A self-consistent mechanics of composite materials, J. Mineral. Petrol. Sci., 1965, 13, 213–222 CrossRef.
- D. R. S. Talbot and J. R. Willis, Variational principles for inhomogeneous non-linear media, J. Appl. Math., 1985, 35, 39–54 Search PubMed.
- P. Ponte Castanẽda, The effective mechanical properties of nonlinear isotropic composites, J. Mineral. Petrol. Sci., 1991, 39, 45–71 Search PubMed.
- A. Molinari, F. El Houdaigui and L. Tóth, Validation of the tangent formulation for the solution of the non-linear eshelby inclusion problem, Int. J. Plast., 2004, 20, 291–307 CrossRef.
- P. Kanouté, D. Boso, J. Chaboche and B. Schrefler, Multiscale methods for composites: A review, Arch. Comput. Methods Eng., 2009, 16, 31–75 CrossRef.
- M. Geers, V. Kouznetsova and W. Brekelmans, Multi-scale computational homogenization: Trends and challenges, J. Comput. Appl. Math., 2010, 234, 2175–2182 CrossRef.
- J. Llorca, C. Gonzalez, J. M. Molina-Aldareguia, J. Segurado, R. Seltzer and F. Sket, et al., Multiscale modeling of composite materials: a roadmap towards virtual testing, Adv. Mater., 2011, 23, 5130–5147 CrossRef CAS PubMed.
- S. Nemat-Nasser and M. Hori, Micromechanics: overall properties of heterogeneous materials, Elsevier, 2013 Search PubMed.
- L. Wu, L. Adam, I. Doghri and L. Noels, An incremental-secant mean-field homogenization method with second statistical moments for elasto-visco-plastic composite materials, Mech. Mater., 2017, 114, 180–200 CrossRef.
- E. B. Tadmor, R. E. Miller and R. S. Elliott, Continuum Mechanics and Thermodynamics: From Fundamental Concepts to Governing Equations, Cambridge University Press, 2011 Search PubMed.
- W. Voigt, Ueber die Beziehung zwischen den beiden Elasticitaetsconstanten isotroper Koerper, Ann. Phys., 1889, 274, 573–587 CrossRef.
- F. Seitz and E. Wigner, On the Constitution of Metallic Sodium, Phys. Rev., 1933, 43(10), 804 CrossRef.
- T. Boehlke and C. Brueggemann, Graphical representation of the generalized Hooke's law, Tech. Mech., 2001, 21(0), 145–158 Search PubMed.
- Z. Hooshmand-Ahoor, M. G. Tarantino and K. Danas, Mechanically-grown morphogenesis of Voronoi-type materials: Computer design, 3D-printing and experiments, 2022 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00496a |
| This journal is © The Royal Society of Chemistry 2023 |


