Dynamic-bond-induced sticky friction tailors non-Newtonian rheology

Abstract

Frictional network formation has become a new paradigm for understanding the non-Newtonian shear-thickening behavior of dense suspensions. Recent studies have exclusively focused on interparticle friction that instantaneously vanishes when applied shear is ceased. Herein, we investigate a friction that emerges from dynamic chemical bridging of functionalized particle surfaces sheared into close proximity. This enables tailoring of both friction magnitude and the time release of the frictional coupling. The experiments use dense suspensions of thiol-functionalized particles suspended in ditopic polymers endcapped with benzalcyanoacetamide Michael-acceptors. The subsequent room temperature, catalyst-free dynamic thia-Michael reactions can form bridging interactions between the particles with dynamic covalent bonds that linger after formation and release in the absence of shear. This chemical friction mimics physical friction but is stickier, leading to tunable rheopexy. The effect of sticky friction on dense suspension rheology is explored by varying the electronic nature of the benzalcyanoacetamide moiety, the molecular weight of the ditopic polymers, the amount of a competitive bonding compound, and temperature. These results demonstrate how dynamic-bond-induced sticky friction can be used to systematically control the time dependence of the non-Newtonian suspension rheology.

---

1 Introduction

Colloidal particles in dense suspensions form networks of frictional contacts when sheared, accounting for the ability to sustain large stresses under load.^1,2 To explore the role of friction in tuning the rheological behavior, and in particular the dramatic, non-Newtonian shear thickening observed in dense suspensions, studies have focused on surface-roughness^3–5 and particle morphology,^6,7 which can be thought of as particle-scale ‘geometric friction’. However, it has remained challenging^8,9 to fabricate particles with different friction coefficients to systematically tune shear thickening phenomena. Furthermore, experiments so far have almost exclusively been limited to frictional interactions where the nature of the attraction was difficult to control.^10,11

To address this challenge and also access sticky frictional forces with extended lifetime, here we explore chemical friction, which functions similarly to physical friction in that interparticle attraction is activated when the applied stress τ is larger than a critical onset stress for shear thickening τ_c and relaxes when the shear is ceased.^2,12,13 Crucially, it is possible to tune the degree of frictional interaction as well as the relaxation time scales by utilizing room temperature thia-Michael dynamic covalent bonds that form between thiol-functionalized silica particles and ditopic polymers endcapped with benzalcyanoacetamide (BCAm) Michael-acceptors (Scheme 1a).¹⁴ This catalyst-free dynamic reaction acts as a non-classical attractive interaction and mimics the process of physical friction. When the thiol-functionalized silica particles are suspended in an excess of the ditopic polymer fluid (molecular weight, ca. 4000 g mol⁻¹), the dynamic thia-Michael bond results in the formation of a polymer brush layer on the particles. When sheared more strongly than τ_c, the forced interaction between the particles results in displacement of some of the grafted polymers and the formation of interparticle polymer bridges that effectively act as chemical friction¹⁴ as illustrated in Scheme 1b. Removal of the stress allows the system to relax over time back to its original state.

Scheme 1 (a) Chemical structures of the benzalcyanoacetaminde (BCAm) endcapped poly(propylene glycol) polymer fluids and their dynamic thia-Michael reaction between the BCAm moieties that act as Michael-acceptors (MAs) and the thiol functional groups on the particle surface (gray). (b) Illustrative sketch of thia-Michael bridging bonds under shear in a dense suspension with an excess of MAs. At low shear stress τ, the thia-Michael reaction results in the formation of a brush layer between the particle and polymer fluid. As particles are sheared into close proximity the ditopic polymer forms particle bridging interactions. Recovery of the original brush layer conformation is delayed due to the relaxation of thia-Michael bonds.

This prior work suggested that the bridging interaction leads to rheopectic behavior where a significant hysteresis in the viscosity is observed between the forward and backward stress sweep. The data suggest that the shift found in the backward sweep originates from the delayed dissociation of the dynamic bridging interaction.¹⁴ The electron-affinity of substituents attached to the phenyl ring (R) of the BCAm Michael-acceptors (MAs) controls the equilibrium of the thia-Michael reaction where more electron-withdrawing –R groups increase the equilibrium constant.^15,16 An increase in the equilibrium constant of the thia-Michael reaction results in more bridging configurations upon application of stress and is analogous to larger friction. As such, room temperature thia–Michael bonds enable access to an unconventional type of ‘chemical’ friction where the suspending medium controls the frictional interactions. The goal of this work was to explore the role of molecular architecture on the rheology of these dynamically bonded suspensions by changing both the molecular weight and –R substituent of the MA-endcapped polymers. In addition, the ability to tune the chemical friction by external controls such as introducing competitive bonding molecules and varying temperature was investigated.

2 Methods

2.1 Materials

p-Toluenesulfonic acid (≥98.5%), benzaldehyde (≥99%), 4-anisaldehyde (98%), 4-nitrobenzaldehyde (98%), 2,2′-(ethylenedioxy)diethanethiol (95%), and (3-mercaptopropyl)trimethoxysilane (95%) were purchased from Sigma-Aldrich. Cyanoacetic acid (97%) was purchased from Alfa Aesar. Silica particles were purchased from Fiber Optic Center (SIOP050-01-1KG). Poly(propylene glycol) (2000 g mol⁻¹) was purchased from Acros Organics. Poly(propylene glycol) bis(2-aminopropyl ether) (230, 2000, and 4000 g mol⁻¹) was purchased from Huntsman (JEFFAMINE® D series). All chemicals were used as received.

2.2 Synthesis of ditopic Michael-acceptor

Ditopic Michael-acceptors were synthesized following a previously reported method.¹⁴ In brief, 2.5 mmol of poly(propylene glycol) bis(2-aminopropyl ether) and 5.5 mmol of cyanoacetic acid were added to a 250 mL round-bottom flask equipped with a Dean–Stark trap. p-Toluenesulfonic acid (0.1 g per 2.5 mmol of poly(propylene glycol) bis(2-aminopropyl ether)) was added to the flask with a mixture of 30 mL toluene and 10 mL dimethylformamide (DMF). Nitrogen gas was purged while the solution was stirred with a magnetic stirring bar at room temperature. The reaction was proceeded by increasing the silicon oil bath temperature to 120 °C. During the reaction, water was removed from the azeotrope mixture of toluene and water through the Dean–Stark trap. The reaction was continued for 4 hour until there no further water was collected in the trap. The remaining toluene was removed from the solution and the resulting cooled down reaction mixture was diluted with 50 mL of chloroform. The product was washed with saturated sodium bicarbonate (NaHCO₃) aqueous solution (×3) and water (×3). The cyanoacetamide-terminated poly(propylene glycol) (P1) was obtained by drying the resulting solution with magnesium sulfate filtering and removing the chloroform using a rotary evaporator.

P1 was further reacted with benzaldehyde to synthesize ditopic Michael-acceptor. 2.5 mmol P1 and 5.5 mmol benzaldehyde were added to a 250 mL flask. 30 mL toluene, 10 mL DMF, and piperdinium acetate (0.1 g per 2.5 mmol of P1) were added to the flask (see ESI,† for the synthesis of piperdinium acetate). The reaction was heated to reflux for 4 hour. The same washing protocols with NaHCO₃ aqueous solution (×3) and water (×3) were used to remove the unreacted reagents and piperdinium acetate. Finally, a BCAm Michael-acceptor with a substituent R = –H attached to the phenyl ring (1H) was synthesized. For Michael-acceptors with different functional groups, other benzaldehyde derivatives (4-anisaldehyde, or 4-nitrobenzaldehyde) were used to synthesize 1N (R = –NO₂) and 1M (R = –OCH₃) using conditions similar to the synthesis of 1H (Fig. S1, see ESI,† for characterization). Poly(propylene glycol)s (PPG) with three different molecular weights M_PPG = 230, 2000, and 4000 g mol⁻¹ were used to vary the molecular weight of Michael-acceptor 1R_MPPG.

2.3 Synthesis of thiol-functionalized silica particle

The silica particles (Fiber Optic Center SIOP050-01-1KG, hydrodynamic diameter d_h = 627 ± 24 nm) were grafted with mercaptopropyl groups following a previously reported method.¹⁷ In a 2 L round-bottom flask, 1.2 L of toluene and 27 g of silica particles were added. The flask was sonicated for 1 hour and stirred for 1 hour. 2.4 mL of (3-mercaptopropyl)trimethoxysilane was added to the flask, and the reaction was heated to reflux for 24 hour. The reaction was then cooled down and the toluene was removed with a rotary evaporator. After drying, the dried particles were washed with ethanol 5 times. The recovered thiol-functionalized particle had d_h = 648 ± 40 nm measured with dynamic light scattering (see ESI†).

2.4 Suspension preparation

Suspensions were prepared by mixing dried particles and an MA oil with a volume fraction of ϕ = 0.52, until no visible dry powder remained, and the suspension looked homogeneous.

2.5 Rheology measurements

Rheology was measured with a stress-controlled rheometer (Anton Paar, MCR301 and MCR702) using a parallel-plate geometry (plate diameter 25 mm). To homogeneously suspend silica particles, suspensions were presheared at shear rate [small gamma, Greek, dot above] = 1 s⁻¹ for 5 min at elevated temperature T = 100 °C. The suspension was then cooled down to room temperature and equilibrated at [small gamma, Greek, dot above] = 5 s⁻¹ for 150 s. Shear rate sweep measurements were performed with a data acquisition rate of 5 s per point at each shear rate. The error bar is estimated from 3 cycles of forward and backward ramps. A pre-shear step ([small gamma, Greek, dot above] = 5 s⁻¹ for 300 s and 100 s for rest) is applied between cycles to mitigate microstructure formation.

3 Results and discussion

3.1 Tailoring chemical friction via thia-Michael dynamic chemistry and molecular weight

The initial focus of this study was on exploring MA-endcapped PPG polymers of different molecular weight to the prior study. As such MA-endcapped PPG polymers where the PPG unit has a number average molecular weight (M_PPG) of 2000 g mol⁻¹ (i.e. half that of the prior study) were prepared with three different –R groups attached to the phenyl ring: methoxy (R = –OCH₃, 1M₂₀₀₀), hydrogen (R = –H, 1H₂₀₀₀), and nitro (R = –NO₂, 1N₂₀₀₀). Prior studies show that the equilibrium constant K_eq of the thia-Michael reaction trends with their electron-withdrawing nature, namely, –NO₂ > –H > –OCH₃ (as shown in Table 1).^14,16 The effect of these different R groups on the chemically-driven frictional interactions was studied with thiol-functionalized particles (ϕ = 0.52) suspended in the MA-endcapped polymers. Fig. 1a–c shows plots of the relative viscosity η_r = η/η_s, where η is the suspension viscosity and η_s is the Newtonian viscosity of the MA-endcapped polymer fluid (see ESI,† for η_s values), as a function of shear stress τ for the thiol particles suspended in the three different MA-endcapped polymer fluids (Fig. S2 shows a plot of viscosity as a function of shear rate, see ESI†). In each case the suspensions exhibit continuous shear thickening at τ > 10 Pa (closed symbols) (at τ < 10 Pa there is a mild shear thinning). Despite the different K_eq's between the particles and three fluids, each shows a similar onset shear stress τ ≈ 10 Pa as well as a similar degree of shear thickening (i.e., slope of η versus τ in the shear thickening regime) as shown by the reference triangles in Fig. 1. The shear thickening is followed by a plateau or mild shear thinning at τ > 100 Pa.

Table 1 Molecular weight of the Michael-acceptor-endcapped poly(propylene glycol)s and equilibrium bonding constant of small molecule analogs with thiol

Substituent,–R	M PPG (g mol^−1)	M MA (g mol^−1)	K eq (M^−1)
a Number-average molecular weight. b Measured by nuclear magnetic resonance spectroscopy. c Values are from small molecule analog study at 25 °C reported in ref. 14.
–OCH3 (1M)	230	760	50
	2000	2980
	4000	5590
–H (1H)	230	790	400
	2000	2940
	4000	5750
–NO2 (1N)	2000	2740	8000
	4000	6070

---

Fig. 1 Relative viscosity η_r = η/η_s for suspensions in 1M₂₀₀₀ (a), 1H₂₀₀₀ (b), and 1N₂₀₀₀ (c) as a function of shear stress τ. Closed symbols: increasing stress ramp. Open symbols: decreasing stress on the ramp's return cycle. Triangles indicate a slope of 0.5 for reference. Error bars are from 3 cycles of forward and backward ramps. The inset in (a) shows the η_r as a function of shear rate [small gamma, Greek, dot above] for the suspension in 1M₂₀₀₀.

However, these three suspensions exhibit striking differences in their apparent time-dependent behavior. This is seen in a pronounced hysteresis of the viscosity between the forward and backward (open symbols in Fig. 1a–c) shear ramp, which increases with increasing K_eq. At low K_eq (R = –OCH₃) the forward and backward ramps are identical (see the inset of Fig. 1a for the viscosity as a function shear rate). At low τ < 1 Pa ([small gamma, Greek, dot above] < 10⁻² s⁻¹), a small initial viscosity increase in the forward ramp is observed (Fig. S2, see ESI†). This is a measurement artifact where the suspensions have not yet achieved a steady state on account of insufficient strain during the allotted time interval.¹⁸ An increased equilibrating time (30 and 90 s per point) measures the consistent steady-state viscosity at τ < 1 Pa and shows that the measured viscosity at all equilibrating times (5, 30, and 90 s) is the steady-state value for τ > 1 Pa (Fig. S3, see ESI†). As seen in Fig. 1c higher K_eq results in a dramatic increase in viscosity during the backward ramp. Time sweeps (Fig. S4, see ESI†) show a clear viscosity increase at a fixed shear rate consistent with dynamic bonds resulting in a time dependent rheology. This anti-thixotropy (or rheopexy) can be attributed to the relaxation time of the dynamic bonds as the bridging interactions are replaced by grafted brushes. When K_eq is larger, the dissociation of thia-Michael bridging interaction is suppressed and thus, the suspension stays in the chemical-friction-induced shear-thickened state for longer before relaxing to the brush layer state during the backward ramp. As a result, the measured viscosity in the backward ramp is larger than the forward ramp and in turn, a reduced magnitude of shear thickening appears from 1H₂₀₀₀ (Fig. 1b) and 1N₂₀₀₀ (Fig. 1c). Interestingly, the effect of the –R group on the rheopectic rheology differs from suspensions in higher molecular weight MA-endcapped PPG (M_PPG = 4000 g mol⁻¹), where rheopexy appears at room temperature, irrespective of the nature of R-substituent on the BCAm moiety. Based on temperature studies of those suspensions it was suggested that rheopexy is observed when the fraction of thiols forming the thia-Michael adduct (p) is > 0.96.¹⁴ However, comparison of the suspensions in 1R₂₀₀₀ and 1R₄₀₀₀ with the same K_eq show that molecular weight of the polymer has an impact on the rheopexy behavior of the suspensions. For example, while the suspension in 1M₄₀₀₀ shows rheopectic behavior, the suspension in 1M₂₀₀₀ shows no rheopexy, even though the fraction of reacted thiol p = 0.97 (i.e. >0.96) (see ESI,† for p estimation for all suspensions and Fig. S5).

To explore in more detail the effect of molecular weight of the MA-endcapped polymers on the chemical friction of these dynamic covalent dense suspensions, MA-endcapped polymers with two different PPG backbone molecular weights, M_PPG = 230 (1R₂₃₀) and 4000 g mol⁻¹ (1R₄₀₀₀), were synthesized, and the rheology of the thiol functionalized silica particles in these polymers was explored. Here, the electronics (–R groups) primarily control K_eq, and any impact of molecular weight is assumed to be minimal.¹⁹ At the suspension packing fraction ϕ = 0.52, the corresponding stoichiometric ratio of thiol groups to MA double bonds is approximately r = [–SH]/[–MA] = 0.01 for M_PPG = 230 g mol⁻¹, r = 0.03 for M_PPG = 2000 g mol⁻¹, and r = 0.13 for M_PPG = 4000 g mol⁻¹. Thus at constant ϕ the three suspensions will have a slightly different number of BCAm group bonding sites. However, it is important to note that all suspensions have a large excess of MA moieties.

For 1M, which has the lowest K_eq, reversible rheological behavior is seen in the forward and backward sweep measurements for M_PPG ≤ 2000 g mol⁻¹ as shown in 1M₂₃₀ (Fig. 2a) and 1M₂₀₀₀ (Fig. 2b). By contrast, rheopexy is observed (Fig. 2c) when the particles are suspended in the higher molecular weight 1M₄₀₀₀ (molecular weight of MA M_MA ≈ 5600 g mol⁻¹). Given that the K_eq of the thia-Michael reaction is equal in all three suspensions, this rheopectic behavior could be accounted for by molecular weight-induced dynamics or entropic contribution of 1M polymers. It is worthy of note that the studied M_MA is below the reported entanglement molecular weights of PPG (M_e ≈ 5300²⁰ or 7000 g mol⁻¹²¹), thus the rheopexy seems not to be a result of MA polymer entanglement.

Fig. 2 Relative viscosity η_rversus shear stress τ of ϕ = 0.52 thiol functionalized silica particle suspensions in different molecular weight BCAm-endcapped poly(propylene glycol)s. The molecular weight of these ditopic polymers is controlled by varying the molecular weight of PPG backbone used to attach the BCAm units, M_PPG = 230 g mol⁻¹ (a) and (d), 2000 g mol⁻¹ (b) and (e) and 4000 g mol⁻¹ (c) and (f). The R substituent on the BCAm is either R = –OCH₃ (a)–(c) or R = –H (d)–(f).

To further explore the origin of the rheopectic behavior, the thiol-functionalized particles were dispersed in a MA-endcapped polymer with larger K_eq's, namely 1H. In 1H₂₃₀ (Fig. 2d), the suspension shows reversible rheology similar to that of weaker bonded suspension. A mild viscosity drop appears in 1H₂₃₀ (Fig. 2d) in the reverse direction and may indicate possible thixotropy in this system. Time-dependent viscosity appears at M_PPG ≥ 2000 g mol⁻¹ as shown in 1H₂₀₀₀ (Fig. 2e) and 1H₄₀₀₀ (Fig. 2f). Comparing the results of the equal molecular weight MA polymers 1M₂₀₀₀ and 1H₂₀₀₀ (Table 1) suggests that the relaxation time scale of dynamic bond bridging is impacted by the strength of the dynamic bridging bonds (i.e., K_eq). As such, the data demonstrates that both the molecular weight of the MA polymer and the bond strength contribute to the rheopectic rheology in these dynamic covalent dense suspensions. Above the critical bonding strength at a given molecular weight, the suspension exhibits rheopectic rheology reflecting the relaxation of the bridging layer. The suspensions in 1N with the highest K_eq are also rheopectic (Fig. S6, see ESI†). Note that for 1M, the slope of shear thickening does vary as M_PPG increases. The fraction of bonded thiol p may play a role in this observed change. This system has the lowest K_eq (ca. 50 M⁻¹) and as such a decrease in p of approximately 5% can be predicted upon increasing molecular weight; p = 0.992 for 1M₂₃₀, p = 0.970 for 1M₂₀₀₀, and p = 0.944 for 1M₄₀₀₀. This effect is not observed in the more strongly bonded 1H and 1N suspensions, which have p > 0.99 for all molecular weights and show almost no change in p (Fig. S5 and Table S1, see ESI†).

3.2 Tailoring chemical friction via competitive bonding thiol additives

If the dynamic bond between the polymer fluid and particles is critical to the frictional interactions and rheopectic behavior of the dense suspensions then the addition of a competitive bonding agent²³ that inhibits the polymer particle bonds should switch off such behavior. Thus the addition of small molecule thiols which can react with the ditopic Michael-acceptor polymer fluid was explored. In these experiments 2,2′-(ethylenedioxy)diethanethiol (EDDT) with dithiol structure is introduced to the suspension with a specific stoichiometric ratio r_fluid = [–SH]_fluid/[–MA] from r_fluid = 0 to 10, where [–SH]_fluid and [–MA] are the molar concentrations of thiol from EDDT and Michael-acceptor groups, respectively. While fixing the volume fraction ϕ = 0.52, five different ratios r_fluid of the suspending medium are used, 0 (no added EDDT), 0.1, 0.5, 2, and 10 (bottom to top in Fig. 3). The total thiol (particle and additive) to Michael-acceptor group molar ratio r in the corresponding suspension is r = 0.03, 0.13, 0.53, 2.04, and 10.05, respectively, i.e., r ≈ r_fluid given the small number of thiols from the particles. As a result, there is an excess of Michael-acceptors on the polymers over the free thiols when r_fluid < 1, which is required to promote the formation of a brush layer on the particles. Note that r_fluid = 1 is avoided to minimize the formation of high molecular polymeric species. At these ratios the degree of polymerization X̄_n is expected to be ≤3, i.e., only oligomeric species are present (using X̄_n = (1 + r̄)/(1 − r̄) with r̄ = r_fluid for r_fluid < 1 and r̄ = r_fluid⁻¹ for r_fluid > 1).²⁴

Fig. 3 Rheology of dense suspensions of thiol functionalized SiO₂ particles suspended in a mixture of 1H₂₀₀₀ and dithiol. η_r is plotted as a function of stress τ. 2,2′-(ethylenedioxy)diethanethiol is added to the suspension to alter the stoichiometric ratio r_fluid from r_fluid = 0 (no added 2,2′-(ethylenedioxy)diethanethiol), 0.1, 0.5, 2, and 10 (from bottom to top). The volume fraction is kept ϕ = 0.52 for all suspensions. Relative viscosity η_r = η/η_s is plotted as a function of shear stress τ. The constraint-based model²² is used to fit reversal rheology curves (solid line). A schematic illustration on the right panel describes the weakening of solvation force as the concentration of 2,2′-(ethylenedioxy)diethanethiol (and r_fluid) increases.

η _r is measured with a forward (closed symbol) and backward (open symbol) ramp and plotted as a function of shear stress τ in Fig. 3. For the suspension in 1H₂₀₀₀, rheopectic behavior is observed up to r_fluid = 0.5, and disappears at r_fluid ≥ 2. This further confirms the hypothesis of our previous study¹⁴ that the antithixotropy in these systems is driven by shear-induced contacts that are stabilized by polymer bridging^25,26 and not particle–particle contacts.^27–29 The added free dithiols competitively deplete the available MA moieties, thereby reducing the strength of the sticky chemical friction between particles. Hence, the extent of shear thickening also decreases. Note the increase in η_r at a low τ as a greater amount of dithiol is added. This tendency of forming a yield stress in a suspension could be accounted for by the weakening of the solvation layer at the surface of particles.^30,31 On account of the high K_eq of the ditopic polymer and thiol group-functionalized particle surface, the particle–solvent interaction provides a strong solvation force in the absence of free dithiol. However, the addition of free dithiol results in less of the ditopic polymers forming dynamic bonds with the particles and therefore, lowers their solvation. As a result, the repulsive force between the particles decreases, leading to the aggregation and the suspension developing a yield stress as the solvation force is suppressed (see illustrative scheme on the right panel of Fig. 3). Control experiments with suspensions in hydroxy-terminated PPG (M_PPG = 2000 g mol⁻¹) and in a 10-to-1 molar ratio mixture of hydroxy-terminated PPG and EDDT show shear-thinning trends without an apparent thickening and confirm the absence of disulfide brush layer or disulfide bridging interaction formation (Fig. S7, see ESI†). In addition, the Raman spectrum of the control suspension with EDDT shows no significant disulfide formation (Fig. S8, see ESI†).

We fit the backward ramps of our flow curves to extract stress and packing fraction scales using the model of Guy et al.^22,32 This model includes a stress scale for the breaking of constraints and additional associated, jamming packing fractions, extending the Wyart–Cates (WC)³³ theory of shear thickening that only includes a single stress scale for the formation of constraints. The generalization by Guy et al. can model a variety of flow curves and we will be using the so-called “class 3a” models, which model flow curves that show shear-thinning at low stresses and shear thickening at higher stresses. In the original use of the class 3a models Guy et al. fit steady state rheology curves for cornstarch suspensions where the constraints being broken at low stress were thought of as rolling constraints and the constraints being formed at higher stresses were thought of as sliding constraints. In this work, the constraints being broken at low stresses are those that arise from interacting brush layers while the constraints being made at higher stresses are those from interparticle bridging. This gives a viscosity η_r = [1 − ϕ/ϕ_J(a, f)]⁻². In this extended model the jamming volume fraction ϕ_J(a, f) is a function of the stress-dependent fraction of adhesive (a) and frictional (f) particle contacts. The onset packing fraction for shear jamming of frictional particles in the absence of adhesion ϕ_m ≡ ϕ_J(a = 0, f = 1), the adhesive loose packing fraction ϕ_alp ≡ ϕ_J(a = 1, f = 1), and adhesive close packing fraction ϕ_acp ≡ ϕ_J(a = 1, f = 0) are used as adjustable parameters in the model fit (see ESI,† for details). This extended model provides a good fit to both the shear thinning and thickening portions of the flow curves (Fig. 3, solid lines). For the systems showing rheopexy (r ≤ 0.5) in Fig. 3 we only fit the backward ramps of the data as those are the steady-state flow curves and therefore the stress scales extracted are not dependent on measurement time as the forward curves would be.

The model fit allows for the extraction of characteristic stress magnitudes for the activation of frictional contact interactions, τ*, and for the deactivation of adhesive contacts, τ_a, and gives further insight into how the introduction of competitive bonding molecules impacts the suspension rheology at each stoichiometric ratio r (Fig. 4a). At all r_fluid, τ* > τ_a indicating that the activation of frictional force requires a larger stress than the one to overcome the adhesion. An increase in τ_a and τ* is observed at r_fluid > 0.5 where the number of free thiol groups exceeds that of MAs, a trend that is consistent with the previously discussed weakening of the solvation of the particles and an increase of attractive interactions between them.

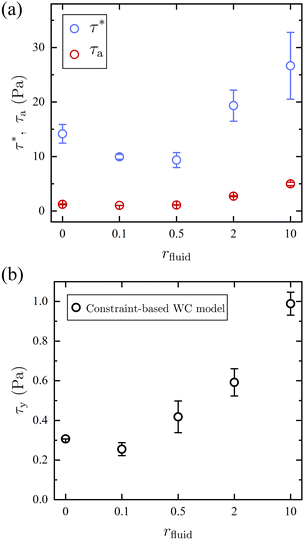Fig. 4 (a) The characteristic stress for activating friction τ* (blue) and deactivating adhesion τ_a (red) is estimated from the modified WC model. (b) Yield stress τ_y of the suspension in 1H₂₀₀₀ mixed with a ratio r_fluid of free thiol molecules from 2,2′-(ethylenedioxy)diethanethiol –SH is estimated using the constraint-based WC model²² by setting ϕ_J = ϕ.

The fits to the flow curves shown in Fig. 3 and corresponding fit parameters shown in Fig. 4 indicate that the stress scales associated with chemical friction are substantially smaller than where contacts are mediated by steric friction. The critical onset stress for thickening is τ* ≤ 27 Pa for all r_fluid and is much lower than in suspensions that shear-thicken via physical friction (i.e., direct contact). For instance, the suspension in 1H₂₀₀₀ shear-thickens at a much lower τ* than charge-stabilized silica particles with d = 1.54 mm at the same packing fraction (τ* ∼ 100 Pa).³⁴ In addition, the critical stress for particles with permanent covalent-bond brush layer follows a power-law relation, suggesting τ* ∼ 145 Pa for d = 648 nm.³⁵ A lower τ* of the dynamic-bond-induced shear thickening suspension may suggest that particles with dynamic bond brush layer are less stable than charge- and permanent brush-stabilized particles. Moreover, different shear thickening mechanisms are at play between the dynamic bond induced chemical and physical friction. The suspension with dynamic covalent bonds requires no direct particle contact to form bridging bonds, whereas a larger stress is required for particles with physical friction to put the particles in direct contact. Hence, the dynamic-bond-induced shear thickening occurs at a lower τ* than conventional shear thickening suspensions.

As mentioned previously there is an increase in viscosity at low τ upon the dithiol addition. This was hypothesized to come from its competitive bonding to the dynamic brushes on the particles which results in increased particle attraction. It, therefore, is reasonable to expect that this increased attraction would be reflected in the yield behavior.³⁶ The yield stress τ_y is estimated using the constraint-based WC model by setting ϕ_J = ϕ (i.e., η_r → ∞).³² The estimated τ_y in Fig. 4b remains constant for r_fluid ≤ 0.5 where [–MA] > [–SH]. For r_fluid ≥ 2, the solvation force is largely reduced, resulting in an increase in τ_y. This abrupt increase in τ_y at r_fluid ≥ 2 further supports that excessive Michael-acceptor moieties over thiols allow for the formation of a (dynamic) brush layer that stabilizes the particles. However, further increase in the amount of free thiol at r_fluid ≥ 2 raises the yield stress. This observation suggests an external control of the repulsive potential of brush layer-stabilized particles. In contrast to the permanently-bonded brush layer,^37,38 a brush layer formed by dynamic covalent bonds allows for systematic control of particle stability by the simple addition of competitive bonding molecules, which reduces the concentration of polymer brushes at equilibrium.

3.3 Temperature-dependence of sticky friction

A governing parameter of sticky friction is the equilibrium of the dynamic thia-Michael bonds in these dynamic covalent dense suspensions. This means that the frictional interactions should also be controllable by temperature. Fig. 5 shows the viscosity η_r as a function of shear stress τ at three temperatures, 25 °C (bottom), 50 °C (middle), and 70 °C (top), for the suspension with ϕ = 0.52 suspended in 1H₂₀₀₀. Increasing the temperature reduces K_eq according to the van't Hoff equation and therefore, decreases the number of thia-Michael bonds for a given concentration. As a result, the sticky friction weakens as temperature increases, thereby removing the rheopectic behavior. Simultaneously, the viscosity at low τ increases due to the weakening of the solvation force. These observations demonstrate again the effect of introducing competitive bonding molecules, whereby the effectiveness of sticky friction weakens with decreasing concentration of active bonding moieties.

Fig. 5 Rheology of dense suspensions of thiol functionalized silica particles in 1H₂₀₀₀. η_r is plotted as a function of shear stress τ. Temperature is raised from 25 °C to 50 °C, and to 70 °C (bottom to top).

4 Conclusions

We demonstrated that the room temperature dynamic nature of thia-Michael bonds can mirror the formation of shear-induced frictional networks. Upon shearing a suspension of particles with room temperature dynamic covalent brushes, formed between the thiols on the particle surface and double bond moieties of a BCAm ditopic polymer fluid, reorganization of the dynamic bonds occurs resulting in polymer bridging interactions between the particles. The experimental results confirm that this dynamic bond-induced bridging serves as shear-induced friction with a long relaxation time, i.e., sticky friction. Control of the molecular weight and equilibrium constant for the thia-Michael dynamic covalent bonds enables systematic tailoring of the rheopectic behavior: (1) decreasing the molecular weight of ditopic MA–polymer inhibits the rheopectic behavior, (2) a larger equilibrium constant between the particle and polymer fluid results in a slower relaxation of bridging interaction and thus enhances rheopexy, and (3) the introduction of competitive bonding thiol additives or temperature control further tunes the bridging interaction formation, granting external controls of the time-dependent rheology and yield-stress.

Such control over the rheological behavior using only a single suspending medium makes these suspensions potentially ideal for applications where a single fluid needs to serve multiple purposes. Furthermore, tuning suspension rheology by changing particle-level properties, such as surface roughness, can be more expensive and time consuming than simply changing the fluid composition. This versatility could be enhanced further as the equilibrium of dynamic covalent chemistries is widely tunable with pH, temperature, and chemical stimuli.^39,40

Author contributions

HK, SJR, and HMJ conceived the research project; HK carried out the experiment; HK, SJR, and HMJ analyzed the data; HK and MvdN conducted the fitting; HK and NDD analyzed the characterization of the polymer; All authors participated in the discussion and writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was primarily supported by the University of Chicago Materials Research Science and Engineering Center (MRSEC), which is funded by the National Science Foundation under award number DMR-2011854. Additional support was provided by the Army Research Laboratory under Cooperative Agreement Number W911NF-20-2-0044. Part of this work was performed under the following financial assistance award 70NANB19H005 from U.S. Department of Commerce, National Institute of Standards and Technology as part of the Center for Hierarchical Materials Design (CHiMaD). HMJ acknowledges additional support from W911NF-21-2-0146 and W911NF-21-1-0038. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation here-in.

Notes and references

1. R. Mari, R. Seto, J. F. Morris and M. M. Denn, J. Rheol., 2014, 58, 1693–1724.
2. E. Brown and H. M. Jaeger, Rep. Prog. Phys., 2014, 77, 046602.
3. C.-P. Hsu, J. Mandal, S. N. Ramakrishna, N. D. Spencer and L. Isa, Nat. Commun., 2021, 12, 1477.
4. C.-P. Hsu, S. N. Ramakrishna, M. Zanini, N. D. Spencer and L. Isa, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5117–5122.
5. S. Jamali and J. F. Brady, Phys. Rev. Lett., 2019, 123, 138002.
6. S. Pradeep, M. Nabizadeh, A. R. Jacob, S. Jamali and L. C. Hsiao, Phys. Rev. Lett., 2021, 127, 158002.
7. N. M. James, H. Xue, M. Goyal and H. M. Jaeger, Soft Matter, 2019, 15, 3649–3654.
8. L. C. Hsiao and S. Pradeep, Curr. Opin. Colloid Interface Sci., 2019, 43, 94–112.
9. N. M. James, C.-P. Hsu, N. D. Spencer, H. M. Jaeger and L. Isa, J. Phys. Chem. Lett., 2019, 10, 1663–1668.
10. J. A. Richards, B. M. Guy, E. Blanco, M. Hermes, G. Poy and W. C. K. Poon, J. Rheol., 2020, 64, 405.
11. E. Brown, N. A. Forman, C. S. Orellana, H. Zhang, B. W. Maynor, D. E. Betts, J. M. DeSimone and H. M. Jaeger, Nat. Mater., 2010, 9, 220–224.
12. H. M. Laun, Angew. Makromol. Chem., 1984, 123, 335–359.
13. B. M. Guy, M. Hermes and W. C. K. Poon, Phys. Rev. Lett., 2015, 115, 088304.
14. G. L. Jackson, J. M. Dennis, N. D. Dolinski, M. van der Naald, H. Kim, C. Eom, S. J. Rowan and H. M. Jaeger, Macromolecules, 2022, 55, 6453–6461.
15. T. M. FitzSimons, F. Oentoro, T. V. Shanbhag, E. V. Anslyn and A. M. Rosales, Macromolecules, 2020, 53, 3738–3746.
16. K. M. Herbert, P. T. Getty, N. D. Dolinski, J. E. Hertzog, D. de Jong, J. H. Lettow, J. Romulus, J. W. Onorato, E. M. Foster and S. J. Rowan, Chem. Sci., 2020, 11, 5028–5036.
17. C. I. Crucho, C. Baleizão and J. P. S. Farinha, Anal. Chem., 2017, 89, 681–687.
18. C. E. Wagner, A. C. Barbati, J. Engmann, A. S. Burbidge and G. H. McKinley, Appl. Rheol., 2016, 26, 36–40.
19. B. Marco-Dufort, R. Iten and M. W. Tibbitt, J. Am. Chem. Soc., 2020, 142, 15371–15385.
20. C. Gainaru and R. Böhmer, Macromolecules, 2009, 42, 7616–7618.
21. B. A. Smith, E. T. Samulski, L. P. Yu and M. A. Winnik, Macromolecules, 1985, 18, 1901–1905.
22. B. Guy, J. Richards, D. Hodgson, E. Blanco and W. Poon, Phys. Rev. Lett., 2018, 121, 128001.
23. M. N. Dominguez, M. P. Howard, J. M. Maier, S. A. Valenzuela, Z. M. Sherman, J. F. Reuther, L. C. Reimnitz, J. Kang, S. H. Cho and S. L. Gibbs, et al. , Chem. Mater., 2020, 32, 10235–10245.
24. P. J. Flory, J. Am. Chem. Soc., 1936, 58, 1877–1885.
25. D. C. Pozzo and L. M. Walker, Colloids Surf., A, 2004, 240, 187–198.
26. J. Zebrowski, V. Prasad, W. Zhang, L. M. Walker and D. Weitz, Colloids Surf., A, 2003, 213, 189–197.
27. J. B. Yannas and R. N. Gonzalez, Nature, 1961, 191, 1384–1385.
28. J. J. Richards, J. B. Hipp, J. K. Riley, N. J. Wagner and P. D. Butler, Langmuir, 2017, 33, 12260–12266.
29. G. Ovarlez, L. Tocquer, F. Bertranda and P. Coussota, Soft Matter, 2013, 9, 5540–5549.
30. S. R. Raghavan, H. J. Walls and S. A. Khan, Langmuir, 2000, 16, 7920–7930.
31. J. Gao, P. M. Mwasame and N. J. Wagner, J. Rheol., 2017, 61, 525–535.
32. J. A. Richards, B. M. Guy, E. Blanco, M. Hermes, G. Poy and W. C. Poon, J. Rheol., 2020, 64, 405–412.
33. M. Wyart and M. E. Cates, Phys. Rev. Lett., 2014, 112, 098302.
34. J. R. Royer, D. L. Blair and S. D. Hudson, Phys. Rev. Lett., 2016, 116, 188301.
35. B. Guy, M. Hermes and W. C. Poon, Phys. Rev. Lett., 2015, 115, 088304.
36. A. Z. Nelson, K. S. Schweizer, B. M. Rauzan, R. G. Nuzzo, J. Vermant and R. H. Ewoldt, Curr. Opin. Solid State Mater. Sci., 2019, 23, 100758.
37. G. H. Fredrickson and P. Pincus, Langmuir, 1991, 7, 786–795.
38. L.-N. Krishnamurthy, N. J. Wagner and J. Mewis, J. Rheol., 2005, 49, 1347–1360.
39. T. M. FitzSimons, E. V. Anslyn and A. M. Rosales, ACS Polym. Au, 2021, 2, 129–136.
40. J. F. Reuther, S. D. Dahlhauser and E. V. Anslyn, Angew. Chem., Int. Ed., 2019, 58, 74–85.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00479a

---