Self-assembly to synchrony of active gels

Abstract

Self-assembly functionalizes active constituents to perform rhythmic activities. Here, our results show that the capillary-Marangoni interaction of irregularly moving gel beads develops complex patterns at the air–liquid interface. The collective behavior of the self-assembled structures exhibits breathing dynamics, polygonal oscillating rings, and cluster synchrony of chains. Interestingly, the trapping of soft particles generates relay synchronization of a rotor. Swarming of clusters is found to form rhythmic shrinking and expanding multiple-ring patterns. The development of self-organized spatiotemporal patterns of our active gel system provides a new way of creating collective oscillations.

---

1. Introduction

Autonomy of active constituents introduces nonlinearity in the form of erratic or regular dynamics at micro- to macro-scales.¹ Their local interaction supports them to function in an organized manner, resulting in self-organized phenomena. Specifically, collective oscillations play a vital role in functioning biological systems, such as pacemaking in neural networks,² heart cells,³ and molecular motors.⁴ In the last few decades, artificial active matter research^5,6 in search of collective behavior has gained immense attention from scientists and laymen alike. Regarding the synchrony of self-oscillating droplets and objects, scientific research has contributed to the synchronization of pentanol,⁷ nitrobenzene,⁸ aniline droplets,⁹ camphor ribbons,¹⁰ boats,^11–13 and thin filaments¹⁴ at the air–liquid interface. Moreover, water-in-oil droplets in railroad-like channel networks¹⁵ and the diffusive coupling of Belousov–Zhabotinsky emulsion oscillators¹⁶ permits phase-locking. In these examples, the individual oscillator pertains to intrinsic periodic oscillations or is spatially confined. On the contrary, here, we deal with a problem where the dynamics of individual gel beads are irregular and their spatial locations are unconfined. In nature, individual organisms often follow an irregular path with no preferred direction, but short range interaction among them within a local group can decrease their erratic motion and cause them to move in harmony. Mimicking such naturally occurring behaviors on the laboratory scale provides the flexibility to tailor the functional properties for practical purposes and create new patterns.

Self-assembly is a widely studied phenomenon where the communication between particle–particle or particle–solvent can result in large-scale, ordered architectures. The nature of forces plays a crucial role in determining the final structure and the assemblies. Capillary interaction at the air–liquid interface aggregates the floating or pinned objects found in everyday examples, such as cereal clumping in a milk bowl¹⁷ and bubbles clustering in the sink.¹⁸ Micro- and nanoparticles can aggregate and create ordered arrays or patterns of particles at interfaces.¹⁹

Nowadays, the emergent dynamical self-assembly, where the organized patterns self-propel, has been a focus issue of active matter. Attractive-repulsive forces of a pair of oil droplets can lead to atomic-like motion.^20,21 In the context of complex patterns, previous studies of active droplets have identified spontaneous rotating clusters²² and dynamical shuffling of droplets.²³ Recent findings have also reported programmable self-assemblies^23–25 and dissipative structures to develop temporal aggregation,²⁶ where particles disappear upon switching off the external stimuli. Moreover, synchronization of self-moving patterns and shuffling of packed aggregation have been established, mainly in the presence of stimuli such as light,²⁷ ultrasound,²⁸ and electromagnetic field.²⁹ The simultaneity of self-assembly in conjunction with the periodic oscillations of each constituent, forming collective synchrony of patterns, is hard to achieve in active particles and not much known in the absence of forcing.

In this paper, we present how the collective spatiotemporal periodic oscillations of self-organized structures can synchronize active gels. Furthermore, a simple model is developed to show the collective oscillations of breathing patterns.

2. Experiment

Analytical grade materials CH₃ COOH (99–100%), ethanol (99–100%), NaOH (pellets) were purchased from VWR chemicals, polysaccharide medium molecular weight chitosan (CS) from Sigma-Aldrich (448877) and GdCl₃·6H₂ O from AlfaAesar.

The chitosan–gadolinium salt sol [0.1 M GdCl₃ in the 0.75 or 1.5 w/v% of CS] in 0.2 M CH₃COOH and sodium hydroxide 3.0 M were prepared with deionized water (Purite 300). For active droplets (CGE, chitosan–gadolinium–ethanol), 1.6 mL ethanol was added in the 10 mL of chitosan–gadolinium salt sol with 0.008 w/v% methylene blue to aid visualization. The mixed CGE solution was stirred for 2 hours and stored overnight in room condition. The passive droplets (CG) were prepared by adding 1.6 mL of deionized water in the chitosan–gadolinium salt sol to maintain the same concentration of chitosan and gadolinium compared with the CGE solutions. The density and viscosity of the solutions, summarized in Table S1 in the ESI,† were measured with a density meter (Anton Paar DMA-550) and with a rotational viscometer (Anton Paar ViscoQC-300), respectively. Surface tension measurements were carried out using Krüss tensiometer.

Experiments were performed at temperature 24 ± 1 °C using circular polyvinyl Petri dishes of inner diameter 8.7 cm or 13.7 cm filled with 60 mL or 150 mL of 3.0 M alkaline solution, respectively. CG or CGE droplets were dripped from a height of ≈1 cm on the alkaline surface using a peristaltic pump (Ismatic Reglo) through the Tygon tube with a needle of inner diameter 0.6 mm (or 1.65 mm). Similar behavior was obtained on decreasing and increasing alkaline solution height to 0.5 cm and 1.5 cm, respectively. Those droplets that adhered to the boundaries or fell onto others during dripping were manually removed. During an experiment we have focused our attention on clusters that are sufficiently far form the rest of the beads and the dish wall, i.e., they can be considered isolated. The characterization of these self-assemblies was based on performing 15–20 experiments for each population size of 4–10.

An Osmo action camera was positioned above the container to record the experiments as videos (30 or 60 frames per second with 1080p resolution), illuminated with a diffusive LED and/or white ceiling light source. The size of raw images (1024 × 768 pixels) were captured using a CCD camera equipped with Vivitar lens. Data were analyzed using MatLab scripts and Fiji ImageJ software with MultiTracker or Mtrack2 Plugins.

3. Results and discussion

The sol–gel transition of CG droplets upon contact with the sodium hydroxide solution on the air–liquid interface compartmentalizes the polymer and the alkaline solution.³⁰ During gel formation, shown in the reaction scheme of Fig. 1, the droplet height and diameter, defined in Fig. 2A, increase and decrease sharply, respectively, before becoming constant in time (Fig. 2B). Even though the density of pre-gel CG solution is less than that of the alkaline solution, the contraction in CG gel layer creates concave menisci on the alkaline surface, which is verified by deflectometry (see Fig. S1 in the ESI†). The developed curved surface induces capillary attraction between the beads, so they approach each other. The grey dots (for five separate experiments) in Fig. 2C show how the relative velocity sharply increases as the beads aproach each other. After reaching a maximal relative speed v_rel = 1.90 ± 0.14 cm s⁻¹, the speed of beads immediately falls to near zero. 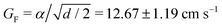The v_rel binned data (black) follow the asymptotic formula for the force of capillary attraction when it is approximately equal to the viscous drag force,^31–34i.e.,where G(2r/d) represents the hydrodynamic mobility, a correction factor of hydrodynamic interactions^31,32,35 given asThe best fit (red-dashed curve) yields and q = 2.31 ± 0.16 cm⁻¹. The blue continuous curve is a fit to eqn (1) with assuming G(z) = 1, which results in G_F = 10.71 ± 1.14 cm s⁻¹ and q = 2.24 ± 0.15 cm⁻¹. Our experimental data in Fig. 2C show that hydrodynamic interactions are considerable only for ≈0.02 cm distance between the beads from their boundaries before the collision. The close agreement of red-dashed and blue curves suggests that, for simplicity, we can limit our discussion to capillary interaction. In eqn (1) the reciprocal of the capillary length depends on the surface tension of the fluid γ, the density difference Δρ and the gravitational acceleration g. Considering the two liquids without the gelation process, q value is estimated to be 1.2 cm⁻¹. Parameter relies on Q,^32,34 which is the measure of liquid surface deformation at the bead with diameter d and on the dynamic viscosity of the solution η. Beads are nearly semi-immersed in the solution, so the correction coefficient f_d in drag force is expected to be 1.³¹ The value of α, determined from fitted value G_F, leads to the estimation of Q ≈ 0.72 mm, which is in accordance with experimental observations, since only minor surface deformation is visible.

Fig. 1 Scheme of the chitosan gelation.

Fig. 2 (A) Side view of the CG bead at (i) t = 2 s and (ii) t = 19 s. Field of view: 0.59 × 0.20 cm². (B) The temporal evolution of bead height h (blue), and diameter d (red). (C) Relative velocity v_rel of the CG beads as a function of the ratio of distance from their centroid r and bead radius d/2. The inset images show beads (i) far from or (ii) close to each other, Δt = 1 s. The concentration of CG(sol) is 0.75 w/v% and d_i = 1.65 mm. The measured data are shown with gray filled circles, the binned data with black hollow circles and their error bars. The red-dashed curve corresponds to the fit of eqn (1) and (2), the blue solid curve to the fit of eqn (1) assuming G(2r/d) = 1.

We have previously shown that self-propulsion of chitosan hydrogel beads could be realized by adding surface-active material ethanol, as a fuel to the chitosan solution, and we observed continuous and intermittent (stop-and-run) motion of the bead before reaching the final stationary state.³⁶ Therefore to make active droplets, we infused ethanol in the CG solutions. When we place the CGE droplets on the alkaline solution, the ethanol diffuses out of the droplet decreasing the surface tension of the liquid around it. In addition, small asymmetry in the shape of the droplet introduces a spatial gradient in the surface tension, and the arising Marangoni force propel the bead along the surface. Initially, the CGE beads continuously move in an unorganized manner independently of one another at high speed, as depicted in Fig. 3A. Note that the sharp falls in speed occur because of the collisions with the Petri dish wall and the beads, verified by comparing the x–y trajectories with the videos. The depletion of ethanol from the droplet gradually decreases the speed of the beads and produces irregular spikes of run-and-stop motion because the weaker flux of ethanol out of the bead cannot maintain a continuous propulsion, similar to our study with a single chitosan bead.³⁶ At this stage, the beads still remain unsynchronized, illustrated by the speed-time series in the inset Fig. 3A. The cessation of individual run phases indicates that geometric asymmetry in the bead cannot create sufficient surface tension gradient any more. A new source in the gradient of surface tension arises, however, from the crowdedness of beads. The ethanol concentration around the beads will be greater in areas adjacent to many beads, leading to smaller surface tension. This then propels the beads away from each other with speeds that are now comparable to that resultant from the capillary attraction. The interplay of these antagonist forces may result in a self-assembly of the nearest beads.

Fig. 3 (A) Speed evolution of four beads as a function of time. (B) Speed of the beads in the ensembled state with images (i and iii) indicating the breathing-in state and (ii) the breathing-out. Field of view of images is 1.70 × 1.75 cm². Nearest neighbor distances of beads (C) in experiments and (D) in simulation. (E) x–y trajectories of the particles with initial positions (0,0), (0.4,0.4), (0.4,−0.4), and (0.8,0). The CS(sol) concentration is 0.75 w/v% and d_i = 1.65 mm.

For the case of two CGE beads, two situations can occur: the beads either move away due to the Marangoni effect or form a pair and self-propel together (see Fig. S2 in the ESI†). For 3–5 beads more complex behavior, synchronization is observed as shown in Fig. 3B for population size of 4 beads, and Fig. S3 (ESI†) for 3 and 5 beads. The inset images in Fig. 3B display the breathing cycle (see Video S1, ESI†), where all beads approach (i and iii) and separate (ii) with their speed is being minimal at the closest and the farthest positions. The beads far from the assembly die in a few seconds, but the organized pattern remains active for a longer duration. Fig. 3C shows that the nearest-neighbor distances of the beads vary irregularly, but the phase remains in sync. The lower threshold of ∼0.63 cm indicates when collisions occur, and the average difference between the maximal and minimal distances of 0.11 ± 0.03 cm provides the repulsion range of the four beads. Our experimental characterization supports that in the assembly state, the repulsion domain is shorter than the range of capillary attraction.

In order to construct a simple model which can recapture the essential dynamics of our experimental system, we have to consider the following. The experimental capillary length l_c is 4.5 mm, which yields an Eötvös number E₀ = d²/l_c² = 1.2 considering the final size of the beads. This means that surface tension effects are comparable to that of gravitational at the interface around a bead. The transient self-organized oscillation of beads only emerges after the intensive self-propulsion of independent active beads has ceased. By this stage a background ethanol concentration is built in the aqueous phase around the beads acting as sources. Although the drift velocity of the beads is small, the Marangoni number (M_a = ud/D) falls in the range of 2000–8000, indicating that diffusion is negligible on the time scale of significant Marangoni flow with D = 2 × 10⁻⁵ cm² s⁻¹. Hence the temporal evolution of the concentration field can be neglected on the time scale of oscillatory motion, and the beads can be approximated as point sources with constant concentration. The constant course diffusion is characterized by a concentration field with the complementary error function,³⁷ hence, the asymptotic concentration gradient takes the form of exp(−r²), which provides the functional form for the gradient of surface tension and for that of the repelling Marangoni force. The dimensionless governing equation can be expressed as

where the term containing C stands for the viscous (Stokes) drag,³³ while F⃑_ij represents the interaction force per unit mass acting on bead i due to bead j at a distance of r_ij. It can be written in the form ofwhere e⃑_ij is the unit vector pointing from bead i towards bead j. The first term in eqn (4) describes repulsion that originates from the concentration gradient of ethanol as discussed above. The second term in eqn (4), related to attraction, is from the capillary force.^31,32,34Eqn (3) defines a 4 × N-variable system for N number of beads. Our simplistic model illustrates that the radial distances between the particles, as shown in Fig. 3D, are synchronized and well-matched with our experiments. The representative trajectories in Fig. 3E indicate that particles 1 and 4 oscillate along the x-axis while 2 and 3 along the y-axis (see Video S2, as well, ESI†). The identical shape of the color trajectories of particles 1–4 represents that the particles move in and out together, i.e., they exhibit breathing dynamics. Varying the initial particle positions influence the dynamics and collective behavior of the system. For example, chimera-like state, the coexistence of synchronized and unsynchronized radial distances between the particles, is possible (see Fig. S4 in the ESI†). The details of the simulations are included in the ESI.†

Besides breathing behavior, more complex dynamics can be observed as factors, such as spatial positions, collision and adhesion/pairing of the beads, influence the spatiotemporal dynamics. For example, the inset image of Fig. 4A shows that beads 2, 4, and 5 form a chain, but 1 and 3 remain free (see Video S3, ESI†). The speed evolution in Fig. 4A illustrates that beads 1–3 oscillate with a higher speed than beads 4 and 5. When beads aggregate, chemical gradients push them away from the central core and capillary interaction organize them into a ring pattern (see Fig. S5 in the ESI†). The self-organized ring pattern can open and close at different positions. The ring shown in Fig. 4B(i) closes and Fig. 4B(ii) opens at the same position resembling inhale and exhale activities (see Video S4, ESI†). Fig. 4B(iii) illustrates that beads 2–7 oscillate with irregular amplitude in synchrony, but bead 1 remains in a nearly steady state or translates with the assembly (x–y trajectories in Fig. S5 in the ESI†). We have also found that the oscillators far from the ring opening mode do not sustain the oscillations for long. Such partial synchrony, where some beads exhibit periodic dynamics in synchrony and the rest stay in a steady state, is also obtained for the self-assembly of three to five beads.

Fig. 4 (A) Speed evolution of five beads aligned in a chain. (B) Ring pattern of seven beads in (i) closed, (ii) open case with (iii) speed profile of the oscillating beads. (C and D) Six beads are assembled in (chain, rotor) shapes, respectively, and (ii and iii) show the speed dynamics. The chitosan concentration is (A and B) 0.75 w/v% and (C and D) 1.5 w/v%. Scale bar = 0.5 cm.

Doubling the CS(sol) concentration in the CGE droplets produces similar dynamic behavior. This concentration increase, however, increases the sol viscosity, resulting in longer bead life because of the stronger cohesive force in the polymer network. An increase in the sol density and a decrease in gel diameter produces stronger capillary forces, hence, greater approaching speed of beads (see Fig. S6 in the ESI†). The longer active propulsion of beads and the arising capillary force together result in various dynamic ordered structures during the transition from initial unordered to the final clustered state. Moreover, the collective oscillations are sustained for a longer duration. Two novel type of patterns form: Fig. 4C(i) represents the chain shape, where beads 3 and 4 adhere, while 1 with 2 and 5 with 6 align at the opposite side. Collectively, they exhibit cluster synchrony, where the outer groups in Fig. 4C(ii) 1,2 and Fig. 4C(iii) 5,6 oscillate with different frequencies, while 3,4 move with the cluster (see Video S5, ESI†). Interestingly, beads oscillate in period-2 dynamics as the outward motion is slow due to slowly increasing and decreasing speed, followed by sharp spikes when the beads move inwards.

Beads' shuffling, collision of a bead to the assembly, or a ring opening–closing process (see Fig. S7 in the ESI†) can induce the trapping of a bead inside a ring of five beads, as depicted in Fig. 4D(i). This self-organized assembly is found to rotate clockwise or anti-clockwise, depending on the initial propel direction of the beads. The speed dynamics in Fig. 4D(ii–iii) show that the beads exhibit oscillatory motion (see Video S6, ESI†). Relay synchronization is also observed, where the speed of bead 2 is in anti-phase with bead 3 but in-phase with bead 4. Note that the anti- and in-phase motion of beads have mild phase drifting, but overall, they maintain the synchronized behavior. When we consider beads 1 and 2, the intermittency of the in-phase and anti-phase region is noticed, and for beads 1 and 5, near anti-phase synchrony is maintained during the oscillatory state of beads (see Fig. S7 in the ESI†). The depletion of ethanol with time decreases the speed of the rotor, which distorts the phases of oscillations in the later stage. We have observed rotating oscillatory pattern only in the case of six beads. Trapping is not sustained for a population size of less than six, while for larger population (N > 6), beads in the ring are crowded and do not have sufficient space to generate the oscillatory rotation. In the case of multiple beads, various clusters form and oscillate synchronously, as shown in Fig. S8 (ESI†). The size of the larger clusters (see Fig. S9, ESI†) increases with time due to the capillary attraction among the beads and smaller clusters.

We have also explored the communication between two groups of gel beads. The interaction of inactive CG particles shows that both groups remain intact in the static assembly after collision (see Fig. S10 in the ESI†). On the other hand, the elongated, elliptical-like configurations of the active groups with population ratios 18 : 15 and 39 : 90—shown by red:blue dots in Fig. 5A(i) and (ii), respectively—transform into circular shape (see Fig. 5A(iii and iv)), indicated by the black dotted lines. In the two groups of beads (red and blue), pairwise interactions dominate as the beads are distributed along chain-like formations. Furthermore, the swarm radii of the particles—defined as , where N is the number of beads, s⃑_i their position vectors, and s⃑_m the position of the collective center of mass—decreases due to clustering of the two assemblies (see Fig. 5B). The disk-like shape of the collective group with multiple ring patterns, as shown in the inset images of Fig. 5B(i–iii), exhibits oscillatory behavior. The decrease in the swarm radii indicates disk shrinking, and the expansion of the disk occurs on increasing R_s (see Video S7, ESI†). Similar behavior is obtained for an assembly of 33 gel beads (see Fig. S11 in the ESI†). During these activities, the active motion of the particles can shuffle the ring connections. When the motion ceases and the system reaches the near equilibrium state, the final configuration of the disk develops multiple islands devoid of beads. Moreover, the 2-D Voronoi diagram using the centroid position of the beads (see Fig. 5C), indicates that polygonal cells with 4–8 edges spread all over the space. Fig. 5D shows that pentagonal and hexagonal cells dominate. We have performed different sets of experiments for population sizes of 99–163 particles, and in all cases a similar probability distribution is observed as shown in Fig. S12 (ESI†). The total Voronoi entropy is 1.59, where P(s) is the probability of polygons with s edges. For a fully regular structure S_vor = 0, and for random distribution of points S_vor = 1.71 has been reported.³⁸ In our case, the high S_vor characterizes a disordered pattern.

Fig. 5 (A) Two active groups (i and ii) before interaction and (iii and iv) in the final state, where the red and blue dots represent the centroid of the beads, and the black dots guide the eye to visualize the shape of the collective group. (B) Swarm radii vs. time with (i–iii) inset images of the corresponding state. Field of view of inset images is 6.73 × 6.43 cm². (C and D) Voronoi diagram and its associated distribution histogram of the number of neighboring beads or edges of the polygon cells s. The concentration of CS(sol) is 1.5 w/v% and d_i = 0.6 mm.

4. Conclusions

Our present system highlights that complex oscillatory patterns can evolve in the low-energy state of self-propelled beads enriching their active life. We have presented a simple, biocompatible gel-based system, where the simultaneous emergence of spatial structures controls the erratic dynamics of their individual constituents. Periodic oscillations of assemblies emerge when the Marangoni force causing repulsion interplays with that of capillary attraction. This paves the way to forming breathing, clustering, and relay mode of synchrony. For larger ensemble of beads, we have also investigated the collective behavior of two active groups: they swarm in disk-like shape and exhibit oscillations. Our findings provide a new method to develop spatiotemporal oscillatory patterns without any master coordinator and can significantly contribute to advancing intelligent collective behavior in swarm robotics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office (K138844) and TKP2021-NVA-19 project. The authors thank the University of Szeged Open Access Fund (6319) for support.

Notes and references

1. M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85, 1143.
2. E. D. Herzog, Neurons and networks in daily rhythms, Nat. Rev. Neurosci., 2007, 8, 790–802.
3. B. O'Rourke, B. M. Ramza and E. Marban, Oscillations of membrane current and excitability driven by metabolic oscillations in heart cells, Science, 1994, 265, 962–966.
4. F. Jülicher and J. Prost, Spontaneous oscillations of collective molecular motors, Phys. Rev. Lett., 1997, 78, 4510.
5. A. Biswas, J. M. Cruz, P. Parmananda and D. Das, First passage of an active particle in the presence of passive crowders, Soft Matter, 2020, 16, 6138–6144.
6. C. Gouiller, F. Raynal, L. Maquet, M. Bourgoin, C. Cottin-Bizonne, R. Volk and C. Ybert, Mixing and unmixing induced by active camphor particles, Phys. Rev. Fluids, 2021, 6, 014501.
7. T. Roy, S. S. Chaurasia, J.-M. Cruz, V. Pimienta and P. Parmananda, Modes of synchrony in self-propelled pentanol drops, Soft Matter, 2022, 18, 1688–1695.
8. S. Sato, H. Sakuta, K. Sadakane and K. Yoshikawa, Self-synchronous swinging motion of a pair of autonomous droplets, ACS Omega, 2019, 4, 12766–12770.
9. Y.-J. Chen, K. Sadakane, H. Sakuta, C. Yao and K. Yoshikawa, Spontaneous oscillations and synchronization of active droplets on a water surface via Marangoni convection, Langmuir, 2017, 33, 12362–12368.
10. J. Sharma, I. Tiwari, D. Das, P. Parmananda, V. S. Akella and V. Pimienta, Rotational synchronization of camphor ribbons, Phys. Rev. E, 2019, 99, 012204.
11. M. I. Kohira, Y. Hayashima, M. Nagayama and S. Nakata, Synchronized self-motion of two camphor boats, Langmuir, 2001, 17, 7124–7129.
12. S. Tanaka, S. Nakata and M. Nagayama, A surfactant reaction model for the reciprocating motion of a self-propelled droplet, Soft Matter, 2021, 17, 388–396.
13. C. Watanabe, S. Tanaka, R. J. G. Löffler, M. M. Hanczyc and J. Górecki, Dynamic ordering caused by a source-sink relation between two droplets, Soft Matter, 2022, 18, 6465–6474.
14. S. Nakata, K. Kayahara, M. Kuze, E. Ginder, M. Nagayama and H. Nishimori, Synchronization of self-propelled soft pendulums, Soft Matter, 2018, 14, 3791–3798.
15. B. Ahn, K. Lee, H. Lee, R. Panchapakesan and K. W. Oh, Parallel synchronization of two trains of droplets using a railroad-like channel network, Lab Chip, 2011, 11, 3956–3962.
16. M. A. Budroni, K. Torbensen, S. Ristori, A. Abou-Hassan and F. Rossi, Membrane structure drives synchronization patterns in arrays of diffusively coupled self-oscillating droplets, J. Phys. Chem. Lett., 2020, 11, 2014–2020.
17. D. Vella and L. Mahadevan, The “Cheerios effect”, Am. J. Phys., 2005, 73, 817–825.
18. M. Nicolson, Math. Proc. Cambridge Philos. Soc., 1949, 288–295.
19. P. A. Kralchevsky and N. D. Denkov, Capillary forces and structuring in layers of colloid particles, Curr. Opin. Colloid Interface Sci., 2001, 6, 383–401.
20. Q. He, D. Liu, W. Huang and J. Wang, Interactions of oil drops induced by the lateral capillary force and surface tension gradients, Langmuir, 2019, 35, 14967–14973.
21. D. Liu, A. Mahmood, D. Weng and J. Wang, Life-like motion of oil drops at the air-liquid interface, Langmuir, 2019, 35, 16146–16152.
22. B. V. Hokmabad, A. Nishide, P. Ramesh, C. Krüger and C. C. Maass, Spontaneously rotating clusters of active droplets, Soft Matter, 2022, 18, 2731–2741.
23. J. Čejková, K. Schwarzenberger, K. Eckert and S. Tanaka, Dancing performance of organic droplets in aqueous surfactant solutions, Colloids Surf., A, 2019, 566, 141–147.
24. M. Rubenstein, A. Cornejo and R. Nagpal, Programmable self-assembly in a thousand-robot swarm, Science, 2014, 345, 795–799.
25. J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Reconfiguring active particles by electrostatic imbalance, Nat. Mater., 2016, 15, 1095–1099.
26. J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Living crystals of light-activated colloidal surfers, Science, 2013, 339, 936–940.
27. A. Aubret, M. Youssef, S. Sacanna and J. Palacci, Targeted assembly and synchronization of self-spinning microgears, Nat. Phys., 2018, 14, 1114–1118.
28. C. Zhou, N. J. Suematsu, Y. Peng, Q. Wang, X. Chen, Y. Gao and W. Wang, Coordinating an ensemble of chemical micromotors via spontaneous synchronization, ACS Nano, 2020, 14, 5360–5370.
29. J. Yan, M. Bloom, S. C. Bae, E. Luijten and S. Granick, Linking synchronization to self-assembly using magnetic Janus colloids, Nature, 2012, 491, 578–581.
30. P. Kumar, D. Horváth and Á. Tóth, Bio-inspired flow-driven chitosan chemical gardens, Soft Matter, 2020, 16, 8325–8329.
31. M.-J. Dalbe, D. Cosic, M. Berhanu and A. Kudrolli, Aggregation of frictional particles due to capillary attraction, Phys. Rev. E, 2011, 83, 051403.
32. N. D. Vassileva, D. van den Ende, F. Mugele and J. Mellema, Capillary forces between spherical particles floating at a liquid-liquid interface, Langmuir, 2005, 21, 11190–11200.
33. A. Dani, G. Keiser, M. Yeganeh and C. Maldarelli, Hydrodynamics of particles at an oil-water interface, Langmuir, 2015, 31, 13290–13302.
34. O. D. Velev, N. D. Denkov, V. N. Paunov, P. A. Kralchevsky and K. Nagayama, Direct measurement of lateral capillary forces, Langmuir, 1993, 9, 3702–3709.
35. G. K. Batchelor, Brownian diffusion of particles with hydrodynamic interaction, J. Fluid Mech., 1976, 74, 1–29.
36. P. Kumar, D. Horváth and Á. Tóth, Sol-gel transition programmed self-propulsion of chitosan hydrogel, Chaos, 2022, 32, 063120.
37. B. Choy and D. D. Reible, Diffusion models of environmental transport, CRC Press, 1999.
38. A. V. Limaye, R. D. Narhe, A. M. Dhote and S. B. Ogale, Evidence for convective effects in breath figure formation on volatile fluid surfaces, Phys. Rev. Lett., 1996, 76, 3762.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00461a

---