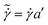Post-liquefaction normospermic human semen behaves as a weak-gel viscoelastic fluid

Abstract

The rheological behavior of human semen is overlooked and essentially unexplored in the scientific literature. Here, we provide the first quantitative experimental evidence that post-liquafaction normospermic human semen behaves as a viscoelastic fluid and the shear moduli can be scaled according to the weak-gel model.

---

Right after ejaculation, semen quickly coagulates into a gel-like viscoelastic medium and then undergoes the so-called liquefaction process usually leading in 20–30 minutes¹ to a low viscosity, watery consistence,² which is considered as one of the hallmarks of healthy (normospermic) semen.

The current view is indeed that any post-liquefaction residual viscoelastic character is a signature of a pathological state. This view, however, is not based on rigorous rheological characterization, since the clinical assessment of semen quality according to the World Health Organization (WHO) guidelines³ includes a rather qualitative and operator-dependent viscosity assay that is made by allowing a sample aspirated in a pipette to freely fall by gravity. A sample is classified of normal viscosity if it leaves the pipette in the form of discrete droplets, while when a liquid thread is formed at the tip of the pipette, the sample is considered of abnormal viscosity (hyperviscosity), especially when the thread length is >2 cm. This measure, however, is sensitive to a combination of different effects, i.e., not only viscous but also elastic properties, and surface tension. The interplay of these different and counteracting effects makes the viscosity measured by the thread method a rather questionable rheological index.

Even from the scientific side, however, only few papers in the literature have been addressed to the rheological characterization of human semen based on rigorous, quantitative methods.⁴ By using a rotational rheometer, it was found that post-liquefaction semen from normospermic donors exhibits a slight decrease of viscosity as a function of the applied shear rate.⁵ Although the presence of shear thinning is suggestive of some dweviation from the classical Newtonian behavior, clear evidence of what is the actual rheological response of post-liquefaction normospermic semen, not only in terms of viscous, but also of elastic parameters, is still lacking, in spite of its physio-pathological relevance.

Here, our main goal is to perform a linear viscoelasticity analysis of normospermic human semen samples and assess their rheological behavior. Furthermore, we aim at correlating the so obtained rheological parameters to clinical data of sperm motility.

The experiments were carried out on 35 human semen samples, collected from men attending the Sterility Center of the Polyclinic of the University of Naples Federico II and evaluated as normospermic based on routine tests. The study was approved in 2019 by the Institutional Ethics Committee of the University of Naples Federico II by protocol No. 382/18 and a written informed consent form was signed by all the participants involved in the study. The latter was conducted in accordance with the principles expressed in the Declaration of Helsinki. The samples were analyzed in the Sterility Center according to the World Health Organization (WHO) guidelines.³ All the samples were used as such and stored at room temperature. A stress-controlled rheometer equipped with a titanium double-gap measuring system was used for the rheological characterization. All measurements were performed at 25 °C within 4 h from collection. Frequency spectra of storage modulus G′ and loss modulus G′′ were obtained by oscillatory shear measurements in the range 0.1–30 rad s⁻¹. To determine the linear viscoelastic regime, each oscillatory test was preceded by strain amplitude sweeps at 1 rad s⁻¹ and 10 rad s⁻¹ with strain amplitudes from 0.1 to 10%. The steady shear measurements were performed in the range 2–1000 s⁻¹, from low to high shear rates and back (up-down curve), providing viscosity vs shear rate curves.

The linear viscoelasticity data of the normospermic samples investigated in this work are shown in Fig. 1a and b and exhibit a large inter-individual variation both for G′ and G′′, spanning almost two orders of magnitude. The viscoelastic spectra of two representative samples having larger (purple squares) and lower (green squares) values of the moduli are presented in Fig. 1c and d, where G′ and G′′ are plotted in the same graph to show at a glance the relative contribution of the elastic and viscous components. One of the main results emerging from these data is that the elastic modulus of most samples is not negligible with respect to the viscous one. Depending on the position of the cross-over frequency between the two moduli, there are cases where the elastic response is even dominant over the viscous one in the frequency range investigated, such as for the sample in Fig. 1d. Therefore, normospermic human semen is in fact a viscoelastic fluid after liquefaction, at variance with the current view of a purely viscous behavior.

Fig. 1 G ′ and G′′ for all the semen samples vs. frequency ω are shown in (a) and (b), respectively. The viscoelastic spectra of two representative samples are shown in (c) and (d).

The question then arises on how to account for the large differences among the viscoelastic spectra of the semen samples. The differences are indeed not only quantitative, but also qualitative (e.g., the cross-over point changes among the samples) and a simple pointwise average of the data does not appear very meaningful. One can reason by analogy with freshly ejaculated or pathological semen samples, where a highly organized molecular network likely due to disulfide bonds and oligosaccharide chains complexed to the peptide core has been hypothesized.⁵ According to this hypothesis, such molecular network is generated upon ejaculation and it is fully disrupted in normospermic samples during the liquefaction process. Having found that post-liquefaction normospermic semen is actually a viscoelastic fluid, one can argue that some residual, though tenuous, network is still present in the seminal plasma (which could provide the viscous response). A microstructure characterized by a tenuous network is the basis of the weak-gel model,⁶ according to which the sample microstructure is made of a particle-based network immersed in a viscous fluid, the former providing the elastic response and the latter the viscous one. However, the presence of a weak molecular network could be due to other factors different from a partial liquefaction of the semen after ejaculation. In the weak gel model it is indeed assumed that the system microstructure is given by a suspension of slightly attractive particles where even small differences of the interparticle potential and of the particle volume fraction can lead to strong changes in the rheological response. It could be envisaged that the weak gel behavior of normospermic semen is also due to the attractive interactions of particles, such as globular proteins and their aggregates.

The weak-gel model is based on the observation that data of G′ and G′′ from different samples can be scaled by independently applying a horizontal and a vertical shift factor. By performing such scaling of the moduli from Fig. 1a and b, the plot of the scaled moduli and vs the scaled frequency [small omega, Greek, tilde] shown in Fig. 2 is obtained. It can be observed that, in spite of the large variability of the raw data, the scaling is quite effective in collapsing the data on the same master curve, which is characterized by a cross-over point separating a dominant elastic response at low frequencies from a dominant viscous one at high frequencies. It can be noticed that the samples with larger values of G′ (such as the one in Fig. 1c) fall to the left of the cross-over point in Fig. 2, where the elastic contribution is dominant. The continuous line in Fig. 2, which corresponds to a power law fit with a 0.9 exponent, provides a good representation of the data in the high frequency range. The validity of the weak-gel scaling is further confirmed in the inset of Fig. 2 by the linear relationship between the vertical and horizontal shift factors b and a/μ, where μ is the highest viscosity measured for each semen sample in the range of shear rate investigated (see Fig. 3), which is representative of the suspending fluid viscosity. A similar result is found by using as the horizontal shift factor the reciprocal of the cross-over frequency divided by μ and as the vertical shift factor the reciprocal of the G′ value corresponding to the plateau observed in the low frequency range (see Fig. S1, ESI†). It can be noticed that classical models of the sol–gel transition, which have been successfully applied to polymeric systems,^7–10 have been also shown to provide a similar scaling.⁸ However, the near-critical gel model predicts a power law evolution of the shifting factors, whereas a linear relationship is found in our data according to the weak gel model.

Fig. 2 The scaled elastic (cloese squares) and viscous (open squares) modulus vs the scaled frequency [small omega, Greek, tilde], where [small omega, Greek, tilde] = ω a, and , a and b being the shift factors. The continuous line is a power law with exponent 0.9. The inset shows the plot of the vertical shift factor b vs. the horizontal shift factor a divided by the high shear viscosity μ, with a slope of 0.12).

Fig. 3 (a) Data of shear stress vs. shear rate for 35 normospermic human semen samples. (b) Same data as in (a) after scaling, where scaled shear rate and scaled shear stress . The inset shows the plot of the vertical b′ vs. the horizontal a’ shift factor, the slope of the being 1.2. The continuous line in (b) is a fit of the equation τ = K[small gamma, Greek, dot above]ⁿ to the experimental data, with K = 0.01 and n = 0.9.

The semen samples were also tested in steady shear flow and the results are presented in Fig. 3a, where shear stress τ is plotted as a function of shear rate [small gamma, Greek, dot above]. As for the viscoelastic spectra, a large scatter can be noticed in the raw data. By horizontal and vertical shifting of the data a good scaling was obtained, as illustrated by the master curve in Fig. 3b and confirmed by the linear relation between the shift factors in the inset of the same figure. The master curve is characterized by a power law behavior at high shear rates with a slope of 0.9. The latter is consistent with the slope of 0.9 found in Fig. 2 for at high frequency where , η being the sample viscosity. At low shear rates, the slope tends to decrease, a trend in line with the behavior of a yield stress fluid, such as a Bingham solid. Similar considerations apply for the data of viscosity vs shear rate, which can be calculated as η = τ/[small gamma, Greek, dot above]. Once again, a rather large variability of viscosity values (in the range 0.004–0.013 Pa·s at low shear rates) can be observed, likely reflecting physiological inter-individual changes in semen composition (Fig. S2, ESI†). We found that, apart from the low shear region, semen viscosity does not change in going from high to low shear rates and viceversa, which suggests a partly reversible rearrangement of an underlying microstructure (Fig. S3, ESI†). The slight decrease of viscosity with shear rate found in the normospermic samples investigated in this work is in agreement with the few results available in the literature.⁵ Other biological fluids, such as blood¹¹ and mucus,¹² exhibit similar shear thinning behavior, which is associated to red blood cells aggregation and deformation in the former and to macromolecular network straining in the latter. Overall, the scaling of shear stress vs shear rate provides further evidence of the validity of the weak-gel model. The steady shear data are consistent with the oscillatory shear data in terms of the limiting slope of G′′ at high frequency and of the high shear value of viscosity μ, which has been used in calculating the horizontal shift factor in the inset of Fig. 2.

Having shown that normospermic semen is a viscoelastic fluid, we next considered whether there is a correlation between rheological properties and some parameters of the spermiogram test. We focused our attention on sperm motility, which can be expected to be somehow influenced by the viscoelastic properties of the medium where the spermatozoa are swimming.^13–17 The motion of spermatozoa is driven by flagellar beating, typically in the range of 10–50 Hz,¹⁸ which propels the cells along a more or less straight trajectory. Such motile behavior is exemplified in Fig. 4a, where a frame of a high-speed microscopy video with spermatozoa swimming in normospermic seminal fluid is shown. In the spermiogram test, cell motility is classified in three main categories based on visual inspection or computer-aided semen analysis: progressive (PR), when spermatozoa move actively along linear or circular trajectories with a large curvature radius, as exemplified in Fig. 4b; non-progressive (NP), encompassing all other patterns with no net cell progression, such as in the case of spermatozoa moving in small circles or when only flagellar beating can be seen; immotility, when no movement is observed. In Fig. 4c the percentage of spermatozoa with progressive motility (from spermiogram data) is plotted as a function of semen viscosity η measured at a shear rate [small gamma, Greek, dot above] of 10 s⁻¹. The continuous line is a linear fit to the data, and the value of the Pearson correlation coefficient (r_P) close to −1 (−0.9994) with P = 0.0006 shows a statistically-significant, strong negative correlation between semen viscosity and sperm motility. This result is in line with a previous study,¹⁹ where however the shear rate was not measured. Here, by exploring different values of [small gamma, Greek, dot above], we show that the correlation is actually dependent on the shear rate. At a shear rate of 2 s⁻¹ essentially no change of motility with η was found (Fig. S4a, ESI†), while a large negative correlation, though not statistically significant, was seen at 100 and 1000 s⁻¹ (Fig. S4b and c, ESI†).

Fig. 4 (a) Microscopy image of spermatozoa in seminal fluid (scale bar is 20 μm). (b) x,y trajectories of 88 spermatozoa referred to the same origin; the sample was sandwiched between a coverslip and a microscope slide according to the WHO guidelines³ and images were taken with a Phantom v711 high-speed video camera at 1200 frame per s at room temperature. Spermatozoa speed ranges between 60–90 μm s⁻¹, in agreement with values found in the literature.²⁰ (c) Plots of spermatozoa motility vs. viscosity at a shear rate of 10 s⁻¹ and (d) vs. elastic modulus G′ and loss modulus G′′ at 10 rad s⁻¹.

Concerning fluid elasticity, we compared progressive sperm motility with G′ at a characteristic frequency of 10 rad s⁻¹, as shown in Fig. 4d. As for the viscosity, sperm motility showed a decreasing trend as a function of G′, although with lower values of r_P (−0.719) and P (0.17). The same trend was found at ω = 1 rad s⁻¹ (Fig. S5a, ESI†), while at ω = 30 rad s⁻¹ a slight correlation was found (Fig. S6a, ESI†). The data of G′ provide altogether some evidence of a suppressing role played by elasticity on spermatozoa motion. A similar negative correlation with sperm motility were also found for G′′ at 10 rad s⁻¹ (see Fig. 4d). Here, a higher value of r_P (−0.88) was obtained as compared to that of G′, and the correlation was statistically significant (P = 0.0205). A weaker dependence of sperm motility on G′′ was found at 1 rad s⁻¹ (Fig. S5b, ESI†), while the correlation was stronger at 30 rad s⁻¹ (Fig. S6b, ESI†), although in both cases the P-value threshold was not met. The same negative correlations of sperm motility with η, G′ and G′′, although weaker, were also obtained by including the in situ motile cells.

While it is quite intriguing that the best correlation between sperm motility and viscosity is found at a value of shear rate (10 s⁻¹) in the range of the flagellar beating frequency (10–50 Hz), all these results can only be interpreted in a statistical sense. In fact, our experiments are based on semen samples as received from the donors without any further manipulation. Hence, sperm motility and semen rheological parameters are not varied independently from each other in the experiments, as it would be needed for a robust assessment of their possible mutual dependence, which is outside the scope of this work.

Conclusions

In conclusion, the main result of this work is the finding that normospermic human semen, though usually considered a purely viscous fluid, is in fact a viscoelastic medium, which can be characterized by measuring the elastic and viscous moduli in the linear regime under oscillatory shear flow. In spite of the large variability of G′ and G′′ among different samples, all the data can be made to collapse on the same master curve thanks to the scaling suggested by the weak-gel model. This remarkable result provides a rationale in classifying human semen by identifying two frequency regions separated by the cross-over point ω*: for ω < ω*, the rheological behavior is dominated by the elastic response, whereas the viscous contribution is dominant for ω > ω*. The peculiar frequency spectrum of semen viscoelasticity suggests that model fluids to mimic spermatozoa motility in human semen should be formulated in such a way that their rheological behavior follows the weak-gel scaling rather than the classical Maxwell model (the latter applies to polymeric solutions, on which most of the model fluids used so far are based).

It should be pointed out that a progressive decline of male fertility as well as semen quality, in terms of sperm concentration and motility^21,22 has been found in the last years,²³ bringing a number of health, psychological and economic issues. Advances in male infertility diagnosis and treatment, however, have been rather limited,²¹ with only few techniques translated from research to clinical practice.^24,25 Therefore, the development of new physiologically-relevant model fluids to study sperm motility in vitro is an important issue,²⁶ the more so in the light of the results of the present work. We found indeed that semen viscoelasticity is strongly correlated with sperm motility. A strong negative correlation between sperm motility and viscoelastic parameters at a shear rate comparable to that of spermatozoa flagellar beating was indeed obtained. This correlation suggests a novel, more rigorous and physiologically-relevant approach based on steady viscosity and shear moduli, in particular at a shear rate/frequency close to that of flagellar beating, to characterize semen rheology as compared to the thread length measurement by visual inspection. In addition to inspiring the development of novel semen testing technologies,²⁷ the viscoelasticity of normospermic semen opens up new avenues for future research addressing the role played by rheological properties (not just viscous, but also elastic ones), and their determinants on male fertility analysis.

Author contributions

G. T. and S. G. conceived and designed the study, and wrote the paper; F. F. performed the experiments; G. T. and F. F. analyzed the data; F. C., I. S. and F. Z. provided the samples; G. T., S. G., F. F., F. C. I. S., S. L. and V. P. discussed the results; S. G. supervised the study. All the authors reviewed the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from PON Ricerca e Innovazione 2014–2020 (CCI 2014IT16M2OP005). Experimental support from Antonella Panarelli is gratefully acknowledged.

References

1. D. H. Owen and D. F. Katz, J. Androl., 2005, 26, 459–469.
2. S. S. Du Plessis, S. Gokul and A. Agarwal, Front. Biosci., Elite Ed., 2013, 5, 224–231.
3. WHO, WHO laboratory manual for the examination and processing of human semen, 2021.
4. G. Tomaiuolo, F. Fellico, V. Preziosi and S. Guido, Interface Focus, 2022, 12, 20220048.
5. G. Mendeluk, F. L. G. Flecha, P. R. Castello and C. Bregni, J. Androl., 2000, 21, 262–267.
6. V. Trappe and D. Weitz, Phys. Rev. Lett., 2000, 85, 449.
7. M. Mours and H. H. Winter, Macromolecules, 1996, 29, 7221–7229.
8. D. Adolf and J. E. Martin, Macromolecules, 1990, 23, 3700–3704.
9. H. H. Winter, Structure and dynamics of polymer and colloidal systems, 2002, pp. 439–470.
10. J. E. Martin, D. Adolf and J. P. Wilcoxon, Phys. Rev. Lett., 1988, 61, 2620.
11. G. Tomaiuolo, A. Carciati, S. Caserta and S. Guido, Rheol. Acta, 2016, 55, 485–495.
12. G. Tomaiuolo, G. Rusciano, S. Caserta, A. Carciati, V. Carnovale, P. Abete, A. Sasso and S. Guido, PLoS One, 2014, 9, e82297.
13. K. Ishimoto, H. Gadêlha, E. A. Gaffney, D. J. Smith and J. Kirkman-Brown, J. Theor. Biol., 2018, 446, 1–10.
14. E. A. Gaffney, K. Ishimoto and B. J. Walker, Front. Cell Dev. Biol., 2021, 9, 710825.
15. L. Emmanuel, J. M. Yeomans and A. Doostmohammadi, Phys. Rev. Fluids, 2020, 5, 023102.
16. A. Furukawa, D. Marenduzzo and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022303.
17. L. E. Becker, S. A. Koehler and H. A. Stone, J. Fluid Mech., 2003, 490, 15–35.
18. J. Teran, L. Fauci and M. Shelley, Phys. Rev. Lett., 2010, 104, 038101.
19. D. Tjioe and S. Oentoeng, Fertil. Steril., 1968, 19, 562–565.
20. D. Katz and H. Dott, Reproduction, 1975, 45, 263–272.
21. R. Nosrati, P. J. Graham, B. Zhang, J. Riordon, A. Lagunov, T. G. Hannam, C. Escobedo, K. Jarvi and D. Sinton, Nat. Rev. Urol., 2017, 14, 707–730.
22. A. Agarwal, A. Mulgund, A. Hamada and M. R. Chyatte, Reprod. Biol. Endocrinol., 2015, 13, 37.
23. P. Sengupta, E. Borges Jr, S. Dutta and E. Krajewska-Kulak, Hum. Exp. Toxicol., 2018, 37, 247–255.
24. C. Dai, Z. Zhang, G. Shan, L.-T. Chu, Z. Huang, S. Moskovtsev, C. Librach, K. Jarvi and Y. Sun, Nat. Rev. Urol., 2021, 18, 447–467.
25. S. Saha, P. Roy, C. Corbitt and S. S. Kakar, Cells, 2021, 10, 1613.
26. J. C. Kirkman-Brown and D. J. Smith, MHR: Basic Sci. Reprod. Med., 2011, 17, 539–544.
27. C. De Jonge, Fertil. Steril., 2012, 97, 260–266.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00443k

‡ Current address: Obstetrics and Gynaecology, Magna Graecia University of Catanzaro, Catanzaro, Italy.

---