Open Access Article
Open Access ArticleStructural characterization of systems with competing interactions confined in narrow spherical shells
Horacio
Serna
 *a,
Ariel G.
Meyra
*a,
Ariel G.
Meyra
 bc,
Eva G.
Noya
bc,
Eva G.
Noya
 d and
Wojciech T.
Góźdź
d and
Wojciech T.
Góźdź
 a
a
aInstitute of Physical Chemistry Polish Academy of Sciences, Kasprzaka 44/52 01-224, Warsaw, Poland. E-mail: hserna@ichf.edu.pl
bIFLYSIB (UNLP,CONICET), 59 No. 789, B1900BTE La Plata, Argentina
cDepartamento de Ingeniería Mecánica, UTN-FRLP, Av. 60 esq. 124, 1900 La Plata, Argentina
dInstituto de Química Física Blas Cabrera, CSIC, C/Serrano 119, 28006 Madrid, Spain
First published on 5th June 2023
Abstract
Systems with short-range attraction and long-range repulsion can form ordered microphases in bulk and under confinement. In fact, confinement has been proven to be a good strategy to induce the formation of novel ordered microphases that might be appealing to the development of functional nanomaterials. Using Grand Canonical Monte Carlo (GCMC) simulations, we study a model colloidal system with competing interactions under confinement in narrow spherical shells at thermodynamic conditions under which the hexagonal phase is stable in bulk. We observe the formation of three parent ordered structures formed by toroidal clusters and two spherical clusters (Type I), toroidal clusters and one spherical cluster (Type II), and toroidal clusters alone (Type III), depending on the radius of the confining shell, that can often coexist with other related structures derived from these parent ones by a simple transformation, in which the system is divided into two hemispheres that are rotated with respect to each other by a given angle. We propose a general method to characterize and predict the structures obtained under confinement in spherical shells in systems able to self-assemble into a hexagonal phase in bulk. We also show that deforming the spherical shells into ellipsoidal ones affects the structure of the system in such a way that helical structures are favoured by prolate ellipsoids and toroidal structures by oblate ellipsoids.
Introduction
Systems with competing attractive and repulsive interactions are ubiquitous. Examples of these systems are block copolymers, oil mixtures with surfactants and water, proteins, polypeptides and colloidal suspension with depletants.1–3 When the ranges of the attraction and repulsion are properly tuned, systems with competing interactions can form a variety of ordered microphases such as spherical clusters forming crystals (cluster-crystals), cylindrical clusters with hexagonal ordering (hexagonal phase), bicontinuous and lamellar. These ordered phases might be important in the development of new technological applications such as templating for nanomaterial synthesis,4,5 catalysis, drug delivery and sensing.6,7 It has been demonstrated, by theory1,8–10 and simulations,11–13 that systems with competing interactions exhibit a universal phase behaviour in bulk. Thus, the conclusions drawn for a specific system of this type can be generalized and inspire new studies on a different one. For instance, results on colloidal systems with competing interactions that are a theoretical platform to study self-assembly might guide the development of the experiments with more complex systems such as block copolymers.Recent studies have shown that by confining systems with competing interactions into pores with the appropriate geometry, new ordered microphases can be induced.14,15 The pore size must be carefully tuned to be commensurate with the periodicity of the target ordered microphases to induce its formation. A poor choice of pore size can produce disordered phases even at thermodynamic conditions under which ordered microphases are stable in bulk.15 For example, with the correct values of the radius and length, cylindrical pores promote the formation of helical structures both in colloidal systems14 and copolymers.16,17 In previous studies, we showed that the confinement in channels with curved walls could strongly affect the structure of colloidal fluids with competing interactions. In particular, we found that at thermodynamic conditions under which the bulk hexagonal phase is stable, the confinement in elliptical pores induces the formation of straight cylindrical clusters.15 In contrast, the cylindrical pores always promote the formation of helical structures.14
Motivated by the importance of commensurability and the presence of curved walls on the structure of systems with competing interactions under confinement, we explore in this paper, by means of Monte Carlo simulations, the behaviour of a colloidal fluid with short-range attraction and long-range repulsion (SALR) confined into narrow spherical shells. This is a quasi-bidimensional system with a geometry that is completely incommensurate with the bulk ordered microphases. We focus on conditions under which the hexagonal phase is stable in bulk since it shows the most interesting behaviour under spherical confinement, as was already shown in a previous work.18
Systems with competing interactions confined in spherical geometries have already been studied. For instance, the phase behaviour of a binary blend of diblock copolymer AB/homopolymer C has been explored using a simulated annealing technique.19 Different combinations of pore surface selectivity to A, B and C species were considered. For the case where the internal surface of the spherical cavity is equally selective to A and B but repulsive to C, phase separation occurs, and the homopolymer forms a big spherical aggregate in the centre of the cavity. Under such conditions, the copolymer (AB) is confined in a spherical shell and its components assemble into either toroidal structures or structures resembling helices. In another work,20 the authors perform a study including simulations and experiments. The system consists of colloidal particles (0.52 μm of diameter) coated with a diblock copolymer. The film thickness is kept in the order of 40 nm. Using cell dynamics computer simulations, they studied the different morphological transformations that the deposited copolymer on the surface of the nanoparticles undergoes for various thermodynamic conditions. They found structures formed by cylindrical micelles that resemble the ordered structures presented here. Adsorbed copolymers on colloidal particles are a good example of a possible experimental realization of the system described in this article. Other options would be tube-forming functionalized colloids21 under spherical confinement or magnetic colloids confined in spherical cavities.22 Also, in a mixture of a symmetrical diblock copolymer with a homopolymer confined in emulsion droplets, helix-like and toroidal structures were observed.23 Similar structures have been predicted by theoretical studies of block copolymers on the surface of a sphere24 and confined into spherical cavities.25–29 In another experimental work,3 spiral-patterned particles synthesized by direct emulsification of polypeptides have been obtained. In this case, the confining surface is a sub-micrometer toluene drop. The structures of dry particles resemble the ones obtained in this paper.
Regarding SALR systems, particles constrained to move on the surface of a sphere have been studied using Monte Carlo simulations. The patterns obtained depend on the radius of the sphere.30,31 Additionally, a molecular dynamics study of a two-dimensional SALR fluid on the surface of a sphere predicted the stability of lamellar structures that form open and closed patterns on the surface. The study also revealed that topological defects could affect the thermodynamic properties.32 In a recent paper, the authors have proved the existence of a cluster-crystal and lamellar phases of a fluid of hard-core SALR disks confined onto the surface of a sphere.33 It has been shown that mixtures of hard spheres and SALR particles with long range cross-attraction might lead to the formation of spherical droplets whose structure resembles those obtained in confined systems.34
Interestingly, many of the structures obtained in previous works are similar to those presented in this article. This suggests that the universality in the behaviour of systems with competing interactions in bulk can be extended to confined systems.
Although systems with competing interactions have been studied under confinement in spherical geometries as we just reviewed, a more comprehensive characterization of the possible self-assembled structures is still missing. Aiming to develop new technological applications, the topological features of the ordered structures and their relationship with the system size are essential.
In this paper, we present a simple method that systematically characterizes the ordered structures and predicts the appropriate geometrical parameters of the spherical shell that lead to a certain type of structure. This method is inspired by the geometrical solutions to the problem of the longest rope on the surface of a sphere as we discussed in a previous work.18 The original problem considered in ref. 35 looks for the longest closed curve (rope) with a constant thickness (diameter of the rope) on the surface of the unit sphere avoiding self-overlapping. Therefore, the curve describes a closed packed rope. The problem can be modified to find optimal open curves too.35 The universality of the ordered structures presented in this paper goes beyond systems with competing interactions in equilibrium since they are also observed in Turing patterns on the surface of a sphere.36–38 The method presented here can also be used to characterize those self-organized structures.
In the last section, we investigate the structure of the system when confined into ellipsoidal shells. We use the spherical shell as a reference and gradually lengthen or shorten the radius along the y axis while keeping the radii along x and z axes constant.
Model and simulation details
The colloidal system is composed of perfectly mono-dispersed spherical particles which interact with each other via a spherical-symmetrical SALR interaction potential. In particular, we consider the square-well-linear potential (SWL), consisting of a hard core, an attractive square-well, and a repulsive ramp. The pair potential is given by the following expression, | (1) |
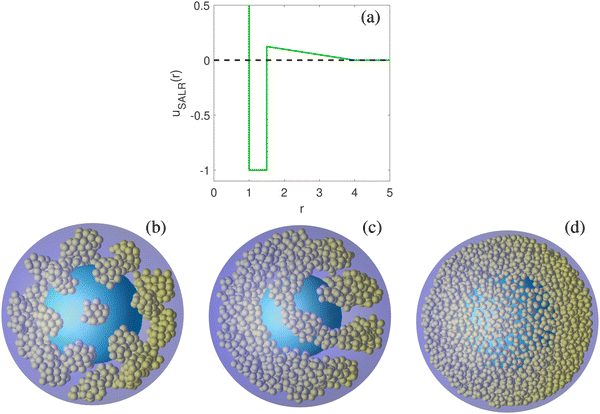
Here, rij denotes the inter-distance between particles i and j, σ is the diameter of the colloidal particles, ε is the depth of the attractive well, λ is the attractive range, ζ denotes the repulsion strength and κ is the repulsion range.39,40 We set the parameter values as: ζ = 0.05, λ = 1.5 and κ = 4.0. We made this choice since the bulk phase diagram has been calculated for this set of parameters,12 and so we have all the thermodynamic information of the system. In addition, the finite range of the potential is convenient for simulations. The phase behaviour of SALR systems is universal and it does not depend on the functional form of the potential. Both in bulk and under confinement, different SALR potentials such as Lennard-Jones + Yukawa11,32,41 and Hard Spheres + Double Yukawa1,13,33 have shown the same qualitative results as those reported for the SWL.12,15,18 A plot of the pair potential is presented in Fig. 1a.
The colloidal fluid is confined into spherical shells with hard walls. The system is finite and quasi bidimensional since we focus on narrow shells. To construct such shells, we define an inner sphere of radius, Rinn, and an outer sphere of radius, Rout. Both spheres are concentric. The region between the two spheres defines the shell in which the particles are allowed to move. Any region outside the shell is prohibited for the particles. We have chosen hard walls to evaluate the pure geometrical effects of confinement on the self-assembled structures. Other scenarios might include attractive or repulsive walls and have been considered in block copolymers under spherical confinement,25,26 where similar structures to those reported here were found, and colloidal systems in the presence of attractive and repulsive flat walls.41–44 We do not expect significant differences when short-range repulsive interactions with the walls are considered. We define the shell region,
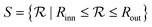 | (2) |
 is the radial coordinate. Based on the shell region, S, we can define the external potential,
is the radial coordinate. Based on the shell region, S, we can define the external potential, | (3) |
 denotes the radial coordinate of particle i. The total energy of the system is thus given by
denotes the radial coordinate of particle i. The total energy of the system is thus given by | (4) |
The structure of the colloidal fluid is investigated by Monte Carlo simulations in the grand canonical ensemble (μ, V, T). All the magnitudes (chemical potential, temperature, internal energy, density, and distance) are reported using σ and ε as units of distance and energy, respectively. The simulated systems contained between 1000 and 2200 particles. We first carried out an equilibration run whose length depends on the system size. The production run consists of 2 × 1010 MC steps, from which 2 × 105 independent configurations were taken for calculating the local density. A Monte Carlo step is defined as a trial move that may be a displacement, addition, or deletion of a particle. We set the displacement attempt probability at 95% and the remaining 5% to the particle exchange attempt. Simulations were performed at the temperature T* = kBT/ε = 0.35 and at values of chemical potential within the range −2.35 ≤ μ/ε = μ* ≤ −2.10. In these thermodynamic conditions, the hexagonal phase is stable in bulk.12 We explore different system sizes in the range 6.5σ ≤ Rout ≤ 13.0σ. The number density of the system is, ρ* = Nσ3/V, where the volume of the spherical shell is, 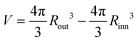 . In Fig. 1, we present snapshots of the system at three different chemical potentials, observing a cluster-crystal with hexagonal symmetry (Fig. 1b, similar to that observed in ref. 33), the hexagonal phase as a coiled cylindrical cluster (Fig. 1c), and one lamella (Fig. 1d). We will only consider the structural properties of the system under thermodynamic conditions at which the hexagonal phase is stable in bulk since it exhibits the most interesting behaviour as we showed in a previous work.18
. In Fig. 1, we present snapshots of the system at three different chemical potentials, observing a cluster-crystal with hexagonal symmetry (Fig. 1b, similar to that observed in ref. 33), the hexagonal phase as a coiled cylindrical cluster (Fig. 1c), and one lamella (Fig. 1d). We will only consider the structural properties of the system under thermodynamic conditions at which the hexagonal phase is stable in bulk since it exhibits the most interesting behaviour as we showed in a previous work.18
We are interested in the formation of a single layer of ordered structure, and thus the width of the spherical shell must be comparable to the diameter of the cylindrical clusters in bulk. We should give more space inside the shell to avoid deformation of the cylindrical clusters due to tight confinement. After some trial runs, we found that a shell width of 6σ yielded good results. This width is compatible with the separation distance between cylindrical clusters in bulk, l0 ≈ 6σ, which is an important geometric parameter to predict the ordered structures as a function of the system size (see Section A predictive and characterization method).
We set, then, the shell width to W = Rout − Rinn = 6σ for all the studied cases. In the limit where W → 0, the system becomes strictly two-dimensional and we expect similar structures to those reported in ref. 33 and 32 for intermediate densities.
An example of the systems we are focusing on is depicted in Fig. 1c. We identify the structure of the colloidal fluid by visual inspection of iso-density surfaces built from the three-dimensional density profiles of the systems,
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent configurations. The iso-density surfaces are obtained by triangulation of the points with a local density, ρiso = 0.4Nσ3/V, using the OpenDX software. Additionally, we use the OVITO software45 to create instantaneous iso-density surfaces.
000 independent configurations. The iso-density surfaces are obtained by triangulation of the points with a local density, ρiso = 0.4Nσ3/V, using the OpenDX software. Additionally, we use the OVITO software45 to create instantaneous iso-density surfaces.
Results and discussion
We run simulations in spherical shells keeping their thickness W = 6σ constant while varying the external radius, so that Rinn = Rout − W. Simulations are performed at T* = 0.35, a temperature that enables a good sampling of all the possible structures for a given shell size. The inner sphere acts as an obstacle for the colloidal particles, but they can interact through it. Thus, for very small spherical shells (Rout < 7.0σ, i.e., Rinn < 1.0σ), the colloidal particles interact repulsively through the inner sphere, and the ordered structures that form instantaneously cannot survive for long at T* = 0.35. Indeed, we found that the minimum radius of the inner sphere that allows the formation of ordered structures at this temperature is approximately Rinn = 1.0σ, a case in which the colloidal particles that are located near the surface of the inner sphere in diametrically opposite positions, experience a low repulsion because the distance between them is almost at the end of the repulsive range of the interaction potential (see eqn (1)).All the structures observed in our simulations can be derived from three fundamental structures. These three fundamental structures are formed by two types of elemental cluster shapes: spheres and tori. Two particles are considered belonging to the same cluster when their distance is lower than the attractive range of the potential, λ = 1.5σ. But, given the characteristic shapes of the clusters under the conditions considered here, they can be directly identified from the iso-density surfaces. The radius of the clusters (spheres and tori) and the separation distance between them are determined by the interplay between attraction and repulsion. The separation distance between clusters must be close to the lattice constant of the hexagonal phase in bulk, l0 ≈ 6σ, and the radius of the clusters to that of the equilibrium radius of the cylindrical clusters, r0 ≈ 1.5σ.14,15
We observe structures composed of: two spheres at the poles and tori in the central region (Type I), one sphere at the pole and tori (Type II), and solely tori (Type III). Examples of these structures are presented in Fig. 2a for a generic shell. These structures are our reference, and from now on we will call them fundamental structures.
Apart from the fundamental structures, the system can self-assemble into structures derived from these fundamental ones. From the fundamental structures (see Fig. 2a), all the solutions of the longest curve with finite thickness on the surface of the unit sphere can be generated as described in ref. 35. The derived structures are formed by cutting the spherical shell into two hemispheres along the longitudinal symmetry plane and then rotating one of the hemispheres about its latitudinal axis by integer multiples of an angle θ that corresponds to the arc length necessary to connect two adjacent clusters. The rotation angle can be calculated by dividing 2π by the number of open toroidal ends and open small hemispheres. Each cut torus has two open ends. When the structure is built of k tori and l spheres (with l = 1 or 2), then the angle of rotation θ can be calculated according to the following formula θ = 2π/(2k + l).
In Fig. 2b, we show the construction of the first derived solution taking as an example the Type III structure, but the same procedure can be applied for the rest. Interestingly, we also observe structures composed of one half of the Type I and the other of Type III. We call these structures the hybrid ones. Hybrid structures are only possible if the angle of formation, θ, is the same in the two different fundamental structures. Thus, the hybrid structures are only possible between Type III with n clusters and Type I with n + 1 clusters. Let us consider a shell formed by one hemisphere of Type III (n) and the other of Type I (n + 1) without any rotation initially (see Fig. 2c left panel). The spherical clusters placed at the poles of Type I (n + 1) perfectly match in the inner region of the toroidal clusters placed at the poles of Type III (n), and thus the clusters of one hemisphere have an offset of θ/2 with respect to the other. Following this, it is clear that only rotations of odd multiples of θ/2 will produce hybrid structures. The number of unique hybrid structures (without considering chirality) is given by the number of odd integers up to n. The structures presented here are optimal solutions of the problem of the longest rope on the surface of a sphere.35 In the original problem, there are no restrictions on the separation between the rope folds, and thus they can lay touching each other at close packing as shown in Fig. 2. In our case, the long-range repulsion of the interaction potential prevents the clusters from merging and then there is a separation between clusters (or folds of the same cluster in the derived structures). Alternatively, we can think about the self-assembled structures as they were closed-packed ropes with a diameter equal to l0. This method of construction not only describes how the ordered structures are formed but also relates them to an optimization problem, which extends the current knowledge of cylinder-forming systems under spherical confinement.30,32,33,46
Following the criteria and method mentioned above, we can predict which fundamental structure will be formed for a given shell size and all the possible derived structures. There are topological differences between the derived structures obtained from fundamental structures of a different type. The resulting derived structures from Type I must have four ends since there will be four semi-spheres as a result of splitting in two halves the two spherical clusters at the poles when the rotation of a hemisphere is performed. The structures derived from Type II always have two ends that correspond to the two semi-spheres in which the spherical cluster placed at the pole is split after a rotation is performed. On the other hand, the structures derived from Type III are always formed by closed clusters. Similarly, the hybrid structures always will have two ends. Based on the geometric considerations of the method, we hypothesize that the fundamental and its derived structures, including the hybrid, are equivalent since all require exactly the same amount of material to be built and should have very similar energies because the distances between clusters are conserved.
In a recent study, density functional theory was used to study the phase behaviour of SALR disks confined to the surface of a sphere, finding that structures very similar to Type I, Type II, Type III, and their derivatives are stable at intermediate densities.33 Although this study considered a different SALR model potential (hard core + double Yukawa with a sharp minimum), these theoretical predictions support the results presented here and their universality. Simulation studies of two dimensional systems on spherical surfaces of colloidal dimers46 and colloidal particles interacting via Lennard-Jones + Yukawa potential32 have also reported the formation of helical structures made out of colloidal stripes that share some topological features with the structures reported here, such as open and closed clusters. However, we found a richer variety of structures and provide a method that explains their formation.
We first discuss the results obtained for small spherical shells. In Fig. 3 we present all the possible structures for shells with Rinn = 1.0σ (a) and 2.5σ (b). We note that for the same chemical potential it is possible to obtain different structures for the same shell size (see Fig. 3(a) the second and the fifth columns; Fig. 3b columns from the second to the sixth). The rest of the structures are obtained within a small range of chemical potentials. Naturally, the average number density and energy per particle are very similar.
 | ||
| Fig. 3 Ordered structures obtained by confining the colloidal fluid into small spherical shells of Rinn = 1.0σ and Rout = 7.0σ (a) and Rinn = 2.5σ and Rout = 8.5σ (b). The iso-density surfaces are presented in white with ρiso = 0.4, and the outer and inner spheres are shown in blue and cyan respectively. The temperature is T* = 0.35 and the chemical potentials, μ*, are shown in the figure. The average number density and energy are also presented for each structure. Above the structures obtained from simulations, we show the geometrical construction of the solutions following the method described in Fig. 2b; the clusters are represented in different colors to follow their new positions after rotations. The fundamental structures are successively rotated by an angle θ = 90° ((a)) and 60° ((b)) clockwise to form all the derived structures. | ||
For both shell sizes presented in Fig. 3, the stable fundamental structures are Type III and Type I. We observed derived structures that can be obtained following the method described above. As predicted, we also found hybrid structures. For the shell with Rinn = 1.0σ the resulting hybrid structure resembles a single helix. For the shell with Rinn = 2.5σ we found two hybrid structures, one corresponding to θ/2 similar to a single helix, and the other corresponding to 3θ/2 which is composed of a closed cluster and an open cluster.
In Fig. 4, we present the results for the spherical shell of Rinn = 4.5σ and Rout = 10.5σ. We find Type III (n = 4, four tori) and Type I (n = 5, two spheres at the poles and three tori) fundamental structures for μ* = −2.180 and −2.170, respectively, with very similar densities and energies. We obtain all the possible derived structures from Type III and Type I within a small range of chemical potential (see Fig. 4a and b, respectively). In Fig. 4a, the θ structure is composed of a closed cluster, whereas the 2θ structure is composed of two closed clusters. In Fig. 4b, the θ structure contains two open clusters and resembles a double-helix; the 2θ structure is composed of three clusters: one closed (in green and cyan) and two open (both in brown). Hybrid structures between Type III and Type I can also be stabilized. In Fig. 4c, we present the hybrid structures, showing that one hemisphere corresponds to Type III (in blue) whereas the other one corresponds to Type I (in red). In the top panel of Fig. 4c, the hemispheres are rotated 67.5° with respect to each other, and in the bottom panel, they are rotated 22.5°. The total number of unique hybrid structures is 2 because up to n = 4 there are two odd numbers: 1 and 3.
 | ||
| Fig. 4 Structures obtained by confining the colloidal fluid into a spherical shell of Rinn = 4.5σ and Rout = 10.5σ. The iso-density surfaces are presented in white with ρiso = 0.40, and the outer and inner spheres are shown in blue and cyan respectively. The temperature is T* = 0.35 and the chemical potentials, μ*, are shown in the figure. The average number density and energy are also presented for each structure. Above the structures obtained from simulations, we show the geometrical construction of the solutions following the method described in Fig. 2b; the clusters are represented in different colors to follow their new positions after rotations. (a) For n = 4 Type III and derived structures, θ = 45°. (b) For n = 5 Type I and derived structures, θ = 45°. (c) Hybrid structures between Type III and Type I. | ||
Fig. 5 shows all the possible structures obtained for the spherical shell with Rout = 11.5σ and Rinn = 5.5σ. The fundamental structure is of Type II composed of one spherical cluster and four torus-shaped clusters. The derived structures are obtained by rotating the fundamental Type II structure clockwise by integer multiples of an angle, θ = 40°. The average energies of all the structures are quite similar (virtually equal for some cases, for example θ and 3θ), only exhibiting small differences within the fluctuations range. The number densities of the systems are also very similar but exhibit an increasing tendency as the chemical potential increases. The derived structures corresponding to rotations of θ, 2θ and 4θ are composed of only one coiled cylindrical cluster. On the other hand, the structure corresponding to a rotation of 3θ is composed of two clusters. The first one is an open cluster resembling a single-helix (shown in green with the ends in blue in Fig. 5, 3θ), and the second one is a closed cluster (shown in cyan and brown in Fig. 5, 3θ). In the θ structure, the two ends of the cylindrical cluster are placed at the same pole. This structure resembles a double helix that closes on itself at the opposite pole. In the 2θ structure, the ends of the cylindrical cluster are separated by one of its folds. Two folds separate the ends of the 3θ structure, but, as already mentioned, the structure is composed of one open cluster and one closed cluster. Finally, the 4θ structure has its ends placed at opposite poles separated by 4 folds. This structure resembles a single helix structure. Note that although the hybrid structure presented in the bottom panel of Fig. 4c is very similar to this structure, they are indeed different because in the former the ends of the structure at the poles head to the same direction, whereas in the latter they head to opposite directions. In a fluid of SALR disks confined to the surface of a sphere, helical structures have been found to be only metastable.33 Our simulations suggest that this type of helical structures is rather stable. These different results might be related to the fact that we are using a SALR potential with a flat minimum, and we are modelling a quasi-bidimensional system, whereas in ref. 33 it used a SALR potential with a very sharp minimum, and the system is strictly bidimensional.
 | ||
| Fig. 5 Structures obtained by confining the colloidal fluid into a spherical shell of Rinn = 5.5σ and Rout = 11.5σ. The iso-density surfaces are presented in white with ρiso = 0.40, and the outer and inner spheres are shown in blue and cyan respectively. The temperature is T* = 0.35 and the chemical potentials, μ*, are shown in the figure. The average number density and energy are also presented for each structure. Above the structures obtained from simulations, we show the geometrical construction of the solutions following the method described in Fig. 2b; the clusters are represented in different colors to follow their new positions after rotations. The Type II fundamental structure is successively rotated an angle θ = 40° clockwise to form all the derived structures. | ||
In Fig. 6, we show all the structures obtained for a shell of Rout = 13.0σ and Rinn = 7.0σ. The fundamental structure is a Type II composed of one spherical cluster and five torus-shaped clusters. Unlike the Rout = 11.5σ shell, all the derived structures are formed by only one open coiled cylindrical cluster. The derived structures follow the same pattern as in the previous case; the ends of the open cluster are placed first at the same pole for a rotation of θ, then the ends are separated by one fold for 2θ and so on. Besides the fact that the average energies and densities are very similar for all the structures, we also observe that two different structures can be obtained under exactly the same thermodynamic conditions (see θ and 5θ structures in Fig. 6). Supported by the results previously discussed (see for example Fig. 3b columns 2–5 and Fig. 4b columns 2 and 3), we suggest that all the possible structures for a given shell size can be obtained for the same thermodynamic conditions. In fact, in long simulations we observe that the system can exchange from one structure to another and likely sampling all the possible structures. In Fig. 7, we present the results at μ* = −2.210 and T* = 0.35 for 1011 MC steps. We observe that the system is in equilibrium since the energy and density fluctuations are within 1% of the mean values. This supports our hypothesis of equivalence between possible structures. Furthermore, we found that the particle fluctuations drive the transitions between structures by favouring the formation of bridges between clusters.
 | ||
| Fig. 6 Structures obtained by confining the colloidal fluid into a spherical shell of Rinn = 7.0σ and Rout = 13.0σ. The iso-density surfaces are presented in white with ρiso = 0.40, and the outer and inner spheres are shown in blue and cyan respectively. The temperature is T* = 0.35 and the chemical potentials, μ*, are shown in the figure. The average number density and energy are also presented for each structure. Above the structures obtained from simulations, we show the geometrical construction of the solutions following the method described in Fig. 2b; the clusters are represented in different colors to follow their new positions after rotations. The Type II fundamental structure is successively rotated at an angle θ = 32.73° clockwise to form all the derived structures. | ||
 | ||
| Fig. 7 A long MC run at μ* = −2.210 and T* = 0.35 for the shell size Rout = 13.0σ that shows how the system fluctuates between different possible structures. The instantaneous energy, u* = u/ε, and number density, ρ*, are shown on the left side. The black dashed lines are the average values. The density and energy fluctuations are within 1% of the mean value, meaning that the system is in equilibrium. On the right side, instantaneous iso-density surfaces of different structures are presented. Orange dots are used as a guide to the eye to indicate the ends of the clusters. The iso-density surfaces are generated by the visualization software OVITO,45 using the Gaussian density method with ρiso = 0.7Nσ3/V. | ||
At this point, it is natural to think about the handedness of the structures presented so far. With the method we have described to obtain the derived structures, we can predict both right and left-handed structures. Although we are just presenting structures obtained in simulations with one handedness, we often observed the formation of chiral structures. However, we did not find any hint that suggests that there is a preference for either handedness.
We expect these structures to form within a range of temperatures, based on the phase diagram reported in ref. 12. Upon increasing the temperature, we anticipate that these structures will melt to a percolating fluid in a first order phase transition. The transition temperature is likely to be different from that in bulk due to the effects of confinement, as often occurs in confined systems in general. For the particular case of SALR systems, shifts in the phase transitions due to confinement have already been reported.41 The transition to a percolating fluid might also be affected by the size of the spherical shell.33
A predictive and characterization method
From our simulations, we identify one simple criterion that must be fulfilled for the system to self-assemble into one or another fundamental structure: the distance from center-to-center, , between the clusters must be of the order of the lattice constant of the hexagonal phase in bulk (l0) to avoid high repulsion between clusters. We also observe that the system still self-assembles into ordered structures when
, between the clusters must be of the order of the lattice constant of the hexagonal phase in bulk (l0) to avoid high repulsion between clusters. We also observe that the system still self-assembles into ordered structures when  because it can adapt both the distance between clusters and the number density within small fluctuations when the available space is smaller than the ideal.
because it can adapt both the distance between clusters and the number density within small fluctuations when the available space is smaller than the ideal.
Based on the evidence we have gathered so far, we have derived some empirical rules that allow us to determine what structures to expect for a given size of the spherical shell. First, we assume l0 = 6.0σ, and W = l0, as in the simulations. The clusters tend to place at the center of the shell which is located at the radial distance Rm = Rinn + W/2. From these parameters we can make an initial estimate of the rotation angle,
 | (6) |
Now, we estimate the number of edges of the regular polygon formed by linking the centres of the cross sections of the clusters inscribed in the circumference of radius Rm, as follows  . The ceil function determines the nearest integer greater than or equal to the argument. Now, if m is an even number, then the number of clusters in the fundamental structure is n = m/2 and the possible structures are Type III with n clusters or Type I with n + 1 clusters. If m is odd, then n = (m + 1)/2 and the possible fundamental structure can only be a Type II with n clusters. After that, we calculate the actual angle of rotation using θ = 2π/(2k + l), where k is the number of tori and l the number of spheres. With this information we can construct all the fundamental and derived structures as a function of the size of the spherical shell.
. The ceil function determines the nearest integer greater than or equal to the argument. Now, if m is an even number, then the number of clusters in the fundamental structure is n = m/2 and the possible structures are Type III with n clusters or Type I with n + 1 clusters. If m is odd, then n = (m + 1)/2 and the possible fundamental structure can only be a Type II with n clusters. After that, we calculate the actual angle of rotation using θ = 2π/(2k + l), where k is the number of tori and l the number of spheres. With this information we can construct all the fundamental and derived structures as a function of the size of the spherical shell.
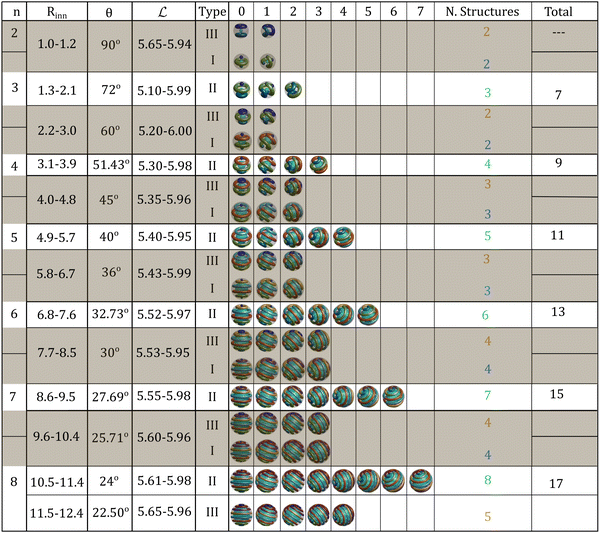
We present in Fig. 8 a catalog of possible structures as a function of the shell size. The number and type of structures are classified by the number of clusters in the fundamental structures, n. For each fundamental structure, there is a range in the internal radius of the shell, Rinn, in which the ordered structures of a given type are stable. We present the angle of formation of the derived structures, θ, and the distance between clusters,  . The numbers above the structures correspond to the clockwise rotations of θ. We only report structures with one handedness. Without considering the hybrid structures, the total number of structures for a given number of clusters follows the relationship 2n + 1. As mentioned before, hybrid structures are only possible between Type III (n) and Type I (n + 1). We shade these structures in the catalog to indicate that they can form hybrids. Note that the maximum values of the ranges of stability of
. The numbers above the structures correspond to the clockwise rotations of θ. We only report structures with one handedness. Without considering the hybrid structures, the total number of structures for a given number of clusters follows the relationship 2n + 1. As mentioned before, hybrid structures are only possible between Type III (n) and Type I (n + 1). We shade these structures in the catalog to indicate that they can form hybrids. Note that the maximum values of the ranges of stability of 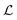 are close to l0, the case in which we obtain ideal structures. Using the catalog, only by knowing the size of the spherical shell can we predict all the structural information of the system, such as the type of the fundamental structure, the number of clusters, the possibility of hybrid structures, the derived structures and so on. The catalog correctly predicts the structures we observed in our simulations in Fig. 3–6. To generalize this catalog to any system with competing interactions able to form a hexagonal phase in bulk when confined in spherical geometries, we only need to know the lattice constant of the hexagonal phase in bulk at equilibrium. The ranges of Rinn provided in the catalog are an estimation using only the geometry of the clusters and the system, and thus they are not strict but a guide for simulation and experimental studies.
are close to l0, the case in which we obtain ideal structures. Using the catalog, only by knowing the size of the spherical shell can we predict all the structural information of the system, such as the type of the fundamental structure, the number of clusters, the possibility of hybrid structures, the derived structures and so on. The catalog correctly predicts the structures we observed in our simulations in Fig. 3–6. To generalize this catalog to any system with competing interactions able to form a hexagonal phase in bulk when confined in spherical geometries, we only need to know the lattice constant of the hexagonal phase in bulk at equilibrium. The ranges of Rinn provided in the catalog are an estimation using only the geometry of the clusters and the system, and thus they are not strict but a guide for simulation and experimental studies.
So far, we have studied in detail the behaviour of the system confined in narrow spherical shells. The simple mathematical model based on rotations of the fundamental structures can explain the formation of all the ordered structures observed in simulations and can be used to predict the possible structures just by knowing the size of the spherical shell and the separation between neighbour cylindrical clusters in the hexagonal phase in bulk. In Fig. 8, we can observe that as the shell grows, the central region of all structures starts to hold simple arrangements of parallel cylindrical clusters which are indistinguishable between them. In the limit of an infinite spherical shell, θ tends toward zero, and then the system behaves as confined into an infinite slit pore. In this limit, the system self-assembles into an arrangement of parallel cylindrical clusters.41
Deforming the spherical shell
Now, we want to study how the structure of the system is modified by deforming the confining spherical shell while we keep its volume constant. For this purpose, we transform the spherical shell into an ellipsoidal shell. We start from the volume of the ellipsoidal shell, | (7) |
 | (8) |
 | (9) |
 | (10) |
The ellipsoidal shell will maintain a spherical cross section in the plane xz, while the transformation occurs along the y axis. Replacing eqn (10) in (9), we obtain:
 | (11) |
The final step is to calculate the volume of the spherical shell we want to keep constant, replace it in eqn (11) and then solve for a for different values of α. If α = 1.0 we have the spherical shell case. For α < 1.0 we shorten the sphere in the y axis converting it into an oblate. For α > 1.0, we elongate the sphere in the y direction converting it into a prolate.
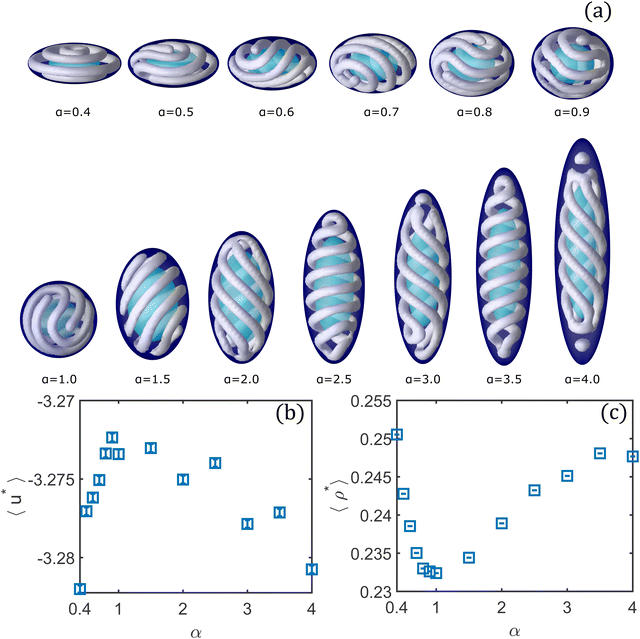
In Fig. 9 we present the results for the system confined in ellipsoidal shells with identical volume to that of the spherical shell at different values of α and under the same thermodynamic conditions (μ* = −2.180, T* = 0.35). The pristine structure obtained in the spherical shell is a cylindrical cluster whose ends are separated by one turn of the cluster (see Fig. 6, 2θ). Note that any of the structures presented in Fig. 6 might be obtained for these thermodynamic conditions. Let us discuss first the structural changes induced by the oblate ellipsoidal shells. In any of the oblate ellipsoidal shells the ends of the cluster are separated by one segment. Instead, we observe ellipsoidal versions of the structures presented in Fig. 6, in which the ends of the cylindrical cluster are separated by two (α = 0.8 and 0.5, corresponding to Fig. 6, 3θ) and three segments (α = 0.9 and 0.6, corresponding to Fig. 6, 4θ). Additionally, for α = 0.7 the cluster forms a double-helix that merges at the opposite pole (corresponding to Fig. 6, 5θ), and for α = 0.4 five tori are formed along the y direction in which the transformation is applied.
In the prolate ellipsoidal shells, we observe that helical structures are highly favoured, being present for all values of α. This behaviour is expected since as the y-axis of the ellipsoidal shells is lengthened, it becomes more similar to a cylindrical shell, geometry that strongly favours the formation of helical structures.14,47 At α = 1.5, a single-helix is formed, but is now somewhat tilted. The ends of the helix are not placed at the highest curvature regions (poles of the ellipsoid) of the shell because in this case the first turn does not have enough room to form without experiencing high repulsion. Regions with less curvature provide more room for the first turn and then avoid high repulsion. At α = 2.0, a penta-helix whose ends merge at the poles in the larger axis is formed. At α = 2.5 and 3.5, the colloidal fluid assembles into a double-helix. For α = 3.0 the helical structure has some defects at the regions of high curvature. We speculate that these defects might be related to the competition of different stable structures driven by small fluctuations in the number of particles as we discussed in the case of the spherical shell (see Fig. 7). Finally, at α = 4.0, we obtain a tetra-helix whose ends merge into tori accompanied by two spherical clusters formed at the poles. Similar structures can be obtained in experiments with confined triblock terpolymers in ellipsoidal droplets.48
Fig. 9b and c show the average energy and density as functions of α, respectively. The transformation to go from spherical to ellipsoidal shells only alters the shape of the system but not its volume. However, the changes in shape cause the colloidal particles to pack in different ways inside the system which are naturally accompanied by density and energy changes. Different values of the parameter α specify different physical systems (different geometry of a shell). The case of the spherical shell (α = 1.0) corresponds to one of the most energetically unfavourable structures (only surpassed by the case of α = 0.9) and also to the worst packing. In contrast, for α = 0.4 the structure made out of toroidal clusters is the most favourable energetically and has the best packing. The other extreme, at α = 4.0, has values of the average energy and number density comparable to those of the α = 0.4 case, suggesting that drastic variations in the system's shape somewhat allows more room for the particles to self-assemble into more favourable structures. The double-helices for α = 2.5 and 3.5 are less favourable than multi-helical structures obtained for α = 2.0, 3.0, respectively. The energy and number density values plotted in Fig. 9b and c are the equilibrium average values for each value of α. These values indicate which geometry is better suited for packing the cylindrical clusters in a shell of the same volume.
Summary and conclusions
We have studied the self-assembly of colloids with competing interactions confined in narrow spherical shells of constant width W = 6σ, under thermodynamics conditions, μ, V and T, at which the hexagonal phase is stable in bulk. We found that the system forms structures composed of clusters with two fundamental shapes: tori and spheres.Depending on the size of the spherical shell, we observed the formation of structures composed of a given number of tori and spheres. We identified three fundamental structures: Type I, Type II and Type III (see Fig. 2). A given type of structure is stable in a spherical shell if the clusters are separated by an arc length comparable to the lattice constant of the hexagonal phase in bulk, and the smallest torus in the structure has a mean external radius of the same order. Apart from the fundamental structures, we observed the formation of derived structures that can be obtained by rotations of one of the hemispheres of the fundamental structures as shown in Fig. 2b. This method is an adaptation of the method used to find the solutions to the problem of the longest rope on the surface of a sphere,35 and thus the structures obtained in the simulations are optimal solutions of this problem. This method is general, and can be applied to characterize the self-assembly of different systems confined in spherical geometries.
All the possible structures for a given shell size have very similar average densities and energies and are obtained within a small range of chemical potential. In fact, we found that different structures can be obtained under the same thermodynamic conditions (see, for example, Fig. 6, for rotations of θ and 5θ, and some structures presented in Fig. 4). Furthermore, we showed that in the same MC run, the system can sample different structures (see Fig. 7). We also observed that the fluctuations of the number of particles often drive the transitions from one structure to another.
For certain sizes of the shell, more than one fundamental structure can fit properly. Thus, we found that the system self-assembles not only into all the possible structures derived from the competing types but also into hybrid structures, in which the hemispheres of the structure correspond to structures of different types (see Fig. 3 and 4).
Using the characterization method described in the paper and our observations, we construct the catalog of Fig. 8. We can predict for which shell size a structure of a given type will be stable. We can extend these predictions to any system with competing interactions that can form a hexagonal phase in bulk and is confined in spherical geometries. We only need to know the lattice constant of the bulk hexagonal phase in equilibrium. We believe that the systematic characterization and prediction of self-assembled structures we present in this paper might be important to the conceptual design of soft nanomaterials that involve systems with competing interactions and spherical geometries. In particular, these findings can guide experiments with block copolymers confined into spherical geometries, allowing a fine tuning of the length scales of the system to obtain specific ordered structures.19,20,49 Regarding colloids, an experimental realization of the system here described would be the recently obtained tube-forming functionalized colloids21 either adsorbed on spherical surfaces or confined into spherical cavities.
Finally, we study the behaviour of the colloidal fluid when the spherical shell is gradually transformed into oblate and prolate ellipsoidal shells. We showed that transforming the spherical shell with Rout = 13.0σ into ellipsoidal ones can induce structural transitions in the colloidal fluid. The transformation was done in such a way the width of the shell and the total volume was kept constant. In particular, we observed that the confinement into oblate shells favours the formation of ordered flattened toroidal structures whereas the prolate shells favour the formation of multi-helical structures. We found that the packing of the system is improved by confinement in both oblate and prolate shells. Based on the internal energy, confinement in spherical shells seems unfavourable compared with confinement in ellipsoidal shells. Interestingly, in the most flattened oblate shell considered (α = 0.4), the colloidal fluid exhibits the best packing and self-assembles into the most energetically favourable structure.
Author contributions
Conceptualisation, H. S., A. G. M., E. G. N and W. T. G.; methodology, H. S., A. G. M, E. G. N. and W. T. G.; software, H. S. and A. G. M.; validation, H. S.; formal analysis, H. S., A. G. M., E. G. N. and W. T. G.; investigation, H. S. and A. G. M.; resources, A. G. M. and W. T. G.; data curation, H. S.; writing—original draft, H. S.; writing—review and editing, H. S., A. G. M., E. G. N. and W. T. G.; visualisation, H. S.; supervision, W. T. G. and E. G. N.; project administration, W. T. G. and E. G. N.; funding acquisition, W. T. G. and E. G. N.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We would like to acknowledge the support from NCN grant No 2018/30/Q/ST3/00434 and from the Agencia Estatal de Investigación and the Fondo Europeo de Desarrollo Regional (FEDER), Grant No PID2020-115722GB-C21.Notes and references
- A. Ciach, J. Pękalski and W. Góźdź, Origin of similarity of phase diagrams in amphiphilic and colloidal systems with competing interactions, Soft Matter, 2013, 9, 6301–6308 RSC.
- J. Ruiz-Franco and E. Zaccarelli, On the Role of Competing Interactions in Charged Colloids with Short-Range Attraction, Ann. Rev. Condens. Matter Phys., 2021, 12, 51–70 CrossRef CAS.
- C. D. Vacogne, C. Wei, K. Tauer and H. Schlaad, Self-assembly of α-helical polypeptides into microscopic and enantiomorphic spirals, J. Am. Chem. Soc., 2018, 140, 11387–11394 CrossRef CAS PubMed.
- H. Hu, M. Gopinadhan and C. O. Osuji, Directed self-assembly of block copolymers: a tutorial review of strategies for enabling nanotechnology with soft matter, Soft Matter, 2014, 10, 3867–3889 RSC.
- G. S. Doerk and K. G. Yager, Beyond native block copolymer morphologies, Mol. Syst. Des. Eng., 2017, 2, 518–538 RSC.
- G. M. Whitesides and B. Grzybowski, Self-assembly at all scales, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- S. Mann, Self-assembly and transformation of hybrid nano-objects and nanostructures under equilibrium and non-equilibrium conditions, Nat. Mater., 2009, 8, 781–792 CrossRef CAS PubMed.
- M. Edelmann and R. Roth, Gyroid phase of fluids with spherically symmetric competing interactions, Phys. Rev. E, 2016, 93, 062146 CrossRef PubMed.
- D. Stopper and R. Roth, Nonequilibrium phase transitions of sheared colloidal microphases: results from dynamical density functional theory, Phys. Rev. E, 2018, 97, 062602 CrossRef CAS PubMed.
- A. Ciach, Combined density functional and Brazovskii theories for systems with spontaneous inhomogeneities, Soft Matter, 2018, 14, 5497–5508 RSC.
- H. Serna, A. D. Pozuelo, E. G. Noya and W. T. Góźdź, Formation and internal ordering of periodic microphases in colloidal models with competing interactions, Soft Matter, 2021, 17, 4957–4968 RSC.
- Y. Zhuang, K. Zhang and P. Charbonneau, Equilibrium phase behavior of a continuousspace microphase former, Phys. Rev. Lett., 2016, 116, 098301 CrossRef PubMed.
- D. Pini and A. Parola, Pattern formation and self-assembly driven by competing interactions, Soft Matter, 2017, 13, 9259–9272 RSC.
- H. Serna, E. G. Noya and W. T. Góźdź, Assembly of helical structures in systems with competing interactions under cylindrical confinement, Langmuir, 2019, 35, 702–708 CrossRef CAS PubMed.
- H. Serna, E. G. Noya and W. T. Góźdź, The influence of confinement on the structure of colloidal systems with competing interactions, Soft Matter, 2020, 16, 718–727 RSC.
- A.-C. Shi and B. Li, Self-assembly of diblock copolymers under confinement, Soft Matter, 2013, 9, 1398–1413 RSC.
- M.-H. Cheng, Y.-C. Hsu, C.-W. Chang, H.-W. Ko, P.-Y. Chung and J.-T. Chen, Blending Homopolymers for Controlling the Morphology Transitions of Block Copolymer Nanorods Confined in Cylindrical Nanopores, ACS Appl. Mater. Interfaces, 2017, 9, 21010–21016 CrossRef CAS PubMed , PMID: 28558189.
- H. Serna, A. G. Meyra, E. G. Noya and W. T. Góźdź, Self-Assembly of Optimally Packed Cylindrical Clusters inside Spherical Shells, J. Phys. Chem. B, 2022, 126, 7059–7065 CrossRef CAS PubMed.
- R. Yang, B. Li and A.-C. Shi, Phase Behavior of Binary Blends of Diblock Copolymer Homopolymer Confined in Spherical Nanopores, Langmuir, 2012, 28, 1569–1578 CrossRef CAS PubMed , PMID: 22148840.
- M. Pinna, S. Hiltl, X. Guo, A. Böker and A. V. Zvelindovsky, Block copolymer nanocontainers, ACS Nano, 2010, 4, 2845–2855 CrossRef CAS PubMed.
- Y. Guo, B. G. P. van Ravensteijn and W. K. Kegel, Self-assembly of isotropic colloids into colloidal strings, Bernal spiral-like, and tubular clusters, Chem. Commun., 2020, 56, 6309–6312 RSC.
- P. Viveros-Méndez, I. Moreno, L. Nuñez-Magos and S. Aranda-Espinoza, Aggregation of superparamagnetic colloids strongly confined in spherical cavities under magnetic fields, Mol. Phys., 2021, 119, e1954254 CrossRef.
- S.-J. Jeon, G.-R. Yi, C. M. Koo and S.-M. Yang, Nanostructures inside colloidal particles of block copolymer/homopolymer blends, Macromolecules, 2007, 40, 8430–8439 CrossRef CAS.
- T. L. Chantawansri, A. W. Bosse, A. Hexemer, H. D. Ceniceros, C. J. Garcia-Cervera, E. J. Kramer and G. H. Fredrickson, Self-consistent field theory simulations of block copolymer assembly on a sphere, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031802 CrossRef PubMed.
- F. Zhao, Z. Xu and W. Li, Self-Assembly of Asymmetric Diblock Copolymers under the Spherical Confinement, Macromolecules, 2021, 54, 11351–11359 CrossRef CAS.
- P. Chen, H. Liang and A.-C. Shi, Microstructures of a cylinder-forming diblock copolymer under spherical confinement, Macromolecules, 2008, 41, 8938–8943 CrossRef CAS.
- B. Yu, B. Li, Q. Jin, D. Ding and A.-C. Shi, Confined self-assembly of cylinder-forming diblock copolymers: effects of confining geometries, Soft Matter, 2011, 7, 10227–10240 RSC.
- S. Li, Y. Jiang and J. Z. Chen, Morphologies and phase diagrams of ABC star triblock copolymers confined in a spherical cavity, Soft Matter, 2013, 9, 4843–4854 RSC.
- J. Wu, S.-T. Chen, S.-B. Li, L.-M. Liu, X.-H. Wang and W.-C. Lang, Simulation of Surface-Induced Morphology Transition and Phase Diagram of Linear Triblock Copolymers under Spherical Confinement, Chin. J. Polym. Sci., 2022, 1–13 Search PubMed.
- G. J. Zarragoicoechea, A. G. Meyra and V. A. Kuz, Pattern formation by interacting particles on the surface of a sphere, Mol. Phys., 2009, 107, 549–554 CrossRef CAS.
- A. G. Meyra, G. J. Zarragoicoechea and V. A. Kuz, Monte Carlo simulation of a binary mixture on the surface of a sphere: lateral phase transition and pattern formation, Mol. Phys., 2010, 108, 1329–1335 CrossRef CAS.
- J. Pekalski and A. Ciach, Orientational ordering of lamellar structures on closed surfaces, J. Chem. Phys., 2018, 148, 174902 CrossRef PubMed.
- S. Franzini, L. Reatto and D. Pini, Phase diagram of SALR fluids on spherical surfaces, Soft Matter, 2022, 18, 186–197 RSC.
- G. Munaò, D. Costa, G. Malescio, J.-M. Bomont and S. Prestipino, Competition between clustering and phase separation in binary mixtures containing SALR particles, Soft Matter, 2022, 18, 6453–6464 RSC.
- H. Gerlach and H. von der Mosel, On sphere-filling ropes, Am. Math. Monthly, 2011, 118, 863–876 CrossRef.
- C. Varea, J. Aragon and R. Barrio, Turing patterns on a sphere, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 60, 4588 CrossRef CAS PubMed.
- D. Lacitignola, B. Bozzini, M. Frittelli and I. Sgura, Turing pattern formation on the sphere for a morphochemical reaction-diffusion model for electrodeposition, Commun. Nonlinear Sci. Numerical Simul., 2017, 48, 484–508 CrossRef.
- R. Nishide and S. Ishihara, Pattern Propagation Driven by Surface Curvature, Phys. Rev. Lett., 2022, 128, 224101 CrossRef CAS PubMed.
- Y. Zhuang and P. Charbonneau, Equilibrium phase behavior of the square-well linear microphase-forming model, J. Phys. Chem. B, 2016, 120, 6178–6188 CrossRef CAS PubMed.
- Y. Zhuang and P. Charbonneau, Recent advances in the theory and simulation of model colloidal microphase formers, J. Phys. Chem. B, 2016, 120, 7775–7782 CrossRef CAS PubMed.
- H. Serna, W. T. Góźdź and E. G. Noya, Structural and Dynamical Behaviour of Colloids with Competing Interactions Confined in Slit Pores, Int. J. Mol. Sci., 2021, 22, 11050 CrossRef PubMed.
- O. Patsahan, M. Litniewski and A. Ciach, Self-assembly in mixtures with competing interactions, Soft Matter, 2021, 17, 2883–2899 RSC.
- A. Ciach, De Virgiliis, A. Meyra and A. Litniewski, M. Pattern Formation in Two-Component Monolayers of Particles with Competing Interactions, Molecules, 2023, 28, 1366 CrossRef CAS PubMed.
- M. Litniewski and A. Ciach, Adsorption in mixtures with competing interactions, Molecules, 2021, 26, 4532 CrossRef CAS PubMed.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- N. Dlamini, S. Prestipino and G. Pellicane, Self-assembled structures of colloidal dimers and disks on a spherical surface, Entropy, 2021, 23, 585 CrossRef PubMed.
- H.-L. Wu, H.-K. Tsao and Y.-J. Sheng, Helical wrapping of diblock copolymers on nanocylinder, J. Taiwan Inst. Chem. Eng., 2017, 81, 104–109 CrossRef CAS.
- X. Dai, X. Qiang, C. Hils, H. Schmalz and A. H. Gröschel, Frustrated microparticle morphologies of a semicrystalline triblock terpolymer in 3D soft confinement, ACS Nano, 2020, 15, 1111–1120 CrossRef PubMed.
- Y.-T. Juan, Y.-F. Lai, X. Li, T.-C. Tai, C.-H. Lin, C.-F. Huang, B. Li, A.-C. Shi and H.-Y. Hsueh, Self-Assembly of Gyroid-Forming Diblock Copolymers under Spherical Confinement, Macromolecules, 2023, 56, 457–469 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |