Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Planar confined water organisation in lipid bilayer stacks of phosphatidylcholine and phosphatidylethanolamine†
Gerome
Vancuylenberg
,
Amin
Sadeghpour
 ,
Arwen I. I.
Tyler
,
Arwen I. I.
Tyler
 and
Michael
Rappolt
and
Michael
Rappolt
 *
*
School of Food Science and Nutrition, Woodhouse Lane, University of Leeds, Leeds, LS2 9JT, UK. E-mail: m.rappolt@leeds.ac.uk
First published on 6th June 2023
Abstract
Phospholipid-based liposomes are abundantly studied in biomembrane research and used in numerous medical and biotechnological applications. Despite current extensive knowledge on membrane nanostructure and its mechanical properties under various environmental conditions, there is still a lack of understanding on interfacial lipid–water interactions. In this work, the nature of the confined water layer for L-α-phosphatidylcholine (egg-PC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dimyristoyl-sn-glycerol-3-phosphocholine (DMPC) and 1,2-dimyristoyl-sn-glycero-3-phosphoethanolamine (DMPE) in the fluid lamellar phase of multilamellar vesicles was investigated. A new model for describing three different water regions is proposed, which have been characterised using a combination of small angle X-ray scattering (SAXS) and densitometry. The three regions concern (i) ‘the headgroup water’, (ii) ‘perturbed water’ near the membrane/water interface and (iii) a core layer of ‘free water’ (unperturbed water). The behaviour of all three layers is discussed as a function of temperature, concerning influences of chain saturation and headgroup type. While the overall water layer and perturbed water layer thickness increase with temperature, the free water layer displays the opposite trend for PCs, and in PEs is completely absent. Furthermore, an estimate of the temperature dependent headgroup orientation is given for both, PCs and PEs. The newly presented structural data deduced from the three-water region model will be useful for future refined molecular dynamics simulations and allow a better theoretical understanding of the attractive van der Waals force between adjacent membranes.
1. Introduction
Amphiphilic lipid self-assemblies belong to the class of lyotropic liquid crystals, and as such, they display a variety of complex mesophases and nanostructures, depending on the environmental conditions, lipid type and molecular shape.1–3 In this study, we focus on the biologically most significant fluid lamellar phase of phospholipids, which form the core matrix of plasma cell membranes.4–6 In particular, we investigated the hydration behaviour of phosphatidylethanolamine (PEs) and phosphatidylcholine (PCs) multilamellar vesicles (MLVs); two very prominent biomimetic model membrane systems.7–11 Generally, liposomes of multilamellar and unilamellar vesicles are widely studied as model systems for understanding the role of the biomembrane matrix in solute interactions, raft formation and fusion processes.12–15 Further to this, their importance is fundamental in the design of nanoparticles for drug delivery,16–19 due to their low toxicity, compatibility with cellular membranes as well as tuneable functionality. More recently, membrane research is focussing on the understanding of essential processes of life through modular reconstitution of artificial and minimal cells,20,21 and the use of giant unilamellar vesicles (GUVs) as bioreactors for artificial cell replication to take place.22 All these applications have been bolstered by the information extracted from studying the fluid lamellar phase.Biomembranes exist in excess of water and the extent of membrane hydration is primarily dictated by the propensity of the headgroup to form hydrogen bonds with interfacial water molecules.23 Elevated temperatures increase the area per lipid due to enhanced chain splay,24 which increases the hydration as the headgroup occupies a larger volume. Another factor influencing chain splay is the number of double bonds along the chain, which dictates the chain disorder, and thus influences in turn the area per lipid. Considering the membrane hydration in each case, PCs are known to hydrate well, displaying a full hydration limit at around 43 wt% of water,7,25 compared to about 25 wt% in PEs.26,27 Further, molecular dynamics (MD) simulations on PC membranes indicate, that a clathrate shell forms around the choline moiety due to the hydrophobicity of the methyl groups,28–30 allowing a greater number of water molecules to become associated with the headgroup of PCs. Additionally, the PC headgroup's greater volume and larger area per lipid provide a greater physical space for interfacial hydration to take place.7 Hydrogen bonding at the lipid/water interface primarily occurs at the oxygen atoms associated with the phosphate of the lipid headgroup as well as at the carbonyl group of the ester linkage in both PCs and PEs.28,31,32 It has also been put forward that inter-bilayer hydrogen bond bridges between adjacent PE membranes prevents the MLVs from swelling.33,34
Our understanding of membrane properties is based on several theoretical aspects. Firstly, the formation of a lipid bilayer is driven by the hydrophobic effect,35 whereby it is energetically more favourable for the polar headgroup to aggregate in an aqueous environment, while the hydrophobic chains will prefer to aggregate among each other.36 Thus, the headgroup interface forms protective layers largely excluding water molecules from the hydrophobic core of the bilayer.37 The first membrane model was suggested by Luzzati,38 dividing the lattice spacing (d-spacing) into a bilayer thickness dLZ and water layer thickness dW. This model describes the lipid/water interface as a sharp boundary, also known as the ‘Gibbs-Dividing Surface’.39 In the fluid phase of PCs and PEs this boundary is close to the position of the phosphate atom of the headgroup.7 Whilst this model is a reasonable approximation, and works well for PCs and PEs to derive structural parameters such as the membrane thickness, it does not reflect the true interfacial details of the distribution of water at the polar/apolar lipid water interface. The next membrane models to gain popularity were bilayer strip models and Gaussian-based bilayer models, which simulate the electron density profiles across the bilayer (Fig. S1, ESI†).40,41 The simplest Gaussian bilayer model describes the electron density profile across the bilayer with three Gaussian distributions, two positive electron density contrasts for each headgroup, and one negative for the chain region.42 From well-ordered fluid membrane stacks (as a rule of thumb, at least four diffraction orders need to be recorded43), the electron density profile (EDP) is directly obtainable from small angle X-ray diffraction experiments,44 while for less-ordered fluid lamellar systems their bilayer structure is commonly analysed by applying global fitting procedures.45,46 Once the refined bilayer EDP is obtained, it is possible to determine the head-to-head distance, dHH, from the positions of the two positive electron density maxima. In order to take into account not only the form factor scattering contributions (arising from bilayer scattering), but also the structure factor contributions (lattice scattering contributions), we applied a global fitting method in this study described in more detail in the Material and methods section and works of Georg Pabst and colleagues.41,47 Importantly, it allows us to additionally evaluate membrane fluctuations in the MLVs, and hence gets hold onto the mechanical behaviour of the bilayers.
As outlined above, great knowledge on the nanostructure of lipid self-assemblies has been accumulated, however, there is still a lack of understanding of membrane behaviour in conjunction with its confined water. Studies are scarce which investigate how the lipid and the confined water layer interact, and rarely a holistic view is applied, treating the lipid/water systems as a single inseparable unit. Exceptions concern the work of Mezzenga and co-workers, who have focussed on the confinement of water in various lipid self-assemblies.48 They have shown that low-temperature crystallisation of molecules into a hexagonal structure is prevented and only amorphous ice forms. Pabst and colleagues included in their latest bilayer modelling also a fixed number of headgroup-bound waters next to an unbound water distribution.49 And more specifically, Kasson et al. have shown that water ordering takes place at the membrane interfaces, when simulating the fusion of two vesicles. This surprisingly leads to a form of hydrophilic confinement of non-bulk-like water behaviour.50 More generally, in terms of the waters’ behaviour relative to the planar lipid bilayer, McIntosh and co-workers have published several studies on membrane hydration and water depth penetration, which suggest vastly differing hydration processes between PCs and PEs.33,34,51,52 Within confined water research, Wurpel et al. used coherent anti-Stokes Raman (CARS) techniques, showing some evidence suggesting weakened hydrogen-bonds (H-bonds), when interlamellar waters were confined in MLVs.53 These weakened H-bonds among interlamellar waters was confirmed again with attenuated total reflection Fourier transform infrared (TR–FTIR).54 More recently it has been suggested in a NMR study that ‘bound water’ near the region of the lipid headgroup is more stable than bulk water, having a more restricted motion and longer stability than that of the bulk.55 This study also supports the idea of distinct water species within the confinement. In all these works, however, there is a lack of discussion on what consequences these observations might have on the bilayer in return.
There remain many open questions regarding membrane behaviour, for which it might be possible that water structuring around the bilayer could give some answers. For example, the incorporation of cholesterol into the bilayer can induce cholesterol-rich domains, so-called liquid ordered (Lo) membrane rafts, which align in radial direction of MLVs or supported lipid films, i.e., Lo-membrane domains register in stacking direction, and are observed as a distinct set of diffraction peaks next to the diffraction peaks of the liquid disordered phase (Ld).56 Cholesterol imbeds itself along the hydrocarbon chain, reducing its degrees of freedom,57 reducing the area per lipid and increasing the membrane thickness, which in turn disrupts the homogeneity of hydration across the membrane, in which Ld and Lo stacked domains coexist.58 To this end, it remains an open question,59 if these confined water differences may have any effect on the stacking alignment of Lo and Ld membranes, respectively. The effect of interfacial water structure might be of great importance for solving this poorly understood phenomenon. Secondly, whilst it is fairly well understood that PEs hydrate poorer than PCs, it is comparatively less understood why this should bring the adjacent bilayers in PEs into such a close separation distance of 0.4–0.5 nm only.60 It seems an additional attractive force contribution is missing to fully understand the thin interlamellar water spacing. Hopefully, these and other open questions can be better understood from more in-depth studies on the confined water structure.
In this study, using a combination of small angle X-ray scattering (SAXS) and densitometry, we are proposing a new distinctive description of individual water regions. Our model accounts for three water layers, namely concerning ‘headgroup water’, ‘perturbed water’ and ‘free water’.
2. Materials and methods
2.1. Materials
L-α-phosphatidylcholine (egg-PC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), dipalmitoyl-sn-glycerol-3-phosphocholine (DMPC), 1,2-dimyristoyl-sn-glycero-3-phosphoethanolamine (DMPE) were purchased from Avanti Polar Lipids (Alabaster, AJ, USA) and used without further purification. All lipids had a purity of >99%, except egg-PC >95%. All lipids were studied exclusively in their fluid phase, therefore all measurements were carried out above their melting temperature Tm. The experimental temperatures ranged from a few degrees above Tm (note, melting points are given in Section 3.1) up to 80 °C.2.2. Densitometry measurements
Samples were prepared in concentrations of 10 mg mL−1 using ultrapure, distilled water (resistance 18 MΩ cm) and vortexed for at least 5 minutes until the lipid was fully dispersed forming MLVs. Density measurements were taken using an Anton-Paar DMA-4500M densitometer (Graz, Austria). The apparatus measures density via the vibrating tube principal.61 We note that the formation of air bubbles within the tube can affect the densitometry measurements quite significantly. Thus, air bubbles were removed by placing the sample in a shaking water bath for 5 minutes and then stirring it on a hot plate at 80 °C for another 5 minutes.Eqn (1) converts the measured density values into the partial specific volume per lipid,61,62
 | (1) |
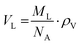 | (2) |
2.3. Small angle X-ray scattering (SAXS)
All samples were prepared by suspending lipids in ultrapure water at differing weight percentages (wt% of lipid) (egg-PC at 40 wt%, DOPC at 40 wt%, DMPC at 25 wt% and DMPE at 20 wt%), and vortexing them at room temperature for 5 minutes until a homogenous dispersion formed. We note that all samples were prepared in excess of water; in order to optimise the SAXS counting statistics of egg-PC and DOPC MLVs, higher weight percentages were chosen for these less ordered systems. Owing to the PEs poorer hydration properties compared to PCs, the DMPE sample was kept at 80 °C for 2–3 minutes in order to facilitate full lipid hydration; upon cooling a homogenous dispersion formed. The samples were then transferred by pipette into 1 mm reusable quartz capillary holder and inserted into a temperature-controlled stage on the SAXSpace instrument (Anton Paar, Graz, Austria).The scattering intensity is a function of the form and structure factors of the sample, expressed with the equation:
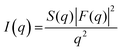 | (3) |
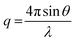 | (4) |
All scattering curves were normalised by the sample transmission and incoming flux, which was achieved by dividing each SAXS curve with the recorded attenuated direct beam intensity. Secondly, the normalised scattering contribution of the empty capillary was subtracted from all other normalised data sets. Thirdly, the pure water SAXS pattern was subtracted from the dispersion SAXS pattern. In this last data reduction step, the excluded water volume was considered.64
All fully corrected scattering patterns were analysed according to the modified Caille theory (MCT),65,66 considering both the bilayer nanostructure and membrane fluctuation. The exact analysis model and underlying grounds have been described elsewhere41 (for an in depth review see Rappolt46). Parameters such as the lamellar repeat distance, d, and the bilayer head-to-head distance, dHH, are directly obtainable from the global fits. The key mechanical fitting parameter, η, known as Caillé parameter or fluctuation parameter, defines the extent of membrane fluctuation. This parameter is directly related to the mean membrane fluctuation distance, σ, via the equation:67
 | (5) |
We note that this global fitting procedure worked well for fully hydrated PC samples, however, it was difficult to obtain satisfactory global fits for DMPE without applying stronger fitting constraints, most probably due to the less suitable structure factor description in this case. Thus, a model free approach was applied. That is, a Fourier analysis was used to obtain the EDPs for DMPE. For centrosymmetric structures such as bilayer stacks, the Fourier summation reduces to only the cosine terms,44 given by the equation:
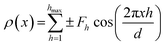 | (6) |
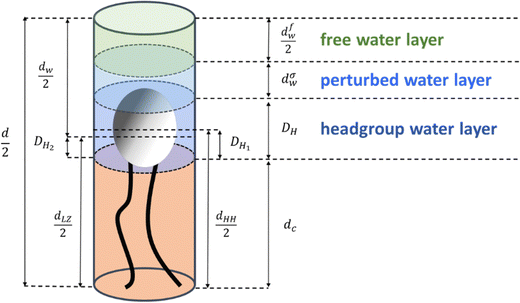
2.4. Definition of three distinct water layers
For our study, we introduce three different regions of water. Fig. 1 shows a schematic of a single lipid and outlines thicknesses of each of its water regions: (i) the ‘headgroup water’ (blue), (ii) ‘perturbed water’ (light blue), and (iii) the ‘free water’ regions (light green). Note, that these highlighted regions are shown per lipid. The overall lipid length is divided into the chain length, dC (the occupied chain volume is shown in light orange in Fig. 1) and the headgroup thickness, DH. The partial headgroup thickness, DH1, measures the distance between the phosphate and the average hydrocarbon chain boundary. An experimentally scrutinized value was published by Nagle and co-workers, reporting DH1 = 0.49 nm for both PCs and PEs,7,33,70 which enables the deduction of the lipid chain length from the experimentally obtainable head-to-head distance, dHH (i.e., the phosphate to phosphate distance). Finally, introducing a second partial headgroup length, DH2, the Luzzati bilayer thickness can be expressed as a function of dHH:| dLZ = dHH + 2(DH2 − DH1) | (7) |
For clarity, all parameters of eqn (7) are defined schematically in Fig. 1 (note, since we display one lipid molecule only, dLZ/2 and dHH/2 are shown). The three water layer thicknesses per lipid, concerning the headgroup, perturbed and free water regions are referred to as (i) DH, (ii) dσw, and (iii) dfw/2. Note, dσw is defined to be equal to σ (eqn (5)) and appears on either side of the free water core, dfw. Finally, the total water layer thickness can be written as:
| dW = d − dLZ = 2dσw + 2(DH − DH2) + dfw | (8) |
We note, that dHH and dLZ for PCs and PEs are not far off, i.e., they are equal to each other within 0.1–0.2 nm,7 and for a first approach estimation can be set equal. However, there is simple way to estimate this deviation 2(DH2–DH1). Since the water volume in the headgroup region, VWH, can be described by the Luzzati method as well as by using the excluded headgroup volumes, VH, approach, we can write:
| (DH − DH2)AL = DHAL − VH | (9) |
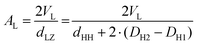 | (10) |
Finally, inserting AL from eqn (10) into eqn (9), we are able to estimate DH2 (see ESI†).
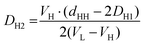 | (11) |
We note that this ansatz can be used as an alternative approach for carrying out tedious and long-lasting gravimetric measurements. Exemplary values on dHH, dLZ and AL of this study are listed together with literature values in Table S2 (ESI†) and show very good agreement.
Specific numbers of waters per water region were calculated, dividing the partial water volumes (ALdσw and AL·dfw/2) by the volume of a single water molecule (VH20 = 0.03 nm3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71). The headgroup thickness DH, was taken from literature to be 0.9 or 0.85 nm for PCs and PEs, respectively,7 and the headgroup volumes derived from the gel-phase to be VH = 0.319 nm3
71). The headgroup thickness DH, was taken from literature to be 0.9 or 0.85 nm for PCs and PEs, respectively,7 and the headgroup volumes derived from the gel-phase to be VH = 0.319 nm3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and 0.252 nm3
7 and 0.252 nm3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 for PCs and PEs, respectively.
8 for PCs and PEs, respectively.
3. Results and discussion
3.1. Volumetric data
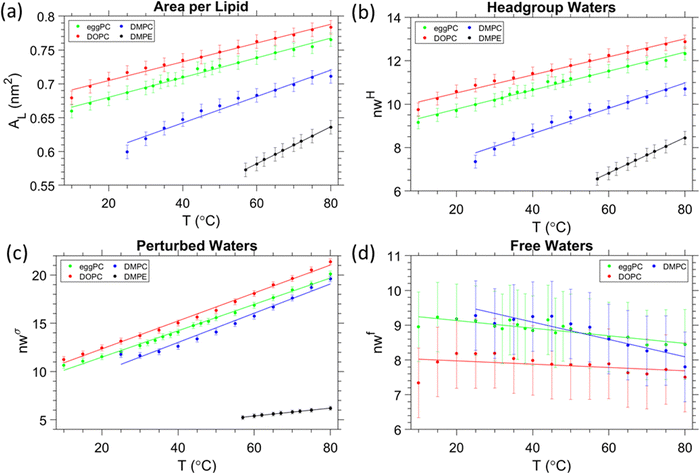
The volume per lipid, VL, was determined from the density measurements and are summarised in Fig. 2. In all cases, a linear increase in the volume per lipid is observed as the temperature increases. The behaviour of the membrane in the fluid phase is relevant to this study, thus for egg-PC and DOPC data were measured from 10 to 80 °C, whereas DMPC was investigated from 25 to 80 °C and DMPE from 57 to 80 °C. We note, that the melting points, TM, for egg-PC, DOPC, DMPC and DMPE, are −15 °C, −17 °C,72,73 24 °C72,73 and 50 °C,72,73 respectively. A higher transition temperature for DMPE of 55 °C was reported by Koynova and Hinz.63 Similarly, we observed in our SAXS experiments an abrupt lattice spacing change at 55 °C (in the heating direction the d-spacing decreases from 5.5 to 5.0 nm), which is in agreement with previous X-ray scattering measurements.74 In order to ensure that all samples were fully in the fluid phase, we have only included data above the main transition.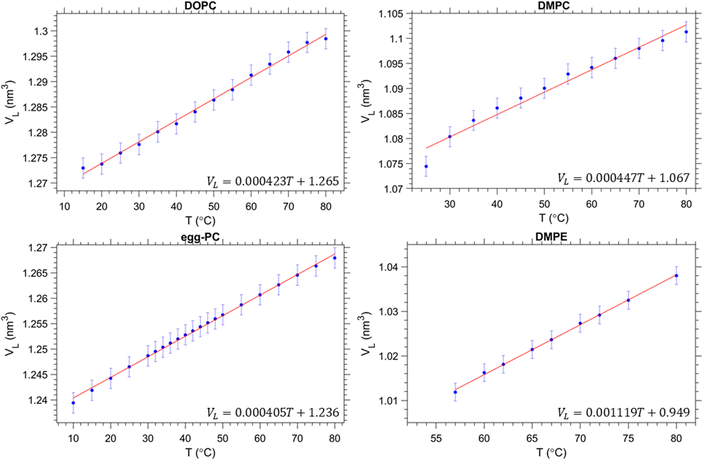 | ||
| Fig. 2 Volumetric data per lipid for each of the samples measured. Our results are in good agreement with previous studies on egg-PC,75 DOPC76 and DMPC.77 Data for DMPE was taken from ref. 63. | ||
3.2. Overview of the bilayer and the three water regions
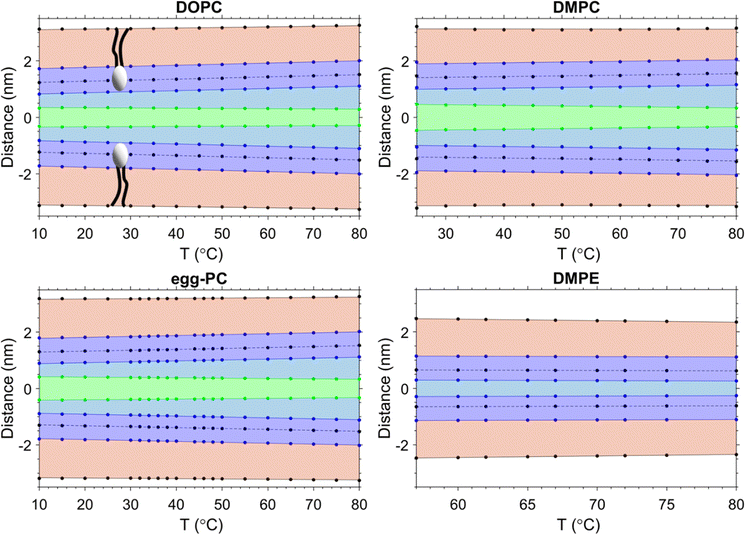
Data from the SAXS curves were analysed to decipher the thicknesses of the different sub-layers of the interstitial water by using eqn (8). The behaviour of the different layers with temperature is summarised in Fig. 3 in schematic diagrams, showing two opposed lipid monolayer leaflets. From top to bottom the layers of the hydrocarbon chains, dC, the headgroup extension layer, DH, the perturbed water layer thickness, dσw, and the free water layer thickness, dfw, are depicted. In all cases, a thinning of the bilayer is observed with increasing temperature, reflecting the extent of chain disorder. As the temperature increases, so does the thermal energy available to the chains, which undergo increasingly trans to gauche conformations,78,79 thinning the bilayer monotonously with temperature. Whilst the bilayer itself thins, the overall d-spacing increases due to the dominant water layer increase, reflecting the swelling of MLVs for all PCs measured. Remarkably, for DMPE the water layer thickness slightly shrinks. That is, the water uptake is greatly reduced, when compared to the PC MLVs (the water uptake will be further discussed in Section 3.5). Membrane fluctuations also tend to increase with temperature as seen by the increase in dσw (its boundaries are given by green and blue lines). Interestingly as the fluctuations increase, dfw shrinks. This was observed in all PCs investigated. The case is very different for DMPE, where the membranes are in such close registry that the opposed perturbed water layers in fact slightly overlap; consequently, there is no free water layer apparent. For this reason, the free water boundaries (green) have been omitted in the DMPE structural data-based schematic. We note that for now we have taken the headgroup thicknesses, DH, to be constant over the entire temperature regime; this simplification will be dropped in Section 3.6 and temperature dependent estimates for DH will be discussed.3.3. Headgroup influence on the interlamellar water regions
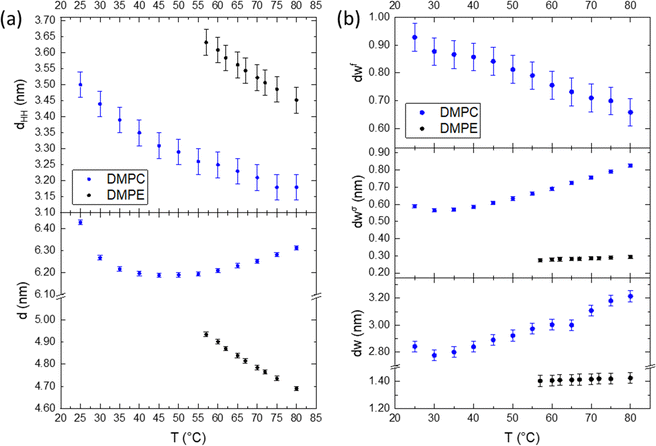
For a better understanding of the influence of the headgroup onto the planar-confined water regions, we compare DMPE vs. DMPC in detail. Fig. 4 summarises the overall behaviour of the membrane and water layers as a function of temperature. The difference between these two lipids is the presence of a choline group for DMPC and an ethanolamine group for DMPE, both conjugated to the phosphate group. Both lipids form hydrogen bonds around the phosphate group, but the hydration level in DMPC is clearly enhanced due to the three methyl groups being associated to water clathrate shells.80,81 Cleary, the behaviour of dw is the most apparent difference between these two lipids, and the influence of the hydrogen bonding and hydration propensity influence this. Membrane fluctuations further increase the water layer thickness in DMPC, as the repulsion between bilayers, due to the Helfrich undulations,82 does increase with the mean membrane fluctuation distance, σ (eqn (5)). As seen in Fig. 4b (middle panel), the perturbed water layer thickness, dσw, of DMPE instead is very constrained, not changing by more than tenth of a nanometre over the entire temperature range. That is, the membrane fluctuations are far less noticeable, when compared to DMPC. This is coupled with the diminished ability to retain water between the bilayer and near the headgroup.81 Further to this, the perturbed water layer is relatively small, leaving very little interstitial water between adjacent membranes, leading to an extreme close registry of adjacent membranes. Most remarkably, is the apparent absence of a free water layer in DMPE. This is markedly different for the case of PCs; coupled to a greater repulsion force acting on DMPC membranes, the MLVs do swell significantly at higher temperature. Nonetheless, the free water layer thickness (Fig. 4b, top panel) decreases with temperature for DMPC, since the water up-take is greatly dominated by the ‘perturbed water’ layer increase.Taking a closer look to Fig. 4a, we can clearly see that the bilayer, dHH, shrinks upon heating in both cases. This is expected as this is mainly dominated by the hydrocarbon chains, which become more disordered as the temperature increases, transferring from trans to gauche states.79 Both lipids have the same fully extended, all-trans state chain length of 1.63 nm, as outlined by Seelig and Seelig79 (note, here dC is defined as (NC − 1) × 0.125 nm, with NC being the number of hydrocarbons and 0.125 nm being the chain-projected C–C bond length). At 80 °C this value reduces by 0.39 nm and 0.53 nm for DMPE and DMPC, respectively, which would amount to four effective gauche states per chain for DMPC and three effective gauche states for DMPE. We note, as described in the common brush model,83 the membrane bending modulus, KC, is proportional to the squared membrane core thickness, (2dC)2, as well to the area compression modulus, KA:
| KC = KA(2dC)2/24 | (12) |
Hence the influence of the bending modulus on the mean fluctuation distance, σ2, is inversely proportional to the ‘deformable’ membrane thickness (note, 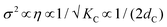 1,67). In simple words, thicker membranes are expected to fluctuate less, leading to a thinner perturbed water layer dσw. The results obtained for DMPE are understood through the brush model, where the membrane is thicker compared to DMPC, therefore the fluctuation distance is shorter. Studies to experimentally measure the bending modulus in DMPE and DMPC have produced varying results,84–87 but a recent simulation study88 determined the bending modules, KC, for DMPE at a value of 22 kBT compared to 14 kBT for DMPC, implying stiffer DMPE membranes. Considering the d-spacing, we see that PC MLVs swell, whilst PEs slightly shrink as a function of temperature, which is in this picture is generally understood on the basis of the differing mechanical properties of the membranes.
1,67). In simple words, thicker membranes are expected to fluctuate less, leading to a thinner perturbed water layer dσw. The results obtained for DMPE are understood through the brush model, where the membrane is thicker compared to DMPC, therefore the fluctuation distance is shorter. Studies to experimentally measure the bending modulus in DMPE and DMPC have produced varying results,84–87 but a recent simulation study88 determined the bending modules, KC, for DMPE at a value of 22 kBT compared to 14 kBT for DMPC, implying stiffer DMPE membranes. Considering the d-spacing, we see that PC MLVs swell, whilst PEs slightly shrink as a function of temperature, which is in this picture is generally understood on the basis of the differing mechanical properties of the membranes.
The Helfrich undulation force depends on the membrane bending modulus as well as the interstitial water layer thickness. However, at small water layer distances (0.4 to 0.8 nm) the repulsive hydration force is dominant, which decays exponentially with dW.89,90 Across all bilayer separations, the van der Waals (VdW) attractive force competes with the two aforementioned repulsive forces, and ultimately, this balance of forces determines the adjacent membrane distance, dW. The attractive VdW force is proportional to the Hamaker constant, which is related to the static dielectric permittivity of the aqueous medium. Changes in the density across the aqueous medium will influence the dielectric permittivity and therefore influences the strength of attraction between adjacent membranes. In general, a decrease in water density decreases the permittivity, causing an increase in the Hamaker constant (for a review see Chapter 13 in Israelachvili's book on ‘Intermolecular and surface forces’91). Considering the density changes across the water layer, it is plausible that the water density is slightly different in each of the defined sub-layers (Fig. 1), due to the influence of the membrane undulations and the degree of headgroup hydration. These supposed water density differences mean that the permittivity is non-uniform across dW, and therefore, in a refined description of the VdW force, the Hamaker constant should be considered to change as a function of distance from the polar/apolar interface. The area per lipid also needs to be considered in the strength of the Hamaker constant. For instance, an increase in the area per lipid decreases the effective surface charge density in the headgroup region, and consequently increases the dielectric permittivity in the interstitial water region.92–94 This increase in permittivity will produce a reduction in the strength of the VdW interaction and allow the water spacing to increase, which is observed in the swelling of PC MLVs.
Similar arguments, but with opposite effect, apply for VdW force in DMPE. In the absence of a free water layer (when only the perturbed, less dense water is apparent) a relative decrease in dielectric permittivity of its interstitial water is expected, and hence a greater overall Hamaker constant. In contrast to PCs, the dominant repulsive force is not given by the Helfrich membrane undulation force, but the water hydration force is dominant at such small membrane to membrane distances.81,95 Remarkably, the very low dW in PE systems has long puzzled the scientific community.33,60 In 1982, Lis et al. considered an increase in the attractive VdW pressure explaining the smaller equilibrium spacings in PE systems but actually reported on too large dW values. This led to other research groups assuming other additional attractive forces in order to overcome the repulsive hydration force in PE membrane stacks. The idea of a solvent-mediated attraction force found some attraction (see ref. 60 and 81 and therein). It has been argued that a small fraction of direct electrostatic and/or indirect hydrogen-bonded water interactions between the NH3+ group in one membrane and the PO4− group in the opposing membrane could account for the additional interaction in PE bilayers.
3.4. Hydrocarbon chain saturation influence on the interlamellar water regions
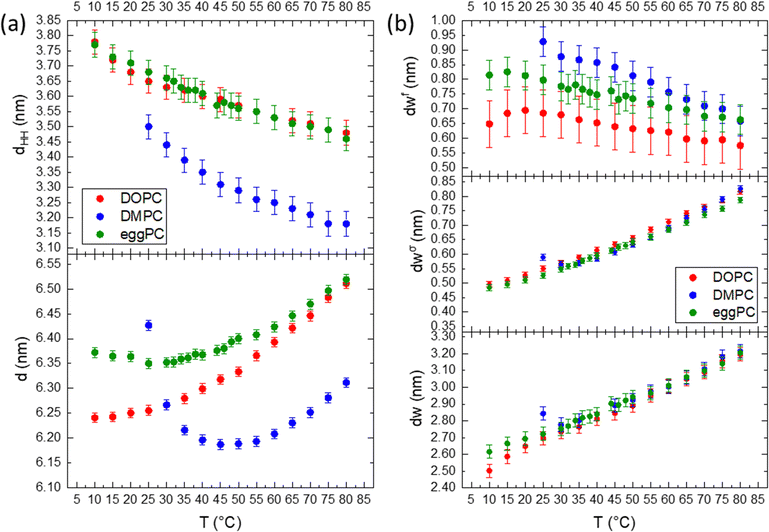
Fig. 5 compares the effect of the hydrocarbon chain and degree of saturation for DMPC, DOPC and egg-PC. All lipids possess the same choline-tipped headgroup. DMPC is fully saturated (C14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 chains), DOPC has monounsaturated chains (C18
0 chains), DOPC has monounsaturated chains (C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and egg-PC is a mixture of lecithins, both with saturated and unsaturated PCs (mostly C16
1) and egg-PC is a mixture of lecithins, both with saturated and unsaturated PCs (mostly C16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and C18
0 and C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).96 In general, across all the parameters described, the hydration behaviour is the same, in that water layer thicknesses increase with temperature as the liposomes swell under the influence of the increasing Helfrich undulation force. The unsaturated chains in DOPC and egg-PC make them more susceptible to chain splay and hence chain disorder, however, their effective chain length is bigger than for DMPC. Hence, the DMPC bilayers are actually thinner, while DOPC and egg-PC bilayers display similar dHH values (Fig. 5a, bottom). According to the brush model (see eqn (12)), the membrane rigidity is not only influenced by the chain fluidity and hence its lateral compressibility modulus, KA, but more strongly to variations in the ‘mechanical’ membrane thickness. We note, that KA does not vary much among PCs containing C14
1).96 In general, across all the parameters described, the hydration behaviour is the same, in that water layer thicknesses increase with temperature as the liposomes swell under the influence of the increasing Helfrich undulation force. The unsaturated chains in DOPC and egg-PC make them more susceptible to chain splay and hence chain disorder, however, their effective chain length is bigger than for DMPC. Hence, the DMPC bilayers are actually thinner, while DOPC and egg-PC bilayers display similar dHH values (Fig. 5a, bottom). According to the brush model (see eqn (12)), the membrane rigidity is not only influenced by the chain fluidity and hence its lateral compressibility modulus, KA, but more strongly to variations in the ‘mechanical’ membrane thickness. We note, that KA does not vary much among PCs containing C14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, C18
0, C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, C18
0, C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and C18
1 and C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrocarbon chains,97 which are predominantly also found in eggPC. Thus, with eggPC and DOPC having significantly bigger bilayer thicknesses than DMPC (Fig. 5a, top), one would expect this to be reflected in a lower membrane rigidity of DMPC bilayers. However, Doktorova et al. pointed out that the classical brush model is not equally applicable to fully saturated lipids, when compared to lipids with unsaturated chains.98 Evidence is put forward that the ‘mechanical’ or ‘deformable’ thickness is relatively bigger for saturated lipids (coming close to dHH), whilst being close to 2dC for unsaturated lipids. Thus, similar ‘mechanical’ membrane thicknesses among eggPC, DOPC and DMPC would explain similar values in dσw. Indeed, our determined η values (Caillé fluctuation parameter) for the studied PCs do not vary much and are in good agreement to literature values, when comparing identical hydration conditions at 30 °C (DMPC: 0.080 compares to 0.077;85 DOPC: 0.081 to 0.09576 and eggPC: 0.073 to 0.08867). Finally, the deviation from a linear water layer thickness trend in DMPC (see 25–30 °C interval), is explained by the effect of anomalous swelling just above the melting point of DMPC,85,99 where the coexistence of gel-like domains in the fluid lamellar bilayer lead to a drop in both the bending rigidity and the bulk compression modulus. The anomalous swelling regime in DMPC also explains the local minima in the recorded d-spacing of DMPC at about 40 °C; while the bilayer thickness monotonously decreases, the MLVs do swell near the melting point as well as at high temperature.
2 hydrocarbon chains,97 which are predominantly also found in eggPC. Thus, with eggPC and DOPC having significantly bigger bilayer thicknesses than DMPC (Fig. 5a, top), one would expect this to be reflected in a lower membrane rigidity of DMPC bilayers. However, Doktorova et al. pointed out that the classical brush model is not equally applicable to fully saturated lipids, when compared to lipids with unsaturated chains.98 Evidence is put forward that the ‘mechanical’ or ‘deformable’ thickness is relatively bigger for saturated lipids (coming close to dHH), whilst being close to 2dC for unsaturated lipids. Thus, similar ‘mechanical’ membrane thicknesses among eggPC, DOPC and DMPC would explain similar values in dσw. Indeed, our determined η values (Caillé fluctuation parameter) for the studied PCs do not vary much and are in good agreement to literature values, when comparing identical hydration conditions at 30 °C (DMPC: 0.080 compares to 0.077;85 DOPC: 0.081 to 0.09576 and eggPC: 0.073 to 0.08867). Finally, the deviation from a linear water layer thickness trend in DMPC (see 25–30 °C interval), is explained by the effect of anomalous swelling just above the melting point of DMPC,85,99 where the coexistence of gel-like domains in the fluid lamellar bilayer lead to a drop in both the bending rigidity and the bulk compression modulus. The anomalous swelling regime in DMPC also explains the local minima in the recorded d-spacing of DMPC at about 40 °C; while the bilayer thickness monotonously decreases, the MLVs do swell near the melting point as well as at high temperature.
As mentioned before for DMPC, the trend in the free water layer spacing (Fig. 5b top panel), is opposite to the dominant increase in the perturbed water layer for all PC samples. At lower temperatures the equilibrium distance between adjacent bilayers, dW, ranks in the order of DMPC > egg-PC > DOPC, most probably reflecting the reverse order of deformable membrane thickness, which in turn dominates the strength of the Helfrich undulation forces. The same ranking in thickness is found for the free water layer thickness.
3.5. Number of water molecules in the three water regions
The area per lipid shows a general increase with temperature (Fig. 6a). DOPC obtained the largest area, owing to the relatively highest disorder in the hydrocarbon chain, arising from the two monounsaturated oleic acid chains (C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9). DMPE has the lowest area per lipid, which is understood due to its relatively small headgroup, and coupled to it, the relatively lowest disorder in the hydrocarbon chain region caused by the lowest number of gauche conformers per saturated myristic acid chains (see discussion in Section 3.3). Another major difference of DMPE MLVs is the fact that they do not swell as compared to PC MLVs. An entirely different balance of forces and poor hydration does explain this exceptional behaviour of the fluid lamellar phase of PEs (see discussion in Section 3.4). In this section, we take a closer look onto the number of waters in the different water regions.
9). DMPE has the lowest area per lipid, which is understood due to its relatively small headgroup, and coupled to it, the relatively lowest disorder in the hydrocarbon chain region caused by the lowest number of gauche conformers per saturated myristic acid chains (see discussion in Section 3.3). Another major difference of DMPE MLVs is the fact that they do not swell as compared to PC MLVs. An entirely different balance of forces and poor hydration does explain this exceptional behaviour of the fluid lamellar phase of PEs (see discussion in Section 3.4). In this section, we take a closer look onto the number of waters in the different water regions.
First, the total number of waters per lipid for DOPC, egg-PC, DMPC (nW = 33, 32 and 24 at 30 °C, respectively) and DMPE (nW = 12 at 60 °C) are in excellent agreement with literature values7,100 (see Table S2, ESI†). Second, a recent small angle scattering model, introducing a fixed hydration shell to the headgroup for improving the quality of fits at lower scattering angles, report on waters per headgroup to be 10–13 of saturated PCs and 16 for loosely-packed monounsaturated PCs.49 More specific values are reported by John Nagle's lab (see ref. 25 and therein) for DMPC (nHW = 7 at 30 °C), egg-PC (nHW = 10 at 30 °C), DOPC (nHW = 11 at 30 °C), and for dilauroyl phosphatidylethanolamine, DLPE (nHW = 6 at 35 °C). Note, to the best of our knowledge, there is no published literature value of nHW for DMPE available, but having the same headgroup and being only two hydrocarbon chains shorter, DLPE nHW values are expected to very similar to those of DMPE. Thus, all published nHW values are in excellent agreement with obtained values in this study (Fig. 6b). In further detail, the (i) number of headgroup waters, the (ii) number of perturbed waters, and the (iii) number of free waters all depend on the trend of AL and their layer thicknesses, DH–DH2, dσw and dfw/2 (Fig. 6b–d). Noteworthy, the number of total water molecules per lipid, the water molecules per headgroup and per perturbed regions do display all the same trend, i.e., DOPC > egg-PC > DMPC > DMPE. That is, they are dominantly influenced by the area per lipid, AL. However, the number of free waters displays the opposite order and are – as noted above – dominated by their extension, dfw/2, which decreases from DMPC > egg-PC > DOPC. For DOPC, the free layer does not change its number of water molecules by a significant amount (less than 1), when compared to egg-PC and DMPC. DOPC also has the lowest gradient for nwf against temperature; −0.0048 °C−1 compared to −0.011 and −0.025 °C−1 for egg-PC and DMPC, respectively. These observations may imply that the free layer of DOPC remains essentially constant over the whole temperature range. This interpretation, as well as the apparent lack of a free layer in DMPE, are used in the next section to roughly estimate the temperature dependent headgroup extension DH.
A final remark shall be given with respect to confined water in non-planar lipid self-assemblies. While this study focusses on planar confined water, the three-water layer model is also applicable to confined water near curved membranes interfaces. Indeed, we have completed a study on the inverse hexagonal phase in greater detail (manuscript in preparation), and would like to herald that it is feasible to introduce the distinction between ‘perturbed’ and ‘free’ water regions in this case. Nonetheless, the situation is more complex, since the mechanical behaviour along the membrane/water interface is not constant in the inverse hexagonal phase, but depends on the locally varying membrane stress (compression vs. decompression zones), which do induce local changes in the thickness of the perturbed water layer.
3.6. Refining the headgroup extension
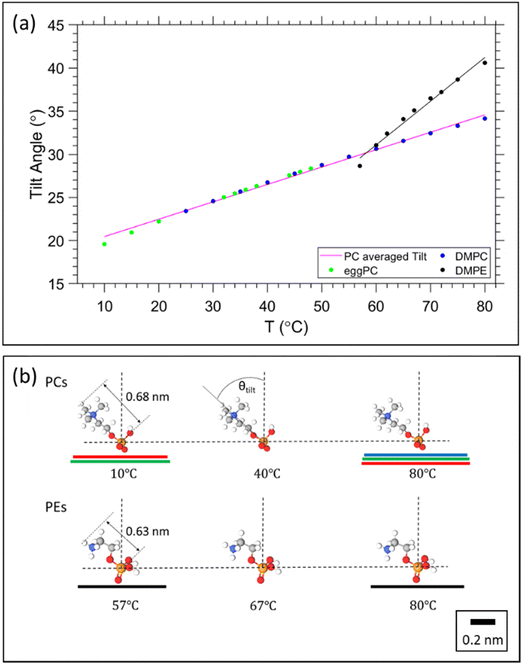
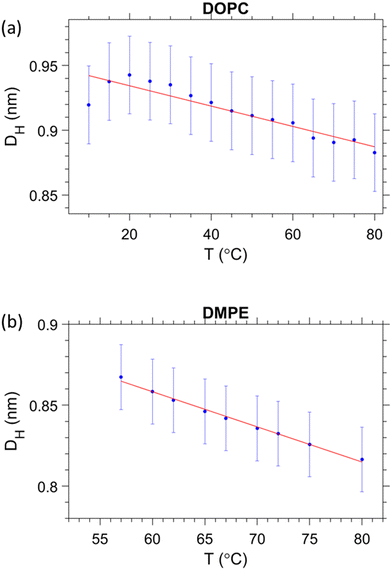
From the estimation of the number of water molecules present in each sub-layer of the confined water strip, a picture of each sub-layers behaviour begins to form. Eqn (8) can be further utilised for the cases of DMPE and DOPC. Here we actually observe that the free water layer thickness in DMPE is practically zero (we note, occurring negative values make no physical sense), and in DOPC the free water layer thickness is constant within error. Thus, our hypothesis is that the apparent trend seen in dfw/2 may actually be caused by a temperature dependent headgroup extension, DH, instead. Our reasoning for this is that the glycerol backbone of the headgroup is commonly assumed to be of constant thickness,101–104 however, the region between the phosphate and tip of the headgroup is more likely to flex and reorient as demonstrated with NMR measurements105,106 as well as shown theoretically and by MD simulations.93,107Starting with DMPE after setting the free water layer to 0 (indicative of the results from SAXS, Fig. 3) and rearranging eqn (8) for DH, we can see that the vertical headgroup extension thins as the temperature increases due to an increase in the tilt angle of phosphate to tip of the headgroup moiety (see Fig. 8). At the onset of the melting temperature, DH is equal to 0.86 nm, which is in good agreement with previously reported values.7 This value then decreases to 0.82 nm at 80 °C. This thinning of the headgroup extension is understandable, when considering the trend of AL that increases with temperature, meaning the headgroup would need to occupy a larger surface area. The headgroup therefore reduces the apparent thickness of DH–DH1 by reorientation of the phosphate to tip of the headgroup extension towards the membrane plane.
In a similar manner, we have set the free water layer for DOPC to a constant value, averaged from high temperature data values obtained in Fig. 5b (top panel). The first values for DH are slightly higher than 0.9 nm, but this is never the less in good agreement with the previously reported values.7 The reduction of headgroup thickness is explained in the same way as for DMPE, whereby the increase in area per lipid is compensated with a thinning of the apparent headgroup thickness, DH. The assumed temperature dependence of DH, slightly alters the number of headgroup waters, which in this scenario do not change by more than a single water molecule. The refined hydration changes are summarised in the ESI† (Fig. S3).
3.7. Estimation of the headgroup tilt
Having obtained a linear regression for the headgroup extension, we can now attempt to estimate its tilt angle. Note, we follow the same assumption as before that the glycerol backbone thickness, DH1, is constant, leaving the portion between the phosphate and the tip of the headgroup to flex and re-orientate. The headgroup thickness, DH, is a projection of the physical extension of the headgroup to the bilayer normal. Thus, to calculate the headgroup tilt angle, it requires the knowledge of the reference length given by the physical distance from the phosphate to the tip of the headgroup, DH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref. For PC and PE we use the literature value of 0.47 nm as the phosphate to nitrogen distance108 and known bond lengths109 as well as bond angles,110 concerning the N–C, C–H and N–H bonds found in the choline and ethanolamine headgroups. This results in DH
ref. For PC and PE we use the literature value of 0.47 nm as the phosphate to nitrogen distance108 and known bond lengths109 as well as bond angles,110 concerning the N–C, C–H and N–H bonds found in the choline and ethanolamine headgroups. This results in DH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref = 0.68 nm and 0.63 nm for PC and PE, respectively (Fig. 8b). The tilt angle, θTilt, is then given by:
ref = 0.68 nm and 0.63 nm for PC and PE, respectively (Fig. 8b). The tilt angle, θTilt, is then given by: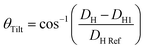 | (13) |
Utilising the obtained headgroup thickness, DH(T) (Fig. 7), we are able to calculate the tilt angle as a function of temperature, and further able to illustrate how much of the area per lipid, AL, is occupied from the precession of the headgroup. The results are summarised in Fig. 8.
 | ||
| Fig. 7 Estimation of the temperature dependent headgroup extension DH for (a) DOPC and (b) DMPE, respectively. | ||
From Fig. 8a, it is clear that the tilt angle increases with temperature, implying that the headgroup tends towards a more horizontal position relative to the bilayer. This result is unsurprising, considering that the area is expanding, whilst the bilayer is thinning and the volume per lipid increases. Theoretical studies and MD simulations confirm that the lipid headgroups tend to a more horizontal position due to thermal movements (rotation), which is more intense at higher temperatures.93,107 The pink line in Fig. 8a represents the averaged linear regression from all the PCs studied; note, all the data points display the same linear trend, since only one linear regression of DH was applied. DMPE displays a stronger tilt angle, which is to be expected, when considering the proximity of adjacent PE bilayers. Fig. 8b, illustrates how the headgroup tilt angle goes hand in hand with the trend in AL. The planar projection of the headgroup length, DH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref, superimposes well with the lateral radius per lipid, √(AL/π).
ref, superimposes well with the lateral radius per lipid, √(AL/π).
4. Conclusions
We have introduced a three-water region model, while commonly only two water regions are considered, i.e., headgroup and interlamellar water. In our model, the interlamellar water region is further divided into free and perturbed water regions, which can be forthrightly determined, when the bilayer nanostructure as well as membrane fluctuations are known. Applying this approach, we have revisited the fluid lamellar phase of PCs and PEs, and particularly chosen these two key lipid species, since they are displaying an extremely different hydration behaviour. Applying this new three-water region model, the following achievements have been made:• We are able to estimate the ‘Gibbs dividing surface’ without the need of gravimetric measurements. That is, we are able to estimate the Luzzati bilayer thickness, dLZ.
• We are providing all standard structural membrane parameters, such as dHH, dC, AL, and VL.
• We give a detailed description of three-water layers and the water numbers per region.
• We provide a rough estimate of the temperature dependent headgroup extension, DH, and its tilt angle.
The presented three-water region model will help to refine existing membrane force descriptions, in particular when revisiting existing models on the attractive van der Waals forces. Note, we expect that the Hamaker constant, H, to be different in the perturbed and free water layer extensions, with Hperturbed being greater as Hfree. The latter notion is in agreement with the extreme differences found for the equilibrium distance of adjacent membranes in PC and PE MLVs, respectively. Finally, due to the refined description of the confined water regions and their temperature behaviour, (‘headgroup’ and ‘perturbed’ water numbers increase with T, while ‘free’ water numbers display a small decreasing temperature dependence), we are able to provide more detailed lipid/water data sets for future refined molecular dynamics simulations.
Author contributions
Conceptualization, data interpretation and revising drafts: GV, AS, AT and MR; data analysis and writing: GV and MR; carrying out experiments: GV.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors are grateful for the funding provided by the EPSRC Centre for Doctoral Training in Soft Matter for Formulation and Industrial Innovation (SOFI2; EP/S023631/1) in the form of a full scholarship for the PhD study of Gerome Vancuylenberg.References
-
M. Rappolt, in Advances in Planar Lipid Bilayers and Liposomes, ed. A. Leitmannova-Liu, Elsevier, Amsterdam, 2006, pp. 253–283 DOI:10.1016/s1554-4516(06)05009-5
.
- J. N. Israelachvili, S. Marcelja, R. G. Horn and J. N. Israelachvili, Q. Rev. Biophys., 1980, 13, 121–200 CrossRef CAS PubMed
.
-
S. Perutkova, M. Daniel, G. Dolinar, M. Rappolt, V. Kralj-Iglic and A. Iglic, in Advances in Planar Lipid Bilayers and Liposomes, ed. A. Leitmannova-Liu and H. T. Tien, Elsevier, Academic Press, Burlington, 2009, vol. 9, pp. 238–278 Search PubMed
.
-
E. Sackmann, in Structure and dynamics of membranes, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995, ch. 1, pp. 1–63 Search PubMed
.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev., 2006, 7, 9–19 CrossRef CAS PubMed
.
-
R. Lipowsky and E. Sackmann, Structure and dynamics of membranes. From cells to vesicles., Elsevier, Amsterdam, 1995 Search PubMed
.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS PubMed
.
-
M. Rappolt, P. Laggner and G. Pabst, in Recent Research Developments in Biophysics, ed. S. G. Pandalai, Transworld Research Network, Trivandrum, 2004, vol. 3, Part II, ch. 20, pp. 365–394 Search PubMed
.
- T. J. McIntosh, Biophys. J., 1980, 29, 237–245 CrossRef CAS PubMed
.
- J. M. Seddon, G. Cevc, R. D. Kaye and D. Marsh, Biochemistry, 1984, 23, 2634–2644 CrossRef CAS PubMed
.
- P. E. Harper, D. A. Mannock, R. N. Lewis, R. N. McElhaney and S. M. Gruner, Biophys. J., 2001, 81, 2693–2706 CrossRef CAS PubMed
.
- T. G. Pomorski, T. Nylander and M. Cárdenas, Adv. Colloid Interface Sci., 2014, 205, 207–220 CrossRef CAS PubMed
.
- D. Papahadjopoulos and N. Miller, Biochim. Biophys. Acta, Rev. Biomembr., 1967, 135, 624–638 CrossRef CAS PubMed
.
- A. Hodzic, P. Zoumpoulakis, G. Pabst, T. Mavromoustakos and M. Rappolt, Phys. Chem. Chem. Phys., 2012, 14, 4780–4788 RSC
.
- S. Aeffner, T. Reusch, B. Weinhausen and T. Salditt, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1609–E1618 CrossRef CAS PubMed
.
- P. Walde, K. Cosentino, H. Engel and P. Stano, ChemBioChem, 2010, 11, 848–865 CrossRef CAS PubMed
.
- C. Chen, S. Zhu, T. Huang, S. Wang and X. Yan, Anal. Methods, 2013, 5, 2150–2157 RSC
.
- F. Sciolla, D. Truzzolillo, E. Chauveau, S. Trabalzini, L. Di Marzio, M. Carafa, C. Marianecci, A. Sarra, F. Bordi and S. Sennato, Colloids Surf., B, 2021, 208, 112054 CrossRef CAS PubMed
.
- Z. Xu, J. M. Seddon, P. A. Beales, M. Rappolt and A. I. I. Tyler, J. Am. Chem. Soc., 2021, 143, 16556–16565 CrossRef CAS PubMed
.
- P. Schwille, J. Spatz, K. Landfester, E. Bodenschatz, S. Herminghaus, V. Sourjik, T. J. Erb, P. Bastiaens, R. Lipowsky, A. Hyman, P. Dabrock, J.-C. Baret, T. Vidakovic-Koch, P. Bieling, R. Dimova, H. Mutschler, T. Robinson, T. Y. D. Tang, S. Wegner and K. Sundmacher, Angew. Chem., Int. Ed., 2018, 57, 13382–13392 CrossRef CAS PubMed
.
- R. Seneviratne, G. Coates, Z. Xu, C. E. Cornell, R. F. Thompson, A. Sadeghpour, D. P. Maskell, L. J. C. Jeuken, M. Rappolt and P. A. Beales, Small, 2023, 2206267 CrossRef CAS PubMed
.
- V. Noireaux and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17669–17674 CrossRef CAS PubMed
.
- G. L. Jendrasiak, J. Nutr. Biochem., 1996, 7, 599–609 CrossRef CAS
.
- G. C. Shearman, O. Ces, R. H. Templer and J. M. Seddon, J. Phys.: Condens. Matter, 2006, 18, S1105–S1124 CrossRef CAS PubMed
.
-
S. Tristram-Nagle, in Membrane Hydration, ed. E. A. Disalvo, Springer, 2015, ch. 2, pp. 17–43 Search PubMed
.
- M. Rappolt, A. Hodzic, B. Sartori, M. Ollivon and P. Laggner, Chem. Phys. Lipids, 2008, 154, 46–55 CrossRef CAS PubMed
.
- M. Rappolt and G. Rapp, Ber. Bunsenges. Phys. Chem., 1996, 100, 1153–1162 CrossRef CAS
.
- C. F. Lopez, S. O. Nielsen, M. L. Klein and P. B. Moore, J. Phys. Chem. B, 2004, 108, 6603–6610 CrossRef CAS
.
- H. E. Alper, D. Bassolino-Klimas and T. R. Stouch, J. Chem. Phys., 1993, 99, 5547–5559 CrossRef CAS
.
- E. Lee, A. Kundu, J. Jeon and M. Cho, J. Chem. Phys., 2019, 151, 114705 CrossRef PubMed
.
- F. Martelli, H.-Y. Ko, C. C. Borallo and G. Franzese, Front. Phys., 2017, 13, 136801 CrossRef
.
- M. Pasenkiewicz-Gierula, Y. Takaoka, H. Miyagawa, K. Kitamura and A. Kusumi, J. Phys. Chem. A, 1997, 101, 3677–3691 CrossRef CAS
.
- T. J. McIntosh and S. A. Simon, Biochemistry, 1986, 25, 4948–4952 CrossRef CAS PubMed
.
- T. J. McIntosh, Chem. Phys. Lipids, 1996, 81, 117–131 CrossRef CAS PubMed
.
- S. Clarke, J. Chem. Educ., 1981, 58, A264 Search PubMed
.
- C. Tanford, Science, 1978, 200, 1012–1018 CrossRef CAS PubMed
.
- W. B. Dowhan, New Compr. Biochem., 2002, 36, 1–35 CAS
.
- V. Luzzati and F. Husson, J. Cell Biol., 1962, 12, 207–219 CrossRef CAS PubMed
.
-
V. A. Parsegian and R. P. Rand, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, North-Holland, 1995, vol. 1, pp. 643–690 Search PubMed
.
- P. Heftberger, B. Kollmitzer, F. A. Heberle, J. Pan, M. Rappolt, H. Amenitsch, N. Kučerka, J. Katsaras and G. Pabst, J. Appl. Crystallogr., 2014, 47, 173–180 CrossRef CAS PubMed
.
- G. Pabst, M. Rappolt, H. Amenitsch and P. Laggner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 4000–4009 CrossRef CAS PubMed
.
- M. C. Wiener, R. M. Suter and J. F. Nagle, Biophys. J., 1989, 55, 315–325 CrossRef CAS PubMed
.
- M. Rappolt, J. Appl. Phys., 2010, 107, 084701 CrossRef
.
- N. Y. D. Li, Š. Perutková, A. Iglič and M. Rappolt, Elektrotehniski Vestnik/Electrotechnical Review, 2017, 84, 69–75 Search PubMed
.
- G. Pabst, Biophys. Rev. Lett., 2006, 1, 57–84 CrossRef CAS
.
-
M. Rappolt, in Advances in Biomembranes and Lipid Self-Assembly, ed. A. Iglic, M. Rappolt and A. J. Garcia-Saez, Elsevier B.V., 2019, vol. 29, pp. 1–21 Search PubMed
.
- P. Heftberger, B. Kollmitzer, F. A. Heberle, J. J. Pan, M. Rappolt, H. Amenitsch, N. Kucerka, J. Katsaras and G. Pabst, J. Appl. Crystallogr., 2014, 47, 173–180 CrossRef CAS PubMed
.
- L. Salvati Manni, S. Assenza, M. Duss, J. J. Vallooran, F. Juranyi, S. Jurt, O. Zerbe, E. M. Landau and R. Mezzenga, Nat. Nanotechnol., 2019, 14, 609–615 CrossRef CAS PubMed
.
- M. P. K. Frewein, M. Doktorova, F. A. Heberle, H. L. Scott, E. F. Semeraro, L. Porcar and G. Pabst, Symmetry, 2021, 13, 1441 CrossRef CAS PubMed
.
- P. M. Kasson, E. Lindahl and V. S. Pande, J. Am. Chem. Soc., 2011, 133, 3812–3815 CrossRef CAS PubMed
.
- T. J. McIntosh and S. A. Simon, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 27–51 CrossRef CAS PubMed
.
- S. A. Simon and T. J. McIntosh, Methods Enzymol., 1986, 127, 511–521 CAS
.
- G. W. H. Wurpel and M. Müller, Chem. Phys. Lett., 2006, 425, 336–341 CrossRef CAS
.
- Z. Arsov, M. Rappolt and J. Grdadolnik, ChemPhysChem, 2009, 10, 1438–1441 CrossRef CAS PubMed
.
- R. Zhang, T. A. Cross, X. Peng and R. Fu, J. Am. Chem. Soc., 2022, 144, 7881–7888 CrossRef CAS PubMed
.
- J. D. Nickels, J. C. Smith and X. L. Cheng, Chem. Phys. Lipids, 2015, 192, 87–99 CrossRef CAS PubMed
.
- H. A. Pérez, L. M. Alarcón, A. R. Verde, G. A. Appignanesi, R. E. Giménez, E. A. Disalvo and M. A. Frías, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183489 CrossRef PubMed
.
- P. Heftberger, B. Kollmitzer, A. Rieder, H. Amenitsch and G. Pabst, Biophys. J., 2015, 108, 854–862 CrossRef CAS PubMed
.
- G. G. Putzel, M. J. Uline, I. Szleifer and M. Schick, Biophys. J., 2011, 100, 996–1004 CrossRef CAS PubMed
.
- T. J. McIntosh and S. A. Simon, Langmuir, 1996, 12, 1622–1630 CrossRef CAS
.
-
O. Kratky, H. Leopold and H. Stabinger, Methods in Enzymology, Academic Press, 1973, vol. 27, pp. 98–110 Search PubMed
.
- A. Hodzic, M. Rappolt, H. Amenitsch, P. Laggner and G. Pabst, Biophys. J., 2008, 94, 3935–3944 CrossRef CAS PubMed
.
- R. Koynova and H.-J. Hinz, Chem. Phys. Lipids, 1990, 54, 67–72 CrossRef CAS PubMed
.
- M. H. J. Koch, P. Vachette and D. I. Svergun, Q. Rev. Biophys., 2003, 36, 147–227 CrossRef CAS PubMed
.
- R. Zhang, S. Tristram-Nagle, W. Sun, R. L. Headrick, T. C. Irving, R. M. Suter and J. F. Nagle, Biophys. J., 1996, 70, 349–357 CrossRef CAS PubMed
.
- R. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 5047–5060 CrossRef CAS PubMed
.
- H. I. Petrache, S. Tristram-Nagle and J. F. Nagle, Chem. Phys. Lipids, 1998, 95, 83–94 CrossRef CAS PubMed
.
- J. Torbet and M. H. F. Wilkins, J. Theor. Biol., 1976, 62, 447–458 CrossRef CAS PubMed
.
- T. J. McIntosh and S. A. Simon, Biophys. J., 1986, 25, 4058–4066 CAS
.
- J. F. Nagle, R. Zhang, S. Tristram-Nagle, W. Sun, H. I. Petrache and R. M. Suter, Biophys. J., 1996, 70, 1419–1431 CrossRef CAS PubMed
.
- M. Gerstein and C. Chothia, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 10167–10172 CrossRef CAS PubMed
.
-
D. J. R. Silvius, Thermotropic Phase Transitions of Pure Lipids in Model Membranes and Their Modifications by Membrane Proteins, John Wiley & Sons, Inc., New York, 1982 Search PubMed
.
- M. Caffrey and J. Hogan, Chem. Phys. Lipids, 1992, 61, 1–109 CrossRef CAS PubMed
.
- M. Rappolt and G. Rapp, Ber. Bunsenges. Phys. Chem., 1996, 100, 1153–1162 CrossRef CAS
.
- S. H. White, R. E. Jacobs and G. I. King, Biophys. J., 1987, 52, 663–665 CrossRef CAS PubMed
.
- S. Tristram-Nagle, H. I. Petrache and J. F. Nagle, Biophys. J., 1998, 75, 917–925 CrossRef CAS PubMed
.
- J. F. Nagle and D. A. Wilkinson, Biophys. J., 1978, 23, 159–175 CrossRef CAS PubMed
.
- W. Pechhold, Kolloid Z. Z. Polym., 1968, 228, 1–38 CrossRef CAS
.
- A. Seelig and J. Seelig, Biochemistry, 1974, 13, 4839–4845 CrossRef CAS PubMed
.
- M. Ge and J. H. Freed, Biophys. J., 2003, 85, 4023–4040 CrossRef CAS PubMed
.
- R. P. Rand and V. A. Parsegian, Biochim. Biophys. Acta, 1989, 988, 351–376 CrossRef CAS
.
- W. Helfrich and R. M. Servuss, Il Nuovo Cimento D, 1984, 3, 137–151 CrossRef
.
-
M. Rappolt and G. Pabst, in Structure and dynamics of membranous interfaces, ed. K. Nag, John Wiley & Sons, Hoboken, 2008, ch. 3, pp. 45–81 Search PubMed
.
- N. Chu, N. Kucerka, Y. Liu, S. Tristram-Nagle and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 041904 CrossRef PubMed
.
- G. Pabst, J. Katsaras, V. A. Raghunathan and M. Rappolt, Langmuir, 2003, 19, 1716–1722 CrossRef CAS
.
- J. F. Nagle, Chem. Phys. Lipids, 2017, 205, 18–24 CrossRef CAS PubMed
.
- M. Mutz and W. Helfrich, J. Phys. France, 1990, 51, 991–1001 CrossRef CAS
.
- C.-P. Chng, Y. Sadovsky, K. J. Hsia and C. Huang, Extreme Mech. Lett., 2021, 43, 101174 CrossRef PubMed
.
- T. J. McIntosh, Curr. Opin. Struct. Biol., 2000, 10, 481–485 CrossRef CAS PubMed
.
- H. I. Petrache, N. Gouliaev, S. Tristram-Nagle, R. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7014–7024 CrossRef CAS
.
-
J. N. Israelachvili, in Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, Boston, 3rd edn, 2011, pp. 253–289 DOI:10.1016/B978-0-12-391927-4.10013-1
.
- E. Gongadze, L. Mesarec, V. Kralj-Iglič and A. Iglič, Mini-Rev. Med. Chem., 2018, 18, 1559–1566 CrossRef CAS PubMed
.
- E. Gongadze, A. Velikonja, Š. Perutkova, P. Kramar, A. Maček-Lebar, V. Kralj-Iglič and A. Iglič, Electrochim. Acta, 2014, 126, 42–60 CrossRef CAS
.
- N. Y. D. Li, D. J. Moore, M. A. Thompson, E. Welfare and M. Rappolt, Chem. Phys. Lipids, 2022, 243, 105165 CrossRef CAS PubMed
.
- T. J. McIntosh, A. D. Magid and S. A. Simon, Biophys. J., 1989, 55, 897–904 CrossRef CAS PubMed
.
- C. N. Blesso, Nutrients, 2015, 7, 2731–2747 CrossRef CAS PubMed
.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed
.
- M. Doktorova, M. V. LeVine, G. Khelashvili and H. Weinstein, Biophys. J., 2019, 116, 487–502 CrossRef CAS PubMed
.
- G. Pabst, H. Amenitsch, D. P. Kharakoz, P. Laggner and M. Rappolt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 9 CrossRef PubMed
.
- D. A. Wilkinson and J. F. Nagle, Biochemistry, 1981, 20, 187–192 CrossRef CAS PubMed
.
- N. Kucerka, M. A. Kiselev and P. Balgavy, Eur. Biophys. J., 2004, 33, 328–334 CrossRef CAS PubMed
.
- N. Kucerka, Y. Liu, N. Chu, H. I. Petrache, S. Tristram-Nagle and J. F. Nagle, Biophys. J., 2005, 88, 2626–2637 CrossRef CAS PubMed
.
- N. Kucerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef CAS PubMed
.
- N. Kucerka, S. Tristram-Nagle and J. F. Nagle, J. Membrane Biol., 2005, 208, 193–202 CrossRef CAS PubMed
.
- J. Seelig, H.-U. Gally and R. Wohlgemuth, Biochim. Biophys. Acta, Biomembr., 1977, 467, 109–119 CrossRef CAS PubMed
.
- T. M. Ferreira, F. Coreta-Gomes, O. H. Samuli Ollila, M. J. Moreno, W. L. C. Vaz and D. Topgaard, Phys. Chem. Chem. Phys., 2013, 15, 1976–1989 RSC
.
- A. M. Lebar, A. Velikonja, P. Kramar and A. Iglič, Bioelectrochemistry, 2016, 111, 49–56 CrossRef CAS PubMed
.
- K. Tu, D. J. Tobias, J. K. Blasie and M. L. Klein, Biophys. J., 1996, 70, 595–608 CrossRef CAS PubMed
.
- G. Herzberg, Am. J. Phys., 1951, 19, 390–391 CrossRef
.
-
I. Buck, J. H. Callomon, K. H. Hellwege, B. Starck, E. Hirota, A. M. Hellwege, K. Kuchitsu, W. J. Lafferty, A. G. Maki and C. S. Pote, Structure Data of Free Polyatomic Molecules/Strukturdaten freier mehratomiger Molekeln, Springer, Berlin Heidelberg, 1976 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00387f |
| This journal is © The Royal Society of Chemistry 2023 |