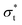Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A many-body dissipative particle dynamics parametrisation scheme to study behaviour at air–water interfaces†
Rachel L.
Hendrikse
 *,
Carlos
Amador
and
Mark R.
Wilson
*,
Carlos
Amador
and
Mark R.
Wilson

Department of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: rachel.hendrikse@durham.ac.uk
First published on 10th May 2023
Abstract
In this article, we present a general parametrisation scheme for many-body dissipative particle dynamics (MDPD). The scheme is based on matching model components to experimental surface tensions and chemical potentials. This allows us to obtain the correct surface and mixing behaviours of complex, multicomponent systems. The methodology is tested by modelling the behaviour of nonionic polyoxyethylene alkyl ether surfactants at an air/water interface. In particular, the influence of the number of ethylene oxide units in the surfactant head group is investigated. We find good agreement with many experimentally obtained parameters, such as minimum surface area per molecule; and a decrease in the surface tension with increasing surfactant surface density. Moreover, we observe an orientational transition, from surfactants lying directly on the water surface at low surface coverage, to surfactants lying parallel or tilted with respect to the surface normal at high surface coverage. The parametrisation scheme is also extended to cover the zwitterionic surfactant lauryldimethylamine oxide (LDAO), where we provide good predictions for the surface tension at maximum surface coverage. Here, if we exceed this coverage, we are able to demonstrate the spontaneous production of micelles from the surface surfactant layer.
1 Introduction
The mesoscopic simulation method of dissipative particle dynamics (DPD1) has found application in modelling systems where more computationally expensive methods struggle. In many soft matter systems, techniques such as molecular dynamics often have limited applicability due to the phenomena of interest occurring on time and length scales that are inaccessible using contemporary computers. Consequently, DPD has found uses in the study of block co-polymers,2–5 lipid bilayers,6–8 nanoparticles9 thermotropic3,10–15 and lyotropic liquid crystalline phases,14,16–24 which often involve large scale molecular organisation and slow dynamics. Molecules in DPD are coarse-grained, replacing multiple atomic sites with a single bead. This approach achieves computational efficiency via a reduction in the complexity of the system, and the use of a smooth, soft-repulsive force acting between beads.One of the main drawbacks of standard DPD is that it can not be used to simulate vapour–liquid co-existence. This is due to the repulsive nature of the interaction force between bead pairs, meaning that DPD can only be used to simulate fluid behaviour in confined spaces, and therefore cannot be used to study systems with free surfaces. In order to simulate vapour–liquid interfaces in standard DPD, researchers have often had to resort to the creation of fictitious ‘vapour beads’.25 To address this limitation, many-body dissipative particle dynamics (MDPD) was developed.26 MDPD is a variation of standard DPD, in which the conservative interaction force between beads is altered to allow for liquid and vapour formation in the same simulation box. This is achieved with the addition of an attractive term in the conservative force. Since its inception, MDPD has found application in areas of research such as droplets,27–29 flow over surfaces,30 bubbles,31 and liquid bridges.32
An additional drawback of the DPD method is that no standard parametrisation scheme exists for assigning the strength of interactions between different bead species (akin to the concept of a force field in molecular dynamics). A number of excellent DPD parametrisation schemes have been developed for various molecules,16,33–44 however, they are usually developed for application to a small selection of molecules (e.g. alkyl ethoxylate surfactants19,43,44), rather than attempting to be more general. A lack of a standard approach makes it difficult to assign off-the-shelf parameters so that DPD can be immediately applied to any particular real system. Furthermore, there is limited existing work developing models for MDPD use, although attempts have been made to connect the interaction parameters in MDPD to real systems.45
In this work, we develop a new MDPD parametrisation scheme, with a particular focus on predicting surface tensions. Moreover, while MDPD has been applied to a variety of research areas, there is limited existing literature using MDPD to study surfactants at an interface, which will be a key focus of this study. Our MDPD model is developed by a top-down coarse-graining scheme, matching to experimental surface tension values for simple systems, in order to find the correct interaction parameters between beads. We also make use of activity coefficients at infinite dilution, in order to find the correct interactions between different types of bead species. We then test this approach by applying it to complex systems containing a mixture of bead species. In particular, we apply our MDPD model to nonionic polyoxyethylene alkyl ether surfactants at an air/water interface. These surfactants are widely used in consumer products, such as laundry detergents and shampoos, and therefore their behaviour is of particular interest. The properties of polyoxyethylene alkyl ethers are strongly dependent on the number of ethylene oxide units in the molecule, and therefore we investigate the impact of varying the size of the head group in our simulations.
The behaviour of these surfactants at the interface has previously been extensively studied experimentally46–53 and using molecular dynamics simulations.54–57 However, MDPD provides a desirable approach to studying these systems and can provide valuable additional insights into what is often complex behaviour. For example, surfactants at an interface can be very difficult to study experimentally. There is often disagreement for surface coverage at the CMC, as determined using neutron reflection, compared with those obtained by surface tension isotherms58,59 (where the surface tension is related to the surface excess by the Gibbs equation). Reasons for these discrepancies are often attributed to the fact that, in order to use the surface tension method, a number of assumptions have to be made about the composition of the surface layer. This is often difficult due to the presence of impurities.59 Molecular dynamics simulations are also typically conducted with a relatively small interfacial area, and can lead to incorrect surface tension calculations depending on the force field used.55
In this article, we begin by outlining the many-body dissipative particle dynamics method, before explaining our approach for creating a new MDPD parametrisation. We investigate the performance of the model by applying it to a variety of simple systems. Following this, we test the parametrisation scheme by studying the effect that the number of ethylene oxide units in polyoxyethylene alkyl ether surfactants has on surfactants at an air/water interface. Finally, we also test a second surfactant, to highlight the transferability of the parametrisation to different types of molecules.
2 Many-body dissipative particle dynamics
In standard DPD, the motion of non-bonded beads is described by a combination of three forces: the conservative force, FCij, dissipative force, FDij and random force, FRij. The conservative force takes the form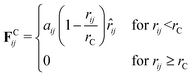 | (1) |
The remaining two non-bonding forces are a pairwise friction-based dissipative (or drag) force FDij and a random pairwise force FRij which, when coupled together, act as the simulation thermostat and maintain hydrodynamics. The dissipative force FDij and random force FRij are given by
FDij = −γωD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (2) |
FRij = σωR(rij)ζij![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ijΔt−1/2, ijΔt−1/2, | (3) |
| ωD = [ωR]2 | (4) |
| σ2 = 2γkBT, | (5) |
Bonding forces are calculated from potentials UBij and UAij. UBij chemically bonds beads to form long chain molecules, while UAij introduces rigidity within the chain or between the beads. These potentials take the harmonic form
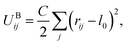 | (6) |
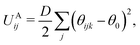 | (7) |
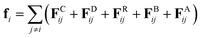 | (8) |
MDPD uses the same random, dissipative, and bonding forces as the standard DPD method. The difference between DPD and MDPD comes in the form of the conservative force, which is modified to include a density-dependent component. The new conservative force takes the form
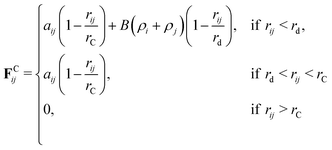 | (9) |
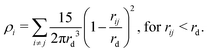 | (10) |
For MDPD, the cutoff rC is usually taken as rC = 1 and the many-body cutoff rd is taken as 0.75.27 The conservative force parameter aij takes a negative value, acting as an inter-particle attraction. The B parameter takes a value 0 < B, meaning that the density dependent part of the conservative force is repulsive. The attractive pairwise term and repulsive many-body term together create a potential that has both attractive and repulsive regions, which can reproduce a van der Waals loop. Hence, MDPD has the capacity to simulate vapour liquid interfaces.27 The no-go theorem61 imposes global B and rd parameters for all particle types, and therefore, in this work, we chose to take the common choices of B = 25 and rd = 0.75.27,62,63 Tuning the aij parameter has an impact on both the surface tension and the mixing energies of each particle. Therefore in order to develop our parametrisation scheme, we first need to obtain relationships between aij, the chemical potential and the surface tension. All simulations described are performed using the DL_MESO software package.64
3 Calculating aij: a parametrisation scheme
For a system which consists of S different bead species, this requires the calculation of S self-interaction values for the aii parameter, and S(S − 1)/2 cross interaction values aij. We approach the calculation of the self-interaction and cross-interaction values differently, as discussed in this section.3.1 Self-interactions
The aii self-interaction parameters are calculated by finding the aii value which reproduces (in MDPD) the experimentally known surface tension for a particular fluid. We wish to create a general approach, such that we have a method of finding an aii value for any possible liquid we may wish to model, provided we have the experimental surface tension. We aim to model water such that 1 bead represents three water molecules, and that long chain molecules are modelled as a series of bonded beads. In this work we focus on molecules which can be represented as a linear chain of beads (i.e. with no branching).In order to find a general relationship between aii and the surface tension, we perform a parameter sweep in the range 25 ≤ aii ≤ 52, with an interval of Δaii = 3. These simulations are conducted in a box with dimensions 10rC × 10rC × 100rC using n = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads, which are initialised with a random initial configuration. We also investigate the influence of bonding on pure systems, by bonding N beads together in a linear chain (N − 1 bonds per chain). We vary N in the range 1 ≤ N ≤ 8, keeping the overall total number of beads n approximately constant. Simulations are performed in the NVT (constant volume and temperature) ensemble, the time step used is Δt = 0.01, and the mass of all beads m = 1.
000 simulation beads, which are initialised with a random initial configuration. We also investigate the influence of bonding on pure systems, by bonding N beads together in a linear chain (N − 1 bonds per chain). We vary N in the range 1 ≤ N ≤ 8, keeping the overall total number of beads n approximately constant. Simulations are performed in the NVT (constant volume and temperature) ensemble, the time step used is Δt = 0.01, and the mass of all beads m = 1.
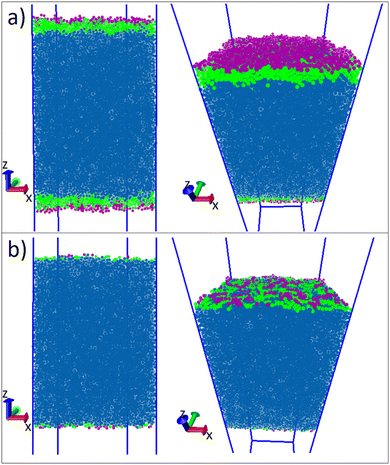
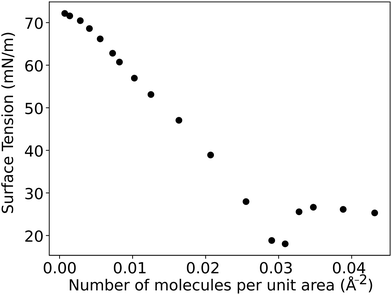
After running the simulation from an initially random placement of molecules, all simulated cases with different aii values eventually form separated regions of liquid and vapour in the simulation box, allowing surface tension to be calculated. An example of the formation of liquid–vapour coexistence from an initial configuration is shown in Fig. 1, where the interface forms in the x–y plane (note that throughout this work we use VMD65 software for creating visualisations). We run these simulations for I = 1.5 × 106 time-steps and, on average, the beads separate into a bulk fluid and vapour after I ≈ 1 × 105, at which point we begin collecting data for calculating the surface tension. The surface tension γ can be calculated using the following definition66–68
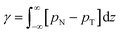 | (11) |
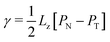 | (12) |
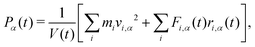 | (13) |
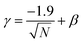 | (14) |
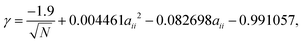 | (15) |
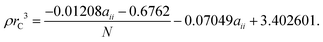 | (16) |
Traditionally, conversion from DPD units into real units is performed by matching the DPD mass density, to the room temperature experimentally known value, thereby defining a value of the length scale rC in real units. Therefore, it is difficult to match both the surface tension and the mass density of every particle species in the system, to those known from experiment. However, for surfactant systems, water is the universally most important solvent, and we, therefore, chose to experimentally match to both the surface tension and density for water at room temperature, in order to obtain a value for rC. Using a value of 72.0 mN m−1 for the surface tension of water at room temperature, kBT = 4.11 × 10−21 J, N = 1, and a coarse graining of 3 water molecules per bead (mass of bead m = 54 g mol−1), allows us to solve eqn (15) and (16) to obtain values rC = 8.53 Å and aWW = −50.683. For all other bead types, we continue to use rC = 8.53 Å for the purpose of converting into real units, and instead obtain values of aii for other bead types by using eqn (15) only.
3.2 Cross interactions
A different approach is required to find values for the mixing interaction parameters of aij when i ≠ j, since it is unlikely that we will always have an experimental surface tension for a mixture of every bead pairing required. In order to find aij we calculate activity coefficients at infinite dilution (γ∞). We calculate ln(γ∞A) using the relation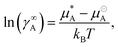 | (17) |
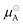 is the chemical potential of pure component A, and
is the chemical potential of pure component A, and 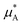 is the chemical potential of A in the mixture at infinite dilution (where the units of chemical potential μ are energy per particle).
is the chemical potential of A in the mixture at infinite dilution (where the units of chemical potential μ are energy per particle).
For computational purposes, the chemical potential of component A in a mixture can be represented using the sum
| μA = μexcessA + μidealA | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρAΛ3 where Λ is the thermal de Broglie wavelength and ρ is the density. The excess potential energy μexcess is calculated via the Widom insertion method as
ρAΛ3 where Λ is the thermal de Broglie wavelength and ρ is the density. The excess potential energy μexcess is calculated via the Widom insertion method as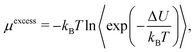 | (19) |
ln(γ∞A) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈exp(−ΔUAA)〉 − ln 〈exp(−ΔUAA)〉 − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈exp(−ΔUAB) 〉 + lnρB/ρA 〈exp(−ΔUAB) 〉 + lnρB/ρA | (20) |
In order to calculate ln(γ∞A) as a function of aAA, aBB and aAB, we perform a parameter sweep in the range 25 ≤ aij ≤ 52 for all three interaction parameters. In contrast to the previous simulations for calculating aii, these simulations are performed using the NPT ensemble in a cubic simulation box. For these simulations, there is no interface and the domain is entirely bulk fluid. Performing NPT simulations allows us to simulate bulk fluid at the correct density for different interaction parameter values. The simulation box is initialised with dimensions 10rC × 10rC × 10rC using n = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads. We equilibrate for I = 1.5 × 106 time-steps using a time step of Δt = 0.001. The domain equilibrates extremely rapidly (I < 3000) to a constant average density before Widom insertions are performed.
000 simulation beads. We equilibrate for I = 1.5 × 106 time-steps using a time step of Δt = 0.001. The domain equilibrates extremely rapidly (I < 3000) to a constant average density before Widom insertions are performed.
Following density equilibration, Widom insertion allows us to determine that ln(γ∞A), as a function of the interaction parameters, can be represented by an equation of the form
| ln(γ∞A) = x1aBB2 + x2aAB2 + x3aBBaAB + x4aBB + x5aAA + x6aAB + x7, | (21) |
3.3 a ij parameters for C12Ej surfactants
Since we aim to be able to apply the parametrisation to predict properties of C12Ej surfactants at an air/water interface, in this section we calculate the required aij parameters for these molecules. Polyoxyethylene alkyl ethers H(CH2)i(OCH2CH2)jOH (often abbreviated as CiEj) are extremely common nonionic surfactants. We coarse grain the surfactant tail such that one alkyl bead (C3) represents three carbon atoms and one head bead (EO) represents a single ethylene oxide unit [OCH2CH2]. The final tail bead of an alkyl chain (C3T) is slightly different to the C3 beads, as it also includes an additional hydrogen atom. Likewise, the end bead (EOT) of the ethylene glycol portion is treated differently, in order to represent the [OCH2CH2OH] unit which terminates the molecule. This coarse graining procedure is shown in Fig. 2.We coarse-grain water beads (W) such that one bead represents three water molecules.
Assuming that the C–C–C angles are tetrahedral (approximately 109.5°) and that the C–C experimental bond is 1.543 Å,69 the separation between three carbon atoms in the alkyl chain (or two adjacent beads) is expected to be around 3.8 Å. The choice of bond length l0 = 0.5 (see Section 2) results in a [CH2CH2CH2]–[CH2CH2CH2] bead separation of l0 = 4.27 Å, which is close to the experimental value. The bond length l0 = 0.5 is also used between beads in the polyethylene glycol portion of the surfactant. Experimentally the distance between successive ethylene oxide units is expected to be around 3.7 Å,70 making this a suitable choice. We note that we also investigated the effect of varying l0 on eqn (15), finding that the bond length actually has very little impact on the surface tension (see ESI† Section S5 for more information).
The values for the activity coefficients at infinite dilution are calculated via COSMO-RS71–73 calculations, and the values are presented in Table 1. COSMO-RS uses quantum chemical calculations in order to model the distribution of charge on molecules, and when combined with statistical thermodynamics can be used to calculate the activity coefficient of a component.74 Once the self-interaction values for each bead species have been determined, the values in Table 1 and eqn (21) are used to determine cross interaction values.
| i↓ / j→ | W | C3 | EO | EOT |
|---|---|---|---|---|
| C3 | 5.0552 | |||
| EO | 0.92710 | 0.46013 | ||
| EOT | −0.34998 | 3.0875 | 0.23774 | |
| C3T | 6.2982 | 0.00040 | 0.46680 | 1.4172 |
In order to find the self-interaction for the EOT bead, aEOT,EOT, we match to the experimental surface tension γ = 45.65 mN m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 for diethylene glycol (note that all experimental surface tensions are taken at room temperature which we define as 25 °C). We approximate the coarse-grained representation of diethylene glycol as two bonded EOT beads (N = 2), using eqn (14) and (15) to determine aEOT,EOT = −39.951.
75 for diethylene glycol (note that all experimental surface tensions are taken at room temperature which we define as 25 °C). We approximate the coarse-grained representation of diethylene glycol as two bonded EOT beads (N = 2), using eqn (14) and (15) to determine aEOT,EOT = −39.951.
For the tail beads, we match to experimental surface tension γ = 25.3 mN m−1 for dodecane,76–78 using four beads (N = 4) to represent this molecule in the coarse-grained representation. We choose to set the self-interactions between all tail beads to be equivalent (i.e. aC3,C3 = aC3T,C3T = aC3,C3T) for ease of matching to experimental surface tension data. Therefore, we determine a self-interaction aC3,C3 = −29.796.
For single ethylene oxide beads, we chose to match to the surface tension of tetraethylene glycol γ = 45.13 mN m−1,79 represented as EOT-EO-EO-EOT. This molecule is more complex than eqn (14) allows for, since the initial parametrisation was developed for bonding between only like bead types. This was applicable for the alkyl chain, as we do not expect there to be a significant difference in the strength of the interaction between the C3 and C3T beads (note that this is supported by the fact that the activity coefficient at infinite dilution of C3T in C3 is found to be nearly zero ln(γ∞A) = 0.0004, indicating that these beads can be treated as equivalent). However, it is expected that there is a great deal of difference between EOT and EO beads. We expect that the hydroxyl groups (OH) play a large part in influencing the surface tension, as interactions between these groups display strong hydrogen bonding. This is highlighted by the relatively large surface tension of ethylene glycol (γ ≈ 48 mN m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75), relative to longer polyethylene glycols.
75), relative to longer polyethylene glycols.
Therefore in order to calculate a value for aEO,EO using experimental data for tetraethylene glycol, we extend the parametrisation to be able to represent molecules bonded with more than one bead type. We perform an additional parameter sweep to represent molecules of form D–(C)l–D where the number l of middle beads C is varied. We perform the parameter sweep for variables aCC, aDD and aCD in the range 28 ≤ aij ≤ 44. The simulations are conducted in the same way as previously described in Section 3.1. When 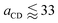 the molecules are observed to crystallise into neat periodic layers, and so these cases are excluded from our general formula fitting, and we fit to simulation cases with 34 ≤ aCD only.
the molecules are observed to crystallise into neat periodic layers, and so these cases are excluded from our general formula fitting, and we fit to simulation cases with 34 ≤ aCD only.
We determine that the surface tension can be fit using an equation of the form
| γ = (MaCC+ (m1N + c1)aCD+ (m2N + c2))aDD + (m3N + c3)aCC+ (m4N + c4)aCD+ (m5N + c5) | (22) |
| Variable | Fitted value |
|---|---|
| M | 5 × 10−3 |
| m 1 | −1.192 × 10−3 |
| c 1 | 1.739 × 10−3 |
| m 2 | 1.748 × 10−2 |
| c 2 | −6.234 × 10−2 |
| m 3 | 3.510 × 10−2 |
| c 3 | − 1.785 × 10−1 |
| m 4 | 3.676 × 10−2 |
| c 4 | 1.750 × 10−1 |
| m 5 | −1.547 |
| c 5 | 1.295 × 10−1 |
Using a combination of eqn (21) and (22), along with the experimental surface tension for tetraethylene glycol and the value of the activity coefficient at infinite dilution in Table 1, allows us to find values aEO,EO = −37.182 and aEO,EOT = −38.847. A table of the final calculated aij parameters for every bead pair is given in Table 3. Note that for each bead pair we must choose one bead to be the solute (particle A in eqn (21)) and one to be the solvent (particle B in eqn (21)) when calculating the cross interaction. We generally choose to define the solvent as the bead which is more abundant (when compared with the abundance of the other bead) in each bead pairing. For example, for aEO,EOT the EOT bead is selected as the solute and EO bead is the solvent. However, since we are varying the number of ethylene oxide groups in the hydrocarbon chain, the relative abundance of head to tail beads varies for our different simulations in this study. For consistency, we chose to use the head groups as the solute and tail beads as the solvent when calculating the aEO,C3 and aEOT,C3T interactions, therefore using the same interaction parameters across all CiEj surfactants.
| a ij | W | C3 | C3T | EO | EOT |
|---|---|---|---|---|---|
| W | −50.683 | −34.686 | −33.578 | −42.134 | −44.654 |
| C3 | — | −29.796 | −29.796 | −34.344 | −33.170 |
| C3T | — | — | −29.796 | −32.360 | −32.644 |
| EO | — | — | — | −37.182 | −38.847 |
| EOT | — | — | — | — | −39.951 |
4 Simulation set-up
Before performing simulations of C12Ej surfactants at an interface, we test the parameters in Table 3 on simpler cases, such as the surface tension of pure fluids or binary mixtures. These simulations are conducted in a box with dimensions 22rC × 22rC × 100rC using n = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads. We note that despite the fact that this surface area is larger than that used to generate eqn (15), the surface tension calculated is independent of the size of the interface (see ESI† Section S4 for details). This is consistent with what is concluded by other researchers.80
000 simulation beads. We note that despite the fact that this surface area is larger than that used to generate eqn (15), the surface tension calculated is independent of the size of the interface (see ESI† Section S4 for details). This is consistent with what is concluded by other researchers.80
The simulations are initialised in a similar way to that described in Section 3.1, that is with a random initial configuration. Molecules form coexisting bulk and vapour phases with two interfaces after around I ≈ 1.5 × 105 time-steps, and in total we run I ≈ 1 × 106 time-steps for collecting data. An exception to this box size is for when we perform a single simulation of a mixture of dodecane and water, which is expected to exhibit phase separation. In this case, we shorten the length of the simulation box and, we use dimensions 22rC × 22rC × 34.03rC using nW = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 12500 dodecane molecules (n = 100
000 and 12500 dodecane molecules (n = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads in total). This box size is chosen such that the water and dodecane fill the simulation box to avoid the formation of dodecane/gas interfaces.
000 simulation beads in total). This box size is chosen such that the water and dodecane fill the simulation box to avoid the formation of dodecane/gas interfaces.
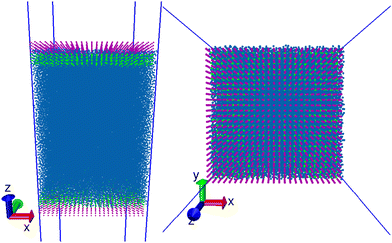
For simulations of surfactants at an air–water interface, surfactants are placed at a pre-equilibrated air/water interface, where the bulk water is generated in the same way as previously described for pure systems (dimensions 22rC × 22rC × 100rC using n = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation beads). Following the generation of the interface, the surfactants are arranged at both surfaces in a grid-like configuration, as shown in Fig. 3.
000 simulation beads). Following the generation of the interface, the surfactants are arranged at both surfaces in a grid-like configuration, as shown in Fig. 3.
The initial configuration places the head groups partially submerged in bulk water, while the tails protrude outwards into the vapour phase, perpendicular to the surface of the water. We then run the simulation for I = 1.5 × 106 time steps, collecting stress tensor values every time step in order to calculate the surface tension. We collect positional data every 1000 time steps, which is used to calculate various properties such as the density profile and orientation of molecules relative to the surface.
5 Complex molecules and binary mixtures
First, the surface tension is calculated for a variety of molecules as pure systems (i.e. single component molecule fluids), in order to confirm that complex molecules can be simulated. Table 4 shows calculated surface tension values for dodecane (C12), tetraethylene glycol (E4) and three polyoxyethylene alkyl ether surfactants, alongside a comparison with experimental values. Overall, we observe good agreement with the available experimental data.Additionally, the parametrisation scheme is also tested on its ability to predict the surface tension of aqueous mixtures of polyethylene glycol. The behaviour of these mixtures is of importance to confirm since the ethylene oxide head group in CiEj surfactants is weakly hydrophilic. Therefore, it can be difficult to predict the correct interaction parameters for these bead types. Here, simulations are set up and initialised in the same manner as the pure simulation case. Fig. 4 shows the surface tension calculated for aqueous mixtures of diethylene glycol, triethylene glycol, and tetraethylene glycol. The surface tensions predicted show very good agreement for triethylene glycol with the experimental data across the composition range and reasonably good agreement for the other two compounds, indicating the correct interaction between ethylene glycol beads and water. The predicted surface tension is most accurate at high and low concentrations, with the mid-range of concentrations showing the most deviation from the experimental measurements. This is to be expected due to the approach of the parametrisation, where self-interactions dominate at high and low concentrations. Additionally, our cross-interactions are calculated using beads at infinite dilution. Therefore, these values may not be fully applicable in the mid-concentration range, and are expected to perform best at lower concentrations. Theoretically, this means that the bulk concentration (the middle of the fluid region) may be different to the overall concentration which is plotted in Fig. 4. However, we find that the thickness of the layer of excess polyethylene glycol molecules near the surface is extremely thin, and therefore the bulk concentration is fairly comparable to the overall concentration. Similarly, in experimental measurements, the surface tension is reported in relation to the bulk concentration because the fraction of surfactant/solute molecules at the interface is minuscule compared to the number of molecules in solution. The accumulation of molecules near the interface also implies that the MDPD surface tension results may be different when the bulk region is extended in the z direction. Therefore, we investigated the impact of box length. Once again, as the excess layer is so thin, we find that there is minimal impact on the results (see ESI† Section S6 for more information).
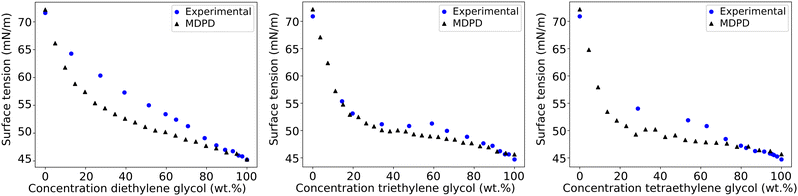 | ||
| Fig. 4 The surface tension calculated using MDPD for diethylene glycol, triethylene glycol, and tetraethylene glycol aqueous solutions. Calculated values are compared with experimental data.81,82 | ||
We find that there is a slight preference for solute molecules to gather near the surface, particularly at lower concentrations. An example of this for diethylene glycol is shown in Fig. 5.
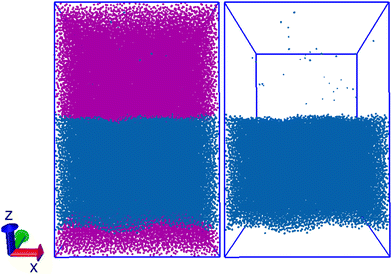
Finally, we also test a mixture of dodecane and water. Fig. 6 shows the expected phase separation which results. We observe there are a small number of water beads in the dodecane bulk, while no dodecane beads reside in the water bulk. This is to be expected given that, while the solubility of each species in the other is very low, the solubility of water in dodecane (65 ppm83) is significantly larger than that of dodecane in water (3.7 ppb84). We find a ratio of ≈1 water bead for every 930 dodecane beads in the dodecane region, resulting in a mass ratio of ≈0.0014 g water per g dodecane, meaning that the concentration of water in dodecane in simulation is somewhat larger than that of experiment (≈20 times larger than experiment). The cross interactions between water and alkane beads are calculated by performing insertions using single C3 beads. We believe that the discrepancy between simulated and experimental solubility may be, in part, due to the fact that we use single (rather than bonded) beads in the parametrisation method. This is supported by the values we calculate for the solubility of water in other alkanes. We performed additional simulations, similar to the one described here for dodecane and water, for nonane and hexane. For reference, the experimental values of water solubility are 79 ppm83 and 94 ppm85 in nonane and hexane respectively. We calculate the water solubility to be 0.00093 (≈12 times larger than experiment) in nonane and 0.00070 (≈7 times larger) in hexane. This shows that increasing the length of the molecule widens the gap between the simulated and experimental results. Therefore, it may be possible to improve the calculated solubility by basing the aij values off the activity coefficients for longer molecules, e.g. dodecane.
6 Application to polyoxyethylene alkyl ethers (C12Ej)
In this section, the parametrisation is tested on C12Ej surfactants at the air/water interface for different surfactants with varying j.6.1 Density profiles
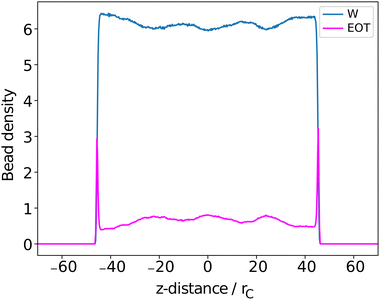
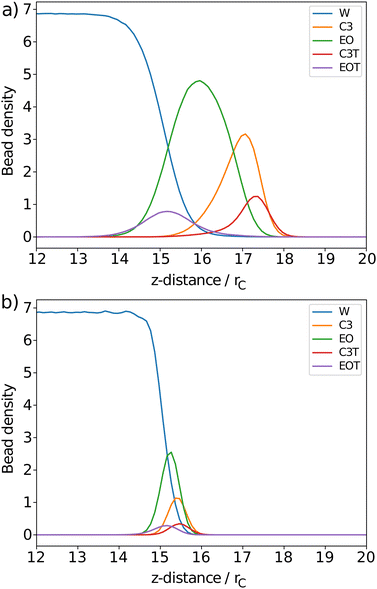
The surfactant behaviour at the interface is shown for two different surface area coverages in Fig. 7. We observed that when the interface has a low density of surfactants (high surface area per surfactant), the surfactant tails tend to remain in contact with the surface of the water. When the number of surfactants at the surface is increased (low surface area per surfactant) the alkyl tails re-orientate such that they are directed towards the gas phase, perpendicular to the liquid–gas interface. This is reflected in the density profiles as shown in Fig. 8,where there is a much greater overlap of the head and tail profiles when the surface coverage is low. When the surface density is increased we also see an enhanced separation between the water and surfactant profiles (particularly for tails). This orientational behaviour at different surface densities is consistent with that observed in similar molecular dynamics studies.55 In all cases, the profiles for tail groups overlap to some extent with those of the head groups. This implies that there is no complete segregation between surfactant head and tails, as is often assumed in theoretical models.86 Theoretical models typically require some knowledge of the behaviour (and thickness) of the adsorption layer, and incorrect assumptions in models can lead to differences between theoretical predictions and experimental results.
6.2 Surface tension
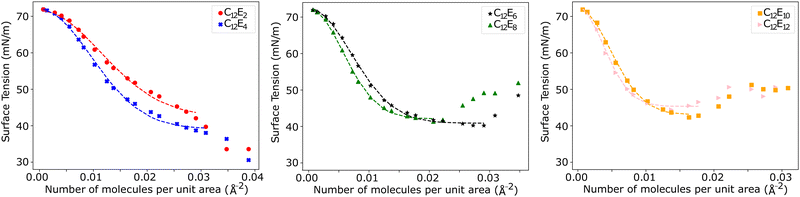
The surface tension is calculated using eqn (12) and plotted as a function of surface coverage for various surfactants in Fig. 9. We observe a smooth decrease in the surface tension with increasing surface coverage. As the number of surfactants at the surface increases, we expect to reach a point where maximum packing is exceeded. The surface tension decreases until the surface reaches what we conclude to be its maximum packing. When the number of ethylene oxide units in the surfactant molecule is large (6 ≥ j), we find that there is a plateau in the surface tension, and after this plateau, the surface tension begins to increase with increasing surfactant surface density. In contrast, at lower numbers of ethylene oxide units (j = 2 and j = 4), when we attempt to initialise simulations with surface densities greater than a maximum density cutoff point (<0.0388 mol Å−2) the simulations become unstable and the surface breaks apart. In these cases, no plateau is observed.Generally, as the number of ethylene oxide units increases, the surface area at maximum packing also decreases, which is experimentally the expected behaviour. However, the overall surface tension drop caused by the surfactants at the interface is lower than that calculated via experiment. The lowest surface tension found for a variety of surfactants is compared with experiment in Table 5. For surfactants with j = 2 and j = 4 we present in the table the surface tension calculated at surface density 0.0388 mol Å−2, however, it is important to note that this is not necessarily comparable with surfactants with 4 < j since there is evidence that the surface is unstable at this high packing.
In principle, for large enough simulations, the critical micelle concentration could be established from the levelling of the surface tension results. However, due to the relatively small amount of bulk water, this isn't a practical approach to determining the CMC. The CMC calculated would differ greatly from that of an experimentally determined value, as in our simulations the surface layer-to-bulk ratio is much larger than that of an experimental vessel. It can be calculated using the results shown in Fig. 9, that this would result in a CMC value which considerably exceeds the reported values for C12Ej surfactants.94 Furthermore, even a single molecule in the bulk water would have a concentration of ≈0.009 wt%, exceeding the expected CMC value of around 0.006 wt%.
6.3 Surfactant layer thickness
Due to the spread of partial density profiles, it is nontrivial to define a layer boundary (and thickness) of the surfactant layer at the surface. However, in order to best compare with existing experimental data,48,52 we obtain the layer thickness by fitting a Gaussian distribution to the density profiles. This profile takes the formn(z) = ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−4(z − ζ)2/σ2) exp(−4(z − ζ)2/σ2) | (23) |
In each simulation, a value is calculated for the thickness of the ethylene oxide group (σh), the alkyl chain (σt), and the overall thickness (σs). This is plotted as a function of surface coverage in Fig. 10 (plotted up to the maximum surface coverage achieved before the surface tension begins to increase). It is shown that the thickness of each component increases largely linearly with the number of molecules at the surface. The thickness of the alkyl chain sublayer is relatively consistent between different C12Ej surfactants, which is to be expected since the tail length is constant for all surfactants. The thickness of the head group portion increases with additional head group beads, this then influences the overall thickness of the surfactant layer.
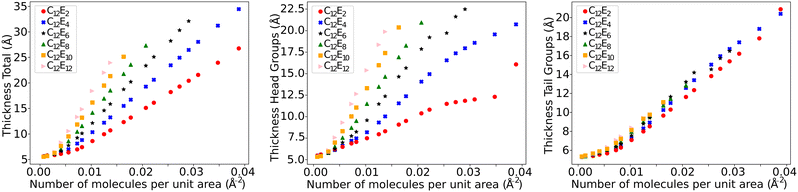 | ||
| Fig. 10 The thickness of the total surfactant layer, as well as the thickness of the head and tail groups individually. | ||
It is of note that, as a result of the overlap of the head and tail profiles demonstrated in Fig. 8, the total thickness is less than the sum of the head and tail thicknesses. Table 6 compares a selection of calculated layer thicknesses with experimental values, showing good agreement between simulation and experiment. The roughness correction provided to the experimental data originates from the fact that the experimentally measured thickness is contributed to by both the intrinsic thickness of the surfactant monolayer (in the direction normal to the surface) and a surface roughness. The surface roughness is thought to primarily originate from capillary waves; thus, the contribution level can be estimated from the surface tension. Therefore, the removal of this roughness contribution allows one to more accurately determine the actual thickness of the layer. This is discussed in more detail in Lu et al.48
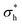 and
and 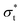 , which are expected to be closer to a realistic value for the thickness. Simulation thicknesses are obtained at surface coverage values: 32.3 Å2 (C12E2), 45.0 Å2 (C12E4), and 72.8 Å2 (C12E12)
, which are expected to be closer to a realistic value for the thickness. Simulation thicknesses are obtained at surface coverage values: 32.3 Å2 (C12E2), 45.0 Å2 (C12E4), and 72.8 Å2 (C12E12)
6.4 Surface coverage
Fig. 9 highlights the differences in the equilibrium surface coverage between the different surfactants tested. We chose to estimate our minimum area per molecule for j > 4 surfactants as the minimum area per molecule before surface tension begins to increase. The calculated values, along with comparable experimental values, are presented in Table 7. The minimum surface area per surfactant increases as the number of ethylene oxide units increases, in agreement with experimental trends.For surfactants with j ≤ 4, the surface becomes unstable at high surfactant density, although in these cases we observe that the surface can be overloaded more easily. At high density, the surface tension continues to decrease, however the surface becomes heavily distorted so that it can no longer be considered a planar interface. Instead, the surface can become extremely convexed, such that the effective surface area of the surfactant layer is increased. This causes the surface tension to appear to be artificially low, due to the increase in area. Furthermore, eqn (12) assumes that the interface is planar to the z-axis, and therefore isn't valid for calculating the surface tension in these cases. Experimentally, we expect the surface to have a surface area per molecule of around 33 Å2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 44 Å2 for C12E2 and C12E4 surfactants respectively.52 These experimental values are in reasonable agreement with the surface coverage value when the smooth relationship between surface tension and surface coverage begins to break down in Fig. 9. We also observe that the surface becomes unstable at this point from the thickness of the head group layer shown in Fig. 10.
and 44 Å2 for C12E2 and C12E4 surfactants respectively.52 These experimental values are in reasonable agreement with the surface coverage value when the smooth relationship between surface tension and surface coverage begins to break down in Fig. 9. We also observe that the surface becomes unstable at this point from the thickness of the head group layer shown in Fig. 10.
6.5 Tilt angle
In order to analyse the orientation of surfactant molecules at the interface, we calculate the average director vector of the surfactant head and tail components, relative to the surface normal (z-direction). The head vector (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) h) is defined as the vector which connects the hydroxyl group (EOT) and the EO atom that is connected to the alkyl tail. Similarly, the tail vector (
h) is defined as the vector which connects the hydroxyl group (EOT) and the EO atom that is connected to the alkyl tail. Similarly, the tail vector (![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) t) is defined as that connecting the first carbon bead (C3) and the final bead in the alkyl tail (C3T). We observe that the tilt angle rotates from its initial configuration (where θh = θt = 0), and therefore we begin collecting data for this calculation after I = 5 × 105 time-steps when the tilt angle has been observed to reach a stable value.
t) is defined as that connecting the first carbon bead (C3) and the final bead in the alkyl tail (C3T). We observe that the tilt angle rotates from its initial configuration (where θh = θt = 0), and therefore we begin collecting data for this calculation after I = 5 × 105 time-steps when the tilt angle has been observed to reach a stable value.
Fig. 11 shows the angle between the average vector and the surface normal, where generally θh and θt decrease as the number of surfactants at the interface increases. This is expected from the observed behaviour (discussed in Section 6.1), where, at low surface densities surfactants lay directly on the water surface. It is interesting to note that the tail angle θt is almost always larger than the head group angle θh, indicating that the surfactant heads are more perpendicular to the interface than the tails are. This somewhat counter-intuitive observation has also been reported in MD studies.55 For surfactants C12E2 and C12E4, the surfactant molecules become almost perfectly perpendicular to the surface at high surface density. However, for other surfactants, the tilt angle generally decreases to a minimum, before increasing again with greater surfactant density.
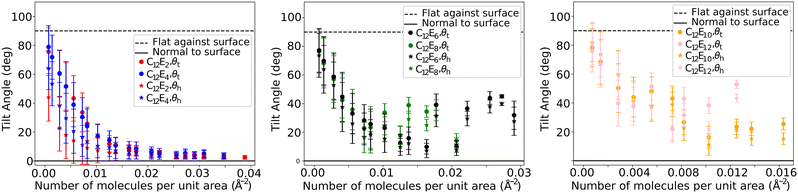 | ||
| Fig. 11 The tilt angle of the head θh and tail θt groups (relative to the surface) of various C12Ej surfactants at different surface coverages. | ||
Experimentally, the tilt angle can be difficult to accurately determine, particularly at low surface coverages. However, at the CMC surface coverage, the alkyl chain tilt angle for C12E12 is reported to be around θt = 45°,48 which is in agreement with the plateau at higher surface coverages for C12E12 in this study. The plateau to larger tilt angles that we find are also consistent with MD studies, where values of θh = 56.8° and θt = 54° for C12E6 surfactants are reported at CMC packing.54
7 Application to other surfactants
One might expect that when the expected maximum packing at the surface is exceeded, molecules are removed from the surface into the bulk. This would increase the minimum area per surfactant and stabilise the surface. The formation of micelles within the bulk should also be expected from the ratio of surfactant molecules to water molecules in the simulation box. For example the expected CMC for C12E8 is around 0.08 mM,94 corresponding to around 10 surfactant molecules in our simulations. While this phenomenon is not observed for C12Ej at the air/water interface, we observe this behaviour when different molecules are tested with other head groups. This surface removal is followed by the formation of micelles in the bulk water. We theorise that the lack of surfactant removal from the surface for C12Ej surfactants is related to the (relatively) weak hydrophilicity of the ethylene oxide head group.Consider zwitterionic surfactant lauryldimethylamine oxide (LDAO), an amine oxide based surfactant with a dodecyl alkyl tail. This molecule is coarse grained as shown in Fig. 12, where the [C2H6NO] head group is represented by a single bead (AO). Here we also demonstrate an approach to finding a value for the self-interaction aii when the surface tension of a pure component is unavailable from existing literature or is unobtainable from experiments. The self-interaction parameter for the AO head group is calculated by matching to experimental data for trimethylamine N-oxide (TMAO), however, anhydrous TMAO exists as a solid at room temperature. Therefore we must calculate a value for aAO,AO by matching to the surface tension for aqueous TMAO, where at a concentration of 15 wt% TMAO solutions have an experimental surface tension of 69.3mN m−1.97,98 The values for ln(γ∞A) are once again calculated using COSMO-RS, where ln(γ∞A) = −10.394 for AO beads at infinite dilution in water, and ln(γ∞A) = 7.0388 for AO beads in baths of hydrocarbon tails at infinite dilution. The amine oxide head group, therefore, displays much more hydrophilic behaviour than the ethylene oxide head groups.
 | ||
| Fig. 12 Coarse-graining procedure illustrated for the LDAO molecule. Beads are coloured according to their type: carbon, C3 (orange); C3T (red); amine oxide, AO (yellow). | ||
In order to find aAO,AO we perform a parameter sweep over aAO,AO in the range −34 ≤ aAO,AO ≤ −26 at intervals of ΔaAO,AO = 1, and for each value the corresponding value of aAO,W is calculated using eqn (21). Simulations are performed at a concentration of 15 wt% TMAO. This allows us to determine values aAO,AO = −30.461 and aAO,W = −48.505. Finally, the interactions with the hydrocarbon tail are calculated as aAO,C3 = aAO,C3T = −21.747.
The calculated surface tension as a function of surface coverage is given in Fig. 13. There is a plateau in the surface tension observed at higher concentrations (initial surface densities ≥0.0328), at which point the surface removes surfactants into the bulk. Fig. 14 shows the formation of micelles at high surfactant densities.
The surface tension at the CMC is experimentally reported as between 25–35 mN m−1,99–101 therefore our plateau to around ≈26 mN m−1 at higher concentrations is consistent with the available experimental data. There is a brief drop (to ≈19 mN m−1) in the surface tension before this plateau at high concentrations. This ‘over drop’ in surface tension is interpreted to be a result of no (or limited) surfactant removal from the interface. Table 8 shows the number of surfactants at the interface following the removal of surfactants into the bulk water. We observe that surfactants are removed from the surface to produce a nearly constant surface density of ≈0.026 mol Å−1. This results in a consistent value calculated for the surface tension. For the data points where the surface tension drops below 20 mN m−1 (where the number of molecules placed at the surface are 1024 and 1089 molecules/interface), the density is significantly higher due to a lack of surfactant removal to the bulk. Therefore the surface needs to have an initialised surface density, which is significantly larger than its desired equilibrium density, in order to see surfactant removal from the surface on the time scale of the simulations.
| No. molecules (initialised) | No. molecules (equilibrated) | Density (Å−2) (initialised) | Density (Å−2) (equilibrated) |
|---|---|---|---|
| a Note that only one of the two surfaces removes surfactant molecules in this case, so the value given is an average. | |||
| 900 | No removal | 0.0255 | 0.0255 |
| 1024 | No removal | 0.0290 | 0.0290 |
| 1089 | 1033.5a | 0.0309 | 0.0293 |
| 1156 | 932 | 0.0328 | 0.0264 |
| 1225 | 912 | 0.0347 | 0.0259 |
| 1369 | 914 | 0.0388 | 0.0259 |
| 1521 | 934 | 0.0431 | 0.0265 |
8 Conclusions
In this work, we have presented a parametrisation scheme for many-body dissipative particle dynamics simulations, which can be used to calculate the surface tension for complex systems. Our application of the parametrisation to C12Ej molecules at an air/water interface allows us to easily study their behaviour at different surface coverages. We obtain good agreement with experimental results, in particular, the trend for surface tension drop and CMC surface coverage for increasing numbers of ethylene oxide groups j. These systems can be difficult to study both experimentally and by using existing molecular dynamics techniques, and therefore MDPD provides a valuable tool for studying surfactant behaviour at the air/water interface.We also find that the parametrisation scheme introduced here provides good predictions for quantities such as the thickness of the surfactant layer and the angle of the surfactants relative to the surface, gaining insight into how the molecules pack at the surface.
We extended our parametrisation scheme to cover lauryldimethylamine oxide surfactants at the air/water interface. In this case, the surface spontaneously removes surfactants into the bulk water when the surface is initialised with a large surface density, in order to optimise the number of surfactants at the surface. This behaviour is difficult to observe in traditional molecular dynamics simulations, where it is far more common to observe an over-drop in the surface tension associated with a distortion of the interface.
It is useful to make some general comments on the applicability of this scheme to other molecules. In this work, we chose to use a bond length of l0 = 0.5rC, which was chosen because it would produce a reasonable bead-bead bond length for a number of different systems. When applying the parametrisation to other molecules, one should take care that the coarse graining chosen produces a bond length which is relatively close to the one which the parametrisation was developed for. Eqn (15) and (22) in particular may differ if a significantly different bond length is chosen. Furthermore, bonded beads are not only subject to bonded interactions (eqn (6) and (7)) but also non-bonded interactions with each other. These non-bonded interactions between bonded beads may result in an alteration of the bond length in the simulation to a value other than exactly l0. Similarly, this parametrisation was developed for linear molecules only but could be extended relatively simply for branched molecules through alteration of eqn (22). Moreover, in this work, we have not included any separate electrostatic interactions, and therefore the parametrisation has not been tested on ionic surfactants or other systems with charged molecules. The extension of this model to charged systems is currently under investigation.
Finally, we note that we have not attempted to use the model to study high surfactant concentrations beyond the (post-CMC) concentration regime when the surface is fully packed and micelles form. However, the emergence of micelles from over-packed LDAO surfaces suggests the possibility of using this parametrisation scheme for studying micellar aggregation numbers and micelle shape.
Data availability
Data supporting this article have been uploaded as part of the ESI.†Author contributions
RH: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. CA: supervision, project administration, writing – review and editing. MW: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the support of Durham University for the use of its HPC facility, Hamilton. RH would like to acknowledge support through a EPSRC/P&G funded Prosperity Partnership grant EP/V056891/1.References
- K. P. Santo and A. V. Neimark, Adv. Colloid Interface Sci., 2021, 298, 102545 CrossRef CAS PubMed.
- R. D. Groot, T. J. Madden and D. J. Tildesley, J. Chem. Phys., 1999, 110, 9739–9749 CrossRef CAS.
- A. Al Sunaidi, W. K. Den Otter and J. H. R. Clarke, Philos. Trans. R. Soc., A, 2004, 362, 1773–1781 CrossRef CAS PubMed.
- A. A. Gavrilov, Y. V. Kudryavtsev and A. V. Chertovich, J. Chem. Phys., 2013, 139, 224901 CrossRef PubMed.
- L. He, Z. Chen, R. Zhang, L. Zhang and Z. Jiang, J. Chem. Phys., 2013, 138, 094907 CrossRef PubMed.
- S. Yamamoto, Y. Maruyama and S.-A. Hyodo, J. Chem. Phys., 2002, 116, 5842–5849 CrossRef CAS.
- X. Chen, F. Tian, X. Zhang and W. Wang, Soft Matter, 2013, 9, 7592–7600 RSC.
- J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061 CrossRef CAS.
- H. Xu, Q. Zhang, H. Zhang, B. Zhang and C. Yin, J. Theor. Comput. Chem., 2013, 12, 1250111 CrossRef.
- A. Al Sunaidi, W. K. Den Otter and J. H. R. Clarke, J. Chem. Phys., 2013, 138, 154904 CrossRef CAS PubMed.
- M. A. Bates and M. Walker, Mol. Cryst. Liq. Cryst., 2010, 525, 204–211 CrossRef CAS.
- M. A. Bates and M. Walker, Phys. Chem. Chem. Phys., 2009, 11, 1893–1900 RSC.
- M. A. Bates and M. Walker, Liq. Cryst., 2011, 38, 1749–1757 CrossRef CAS.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8876–8883 RSC.
- R. L. Anderson, D. J. Bray, A. Del Regno, M. A. Seaton, A. S. Ferrante and P. B. Warren, J. Chem. Theory Comput., 2018, 14, 2633–2643 CrossRef CAS PubMed.
- A. Khedr and A. Striolo, J. Chem. Theory Comput., 2018, 14, 6460–6471 CrossRef CAS PubMed.
- E. Lavagnini, J. L. Cook, P. B. Warren and C. A. Hunter, J. Phys. Chem. B, 2021, 125, 3942–3952 CrossRef CAS PubMed.
- E. Lavagnini, J. L. Cook, P. B. Warren, M. J. Williamson and C. A. Hunter, J. Phys. Chem. B, 2020, 124, 5047–5055 CrossRef CAS PubMed.
- M. Walker, A. J. Masters and M. R. Wilson, Phys. Chem. Chem. Phys., 2014, 16, 23074–23081 RSC.
- M. Walker and M. R. Wilson, Soft Matter, 2016, 12, 8588–8594 RSC.
- N. Denham, M. C. Holmes and A. V. Zvelindovsky, J. Phys. Chem. B, 2011, 115, 1385–1393 CrossRef CAS PubMed.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS PubMed.
- C. R. Wand, M. Panoukidou, A. Del Regno, R. L. Anderson and P. Carbone, Langmuir, 2020, 36, 12288–12298 CrossRef CAS PubMed.
- X. Wang, K. P. Santo and A. V. Neimark, Langmuir, 2020, 36, 14686–14698 CrossRef CAS PubMed.
- I. Pagonabarraga and D. Frenkel, J. Chem. Phys., 2001, 115, 5015–5026 CrossRef CAS.
- P. B. Warren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 066702 CrossRef CAS PubMed.
- N. Ghorbani and A. Pishevar, Comput. Part. Mech., 2017, 5, 113–123 CrossRef.
- S. Aphinyan, E. Y. M. Ang, J. Yeo, T. Y. Ng, R. Lin, Z. Liu and K. R. Geethalakshmi, Modell. Simul. Mater. Sci. Eng., 2019, 27, 055005 CrossRef CAS.
- L. Ren, H. Hu, L. Bao, M. Zhang, J. Wen and L. Xie, Phys. Fluids, 2021, 33, 072001 CrossRef CAS.
- C.-J. Wu, K.-C. Chu, Y.-J. Sheng and H.-K. Tsao, J. Phys. Chem. C, 2017, 121, 17932–17940 CrossRef CAS.
- Y.-E. Liang, Y.-H. Weng, H.-K. Tsao and Y.-J. Sheng, Langmuir, 2016, 32, 8543–8549 CrossRef CAS PubMed.
- R. D. Groot, Langmuir, 2000, 16, 7493–7502 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- G. Kacar, E. A. J. F. Peters and G. de With, EPL, 2013, 102, 40009 CrossRef.
- M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Chem. Theory Comput., 2015, 11, 4395–4403 CrossRef CAS PubMed.
- M.-T. Lee, R. Mao, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2016, 120, 4980–4991 CrossRef CAS PubMed.
- A. Maiti and S. McGrother, J. Chem. Phys., 2004, 120, 1594–1601 CrossRef CAS PubMed.
- L. Rekvig, M. Kranenburg, J. Vreede, B. Hafskjold and B. Smit, Langmuir, 2003, 19, 8195–8205 CrossRef CAS.
- K. P. Travis, M. Bankhead, K. Good and S. L. Owens, J. Chem. Phys., 2007, 127, 014109 CrossRef PubMed.
- A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802 CrossRef CAS PubMed.
- A. Vishnyakov, R. Mao, M.-T. Lee and A. V. Neimark, J. Chem. Phys., 2018, 148, 024108 CrossRef PubMed.
- R. L. Anderson, D. Bray, A. S. Ferrante, M. G. Noro, I. P. Stott and P. Warren, J. Chem. Phys., 2017, 147, 094503 CrossRef PubMed.
- A. Truszkowski, M. Epple, A. Fiethen, A. Zielesny and H. Kuhn, J. Colloid Interface Sci., 2013, 410, 140–145 CrossRef CAS PubMed.
- P. Vanya, P. Crout, J. Sharman and J. A. Elliott, Phys. Rev. E, 2018, 98, 033310 CrossRef CAS.
- E. C. Wijaya, F. Separovic, C. J. Drummond and T. L. Greaves, Phys. Chem. Chem. Phys., 2016, 18, 24377–24386 RSC.
- S. R. Goates, D. A. Schofield and C. D. Bain, Langmuir, 1999, 15, 1400–1409 CrossRef CAS.
- J. R. Lu, T. J. Su, Z. X. Li, R. K. Thomas, E. J. Staples, I. Tucker and J. Penfold, J. Phys. Chem. B, 1997, 101, 10332–10339 CrossRef CAS.
- J. R. Lu, Z. X. Li, R. K. Thomas, E. J. Staples, L. Thompson, I. Tucker and J. Penfold, J. Phys. Chem., 1994, 98, 6559–6567 CrossRef CAS.
- J. R. Lu, Z. X. Li, R. K. Thomas, E. J. Staples, I. Tucker and J. Penfold, J. Phys. Chem., 1993, 97, 8012–8020 CrossRef CAS.
- J. R. Lu, E. M. Lee, R. K. Thomas, J. Penfold and S. L. Flitsch, Langmuir, 1993, 9, 1352–1360 CrossRef CAS.
- J. R. Lu, Z. X. Li, T. J. Su, R. K. Thomas and J. Penfold, Langmuir, 1993, 9, 2408–2416 CrossRef CAS.
- J. R. Lu, E. A. Simister, E. M. Lee, R. K. Thomas, A. R. Rennie and J. Penfold, Langmuir, 1992, 8, 1837–1844 CrossRef CAS.
- J. Chanda and S. Bandyopadhyay, J. Chem. Theory Comput., 2005, 1, 963–971 CrossRef CAS PubMed.
- L. Shi, N. R. Tummala and A. Striolo, Langmuir, 2010, 26, 5462–5474 CrossRef CAS PubMed.
- S. Bandyopadhyay and J. Chanda, Langmuir, 2003, 19, 10443–10448 CrossRef CAS.
- V. Cuny, M. Antoni, M. Arbelot and L. Liggieri, Colloids Surf., A, 2008, 323, 180–191 CrossRef CAS.
- E. A. Simister, R. K. Thomas, J. Penfold, R. Aveyard, B. P. Binks, P. Cooper, P. D. I. Fletcher, J. R. Lu and A. Sokolowski, J. Phys. Chem., 1992, 96, 1383–1388 CrossRef CAS.
- J. Penfold and R. K. Thomas, Phys. Chem. Chem. Phys., 2022, 24, 8553–8577 RSC.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- P. B. Warren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 045303 CrossRef PubMed.
- Y.-C. Li, H. Liu, X.-R. Huang and C.-C. Sun, Mol. Simul., 2011, 37, 875–883 CrossRef CAS.
- A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2012, 8, 787–791 CrossRef CAS PubMed.
- M. A. Seaton, The DL_MESO Mesoscale Simulation Package, STFC Computational Science and Engineering Department, 2012, http://www.ccp5.ac.uk/DL_MESO.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1949, 17, 338–343 CrossRef CAS.
- G. Jiménez-Serratos, C. Vega and A. Gil-Villegas, J. Chem. Phys., 2012, 137, 204104 CrossRef PubMed.
- E. de Miguel and G. Jackson, J. Chem. Phys., 2006, 125, 164109 CrossRef PubMed.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19 RSC.
- J. E. Mark and P. J. Flory, J. Am. Chem. Soc., 1965, 87, 1415–1423 CrossRef CAS.
- A. Klamt and F. Eckert, Fluid Phase Equilib., 2000, 172, 43–72 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- E. Mullins, R. Oldland, Y. A. Liu, S. Wang, S. I. Sandler, C.-C. Chen, M. Zwolak and K. C. Seavey, Ind. Eng. Chem. Res., 2006, 45, 4389–4415 CrossRef CAS.
- H. Alasiri and W. G. Chapman, J. Mol. Liq., 2017, 246, 131–139 CrossRef CAS.
- J. J. Jasper, J. Phys. Chem. Ref. Data, 1972, 1, 841–1010 CrossRef CAS.
- M. Sánchez-Rubio, B. Gordillo and D. S. Rushforth, J. Chem. Educ., 1983, 60, 70 CrossRef.
- A. I. Vogel, J. Chem. Soc., 1946, 133–139 RSC.
- D. J. Luning Prak, S. M. Alexandre, J. S. Cowart and P. C. Trulove, J. Chem. Eng. Data, 2014, 59, 1334–1346 CrossRef CAS.
- Y. Yu, X. Yue, S. Zhang, B. Li, C. Hao and J. Ye, J. Mol. Liq., 2020, 301, 112483 CrossRef CAS.
- F. Goujon, A. Dequidt, A. Ghoufi and P. Malfreyt, J. Chem. Theory Comput., 2018, 14, 2644–2651 CrossRef CAS PubMed.
- S. K. Begum, R. J. Clarke, M. S. Ahmed, S. Begum and M. A. Saleh, J. Mol. Liq., 2013, 177, 11–18 CrossRef CAS.
- S. K. Begum, R. J. Clarke, M. S. Ahmed, S. Begum and M. A. Saleh, J. Chem. Eng. Data, 2011, 56, 303–306 CrossRef CAS.
- P. Schatzberg, J. Phys. Chem., 1963, 67, 776–779 CrossRef CAS.
- C. Sutton and J. A. Calder, Environ. Sci. Technol., 1974, 8, 654–657 CrossRef CAS.
- J. Roddy and C. Coleman, Talanta, 1968, 15, 1281–1286 CrossRef CAS PubMed.
- M. Peng and A. V. Nguyen, Adv. Colloid Interface Sci., 2020, 275, 102052 CrossRef CAS PubMed.
- C.-T. Hsu, M.-J. Shao and S.-Y. Lin, Langmuir, 2000, 16, 3187–3194 CrossRef CAS.
- S.-Y. Lin, Y.-Y. Lin, E.-M. Chen, C.-T. Hsu and C.-C. Kwan, Langmuir, 1999, 15, 4370–4376 CrossRef CAS.
- C. M. Persson, U. R. M. Kjellin and J. C. Eriksson, Langmuir, 2003, 19, 8152–8160 CrossRef CAS.
- B. V. Zhmud, F. Tiberg and J. Kizling, Langmuir, 2000, 16, 2557–2565 CrossRef CAS.
- J. Liley, J. Penfold, R. Thomas, I. Tucker, J. Petkov, P. Stevenson, I. Banat, R. Marchant, M. Rudden and J. Webster, J. Colloid Interface Sci., 2019, 534, 64–71 CrossRef CAS PubMed.
- D. F. Anghel, S. Saito, A. Băran, A. Iovescu and M. Corniţescu, Colloid Polym. Sci., 2007, 285, 771–779 CrossRef CAS.
- T. Joshi, B. Bharatiya and K. Kuperkar, J. Dispersion Sci. Technol., 2008, 29, 351–357 CrossRef CAS.
- W. C. Swope, M. A. Johnston, A. I. Duff, J. L. McDonagh, R. L. Anderson, G. Alva, A. T. Tek and A. P. Maschino, J. Phys. Chem. B, 2019, 123, 1696–1707 CrossRef CAS PubMed.
- E. H. Crook, D. B. Fordyce and G. F. Trebbi, J. Phys. Chem., 1963, 67, 1987–1994 CrossRef CAS.
- S. B. Sulthana, P. V. C. Rao, S. G. T. Bhat, T. Y. Nakano, G. Sugihara and A. K. Rakshit, Langmuir, 2000, 16, 980–987 CrossRef CAS.
- Y.-T. Liao, A. C. Manson, M. R. DeLyser, W. G. Noid and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2479–2484 CrossRef CAS PubMed.
- M. Auton, A. C. M. Ferreon and D. W. Bolen, J. Mol. Biol., 2006, 361, 983–992 CrossRef CAS PubMed.
- R. Wang, Y. Li, Y. Song and L. Zhi, J. Surfactants Deterg., 2014, 17, 223–229 CrossRef CAS.
- K. D. Thompson, E. P. Danielson, K. N. Peterson, N. O. Nocevski, J. T. Boock and J. A. Berberich, Langmuir, 2022, 38, 4090–4101 CrossRef CAS PubMed.
- R. A. Abdel-Rahem, S. Niaz, A. M. Altwaiq, M. Esaifan, M. B. A. Bitar and A. A. Bawab, Tenside, Surfactants, Deterg., 2022, 59, 144–158 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00276d |
| This journal is © The Royal Society of Chemistry 2023 |