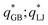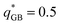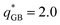Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase behaviour of mixtures of charged soft disks and spheres†
Valerio
Mazzilli
 ab,
Katsuhiko
Satoh
ab,
Katsuhiko
Satoh
 *c and
Giacomo
Saielli
*c and
Giacomo
Saielli
 *ab
*ab
aDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: giacomo.saielli@unipd.it
bCNR-ITM, Institute on Membrane Technology, Padova Unit, Via Marzolo, 1, 35131 Padova, Italy
cDepartment of Chemistry, Osaka Sangyo University, Daito, Osaka, 574-8530, Japan. E-mail: ksatoh@las.osaka-sandai.ac.jp
First published on 13th April 2023
Abstract
We have investigated the phase behaviour of mixtures of soft disks (Gay-Berne oblate ellipsoids, GB) and soft spheres (Lennard-Jones, LJ) with opposite charge as a model of ionic liquid crystals and colloidal suspensions. We have used constant volume Molecular Dynamics simulations and fixed the stoichiometry of the mixture in order to have electroneutrality; three systems have been selected GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, GB
2, GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and GB
1 and GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 2
LJ = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For each system we have selected three values of the scaled point charge q* of the GB particles, namely 0.5, 1.0 and 2.0 (and a corresponding negative scaled charge of the LJ particles that depends on the stoichiometric ratio). We have found a very rich mesomorphism with the formation, as a function of the scaled temperature, of the isotropic phase, the discotic nematic phase, the hexagonal columnar phase and crystal phases. While the structure of the high temperature phases was similar in all systems, the hexagonal columnar phases exhibited a highly variable morphology depending on the scaled charge and stoichiometry. On the one hand, GB
1. For each system we have selected three values of the scaled point charge q* of the GB particles, namely 0.5, 1.0 and 2.0 (and a corresponding negative scaled charge of the LJ particles that depends on the stoichiometric ratio). We have found a very rich mesomorphism with the formation, as a function of the scaled temperature, of the isotropic phase, the discotic nematic phase, the hexagonal columnar phase and crystal phases. While the structure of the high temperature phases was similar in all systems, the hexagonal columnar phases exhibited a highly variable morphology depending on the scaled charge and stoichiometry. On the one hand, GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 systems form lamellar structures, akin to smectic phases, with an alternation of layers of disks (exhibiting an hexagonal columnar phase) and layers of LJ particles (in the isotropic phase). On the other hand, for the 2
2 systems form lamellar structures, akin to smectic phases, with an alternation of layers of disks (exhibiting an hexagonal columnar phase) and layers of LJ particles (in the isotropic phase). On the other hand, for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry we observe the formation of a frustrated hexagonal columnar phase with an alternating tilt direction of the molecular axis. We rationalize these findings based on the structure of the neutral ion pair dominating the behaviour at low temperature and high charge.
1 stoichiometry we observe the formation of a frustrated hexagonal columnar phase with an alternating tilt direction of the molecular axis. We rationalize these findings based on the structure of the neutral ion pair dominating the behaviour at low temperature and high charge.
Introduction
Ionic Liquid Crystals (ILCs) are materials composed of ions, typically organic cations and inorganic anions as normally observed in Ionic Liquids (ILs), and exhibiting Liquid Crystal (LC) phases as a function of the temperature.1,2 They combine together the solvent properties of ILs with the partially ordered and anisotropic conductive properties of LCs, making them attractive materials wherever charge/mass transport is sought, e.g. as electrolyte for Li-ion batteries,3 dye-sensitized solar cells4 and/or membranes for selective ion/water transport.5,6 In particular, discotic ILCs based on derivatives of gallic acid, have been used to make polymeric membranes exploiting the nano-sized channels formed in columnar (Col) and cubic phases.7,8Computer simulations of ILCs are a useful complementary tool to investigate the structural and dynamic properties of these materials. Typically, fully atomistic (FA) simulations are used to study details of the molecular organization at a given temperature and a given phase.7,9,10 The complexity of the systems, however, makes difficult to explore the whole phase diagram using FA force fields. Moreover, several important aspects of ILCs do not depend on the details of the chemical structure, rather on more general parameters such as the molecular size and shape and the charge position within the molecule, as well as its magnitude. To this end, interesting results on the factors stabilizing ionic nematic (Nem) phases vs smectic phases of rod-like molecules have been obtained using highly coarse-grained models of ILCs, e.g. mixtures of charged hard spherocylinders and hard spheres11 or mixtures of soft Gay-Berne ellipsoids and Lennard-Jones spheres.12–17
On the other hand, ionic discotic systems have been less studied, using highly coarse-grained models, with some notable exceptions of colloidal suspensions of platelet particles using Monte Carlo simulations.18,19 However, to the best of our knowledge, there are no reports in the literature of simulations of mixtures of oppositely charged discotic and spherical soft particles as models of discotic ILCs. Recently we presented a detailed analysis of the structural properties of mixtures of non-charged soft particles made of Gay-Berne (GB) disks and Lennard-Jones (LJ) spheres.20 The phase behaviour of the mixtures at various compositions was dominated by the excluded volume interactions leading to phase separation. At high temperature the systems were in an isotropic (Iso), homogeneous mixed phase; by lowering the temperature, a phase separation took place resulting in an isotropic phase rich in LJ particles with some GB disks, and a liquid-crystalline phase almost exclusively composed by GB disks exhibiting nematic and hexagonal columnar phases at different temperatures. Depending on the mixture composition, the phase separation could take place at the transition between the high temperature isotropic mixed phase and the discotic nematic phase (for mixtures rich in LJ particles) or at lower temperatures when the GB disks formed a hexagonal columnar phase (for mixtures rich in GB particles). In the latter case, a homogeneous discotic nematic phase with the LJ particles dissolved in the GB “solvent” was observed.20
In this work we wish to extend our studies by investigating how the presence of opposite charges on the soft GB disks and LJ spheres affects the phase behaviour of the mixtures. Because of the presence of a fixed charge, the cation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion ratio of the mixture is also fixed to guarantee electroneutrality, therefore the systems should be considered as pure ionic liquid compounds made by a stoichiometric amount of GB and LJ particles, rather than mixtures, since the composition cannot be varied freely. We selected three GB
anion ratio of the mixture is also fixed to guarantee electroneutrality, therefore the systems should be considered as pure ionic liquid compounds made by a stoichiometric amount of GB and LJ particles, rather than mixtures, since the composition cannot be varied freely. We selected three GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ stoichiometries: 1
LJ stoichiometries: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 that could be considered as representing ILCs with, respectively a doubly charged cation and a singly charged anion; a cation/anion pair with the same charge (in magnitude); a singly charged cation and a doubly charged anion.
1 that could be considered as representing ILCs with, respectively a doubly charged cation and a singly charged anion; a cation/anion pair with the same charge (in magnitude); a singly charged cation and a doubly charged anion.
Computational details
MD simulations
We used the software package LAMMPS21 for the Molecular Dynamics (MD) simulations. These were run in the NVT ensemble using a cut-off distance of 1.6 scaled units for the van der Waals interaction, and 4.0 scaled units for the Coulomb interactions and a Nosé–Hoover thermostat22,23 to control the temperature. The total number of particles (Ntot) in all the systems were above 5000 to achieve a negligible size effect, as demonstrated in our previous work.13 Three GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ stoichiometries were simulated with cation
LJ stoichiometries were simulated with cation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion ratio of 1
anion ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; the corresponding scaled charges, q*, were set to proper values to guarantee electroneutrality, that is +q*/−1/2q*, +q*/−q* and +q*/−2q*, respectively, see Table 1. The scaled point charges are at the center of mass of the two particles and the electrostatic interactions were computed using the Coulomb potential with particle–particle particle–mesh solver (pppm)24 for long range interaction setting an accuracy on the forces of 10−6. Errors on the forces are calculated in LAMMPS following ref. 25 and 26. The cutoff and accuracy determine the size of the grid for the pppm calculations. Typical grids for our systems are in the range 48 × 48 × 48 for 1
1; the corresponding scaled charges, q*, were set to proper values to guarantee electroneutrality, that is +q*/−1/2q*, +q*/−q* and +q*/−2q*, respectively, see Table 1. The scaled point charges are at the center of mass of the two particles and the electrostatic interactions were computed using the Coulomb potential with particle–particle particle–mesh solver (pppm)24 for long range interaction setting an accuracy on the forces of 10−6. Errors on the forces are calculated in LAMMPS following ref. 25 and 26. The cutoff and accuracy determine the size of the grid for the pppm calculations. Typical grids for our systems are in the range 48 × 48 × 48 for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,
2,  to a maximum of 144 × 144 × 144 for the 2
to a maximum of 144 × 144 × 144 for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,
1, 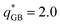 . All the systems have the same packing fraction (η) equal to 0.5023, which is the same used in our previous work with mixtures of uncharged particles.20 Simulations were run in cascade starting from a high-temperature isotropic mixed phase. Cooling runs were followed by heating runs to assess the presence of hysteresis. Each simulation at a given temperature consisted of at least 1 M timesteps of which the last 500 k timesteps were used for production. Temperatures closer to transition points needed longer simulations, up to 3 M timesteps, to be properly equilibrated. In some cases, however, hysteresis could not be removed. The timestep was set to 0.0005 scaled units.
. All the systems have the same packing fraction (η) equal to 0.5023, which is the same used in our previous work with mixtures of uncharged particles.20 Simulations were run in cascade starting from a high-temperature isotropic mixed phase. Cooling runs were followed by heating runs to assess the presence of hysteresis. Each simulation at a given temperature consisted of at least 1 M timesteps of which the last 500 k timesteps were used for production. Temperatures closer to transition points needed longer simulations, up to 3 M timesteps, to be properly equilibrated. In some cases, however, hysteresis could not be removed. The timestep was set to 0.0005 scaled units.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ, the number of GB and LJ particles, NGB
LJ, the number of GB and LJ particles, NGB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NLJ, the scaled charges,
NLJ, the scaled charges,  and
and  , and the scaled densities, ρ*. Packing fraction η = 0.5023
, and the scaled densities, ρ*. Packing fraction η = 0.5023
Gay-Berne model potential
We have used the Gay-Berne potential implementation for the disks as described by Bates and Luckhurst in ref. 27 and therein called GBDII. This parametrization of the GB potential features the ratio of the face-to-face vs. the edge-to-edge contact distance, σf/σe equal to 0.345; the ratio of the face-to-face vs edge-to-edge well depth, εf/εe, equal to 5.0; and the additional two parameters of the GB potential, μ, and ν (see ref. 27 for more details) equal to 1 and 2, respectively. Moreover, the selected parametrization adopts an interaction potential which is shifted and scaled with respect to σf. With this choice of the parameters, the GB disks have the three diameters, σe, σe, σf equal to 1.0, 1.0, 0.345 σ0 units, respectively. The LJ spheres in our mixtures have a diameter of 0.345 σ0 units. The mixed GB–LJ interaction potential is based on the work of Berardi et al.28 as implemented in LAMMPS.29 Both particles are treated as special cases of biaxial GB particles with two (for the disks) and three (for the spheres) equal diameters. Therefore, care must be exercised to remove the unphysical rotational degrees of freedom for a proper equilibration of the rotational temperatures.13,14 The scaled quantities are defined as follows: the scaled potential energy, U* = U/ε0; the scaled distance, r* = r/σ0; the scaled volume, V* = V/σ03; the scaled number density, ρ* = Ntot/V*; the scaled temperature, T* = kBT/ε0; the scaled pressure, p* = pσ03/ε0; the scaled moment of inertia, I⊥* = I⊥/mσ02; the scaled time, ; the scaled charge
; the scaled charge  , where ε0 is the vacuum permittivity, while the packing fraction is given by η = NVm*/V*, where Vm* is the scaled molecular volume. Though we are dealing with soft particles, the volume is calculated taking the contact distance defined above.
, where ε0 is the vacuum permittivity, while the packing fraction is given by η = NVm*/V*, where Vm* is the scaled molecular volume. Though we are dealing with soft particles, the volume is calculated taking the contact distance defined above.
The mass, m, the potential well depth, ε0, and the contact distance, σ0 = σe, are the parameters (all set to 1) used to scale all quantities. Please note that σ0 is used to scale the quantities above while, as mentioned already, σf is used to shift and scale the Gay-Berne potential, see ref. 27 for more details. Although the mass of typical cations in real systems is expected to be larger than the mass of typical anions, our choice to set both to 1 reduces the number of variable parameters and does not impact on the structural properties and phase behaviour since the space of coordinates and momenta are independent, that is the mass only affects the dynamic properties, which are not considered here.
Structural analysis
The assignment of the phase type has been done by visual inspection of the snapshots, by the analysis of the isotropic radial distribution functions (RDF) of the distance between GB–GB, LJ–LJ and GB–LJ pairs as well as using the RDF resolved along the parallel and perpendicular direction with respect to the director of the phase. To this end, we have selected GB particle pairs as follows, according to the procedure by Bates and Luckhurst:27 for the parallel RDF, , we consider only those pairs whose perpendicular component of the distance,
, we consider only those pairs whose perpendicular component of the distance,  , is less than 0.6σ0, while for the perpendicular RDF,
, is less than 0.6σ0, while for the perpendicular RDF, 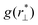 , we consider only those pairs whose parallel component of the distance,
, we consider only those pairs whose parallel component of the distance,  , is less than 0.6σ0. This guarantees that we are exploring the RDF in a relatively thin cylinder parallel to the director and in a relatively thin plane perpendicular to the director, respectively. In addition to the RDF, we have calculated the orientational and the hexatic order parameters. The second rank orientational order parameter, 〈P2〉, for the GB disks only, is obtained from the Q tensor, eqn (1), as the maximum eigenvalue of
, is less than 0.6σ0. This guarantees that we are exploring the RDF in a relatively thin cylinder parallel to the director and in a relatively thin plane perpendicular to the director, respectively. In addition to the RDF, we have calculated the orientational and the hexatic order parameters. The second rank orientational order parameter, 〈P2〉, for the GB disks only, is obtained from the Q tensor, eqn (1), as the maximum eigenvalue of | (1) |
 | (2) |
The Iso-to-Nem transition temperatures were estimated as follows: the system is in the isotropic phase when the orientational order parameter is lower than 0.2; it is in the nematic phase when the orientational order parameter is higher than 0.4. For intermediate values, we note a possible coexistence of domains of nematic phase still not uniformly oriented because of a residual short-range microphase segregation between particles of different shape. This definition is slightly different from what we used in ref. 20 for the non-charged systems. There, we observed two different situations: for GB-rich mixtures, the Iso-to-Nem transition appeared almost second order and we assumed the phase to be nematic already at temperatures where 〈P2〉 was higher than 0.2, thus neglecting the small intermediate range. For LJ-rich systems, the Iso-to-Nem transition occurred together with a macroscopic phase separation, requiring the calculation of the order parameters separately for the two phases, the GB phase and the LJ phase. Here, since the charged systems do not show a macroscopic phase separation, due to the electrostatic interaction, we prefer to use for all systems a consistent definition of isotropic and nematic phase, as defined above: nematic phase for 〈P2〉 > 0.4 (and for 〈Ψ6〉 = 0.0), isotropic phase for 〈P2〉 < 0.2, intermediate phase in the other cases. Moreover, the 〈P2〉 values are nicely reproduced during the heating and cooling run and no hysteresis is detected at the Iso-to-Nem transition, therefore the intermediate phase is not a metastable state, rather the transition is, in those cases, a very weak first order one.
In contrast, for some Nem-to-Col transitions, some hysteresis is present. In such cases we estimated the temperature of the phase transition as an average between the highest temperature of the heating run, before the transition 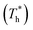 and the lowest of the cooling run, also before the transition,
and the lowest of the cooling run, also before the transition,  using eqn (3):31
using eqn (3):31
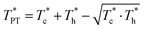 | (3) |
Results and discussion
We will discuss in the following the results for the three stoichiometries selected (GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as a function of temperature and scaled charge through the analysis of the order parameters, the radial distribution functions, and some selected snapshots. For the sake of comparison, we will include in the discussion also some of the results of our previous work,20 where mixtures of uncharged particles (q* = 0.0) were simulated.
1) as a function of temperature and scaled charge through the analysis of the order parameters, the radial distribution functions, and some selected snapshots. For the sake of comparison, we will include in the discussion also some of the results of our previous work,20 where mixtures of uncharged particles (q* = 0.0) were simulated.
GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) LJ 1
LJ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2
2
The phase behaviour of the systems with stoichiometry GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (modelling an ionic liquid crystal with a discotic divalent cation and a spherical monovalent anion) is shown in Fig. 1 for the various scaled charges used, where we report the 〈P2〉 and 〈Ψ6〉 order parameters as a function of the scaled temperature. Representative snapshots can be found in Fig. 2. The trend of the short-range potential energy and electrostatic term can be found in ESI,† Fig. S4, S8 and S12.†
2 (modelling an ionic liquid crystal with a discotic divalent cation and a spherical monovalent anion) is shown in Fig. 1 for the various scaled charges used, where we report the 〈P2〉 and 〈Ψ6〉 order parameters as a function of the scaled temperature. Representative snapshots can be found in Fig. 2. The trend of the short-range potential energy and electrostatic term can be found in ESI,† Fig. S4, S8 and S12.†
The system with  has been already described in details in ref. 20. The charged systems with
has been already described in details in ref. 20. The charged systems with  and
and  have a similar qualitative behaviour. At high reduced temperatures they are in an isotropic and homogeneously mixed phase, see Fig. 2a, for
have a similar qualitative behaviour. At high reduced temperatures they are in an isotropic and homogeneously mixed phase, see Fig. 2a, for  , (additional snapshots for the other systems can be found in ESI†) and the order parameters 〈P2〉 and 〈Ψ6〉 are close to zero. By lowering T* we observe an increase in the orientational order of the disks, while 〈Ψ6〉 remains close to zero, therefore the phase observed is a nematic discotic, see Fig. 2b. As mentioned already, when the orientational order parameter is above 0.4 the phase is considered nematic, while for 〈P2〉 < 0.2 it is considered isotropic. When 〈P2〉 values are between 0.2 and 0.4 we observe the formation of nematic domains of GB particles within the box which, however, do not coherently align all in the same direction, resulting in a low orientational order parameter. This is partly due to a short-ranged microphase separation (especially for the low-charge system
, (additional snapshots for the other systems can be found in ESI†) and the order parameters 〈P2〉 and 〈Ψ6〉 are close to zero. By lowering T* we observe an increase in the orientational order of the disks, while 〈Ψ6〉 remains close to zero, therefore the phase observed is a nematic discotic, see Fig. 2b. As mentioned already, when the orientational order parameter is above 0.4 the phase is considered nematic, while for 〈P2〉 < 0.2 it is considered isotropic. When 〈P2〉 values are between 0.2 and 0.4 we observe the formation of nematic domains of GB particles within the box which, however, do not coherently align all in the same direction, resulting in a low orientational order parameter. This is partly due to a short-ranged microphase separation (especially for the low-charge system  ) with the formation of domains of LJ particles that can also be seen in Fig. 2b. This explains the stable formation of an intermediate phase (observed on heating and cooling) with a low orientational order parameter. With these boundaries set, the transition temperatures isotropic-to-intermediate phase
) with the formation of domains of LJ particles that can also be seen in Fig. 2b. This explains the stable formation of an intermediate phase (observed on heating and cooling) with a low orientational order parameter. With these boundaries set, the transition temperatures isotropic-to-intermediate phase  and intermediate-to-nematic
and intermediate-to-nematic  are determined and their values are reported in Table 2 together with the Nem-to-Col transition temperatures
are determined and their values are reported in Table 2 together with the Nem-to-Col transition temperatures  , which will be discussed later. The systems do not show hysteresis when undergoing Iso-to-Nem transition as can be seen from the 〈P2〉, Fig. 1, since the results of the cooling and heating run are superimposable.
, which will be discussed later. The systems do not show hysteresis when undergoing Iso-to-Nem transition as can be seen from the 〈P2〉, Fig. 1, since the results of the cooling and heating run are superimposable.
GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ LJ |
||||
|---|---|---|---|---|
| a Data from ref. 20. | ||||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0a 0.0a |
8.125 | 7.25 | 5.772 |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.25 −0.25 |
6.750 | 5.626 | 3.250 | |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.5 −0.5 |
4.800 | 4.500 | 2.400 | |
2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.0 −1.0 |
2.150 | 2.100 | 1.300 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0a 0.0a |
9.025 | 7.75 | 4.507 |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.5 −0.5 |
8.000 | 7.250 | 2.675 | |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.0 −1.0 |
6.750 | 5.750 | 2.125 | |
2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −2.0 −2.0 |
2.000 | 1.500 | 1.250 | |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0a 0.0a |
10.75 | 9.25 | 4.127 |
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.0 −1.0 |
9.750 | 9.000 | 2.775 | |
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −2.0 −2.0 |
8.400 | 7.800 | 2.250 | |
2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −4.0 −4.0 |
4.400 | 4.000 | 1.900 | |
Further cooling of the  and 1.0 systems, enhances the orientational order, thus increasing 〈P2〉 values. Moreover, they undergo a transition to another phase, as can be seen in Fig. 2c (for
and 1.0 systems, enhances the orientational order, thus increasing 〈P2〉 values. Moreover, they undergo a transition to another phase, as can be seen in Fig. 2c (for  ). The phase transition can be detected by the small jump in the 〈P2〉 values and by the large jump in the 〈Ψ6〉 trends reported in Fig. 1. This indicates a clear first order transition to a columnar hexagonal phase. As can be seen in Fig. 2d this is accompanied by a significant micro-phase segregation between disks and spheres resulting in a lamellar-like structure. This issue will be discussed more in details below. The systems show a hysteresis in the Nem-to-Col transitions when the particles bear no charges. This is due to the phase separation of GB and LJ particles that takes place in the zero-charge systems and it has been discussed in our previous paper.20 In contrast, when
). The phase transition can be detected by the small jump in the 〈P2〉 values and by the large jump in the 〈Ψ6〉 trends reported in Fig. 1. This indicates a clear first order transition to a columnar hexagonal phase. As can be seen in Fig. 2d this is accompanied by a significant micro-phase segregation between disks and spheres resulting in a lamellar-like structure. This issue will be discussed more in details below. The systems show a hysteresis in the Nem-to-Col transitions when the particles bear no charges. This is due to the phase separation of GB and LJ particles that takes place in the zero-charge systems and it has been discussed in our previous paper.20 In contrast, when  and 1.0 they possess small or negligible hysteresis in the Nem-to-Col transition due to the electrostatic interactions that oppose the particle-demixing process. The net jumps in 〈Ψ6〉 coincide with the transition temperature nem-to-Col
and 1.0 they possess small or negligible hysteresis in the Nem-to-Col transition due to the electrostatic interactions that oppose the particle-demixing process. The net jumps in 〈Ψ6〉 coincide with the transition temperature nem-to-Col  for the system with
for the system with  and 1.0. Further cooling shows another small jump in 〈P2〉 values other than the one for Nem-to-Col transition suggesting the formation of a crystalline phase that is not further investigated here.
and 1.0. Further cooling shows another small jump in 〈P2〉 values other than the one for Nem-to-Col transition suggesting the formation of a crystalline phase that is not further investigated here.
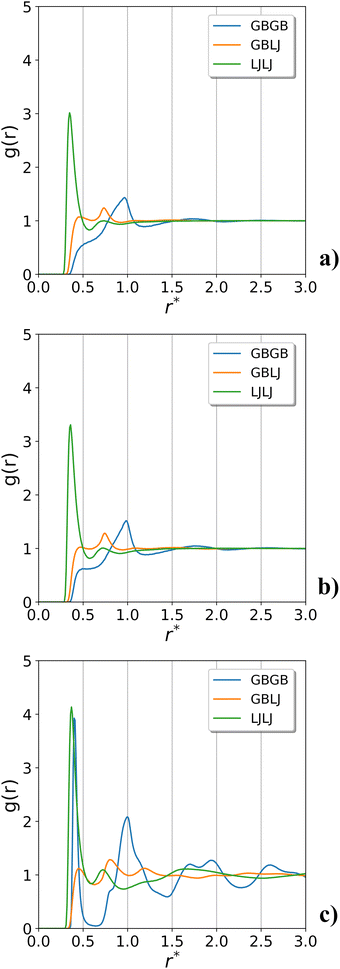
The RDF of the different particle pairs within the system, are reported in Fig. 3. In panel (a) we note the lack of long-range correlation typical of an isotropic phase. Similar profiles are observed for the nematic phase, which also lacks any positional order. In contrast in Fig. 3c we see a strong correlation for the GB–GB pairs indicating the presence of long-range positional order.
It is noteworthy, however, that the disks are not perfectly stacked face-to-face in the columnar hexagonal phase. In fact, by looking at the GB–GB trace, the first peak is found at r* greater than 0.345 (which is the diameter of the spheres and the short axis of the ellipsoids), thus indicating that the disks’ centres do not perfectly stack on top of each other. Moreover, the columnar hexagonal phase is not characterized by long columns since these are limited by the layered structure, see Fig. 2d. This point will be discussed in more details below.
While the systems with  and 1.0 behave in a qualitatively similar way and show analogous phase sequence, the system with
and 1.0 behave in a qualitatively similar way and show analogous phase sequence, the system with  behaves somewhat differently. The isotropic mixed phase is strongly stabilized by the larger charge. As the T* is lowered, 〈P2〉 shows a net jump, suggesting a first order transition, but the nematic phase appears to be stable for a small range of T* before undergoing the Nem-to-Col transition. Moreover, there is a significant hysteresis between the cooling and heating runs, see Fig. 1. This different behaviour can be certainly ascribed to a stronger electrostatic interaction which favours the formation of tightly interacting ion pairs (which are actually formed by two LJ spheres and one GB disk because of the stoichiometry of the phase).
behaves somewhat differently. The isotropic mixed phase is strongly stabilized by the larger charge. As the T* is lowered, 〈P2〉 shows a net jump, suggesting a first order transition, but the nematic phase appears to be stable for a small range of T* before undergoing the Nem-to-Col transition. Moreover, there is a significant hysteresis between the cooling and heating runs, see Fig. 1. This different behaviour can be certainly ascribed to a stronger electrostatic interaction which favours the formation of tightly interacting ion pairs (which are actually formed by two LJ spheres and one GB disk because of the stoichiometry of the phase).
To summarize, the introduction of electrostatic interactions disfavors the phase separation observed in the non-charged systems.20 Nonetheless, a tendency in the segregation of the GB and the LJ particles is still present and it is manifested, as shown above, by the formation of layers of oppositely charged particles in a similar fashion to lyotropic lamellar phases33 or smectic phases of rod-like LCs. A similar alternation of layers was reported also in ref. 34 where a system of oppositely charged discotic particle was investigated. The Authors observed the formation of a “smectic” phase where each alternating layer consisted of disks of the same charge. On the other hand, charged colloidal spherical particles were also found to exhibit a fluid layered structure,35 as well as the so-called inverse patchy colloids36 modeled by a sphere with two charged regions at the poles and an oppositely charged equatorial belt. These observations point to the charge as the main ordering mechanism responsible to the layers formation, while the particle's shape is likely to play a minor role.
Representative low T* snapshots of GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 systems are reported in Fig. 4 to clearly highlight the effect of the charge. It appears that increasing the charge has the effect of reducing the thickness of the lamellae, therefore producing more intercalated discotic phases. This effect can be ascribed to the increased repulsion between like particles (forming a given layer) for higher charges. We calculated the layers thickness of the GB and LJ layers by inspection of the density profile projected along the nematic director, see Fig. 5. The width at half height of the LJ and GB density profile can be taken as a measure of the thickness of the respective layers; these values are also reported in Table 3. Finally, in Fig. S3, S7 and S11 in ESI† we report the RDF of GB–GB distance resolved parallel and perpendicular to the director,
2 systems are reported in Fig. 4 to clearly highlight the effect of the charge. It appears that increasing the charge has the effect of reducing the thickness of the lamellae, therefore producing more intercalated discotic phases. This effect can be ascribed to the increased repulsion between like particles (forming a given layer) for higher charges. We calculated the layers thickness of the GB and LJ layers by inspection of the density profile projected along the nematic director, see Fig. 5. The width at half height of the LJ and GB density profile can be taken as a measure of the thickness of the respective layers; these values are also reported in Table 3. Finally, in Fig. S3, S7 and S11 in ESI† we report the RDF of GB–GB distance resolved parallel and perpendicular to the director,  and
and  , respectively. They confirm the assignment of the phases in agreement with the isotropic RDF of Fig. 3, while giving some additional information concerning the ordered phase. The in-plane correlation is typical of a hexagonal arrangement: for an ideal case of planar hexagonal lattice of disks we would observe a peak at 1.00 (the first shell) and a double peak at 1.732 and 2.00 (the second shell). These are clearly visible in all the isotropic RDFs and
, respectively. They confirm the assignment of the phases in agreement with the isotropic RDF of Fig. 3, while giving some additional information concerning the ordered phase. The in-plane correlation is typical of a hexagonal arrangement: for an ideal case of planar hexagonal lattice of disks we would observe a peak at 1.00 (the first shell) and a double peak at 1.732 and 2.00 (the second shell). These are clearly visible in all the isotropic RDFs and  , though the peaks are slightly scaled down because of some degree of interdigitation of the disks. More interesting is the parallel component: for the
, though the peaks are slightly scaled down because of some degree of interdigitation of the disks. More interesting is the parallel component: for the  system, the lack of a long range structure in the
system, the lack of a long range structure in the  (see Fig. S3 in ESI†) clearly suggests that the short columns existing within each discotic layer do not correlate with the columns in the next discotic layer. In contrast, for the thinner layers of the systems with higher charge the columns are correlated through the whole box (see Fig. S7 and S11 in ESI†).
(see Fig. S3 in ESI†) clearly suggests that the short columns existing within each discotic layer do not correlate with the columns in the next discotic layer. In contrast, for the thinner layers of the systems with higher charge the columns are correlated through the whole box (see Fig. S7 and S11 in ESI†).
GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) LJ 1
LJ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
We now consider the GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 systems. Again, they have similar trends when
1 systems. Again, they have similar trends when  are 0.0, 0.5 or 1.0. These systems do not possess order at high T* (〈P2〉 and 〈Ψ6〉 both close to zero, see Fig. 6), thus being isotropic and homogeneously mixed, e.g. see Fig. 7a for some representative snapshots. Moreover, the radial distribution functions, Fig. S14 and S18 in ESI,† do not show any long-range order for the different particle pairs, thus confirming an isotropic mixed phase. As the T* is lowered all the systems undergo a transition to a more ordered phase as can be appreciated by looking again at the relevant snapshot in Fig. 7b and the radial distribution functions in ESI.† As for the GB
are 0.0, 0.5 or 1.0. These systems do not possess order at high T* (〈P2〉 and 〈Ψ6〉 both close to zero, see Fig. 6), thus being isotropic and homogeneously mixed, e.g. see Fig. 7a for some representative snapshots. Moreover, the radial distribution functions, Fig. S14 and S18 in ESI,† do not show any long-range order for the different particle pairs, thus confirming an isotropic mixed phase. As the T* is lowered all the systems undergo a transition to a more ordered phase as can be appreciated by looking again at the relevant snapshot in Fig. 7b and the radial distribution functions in ESI.† As for the GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the systems show negligible hysteresis in the Iso-to-Nem transition (transition temperatures are reported in Table 2.) By continuing to lower T* we bring the systems into a columnar hexagonal phase (Fig. 7c). The transition Nem-to-Col is a sharp first order transition, as can be seen for 〈Ψ6〉 trends in Fig. 6. The systems with
2, the systems show negligible hysteresis in the Iso-to-Nem transition (transition temperatures are reported in Table 2.) By continuing to lower T* we bring the systems into a columnar hexagonal phase (Fig. 7c). The transition Nem-to-Col is a sharp first order transition, as can be seen for 〈Ψ6〉 trends in Fig. 6. The systems with  and 1.0 show negligible hysteresis in the Nem-to-Col transition, while the system with zero-charge shows a small hysteresis due to the demixing process of uncharged particles.20
and 1.0 show negligible hysteresis in the Nem-to-Col transition, while the system with zero-charge shows a small hysteresis due to the demixing process of uncharged particles.20
The system with  has, again, a partly different behaviour compared to the system with
has, again, a partly different behaviour compared to the system with 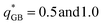 , nonetheless it behaves similarly to the system with
, nonetheless it behaves similarly to the system with  and GB
and GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry. It is isotropic for a broad range of temperatures, as can be seen from Fig. 6 the 〈P2〉 and 〈Ψ6〉 order parameters are close to 0, down to T* = 2.0. As the T* is lowered the system undergoes two distinct first order phase transitions with sharp jumps in 〈P2〉 and 〈Ψ6〉 values. The nematic phase has a small thermal range of existence and it shows no hysteresis in the Iso-to-Nem transition. On the other hand, the Nem-to-Col transition shows a small hysteresis (see Table 2).
2 stoichiometry. It is isotropic for a broad range of temperatures, as can be seen from Fig. 6 the 〈P2〉 and 〈Ψ6〉 order parameters are close to 0, down to T* = 2.0. As the T* is lowered the system undergoes two distinct first order phase transitions with sharp jumps in 〈P2〉 and 〈Ψ6〉 values. The nematic phase has a small thermal range of existence and it shows no hysteresis in the Iso-to-Nem transition. On the other hand, the Nem-to-Col transition shows a small hysteresis (see Table 2).
The low T* snapshots of GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and all the different charges are reported in Fig. 8. The macroscopic phase separation of uncharged LJ and GB occurs at low T* and two distinct phases are found: a columnar hexagonal one and an isotropic one.20 The introduction of charges disfavors the de-mixing process and the segregation of phases. However, for the relatively small charge of 0.5, see Fig. 8b, we still observe a clear short-range microphase segregation between disks and speres, while increasing the value of q* leads to a more homogeneous distribution of spheres within the GB matrix.
1 and all the different charges are reported in Fig. 8. The macroscopic phase separation of uncharged LJ and GB occurs at low T* and two distinct phases are found: a columnar hexagonal one and an isotropic one.20 The introduction of charges disfavors the de-mixing process and the segregation of phases. However, for the relatively small charge of 0.5, see Fig. 8b, we still observe a clear short-range microphase segregation between disks and speres, while increasing the value of q* leads to a more homogeneous distribution of spheres within the GB matrix.
In contrast to the previous stoichiometry, however, the amount of spheres is not sufficient to promote the formation of separate layers of LJ particles, rather relatively small domains with finite size are formed. Moreover, as the GB disks charge increases (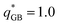 and
and  in Fig. 8c and d) the structure of columnar hexagonal phase boxes varies. The electrostatic interactions between GB–GB particles disfavour the face-to-face configuration and the even distribution of disks within the box produces columns with some disorder. Nonetheless, the GB particles form planes of disks arranged in a hexagonal fashion (see Fig. 7c) for a top view). These observations are confirmed by the parallel and perpendicular RDF in Fig. S15, S19 and S23 in ESI:† while for the systems with small and medium charge (
in Fig. 8c and d) the structure of columnar hexagonal phase boxes varies. The electrostatic interactions between GB–GB particles disfavour the face-to-face configuration and the even distribution of disks within the box produces columns with some disorder. Nonetheless, the GB particles form planes of disks arranged in a hexagonal fashion (see Fig. 7c) for a top view). These observations are confirmed by the parallel and perpendicular RDF in Fig. S15, S19 and S23 in ESI:† while for the systems with small and medium charge ( and
and  ) there is a clear long-range structure of
) there is a clear long-range structure of  , for the systems with
, for the systems with  we note a less clear pattern indicating a loss of correlation for the face-to-face stacking of disks within a column.
we note a less clear pattern indicating a loss of correlation for the face-to-face stacking of disks within a column.
GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) LJ 2
LJ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
Finally, we discuss the results for the GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 2
LJ = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 systems. A behaviour qualitatively similar to the previous stoichiometries is found for the systems with
1 systems. A behaviour qualitatively similar to the previous stoichiometries is found for the systems with  , 0.5 and 1.0. At high T*, an isotropic mixed phase is present in all the systems, as can be seen in Fig. 9 since 〈P2〉 and 〈Ψ6〉 order parameters are close to 0. A snapshot of the box in Fig. 10a confirms the assignment as well as the RDFs of the particles’ pairs (Fig. S26 and S30 in ESI†) show no long-range positional order. Cooling down the temperature results in the discotic nematic phase followed by a hexagonal columnar phase, see Fig. 10b and c and Table 2. The systems show negligible hysteresis for the Iso-to-Nem transitions and small hysteresis in the Nem-to-Col transition. Low-temperature trends of 〈P2〉 suggest the transition to other liquid crystalline phases which are not further investigated here. For this case with GB
, 0.5 and 1.0. At high T*, an isotropic mixed phase is present in all the systems, as can be seen in Fig. 9 since 〈P2〉 and 〈Ψ6〉 order parameters are close to 0. A snapshot of the box in Fig. 10a confirms the assignment as well as the RDFs of the particles’ pairs (Fig. S26 and S30 in ESI†) show no long-range positional order. Cooling down the temperature results in the discotic nematic phase followed by a hexagonal columnar phase, see Fig. 10b and c and Table 2. The systems show negligible hysteresis for the Iso-to-Nem transitions and small hysteresis in the Nem-to-Col transition. Low-temperature trends of 〈P2〉 suggest the transition to other liquid crystalline phases which are not further investigated here. For this case with GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 2
LJ = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, at variance with the previously discussed stoichiometries, the system with a relatively high charge,
1, at variance with the previously discussed stoichiometries, the system with a relatively high charge, 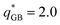 , appears to behave qualitatively in a similar way to its homologues with low-charge, see Fig. 9. Likely, the abundance of GB particles stabilizes the nematic phase resulting in a wider T* range of thermal stability of the discotic nematic phase. Moreover, the onset of a columnar hexagonal phase occurs at a higher T* compared to the other stoichiometries. The system shows no hysteresis in the Iso-to-Nem transition, while a small hysteresis is found when the system has a Nem-to-Col transition.
, appears to behave qualitatively in a similar way to its homologues with low-charge, see Fig. 9. Likely, the abundance of GB particles stabilizes the nematic phase resulting in a wider T* range of thermal stability of the discotic nematic phase. Moreover, the onset of a columnar hexagonal phase occurs at a higher T* compared to the other stoichiometries. The system shows no hysteresis in the Iso-to-Nem transition, while a small hysteresis is found when the system has a Nem-to-Col transition.
As for the other two stoichiometries investigated, we check the morphology of the low-temperature phases. The snapshots of the boxes with different charge are reported in Fig. 11 and, as we can appreciate, the hexagonal columnar order is present in all cases. Moreover, except for the uncharged systems, the microphase segregation is quite inhibited.
Introducing the charge ( , Fig. 11b), improves the dispersion of LJ particles within the box. The relatively low charge on GB particles enables the disks to be stacked face-to-face, producing highly aligned columns surrounded by negatively charged LJ particles. When the charge on GB particles increases (
, Fig. 11b), improves the dispersion of LJ particles within the box. The relatively low charge on GB particles enables the disks to be stacked face-to-face, producing highly aligned columns surrounded by negatively charged LJ particles. When the charge on GB particles increases ( , Fig. 11c) the columns tend to be made of tilted disks, since LJ particles,
, Fig. 11c) the columns tend to be made of tilted disks, since LJ particles,  , act like the system at GB
, act like the system at GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and
1 and 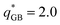 , Fig. 11d). Interestingly, the
, Fig. 11d). Interestingly, the  system forms a unique structure at low T* values with a 〈P2〉 that never exceed 0.8 (as indicated by the more green shades of the particles), suggesting looser stacking of the disks, as can be seen in Fig. 11d. The LJ particles are evenly distributed within the simulation box. Moreover, two GB particles assemble into a “V” shaped motif with a LJ sphere in-between the “V” formed by two disks.
system forms a unique structure at low T* values with a 〈P2〉 that never exceed 0.8 (as indicated by the more green shades of the particles), suggesting looser stacking of the disks, as can be seen in Fig. 11d. The LJ particles are evenly distributed within the simulation box. Moreover, two GB particles assemble into a “V” shaped motif with a LJ sphere in-between the “V” formed by two disks.
In Fig. 12 we show the same snapshot also presented in Fig. 11d, but using a different colouring scheme for the disks. These are now green or red depending on the sign of the tilt of the disk axis with respect to the director. Using these colours it appears clear that there is an alternation of layers with a different tilt in the hexagonal columnar phase.
 | ||
| Fig. 12 The “V” motif is represented on the left, while on the right the same snapshots as in Fig. 11d is shown. The slight deviations from the nematic director are highlighted in red and green depending on the direction of the tilt. | ||
The parallel RDF in Fig. S35 of ESI† confirms a complex arrangement of the disks in the frustrated columnar phase of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system with
1 system with  in contrast to the systems with a lower charge where the columns are well defined (see Fig. S27 and S31 in ESI†). In particular, the peak in
in contrast to the systems with a lower charge where the columns are well defined (see Fig. S27 and S31 in ESI†). In particular, the peak in  at
at  , which is observed only in this system, corresponds to two disks arranged as the insert of Fig. 12.
, which is observed only in this system, corresponds to two disks arranged as the insert of Fig. 12.
General discussion
To compare the results obtained we group together the important information in Fig. 13. The thermal ranges of existence of the different phases are indicated with different colours for the various of GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ stoichiometries and
LJ stoichiometries and  charge. The systems are all characterized by a high T* isotropic phase and a low T* columnar hexagonal phase. In between these two boundaries the systems develop discotic nematic order. The overall effect of the introduction of charges is to lower all the transition temperatures, both
charge. The systems are all characterized by a high T* isotropic phase and a low T* columnar hexagonal phase. In between these two boundaries the systems develop discotic nematic order. The overall effect of the introduction of charges is to lower all the transition temperatures, both  and
and 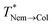 . Moreover, the GB-rich systems have a nematic phase extending for a broader range of temperatures compared to the GB-poor ones. This is reasonable since the GB disks are the nematogenic particles. On the other hand, the columnar hexagonal order and
. Moreover, the GB-rich systems have a nematic phase extending for a broader range of temperatures compared to the GB-poor ones. This is reasonable since the GB disks are the nematogenic particles. On the other hand, the columnar hexagonal order and  it is somewhat affected by the GB content having all the transition T* comparable among all the systems. The effect is, however, to reduce the thermal range of the columnar phase in the GB-rich systems.
it is somewhat affected by the GB content having all the transition T* comparable among all the systems. The effect is, however, to reduce the thermal range of the columnar phase in the GB-rich systems.
 | ||
Fig. 13 Diagram of the transition temperatures (see Table 2) of all the systems studied as a function of GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ stoichiometry and LJ stoichiometry and  . On the left GB . On the left GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1 LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, in the centre GB 2, in the centre GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1 LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and on the right GB 1 and on the right GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 2 LJ = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries are reported. Each GB 1 stoichiometries are reported. Each GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ stoichiometry consists of 4 different charges: LJ stoichiometry consists of 4 different charges:  ,20 0.5, 1.0 and 2.0. Each color represents the phase in which the system is found: isotropic (yellow), nematic (purple), columnar (blue). The grey area is the intermediate region with weak nematic order. ,20 0.5, 1.0 and 2.0. Each color represents the phase in which the system is found: isotropic (yellow), nematic (purple), columnar (blue). The grey area is the intermediate region with weak nematic order. | ||
The state points investigated cover a wide range of scaled pressures, as can be seen in Fig. S37 in ESI.† Similar values were found for the non-charged mixtures20 as well as for the pure discotic GB investigated by Bates and Luckhurst.27
We also report in Table 4 a summary of the type of columnar mesophases formed, for an easier reference. We focus on the Col phase since all systems exhibit similar isotropic and nematic phases, the main differences among them being in the degree of nano-segregation, which is absent for the highly charged cases and not-negligible (even though limited in scale) for the weakly charged ones.
| 0.5 | 1.0 | 2.0 | |
|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
Thick Lam, Hex Col within GB layers, no correlation between different layers | Medium Lam, columns correlated through several layers | Thin Lam, columns correlated through several layers |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Hex Col, average correlation along a column | Hex Col, weak correlation along a column | Hex Col, very weak correlation along a column |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Hex Col, high correlation along a column | Hex Col, high correlation along a column | Frustrated Hex Col with modulated tilt of the director |
Finally, we wish to make some attempts to connect the results of our simulations with available experimental data. The large majority of thermotropic discotic ionic liquid crystals only form columnar mesophases.37 Some typical examples made by a disk-like cation and a small spherical anion are compounds 1 and 2 in Fig. 14, with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. Depending on the alkyl chain length and metal ion, the metallomesogens 1 have a columnar hexagonal phase between room temperature and 250 °C.38 Similarly, the 2,4,6-triarylpyrylium tetrafluoroborates 2 have a columnar phase between room temperature and 200 °C.39 In contrast to the results of the simulations, discotic nematic phases are very rare in real systems.2 This is likely due to the necessity of having relatively long alkyl chains on the discotic particles, see Fig. 14, to enhance fluidity; the chains, however, also promote nano-segregation between the ionic parts and the hydrophobic tails, similarly to the mechanism of formation of smectic phase in calamitic ILCs.40,41 Therefore, the simulations suggests that in order to favour discotic nematic phases, short chains are needed so that nano-segregation will not dominate the phase behaviour.
1 stoichiometry. Depending on the alkyl chain length and metal ion, the metallomesogens 1 have a columnar hexagonal phase between room temperature and 250 °C.38 Similarly, the 2,4,6-triarylpyrylium tetrafluoroborates 2 have a columnar phase between room temperature and 200 °C.39 In contrast to the results of the simulations, discotic nematic phases are very rare in real systems.2 This is likely due to the necessity of having relatively long alkyl chains on the discotic particles, see Fig. 14, to enhance fluidity; the chains, however, also promote nano-segregation between the ionic parts and the hydrophobic tails, similarly to the mechanism of formation of smectic phase in calamitic ILCs.40,41 Therefore, the simulations suggests that in order to favour discotic nematic phases, short chains are needed so that nano-segregation will not dominate the phase behaviour.
Despite the observation above, concerning the ubiquitous presence of columnar phases of discotic ILCs, some cases have been reported in the literature concerning ionic discotic molecules forming lamellar phases, as we have observed in our simulations. For example, Sørensen et al.42,43 have synthesized and characterized ionic discotic compounds 3 in Fig. 14 and observed a lamellar structure with alternation of planes of cations and anions. Camerel et al.44 reported a series of Cu complexes with 1,10-phenantroline derivatives (4 in Fig. 14) forming lamellar phases, even though in this case the layering was promoted by the nano-segregation between the ionic cores and the alkylic regions.
Finally, it is noteworthy that mixtures of oppositely charged nanoparticles (NPs) of spherical and discotic shape have been very recently prepared.45 The system investigated experimentally is somewhat different from our simulations since the spherical NPs are much larger than the discotic NPs, nonetheless, the Authors speculate on how the charge of the NPs is the key factor opposing the aggregation of the same type of NPs together, thus preventing a phase separation. Moreover, nowadays it is possible to fabricate NPs of any shape and size,46,47 therefore we expect that after an appropriate control of the charge, more and more systems similar to the ones we have investigated in this work, will be experimentally accessible.
Conclusions
We have investigated the phase behaviour of mixtures of charged soft oblate ellipsoids (disks) and soft spheres as models of discotic ionic liquid crystals and possibly colloidal suspensions. The systems exhibited a rich mesomorphism as a function of the temperature at fixed packing fraction. We have observed isotropic, discotic nematic and hexagonal columnar phases, as expected, but also unusual lamellar phases formed by an alternation of disks and spheres as well as frustrated columnar phases with an alternating tilt of the director.The presence of a opposite charge on the two types of particles prevents the macroscopic phase separation which is observed in the non-charged cases studied in our previous paper.20 However, the excluded volume interactions are still important when the magnitude of the charge is relatively low and the volume fraction of spheres is relatively large. This combined effect leads to a lamellar structure where layers of disks are alternating with layers of spheres. Although such arrangement might be difficult to be realized at a molecular level (that is for common ILC systems), it appears as a reasonable option for colloidal suspension of mixtures of oppositely charged nanoparticles, where the magnitude of the electrostatic interaction can be modulated more freely by a proper design of the chemical composition of the surface of the nanoparticle itself.
At low temperature, and for the largest charge studied, 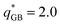 (which, for the three stoichiometries 1
(which, for the three stoichiometries 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 corresponds to an opposite charge on the LJ particles of −1.0, 2.0 and 4.0, respectively), the phase structure is strongly influenced by structure of the minimum neutral ion pair, which is a disk paired with two spheres for the 1
1 corresponds to an opposite charge on the LJ particles of −1.0, 2.0 and 4.0, respectively), the phase structure is strongly influenced by structure of the minimum neutral ion pair, which is a disk paired with two spheres for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 systems, a disk paired with one sphere for the 1
2 systems, a disk paired with one sphere for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system and a sphere paired with two disks for the 2
1 system and a sphere paired with two disks for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system. The necessity of an efficient packing of the neutral unit leads to rather different structures. For the 1
1 system. The necessity of an efficient packing of the neutral unit leads to rather different structures. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 system, we have an alternation of layers of disks and spheres that for the highest charge case have a very low thickness, almost corresponding to just one particle per layer. For the 1
2 system, we have an alternation of layers of disks and spheres that for the highest charge case have a very low thickness, almost corresponding to just one particle per layer. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system, we have a hexagonal columnar phase with a well-defined hexagonal arrangement of disks in the plane perpendicular to the director, but the columns appear poorly defined. Finally, for the case with an excess of GB particles (and where the volume fraction of spheres is therefore very low), the 2
1 system, we have a hexagonal columnar phase with a well-defined hexagonal arrangement of disks in the plane perpendicular to the director, but the columns appear poorly defined. Finally, for the case with an excess of GB particles (and where the volume fraction of spheres is therefore very low), the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system, we observe a hexagonal columnar phase but where the tilt of the symmetry axis of the disk is not constant, rather it varies giving rise to a wave-like pattern.
1 system, we observe a hexagonal columnar phase but where the tilt of the symmetry axis of the disk is not constant, rather it varies giving rise to a wave-like pattern.
Finally, the observed dependence of the layer thickness, for GB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LJ = 1
LJ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometries, of the lamellae found in the low-temperature phases it is indeed an interesting issue that we plan to investigate in more details in the future in order to establish a relationship with the charge magnitude. This will provide a useful tool to “measure” the tendency of phase separation between particles of different shape as due to excluded volume effects.
2 stoichiometries, of the lamellae found in the low-temperature phases it is indeed an interesting issue that we plan to investigate in more details in the future in order to establish a relationship with the charge magnitude. This will provide a useful tool to “measure” the tendency of phase separation between particles of different shape as due to excluded volume effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the C3P community of the Department of Chemical Sciences of the University of Padova for the allocation of computing resources. We also thank the CINECA Supercomputing Centre (Bologna, Italy) for granting cpu time through the ISCRA project nr. HP10B8AOVV.Notes and references
- K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Ionic Liquid Crystals: Versatile Materials, Chem. Rev., 2016, 116(8), 4643–4807, DOI:10.1021/cr400334b.
- N. Kapernaum, A. Lange, M. Ebert, M. A. Grunwald, C. Haege, S. Marino, A. Zens, A. Taubert, F. Giesselmann and S. Laschat, Current Topics in Ionic Liquid Crystals, ChemPlusChem, 2022, 87(1), e202100397, DOI:10.1002/cplu.202100397.
- Q. Ruan, M. Yao, D. Yuan, H. Dong, J. Liu, X. Yuan, W. Fang, G. Zhao and H. Zhang, Ionic Liquid Crystal Electrolytes: Fundamental, Applications and Prospects, Nano Energy, 2023, 106, 108087, DOI:10.1016/j.nanoen.2022.108087.
- N. Yamanaka, R. Kawano, W. Kubo, N. Masaki, T. Kitamura, Y. Wada, M. Watanabe and S. Yanagida, Dye-Sensitized TiO2 Solar Cells Using Imidazolium-Type Ionic Liquid Crystal Systems as Effective Electrolytes, J. Phys. Chem. B, 2007, 111(18), 4763–4769, DOI:10.1021/jp0671446.
- J. Kloos, N. Joosten, A. Schenning and K. Nijmeijer, Self-Assembling Liquid Crystals as Building Blocks to Design Nanoporous Membranes Suitable for Molecular Separations, J. Memb. Sci., 2021, 620, 118849, DOI:10.1016/j.memsci.2020.118849.
- K. Salikolimi, A. A. Sudhakar and Y. Ishida, Functional Ionic Liquid Crystals, Langmuir, 2020, 36(40), 11702–11731, DOI:10.1021/acs.langmuir.0c01935.
- Y. Ishii, N. Matubayasi and H. Washizu, Nonpolarizable Force Fields through the Self-Consistent Modeling Scheme with MD and DFT Methods: From Ionic Liquids to Self-Assembled Ionic Liquid Crystals, J. Phys. Chem. B, 2022, 126(24), 4611–4622, DOI:10.1021/acs.jpcb.2c02782.
- T. Sakamoto, T. Ogawa, H. Nada, K. Nakatsuji, M. Mitani, B. Soberats, K. Kawata, M. Yoshio, H. Tomioka and T. Sasaki, et al., Development of Nanostructured Water Treatment Membranes Based on Thermotropic Liquid Crystals: Molecular Design of Sub-Nanoporous Materials, Adv. Sci., 2018, 5(1), 1700405, DOI:10.1002/advs.201700405.
- M. R. Schenkel, J. B. Hooper, M. J. Moran, L. A. Robertson, D. Bedrov and D. L. Gin, Effect of Counter-Ion on the Thermotropic Liquid Crystal Behaviour of Bis(Alkyl)-Tris(Imidazolium Salt) Compounds, Liq. Cryst., 2014, 41, 1668–1685, DOI:10.1080/02678292.2014.948087.
- G. Saielli, The Effect of Hydration on the Stability of Ionic Liquid Crystals: MD Simulations of [C14C1im]Cl and [C14C1im]Cl·H2O, Phys. Chem. Chem. Phys., 2021, 23(42), 24386–24395, 10.1039/D1CP03757A.
- C. Avendaño, A. Gil-Villegas and E. González-Tovar, A Monte Carlo Simulation Study of Binary Mixtures of Charged Hard Spherocylinders and Charged Hard Spheres, Chem. Phys. Lett., 2009, 470(1), 67–71, DOI:10.1016/j.cplett.2009.01.017.
- C. Haege, S. Jagiella and F. Giesselmann, Towards Nematic Phases in Ionic Liquid Crystals – A Simulation Study, Chem. Phys. Chem., 2023, 24(1), e202200424, DOI:10.1002/cphc.202200424.
- G. Saielli, T. Margola and K. Satoh, Tuning Coulombic Interactions to Stabilize Nematic and Smectic Ionic Liquid Crystal Phases in Mixtures of Charged Soft Ellipsoids and Spheres, Soft Matter, 2017, 13(30), 5204–5213, 10.1039/c7sm00612h.
- G. Saielli and K. Satoh, A Coarse-Grained Model of Ionic Liquid Crystals: The Effect of Stoichiometry on the Stability of the Ionic Nematic Phase, Phys. Chem. Chem. Phys., 2019, 21(36), 20327–20337, 10.1039/c9cp03296g.
- T. Margola, G. Saielli and K. Satoh, MD Simulations of Mixtures of Charged Gay-Berne and Lennard-Jones Particles as Models of Ionic Liquid Crystals, Mol. Cryst. Liq. Cryst., 2017, 649(1), 50–58, DOI:10.1080/15421406.2017.1303918.
- H. Bartsch, M. Bier and S. Dietrich, The Role of Counterions in Ionic Liquid Crystals, J. Chem. Phys., 2021, 154(1), 14901, DOI:10.1063/5.0034314.
- T. Margola, K. Satoh and G. Saielli, Comparison of the Mesomorphic Behaviour of 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Mixtures of Charged Gay-Berne GB(4.4,20.0,1,1) and Lennard-Jones Particles, Crystals, 2018, 8(10), 371, DOI:10.3390/cryst8100371.
2 Mixtures of Charged Gay-Berne GB(4.4,20.0,1,1) and Lennard-Jones Particles, Crystals, 2018, 8(10), 371, DOI:10.3390/cryst8100371. - L. Morales-Anda, H. H. Wensink, A. Galindo and A. Gil-Villegas, Anomalous Columnar Order of Charged Colloidal Platelets, J. Chem. Phys., 2012, 136(3), 34901, DOI:10.1063/1.3673877.
- S. Jabbari-Farouji, J.-J. Weis, P. Davidson, P. Levitz and E. Trizac, Interplay of Anisotropy in Shape and Interactions in Charged Platelet Suspensions, J. Chem. Phys., 2014, 141(22), 224510, DOI:10.1063/1.4903045.
- V. Mazzilli, K. Satoh and G. Saielli, Mixtures of Discotic and Spherical Soft Particles: De-Mixing, Liquid Crystal Behaviour and Relative Solubility, J. Mol. Liq., 2022, 347, 117973, DOI:10.1016/j.molliq.2021.117973.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., LAMMPS - a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- S. Nosé, A Molecular Dynamics Method for Simulations in the Canonical Ensemble, Mol. Phys., 1984, 52(2), 255–268, DOI:10.1080/00268978400101201.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31(3), 1695–1697, DOI:10.1103/PhysRevA.31.1695.
- R. Hockney and J. Eastwood, Computer Simulation Using Particles, Adam Hilger, New York, 1989 Search PubMed.
- J. Kolafa and J. W. Perram, Cutoff Errors in the Ewald Summation Formulae for Point Charge Systems, Mol. Simul., 1992, 9(5), 351–368, DOI:10.1080/08927029208049126.
- M. Deserno and C. Holm, How to Mesh up Ewald Sums. II. An Accurate Error Estimate for the Particle–Particle–Particle-Mesh Algorithm, J. Chem. Phys., 1998, 109(18), 7694–7701, DOI:10.1063/1.477415.
- M. A. Bates and G. R. Luckhurst, Computer Simulation Studies of Anisotropic Systems. XXVI. Monte Carlo Investigations of a Gay–Berne Discotic at Constant Pressure, J. Chem. Phys., 1996, 104(17), 6696–6709, DOI:10.1063/1.471387.
- R. Berardi, C. Fava and C. Zannoni, A Gay–Berne Potential for Dissimilar Biaxial Particles, Chem. Phys. Lett., 1998, 297(1–2), 8–14, DOI:10.1016/S0009-2614(98)01090-2.
- W. M. Brown, M. K. Petersen, S. J. Plimpton and G. S. Grest, Liquid Crystal Nanodroplets in Solution, J. Chem. Phys., 2009, 130(4), 44901, DOI:10.1063/1.3058435.
- D. R. Nelson and B. I. Halperin, Dislocation-Mediated Melting in Two Dimensions, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19(5), 2457–2484, DOI:10.1103/PhysRevB.19.2457.
- E. K. Lindenberg and G. N. Patey, Melting Point Trends and Solid Phase Behaviors of Model Salts with Ion Size Asymmetry and Distributed Cation Charge, J. Chem. Phys., 2015, 143(2), 24508, DOI:10.1063/1.4923344.
- A. T. Gabriel, T. Meyer and G. Germano, Molecular Graphics of Convex Body Fluids, J. Chem. Theory Comput., 2008, 4(3), 468–476, DOI:10.1021/ct700192z.
- H. Kumar, A. Sureshkumar, N. Badduri and V. Jain, A Review on Lyotropic Liquid Crystals and Its Potential Applications, Nanosci. Nanotechnol. –Asia, 2021, 11(6), e070921191139, DOI:10.2174/2210681211666210204114532.
- G. C. Ganzenmueller and G. N. Patey, Charge Ordering Induces a Smectic Phase in Oblate Ionic Liquid Crystals, Phys. Rev. Lett., 2010, 105(13), 137801, DOI:10.1103/PhysRevLett.105.137801.
- F. Smallenburg and M. Dijkstra, Phase Diagram of Colloidal Spheres in a Biaxial Electric or Magnetic Field, J. Chem. Phys., 2010, 132(20), 204508, DOI:10.1063/1.3425734.
- E. G. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Phase Diagram of Inverse Patchy Colloids Assembling into an Equilibrium Laminar Phase, Soft Matter, 2014, 10(42), 8464–8474, 10.1039/C4SM01559B.
- S. K. Pal and S. Kumar, Ionic Discotic Liquid Crystals: Recent Advances and Applications, Biosensors Nanotechnology, 2014, pp. 267–314 DOI:10.1002/9781118773826.ch9.
- H.-C. Wu, J.-H. Sung, C.-D. Yang and C. K. Lai, Ionic Hexagonal Columnar Metallomesogens Derived from Tetrabenzo[b,f,j,n] [1,5,9,13]Tetraazacyclohexadecine, Liq. Cryst., 2001, 28(3), 411–415, DOI:10.1080/02678290010017926.
- P. Davidson, C. Jallabert, A. M. Levelut, H. Strzelecka and M. Veber, Synthesis and X-Ray Study of New Columnar Heteroaromatic Salts, Liq. Cryst., 1988, 3(1), 133–137, DOI:10.1080/02678298808086357.
- Y. Ji, R. Shi, Y. Wang and G. Saielli, Effect of the Chain Length on the Structure of Ionic Liquids: From Spatial Heterogeneity to Ionic Liquid Crystals, J. Phys. Chem. B, 2013, 117(4), 1104–1109, DOI:10.1021/jp310231f.
- Y.-L. Wang, B. Li and A. Laaksonen, Coarse-Grained Simulations of Ionic Liquid Materials: From Monomeric Ionic Liquids to Ionic Liquid Crystals and Polymeric Ionic Liquids, Phys. Chem. Chem. Phys., 2021, 23(35), 19435–19456, 10.1039/D1CP02662C.
- T. J. Sørensen, C. B. Hildebrandt, M. Glyvradal and B. W. Laursen, Synthesis, Optical Properties and Lamellar Self-Organization of New N,N′,N′′-Trialkyl-Triazatriangulenium Tetrafluoroborate Salts, Dye. Pigment., 2013, 98(2), 297–303, DOI:10.1016/j.dyepig.2013.03.006.
- T. J. Sørensen, C. B. Hildebrandt, J. Elm, J. W. Andreasen, A. Ø. Madsen, F. Westerlund and B. W. Laursen, Large Area, Soft Crystalline Thin Films of N,N′,N′′-Trialkyltriazatriangulenium Salts with Homeotropic Alignment of the Discotic Cores in a Lamellar Lattice, J. Mater. Chem., 2012, 22(11), 4797–4805, 10.1039/C2JM15954F.
- F. Camerel, P. Strauch, M. Antonietti and C. F. J. Faul, Copper–Metallomesogen Structures Obtained by Ionic Self-Assembly (ISA): Molecular Electromechanical Switching Driven by Cooperativity, Chem. – Eur. J., 2003, 9(16), 3764–3771, DOI:10.1002/chem.200204693.
- G. Rezvan, M. Esmaeili, M. Sadati and N. Taheri-Qazvini, Hybrid Colloidal Gels with Tunable Elasticity Formed by Charge-Driven Assembly between Spherical Soft Nanoparticles and Discotic Nanosilicates, J. Colloid Interface Sci., 2022, 627, 40–52, DOI:10.1016/j.jcis.2022.07.039.
- Y. C. Saraswat, F. Ibis, L. Rossi, L. Sasso, H. B. Eral and P. Fanzio, Shape Anisotropic Colloidal Particle Fabrication Using 2-Photon Polymerization, J. Colloid Interface Sci., 2020, 564, 43–51, DOI:10.1016/j.jcis.2019.12.035.
- J. A. Champion, Y. K. Katare and S. Mitragotri, Making Polymeric Micro- and Nanoparticles of Complex Shapes, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(29), 11901–11904, DOI:10.1073/pnas.0705326104.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00223c |
| This journal is © The Royal Society of Chemistry 2023 |