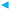Effect of scission on alignment of nonionic surfactant micelles under shear flow

Abstract

We investigate the alignment of wormlike micelles under shear flow with dissipative particle dynamics simulations of nonionic surfactant solutions. To reveal the effect of micellar scission on alignment, we evaluate the shear-rate dependence of the mean orientation angle and the average lifetime of micelles for fixed aggregation numbers. Our numerical results demonstrate the presence of two distinct shear-rate regimes of micellar alignment. In the low shear-rate regime, where flow-induced scission does not occur, wormlike micelles align more in the flow direction with the shear rate. In contrast, flow-induced scission suppresses micellar alignment in the high shear-rate regime. In addition, comparing the alignment of wormlike micelles with that of polymers without scission, we find that the mean orientation angle of wormlike micelles is larger than that of polymers when flow-induced scission occurs. This comparison confirms that flow-induced scission yields the unique behavior of micellar alignment. Furthermore, we demonstrate that flow-induced scission suppresses micellar alignment for fixed aggregation numbers by reducing the effective longest relaxation time of micelles.

---

1. Introduction

One of the significant differences between polymers and wormlike micelles is the underlying mechanism of their structure formation. Polymers are based on covalent bonds, whereas surfactant micelles are on weak non-bonded interactions. Thus, unlike polymers, micelles constantly exhibit scission and recombination. It is important to understand how this difference affects their properties. A crucial example is turbulent drag reduction by adding polymers and surfactants.^1,2 Since the flow statistics are similar for both additives,³ polymers and surfactant micelles have similar roles in modulating turbulence. However, there is an indispensable difference originating from their formation mechanisms. Since polymers are formed through covalent bonds, their structures never recover once they are broken by strong shear flows.⁴ Due to this irreversibility, the drag reduction efficiency by polymer additives declines with time.^5–7 In contrast, since the driving force for micellization is a non-bonded interaction, surfactants can form micelles again after scission.⁸ Thus surfactant solutions are less affected by mechanical degradation than polymers.⁹ This property makes surfactants more suitable for closed-loop systems such as air conditioning systems.^10,11 Therefore, developing technologies using polymer and surfactant solutions requires a fundamental knowledge of their different properties arising from their formation mechanisms.

Here, we explore whether micellar scission kinetics yields a difference in alignment behavior under shear flow. In general, the alignment of wormlike micelles and polymers is closely related to the rheological properties of their solutions. Since surfactants and polymers are often added to solutions to control rheology,^12–14 it is indispensable to understand their alignment properties. Many studies have been conducted on polymer alignment using theoretical, experimental, and numerical approaches.^15–18 It is well known that polymers under shear flow align more in the flow direction as the shear rate increases. Similarly to polymers, numerous studies have reported that rodlike and wormlike micelles also align in the flow direction.^19–26 However, little is known about the effect of scission on micellar alignment, although recent experimental results suggest that the scission effect on the micellar alignment emerges for high shear rates. Arenas-Gómez et al.²⁵ conducted simultaneous measurements of the viscosity and alignment of wormlike micelle solutions. They revealed that the orientation parameter exhibits nonmonotonic dependence on the shear rate. They attributed the decrease in the orientation parameter to the decreased contour length due to increased scission frequency. Recently, King et al.²⁶ investigated the alignment and viscosity of concentrated wormlike micelle solutions. They demonstrated that the saturation of alignment occurs for high shear rates, indicating the scission effect. However, it is difficult to experimentally measure the scission frequency and observe the structures and dynamics of individual micelles in flowing solutions. Thus the effect of scission on micellar alignment remains unclear.

Molecular simulations allow us to overcome these difficulties and reveal the relationship between alignment and scission. Although some studies investigated the alignment of rodlike and wormlike micelles using molecular simulations,^27–30 little has been done to reveal the effect of scission.³¹ Huang et al.²⁸ used a mesoscopic model incorporating a kinetic model for scission and recombination into linear chains and examined alignment and scission under shear flow. Although they reported the saturation of alignment for high shear rates, they attributed this saturation to finite-size effects under strong shear flows. Sambasivam et al.³⁰ investigated alignment and scission of a single rodlike micelle under shear flow with the coarse-grained molecular dynamics (CGMD) method. They found that when the Weissenberg number Wi = τ[small gamma, Greek, dot above] defined as the product of the shear rate [small gamma, Greek, dot above] and the rotational relaxation time τ is larger than 1, a rodlike micelle aligns in the flow direction exhibiting tumbling dynamics. They also showed that elongation of micelles by shear flow leads to micellar scission for large Wi. However, there was no comparison between alignment and scission for given Wi. Although it is worth noting that Carl et al.³¹ found that the saturation of the mean alignment angle can occur due to a decrease in the average chain length, there is still room for studying micellar alignment under shear flow in terms of scission.

In the present study, we investigate the effect of scission on micellar alignment through detailed analysis of both alignment and scission using molecular simulations. There are two significant issues for solving this problem. One is the evaluation of statistical properties of scission. Observing many scission events requires a high computational cost. To overcome this difficulty, we employ the dissipative particle dynamics (DPD) method. Thanks to coarse-graining and soft repulsive interactions, DPD allows us to simulate large systems for long time scales with a low computational cost. In fact, our previous study³² demonstrated that DPD is suitable for evaluating the statistical properties of micellar lifetimes. In addition, surfactant and water molecules are explicitly considered in DPD simulations. Thus we do not rely on a kinetic model for the scission and recombination of micelles.^33–35 The other issue is the polydispersity of the aggregation number of micelles. When a concentration is high enough for wormlike micelles to exist, micelles of different sizes coexist in the solution. In addition, the distribution changes for high shear rates due to increased scission frequency.³² Thus statistics over all the micelles in the system, often used in previous studies,^28,29,33,36 could demonstrate only the combined effect of the changes in the micellar properties and distributions. Here, we employ conditional statistics based on the aggregation number used in our previous study.³² This analysis method separates the effect of individual micellar properties and distributions of the aggregation number. In addition, this method allows us to directly compare the alignment of individual micelles with that of polymers to reveal the effect of micellar scission on alignment. In the following, we will quantitatively show that flow-induced scission suppresses micellar alignment even for fixed aggregation numbers.

2. Method

2.1 DPD governing equations

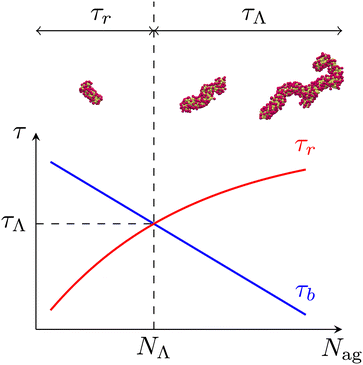
In the present study, we use the DPD method to conduct molecular simulations of nonionic surfactant solutions. In DPD simulations, a single DPD particle represents a group of atoms and molecules. The motion of a DPD particle obeyswhere m_i and v_i are the mass and velocity of the ith particle, respectively; and F^C_ij, F^D_ij, and F^R_ij are the conservative, dissipative, and random forces exerted on the ith particle by the jth particle, respectively. Note that the bond force F^B_ij is added in eqn (1) for surfactants and polymers. The conservative force acts as a repulsive force in the form ofwhere a_ij is the conservative force coefficient between the ith and jth particles, r_c is the cutoff distance, r_ij = r_i − r_j, r_ij = |r_ij|, and e_ij = r_ij/r_ij with r_i being the position of the ith particle. The dissipative and random forces are expressed as

F^D_ij = −γw^D(r_ij)(e_ij·v_ij)e_ij (v_ij = v_i − v_j) (3)

and

F^R_ij = σw^R(r_ij)θ_ije_ij, (4)

where γ and σ are the dissipative and random force coefficients, respectively; and w^D(r_ij) and w^R(r_ij) are the weight functions of the dissipative and random forces, respectively. In eqn (4), θ_ij is a random variable that satisfies

θ_ij(t) = θ_ji(t) (5)

〈θ_ij(t)〉 = 0 (6)

〈θ_ij(t)θ_kl(t′)〉 = (δ_ikδ_jl + δ_ilδ_jk)δ(t − t′) (7)

where δ_ij is the Kronecker delta, δ(t) is the delta function, and 〈·〉 denotes the ensemble average. The fluctuation dissipation theorem requires that γ, σ, w^D(r_ij), and w^R(r_ij) satisfy

w^D(r_ij) = [w^R(r_ij)]² (8)

and

σ²= 2γk_BT, (9)

where k_B is the Boltzmann constant and T is the temperature of the system.³⁷ Following ref. 38, we set the weight function w^R(r_ij) asIn what follows, we use simulation units with k_BT = m = r_c = 1.

2.2 Surfactant model

The model of a nonionic surfactant molecule contains a hydrophilic head particle and two hydrophobic tail particles. Three surfactant particles are connected by two harmonic springs expressed by

F^B_ij = −k_s(r_ij − r_eq)e_ij, (11)

where k_s is the spring constant and r_eq is the equilibrium bond distance. Table 1 shows the simulation parameters for surfactant solutions. Here, N is the total number of DPD particles, ρ is the number density of DPD particles, ϕ is the volume fraction of surfactants, and a_ij is the conservative force coefficient between different types of particles. The subscripts indicate the types of particles; namely, h, t, and w denote head, tail, and water particles, respectively. We choose ϕ = 0.05 because a sufficient number of wormlike micelles exist in the system with this volume fraction, as confirmed in our previous study.³² Additionally, there is no entanglement effect in the considered system because the mean squared displacement of surfactants (see Fig. 6 of ref. 32) does not exhibit a power law specific to a reptation motion.³⁹ DPD simulations of surfactant solutions are performed in a cubic box of size 60 × 60 × 60.

Table 1 DPD simulation parameters for surfactant solutions. N is the total number of DPD particles, ρ is the number density of DPD particles, σ is the random force coefficient, ϕ is the volume fraction of surfactants, k_s is the spring constant, r_eq is the equilibrium bond distance, and a_ij is the conservative force coefficient between different types of particles. The subscripts indicate the types of particles; namely, h, t, and w denote head, tail, and water particles, respectively

N	ρ	σ	ϕ	k s	r eq	a hh	a ht	a hw	a tt	a tw	a ww
648 000	3	3	0.05	50	0.8	25	60	20	25	60	25

---

2.3 Polymer model

In the present study, we conduct DPD simulations of polymer solutions for comparison. We employ the fully flexible polymer model used in the previous study.⁴⁰ Linear polymer chains consist of N_m beads, and adjacent beads in a polymer are connected by finitely extensible nonlinear elastic (FENE) springs expressed bywhere k_F is the spring constant and r_max is the maximum bond distance. Table 2 shows the simulation parameters for polymer solutions. DPD simulations of polymer solutions are performed in a cubic box of size 50 × 50 × 50.

Table 2 DPD simulation parameters for polymer solutions. N is the total number of DPD particles, N_m is the number of beads in a chain, ρ is the number density of DPD particles, σ is the random force coefficient, ϕ is the volume fraction of polymers, k_F is the spring constant, r_eq is the equilibrium bond distance, r_max is the maximum bond distance, and a_ij is the conservative force coefficient between different types of particles. The subscripts indicate the types of particles; namely, p and w denote polymer and water particles, respectively

N	N m	ρ	σ	ϕ	k F	r eq	r max	a pp	a pw	a ww
375 000	50	3	3	0.05	40	0.7	2	25	25	25

---

2.4 Simulation details

To integrate the equations of motion, we use the modified velocity Verlet method³⁸ with the time step Δt = 0.04 and the parameter λ = 0.65 introduced in this algorithm. We have confirmed that these parameters realize sufficiently accurate temperature control. To generate a uniform shear flow, we use the Lees–Edwards boundary condition⁴¹ and the SLLOD equations.⁴² We impose a random initial configuration and conduct equilibrium simulations for 20 000 time units for surfactant solutions and 8000 time units for polymer solutions, achieving statistically steady values of the potential energy. After that, we conduct non-equilibrium simulations by imposing shear flow. Conditional statistics for micelles introduced in Section 2.5 require DPD simulations for a long time to obtain sufficiently accurate results. Thus we conduct non-equilibrium simulations of surfactant solutions for 40 000–160 000 time units depending on the shear rate.

We perform all the DPD simulations using our in-house code.

2.5 Analysis details

To evaluate individual micellar properties, we need to identify micelles in the system. We define micelles adopting the method used in previous studies.^43,44 In this method, two surfactant molecules belong to a common cluster if a hydrophobic particle of one surfactant molecule is within r_c (=1) of a hydrophobic particle of the other. If a cluster has an aggregation number N_ag larger than a threshold value n_mic (=10), then we regard the cluster as a micelle. Since we focus mainly on micelles with N_ag ≳ 50, our results are practically insensitive to the choice of n_mic.

To investigate N_ag dependence of micellar properties, we use conditional statistics based on N_ag instead of statistics over all the micelles in the system. Specifically, to evaluate the micellar properties for given N_ag, we use the data for micelles having aggregation numbers that lie in [N_ag − ΔN_ag,N_ag + ΔN_ag], where we set ΔN_ag = 0.05N_ag. In the following, the micellar orientation angle is conditioned by instantaneous N_ag, whereas the micellar lifetime is conditioned by the value of N_ag before scission.

3. Results

One of the most intriguing observations in the present study is that flow-induced scission, which occurs for high shear rates, suppresses micellar alignment in the flow direction even for fixed aggregation numbers N_ag. To quantitatively demonstrate the effect of scission on micellar alignment, we evaluate the shear-rate dependence of the micellar lifetime and alignment.

3.1 Alignment

In this subsection, we examine the micellar alignment under shear flow. First, we define micellar orientation angles. In the present study, we define the micellar direction as the eigenvector e⁽¹⁾ of the gyration tensor G_ij corresponding to the largest eigenvalue. Here, G_ij is defined aswhere Δr_k,i is the ith component of the relative position vector of the kth surfactant particle with respect to the center of mass of the micelle, and N_sur (=3N_ag) is the number of surfactant particles in the micelle. Fig. 1 shows the micellar structures and the corresponding e⁽¹⁾. We confirm that e⁽¹⁾ represents the global orientation of micelles. Since micelles form branched structures more often as N_ag increases (see Fig. 12 of ref. 32), it may also be important to consider the local orientation of branched micelles as shown in Fig. 1(b). However, for simplicity, we investigate the global alignment using e⁽¹⁾ in the following. Fig. 2 shows the definition of micellar angles θ and φ. To investigate micellar alignment in the flow direction, we focus on φ. Note that φ ∈ [−π/2, π/2) because e⁽¹⁾ is equivalent to −e⁽¹⁾ in our definition.

Fig. 1 Eigenvector e⁽¹⁾ of the gyration tensor G_ij corresponding to the largest eigenvalue for (a) N_ag = 300 and (b) N_ag = 500. Hydrophilic and hydrophobic particles are indicated in red and yellow, respectively.

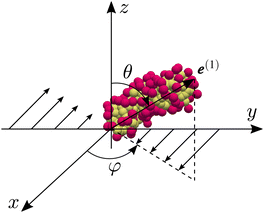Fig. 2 Definition of angles θ and φ of micelles. The micellar direction is defined as the eigenvector e⁽¹⁾ of the gyration tensor G_ij corresponding to the largest eigenvalue.

A key point of our analysis is that we rely on conditional statistics based on N_ag instead of statistics over all the micelles in the system. The inset of Fig. 3 shows the probability density function (PDF) P(N_ag) of N_ag for the shear rate [small gamma, Greek, dot above] = 0.005. Note that the temporally averaged values are shown. We find that micelles of various sizes coexist in the system for the considered volume fraction ϕ. Fig. 3 shows the PDF P(φ) of φ for various N_ag, which demonstrates that the statistical properties of micellar alignment significantly depend on N_ag for given [small gamma, Greek, dot above]. Therefore, the analysis using the information on all the micelles in the system, as conducted in previous studies,^28,29 reflects not only individual micellar dynamics but also the distribution of N_ag. In particular, since P(N_ag) for high shear rates greatly differ from that at equilibrium due to flow-induced scission (see Fig. 10 of ref. 32), this change in P(N_ag) complicates the interpretation of the results. We overcome this difficulty using conditional statistics based on N_ag defined in Section 2.5, which enables us to investigate the alignment properties of individual micelles.

Fig. 3 PDF P(φ) of the orientation angle φ for [small gamma, Greek, dot above] = 0.005. Different curves correspond to different values of the aggregation number: N_ag = 70, 100, 200, and 400 from thinner (and darker) to thicker (and lighter) lines. The inset shows PDF P(N_ag) of N_ag for [small gamma, Greek, dot above] = 0.005. The vertical black dashed line indicates the mean orientation angle [small phi variant, Greek, macron] defined by eqn (14), and the vertical dotted red line indicates the conventional mean orientation angle χ_G defined by eqn (15) for N_ag = 400.

In the following, we characterize [small gamma, Greek, dot above] dependence of micellar alignment with a mean orientation angle. Note that given a set of n angles {φ₁, φ₂, …, φ_n}, the arithmetic mean 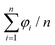is inappropriate as a mean orientation angle due to the periodicity of φ_i. For instance, the arithmetic mean of φ₁ = π/2 − ε and φ₂ = −π/2 + ε is zero even when ε ≪ 1, which is misleading because φ₁ ≃ φ₂ ≃ π/2 modulo π. Here, we define a mean orientation angle [small phi variant, Greek, macron] as

where arg (·) denotes the argument of a complex number.⁴⁵ Doubling φ_i leads to 2φ_i ∈ [−π, π). Instead of the arithmetic mean of 2φ_i, we consider that of e^2iφ_i to avoid the problem due to the periodicity. Then we obtain [small phi variant, Greek, macron] by dividing the mean direction of 2φ_i by 2. We show [small phi variant, Greek, macron] of micelles with N_ag = 400 for [small gamma, Greek, dot above] = 0.005 by a vertical black dashed line in Fig. 3 as an example. It verifies that [small phi variant, Greek, macron] is a characteristic angle of wormlike micelles. For comparison, we also show the conventional mean orientation angle χ_G^17,46 defined byin Fig. 3. We observe that [small phi variant, Greek, macron] and χ_G show similar values. Thus the definition of the mean orientation angle has little effect on the following results.

Fig. 4 shows [small gamma, Greek, dot above] dependence of [small phi variant, Greek, macron] for various N_ag. Two important features are evident in this result. First, N_ag dependence of [small phi variant, Greek, macron] for fixed [small gamma, Greek, dot above] indicates that there exists a threshold aggregation number N_Λ above which [small phi variant, Greek, macron] remains constant. For N_ag ≥300, [small phi variant, Greek, macron] collapses on a single function of [small gamma, Greek, dot above] irrespective of N_ag. In contrast, [small phi variant, Greek, macron] of micelles with N_ag ≤ 130 decreases as N_ag increases for fixed [small gamma, Greek, dot above]. These observations indicate that the longest relaxation time of micelles increases with N_ag for N_ag ≲ N_Λ and remains constant for N_ag ≳ N_Λ. We will explain how to evaluate the values of the longest relaxation time and N_Λ in Section 4. Second, [small gamma, Greek, dot above] dependence of [small phi variant, Greek, macron] for fixed N_ag exhibits a nonmonotonic behavior. Here, we explain this nonmonotonic dependence focusing on the results for N_ag ≥ 300. For [small gamma, Greek, dot above] ≤ 0.005, [small phi variant, Greek, macron] decreases as [small gamma, Greek, dot above] increases, indicating that micelles align more in the flow direction for lager [small gamma, Greek, dot above]. In contrast, for [small gamma, Greek, dot above] > 0.005, [small phi variant, Greek, macron] decreases more slowly and slightly increases for [small gamma, Greek, dot above] ≥ 0.02. This is an intriguing phenomenon because [small phi variant, Greek, macron] of polymers monotonically decreases as [small gamma, Greek, dot above] increases, as described below (see Fig. 8). Interestingly, the saturation of alignment was also reported for amphiphilic Janus colloids,⁴⁷ which suggests the general alignment behavior of self-assembled clusters. In the next subsection, we will explore the origin of the alignment behavior by evaluating the micellar lifetime under shear flow.

Fig. 4 Mean orientation angle [small phi variant, Greek, macron] of micelles as a function of the shear rate [small gamma, Greek, dot above] for N_ag = 70 (), 90 (), 130 (), 300 (●), 400 () and 500 (). For comparison, [capital Phi, Greek, macron] defined as [small phi variant, Greek, macron] obtained with all the data for micelles with N_ag ≥ 50 is plotted (◊).

Before closing this subsection, we refer to the results without using conditional statistics. We define [capital Phi, Greek, macron] as [small phi variant, Greek, macron] obtained with eqn (14) using all the data for micelles with N_ag ≥ 50. In Fig. 4, we show [capital Phi, Greek, macron] as a function of [small gamma, Greek, dot above]. In the case of the examined parameters, since a sufficient number of micelles with N_ag ≳ N_Λ exist in the system, [small phi variant, Greek, macron] for N_ag ≳ N_Λ and [capital Phi, Greek, macron] exhibit similar behavior. Specifically, [capital Phi, Greek, macron] does not decrease toward zero when increasing [small gamma, Greek, dot above], which was also observed in a previous study³¹ modeling linear micelles as breakable bead-spring chains. However, due to the contributions from micelles with N_ag ≲ N_Λ, [capital Phi, Greek, macron] is larger than [small phi variant, Greek, macron] for N_ag ≳ N_Λ. In summary, since [capital Phi, Greek, macron] depends on P(N_ag), interpretation of [capital Phi, Greek, macron] may not be straightforward, especially when comparing results between different parameters.

3.2 Effect of scission

In the previous subsection, we have seen that [small phi variant, Greek, macron] of wormlike micelles exhibits a nontrivial dependence on [small gamma, Greek, dot above]. To reveal its origin, we investigate the effect of scission on micellar alignment. To quantitatively evaluate micellar scission, we focus on the micellar lifetime t_b defined as the time between micellar birth and scission. We estimate a survival function S(t_b), which gives the probability that micelles survive beyond a certain time t_b, using the Kaplan–Meier method.⁴⁸ Then, we fit S(t_b) with C₀ exp(−t_b/τ_b) to obtain the average lifetime τ_b. The definition of micellar scission and the method to evaluate τ_b are the same as in our previous study.³² In this subsection, we will show the results of micelles with N_ag larger than N_Λ because more than 65% of surfactants in the system belong to micelles with N_ag ≳ N_Λ at equilibrium. In addition, micelles with N_ag ≳ N_Λ have the slowest timescale in the system as described in Section 4. In other words, they align most in the flow direction. We will discuss the alignment of micelles with N_ag ≲ N_Λ in Section 4.

To explore the relationship between alignment and scission, we show [small gamma, Greek, dot above] dependence of [small phi variant, Greek, macron] and τ_b for various N_ag (>N_Λ) in Fig. 5. To focus on the flow effect, we normalize τ_b by the value τ⁰_b at equilibrium for given N_ag. We find that τ_b/τ⁰_b also follows a single function of [small gamma, Greek, dot above] irrespective of N_ag (>N_Λ) as well as [small phi variant, Greek, macron]. The bottom panel of Fig. 5 demonstrates that τ_b/τ⁰_b ≃ 1 for [small gamma, Greek, dot above] ≲ 0.005, indicating that flow-induced scission does not occur, whereas τ_b/τ⁰_b ≲ 1 for [small gamma, Greek, dot above] ≳ 0.005 due to flow-induced scission. We show this threshold shear rate [small gamma, Greek, dot above]_c (=0.005) for flow-induced scission in Fig. 5 to emphasize the effect of flow-induced scission. The top panel of Fig. 5 demonstrates that the alignment behavior changes around [small gamma, Greek, dot above]_c. This indicates that flow-induced scission, which occurs for [small gamma, Greek, dot above] ≳ [small gamma, Greek, dot above]_c, suppresses micellar alignment. It is worth emphasizing that Fig. 5 shows [small phi variant, Greek, macron] of micelles with a given N_ag obtained with conditional statistics instead of the average values over all the micelles. Thus, the increase in the number of small micelles due to flow-induced scission cannot explain the suppression of alignment. Although the present study focuses on the relationship between alignment and scission of micelles under shear flow, their effect on the rheological properties is an important aspect. In our previous study,³² we have shown that the considered solutions have viscoelasticity and exhibit shear thinning. In this system, both alignment and flow-induced scission contribute to the shear thinning. Constitutive models based on the microscopic dynamics and kinetics of micelles (e.g.ref. 49) will allow a systematic study on the effect of alignment and flow-induced scission on the rheological properties, which is an important near-future study.

Fig. 5 Shear-rate [small gamma, Greek, dot above] dependence of the mean orientation angle [small phi variant, Greek, macron] (top panel) and the average lifetime τ_b (bottom panel) normalized by the value τ⁰_b at equilibrium for N_ag = 300 (●), 400 (), and 500 (). The black dotted line indicates [small gamma, Greek, dot above] = [small gamma, Greek, dot above]_c. Open symbols in the top panel indicate the results of the larger system (N = 3 000 000).

To confirm whether finite system sizes affect micellar alignment, we show the results of the system composed of N = 3 000 000 particles in Fig. 5. Since these results agree with those of N = 648 000, finite system sizes have little effect on the micellar alignment. In the next section, we demonstrate that the nontrivial [small gamma, Greek, dot above] dependence of [small phi variant, Greek, macron] (Fig. 5) is specific to wormlike micelles by conducting a similar analysis for polymer models without scission.

Before closing this subsection, we refer to the orientational dynamics of micelles before scission. To observe the typical dynamics of micelles before scission, we show φ of micelles that survive for O(τ_b) as a function of time t − t* in Fig. 6. Here, [small gamma, Greek, dot above] = 0.01, and t* is the time when scission occurs. Since τ_b is smaller than the rotational relaxation time τ_r for N_ag = 300 as described in Section 4.1, φ does not exhibit significant variations. This is evident by observing that φ of micelles with N_ag = 130, for which τ_b ≳ τ_r, fluctuates between −π/2 and π/2 before scission. Consequently, micellar recombination plays an essential role in the distribution of φ when τ_b ≲ τ_r. Thus it is an important near-future study to investigate micellar alignment in terms of recombination.^34,50,51

Fig. 6 Orientation angle φ of micelles that survive for O(τ_b) as a function of time t − t* before scission for [small gamma, Greek, dot above] = 0.01. Different colors correspond to different values of N_ag: black, 130; red, 300. Different line styles correspond to different samples of micelles.

4. Discussion

4.1 Comparison with polymers

Comparing the mean orientation angle [small phi variant, Greek, macron] with the average lifetime τ_b has demonstrated that flow-induced scission suppresses micellar alignment (Fig. 5). Here, we compare the alignment of micelles with that of polymers to demonstrate the unique properties of micellar alignment.

Since wormlike micelles and polymers have different timescales, we introduce the Weissenberg number Wi = τ[small gamma, Greek, dot above] defined as the product of the longest relaxation time τ and the shear rate [small gamma, Greek, dot above]. We estimate τ of polymers by fitting the autocorrelation function C(t) of the end-to-end vector with an exponential function C₀ exp (−t/τ).⁴⁰ We obtain τ = 148 in the case of the examined parameters.

We evaluate the longest relaxation time τ(N_ag) of unentangled micelles from the rotational relaxation time τ_r(N_ag) and the average lifetime τ_b(N_ag). Specifically, we use the formula

proposed in our previous study.³² Here, we introduce a certain aggregation number N_Λ which satisfies τ_r(N_Λ) = τ_b(N_Λ) and define τ_Λ as τ_r(N_Λ). Fig. 7 shows the schematic of the longest relaxation time. In general, τ_r is a monotonically increasing function of N_ag.³² However, relaxation modes such that τ_r(N_ag)>τ_b(N_ag) disappear due to the scission of micelles. Therefore, the intersection of τ_r(N_ag) and τ_b(N_ag) determines the largest timescale in the system. In other words, N_Λ defines the largest segment that behaves similarly to polymer chains (i.e., chains without scission kinetics). Consequently, micelles with N_ag ≳ N_Λ have a common longest relaxation time τ_Λ. This is consistent with the fact that [small phi variant, Greek, macron] and τ_b/τ⁰_b are independent of N_ag (>N_Λ) for fixed [small gamma, Greek, dot above] (Fig. 5). The methods to evaluate τ_r and τ_b are the same as in our previous study.³² We obtain τ(70) = 72, τ(90) = 203, τ(130) = 586, τ(300) = τ(400) = τ(500) = τ_Λ = 796 and N_Λ = 169.

Fig. 7 Schematic of the longest relaxation time of micelles. The intersection of the rotational relaxation time τ_r and the average lifetime τ_b defines τ_Λ and N_Λ. Since τ_b is larger than τ_r for N_ag ≲ N_Λ, the rotational relaxation of micelles is not affected by their scission. In contrast, relaxation modes such that τ_r ≳ τ_Λ disappear due to the rapid scission of large micelles with N_ag ≳ N_Λ. As a result, micelles with N_ag ≳ N_Λ are characterized by a common longest relaxation time τ_Λ.

Fig. 8 shows Wi dependence of [small phi variant, Greek, macron] for polymers and micelles. We confirm that [small phi variant, Greek, macron] of polymers obeys [small phi variant, Greek, macron] ∝ Wi^−0.45 for Wi ≳ 1. A similar power law was reported in previous studies,^16,46,52,53 with a slightly different definition of a mean orientation angle. It is interesting to focus on the threshold Weissenberg number Wi_c = τ_Λ[small gamma, Greek, dot above]_c for flow-induced scission of micelles with N_ag ≳ N_Λ. The alignment behavior of micelles with N_ag ≳ N_Λ deviates from that of polymers above Wi_c. Two important features are evident in this result. First, we confirm that [small phi variant, Greek, macron] of wormlike micelles and polymers collapse on a single function of Wi for Wi ≲ Wi_c, indicating the similar alignment behavior of wormlike micelles and polymers when flow-induced scission does not occur. In addition, this collapse verifies that eqn (16) proposed in our previous study³² yields a quantitatively valid value of τ(N_ag). Second, wormlike micelles have larger values of [small phi variant, Greek, macron] than polymers for Wi ≳ Wi_c, indicating that flow-induced scission suppresses micellar alignment compared with polymers. So far, we have mainly focused on micelles with N_ag ≳ N_Λ. Here, we investigate the alignment of micelles with N_ag ≲ N_Λ in a similar way. Fig. 8 demonstrates that [small phi variant, Greek, macron] of micelles with N_ag ≲ N_Λ collapse on the same function for Wi ≲ Wi_c. This collapse shows that we can consider N_ag dependence of [small phi variant, Greek, macron] shown in Fig. 4 by using eqn (16). Similarly to micelles with N_ag ≳ N_Λ, [small phi variant, Greek, macron] of micelles with N_ag ≲ N_Λ is larger than that of polymers for Wi ≳ Wi_c. Thus, the alignment of micelles with N_ag ≲ N_Λ is also suppressed for high shear rates. However, since [small phi variant, Greek, macron] has different values depending on N_ag for fixed Wi (≳ Wi_c), more detailed investigations are required to explain the degree of the alignment suppression. In the following, we again focus on the alignment of wormlike micelles with N_ag ≳ N_Λ, which are characterized by a common longest relaxation time τ_Λ.

Fig. 8 Mean orientation angle [small phi variant, Greek, macron] as a function of the Weissenberg number Wi for polymers (○) and micelles: N_ag = 70 (), 90 (), 130 (), 300 (●), 400 () and 500 (). The vertical black dotted line indicates Wi = Wi_c. The black dashed line indicates [small phi variant, Greek, macron]∝Wi^−0.45.

We also confirm the suppression of micellar alignment through visualization of wormlike micelles and polymers for given Wi. For surfactant solutions, we define the Weissenberg number of the system as Wi = τ_Λ[small gamma, Greek, dot above]. We first focus on the alignment of wormlike micelles and polymers for Wi ≲ Wi_c, where flow-induced scission of micelles does not occur. Fig. 9(a) shows micelles with 200 ≤ N_ag ≤ 600 for Wi = 2.4, and Fig. 9(c) shows some polymers which are randomly chosen for Wi = 3.0. They exhibit a qualitatively similar alignment behavior for Wi ≲ Wi_c. Incidentally, since surfactants consist of three DPD particles, micelles are slightly thicker than polymers. Indeed, the mean end-to-end distance of surfactants gives a rough estimate of the micellar radius R ≃ 1.43. Using longer surfactant models will reveal the effect of micellar thickness on alignment.

Fig. 9 Visualization of micelles with 200 ≤ N_ag ≤ 600 for (a) Wi = 2.4 and (b) Wi = 48, and polymers for (c) Wi = 3.0 and (d) Wi = 44. Hydrophilic and hydrophobic particles are indicated in red and yellow, respectively (a and b). The number N_m of beads in a polymer is 50, and some of the polymers in the system are shown for clarity (c and d). The volume fraction ϕ of surfactants and polymers is (a, c and d) 0.05 and (b) 0.1.

Next, we investigate their alignment for Wi ≳ Wi_c, where flow-induced scission occurs. Fig. 9(b) shows micelles with 200 ≤ N_ag ≤ 600 for Wi = 48, and Fig. 9(d) shows some polymers which are randomly chosen for Wi = 44. Note that, for clarity, we use the data for ϕ = 0.1 in Fig. 9(b) because the number of micelles with 200 ≤ N_ag ≤ 600 significantly decreases for large Wi due to flow-induced scission. We have confirmed that wormlike micelles exhibit similar alignment properties for ϕ = 0.1 as in the case of ϕ = 0.05. We observe in Fig. 9(d) that polymers considerably align in the flow direction, whereas wormlike micelles slightly tilt from the flow direction in Fig. 9(b). These observations are consistent with the quantitative results shown in Fig. 8. We then conclude that visualization also demonstrates the suppression of micellar alignment for Wi ≳ Wi_c. In the next subsection, we consider the mechanism of the suppression of micellar alignment focusing on the effective longest relaxation time under shear flow.

4.2 Effective longest relaxation time

We have shown that, for high shear rates, flow-induced scission occurs (Fig. 5) and suppresses micellar alignment compared with polymers (Fig. 8 and 9). This subsection demonstrates that flow-induced scission suppresses micellar alignment for fixed N_ag by reducing the effective longest relaxation time. As mentioned above, we focus on micelles with N_ag ≳ N_Λ. Such micelles have a common longest relaxation time τ_Λ and exhibit the most significant alignment of all the micelles in the system.

Let us now demonstrate that the decrease in the effective longest relaxation time τ_Λ causes the suppression of micellar alignment for high shear rates. Here, we propose a scenario that flow-induced scission reduces τ_b for [small gamma, Greek, dot above] ≳ [small gamma, Greek, dot above]_c and then shifts τ_Λ and N_Λ shown in Fig. 7 towards lower values. To verify this scenario, we focus on the fact that micelles with N_ag ≳ N_Λ are characterized by a common longest relaxation time τ_Λ. On the basis of this fact, we investigate whether N_Λ changes for [small gamma, Greek, dot above] ≳ [small gamma, Greek, dot above]_c to confirm the reduction of τ_Λ. Fig. 10 shows [small phi variant, Greek, macron] as a function of N_ag for various [small gamma, Greek, dot above]. Note that, for clarity, we subtract the average value over micelles with N_ag ≥ N_Λ from [small phi variant, Greek, macron] for each [small gamma, Greek, dot above]. In Fig. 10, we show N_Λ at equilibrium by a vertical dotted line for comparison. For [small gamma, Greek, dot above] ≤ [small gamma, Greek, dot above]_c, the behavior of [small phi variant, Greek, macron] changes around N_Λ. For N_ag ≲ N_Λ, [small phi variant, Greek, macron] depends on N_ag because the micellar alignment is characterized by τ_r(N_ag). In contrast, since τ_Λ is a common longest relaxation time of micelles with N_ag ≳ N_Λ, [small phi variant, Greek, macron] is independent of N_ag for N_ag ≳ N_Λ. Most notably, for [small gamma, Greek, dot above] > [small gamma, Greek, dot above]_c, the plateau regime of [small phi variant, Greek, macron] extends to a lower N_ag as [small gamma, Greek, dot above] increases. This indicates that N_Λ decreases as [small gamma, Greek, dot above] increases. In other words, the effective longest relaxation time also decreases for [small gamma, Greek, dot above] > [small gamma, Greek, dot above]_c. We, therefore, conclude that flow-induced scission promotes micellar scission and reduces the effective longest relaxation time τ_Λ, leading to the suppression of micellar alignment even for fixed N_ag.

Fig. 10 Difference between the mean orientation angle [small phi variant, Greek, macron] and its average over micelles with N_ag ≥ N_Λ as a function of N_ag. Different symbols denote the results for different values of the shear rate: [small gamma, Greek, dot above] = 0.003, ●; 0.005, ; 0.02, ; 0.05, . Solid lines indicate the results for [small gamma, Greek, dot above] ≤ [small gamma, Greek, dot above]_c and dashed lines indicate those for [small gamma, Greek, dot above] > [small gamma, Greek, dot above]_c. The vertical black dotted line indicates N_Λ at equilibrium.

5. Conclusions

We have conducted DPD simulations of nonionic surfactant solutions under shear flow to investigate the effect of scission on the alignment of wormlike micelles. The most important conclusion is that flow-induced scission suppresses micellar alignment even for fixed aggregation numbers N_ag. One may think that the suppression is obvious because flow-induced scission shortens micelles, i.e., decreases N_ag, thus promoting their rotational relaxation. However, we emphasize that the suppression of micellar alignment can occur even for fixed N_ag. We have verified the conclusion by evaluating the shear-rate [small gamma, Greek, dot above] dependence of the average lifetime τ_b and the mean orientation angle [small phi variant, Greek, macron] for fixed N_ag (Fig. 5). Specifically, when [small gamma, Greek, dot above] exceeds a threshold shear rate [small gamma, Greek, dot above]_c, τ_b becomes smaller than the value τ⁰_b at equilibrium and [small phi variant, Greek, macron] does not show such a decrease as when [small gamma, Greek, dot above] ≲ [small gamma, Greek, dot above]_c. Comparing the alignment of micelles with that of polymers (i.e., chains without scission kinetics) has provided further evidence that flow-induced scission suppresses micellar alignment for fixed N_ag (Fig. 8). To introduce the Weissenberg number Wi = τ[small gamma, Greek, dot above] defined as the product of the longest relaxation time τ and [small gamma, Greek, dot above], we have evaluated τ of micelles using the method proposed in our previous study.³² This method, which considers the effect of scission kinetics on micellar relaxation, has allowed us to compare the alignment of micelles and polymers appropriately. When Wi is smaller than the threshold Weissenberg number Wi_c = τ[small gamma, Greek, dot above]_c for flow-induced scission, [small phi variant, Greek, macron] of both micelles and polymers follows a single function of Wi. This collapse indicates the similar alignment behavior of micelles and polymers when flow-induced scission does not occur. In contrast, [small phi variant, Greek, macron] of micelles is larger than that of polymers for Wi ≳ Wi_c. Such deviation of [small phi variant, Greek, macron] above Wi_c confirms that flow-induced scission suppresses micellar alignment for fixed N_ag. Visualization also has shown that wormlike micelles tilt more from the flow direction than polymers for given Wi (≳Wi_c) (Fig. 9).

To explain the mechanism of the alignment suppression due to flow-induced scission, we have considered the effective longest relaxation time of micelles. Then we have demonstrated that the decrease in the effective longest relaxation time due to flow-induced scission plays a crucial role in suppressing micellar alignment. The concept of the micellar longest relaxation time (Fig. 7) predicts that the reduction of τ_b due to flow-induced scission decreases the effective longest relaxation time τ_Λ under shear flow. We have verified this prediction by evaluating N_ag dependence of [small phi variant, Greek, macron] (Fig. 10). According to the concept, when N_ag is larger than a certain aggregation number N_Λ, micelles are characterized by a common longest relaxation time τ_Λ. Indeed, we have found that when [small gamma, Greek, dot above] is smaller than [small gamma, Greek, dot above]_c, [small phi variant, Greek, macron] is independent of N_ag for N_ag ≳ N_Λ. In contrast, for [small gamma, Greek, dot above] ≳ [small gamma, Greek, dot above]_c, the plateau regime of [small phi variant, Greek, macron] extends to a lower N_ag as [small gamma, Greek, dot above] increases. This observation shows that flow-induced scission reduces N_Λ and consequently reduces the effective Weissenberg number Wi = τ_Λ[small gamma, Greek, dot above] of wormlike micelles with fixed N_ag (≳N_Λ) compared with the case without flow-induced scission, which is a major origin of the alignment suppression.

In the present study, we have quantitatively shown that flow-induced scission suppresses micellar alignment even for fixed N_ag and qualitatively explained the mechanism of this phenomenon through the decrease in the effective longest relaxation time under shear flow. However, we have yet to quantitatively explain the alignment behavior of micelles for Wi ≳ Wi_c, where flow-induced scission occurs. For example, it is not completely clear why [small phi variant, Greek, macron] exhibits the nonmonotonic dependence on Wi (Fig. 8). To explain the degree of alignment suppression, we first need to quantify the effective longest relaxation time. In addition, it is likely that we need to consider the direct coupling between the orientational dynamics and scission kinetics of individual micelles under shear flow. These are left for future studies.

Author contributions

Yusuke Koide: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. Susumu Goto: conceptualization, funding acquisition, project administration, resources, supervision, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The present study was supported in part by JSPS Grants-in-Aid for Scientific Research (20H02068 and 21J21061). The DPD simulations were mainly conducted under the auspices of the NIFS Collaboration Research Programs (NIFS20KNSS145). A part of the simulations was conducted using the JAXA Supercomputer System Generation 3 (JSS3).

Notes and references

1. C. M. White and M. G. Mungal, Annu. Rev. Fluid Mech., 2008, 40, 235–256.
2. J. L. Zakin, B. Lu and H.-W. Bewersdorff, Rev. Chem. Eng., 1998, 14, 253–320.
3. L. Warwaruk and S. Ghaemi, J. Fluid Mech., 2021, 917, A7.
4. S. A. Vanapalli, S. L. Ceccio and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16660–16665.
5. J. M. J. Den Toonder, A. A. Draad, G. D. C. Kuiken and F. T. M. Nieuwstadt, Appl. Sci. Res., 1995, 55, 63–82.
6. A. S. Pereira, R. M. Andrade and E. J. Soares, J. Non-Newtonian Fluid Mech., 2013, 202, 72–87.
7. E. J. Soares, J. Non-Newtonian Fluid Mech., 2020, 276, 104225.
8. Z. Chu, C. A. Dreiss and Y. Feng, Chem. Soc. Rev., 2013, 42, 7174.
9. S. Tamano, H. Ikarashi, Y. Morinishi and K. Taga, J. Non-Newtonian Fluid Mech., 2015, 215, 1–7.
10. B. Yu, F. Li and Y. Kawaguchi, Int. J. Heat Fluid Flow, 2004, 25, 961–974.
11. A. Krope and L. C. Lipus, Appl. Therm. Eng., 2010, 30, 833–838.
12. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
13. L. Zhong, M. Oostrom, M. J. Truex, V. R. Vermeul and J. E. Szecsody, J. Hazard. Mater., 2013, 244–245, 160–170.
14. P. A. Cornwell, Int. J. Cosmet. Sci., 2018, 40, 16–30.
15. C. M. Schroeder, R. E. Teixeira, E. S. Shaqfeh and S. Chu, Phys. Rev. Lett., 2005, 95, 018301.
16. C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 1967–1978.
17. C.-C. Huang, R. G. Winkler, G. Sutmann and G. Gompper, Macromolecules, 2010, 43, 10107–10116.
18. R. G. Winkler, J. Chem. Phys., 2010, 133, 164905.
19. J. B. Hayter and J. Penfold, J. Phys. Chem., 1984, 88, 4589–4593.
20. V. Croce, T. Cosgrove, C. A. Dreiss, S. King, G. Maitland and T. Hughes, Langmuir, 2005, 21, 6762–6768.
21. S. Förster, M. Konrad and P. Lindner, Phys. Rev. Lett., 2005, 94, 017803.
22. M. Takeda, T. Kusano, T. Matsunaga, H. Endo, M. Shibayama and T. Shikata, Langmuir, 2011, 27, 1731–1738.
23. C. R. López-Barrón, A. K. Gurnon, A. P. R. Eberle, L. Porcar and N. J. Wagner, Phys. Rev. E, 2014, 89, 042301.
24. A. K. Gurnon, C. López-Barrón, M. J. Wasbrough, L. Porcar and N. J. Wagner, ACS Macro Lett., 2014, 3, 276–280.
25. B. Arenas-Gómez, C. Garza, Y. Liu and R. Castillo, J. Colloid Interface Sci., 2020, 560, 618–625.
26. J. P. King, C. S. G. Butler, S. W. Prescott, A. V. Sokolova, L. de Campo, A. P. Williams and R. F. Tabor, Phys. Fluids, 2022, 34, 083104.
27. C.-C. Huang, H. Xu and J.-P. Ryckaert, Europhys. Lett., 2008, 81, 58002.
28. C.-C. Huang, J.-P. Ryckaert and H. Xu, Phys. Rev. E, 2009, 79, 041501.
29. J. Wei, Y. Kawaguchi, B. Yu, F. Li and C. Zhang, Nonlinear Dyn., 2010, 61, 503–515.
30. A. Sambasivam, A. V. Sangwai and R. Sureshkumar, Phys. Rev. Lett., 2015, 114, 158302.
31. W. Carl, R. Makhloufi and M. Kröger, J. Phys. II, 1997, 7, 931–946.
32. Y. Koide and S. Goto, J. Chem. Phys., 2022, 157, 084903.
33. M. Kröger and R. Makhloufi, Phys. Rev. E, 1996, 53, 2531.
34. C.-C. Huang, H. Xu and J.-P. Ryckaert, J. Chem. Phys., 2006, 125, 094901.
35. J. T. Padding, W. J. Briels, M. R. Stukan and E. S. Boek, Soft Matter, 2009, 5, 4367–4375.
36. J. T. Padding, E. S. Boek and W. J. Briels, J. Chem. Phys., 2008, 129, 074903.
37. P. Español and P. Warren, Europhys. Lett., 1995, 30, 191.
38. R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435.
39. K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086.
40. W. Jiang, J. Huang, Y. Wang and M. Laradji, J. Chem. Phys., 2007, 126, 044901.
41. A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921.
42. D. J. Evans and G. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Cambridge University Press, 2008.
43. A. Vishnyakov, M.-T. Lee and A. V. Neimark, J. Phys. Chem. Lett., 2013, 4, 797–802.
44. M.-T. Lee, R. Mao, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2016, 120, 4980–4991.
45. N. I. Fisher, Statistical Analysis of Circular Data, Cambridge University Press, 1995.
46. C. Aust, M. Kröger and S. Hess, Macromolecules, 1999, 32, 5660–5672.
47. Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2020, 16, 476–486.
48. E. L. Kaplan and P. Meier, J. Am. Stat. Assoc., 1958, 53, 457–481.
49. R. J. Hommel and M. D. Graham, J. Non-Newtonian Fluid Mech., 2021, 295, 104606.
50. B. O'Shaughnessy and J. Yu, Phys. Rev. Lett., 1995, 74, 4329–4332.
51. J. T. Padding and E. S. Boek, Europhys. Lett., 2004, 66, 756.
52. R. E. Teixeira, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 581–592.
53. M. Q. Tu, M. Lee, R. M. Robertson-Anderson and C. M. Schroeder, Macromolecules, 2020, 53, 9406–9419.

---