 Open Access Article
Open Access ArticleReply to the ‘Comment on “Simulations of ionization equilibria in weak polyelectrolyte solutions and gels”’ by J. Landsgesell, L. Nová, O. Rud, F. Uhlík, D. Sean, P. Hebbeker, C. Holm and P. Košovan, Soft Matter, 2019, 15, 1155–1185
Peter
Košovan
 *a,
Jonas
Landsgesell
b,
Lucie
Nová
*a,
Jonas
Landsgesell
b,
Lucie
Nová
 a,
Filip
Uhlík
a,
David
Beyer
a,
Filip
Uhlík
a,
David
Beyer
 b,
Pablo M.
Blanco
b,
Pablo M.
Blanco
 c,
Roman
Staňo
c,
Roman
Staňo
 de and
Christian
Holm
de and
Christian
Holm
 *b
*b
aDepartment of Physical and Macromolecular Chemistry, Charles University, Hlavova 8, 128 00 Prague 2, Czech Republic. E-mail: peter.kosovan@natur.cuni.cz
bInstitute for Computational Physics, University of Stuttgart, Allmandring 3, Stuttgart, Germany. E-mail: holm@icp.uni-stuttgart.de
cMaterials Science and Physical Chemistry Department & Research Institute of Theoretical and Computational Chemistry, University of Barcelona, 08028 Barcelona, Catalonia, Spain
dFaculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria
eVienna Doctoral School in Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria
First published on 9th May 2023
Abstract
Levin and Bakhshandeh suggested in their comment that (1), we stated in our recent review that pH–pKA is a universal parameter for titrating systems, that (2), we omitted to mention in our review the broken symmetry of the constant pH algorithm, and that (3), a constant pH simulation must include a grand-canonical exchange of ions with the reservoir. As a reply to (1), we point out that Levin and Bakhshandeh misquoted and hence invalidated our original statement. We therefore explain in detail under which circumstances pH–pKA can be a universal parameter, and also demonstrate why their numerical example is not in contradiction to our statement. Moreover, the fact that pH–pKA is not a universal parameter for titrating systems is well known in the pertinent literature. Regarding (2), we admit that the symmetry-breaking feature of the constant pH algorithm has escaped our attention at the time of writing the review. We added some clarifying remarks to this behavior. Concerning (3), we point out that the grand-canonical coupling and the resultant Donnan potential are not features of single-phase systems, but are essential for two-phase systems, as was shown in a recent paper by some of us, see J. Landsgesell et al., Macromolecules, 2020, 53, 3007–3020.
1 Is pH–pKA a universal parameter?
Levin and Bakhshandeh showed in their comment on our review article1 that pH–pKA is not a universal parameter for titrating systems. They also presented examples when this universality is not maintained. All these facts are not new and they are widely known in the pertinent literature. This was also stated in our review,1 as well as in a previous paper by some of us.2 However, Levin and Bakhshandeh quoted us incorrectly, omitting some relevant words and adding others, which effectively invalidated our original statement. As a matter of fact, we did not state in our review that “pH–pKAis a universal parameter for titrating systems”, but we wrote “according to eqn (13), variations of pKAin the RxMC K sweeping mode gives the same degree of dissociation as the variation of pH in the cpH method because the universal parameter is (pH–pKA), provided that all other conditions are the same”. Later we will show that our statement is certainly correct within the limitations of eqn (13), as discussed in the review. So, the short answer to the comment could be that we agree with their initial statements about the absence of universality with respect to pH–pKA. Nevertheless, the discussion in the comment presents additional points, some of which we find highly questionable.Eqn (4) of the comment can be rearranged to analyze its symmetry with respect to pH–pKA:
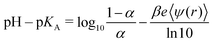 | (1) |
At extreme pH values, the electrostatic potential depends on the pH but is not uniquely determined by α. More precisely, it is not uniquely determined by α if the concentration of H+ and OH−, determined by the pH value, is higher than the concentration of added salt. Under these conditions, H+ or OH− ions and their counterions significantly contribute to the ionic strength of the solution. Then, a change in pH at a fixed concentration of added salt changes also the screening length. As a result, ψ is no longer uniquely determined by α.
The numerical results presented in the comment after eqn (5) do not contradict but actually corroborate the statements given in our review.1 After eqn (5) of the comment, the authors compare calculations at pH = 1 and pH = 6 in salt-free solution, noting that “there is no universality”. In salt-free solutions, the ionic strength is controlled by the concentration of H+ or OH− ions and their counterions. Therefore, if pH = 1 then I ≈ 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M, and if pH = 6 then I ≈ 10−6
M, and if pH = 6 then I ≈ 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M. Universal dependence of α on pH–pKA should not be expected when comparing results at such different ionic strengths because the requirement that all other conditions are the same is not fulfilled.
M. Universal dependence of α on pH–pKA should not be expected when comparing results at such different ionic strengths because the requirement that all other conditions are the same is not fulfilled.
Levin and Bakhshandeh disputed that we have confirmed this universality when comparing RxMC and cpH simulations in our review. However, they omitted the context in which this statement was made in the review. In section 3.3 of the review, we identified a convenient range of the cpH algorithm3 as 3 ≲ pH ≲ 11. Outside this range, artifacts may occur because, by construction, the acceptance probability of the cpH algorithm strictly imposes that pH–pKA be the universal parameter. The algorithm neglects that a change in the pH implies a change in the screening length and this change is significant outside the convenient range. For this reason, the cpH algorithm should be regarded as an approximation which works well in the convenient range of pH but can fail outside this range. In ref. 2, we showed not only that pH–pKA is the universal parameter, provided that all conditions are the same, but also that deviations occur under specific conditions, when this requirement cannot be fulfilled.
2 Symmetry-breaking in the constant pH algorithm
Levin and Bakhshandeh also indicated that the constant pH algorithm has a broken symmetry, citing the work by Labbez and Jönsson,4 which we admittedly were not aware of at the time of writing the review. It must be clarified that this symmetry-breaking is an implementation feature of the constant pH algorithm. As such, it is unrelated to pH–pKA being a universal parameter for titrating systems, which was discussed in the previous section.Labbez and Jönsson4 proposed a correction to the cpH algorithm which prevents this symmetry breaking. In their comment, Levin and Bakhshandeh proposed a modification of this correction, claiming that it should work under all conditions. In fact, the proposed modification does not work under all conditions but it only works under a narrower range of conditions than the original correction by Labbez and Jönsson.4
Labbez and Jönsson noted that the protonation/deprotonation reaction could be implemented in two different ways, which should be equivalent in principle,
| HA ⇌ A− + Y+ addition of cation procedure, ACP | (2) |
| X− + HA ⇌ A− deletion of anion procedure, DAP | (3) |
The correction proposed by Labbez and Jönsson4 was presented as eqn (7) in the comment, albeit using a different notation. Labbez and Jönsson noted that their correction “amounts to simply correct the trial energy of titration, eqn (3), by the excess chemical potential of the ‘unwanted’ ion”.4 Assuming that the amount of salt ions in the box is sufficient, then
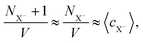 | (4) |
 | (5) |
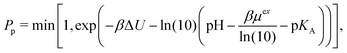 | (6) |
 . Therefore, the excess chemical potential is constant as long as the ionic strength is constant. At an extreme pH, the ionic strength is not constant. In such a case, the correction is not constant either but becomes a function of the pH, not only shifting the results along the pH scale but also affecting the shape of the curve.
. Therefore, the excess chemical potential is constant as long as the ionic strength is constant. At an extreme pH, the ionic strength is not constant. In such a case, the correction is not constant either but becomes a function of the pH, not only shifting the results along the pH scale but also affecting the shape of the curve.
Labbez and Jönsson demonstrated that this corrected algorithm yields consistent results for both procedures, ACP and DAP. They also showed that this correction can be particularly important for simulating highly charged surfaces of colloidal particles, similar to those studied by the authors of the comment. The practical problem of using this correction is that the activity coefficients (chemical potentials) of the ions are not known in advance. Nevertheless, this problem can be solved by using the Widom insertion to measure the activity coefficients during the same simulation.
Levin and Bakhshandeh proposed further modifying of the correction by Labbez and Jönsson,4 claiming that at pH < 7 one can use the approximation pH ≈ pCl. This approximation is valid only in salt-free solutions to which HCl has been added to adjust the pH. However, under most conditions, this approximation is not applicable, e.g. in a 0.1 M NaCl (pCl ≈ 1) solution at pH = 5, used by the authors in the subsequent paragraphs. Therefore, while the correction by Labbez and Jönsson4 is important for using the cpH algorithm, the modification proposed by Levin and Bakhshandeh has a very limited utility.
The original cpH algorithm was formulated without an explicit counterion in the chemical reaction and without symmetry breaking.3 However, this formulation does not preserve electroneutrality and, therefore, is compatible only with the Debye–Hückel potential used in the original work.3 If the cpH algorithm is used with full Coulomb electrostatics in periodic boundary conditions, the counterion is required to preserve electroneutrality. This symmetry breaking and the related correction were not discussed in the review. However, we emphasize that this correction only deals with the broken symmetry of the constant pH algorithm but it is not directly connected to the symmetry of eqn (1), discussed in the preceding section.
3 The Donnan potential
In the remaining text of the comment, Levin and Bakhshandeh elaborate on their claim that “It is actually possible to forgo the pairing of hydronium and of anion during the titration moves, but at the cost of introducing the Donnan potential between system and the reservoir” using an explicit grand-canonical coupling to a reservoir via insertion or deletion of ions. Experimentally, a desired pH and salt concentration in a macromolecular or colloidal solution can be obtained in various ways, some of which result in the Donnan potential, while others do not. For example, if we add the desired amount of salt and adjust the pH by acid or base, or use a buffer solution, we obtain a single-phase system without any Donnan potential. Alternatively, a fixed pH can be obtained also by coupling the macromolecular solution (system) to a an ionic solution (reservoir) via a semi-permeable membrane, as in dialysis. In the latter case, the Donnan potential appears between the system and the reservoir. Therefore, the claim that “grand canonical insertion/deletion moves of ions must be included in the simulation” is not true in general. It is true only if one intends to simulate a two-phase system as described above.In our opinion, the discussion of acid–base equilibria in two-phase systems is beyond the scope of the comment because such systems have not been addressed in the review.1 Nevertheless, these systems are discussed in the comment, based on multiple inaccurate statements which ultimately lead to erroneous conclusions. Therefore, these inaccuracies must also be addressed in our reply.
The authors of the comment used arbitrary definitions of activity and pH, inconsistent with how these quantities are defined by IUPAC.5,6 According to IUPAC, pH is defined as the chemical potential of the H+ ion. This chemical potential does not include the Donnan potential, in contrast to the electrochemical potential. Additionally, the IUPAC definition of pH addresses how this quantity is measured. In the pH measurements the Donnan potentials of the H+ ion and its counterion cancel each other. While this nuance is unimportant in many situations, it is essential when considering acid–base equilibria in two-phase systems with the Donnan potential on the interface, such as colloidal solutions separated from a buffer solution by a semi-permeable membrane. The electrochemical potentials of small ions, including the H+ ion, are equal on each side of the membrane, but the pH value is different. This difference in pH is also evidenced by experimental measurements in membrane-based separation processes.7 Nevertheless, Levin and Bakhshandeh stated in their recent publication8 that “electrochemical potential of an ion inside the system and in the reservoir is the same. Recall that inside the simulation cell, the electrochemical potential of an ion includes the Donnan potential. This means that the activity of hydronium ion is the same inside the cell, and in the reservoir, therefore, the pH inside the simulation cell and the reservoir is the same.” This is a fundamental flaw of their arguments which leads to further misinterpretations.
The original constant pH method was formulated to represent a macromolecular solution, where the implicit solvent (water) or a buffer serves as a virtual reservoir of H+ ions. This represents a single-phase system without the Donnan potential. Therefore, salt concentration and pH in the system are the input parameters. A macromolecular solution coupled to an ionic solution via a semi-permeable membrane is a two-phase system, where the difference in salt concentrations between the system is determined by the Donnan potential. The Donnan potential affects not only the salt concentration but also the partitioning of H+ ions, so the pH in the system is different from that in the reservoir. When Levin and Bakhshandeh compare a constant pH simulation at a given salt concentration and pH in the system to a grand-canonical simulation using the same values of salt concentration and pH in the reservoir, they are comparing these systems under different conditions. Unsurprisingly, the results from the cpH method, presented in Table I of the comment, differ from the other two methods with explicit grand-canonical coupling and the Donnan potential.
The comment further claims that a correct simulation of the Donnan partitioning makes the GCMC and titration moves independent. Barr and Panagiotopoulos9 are cited in the context of the same sentence, but they considered only the Donnan partitioning of salt ions and did not consider titration. The simulation method for titration combined with explicit coupling to a reservoir was introduced in our recent work10 which was published after our review article.1 A few months later an equivalent formulation was presented by Curk and Luijten.11 Both studies demonstrated that the titration and exchange of ions are mutually coupled because the Donnan partitioning affects also the H+ ions. They also showed that this coupling can be successfully achieved when employing the RxMC method which explicitly accounts for the number of H+ ions in the acceptance probabilities. Levin and Bakhshandeh claimed in their comment that “The canonical acceptance probabilities, eqn (9), do not depend on pH of solution”, although this equation explicitly states that the acceptance probability depends on the number of H+ ions in the system. Consequently, the pH in the simulated system differs from that in the reservoir by the Donnan potential. The method proposed by Levin, Bakhshandeh et. al. in ref. 8,12 does not account for this difference. The consequences of disregarding this difference are unclear at the moment. The discussion of these consequences is beyond the scope of our reply to this comment but will be addressed in a forthcoming review article.
4 Conclusion
In conclusion, we have demonstrated that in many cases the degree of ionization is a universal function of pH–pKA, provided that all other conditions remain the same. Within the mean-field picture, eqn (1) retains this universality as long as the electrostatic potential is uniquely determined by the ionization degree. This universality breaks down if a change in pH cannot be achieved without significantly affecting the ionic strength of the solution, thereby breaking the requirement that all other conditions remain the same. We have shown that all numerical examples, provided by the authors of the comment, did not fulfill the requirement that all other conditions remain the same. Therefore, the observed differences in the numerical results do not contradict but in fact corroborate our statements. Nevertheless, we did not discuss the symmetry-breaking in the constant pH algorithm in our review. This feature has been first discussed and corrected by Labbez and Jönsson.4 Finally, the discussion of the acid–base equilibria in two-phase systems, coupled to a reservoir of small ions, goes beyond the scope of the original review and of the comment. This topic will be covered in a forthcoming review paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PK acknowledges the financial support of the Czech Science Foundation, Grant 21-31978J. P. M. B. also acknowledges the financial support of the Margarita Salas grant from the University of Barcelona (funded by the Spanish Ministry of Universities and the European Union). CH acknowledge support through the Cluster of Excellence EXC 2075 SimTech, funded by the German Science Foundation (DFG), grant no. 390740016 and further DFG funding under grants no. 397384169, 451980436, 429529433, and 268449726. RS acknowledges the financial support by the Doctoral College Advanced Functional Materials – Hierarchical Design of Hybrid Systems DOC 85 doc.funds funded by the Austrian Science Fund (FWF).References
- J. Landsgesell, L. Nová, O. Rud, F. Uhlík, D. Sean, P. Hebbeker, C. Holm and P. Košovan, Soft Matter, 2019, 15, 1155–1185 RSC.
- J. Landsgesell, C. Holm and J. Smiatek, Eur. Phys. J.-Spec. Top., 2017, 226, 725–736 CrossRef CAS.
- C. E. Reed and W. F. Reed, J. Chem. Phys., 1992, 96, 1609–1620 CrossRef CAS.
- C. Labbez and B. Jönsson, in Applied Parallel Computing. State of the Art in Scientific Computing, ed. B. Kågström, E. Elmroth, J. Dongarra and J. Wásniewski, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, vol. 4699, pp. 66–72 Search PubMed.
- McNaught and Wilkinson, IUPAC, Compendium of Chemical Terminology, 2nd edn (the “Gold Book”), 1997.
- R. P. Buck, S. Rondinini, A. K. Covington, F. G. K. Baucke, C. M. A. Brett, M. F. Camoes, M. J. T. Milton, R. Mussini, R. Naumann, K. W. Pratt, P. Spitzer and G. S. Wilson, Pure Appl. Chem., 2002, 74, 2169 CrossRef CAS.
- T. Briskot, N. Hillebrandt, S. Kluters, G. Wang, J. Studts, T. Hahn, T. Huuk and J. Hubbuch, J. Membr. Sci., 2022, 648, 120333 CrossRef CAS.
- A. Bakhshandeh, D. Frydel and Y. Levin, J. Chem. Phys., 2022, 156, 014108 CrossRef CAS PubMed.
- S. A. Barr and A. Z. Panagiotopoulos, J. Chem. Phys., 2012, 137, 144704 CrossRef CAS.
- J. Landsgesell, P. Hebbeker, O. Rud, R. Lunkad, P. Košovan and C. Holm, Macromolecules, 2020, 53, 3007–3020 CrossRef CAS.
- T. Curk and E. Luijten, Phys. Rev. Lett., 2021, 126, 138003 CrossRef CAS PubMed.
- A. Bakhshandeh, D. Frydel and Y. Levin, Langmuir, 2022, 38(45), 13963–13971 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |
