Effect of surfactant concentration on diffusion and microstructure in water-in-oil emulsions studied by low-field benchtop NMR and optical microscopy

Abstract

Emulsions are ubiquitous in many consumer products, including food, cosmetics and pharmaceuticals. Whilst their macroscopic characterisation is well-established, understanding their microscopic behaviour is very challenging. In our previous work we investigated oil-in-water emulsions by studying the effect of water on structuring and dynamics of such systems. In the present work, we investigate the effect of surfactant concentration on microstructure and diffusion within the water-in-oil emulsion system by using low-field pulsed-field gradient (PFG) NMR studies carried out with a benchtop NMR instrument, in conjunction with optical imaging. The results reveal that at high surfactant concentration the formation of smaller droplets gives rise to a third component in the PFG NMR attenuation plot, which is mostly attributed to restricted diffusion near the droplet boundaries. In addition, structuring effects due to increase in surfactant concentration at the boundaries could also contribute to further slowing down water diffusion at the boundaries. As the surfactant concentration decreases, the average droplet size becomes larger and both restriction and structuring effects at the droplet boundaries become less significant, as suggested by the PFG NMR plot, whereby the presence of a third diffusion component becomes less pronounced.

---

Introduction

Emulsions are colloidal systems consisting in a dispersion of droplets of an immiscible liquid within another one representing the continuous phase.^1,2 They are used in several industrial fields such as food, cosmetics, pharmaceuticals, chemicals and refineries.^3–5 Because of the oil and water immiscibility, such complex fluids are thermodynamically unstable and tend to phase separate over time.^6,7 To slow down the phase separation process, emulsions are stabilised with surfactants, which are amphiphilic molecules containing a non-polar long-chain hydrocarbon and a polar headgroup, which tend to adsorb at the interfaces and reduce the interfacial tension between the two phases.^3,8–10

Due to their use in industrial applications and in daily life products, emulsions stability is an important parameter to control and it is related to emulsion microstructure, in terms of droplet size distribution and morphology. Elucidating emulsion microstructure is therefore a key issue for understanding their behaviour as well as rationalising their design and applications. Unlike bulk properties of these complex fluids, which can be measured by many techniques, such as rheological measurements,^11,12 emulsion properties at the microstructural level are more challenging to probe and many key points need to be fully understood. For example, while in water solutions surfactant molecules above a critical concentration (CMC) arrange themselves into organised molecular assemblies known as micelles,^13,14 in droplet-based systems, part of surfactant molecules tend to migrate toward the oil–water interface to stabilize the emulsion and the rest remains in bulk phase as micelles. Surfactant arrangement and partitioning between the bulk (either of the continuous or dispersed phase) and the interface of the droplet is however far from being understood.^15–19

In addition to surfactant microstructure, water structuring at the interface in the presence of surfactants is also a debated question. Some evidence of the complex interactions between water and surfactant molecule is provided by the study of water diffusion in micelles,²⁰ whereby water molecules can form strong hydrogen bonds with the polar heads of surfactants (bound water). When reverse micelles (i.e., micelles with surfactant tails outside and polar heads inside) are present,^21,22 water in the internal pool has been described by a shell and core model, with the shell corresponding to water molecules close to surfactant polar heads.²⁰ The results on reverse micelles have also shown that the presence of the interface more than its chemical nature is the primary factor altering water diffusion.²³

More difficult to investigate is the microstructure-transport relationship in emulsion systems. In this context, nuclear magnetic resonance (NMR) spectroscopy offers unique insights for studying dynamics in liquids^24–28 and more complex systems, such as emulsions,^1,29–33 surfactant solutions³⁴ and gels.³⁵ Several NMR studies of emulsions have been carried out, in particular those of Johns et al.,^1,36 have focused on non-invasive monitoring of the droplet size distribution (DSD). These authors³⁶ applied pulsed-field gradient (PFG) NMR and regularisation techniques to retrieve a DSD without assuming a lognormal form as several studies have done. Other authors used PFG NMR to probe droplet size distribution.^3,37 Ambrosone et al.³⁸ found a very good agreement for droplet size determination using NMR and optical microscope measurements. The PFG NMR technique to study droplet size was also used in conjunction with a microfluidic device, which was used to create a monodisperse PDMS oil in water emulsions. Results were compared with optical microscopy, confocal laser scanning microscopy (CLSM) and laser diffractions measurements³⁹ and showed the presence of a minimum in NMR q-space due to restricted diffusion of the molecules within the droplets. PFG NMR has also been demonstrated to be a successful tool for evaluating the DSD of multiple emulsion.³ For example, Wolf et al.⁴⁰ have used PFG NMR measurements to study droplet size of the inner phase of a w/o/w double emulsion and found to be consistent with results from laser light diffraction.

More recently, D’Agostino et al.⁴¹ combined NMR studies with CLSM measurements to investigate the evolution of emulsion microstructure in a phase inversion process as a function of water concentration. In this work, the effect of water in oil-in-water (o/w) emulsions, that is, the oil being the dispersed phase (droplets), was probed and results suggested that the addition of water at different concentrations leads to a significant structuring of the oil-rich phase in the presence of surfactant(s), which was explained by the presence of aggregates in the oil phase as reverse micelle structures.

In the current work, we investigate from an experimental point of view the effect of surfactant concentration on diffusion behaviour in water-in-oil (w/o) emulsions. These systems are important in many areas such as in oil recovery,⁴² yet the transport properties of these systems are challenging to probe. PFG NMR diffusion techniques are used to probe diffusion of the various species in both phases of the emulsions and combined with optical microscopy and rheology measurements in order to determine how the surfactant concentration affects the morphology of the produced emulsions and the mobility within them.

Experimental section

Materials

Soybean oil was purchased from Sigma-Aldrich and has a viscosity of η = 0.06 Pa s, a density of ρ_oil = 0.9138 kg L⁻¹ at room temperature and an average molecular weight of ∼900 kg kmol⁻¹.⁴³ Brij 58 (C16E20, polyoxyethylene-20 hexadecyl ether), purchased from Sigma-Aldrich, is a non-ionic hydrophilic surfactant with an average molecular weight of 1120 g mol⁻¹ and a critical micellar concentration of CMC = 0.01 mM.^7,44 Deionised water was supplied by Millipore.

Sample preparation

Water in oil (w/o) emulsions were prepared by using soybean oil as the continuous phase with water plus Brij 58 at different surfactant concentrations as the dispersed phase. Firstly, the hydrophilic surfactant was dissolved into deionised water, at concentrations ranging from ∼10⁻⁵ to ∼2 × 10⁻¹ M. Then, the oil phase was filtered with a 0.20 μm acetate cellulose syringe filter to remove any impurity and then emulsions, with a volume of disperse phase equal to ϕ = 0.1, were prepared by mixing water/surfactant solution and oil in a beaker on a magnetic stirring plate at room temperature for about 15 minutes. Further details on sample preparation have been reported in a previous study.⁷

NMR measurements and data analysis

NMR experiments were performed at room temperature using a Spinsolve Magritek 43 MHz, equipped with a magnetic field gradient up to 164 mT m⁻¹. The emulsion samples were placed into 5 mm NMR tubes. ¹H NMR spectra were acquired using pulse length of 18 μs, with a pulse amplitude of −6 dB for the 90° pulse and 0 dB for the 180° pulse, a receiver gain of 52 and acquiring 8192 points in the time domain with a dwell time of 50 μs. Pulsed-field gradient (PFG) NMR diffusion experiments were carried out using the pulsed gradient stimulated echo (PGSTE) pulse sequence and the signal decay data were fitted using the Stejskal–Tanner equation⁴⁵ for multi-exponential signal decay:⁴⁶In eqn (1)E₀ is the echo signal in absence of gradient, D_i is the self-diffusion coefficient of the molecules with population p_i, Δ is the observation time for diffusion, δ the duration of a single magnetic field gradient pulse, g is the strength of the magnetic field gradient pulse and γ represents the gyro-magnetic ratio of the nucleus being studied (i.e., ¹H in our case).¹ The expression is simplified introducing the so-called b-factor, .

The n value in eqn (1) represents the number of different diffusion components within the system under investigation. Experiments were conducted at room temperature acquiring approximately sixteen gradient points, using gradient duration times in the range 20–40 ms, a gradient ramp time of 0.1 ms ramped in 10 steps, a gradient stabilisation delay of 1 ms, a number of scans in the range 16–32, two dummy scans and a repetition time of 5000 ms, with each experiment taking approximately 30–60 min.

Regularisation was used to obtain distributions of diffusion coefficients from the PGSTE data. This involves inversion using the Tikhonov regularisation method with general cross-validation (GCV) to choose the regularisation parameter.³⁶ The PFG NMR signal attenuation was fitted by using a Matlab R2018 algorithm with a 64 logarithmic step fit with values in the range of 10⁻¹² to 10⁻⁸ m² s⁻¹ Such algorithm is based on the Stejskal–Tanner model, and the distributions were normalised such that .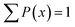

Microscopy imaging

For each sample droplet images were acquired by using an inverted microscope (Zeiss Axiovert S100 TV) connected to a video camera. In all the experiments, observations were performed in bright field using a 20×/0.30 ph1 objective. Droplet diameters were analysed using a commercial software (Image Pro-Plus) and droplet size distribution was obtained using the same software.

Results and discussion

NMR spectra

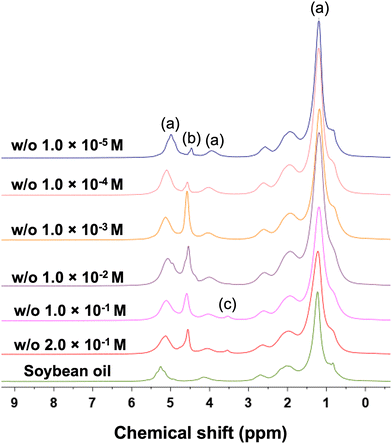
Fig. 1 shows the ¹H NMR spectra for all the emulsions studied here and for the pure soybean oil. It is possible to identify the spectral features of the various components in the emulsion: peaks (a), range 0–3 ppm, 3.5–4.5 ppm and 5–6 ppm, represent the NMR signal of the soybean oil; peak (b), range 4.5–5 ppm is assigned to water; finally peak (c), range 3.5–4, ppm, is assigned to the Brij 58 surfactant, in particular to the polyoxyethylene headgroup and α-CH₂ of the surfactant.⁴⁷ This assignment is supported also by NMR spectra of the solution water plus Brij 58 at the same concentration, which is without the oil (see Fig. S2c, ESI†). It is possible to note that the spectral feature of the surfactant is present only at high concentrations while below 10⁻¹ M the signal becomes not visible anymore as it is overwhelmed by the oil and water signals. It is noted that variation of the relative intensities of the oil (a) and the water (b) peaks across samples, especially for those at low surfactant concentration, might be due to the emulsion becoming unstable, which might lead to separation of phases, hence determine a different amount of water in the control volume.

Fig. 1 ¹H NMR spectra of soybean oil and emulsions used in this work showing labels on the spectral features used for our analysis. Peaks (a), range 0–3 ppm, 3.5–4.5 ppm and 5–6 ppm, represent the NMR signal of the soybean oil; peak (b), range 4.5–5 ppm is assigned to water; peak (c), range 3.5–4 ppm, represents the Brij 58.

Diffusion in the continuous (oil) phase of the emulsion

PGSTE measurements were carried out to evaluate the self-diffusion coefficient of the species within the emulsions in order to understand the mobility of such species and how this is affected by the location in which diffusion occurs, continuous or dispersed phase, as well as the concentration of surfactant used. We begin our analysis on the behaviour of the continuous phase, that is, the soybean oil, and we start our analysis on the pure soybean oil. The PGSTE log attenuation plot for pure soybean oil is depicted in Fig. 2a and shows the typical behaviour of unrestricted diffusion, that is, a linear behaviour that is independent of the observation time. The diffusion coefficient of the pure soybean oil, which is the negative value of the slope of the plot, is 1.34 × 10⁻¹¹ m² s⁻¹. Denkova et al.³⁷ previously reported a self-diffusion coefficient for soybean oil is 1.15 × 10⁻¹¹ m² s⁻¹ at 23 °C, which is in good agreement with our results.

Fig. 2 (a) PGSTE plot for pure soybean oil; (b) PGSTE plot for soybean oil in w/o at surfactant concentration of 2 × 10⁻¹ M; (c) PGSTE plot for soybean oil in w/o at surfactant concentration of 10⁻⁴ M. Solid lines are fittings to eqn (1) with n = 1.

We now focus our attention on the behaviour of the oil phase in the emulsions by monitoring the PGSTE signal attenuation for the NMR signal in the range 0–3 ppm, which represents the aliphatic peaks of the soybean oil. For the sake of brevity, we report only two emulsions for the oil phase, shown in Fig. 2b and c. Similarly, to the pure oil, the PGSTE log plots show a linear and this is largely expected because the oil is the continuous phase, hence it will experience unrestricted diffusion. The self-diffusion coefficients measured for the oil in those two emulsions are approximately the same as that measured for pure soybean oil, with values of 1.30 × 10⁻¹¹ m² s⁻¹ for 2 × 10⁻¹ M and 1.35 × 10⁻¹¹ m² s⁻¹ for 10⁻⁴ M.

Diffusion in the dispersed (water/surfactant) phase of the emulsion

We now focus the attention on the behaviour of the dispersed phase within the emulsions. The dispersed phase of the emulsion is made of water droplets stabilised by the Brij 58 surfactant. For samples with Brij 58 concentration higher than the critical micelle concentration (CMC = 0.01 m M) it is possible to observe the spectral region for the Brij 58 (see Fig. 1). Data on Brij 58 diffusion in the emulsion system and in pure water are reported in the ESI† (Fig. S2, S3 and Table S1).

In the dispersed phase we are interested in understanding the behaviour of the water species. When we started our investigation, we noticed a very peculiar behaviour of the diffusion of the water peak. Using low magnetic field gradient values, up to 10 mT m⁻¹, we can clearly pick up a fast diffusion component of the water signal, at approximately 4.7 ppm, which is significantly faster than that of the oil signal in the continuous phase, at approximately 5.5 ppm. This can be seen in Fig. 3a, which shows the PGSTE spectra for the w/o 2 × 10⁻¹ M sample, whereby during the diffusion experiments the diffusion signal decay of the 4.7 ppm water resonance is significantly faster than the decay of the 5.5 ppm oil signal, the latter showing no appreciable PGSTE attenuation in the range of magnetic field gradients used.

Fig. 3 (a) PGSTE NMR signal attenuation of w/o emulsion at surfactant concentration of 2 × 10⁻¹ M at low b-factor values (i.e., with a maximum magnetic field gradient value of g = 10 mT m⁻¹); (b) PGSTE NMR signal attenuation of w/o emulsion at surfactant concentration of 2 × 10⁻¹ M at high b-factor values (i.e., with a maximum magnetic field gradient value of g = 163 mT m⁻¹).

From Fig. 3a it is clear that despite a first rapid attenuation of the water signal, a significant proportion of this signal does not decay using a maximum magnetic field gradient of 10 mT m⁻¹. To further investigate this behaviour, we significantly increased the magnetic field gradient values in our PGSTE experiments up to a value of 163 mT m⁻¹. In a first qualitative assessment, shown in Fig. 3b, we can now see that using such values of magnetic field gradient, after a first rapid decay of the water peak at 4.7 ppm relative to that of the oil at 5.5 ppm, the decay of the water signal slows down significantly compared to that of the oil peak at 5.5 ppm, the latter showing almost full decay to the noise level. Indeed, when the highest value of the magnetic field gradient is reached, the oil peak has decayed to almost the baseline level whereas a residual water signal remains.

This finding indicates that water inside the droplet has basically two components with very different decay rates:

(i) A first, fast decaying component of the intra-droplet water, which is faster than the decay associated to the diffusion of the oil in the continuous phase;

(ii) A second, slow decaying component of the intra-droplet water, which is much slower than the decay associated to the diffusion of the oil in the continuous phase.

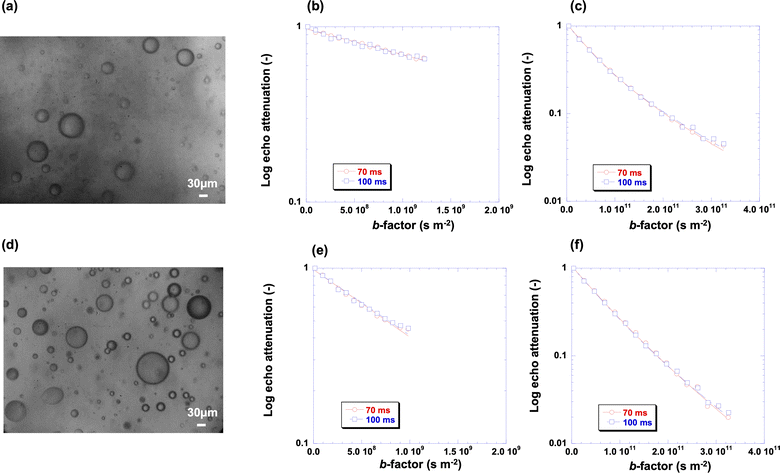
This finding is counter-intuitive since water would be expected to diffuse faster than the oil, based on the viscosity of the bulk fluids. In order to unravel this behaviour, we coupled NMR diffusion measurements with optical microscopy. Fig. 4 shows the microscopy images of the emulsions at different surfactant concentrations studied in this work and the associated PGSTE plots, both using high (163 mT m⁻¹) and low (10 mT m⁻¹) values of the maximum magnetic field gradient, for probing the slower and faster diffusion components, respectively (PGSTE plots for more samples are reported in Fig. S4 of the ESI†). The signal decays reported in the plots is that of the spectral features in the range 4.5–6 ppm in Fig. 1, which contains the peak of water (region 4.5–5 ppm) and the peak of the oil phase (region 5–6 ppm). Due to the proximity of the two signals, integration of both peaks gives a more comprehensive picture of the behaviour of the oil and water species in the emulsion as it ensures that both the full signals of water and oil are included in the PGSTE decay. We stress however that the focus here is on the water peak, which is the dispersed phase of the emulsion, whereas the oil peak is representative of the continuous phase already investigated.

Fig. 4 (a) Optical microscopy image of emulsion at 2 × 10⁻¹ M surfactant concentration and associated PGSTE plots at (b) data at low b-factor values and (c) data at high b-factor values; (d) optical microscopy images of emulsion at 10⁻² M surfactant concentration and associated PGSTE plots at (e) low b-factor values and (f) high b-factor values. Solid lines are fittings to eqn (1) with n = 1 for (b) and (e) and n = 2 for (c) and (f). The scale bar in the optical microscopy images is 30 μm.

The PGSTE plots at low values of b-factor, that is, using a maximum value of g = 10 mT m⁻¹, show a linear behaviour, which is attributed to the fast diffusion water inside the droplet, as expected from Fig. 3a; conversely, the PGSTE plots at high values of b-factor, that is, using a maximum value of g = 163 mT m⁻¹, show a non-linear behaviour, which is associated to the presence of a multi-component diffusion behaviour as previously discussed, in particular the slow diffusion component for the water signal at 4.7 ppm and in addition the decay of the oil signal at 5.5 ppm, see Fig. 3b.

Indeed, the minimum number of components to fit satisfactorily using eqn (1) the decay of the water signal is with n = 2. Note that the change in diffusion observation time from 70 ms to 100 ms has no significant effect on the shape of the plots.

The presence of a total of three components within our systems was also verified by carrying out the analysis of PGSTE data using an alternative method, that is, inversion of the PGSTE data using the Tikhonov regularisation method. The distribution of diffusion coefficients in Fig. 5 and shows clearly the presence of three diffusion populations, which agrees with the analysis shown in Fig. 4. We note that the data in Fig. 5 should be considered only in terms of number of peaks (i.e., diffusing populations) and mean values of diffusivity for each peak. Other features, such as the broadness of the peaks, are not necessarily representative of the physical system and are related to the mathematical aspects of the regularisation procedure.

Fig. 5 Distribution of diffusion coefficients for the investigated emulsions. The data sets there are three populations present consistent with analysis that there are three diffusion populations in the sample, an oil diffusion coefficient population (i = 2) can be observed in-between the slow water (i = 3) and fast water (i = 1) diffusing populations.

In summary, based on experimental evidence, our emulsions systems are characterised by three distinctive regions:

(a) i = 1 is the fast-decaying signal of water inside the droplet;

(b) i = 2 is the diffusion decay of the oil in the continuous phase;

(c) i = 3 is the slow decaying signal of water inside the droplet.

The oil component of the distribution, i = 2, has a diffusion coefficient of the same order of magnitude of that of the pure soybean oil (1.34 × 10⁻¹¹ m² s⁻¹), in particular 2.19 × 10⁻¹¹ m² s⁻¹ for the 2 × 10⁻¹ M samples, and 2.30 × 10⁻¹¹ m² s⁻¹ for 10⁻² M sample. These are essentially the same values obtained by an independent analysis of the PGSTE decay of the signal in the region 0–3 ppm, which is unambiguously that of the soybean only, and confirms that our assignment of the oil peak is correct. Values of self-diffusion coefficients are reported in more detail in Table S3 (ESI†).

Having resolved the diffusion component of the oil peak (at 5.5 ppm) we now turn our attention to more complex behaviour of water. As previously highlighted, based on the findings reported in Fig. 3, the component i = 1 is assigned to the fast water inside the droplet, in particular the water species diffusing in the bulk of the droplet. The values of diffusivity obtained for this component are in the range 10⁻¹⁰ and 10⁻⁹ m² s⁻¹, centred at approximately 7 × 10⁻¹⁰ m² s⁻¹, which is significantly faster than the oil diffusion and but slower (i.e., at low surfactant concentrations) to the diffusion of bulk water at the same temperature (approximately 2.42 × 10⁻⁹ m² s⁻¹) or diffusion of water in solutions of water/surfactant at the same concentration (see Fig. S2a and Table S1, ESI†). This component is ascribed to bulk diffusion of water inside the droplet, which is slower than bulk water, possibly due to an increase in local concentration of the surfactant within the droplets relative to a continuous bulk solution water/surfactant, which then increases the local viscosity within the droplets resulting in slower mobility of the bulk water within the droplet relative to a continuous water/surfactant phase.

Having established that this fast component is that of water diffusing inside the droplets, it is important to assess whether we are in the presence of totally restricted diffusivity, that is, diffusion dominated by collisions of the water molecules with the droplet interface boundary. In order to assess the significance of this phenomenon for our systems, we have calculated the root mean square displacement (RMSD) of the diffusing water inside the droplet according to:

Fully restricted diffusion within the droplet becomes significant if RMSD ≫ d,⁴¹ with d being the diameter of the droplet. Assuming a bulk diffusion inside the droplet of approximately 7 × 10⁻¹⁰ m² s⁻¹ which is the value of the fast water component, for an observation time of 70 ms we obtain a RMSD of approximately 9.9 μm. If we compare this value with the average droplet size of the various emulsions studied here (see Table S2, ESI†), we can note that for emulsions obtained at surfactant concentrations of 2 × 10⁻¹ M and 10⁻¹ M we have that RMSD ∼ d. This cross-over condition implies that water molecules start to feel restriction effects inside the droplet although not fully restricted. Therefore, it is plausible to assume that for such emulsions, the third component arising from the curvature of the PGSTE plot, i = 3, can be attributed to water molecules diffusing near the droplet boundaries and experiencing the restriction of the droplet “wall”. As surfactant concentration decreases, the droplet size increases and for surfactant concentration of 10⁻² M, and below, we generally have that RMSD < d. In this case, we expect the effect of diffusion occurring at the droplet boundary to become less significant and indeed, by inspection of the PGSTE plots in Fig. 6, we note that the curvature associated to the third component, attributed to restricted diffusion near the droplet boundary, becomes less significant and tends to merge with the fast diffusion component of water.

Fig. 6 (a) Optical microscopy image at 10⁻³ M surfactant concentration and associated PGSTE plots at (b) data at low b-factor values and (c) data at high b-factor values; (d) optical microscopy image at 10⁻⁵ M surfactant concentration and associated PGSTE plots at (e) low b-factor values and (f) high b-factor values. Solid lines are fittings to eqn (1) with n = 1 for (b) and (e) and n = 2 for (c) and (f). The scale bar is 30 μm.

We note that another possibility potentially responsible for the presence of the third diffusion component is droplet diffusion, that is, the Brownian diffusion of the droplet in the continuous phase. This process is negligible in concentrated system, but may arise in more diluted systems.⁴⁸ In order to verify the significance of this process in our system, we have calculated the expected self-diffusion coefficient of the droplets using the Stoke–Einstein equation:

where η is the viscosity of the continuous oil phase (in which the droplets are immersed), k_B Boltzmann constant and R the average droplet radius in our systems obtained from microscopy analysis. From eqn (3) we obtain expected droplets diffusivity in the order of 10⁻¹⁶ m² s⁻¹; this value is much smaller than the actual diffusion coefficients measured by PGSTE measurements and to be able to probe such values of diffusivity much higher gradients would be needed, which cannot be achieved due to technical limitations of the instrument. As such, under our experimental conditions we can neglect the Brownian motion of the droplets in the continuous oil phase. It is noted that there could be the possibility of interdroplet diffusion of water as well; however, we can also neglect this contribution since the amount of water in the continuous oil phase is expected to be very small and its NMR signal would be weak and overwhelmed by the contribution of water droplets. We can therefore assign the slow decaying component of the plots in Fig. 4 to the water inside the droplet experiencing restriction at the droplet boundaries.

It should be mentioned that given that we are not in a fully restricted diffusion regime, other factors may contribute to generated curvature associated to the slow-decaying water signal, such as structuring effects at the droplet interface due to a local increase of surfactant concentration at the interface, which has been previously predicted by molecular modelling.¹⁵ Indeed, it is known that surfactant molecules tend to saturate the interface between the oil and the water to stabilise the system but once the interface is covered, and above the CMC, surfactant molecules tend to self-assembly into micelles even nearby the interface by making it a complex and heterogeneous layer.⁴⁹ This leads to a significant structuring of the liquid phase at the droplet interface, leading to the remarkably low diffusion of water. These findings are in line with previous results⁵⁰ on flat liquid–vapour aqueous interfaces in presence of alkyl poly(ethylene oxide) surfactant monolayers (i.e., the same family of the surfactant used in this study), where the presence of water species forming strong hydrogen bonds in a tetrahedrally coordinated structure similar to that of bulk ice has been suggested. In addition the ethylene oxide chains elicit an ordering of the hydrating water molecules,⁵¹ even though the chains are disordered in the liquid-like interfacial phase of surfactant molecules. Our results could hence provide some evidence of strongly bound water species at the interface. One result that supports this additional effect contributing to the slow decaying water signal is that the shift from a two-component towards a single component behaviour, that is, the slow-decaying component becoming negligible, occurs at approximately the CMC of the emulsion. This finding suggests that below the CMC the surfactant ability to form such structuring at the water droplet interface decreases significantly.⁴⁹ We stress however that whilst there is some evidence for such structuring effects, this is not conclusive and more work would be needed to elucidate this aspect, which will be the subject of future research in this area.

Conclusions

The role of surfactant(s) in emulsions is essential in emulsification processes for determining system microstructure and stability.^7,52,53 In droplet-based systems, surfactants rearrange themselves and distribute, both in bulk and at the interface, according to their chemical structure and concentration but there are many points relating to this process at the microscopic scale that remains unexplored. This work shows that the combination of PFG NMR diffusion measurements and optical microscopy is a powerful tool for assessing both evolution of w/o emulsion microstructure as well as probe transport properties, giving a comprehensive picture of both morphology and dynamics in these systems. The results obtained suggest that at high surfactant concentration a third diffusion component in the PFG NMR attenuation plot is observed, which can be mostly explained by the formation of smaller droplets that leads towards a restricted diffusion near the droplet boundaries. In addition, structuring effects in higher surfactant concentration emulsions may also contribute to further slowing down water diffusion. As the surfactant concentration decreases, effects of restrictions on water diffusion inside the droplet become less significant due to the average droplet size becoming larger. The approach proposed in this work is able to study both microstructure and transport in water-in-oil emulsions as a function of surfactant concentration, which are important aspects to consider when designing such systems.

Author contributions

Carmine D’Agostino: conceptualization, methodology, validation, formal analysis, investigation, writing–original draft preparation. Valentina Preziosi: conceptualization, methodology, validation, formal analysis, investigation, writing–original draft preparation, funding acquisition. Giuseppina Caiazza and Maria Vittoria Maiorino: formal analysis, investigation. Einar Fridjonsson: formal analysis, investigation, writing–review and editing. Stefano Guido: writing–review and editing, supervision. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

V. Preziosi gratefully acknowledges funding from the STAR Linea1/2018 project and FISR 2020 project (FISR2020IP_01635). C. D’Agostino would like to acknowledge the EPSRC (grant no. EP/S019138/1) for funding his research activities. G. Caiazza and M. V. Maiorino would like to acknowledge the Erasmus plus Traineeship programme for funding their research activities at the University of Manchester. For the purpose of open access, the authors have applied a creative commons attribution (CC BY) licence (where permitted by UKRI, ‘open government licence’ or ‘creative commons attribution no-derivatives (CC BY-ND) licence’ may be stated instead) to any author accepted manuscript version arising.

Notes and references

1. M. L. Johns, Curr. Opin. Coll. Interface Sci., 2009, 14, 178–183.
2. J. Bibette, F. L. Calderon and P. Poulin, Rep. Prog. Phys., 1999, 62, 969.
3. R. Bernewitz, G. Guthansena and H. P. Schuchmann, Magn. Reson. Chem., 2012, 49, S93–S104.
4. F. Goodarzi and S. Zendehboudi, Can. J. Chem. Eng., 2019, 97, 281–309.
5. D. Wang, D. Yang, C. Huang, Y. Huang, D. Yang, H. Zhang, Q. Liu, T. Tang, M. G. El-Din and T. Kemppi, Fuel, 2021, 286, 119390.
6. T. F. Tadros, Emulsion Form. Stab., 2013, 1, 1–75.
7. R. D'Apolito, A. Perazzo, V. Preziosi, M. D'Antuono, G. Tomaiuolo, R. Miller and S. Guido, Langmuir, 2018, 34, 4991–4997.
8. R. Miller and G. Kretzschmar, Adv. Colloid Interface Sci., 1991, 37, 97–121.
9. J. Sjoblom, Emulsions and emulsion stability, Taylor and Francis, 2005.
10. M. Zembyla, B. S. Murray and A. Sarkar, Trends Food Sci. Technol., 2020, 104, 49–59.
11. Y. Otsubo and R. K. Prud'homme, Rheol. Acta, 1994, 33, 29–37.
12. R. Pal, AIChE J., 1996, 42, 3181–3390.
13. A. Domínguez, A. Fernández, N. González, E. Iglesia and L. Montenegro, J. Chem. Educ., 1997, 74, 1227.
14. M. Monduzzi and B. Lindman, Curr. Opin. Colloid Interface Sci., 2019, 44, 14–22.
15. P. Posocco, A. Perazzo, V. Preziosi, E. Laurini, S. Pricl and S. Guido, RSC Adv., 2016, 6, 4723–4729.
16. P. Levitz, Langmuir, 1991, 7, 1595–1608.
17. V. Fainerman, R. Miller, E. Aksenenko, A. Makievski, J. Krägel, G. Loglio and L. Liggieri, Adv. Colloid Interface Sci., 2000, 86, 83–101.
18. P. Joos and J. Van Hunsel, Colloids Surf., 1988, 33, 99–108.
19. H. A. Stone, J. Fluid Mech., 2010, 645, 1–25.
20. B. Bagchi, Water in Biological and Chemical Processes: From Structure and Dynamics to Function, Cambridge University Press, Cambridge, 2013, pp. 261–276.
21. A. A. Bakulin, D. Cringus, P. A. Pieniazek, J. L. Skinner, T. L. Jansen and M. S. Pshenichnikov, J. Phys. Chem. B, 2013, 117, 15545–15558.
22. E. E. Fenn, D. B. Wong, C. H. Giammanco and M. Fayer, J. Phys. Chem. B, 2011, 115, 11658–11670.
23. E. E. Fenn, D. B. Wong and M. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15243–15248.
24. C. D'Agostino, M. Mantle, L. Gladden and G. Moggridge, Chem. Eng. Sci., 2012, 74, 105–113.
25. C. D'Agostino, M. D. Mantle, L. F. Gladden and G. D. Moggridge, Chem. Eng. Sci., 2012, 74, 105–113.
26. C. D'Agostino, J. A. Stephens, J. D. Parkinson, M. D. Mantle, L. F. Gladden and G. D. Moggridge, Chem. Eng. Sci., 2013, 95, 43–47.
27. Q. Zhu, C. D'Agostino, M. Ainte, M. D. Mantle, L. F. Gladden, O. Ortona, L. Paduano, D. Ciccarelli and G. D. Moggridge, Chem. Eng. Sci., 2016, 147, 118–127.
28. F. Franconi, L. Lemaire, J.-C. Gimel, S. Bonnet and P. Saulnier, J. Controlled Release, 2021, 337, 155–167.
29. I. Lönnqvist, A. Khan and O. Söderman, J. Colloid Interface Sci., 1991, 144, 401–411.
30. N. N. Ling, A. Haber, E. F. May, E. O. Fridjonsson and M. L. Johns, Chem. Eng. Sci., 2017, 160, 362–369.
31. Z. Gong, M. H. Tootoonchi, C. A. Fraker and J. D. Walls, Phys. Chem. Chem. Phys., 2021, 23, 19244–19254.
32. R. Bernewitz, U. Schmidt, H. Schuchmann and G. Guthausen, Colloids Surf., A, 2014, 458, 10–18.
33. E. O. Fridjonsson, B. F. Graham, M. Akhfash, E. F. May and M. L. Johns, Energy Fuels, 2014, 28, 1756–1764.
34. S. J. Law and M. M. Britton, Langmuir, 2012, 28, 11699–11706.
35. C. D'Agostino, R. Liuzzi, L. F. Gladden and S. Guido, Soft Matter, 2017, 13, 2952.
36. K. G. Hollingsworth and M. L. Jhons, J. Colloid Interface Sci., 2003, 258, 383–389.
37. P. S. Denkova, S. Tcholakova, N. D. Denkov, K. D. Danov, B. Campbell, C. Shawl and D. Kim, Langmuir, 2004, 20, 11402–11413.
38. L. Ambrosone, S. Murgia, G. Cinelli, M. Monduzzi and A. Ceglie, J. Phys. Chem. B, 2004, 108, 18472–18478.
39. A. Woodward, T. Cosgrove, J. Espidel, P. Jenkins and N. Shaw, Soft Matter, 2007, 3, 627–633.
40. F. Wolf, L. Hecht, H. P. Schuchmann, E. H. Hardy and G. Guthausen, Eur. J. Lipid Sci. Technol., 2009, 111, 730–742.
41. C. D'Agostino, V. Preziosi, A. Khan, M. Mantle, E. Fridjonsson and S. Guido, J. Colloid Interface Sci., 2019, 551, 138–146.
42. A. Perazzo, G. Tomaiuolo, V. Preziosi and S. Guido, Adv. Colloid Interface Sci., 2018, 256, 305–325.
43. T. W. Patzek, Bull. Sci., Technol. Soc., 2009, 29, 194–204.
44. A. Patist, S. S. Bhagwat, K. W. Penfield, P. Aikens and D. O. Shah, J. Surfactants Deterg., 2000, 3, 53–58.
45. J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526.
46. M. Schönhoff and O. Söderman, J. Phys. Chem. B, 1997, 101, 8237–8242.
47. H. Heins, T. Sokolowski, H. Stöckmann and K. Schwarz, Lipids, 2007, 42, 561–572.
48. T. Garasanin, T. Cosgrove, L. Marteaux, A. Kretschmer, A. Goodwin and K. Zick, Langmuir, 2002, 18, 10298–10304.
49. H. B. De Aguiar, M. L. Strader, A. G. de Beer and S. Roke, J. Phys. Chem. B, 2011, 115, 2970–2978.
50. E. Tyrode, C. M. Johnson, A. Kumpulainen, M. W. Rutland and P. M. Claesson, J. Am. Chem. Soc., 2005, 127, 16848–16859.
51. C. D. Bain, J. Chem. Soc., Faraday Trans., 1995, 91, 1281–1296.
52. P. Wilde, Curr. Opin. Colloid Interface Sci., 2000, 5, 176–181.
53. H. Stone and L. Leal, J. Fluid Mech., 1990, 220, 161–186.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00113j

‡ These two authors contributed equally to this work and are co-first authors.

---