 Open Access Article
Open Access Article3-D rotation tracking from 2-D images of spherical colloids with textured surfaces†
Vincent
Niggel
 ,
Maximilian R.
Bailey
,
Maximilian R.
Bailey
 ,
Carolina
van Baalen
,
Carolina
van Baalen
 ,
Nino
Zosso
,
Nino
Zosso
 and
Lucio
Isa
and
Lucio
Isa
 *
*
Laboratory for Soft Materials and Interfaces, Department of Materials, ETH Zurich, CH-8093, Zurich, Switzerland. E-mail: lucio.isa@mat.ethz.ch
First published on 31st March 2023
Abstract
Tracking the three-dimensional rotation of colloidal particles is essential to elucidate many open questions, e.g. concerning the contact interactions between particles under flow, or the way in which obstacles and neighboring particles affect self-propulsion in active suspensions. In order to achieve rotational tracking, optically anisotropic particles are required. We synthesise here rough spherical colloids that present randomly distributed fluorescent asperities and track their motion under different experimental conditions. Specifically, we propose a new algorithm based on a 3-D rotation registration, which enables us to track the 3-D rotation of our rough colloids at short time-scales, using time series of 2-D images acquired at high frame rates with a conventional wide-field microscope. The method is based on the image correlation between a reference image and rotated 3-D prospective images to identify the most likely angular displacements between frames. We first validate our approach against simulated data and then apply it to the cases of: particles flowing through a capillary, freely diffusing at solid–liquid and liquid–liquid interfaces, and self-propelling above a substrate. By demonstrating the applicability of our algorithm and sharing the code, we hope to encourage further investigations in the rotational dynamics of colloidal systems.
1 Introduction
Colloidal particles, i.e. objects with a size between a few nanometers and few micrometers, are subjected to incessant, thermally-driven random collisions with surrounding fluid molecules, which are responsible for their diffusive, or Brownian, motion. A rigid body moving in three dimensions has six degrees of freedom – three positional and three orientational ones – and the most generic form to describe the dynamics of arbitrarily shaped colloids is via a system of six Langevin equations, where viscous (Stokes) drag forces and torques balance thermal ones. For an arbitrary shape, translation and rotation can be coupled, leading to a hydrodynamic friction tensor with up 21 independent elements.1 More symmetric shapes require fewer coefficients,2,3 down to the case of sphere-like objects, whose motion is fully described by one translational and one rotational drag coefficient, directly connected to the particle's translational and rotational diffusivity, DT and DR, via simple Stokes–Einstein relations. However, even for colloidal spheres, symmetry in the dynamics may be broken by interactions with confining walls.4–6 In addition to stochastic diffusive motion, particles can also be made to translate or rotate deterministically along prescribed directions in the presence of external fields, such as flow, magnetic or electric fields, thus also requiring the determination of three translational and three angular velocities. Finally, any combination of diffusive and deterministic motion is possible, such as in the case of active Brownian motion, where a particle has a self-generated constant propulsion velocity, whose direction is randomised by rotational diffusion, and which is superimposed to translational random displacements.7 From these arguments it follows that a full description of the motion of colloidal particles under a range of different conditions requires one to characterise both their translational and angular displacements in three dimensions (3-D).Since seminal efforts in the 90's, e.g.,8,9 tracking particle translation from microscopy images has today become a common task, recently also exploiting machine-learning approaches,10,11 with ramifications across different disciplines.12 In contrast, tracking the rotational motion of colloidal particles has received significantly less attention.13 Tracking rotation is in fact easily achievable for shape-anisotropic particles,1,3,14–21 but it is impossible for uniform spherical colloids. However, colloidal spheres are ubiquitous model systems and unravelling their rotational motion plays an important role in a broad range of physical problems, e.g. in dense quiescent suspensions approaching dynamical arrest (glass transition),22–24 for individual self-propelling colloids in proximity to a confining wall25 or at higher concentrations, where dynamic clustering occurs,26,27 and for concentrated systems under shear.28 Moreover, the presence of potential coupling between rotational and translational motion renders the accurate characterisation of the former highly important in many additional situations.29–31
The key impediment to the direct evaluation of a particle's orientation is the requirement for optical anisotropy,13 as exploited in earlier depolarised light-scattering studies,32 which is however not common for most spherical colloids. Optical anisotropy can nonetheless be achieved by incorporating a non-centered fluorescent component within the particles during synthesis23,24,33 or after synthesis, e.g. by photobleaching,34 or by preparing asymmetrically-coated particles, i.e. Janus particles.35–38 More recently, Ilhan et al. demonstrated the tracking of the 3-D rotations of colloidal particles having an overall spherical shape, but presenting a non-uniform fluorescence signal due to the presence of fluorescent asperities onto their surfaces (raspberry particles).39 They then used these particles to probe the effect of surface roughness on the rotational dynamics of a colloidal suspension approaching the glass transition.40
Currently, most experimental approaches to directly measure 3-D rotation require three-dimensional imaging, typically achieved by performing z-scans with a confocal microscope. Besides the requirement for sophisticated equipment, this approach is ill-suited for the rapid tracking of particle rotations, as images from different focal planes must be acquired continuously (z-stacks), introducing significant delays in the effective volumetric frame rate. Ideally, the acquisition rate of the image stacks should be much faster than the characteristic time of rotation to avoid image distortions, which limits investigations to slow dynamics, contrasting with the various situations where particles undergo rapid rotations, e.g. under flow.
Here, we demonstrate a method to track the 3-D rotations of optically heterogeneous colloids, i.e. raspberry particles similar to those used by Ilhan et al.39,40 and whose translational motion is restricted to the xy plane, from 2-D wide-field microscopy images at fast acquisition times. In contrast to the method used by Ilhan and co-workers, who directly tracked the fluorescent asperities in 3-D, we retrieve the 3-D angular displacements by analysing the local changes in the particles’ surface texture resulting from said rotations. This approach has been previously used to investigate the rotations of macroscopic objects,41,42 but, to the best of our knowledge, it has not yet been applied to colloidal systems. In the following, we describe the detailed steps of our approach, and evaluate the effects of imaging and tracking parameters on its accuracy against the ground truth by using simulated images. We conclude by applying our method to three distinct experimental cases of widespread interest, namely: particles under flow in a microchannel, free particles diffusing at a glass–water and at an oil–water interface, and active particles self-propelling above a glass substrate.
2 Materials and methods
2.1 Materials
Tetraethyl orthosilicate (TEOS, ≥99%, 250 mL) and a Poly(diallyldimethylammonium chloride) (PolyDADMAC) aqueous solution (average Mw 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00
00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–5
000–5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 00
00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 20 wt% in H2O) were acquired from Sigma-Aldrich. Ethanol (EtOH, absolute for analysis, 1 L) was acquired from Merck. An ammonium hydroxyde aqueous solution (NH4OH in water, 25% v/v, 1 L) was acquired from VWR Chemicals. The small silica particles used as asperities, i.e. “berries”, (200 nm, 10 mg mL−1 in water) were acquired from nanoComposix. The small polystyrene particles used as fluorescent berries (Fluospheres) were acquired from ThermoFischer scientific.
000, 20 wt% in H2O) were acquired from Sigma-Aldrich. Ethanol (EtOH, absolute for analysis, 1 L) was acquired from Merck. An ammonium hydroxyde aqueous solution (NH4OH in water, 25% v/v, 1 L) was acquired from VWR Chemicals. The small silica particles used as asperities, i.e. “berries”, (200 nm, 10 mg mL−1 in water) were acquired from nanoComposix. The small polystyrene particles used as fluorescent berries (Fluospheres) were acquired from ThermoFischer scientific.
2.2 Particle synthesis
Our particle synthesis is based on a previously reported heterogeneous aggregation method43 and is similar to the one used by Ilhan et al.39 We first started with the synthesis of silica core particles with a diameter of 3.5 μm following the Stöber method. For this, we injected a mixture of ethanol and TEOS (80% of EtOH and 20% TEOS in volume) drop-wise for 3 hours in 4.3 mL EtOH and 1.7 mL NH4OH. We also co-injected 15 mL of NH4OH after 12.5 min for 2 hours. The mixture was mixed for another 20 minutes before centrifuging several times to collect and clean the silica core particles. We then took 30 mg of those silica core particles and inverted their surface charge by diluting them with 20 mL of an aqueous solution of PolyDADMAC at a concentration of 0.025 wt%. After centrifugation and redispersion in water several times, the particles were finally redispersed in 3.5 mL double-deionized water before adding 15 μL of 200 nm fluorescent polystyrene berries at 1 wt% followed by 100 μL of 200 nm silica berries at 1 wt% under stirring. 22.5 mL of ethanol and 3.6 mL of ammonia were added to the previous suspension before injecting 1.5 mL of a 95% ethanol- 5% TEOS mixture at 180 μL min−1 before stirring for 20 more minutes to grow a silica shell around the particles and chemically bind the berries to the silica cores. We injected the ethanolic silica precursor solution twice more before placing the particles in a sonicator bath, and finally collected them by centrifugation. Our final particles have a diameter of approximately 4 μm, and a root mean square (RMS) roughness value of 60 nm (see Fig. SI1, ESI†).Janus catalytic microswimmers were obtained by metal deposition onto the fluorescent raspberry particles produced as described above. First, 60 μL of a 0.5 mg mL−1 particle solution was spread onto a microscopy slide that had been exposed to air plasma for 2 minutes at 5 × 10−2 mbar (Harrick, Plasma cleaner PDC-32G). After drying, the particles were coated by a 5 nm Pt layer using a sputter-coating machine (Safematic, CCU-010). The resulting Janus particles were subsequently detached from the glass slide by 2 minutes of ultra-sonication in 50 mL double-deionised water, and finally concentrated into a volume of 0.5 mL.
2.3 Particle imaging
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with isopropanol (Sigma Aldrich), and ultrasonicated for 2 minutes. Subsequently, 0.5 μL of the spreading solution was injected at the water–hexadecane interface through the oil phase using a micro syringe pipette with a flat PFTE tip (Hamilton, 701 N Micro SYR Pipette). Particles at the interface were finally imaged using a water Dip-In objective (CFI Apochromat NIR 60X W) mounted on an Nikon LV-ECON upright microscope equipped with Hamamatsu Orca Flash 4.0 v3 camera. A sketch of the experimental setup can be found in Fig. SI2-B, ESI.† The 498 × 420 pixel images were acquired at 20 fps.
1 ratio with isopropanol (Sigma Aldrich), and ultrasonicated for 2 minutes. Subsequently, 0.5 μL of the spreading solution was injected at the water–hexadecane interface through the oil phase using a micro syringe pipette with a flat PFTE tip (Hamilton, 701 N Micro SYR Pipette). Particles at the interface were finally imaged using a water Dip-In objective (CFI Apochromat NIR 60X W) mounted on an Nikon LV-ECON upright microscope equipped with Hamamatsu Orca Flash 4.0 v3 camera. A sketch of the experimental setup can be found in Fig. SI2-B, ESI.† The 498 × 420 pixel images were acquired at 20 fps.
2.4 3-D rotation computation
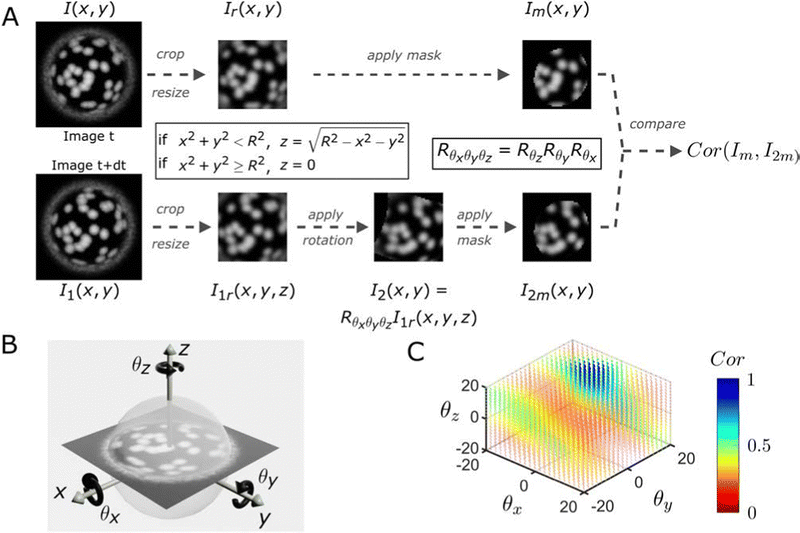
We first test the method on simulated images and then apply it to different experimental situations. Details on the simulation of the raspberry particles can be found in the ESI† (Fig. SI5–SI13). A schematic outlining the different steps of our method is presented in Fig. 1. We start from a 2-D image I(x, y) at time t, which shows a top view of a simulated raspberry-like particle, and compare it to a later image I1(x, y) at time t + dt, which shows a top view of the same particle after rotation by a specified angle. I(x, y) is defined as the reference image, while I1(x, y) will be used to generate the rotated images for comparison.
To retrieve the angular displacements, a direct orthonormal coordinate system with in-plane axes x and y, and a normal, out-of-plane axis z must first be defined. We also need to define the 3-D rotation matrix, which in our case is Rθxθyθz = RθzRθyRθx. This rotation is the composition of a first rotation Rθx of angle θx around the x axis, followed by a rotation Rθy of angle θy around the y axis and finally a rotation Rθz of angle θz around the z axis. Having defined the coordinate system, it is now possible to apply different transforms and create the prospective images.
The images I(x, y) and I1(x, y) are first cropped and resized to decrease computational times while retaining sufficient information and spatial resolution. Since we assume that the recorded images are projections of a spherical particle with randomly distributed fluorescent asperities onto a plane above its equator, the information is denser at the particle center than at its border (i.e., the pixels in the center of the projection correspond to a smaller area of the particle surface and thus allow for the detection of smaller out-of-plane rotations, see Fig. SI16, ESI†). This consideration allows identifying a suitable range for cropping, whose choice influences the precision of the measured angles as well as the range of angular displacements that can be extracted (see Fig. SI17, ESI†). Usually, our cropping is slightly bigger than the size of the mask we will apply in a later step (see Fig. SI18, ESI†). After this first processing step, we thus obtain two new images Ir(x, y) and I1r(x, y). Since we assume that the particle radius R is known and that the spherical particles are centered in the image, we can associate each (x, y) pixel of I1r(x, y) to a height z, where with 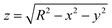 if x2 + y2 < R2 and z = 0 everywhere else. We can then compute the new position [x1, y1, z1] = Rθxθyθz[x, y, z] of each pixel of I1r and, by using a linear interpolant, we can create the rotated image I2 from the rotation Rθxθyθz of I1r (see Fig. SI19, ESI†).
if x2 + y2 < R2 and z = 0 everywhere else. We can then compute the new position [x1, y1, z1] = Rθxθyθz[x, y, z] of each pixel of I1r and, by using a linear interpolant, we can create the rotated image I2 from the rotation Rθxθyθz of I1r (see Fig. SI19, ESI†).
At this stage, we apply the same mask to Ir and I2 to remove unwanted information from the images. The mask is the rotated image of a disk with the same rotation Rθxθyθz. This disk mask selects data with a circular symmetry from our original square images, and it is necessary to discard pixels that are further away from the particle center and that are excluded in our correlation process (see Fig. SI15, ESI†). We then assess the correlation between the masked reference image Im and the rotated image I2m by using the corr2 function from MATLAB based on the pixel intensity of the images. This procedure is performed for all combinations of angles (θx, θy, θz) defined by the user and the most likely 3-D rotation is defined as the rotation which maximises the correlation between Im and I2m.
A detailed discussion on the applicability of the method, on the influence of the image, tracking and experimental parameters is presented in the ESI† (Fig. SI20–SI27) together with the 3D rotation registration codes. The codes for simulation and 3D rotation registration are custom written in and run on Matlab R2020b on a Lenovo P52 (Intel Core, i7-8850H CPU @ 2.60 GHz (6 Core), 16 GB RAM).
3 Results
3.1 Tracking performance versus other methods
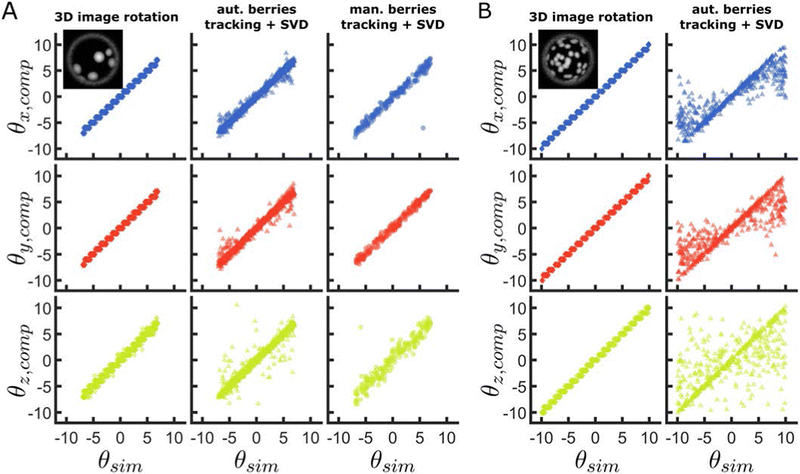
To evaluate the performance of our method on representative data and against other approaches to track 3-D rotation, we extract the angular displacements of simulated raspberry particles using different algorithms, and compare them to their ground-truth values. Specifically, we compare our method against the rotations calculated by applying singular value decomposition (SVD) to the berry (asperities) positions, determined either using automatic detection (Fig. SI28, ESI†), or by manual selection (Fig. SI29, ESI†). Using SVD, the rotation matrix that transforms an initial vector of coordinates into the corresponding final vector can be determined39,42 and used to extract the rotation angles.We begin by analysing the rotation of raspberry particles with a small number of large berries (Fig. 2A). From the calculated angular displacements, we observe that all methods are able to track the ground-truth rotation around all axes, however, the spread in the measured θz,comp is greater than for the two other rotations. We also note that, in all dimensions, our correlation-based approach appears to provide higher precision than SVD using the locations of berries. This is not a consequence of the SVD method, but is instead due to increased errors in locating and tracking single asperities. In fact, the automatic berry tracking method we use presents issues when the asperities are too close to each other, or when individual berries disappear out of the field of view due to the rotation (Fig. SI30, ESI†). Manually selecting the berry centres reduces the degree of matching error compared to the automated case, as reflected in the increased precision of the rotations extracted using SVD, nonetheless, the process is time-consuming and can still lead to tracking errors from limited spatial resolution or due to human error.
We then increase the number of berries while decreasing their average size, and evaluate the precision of our correlation-based method compared to the SVD method applied on berry centres which are localised with automated tracking (Fig. 2B). The performance of our method appears to improve with an increasing number of smaller berries, due to the larger number of features available to compute the correlation. This contrasts with the clearly decreased precision of the alternative approach using SVD, which likely arises due to an amplification of tracking issues for displacements that start to approach the inter-asperity distance.
From the comparison of our method with alternatives using SVD on the tracked asperity centres, we find that an image-correlation-based method provides higher precision in tracking the rotation of raspberry particles around all 3-D axes. However, we note that our method rotates images by discrete angles, whereas SVD provides a continuous range of angular displacements. The size of the discrete space evaluated increases the prospective images by N3 (assuming each dimension is evaluated with the equal number of angles N), and is therefore an important parameter to evaluate to optimise computation time. A systematic study of the influence of other parameters on tracking accuracy is given in the Supporting Information as previously mentioned (Fig. SI20–SI27, ESI†). Moreover, as previously outlined, this method works for any textured surface that does not have any rotational symmetry. It is therefore applicable to systems other than raspberry-like particles (Fig. SI31, ESI†).
3.2 Particles in capillary flow
As a first example of our method's applicability, we track the translation and rotation of dilute particle suspensions flowing in a thin rectangular glass capillary under an externally-imposed flow (see Fig. 3A). An example of particles flowing in the capillary is shown in the Movie SM1, ESI.† For our experimental particles, the protrusion of the center of the berries relative to the surface of the core sphere corresponds to less than 5% of the overall particle radius, and we therefore neglect it in the computation. However, in the case of greater protrusions, an effective radius may be considered for the image transformations. Details on the effect of deviations of the assumed particle radius are found in Fig. SI25, ESI.†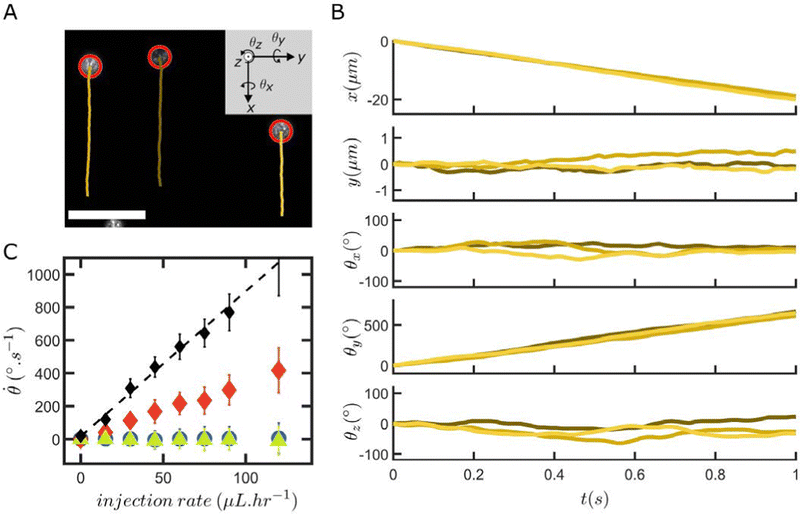 | ||
Fig. 3 (A) Example image with 3 particles on the bottom of a rectangular glass capillary and corresponding trajectories for an injection rate of 60 μL h−1. The white scale bar represents 20 μm. (B) Positional and angular coordinates of the three particles shown in A as a function of time. (C) Average rolling speed ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) x (blue circles), x (blue circles), ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) y (red diamonds) and y (red diamonds) and ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) z (green triangles) of the particles as a function of the injection rate. The black diamonds show the expected values for pure rolling with z (green triangles) of the particles as a function of the injection rate. The black diamonds show the expected values for pure rolling with ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) = 360° × = 360° × 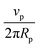 , with vp the experimental average velocity of the particles for the different injection rates (see Fig. SI32, ESI†) and Rp the particle radius. The black dashed line shows a linear fit of the pure rolling speed vs. injection rate. The error bars correspond to the standard deviation of the data. , with vp the experimental average velocity of the particles for the different injection rates (see Fig. SI32, ESI†) and Rp the particle radius. The black dashed line shows a linear fit of the pure rolling speed vs. injection rate. The error bars correspond to the standard deviation of the data. | ||
Given the geometry of the problem, at the centre of the channel at its bottom surface, the flow induces translation along the channel (x-axis) and rotation along the principal shear direction (y-axis). We first localize and track the particles’ centres using the in-built MATLAB imfindcircles function and show that they move with a constant velocity vp in the x direction and only exhibit small positional fluctuations in the y direction (see Fig. 3B). Moreover, the density difference with the fluid causes them to sediment to the channel bottom wall and we neglect displacements in the z direction. Using our image correlation approach for 3-D rotation registration, we are then able to track the angular displacements in x, y, and z over time (also see Fig. 3B). We find that the particles steadily rotate around the y axis with a constant angular velocity as they roll on the channel's bottom surface. Both the translational and the rolling velocity ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) grow linearly with the externally imposed flow rate (see Fig. 3C and Fig. SI32, ESI†). However, the measured values of rotation around the y-axis are below the theoretical prediction for pure rolling (see black symbols in Fig. 3C), indicating that they also slide on the glass capillary surface. Rotations around the two other axes are significantly smaller, and thus the particle motion is essentially confined in 1D. The data suggest a constant ratio of sliding to rolling motion under these experimental conditions, i.e., a constant ratio between the values of the black and red diamonds as a function of injection rate in Fig. 3C, which would be interesting to characterize further beyond these initial experiments as a function of particle and substrate properties. This method can be extended to denser suspensions flowing in a thin capillary, allowing comparison between the translational and rotational velocities beyond the dilute case (see Fig. SI34, ESI†)
grow linearly with the externally imposed flow rate (see Fig. 3C and Fig. SI32, ESI†). However, the measured values of rotation around the y-axis are below the theoretical prediction for pure rolling (see black symbols in Fig. 3C), indicating that they also slide on the glass capillary surface. Rotations around the two other axes are significantly smaller, and thus the particle motion is essentially confined in 1D. The data suggest a constant ratio of sliding to rolling motion under these experimental conditions, i.e., a constant ratio between the values of the black and red diamonds as a function of injection rate in Fig. 3C, which would be interesting to characterize further beyond these initial experiments as a function of particle and substrate properties. This method can be extended to denser suspensions flowing in a thin capillary, allowing comparison between the translational and rotational velocities beyond the dilute case (see Fig. SI34, ESI†)
3.3 Freely rotating particles at interfaces
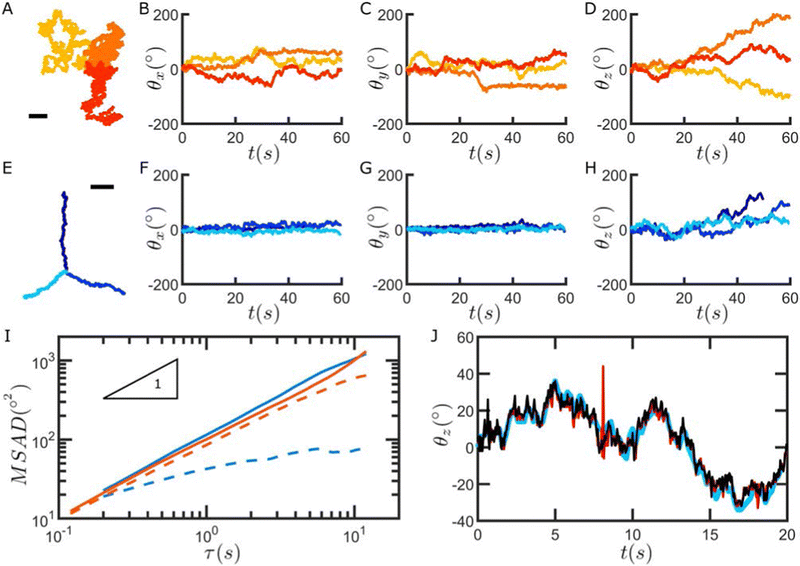
We next apply our method to track the Brownian rotation of particles close to a glass substrate and after adsorption to a hexadecane/water interface. An example of a particle freely diffusing in water close to a glass substrate is shown in the Movie SM2, ESI† while the Movie SM3, ESI† shows the case of a particle absorbed at a fluid–fluid interface.Fig. 4A–D show the trajectories (A) and the angular coordinates (B–D) as a function of time of three particles freely diffusing in water in proximity to a glass substrate. The data clearly show that the particles are rotating in three dimensions, with larger total angular displacements for in-plane (z) rotations. The situation is different when similar particles are instead adsorbed at a fluid–fluid interface. Recording the x, y and z angular coordinates as a function of time shows that the out-of-plane rotation (x and y) is greatly suppressed, with particles only fluctuating around their initial angular position (F–G), while the in-plane, z rotation is unrestricted (H). Additionally, at fluid interfaces, drift is more likely to be present, causing a combination of diffusive and advective translational motion, as seen in the particle trajectories (E) and in the corresponding mean square displacements (Fig. SI35, ESI†).
The time series of the angular positions can be used to calculate the mean squared angular displacements (MSAD) of the particles, which we report in Fig. 4I. Here we plot the MSAD down to ≈0.1 s because the angular displacements at shorter times are below the tracking resolution of our method, but in principle, for sufficiently large angular displacements, the MASD can be calculated all the way down to the camera acquisition rate. We note that in the case of a particle freely diffusing above a substrate, the MSAD of the rotations in x, y, and z are comparable (see Fig. 4I, orange curves, and Fig. SI36, ESI†). We also stress that the MSAD we show is the cumulative MSAD (see Fig. SI38, ESI†) and that the value we compute is practically independent of the rotation order (see Fig. SI39, ESI†). By fitting the MSAD, averaged over the three particles, we obtain a rotational diffusion coefficient ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) R = 0.0141 rad2 s−1 (see ESI,† section “Freely-rotating particles” for more details).
R = 0.0141 rad2 s−1 (see ESI,† section “Freely-rotating particles” for more details).
At the water–hexadecane interface, we see that the particles undergo in-plane rotational diffusion with a diffusion coefficient comparable to that of the particles close to the substrate (solid blue line in Fig. 4I, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) R = 0.0176 rad2 s−1). Conversely, the rotations of the particles in the x- and y-directions are significantly hindered, and the MASD shows a clearly sublinear time dependence and a plateau at long times (dashed blue line in Fig. 4I).
R = 0.0176 rad2 s−1). Conversely, the rotations of the particles in the x- and y-directions are significantly hindered, and the MASD shows a clearly sublinear time dependence and a plateau at long times (dashed blue line in Fig. 4I).
Rough raspberry silica particles adsorbed at fluid interfaces have been shown to exhibit contact-line pinning, such that, after spreading, particles are effectively trapped at a given orientation relative to the interface and can only locally fluctuate without freely rotating out of the interface plane. This scenario follows previous literature studies that ascribe it to contact-line pinning induced by surface heterogeneities for many different particle types, e.g.45–49 Since contact-line pinning effectively confines particle rotation in 2-D at the fluid interface, under these experimental conditions, our 3-D approach can be directly compared to additional approaches to track 2-D rotation, such as 2-D image rotation, or methods based on Fourier transforms (ref. 50, 51). Despite allowing for 3-D rotation of the images to determine the maximum correlation, our method compares favourably with alternatives that only track rotations in 2-D, as can be seen in Fig. 4J. More information on the methods we used for the 2-D rotation tracking can be found in Fig. SI40 and SI41, ESI.†
3.4 Microswimmers
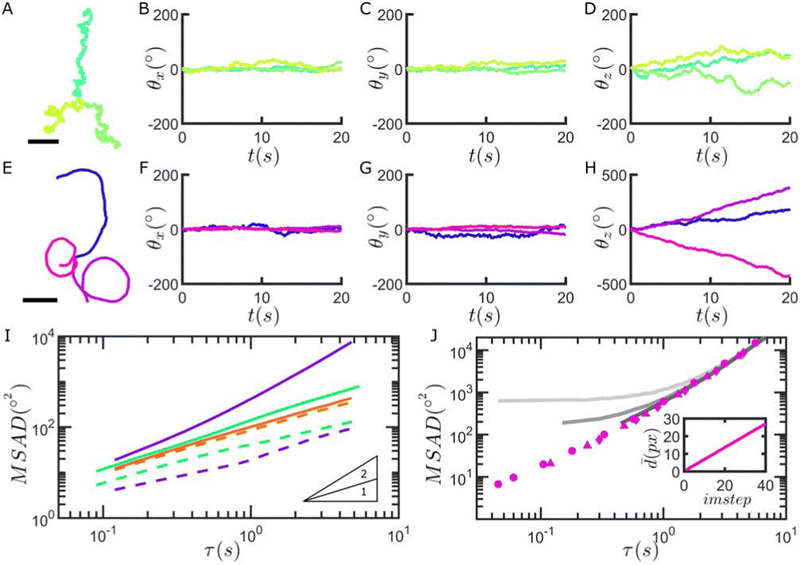
As a final application of our method, we investigate the rotational motion of Janus catalytic microswimmers, produced by asymmetrically depositing Pt thin films onto the raspberry particles.52 The uneven distribution of catalyst on the particle surface self-generates chemical gradients in the presence of a fuel (i.e. H2O2), inducing flows which in turn lead to microswimmer propulsion.53–55 The rotational diffusion coefficients DR of active particles are typically indirectly extracted from their motion using analytical expressions for their MSD assuming idealised models of motion, such as the active Brownian particle model,56 while direct measurements of the rotational motion of spherical Janus microswimmers have to date been restricted to exploiting the optical asymmetry between the metal cap and the supporting particle material.38,46,57,58Fig. 5 shows that we are able to record the rotational motion of the particles as they self-propel. We first perform control experiments in the absence of a chemical fuel (H2O2), and find that the presence of an ∼5 nm Pt cap already affects the out-of-plane particle rotation in comparison to the same particles without a Pt cap (see Fig. 5B, C and I). This is in good agreement with previous Brownian dynamics simulations, which found a preferential cap-down configuration due to a quenching of thermal rotation, caused by gravitational torque arising from the asymmetry in particle density.59
As described above, with the introduction of H2O2, the Janus raspberry microswimmers produce chemical gradients, which also affect their rotational dynamics in the presence of a confining boundary.60 Specifically, angular fluctuations around the x- and y-axes appear to be further damped when the particles become active (see Fig. 5F, G and I). Furthermore, asymmetries present from the berries and potentially uneven Pt film coverage introduce chirality to the microswimmers’ motion, in turn affecting the particle rotation in-plane and increasing the corresponding MSAD (see Fig. 5E, H and I). Examples of Janus raspberry particles with and without hydrogen peroxide are shown in the Movies SM4 and SM5, ESI,† respectively.
We can finally compare the angular displacements obtained using our image correlation-based method with values extracted from particle displacements, assuming that rotations are restricted to 2-D. If the orientation vector of the catalytic cap is assumed to be identical to the direction of motion of the particle, consecutive angular displacements can be determined from the translational motion of the particles.61–63 However, as shown in Fig. 5J, the latter approach performs worse than our methodology at short time-intervals due to the overestimation of detected angular displacements deriving from positional fluctuations (see Fig. SI43, ESI†). Finally, it is worth stressing that the orientation of the microswimmers may not be truly restricted in 2-D in some cases, and might be better described by an intermediate between unrestricted 3-D and confined 2-D rotation, depending on their swimming properties.64 Therefore, by decoupling the measurement of angular displacement from motion, our method is applicable to a wider range of active matter systems, removing the required assumption of e.g. confined 2-D rotation or a constant modulus of velocity.
4 Conclusions
In conclusion, we report here an alternative method to track the 3-D rotation of spherical colloids with textured surfaces from 2-D image sequences, that enables simpler experimental conditions and faster acquisition. In its current implementation, our approach is restricted to particles moving primarily within a plane, such that they can be imaged for extended amounts of time at high frame rates without moving the microscope focal plane, thus being effective in situations complementary to those where full 3-D imaging is required. Our method is based on the comparison between one image of a particle and its hypothetical 3-D rotated projections, and can track 3-D rotation angles from 2-D images, as verified by simulations. In particular, our approach allows 3-D angular tracking at smaller time-steps compared to confocal microscopy. The computational cost of our approach depends on the image size and on the discretisation of the angular space, which need to be optimized under different experimental conditions to maximise accuracy and minimise analysis time. Logically, the computational time decreases by reducing the image size image_size or increasing the size of the angle increments ang_step evaluated. However, both operations reduce tracking accuracy, such that a compromise must be found in each case. Moreover, compared to methods based on feature tracking combined with SVD, which are computationally faster, our correlation-based approach offers a real alternative when the feature tracking fails, while rigid rotations of the surface texture can be still be detected. Additionally, in the current applications of the method, real-time rotation tracking is not required and computation is run offline.Using simulated data, we have also evaluated the impact of errors in the estimation of particle size or particle center localisation on our method's precision, and we showed that adjusting the coverage of fluorescent features allows for improved tracking performance. We found that it is also important that radius of the particles is properly defined, and the particle centre is tracked accurately not to affect the precision of the analysis. The selection of these parameters is highly dependent on the experimental conditions used, and therefore evaluating the performance of the model using simulated data, i.e. generated by the code that we provide, prior to application to experimental data is advised.
We finally illustrated that our 3-D registration rotation method is applicable to a broad range of experimental situations, enabling extraction of detailed information on rotational dynamics. For instance, we showed that particles in a glass capillary undergo both rolling and sliding on the surface under flow. Elucidating the contact conditions of particles under shear will help shed light on open questions in the rheology of dense suspensions where the relative roles of sliding and rolling friction, adhesion and hydrodynamic lubrication are under scrutiny.28 In particular, we envisage that our approach may be used to visualise whether the relative rotations between neighbouring particles are affected by contacts under shear, e.g. imaged in the stagnation plane of a rheo-confocal setup.65 Even if the contact region cannot be imaged with high-resolution, rotations are in any case detected using the central part of the particle images, which would still allow for rotation mapping. We also showed that the rotation of particles at an oil–water interface can be directly measured, which offers additional insight into the motion of particles at fluid interfaces,47,66 towards the realization of materials with tailored interfacial mechanical properties.67 Last but not least, we showed that the direct measurement of the rotation of active particles in 3-D offers better accuracy than methods based on their translational motion, and holds promise to provide useful inputs in extracting dynamics and interactions within ensembles of microswimmers.68 We expect that growing interest will continue developing in characterizing the rotational dynamics of colloidal particles under different conditions, and hope that our method will enable soft matter community to explore new questions.
Data availability
The codes for the simulations and analysis used in this work are available at https://github.com/VincentNiggel/3Drotationsimulation.Author contributions
Author contributions are defined based on the credit (Contributor Roles Taxonomy) and listed alphabetically. Conceptualization: L. I., V. N.; data curation: V. N.; formal analysis: M. R. B., V. N.; funding acquisition: L. I.; investigation: C. v. B., M. R. B., V. N., N. Z.; methodology: C. v. B., M. R. B., V. N., N. Z.; project administration: M. R. B., L. I., V. N.; software: M. R. B., V. N.; supervision: M. R. B., L. I., V. N.; validation: M. R. B., V. N.; visualization: C. v. B., M. R. B., L. I., V. N.; writing – original draft: C. v. B., M. R. B., L. I., V. N.; writing – review and editing: C. v. B., M. R. B., L. I., V. N.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank André Studart for kindly providing access to SEM facilities. This project has received funding from the European Research Council (ERC) under the the European Unions Horizon 2020 research and innovation program grant agreement No. 101001514 and from the MCSA-ITN-ETN “ActiveMatter” Grant agreement No. 812780.References
- D. J. Kraft, R. Wittkowski, B. ten Hagen, K. V. Edmond, D. J. Pine and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 050301 CrossRef PubMed.
- M. Hoffmann, C. S. Wagner, L. Harnau and A. Wittemann, ACS Nano, 2009, 3, 3326–3334 CrossRef CAS PubMed.
- A. Chakrabarty, A. Konya, F. Wang, J. V. Selinger, K. Sun and Q.-H. Wei, Langmuir, 2014, 30, 13844–13853 CrossRef CAS PubMed.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- A. Goldman, R. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–651 CrossRef CAS.
- J. A. Rivera-Moran, Y. Liu, S. Monter, C.-P. Hsu, P. Ruckdeschel, M. Retsch, M. Lisicki and P. R. Lang, Soft Matter, 2021, 17, 10301–10311 RSC.
- B. ten Hagen, S. van Teeffelen and H. Löwen, J. Phys.: Condens. Matter, 2011, 23, 194119 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- H. Qian, M. Sheetz and E. Elson, Biophys. J., 1991, 60, 910–921 CrossRef CAS PubMed.
- B. Midtvedt, S. Helgadottir, A. Argun, J. Pineda, D. Midtvedt and G. Volpe, Appl. Phys. Rev., 2021, 8, 011310 CAS.
- M. R. Bailey, F. Grillo and L. Isa, Soft Matter, 2022, 18, 7291–7300 RSC.
- G. Muñoz-Gil, G. Volpe, M. A. Garcia-March, E. Aghion, A. Argun, C. B. Hong, T. Bland, S. Bo, J. A. Conejero, N. Firbas, Ò. Garibo i Orts, A. Gentili, Z. Huang, J.-H. Jeon, H. Kabbech, Y. Kim, P. Kowalek, D. Krapf, H. Loch-Olszewska, M. A. Lomholt, J.-B. Masson, P. G. Meyer, S. Park, B. Requena, I. Smal, T. Song, J. Szwabiński, S. Thapa, H. Verdier, G. Volpe, A. Widera, M. Lewenstein, R. Metzler and C. Manzo, Nat. Commun., 2021, 12, 6253 CrossRef PubMed.
- S. M. Anthony and Y. Yu, Anal. Methods, 2015, 7, 7020–7028 RSC.
- I. Chung, K. T. Shimizu and M. G. Bawendi, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 405–408 CrossRef CAS PubMed.
- D. Mukhija and M. J. Solomon, J. Colloid Interface Sci., 2007, 314, 98–106 CrossRef CAS PubMed.
- T. H. Besseling, M. Hermes, A. Kuijk, B. de Nijs, T.-S. Deng, M. Dijkstra, A. Imhof and A. van Blaaderen, J. Phys.: Condens. Matter, 2015, 27, 194109 CrossRef CAS PubMed.
- J. Roller, A. Laganapan, J.-M. Meijer, M. Fuchs and A. Zumbusch, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018072118 CrossRef CAS PubMed.
- R. Colin, M. Yan, L. Chevry, J.-F. Berret and B. Abou, EPL, 2012, 97, 30008 CrossRef.
- G. L. Hunter, K. V. Edmond, M. T. Elsesser and E. R. Weeks, Opt. Express, 2011, 19, 17189–17202 CrossRef CAS PubMed.
- S. Coertjens, R. De Dier, P. Moldenaers, L. Isa and J. Vermant, Langmuir, 2017, 33, 2689–2697 CrossRef CAS PubMed.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- K. V. Edmond, M. T. Elsesser, G. L. Hunter, D. J. Pine and E. R. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17891–17896 CrossRef CAS PubMed.
- L. C. Hsiao, I. Saha-Dalal, R. G. Larson and M. J. Solomon, Soft Matter, 2017, 13, 9229–9236 RSC.
- T. Yanagishima, Y. Liu, H. Tanaka and R. P. A. Dullens, Phys. Rev. X, 2021, 11, 021056 CAS.
- J. Simmchen, J. Katuri, W. E. Uspal, M. N. Popescu, M. Tasinkevych and S. Sánchez, Nat. Commun., 2016, 7, 10598 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- A. Singh, C. Ness, R. Seto, J. J. de Pablo and H. M. Jaeger, Phys. Rev. Lett., 2020, 124, 248005 CrossRef CAS PubMed.
- M. Lisicki, B. Cichocki and E. Wajnryb, J. Chem. Phys., 2016, 145, 034904 CrossRef PubMed.
- A. Neild, J. T. Padding, L. Yu, B. Bhaduri, W. J. Briels and T. W. Ng, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041126 CrossRef PubMed.
- K. Yeo, E. Lushi and P. M. Vlahovska, Phys. Rev. Lett., 2015, 114, 188301 CrossRef PubMed.
- V. Degiorgio, R. Piazza and R. B. Jones, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 2707–2717 CrossRef CAS PubMed.
- B. Liu and A. Böker, Soft Matter, 2016, 12, 6033–6037 RSC.
- S. Schiwek, T. Meckel, R. W. Stark and C. Dietz, J. Appl. Phys., 2016, 119, 194304 CrossRef.
- S. M. Anthony, L. Hong, M. Kim and S. Granick, Langmuir, 2006, 22, 9812–9815 CrossRef CAS PubMed.
- C. J. Behrend, J. N. Anker, B. H. McNaughton and R. Kopelman, J. Magn. Magn. Mater., 2005, 293, 663–670 CrossRef CAS.
- Z. Jalilvand, H. Haider, J. Cui and I. Kretzschmar, Langmuir, 2020, 36, 6880–6887 CrossRef CAS PubMed.
- A. Wittmeier, A. Leeth Holterhoff, J. Johnson and J. G. Gibbs, Langmuir, 2015, 31, 10402–10410 CrossRef CAS PubMed.
- B. Ilhan, J. J. Schoppink, F. Mugele and M. H. Duits, J. Colloid Interface Sci., 2020, 576, 322–329 CrossRef CAS PubMed.
- B. Ilhan, F. Mugele and M. H. Duits, J. Colloid Interface Sci., 2022, 607, 1709–1716 CrossRef CAS PubMed.
- R. Zimmermann, Y. Gasteuil, M. Bourgoin, R. Volk, A. Pumir and J.-F. Pinton, Rev. Sci. Instrum., 2011, 82, 033906 CrossRef PubMed.
- D. Barros, B. Hiltbrand and E. K. Longmire, Exp. Fluids, 2018, 59, 104 CrossRef.
- M. Zanini, C.-P. Hsu, T. Magrini, E. Marini and L. Isa, Colloids Surf., A, 2017, 532, 116–124 CrossRef CAS.
- I. Buttinoni, Z. A. Zell, T. M. Squires and L. Isa, Soft Matter, 2015, 11, 8313–8321 RSC.
- X. Wang, M. In, C. Blanc, P. Malgaretti, M. Nobili and A. Stocco, Faraday Discuss., 2016, 191, 305–324 RSC.
- X. Wang, M. In, C. Blanc, A. Würger, M. Nobili and A. Stocco, Langmuir, 2017, 33, 13766–13773 CrossRef CAS PubMed.
- A. Stocco, B. Chollet, X. Wang, C. Blanc and M. Nobili, J. Colloid Interface Sci., 2019, 542, 363–369 CrossRef CAS PubMed.
- M. Zanini, C. Marschelke, S. E. Anachkov, E. Marini, A. Synytska and L. Isa, Nat. Commun., 2017, 8, 15701 CrossRef CAS PubMed.
- K. Dietrich, D. Renggli, M. Zanini, G. Volpe, I. Buttinoni and L. Isa, New J. Phys., 2017, 19, 065008 CrossRef.
- E. De Castro and C. Morandi, IEEE Trans. Pattern Anal. Mach. Intell., 1987, PAMI-9, 700–703 Search PubMed.
- P. Kostelec and S. Periaswamy, Mod. Signal Process., 2003, 46, 161–184 Search PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed.
- M. N. Popescu, S. Dietrich, M. Tasinkevych and J. Ralston, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 351–367 CrossRef CAS PubMed.
- M. R. Bailey, N. Reichholf, A. Flechsig, F. Grillo and L. Isa, Part. Part. Syst. Charact., 2022, 39, 2100200 CrossRef CAS.
- H. Löwen, J. Chem. Phys., 2020, 152, 040901 CrossRef PubMed.
- M. A. Fernandez-Rodriguez, F. Grillo, L. Alvarez, M. Rathlef, I. Buttinoni, G. Volpe and L. Isa, Nat. Commun., 2020, 11, 4223 CrossRef CAS PubMed.
- C. Lozano, J. R. Gomez-Solano and C. Bechinger, Nat. Mater., 2019, 18, 1118–1123 CrossRef CAS PubMed.
- A. Rashidi, S. Razavi and C. L. Wirth, Phys. Rev. E, 2020, 101, 042606 CrossRef CAS PubMed.
- W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438 RSC.
- M. R. Bailey, F. Grillo, N. D. Spencer and L. Isa, Adv. Funct. Mater., 2022, 32, 2109175 CrossRef CAS.
- R. Mestre, L. S. Palacios, A. Miguel-López, X. Arqué, I. Pagonabarraga and S. Sánchez, Extraction of the propulsive speed of catalytic nano- and micro-motors under different motion dynamics, 2020, https://arxiv.org/abs/2007.15316.
- K. Dietrich, G. Volpe, M. N. Sulaiman, D. Renggli, I. Buttinoni and L. Isa, Phys. Rev. Lett., 2018, 120, 268004 CrossRef CAS PubMed.
- X. Zheng, B. ten Hagen, A. Kaiser, M. Wu, H. Cui, Z. Silber-Li and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032304 CrossRef PubMed.
- G. Colombo, R. Massaro, S. Coleman, J. Läuger, P. Va Puyvelde and J. Vermant, Korea Aust. Rheol. J., 2019, 31, 229–240 CrossRef.
- G. Boniello, C. Blanc, D. Fedorenko, M. Medfai, N. B. Mbarek, M. In, M. Gross, A. Stocco and M. Nobili, Nat. Mater., 2015, 14, 908–911 CrossRef CAS PubMed.
- P. J. Beltramo, M. Gupta, A. Alicke, I. Liascukiene, D. Z. Gunes, C. N. Baroud and J. Vermant, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10373–10378 CrossRef CAS PubMed.
- M. Ruiz-Garcia, C. M. B. Gutierrez, L. C. Alexander, D. G. A. L. Aarts, L. Ghiringhelli and C. Valeriani, Discovering dynamic laws from observations: the case of self-propelled, interacting colloids, 2022, https://arxiv.org/abs/2203.14846.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of experimental procedures and report of additional syntheses. See DOI: https://doi.org/10.1039/d3sm00076a |
| This journal is © The Royal Society of Chemistry 2023 |

![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)