Probing local lateral forces of focal adhesions and cell–cell junctions of living cells by torsional force spectroscopy

Abstract

The number and strength of mechanical connections of cells to their local environment can be indicative of their migration and invasion potential. Gaining direct access to the mechanical properties of individual connections and bringing them into a relationship with the state of disease, however, is a formidable task. Here, we present a method to directly sense focal adhesions and cell–cell contacts with a force sensor to quantify the lateral forces of their anchoring points. We found local lateral forces of 1.0–1.5 nN for focal adhesions and slightly higher values at the interfaces between cells where cell–cell contacts are located. Interestingly, a modified surface layer was observed exhibiting considerably reduced tip friction directly next to the area of a retracting cell edge on the substrate. We expect that this technique can improve the understanding of the relationship between mechanical properties of cell connections and the pathological state of cells in the future.

---

1. Introduction

Cancer is considered as one of the major causes of deaths worldwide.¹ Throughout their development, cancerous cells detach from the primary tumor, circulate through the body via the lymphatic or blood system and settle in foreign organ tissues known as the spreading process. Adhesion within their native tissue is generated and organized by cell–cell contacts, in particular by adherens junctions,² tight junctions,³ desmosomes⁴ or gap junctions⁵ within cell layers and by focal adhesions⁶ to the extracellular matrix (ECM) which play a crucial role in malignancy. For the spread of cancer, a fundamental process is detachment, where cancerous cells break their connections to their environment. To thoroughly understand the physics of detachment and specifically to quantify the strength of binding efficiently, meaningful and conclusive measures to assess adhesion are of utmost importance. Currently, there are various optical approaches to conceive the mechanical stress of cells with their surroundings.^7–10 For example, Zaoh et al.¹¹ developed membrane DNA tension probes to visualize tensile forces at cell junctions. Monolayer stress microscopy allowed for the discovery of collective migration phenomena where neighboring cells joined forces to transmit appreciable normal stress across the cell–cell junction, but migrated along orientations of minimal intercellular shear stress.¹² A recent review of single-cell adhesion force kinetics and applications explaining existing approaches can be found in ref. 13. Suspended epithelial cell monolayers could reveal the tensile planar mechanical properties in isolation from their substrate.¹⁴ On the other hand, colloidal probes attached to a force lever can quantify apical surface supracellular mechanical properties in polarized epithelium.¹⁵ Additionally, there are many more methods to probe traction, lateral forces for cell contacts, forces exerted by cells to their substrate/vicinity or within cells by e.g. optical tweezers,^16,17 traction force microscopy,^18–21 atomic force microscopy,^22,23 single molecule fluorescence force spectroscopy²⁴ or magnetic twisting devices using microbeads.²⁵ Mandriota et al.²⁶ developed an elegant approach with adapted T-shaped cantilevers^27,28 for cell stiffness imaging to reveal a mechanistic link between intracellular forces and cell stiffness at the nanoscale. With their approach and model it is not only possible to calculate important quantities such as tension within actin bundles, cell cortex and plasma membrane but also feasible to determine a coupling distance that determines how far effects of a locally exerted force are transmitted to the neighboring region of the cell.²⁶ Here, we present a methodology based on force spectroscopy which maps the lateral forces of the cell periphery as a function of the indentation depth and facilitates the creation of layer-by-layer lateral force images with high lateral and depth precision exhibiting the potential to quantify individual bindings among cells and between cells and the substrate. In contrast to the aforementioned approaches, we utilize a sharp probe on a force sensor to directly sense the mechanical stress of cell connections with the ability to address individual junctions. Static and dynamic force mapping of cells^29–35 and soft matter^36–39 has the advantage to extract multiple observables in various layers of the specimen. An extensive review about the nanomechanical mapping of soft materials was recently provided by Garcia.⁴⁰ We focused in this study on a torsional oscillation of the force sensor to establish a procedure that can quantify lateral forces of soft matter in different indentation depths.

2. Materials and methods

2.1. Cell culturing and fluorescence microscopy

BT-20 cells, epithelial cells from a triple-negative breast cancer were received by our laboratory from CLS Cell Lines Service GmbH (Eppelheim, Germany) and cultivated in cell flasks in a culture medium consisting of 50% Dulbecco's Modified Eagle Medium (DMEM, Merck KGaA, Darmstadt, Germany) and 50% nutrient mixture F-12 (GibcoTM Ham's F-12 nutrient mixture, Fisher Scientific GmbH, Schwerte, Germany) in an incubator at 37 °C and 5% CO₂. For sample preparation, cells were detached from the flasks using Trypsin-EDTA (0.05%, Life Technologies GmbH, Darmstadt, Germany) and grown on round glass disks in a small Petri dish over night. The glass disks were plasma treated for a high cell adhesion without further coating and tagged with star-shaped scratches on the bottom side prior to sample preparation to have markers on the sample that helped finding the same imaging region measured by force mapping with the fluorescence microscope for the purpose of relating lateral forces with locations of the color-labeled focal adhesions. To this end, the glass disks including the cells were dismounted from the atomic force microscope (AFM) and prepared for staining in the following steps. First, cells were washed in phosphate-buffered saline (PBS) before and after fixation in a 3.7% formaldehyde (Merck KGaA, Darmstadt, Germany) containing PBS solution for 15 min. For permeabilization of cell membranes, cells were immersed in a 0.5% Triton X-100 (Acros Organics, Geel, Belgium) followed by two times washing with PBS. Subsequently, the cells were blocked to avoid unspecific binding in 1% BSA/PBS (Thermofisher Scientific, Rockford, IL) for 20 min. Cells were stained with vinculin-binding antibodies conjugated with Alexa Fluor 488 (vinculin monoclonal antibody (7F9), eBioscience™, Affymetrix Inc., Santa Clara, CA) in a mixture with 1% BSA/PBS at a ratio of 1 : 500 (7F9:BSA/PBS). Afterwards, the cells were exposed to 50 μL of the final staining solution for 1 h on a Parafilm surface at room temperature. Eventually, the disks were mounted on coverslips for fluorescence microscopy. With the help of the markers prepared on the glass substrate before measuring the force maps, the region of interest could be found in bright field mode with the optical microscope (Axio Observer Z1, Carl Zeiss AG, Oberkochen, Germany). Fluorescence images were captured at a wavelength λ = 493 nm and exposure times of t = 1 s on an AxioCam HSm Camera from the same manufacturer.

2.2. Cell viability assessment

We employed the ThermoFisher Scientific Live/Dead Viability/Cytotoxicity kit for mammalian cells (Cat. No. L3224) to discern between live and dead cells following torsional force spectroscopy. This kit utilizes two commonly used microscope filters (FITC and RFP) to assess cell viability based on intracellular esterase activity and plasma membrane integrity. For this purpose, a staining solution was prepared by adding 5 μL of calcein AM and 20 μL of ethidium homodimer-1 to 10 mL of DPBS. Subsequently, 200 μL of the staining solution was directly applied to the sample, followed by a 30 minute incubation at 20 °C. The sample, marked by scratches, was then mounted onto the fluorescence microscope, and the same region that was mapped using torsional force microscopy was located with the assistance of bright field imaging. Fluorescence images of live cells (with intact cell membranes, detected by calcein) were captured using a calcein optical filter. In contrast, images of dead cells (with damaged cell membranes, detected by Ethidium homodimer-1) were obtained using a rhodamine optical filter.

2.3. Force microscopy

Cells were mechanically mapped with a Cypher S (Asylum Research, Oxford Instruments, Santa Barbara, CA) atomic force microscope in CO₂ independent DMEM medium (Merck KGaA, Darmstadt, Germany) using the standard liquid cell holder. The photothermal excitation was realized with the built-in blueDrive™ system possessing an excitation laser at λ = 405 nm. Force maps were taken at a lateral resolution of 128 × 128 with 2 μm z-length at a sample rate of 10 kHz and an oscillation frequency of 2 Hz triggered at a force of 2 nN maximum. For the cantilever calibration, the optical lever sensitivity of the cantilever for the vertical bending was measured pushing the tip on a stiff silicon substrate and relating the z-motion of the scanner piezo (in nm) with the vertical deflection on the photodiode (in volts). For the lateral direction, the scan direction was set to 90° (perpendicular to the cantilever length symmetry axis), the tip was pressed on a flat silicon(-oxide) surface with 2 nN and 10 nm were scanned with 256 × 256 pixels in contact mode. Such tiny image areas resulted in stiction between tip and surface during the scan, thus allowing for correlating the motion of the laser on the photodiode in the lateral direction (in volts) with the lateral motion of the scanner in the x-direction (in nm) for torsional calibration. Subsequently, the flexural spring constant was calibrated with the thermal noise method⁴¹ whereas the torsional stiffness was determined based on the theory of Green et al.⁴² For the Cont-GD-G cantilevers (Budget Sensors, Innovative Solutions Bulgaria Ltd, Bulgaria) used in this study, we obtained the following typical values: first flexural force constant k_flex = 0.2–0.3 N m⁻¹; first torsional torque constant k_tor = (0.8–1.0) × 10⁻⁸ N m rad⁻¹; first torsional resonance frequency f_tor,0 = 50–80 kHz (in liquid culture medium); nominal tip radius R = 10 nm. Observables that were recorded during mapping: vertical deflection of the cantilever D, z-piezo position z, torsional drive amplitude a_tor and torsional resonance frequency f_tor,0. In a previous study,³¹ deeply buried cellular components such as nucleoli could be visualized which demonstrate the sub-surface detection capability of this technique. Penetration of the cell membrane depends on the sharpness of the cantilever and the applied forces. Under the conditions chosen here (tip radii <10 nm, applied force 2 nN), we expect a penetration of the tip through the membrane as well as a compression of the cell membrane/structure beneath the tip. Based on the range of tip indentation (up to 2 μm) and the indenter's geometry, it is reasonable to assume that the tip creates a hole in the membrane of similar dimensions, resulting in irreversible damage to the membrane. To confirm the membrane's integrity, we conducted a cell viability assessment following the acquisition of torsional force maps. Remarkably, we were able to demonstrate the membrane's integrity in the same cell. Moreover, the presence of a plateau of constant force in numerous individual force-distance curves, similar to the findings of Penedo et al.⁴³ using needle-shaped tips, suggests that the membrane undergoes stretching before the tip penetrates and senses subsurface features such as desmosomes and focal adhesions. Given the demonstrated membrane integrity, it is reasonable to propose that the created hole closes reversibly upon withdrawal (refer to the proposed tip-sample interaction mechanism in the ESI,† Fig. S1 and S2). Furthermore, the ability to perform repeated measurements on individual cells and the observation of subsequent mitotic events in the incubator indicate cell viability following the measurements, suggesting that this technique does not cause significant cell damage.

2.4. Image processing

From the recorded observables, images of the local tip-sample contact point d₀(x,y), maximum indentation δ_max(x,y), local elastic modulus E(x,y,z), local vertical force F_v(x,y,z) and lateral force F_L(x,y,z) could be deduced. To this end, “force curves” consisting of the cantilever deflection data D at each z-piezo position served as the basis for further analytical processing of the other observables. For each individual force curve, the noise was removed by a Gauss filter followed by a baseline correction (line fit) facilitating a reliable determination of the contact point d₀ between tip and sample as the first point in the z-direction where the deflection value exceeded the standard deviation of the baseline values more than a defined threshold (10×). From the contact point, the indentation depth could be calculated by δ = z−d₀−D. The individual maps can then be displayed as a two-dimensional surface map (through the xy-plane) at a certain z-height. The lateral force F_L(x,y,z) at each indentation depth for all force curves were deduced from the recorded torsional frequency-shift values according to eqn (1). Maps were created and plotted as color-coded images using a home-built program written in Matlab 2021a (MathWorks®, Natick, MA) based on a code provided by Welker et al.⁴⁴ and shown as is, i.e. unfiltered in the Fig. 2 and 3.

3. Results and discussion

3.1. Mapping the lateral forces as function of the cell depth

Fig. 1 illustrates the excitation and detection scheme for torsional force spectroscopy. Based on standard force mapping,³¹ the tip touches the surface of the specimen and indents into it with a chosen oscillation frequency while scanning across the sample. The maximum indentation depth into the cell specimen can be accurately specified by the force setpoint F_set. A torsional vibration^45,46 is generated by photothermal excitation where a power-modulated laser beam periodically heats the cantilever at its base with a frequency matching the first torsional resonance frequency. Note that the excitation laser must be located off the cantilever's length symmetry axis (considering the plane view) towards the edge (see Fig. 1 and 2). Consequently, the apex of the tip performs an oscillation that is in first approximation parallel to the substrate and hence sensitive to in-plane (lateral) sample forces.^43,47,48 The vertical photodiode signal induced by the detection laser can be analyzed to deduce topography, loading force, cumulative as well as local elastic modulus. The lateral signal is fed into phase-locked loop electronics to track the instantaneous torsional resonance frequency of the cantilever and maintain the desired oscillation amplitude A_tor, varying the power of the excitation laser (drive amplitude a_tor). The in-plane tip-sample conservative forces as a function of the indentation depth δ can then be deduced from the torsional resonance frequency shift using the relationship established by Sader–Jarvis:^49,50where k_ip is the in-plane tip-sample force constant k_ip = k_tor/h_tip² which can be considered as lateral spring constant at the tip position and calculated as the ratio of the torsional stiffness of the cantilever and the square of the tip height h_tip.⁵¹ The half-fractional derivative of the frequency shift in eqn (1) is required to deduce forces for the large amplitude case. The drive amplitude is simply a measure for the energy dissipated in the sample during the oscillation. From the in-plane tip-sample forces we then obtain the local lateral forces F_L(x,y,z) when mapping the specimen.

Fig. 1 Scheme of the excitation and detection setup for mapping living cells by torsional force microscopy. The tip periodically indents into the cells while sensing the in-plane forces via torsional cantilever vibration. δ is the local indentation depth of the tip into the sample.

Fig. 2 Selection of the region of interest. (a) Scheme of the scan area with respect to two adjacent cells under investigation. To avoid interferences during spectroscopy a super-luminescence photodiode (SL diode) was used. (b) Map of the indentation depth of the tip into the sample. Total image area 30 × 30 μm².

To acquire the mechanical properties of focal adhesions, the region of interest (ROI) was set to the periphery of both cells (Fig. 2). Fig. 2a schematically shows the alignment of the cantilever with respect to the positions of the two adjacent cells under investigation. As it can be deduced from the 30 × 30 μm² indentation map shown in Fig. 2b, the cell height in the periphery is comparably low and the tip can completely penetrate through the cell down to the substrate where focal adhesions are situated. The cell boundaries are also clearly apparent in the indentation map (highlighted by green dashed lines). The substrate area can be derived from the low indention depth in the left portion of the map. For clarity, henceforth, we refer to cell #1 for the cell at the top and cell #2 for the cell located at the bottom of the map.

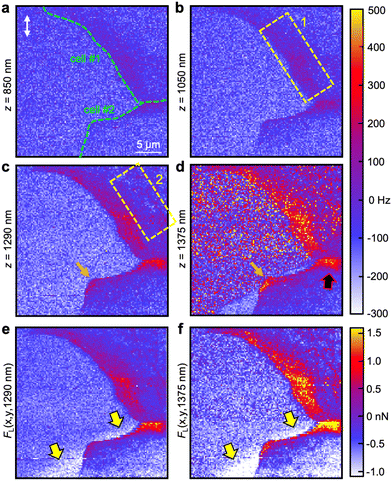
Fig. 3 shows the frequency-shift maps of the torsional cantilever oscillation mode (Fig. 3a–d) as well as the calculated lateral forces (Fig. 3e and f) at various z-depths beneath the cell surfaces (z = 0). The extracted frequency-shift values at z = 850 nm reveal weak interactions between the laterally oscillating tip and cell structures close to the substrate at locations of the periphery. These structures become increasingly evident the more the tip penetrates toward the substrate (Fig. 3b–d). At z = 1050 nm, a belt of repulsive interactions (Δf ≈ 50–100 Hz) located at the periphery and orientated along the edge of cell #1 is visible (enclosed by the yellow dashed box 1). Additionally, the interface of the two adjacent cells features a stripe of higher frequency shift than the surrounding area. At z = 1290 nm single spots of high lateral interaction as well as a network (enclosed by the yellow dashed box 2) appear a few micrometers apart from the edge of cell #1 closer to the nucleus. Also, lateral interactions at the edge of cell #2 emerge. In Fig. 3d (z = 1375 nm), the tip is very close to the substrate, discernible by the lateral interactions that occur on the substrate. The interactions within the cell periphery and at the cell–cell interface (black-red arrow), however, are substantially stronger and in the range of F_L = 1.0–1.5 nN at the rim of cell #1 and 1.5–2.0 nN at the interface between cell #1 and cell #2 as deduced by eqn (1) and mapped in Fig. 3e for the z = 1290 nm layer and Fig. 3f for the z = 1375 nm layer, respectively. Also, the network of strong lateral forces slightly apart from the edge of cell #1 is evident in the map of Fig. 3f. Mandriota et al.²⁶ employed specialized T-shaped cantilevers to conduct force spectroscopy measurements and determine intracellular forces by analyzing stiffness maps. Their developed model, which treats actin bundles as tensioned beams resting on an elastic foundation, enabled the calculation of bundle tension magnitude based on local stiffness. The deduced tensions in fibroblast bundles were found to range in the order of a few nanonewtons. While the cells examined were of different types, we assert that the close agreement between the lateral force values obtained near focal adhesions (mechanically connected to the actin cytoskeleton) and cell–cell junctions using a laterally oscillating tip validates our methodology. It should be noted that torsional force spectroscopy specifically detects in-plane (lateral) forces, making it sensitive to tensions directed along the substrate plane, such as those arising from the actin-focal-adhesion-substrate network or cell–cell junctions. The ability of this method to detect sub-surface structures based on inter- and intramolecular forces, which are not directly measurable through out-of-plane tip vibrations, has been demonstrated on model systems consisting of heterogeneous polymers in ref. 43. Note that there are regions of weak lateral forces in the range F_L = −(1.0–1.5) nN close to the edge of cell #2 on the substrate side apparent in both force images (highlighted by yellow-black arrows). The complete emergence of focal adhesions and cell–cell junctions with increasing tip indentation can be tracked in the Movies S1 and S2 (ESI†).

Fig. 3 Torsional force spectroscopy maps at various subsurface cell layers visualizing the lateral forces of focal adhesions and adherens junctions. (a) Distribution of the local frequency shift at a layer of z = 850 nm beneath the highest tip-sample contact point depicting focal adhesions at the leading edge of the cell. (b) Indenting further (z = 1050 nm) gives access to the lateral forces of focal adhesions closer to the nucleus (region 1 enclosed by dashed rectangles). (c) At z = 1290 nm, a network of strong lateral forces (region 2) becomes apparent as well as the strong lateral forces of adherens junctions (marked by the black-red arrow). (d) Cell #2 (cell at bottom of image) is weakly attached to the glass substrate compared to cell #1 as it depicts only a few spots of high lateral forces for z = 1375 nm at the edge of the cell periphery (orange arrows). (e)–(f) Calculated lateral forces F_L(x,y,z) at the same z-depths as in (c and d), respectively. Note: there are regions of attractive lateral forces on the substrate side adjacent to the cell periphery of cell #2 (highlighted by the yellow-black arrows).

3.2. Identification of focal adhesions and cell–cell junctions as origin for locations with high local shear strengths

Based on the locations of strong lateral forces detected here, we hypothesize that these structures in the cell periphery are either associated with cell connections to the substrate, i.e. focal adhesions, or with cell–cell junctions because these structures are aligned parallel to the substrate and thus exhibit a strong resistance against shear load. To prove this hypothesis, we stained vinculin with vinculin-binding antibodies immediately after performing the mechanical mapping. Vinculin is a focal adhesion protein that anchors the extracellular matrix through integrins to the actomyosin cytoskeleton. It is also associated with cell–cell junctions and hence it is in the focus of cell mechanical measurements and a key protein regulating the transmission of contractile forces.⁵² In another data set, we mapped the periphery of a cell, extracted the lateral frequency-shift image (Fig. 4a), marked the contour of the cell edge (Fig. 4b), and transparently visualized areas of highest lateral force. Before the measurement, we prepared markers in which vicinity we chose the region of interest (see Methods for details). After staining the cells, we focused on the same region by fluorescence microscopy. With the help of the cell contour (white cyan solid line Fig. 4b) drawn in the frequency-shift image and the edge of the cell visible in the fluorescence microscopy image, we could identify the same position and overlay both images. As can be seen in Fig. 4c there is a convincing match of both images. The transparent regions in the torsional frequency-shift map correspond to nearly all spots of highest fluorescence intensity (Fig. 4d and e). The match between both images was corroborated by a Pearson correlation coefficient analysis of different sub-areas within the cell location (red frames in Fig. 4f) which exhibited a clear correlation for most of the areas. However, very low as well as negative coefficients were also calculated for some regions and two mismatches are apparent between high lateral force regions and the potential locations of focal adhesions (green encircled spots in Fig. 4b and e). Reasons for this discrepancy could be due to (i) differences in lateral strength between vinculin-rich areas, (ii) partial cell detachment from the substrate and (iii) cell locomotion during the time between unmounting the sample from the AFM and fixing the cell, (iv) slight misalignment between the two images when manually overlaying as well as (v) noise in the force map. Nevertheless, most of vinculin-rich areas were successfully identified by torsional force spectroscopy. With this procedure, we could unambiguously identify locations of strong lateral forces as anchor positions of the cell associated with the vinculin protein. Hence, we conclude that torsional force spectroscopy is highly sensitive to focal adhesions and cell–cell junctions. It is worth mentioning that we simultaneously recorded dissipation maps in the in-plane direction and force maps in the out-of-plane direction (not shown). For the first ones, we do not observe any significant contrast in all z-layers which is indicative for the conservative character of the binding components of the cell. For the latter ones, we do obtain contrast at positions of focal adhesions and cell–cell junction, however, not as good resolved as in the lateral channel as a consequence of the stiff underlaying substrate to which the torsional oscillation modes remain unaffected.

Fig. 4 Torsional force spectroscopy mapping with subsequent fluorescence microscopy imaging. (a) Original torsional frequency shift map at a layer z = 1796 nm beneath the highest tip-sample contact point. The color scale has been chosen to show regions of highest values transparent. (b) Map shown in (a) with regions of highest values highlighted by solid black lines. The cell boundary to the substrate was marked by a solid cyan line. (c) Overlay of the fluorescence microscopy image of a BT20 cell with the torsional frequency-shift map. Vinculin proteins were stained with vinculin monoclonal antibodies. The image was captured at a wavelength of λ = 493 nm and an exposure time of t = 1 s. There is a convincing match between regions of the highest torsional frequency-shift values and vinculin-rich areas. (d) Zoom into the fluorescence image. (e) Fluorescence image of (d) highlighting the transparent regions of highest torsional frequency shift (lateral force) found with the help of (c). Two mismatches were located between high lateral force and potential location of focal adhesions (green marked areas). Nearly all vinculin-rich areas have been successfully identified by torsional force spectroscopy. (f) Pearson correlation coefficient analysis of various sub-areas (marked by frames) between fluorescence image (left) and lateral force map (right). The latter has been changed to 8-bit grayscale format and smoothed to remove noise and for better comparability.

3.3. Anchored cell vs. cell in locomotion

Strikingly, compared to cell #2, cell #1 exhibits a relatively large area containing focal adhesions which is visible as a broad belt of strong lateral forces located at the edge of the cell close (Fig. 3e) and immediate to the substrate (Fig. 3f). Cell #2 possesses merely two main anchor points: a cell–cell junction as a mechanical connection to cell #1 (highlighted by a black-red arrow, Fig. 3d) and focal adhesions to the glass substrate at the corner of the cell edge (orange arrow). We conclude that cell #2 is either in the state of detachment or more plausible, we observe the rear of a cell that is pushed forward by its leading-edge (outside of ROI). Suggested and experimentally substantiated by Ofera et al.,⁵³ when a cell is in motion, the cell front is pushed by concerted self-assembly of actin filament network acting on the membrane. Consequently, force is generated within the cell and transmitted via cell membrane, a lipid layer that can be considered as 2D fluid, eventually detaching actin residues at the rear of the cell (within ROI) and most likely recycling remaining cell adhesions to the substrate.⁵⁴ There is also a gradient of F-actin density from the leading edge to the rear of the cell increasing toward the front. The lack of an obvious focal adhesion network slightly off the edge as it is observable for cell #1 fits well to this assumption because vinculin is involved in cell adhesion as a linker between integrin adhesion molecules and the actin cytoskeleton, in other words, it mechanically connects actin filaments to the membrane and in turn to the substrate. Hence, if there is no vinculin apparent at the substrate, there is no actin present. The assumption of ongoing cell locomotion is further corroborated by the fact that we detected substantially weaker lateral forces in the vicinity of the edge of cell #2 (approx. −1.5 nN, white areas in Fig. 3e and f, highlighted by the yellow-black arrows) than on the rest of the substrate. We conclude that tip friction is considerably reduced either due to a modification of the substrate by the cell or a thin layer of residual protein leftovers from before cell retraction. Both are reasonable scenarios because a chemically modified substrate would be associated with a change in mechanical properties and residual proteins could ease tip sliding and act as a lubricant film on the substrate.

It should be emphasized that torsional force microscopy accomplished in the liquid medium is best performed with a photothermal cantilever excitation method to foster a sufficiently high signal-to-noise ratio and to prevent unwanted resonances. Not many commercial AFMs are currently equipped with a photothermal drive. Additionally, the imaging mode is not standard, can be time-consuming (up to ≈ 2 h per image), difficult to upscale in terms of higher throughputs and can be demanding to be performed in liquids with calibration needed for each cantilever eigenmode (see Materials and methods). Moreover, AFMs having this option and also capable of correlative fluorescence imaging are rare. Hence, at the current state the availability of this method will be limited to a few laboratories and further research and development by the manufacturers need to be done in order to promote the technique to a general tool for mechanobiology. Nevertheless, it is currently the only method that allows for directly probing the lateral forces of cells with nanoscale precision. Furthermore, torsional force spectroscopy is arbitrarily expandable with additional oscillation modes for the three-dimensional mechanical characterization or acquiring complementary physical properties. Hence, we expect the method to become a valuable tool to supplement biophysics, biology, cancer stage diagnostics and medical pathology in general in the medium-term future because it allows for the quantification of cell adherents with high lateral precision that could potentially be correlated with the pathological state of individual cells.

4. Conclusions

In conclusion, we present a method based on force microscopy that exploits the torsional oscillation of a cantilever to detect sub-surface lateral forces in living cells. In a combination with fluorescence microscopy, regions of high lateral forces could be identified as vinculin enriched areas. Since vinculin is a protein involved in cell–matrix and cell–cell junctions, these locations can be attributed to the presence of focal adhesions or integrin/cadherin aggregations with enhanced shear stress compared to their surroundings. The focal adhesions were mainly concentrated at the edge of the cells, however, networks of them were also found slightly off the edge towards cell nuclei. The cell–cell interface appeared as a band of high lateral forces due to the existence of cell–cell junctions along the connection. We stress that this is a proof-of-principle study and that the method in the current state is not calibrated to relate the measured lateral forces with the degree of maturity of cell-to-cell junctions. The observation of the layer formation at the cell edge demonstrates the sensitivity of the technique in terms of mechanical properties and friction. It shows the complementary nature of the additional tip vibration facilitating the visualization of highly viscous surface layers otherwise not accessible. We also note that with our current setup mechanical characterization of the living cells by force spectroscopy and the identification of cell components in the fixed state by fluorescence microscopy is accomplished with two separated instruments. A combined setup would allow for correlative imaging without delays between mechanical cell characterization and component identification by live cell staining.

Author contributions

C. D. conceived and designed the experiments. K. W., J. B. and C. D. performed the experiments. A. A. supervised the cell culturing and staining. N. S., A.-L. E. and M. D. coded the Matlab programs. K. W., J. B. and C. D. analyzed the results. C. D. drafted the manuscript. All authors discussed the results and helped to finalize the manuscript.

Data availability

All data supporting the findings and conclusions of this study are available within the paper. All other relevant data are available from the corresponding author upon reasonable request. Source data are provided with this paper.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors thank the Deutsche Forschungsgemeinschaft (Project numbers 318205773 and 407750697) for financial support.

Notes and references

1. J. Ferlay, M. Colombet, I. Soerjomataram, D. M. Parkin, M. Pineros, A. Znaor and F. Bray, Int. J. Cancer, 2021, 149, 778–789.
2. T. J. C. Harris and U. Tepass, Nat. Rev. Mol. Cell Biol., 2010, 11, 502–514.
3. L. Shen, C. R. Weber, D. R. Raleigh, D. Yu and J. R. Tumer, in Annual Review of Physiology, ed. D. Julius and D. E. Clapham, 2011, vol. 73, pp. 283–309.
4. S. Getsios, A. C. Huen and K. J. Green, Nat. Rev. Mol. Cell Biol., 2004, 5, 271–281.
5. N. M. Kumar and N. B. Gilula, Cell, 1996, 84, 381–388.
6. K. Burridge and M. ChrzanowskaWodnicka, Annu. Rev. Cell Dev. Biol., 1996, 12, 463–518.
7. R. Serrano, A. Aung, Y. T. Yeh, S. Varghese, J. C. Lasheras and J. C. Del Alamo, Biophys. J., 2019, 117, 111–128.
8. X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler and J. J. Fredberg, Nat. Phys., 2009, 5, 426–430.
9. M. Prabhune, F. Rehfeldt and C. F. Schmidt, J. Phys. D: Appl. Phys., 2017, 50, 233001.
10. I. Schoen, W. Hu, E. Klotzsch and V. Vogel, Nano Lett., 2010, 10, 1823–1830.
11. B. Zhao, C. O'Brien, A. P. K. K. K. Mudiyanselage, N. Li, Y. Bagheri, R. Wu, Y. Sun and M. You, J. Am. Chem. Soc., 2017, 139, 18182–18185.
12. D. T. Tambe, C. C. Hardin, T. E. Angelini, K. Rajendran, C. Y. Park, X. Serra-Picamal, E. H. Zhou, M. H. Zaman, J. P. Butler, D. A. Weitz, J. J. Fredberg and X. Trepat, Nat. Mater., 2011, 10, 469–475.
13. A. Shinde, K. Illath, P. Gupta, P. Shinde, K. T. Lim, M. Nagai and T. S. Santra, Cells, 2021, 10, 577.
14. A. R. Harris, L. Peter, J. Bellis, B. Baum, A. J. Kabla and G. T. Charras, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16449–16454.
15. A. X. Cartagena-Rivera, C. M. Van Itallie, J. M. Anderson and R. S. Chadwick, Nat. Commun., 2017, 8, 1030.
16. C. Arbore, L. Perego, M. Sergides and M. Capitanio, Biophys. Rev., 2019, 11, 765–782.
17. C. G. Galbraith, K. M. Yamada and M. P. Sheetz, J. Cell Biol., 2002, 159, 695–705.
18. A. K. Harris, P. Wild and D. Stopak, Science, 1980, 208, 177–179.
19. H. Colin-York, Y. Javanmardi, L. Barbieri, D. Li, K. Korobchevskaya, Y. Guo, C. Hall, A. Taylor, S. Khuon, G. K. Sheridan, T. L. Chew, D. Li, E. Moeendarbary and M. Fritzsche, Nano Lett., 2019, 19, 4427–4434.
20. W. R. Legant, C. K. Choi, J. S. Miller, L. Shao, L. Gao, E. Betzig and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 881–886.
21. M. Ghibaudo, A. Saez, L. Trichet, A. Xayaphoummine, J. Browaeys, P. Silberzan, A. Buguin and B. Ladoux, Soft Matter, 2008, 4, 1836–1843.
22. C. M. Franz and D. J. Muller, J. Cell Sci., 2005, 118, 5315–5323.
23. K. Haase and A. E. Pelling, J. R. Soc., Interface, 2015, 12, 20140970.
24. C. Grashoff, B. D. Hoffman, M. D. Brenner, R. Zhou, M. Parsons, M. T. Yang, M. A. McLean, S. G. Sligar, C. S. Chen, T. Ha and M. A. Schwartz, Nature, 2010, 466, 263–266.
25. N. Wang, J. P. Butler and D. E. Ingber, Science, 1993, 260, 1124–1127.
26. N. Mandriota, C. Friedsam, J. A. Jones-Molina, K. V. Tatem, D. E. Ingber and O. Sahin, Nat. Mater., 2019, 18, 1071–1077.
27. M. Dong, S. Husale and O. Sahin, Nat. Nanotechnol., 2009, 4, 514–517.
28. M. Dong and O. Sahin, Nat. Commun., 2011, 2, 247.
29. C. R. Guerrero, P. D. Garcia and R. Garcia, ACS Nano, 2019, 13, 9629–9637.
30. Y. M. Efremov, D. M. Suter, P. S. Timashev and A. Raman, Sci. Rep., 2022, 12, 529.
31. L. Stühn, A. Fritschen, J. Choy, M. Dehnert and C. Dietz, Nanoscale, 2019, 11, 13089–13097.
32. C. Roduit, S. Sekatski, G. Dietler, S. Catsicas, F. Lafont and S. Kasas, Biophys. J., 2009, 97, 674–677.
33. C. Roduit, G. Longo, I. Benmessaoud, A. Volterra, B. Saha, G. Dietler and S. Kasas, J. Mol. Recognit., 2012, 25, 241–246.
34. A. Raman, S. Trigueros, A. Cartagena, A. P. Z. Stevenson, M. Susilo, E. Nauman and S. A. Contera, Nat. Nanotechnol., 2011, 6, 809–814.
35. A. Wang, K. Vijayraghavan, O. Solgaard and M. J. Butte, ACS Nano, 2016, 10, 257–264.
36. A. Knoll, R. Magerle and G. Krausch, Macromolecules, 2001, 34, 4159–4165.
37. M. Zerson, E. C. Spitzner, C. Riesch, R. Lohwasser, M. Thelakkat and R. Magerle, Macromolecules, 2011, 44, 5874–5877.
38. M. Dehnert and R. Magerle, Nanoscale, 2018, 10, 5695–5707.
39. M. R. Uhlig, S. Benaglia, R. Thakkar, J. Comer and R. Garcia, Nanoscale, 2021, 13, 5275–5283.
40. R. Garcia, Chem. Soc. Rev., 2020, 49, 5850–5884.
41. H. J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1–7.
42. C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 2004, 75, 1988–1996.
43. C. Dietz, Nanoscale, 2018, 10, 460–468.
44. J. Welker, E. Illek and F. J. Giessibl, Beilstein J. Nanotechnol., 2012, 3, 238–248.
45. T. Meier, B. Eslami and S. D. Solares, Nanotechnology, 2016, 27, 085702.
46. F. F. Canova, S. Kawai, C. de Capitani, K. I. Kanno, T. Glatzel, B. Such, A. S. Foster and E. Meyer, Phys. Rev. Lett., 2013, 110, 203203.
47. A. L. Eichhorn and C. Dietz, Adv. Mater. Interfaces, 2021, 8, 2101288.
48. A. L. Eichhorn, M. Hoffer and C. Dietz, Carbon, 2022, 200, 124–133.
49. J. E. Sader and S. P. Jarvis, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 012303.
50. J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801–1803.
51. P. A. Thoren, A. S. de Wijn, R. Borgani, D. Forchheimer and D. B. Haviland, Nat. Commun., 2016, 7, 13836.
52. C. T. Mierke, Cell Biochem. Biophys., 2009, 53, 115–126.
53. N. Ofera, A. Mogilner and K. Keren, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20394–20399.
54. A. D. Bershadsky and M. M. Kozlov, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20275–20276.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01685k

‡ These authors contributed equally.

---