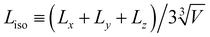Impact of granular inclusions on the phase behavior of colloidal gels

Abstract

Colloidal gels formed from small attractive particles are commonly used in formulations to keep larger components in suspension. Despite extensive work characterising unfilled gels, little is known about how the larger inclusions alter the phase behavior and microstructure of the colloidal system. Here we use numerical simulations to examine how larger ‘granular’ particles can alter the gel transition phase boundaries. We find two distinct regimes depending on both the filler size and native gel structure: a ‘passive’ regime where the filler fits into already-present voids, giving little change in the transition, and an ‘active’ regime where the filler no longer fits in these voids and instead perturbs the native structure. In this second regime the phase boundary is controlled by an effective colloidal volume fraction given by the available free volume.

---

1 Introduction

Dispersions of attractive colloids can form solid-like gels characterized by a system-spanning network of arrested particles.^1–3 These colloidal gels are ubiquitous, encountered in disparate industries ranging from food and personal care products to building materials and catholyte slurries.^4–7 While there has been considerable progress in understanding the formation, structure and rheology of ‘model’ colloidal gels formed from (nearly) uniformly sized spheres,^8–11 most practical gels are more complex. In particular, colloidal gels frequently serve as a carrier for larger, non-Brownian ‘granular’ components (typical size ≳10 μm). In such composites, the gel often acts as a rheology modifier to prevent sedimentation. In some applications the gel network itself may be desired, for example catholyte slurries for battery manufacturing rely on a conductive carbon black gel to provide connectivity between the active Li-ion ‘grains’.

It is thus critical to understand how granular inclusions alter the colloidal gel phase. Recent work examining the influence of inclusions on gel rheology suggests they have a significant impact,^12,13 even introducing new phenomena such as rheological bi-stability in these filled systems.¹⁴ This previous work has largely focused on systems deep into the gel state, so it remains unclear how granular inclusions alter the gel transition and phase behavior (but see Jiang and Seto¹⁵).

For uniformly-sized colloidal spheres, the gelation phase boundaries depend on the colloid concentration and attraction strength, and there has been extensive work mapping these boundaries in a variety of systems.^11,16–25 In depletion gels there is good agreement between gelation and the gas–liquid spinodal boundary,²⁶ though there remains some debate concerning the generality of this agreement and the relative roles of percolation and clustering at the gel transition.^23–25,27

The inclusion of larger grains introduces additional control parameters which can potentially alter these phase boundaries. For simple ‘hard’ grains interacting solely through their excluded volume, their influence will be set by the filler concentration and the size ratio r_L/r_S between the large (L) grains and the smaller (S) colloids. These granular inclusions reduce the free volume available to the colloids relative to the total volume, but the interplay between the inclusions and gel structure is non-trivial, as colloidal gels can be heterogeneous on length scales ≫r_S.^3,28,29

Here we characterise the influence of hard granular inclusions on the colloidal gel phase boundaries using numerical simulations, where the particle sizes, interactions and volume fractions can all be precisely varied. We find that the relative sizes of the inclusions and the void spaces present in the unfilled gels is the key parameter governing the phase behavior of the filled systems.

2 Methods

We simulate the trajectories of 10⁴ colloidal and a smaller number of granular spheres in a periodic box (volume V), using LAMMPS.³⁰ Motion is governed by the Langevin equation, which for particle i reads m_idU_i/dt =F^H_i + F^B_i + F^P_i, with m_i = (4/3)πr_i³ρ and U_i the particle mass and velocity respectively (we assume density ρ matching between all particle species and the solvent). The hydrodynamic force F^H_i= −6πηr_i(U_i − U^∞_i) captures Stokes drag on a sphere of radius r_i, with U^∞_i the background fluid velocity at the sphere centre (generally set to 0 except under oscillatory shear).

Brownian forces are generated as 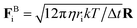, where Δt is the timestep, kT the thermal energy and the elements of the vector R are drawn from a Gaussian distribution with zero-mean and no time correlation. The characteristic diffusive timescale for a particle with radius r_i is thus 6πηr_i³/kT. To avoid crystallisation in the small colloids, we use a binary size mixture with radii r_S and 1.4r_S (mixed equally by number), while the larger grains are monodisperse with radius r_L varying from 8r_S to 24r_S. Since the diffusion time scales as r_i³, for the larger grains it is >500 times longer than the colloidal timescale τ_B = 6πηr_S³/kT, so that even though Brownian forces are applied uniformly to all particles the larger grains are effectively non-Brownian.

Colloids (labeled i and j) at a distance r and surface-to-surface separation δ_ij = r − (r_i + r_j) interact via a Morse potential, giving a pairwise force with n_ij the center-to-center unit vector. This potential gives finite-ranged attraction, and repulsion for overlapping particles (δ_ij < 0). The interaction length scale is set as κ_ij⁻¹ = (r_i + r_j)/200 to give short-ranged attraction. We evaluate the force when δ_ij < 0.03(r_i + r_j) (following conventional practice, see e.g. Sciortino et al.³¹), beyond which the attractive force is <1% of its maximum value. We defined contacts using the same threshold of δ_ij, having verified that a more stringent criteria does not affect any of the conclusions we draw. The depth of the attractive potential ε is varied between kT and 20kT, with a variable step size to refine our estimates of the gelation point. Colloid–granular and granular–granular contact forces are modeled as linear springs F^p_ij = −k_nδ_ijn_ij, with a stiffness k_n set sufficiently large (k_nr_S²/kT = 5 × 10⁴) to approximate hard-sphere interactions. The timestep Δt is set to 10⁻⁴, substantially smaller than the Brownian time τ_B, the contact time and the inertial relaxation time τ_i = r_S²ρ/η (with η sufficiently large that τ_i ≪ τ_B).

We characterise the mechanical response of steady-state structures by applying an oscillatory shear through the liquid streaming velocity as U^∞_i(t,y_i) = y_iγ₀sin ωt and turning off the Brownian forces. We remain in the low amplitude regime by setting γ₀ = 0.005, and set ω such that inertia plays no role (in practice this is achieved when ωτ_i ≤ 0.005). The bulk shear stress is computed as 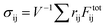(with the sum being over all interacting pairs), and the viscoelastic moduli G′ and G′′ are computed from the Fourier transform of σ_xy averaged over 50 shear cycles. All results for both the elastic moduli and L_iso are averages from at least 6 independent realisations with randomized granular and colloidal initial positions. We simulated a larger system of 10⁵ colloids with r_L/r_S = 24 inclusions and confirmed that its results are consistent with the 10⁴ system both in terms of L_iso and in the distribution of isostatic cluster sizes.

3 Results and discussion

The system initially equilibrates at a prescribed volume fraction in the absence of colloidal attraction, after which the interaction potential with depth ε/kT is turned on and the system evolves for up to 10⁴τ_B to reach a steady state. To map the phase behavior of these systems, we vary ε/kT along with the colloidal and granular volume fractions, ϕ_S = V_s/V and ϕ_L = V_L/V. These volume fractions are defined as the volume occupied by the colloids (grains), V_s (V_L), relative to the total volume of the cubic simulation box, so that increasing ϕ_L at fixed ϕ_S decreases the free volume available to the colloids.

3.1 Isostaticity percolation and mechanical response

To explore how large granular inclusions alter the colloidal microstructure, we characterize networks of isostatic particles, defined as colloids with N ≥ 6 contacts. This follows from the Maxwell criteria for stability in a system with pairwise central forces, requiring that constraints balance the degrees of freedom.³² While this isostaticity criterion is typically considered globally in the context of granular packings,³³ it has been suggested that networks of locally isostatic particles control the rigidity of colloidal gels.^9,34 Specifically, recent experimental work suggests the gel transition coincides with the formation of a percolating network of isostatic particles.³⁵

We define contacts among attractive colloids as pairs (radii r_i and r_j) within a separation 0.03(r_i + r_j). To characterise the distance from isostaticity percolation, we first remove colloids with N < 6 contacts and then identify clusters of isostatic particles. The isostatic length, L_iso, gives the mean length of the largest isostatic cluster in all three spatial dimensions relative to the box size (Fig. 1(A)), so that L_iso = 1 corresponds to isotropic isostaticity percolation (in principle L_iso may exceed unity once the periodic box is unwrapped, in which case we limit it to this value).

Fig. 1 Isostaticity percolation and its relation to the mechanical response. (A) Procedure for determining L_iso. Left to right: Isostatic colloids with N ≥ 6 contacts (red) are isolated and contacting clusters identified. The isostatic length is computed from the span of the largest cluster, (). (B) Time evolution of 1 − L_iso for an unfilled system (ϕ_S = 0.2, ϕ_L = 0) at varying attraction ε/kT. (C) Steady-state 1 − L^ss_iso (black, left axis) and viscoelastic moduli G′ and G′′ (red filled and open symbols, respectively, right axis) verses ε/kT. Green arrow highlights the coincidence between the crossover G′ = G′′ and 1 − L^ss_iso → 0. Inset: Rendering of a steady-state (t/τ_B > 10³) gel state for ε/kT = 5.6 with ϕ_S = 0.2, ϕ_L = 0. (D) and (E) reproduce (B) and (C), respectively, for a filled system with ϕ_S = 0.20, ϕ_L = 0.3. Inset in (E) shows a rendering with granular inclusions (yellow) at ε/kT = 5.6. Error bars in (C) and (E) indicate the standard deviation from 6 realisations. Dotted lines in (C) and (E) (and later figures) are used to indicate data crossing the broken y-axis.

In pure colloidal suspensions (ϕ_L = 0), the colloids are initially well-dispersed, with L_iso ≈ 0 (so that 1 − L_iso ≈ 1). Turning on the attraction ε at time t = 0 causes clusters to form and grow, reflected in an increase in L_iso(t) with time (Fig. 1(B)). As time progresses this initial growth slows and the isostatic length approaches a plateau at some steady-state value L^ss_iso at long times (t ≳ 10³–10⁴τ_B). The growth of L_iso(t) depends on the attraction strength, with strongly attractive colloids rapidly reaching isostaticity percolation at L^ss_iso = 1 (1 −L^ss_iso = 0) while with weaker attraction L_iso instead appears to plateau at some steady-state value L^ss_iso < 1, short of the percolation threshold. Reaching steady states in L_iso(t) gets progressively slower as we approach the critical interaction energy ε*, and truncating our time series at 10³–10⁴τ_B limits our resolution in ε* to ±0.1kT. This limitation will not affect the outcomes of our work, and future studies aiming to obtain ε* with greater precision will require substantially larger particle numbers and run times.

We apply small amplitude oscillatory shear γ(t) = γ₀ sin ωt to extract the viscoelastic moduli G′ and G′′ for the structures obtained at the end of each time series. We find a transition from liquid-like states (G′ < G′′) to solid-like states (G′ > G′′) as the attraction strength ε is increased (Fig. 1(C)), indicating the emergence of a solid-like gel. The crossover point where G′ = G′′ occurs as L^ss_iso approaches unity at interaction energy ε* indicating that the gel transition coincides with isostaticity percolation in agreement with Tsurusawa et al.³⁵ We verified this agreement holds for ϕ_S ≤ 0.4, and that our phase diagram reported below is consistent with that obtained purely via rheology.

3.2 Role of granular inclusions

The addition of granular inclusions gives qualitatively similar behavior in both the evolution of L_iso with time and the mechanical response of the steady state structures, Fig. 1(D) and (E). We again find good agreement between isostaticity percolation (L^ss_iso = 1) and the emergence of mechanical rigidity (G′ = G′′), indicated by green arrows in Fig. 1(C) and (E). Comparing these transition points for filled (r_L = 8r_S, ϕ_L = 0.3) and unfilled systems both at ϕ_S = 0.2, we find that the inclusions aid gelation with a reduced ε* in the filled system.

To understand this shift in the gelation point, we examine how granular inclusions alter the structure and distribution of the isostatic colloidal particles. In a pure colloidal system below the gel transition, ε = 5.1kT = 0.94ε* and ϕ_S = 0.2, there are numerous disjoint clusters of isostatic particles (Fig. 2(A)) and the system remains well below the isostatic percolation threshold. The inclusion of the larger grains increases the number of isostatic colloidal particles, enabling them to instead form a large connected network which percolates across the sample for ϕ_L = 0.4 (Fig. 2(B)).

Fig. 2 Contrasting effects of granular inclusions. Shown are snapshots of steady-state (t = 10³–10⁴τ_B) configurations, with ϕ_S = 0.2 and ε = 0.94ε₀* for (A) ϕ_L = 0 and; (B) ϕ_L = 0.4. Only isostatic colloids are rendered, with the largest cluster shown in red. Larger grains are shown (grey) in (B). (C) and (D) 1 − L^ss_iso(ϕ_L) at varying ε for (C) ϕ_S = 0.2 and (D) ϕ_S = 0.1. Values for ε given relative to the gelation point in the unfilled system, ε₀*, with ε₀* = 5.3kT for ϕ_S = 0.2 and ε₀* = 6.1kT for ϕ_S = 0.1. Dashed squares (a) and (b) indicate states rendered in (A) and (B), respectively. (E) and (F) probability distribution of the number of contacts per particle as a function of ϕ_L, for (E) ϕ_S = 0.2, ε = 5.1kT and (F) ϕ_S = 0.07, ε = 6.6kT. Both cases cross the phase boundary as ϕ_L is increased.

This observation is reflected in the microstructural statistics: for fixed ϕ_S = 0.2, we find that L^ss_iso of an initially liquid system increases dramatically with increasing ϕ_L (Fig. 2(C)), mirrored by a shift to larger N in the probability distribution of particle contact numbers (Fig. 2(E)). Defining ε₀* ≡ ε*(ϕ_L = 0) the critical interaction energy in the unfilled system, granular inclusions can take a system initially quite far from the gelation point (ε = 0.91ε₀* and L^ss_iso ≈ 0) nearly up to the transition point L^ss_iso ≈ 0.98 as ϕ_L increases up to ϕ_L = 0.4. Increasing the interaction energy to ε/ε₀* = 0.96, the volume of granular filler needed to drive isostaticity percolation decreases, so that the gelation boundary ε* where L^ss_iso reaches unity continuously shifts to lower values with increasing ϕ_L.

Since the free volume available to the colloids decreases with increasing ϕ_L, one might expect this described increase in the number of isostatic particles, and hence an increase in L^ss_iso in the filled system. Furthermore, the gel phase boundary for unfilled systems, ε₀*(ϕ_S), is a decreasing function of ϕ_S, at least at low to moderate concentrations.^16–25 This suggests the possibility of capturing the shifting gel point with granular inclusions simply in terms of the reduced free volume available to the colloids. In this picture, one would expect the filler to have more pronounced effect at lower colloid concentrations, where the curve ε₀*(ϕ_S) is steepest. However, simulations with ϕ_S = 0.1 (and lower) instead show the opposite, with the inclusion of large grains giving only a modest increase in L^ss_iso (Fig. 2(D)), having little to no effect on P(N) (Fig. 2(F)), and generating only minor shifts in the gelation phase boundary. This unexpected result demonstrates that a universal picture in which the gel state is defined entirely by an effective colloidal volume fraction does not apply.

3.3 Fillers and voids

To understand the reduced filler impact at low ϕ_S, we look at how the microstructure of the colloidal phase varies with concentration. Specifically, we focus on the size distribution of the empty voids between the colloids at (or close to) the gel transition.³⁶ We compute this distribution by dividing the simulation volume into cubic cells (length r_S) and then finding the largest possible sphere (radius r_v) centered in each cell that avoids intersecting a colloidal particle (so that larger grains are treated as empty voids). Normalised histograms of these local void radii give the void size distribution P(r_v).

For an unfilled colloidal system with ϕ_S = 0.2 close to the gel transition (ε = 5.3kT ≈ ε₀*), this distribution is nearly flat up to r_v ≈ 3r_S and then falls off rapidly as r_v increases further (Fig. 3(A)) with voids larger than r_v ≈ 6r_S exceedingly rare. While precisely characterizing the rare-event tails in P(r_v) would require significant computational effort, we can define an effective maximum void size P(r^max_v) = 10⁻⁴, as voids larger then this are effectively absent in our observed configurations. Adding larger granular inclusions, with r_L = 8r_S > r^max_v, perturbs the colloidal microstructure and shifts the shoulder in P(r_v) to higher radii ≈r_L, reflecting the voids created by the large grains.

Fig. 3 Void-volumes in filled and unfilled systems near the gel boundary. Normalized colloidal void size distribution P(r_v) for (A) ϕ_S = 0.2 (ε = 5.3kT ≈ ε₀*) and (B) ϕ_S = 0.1 (ε = 6.3kT ≈ ε₀*) at varying ϕ_L. The large particle size is r_L = 8r_S (highlighted by black dashed vertical lines), with the exception of the red filled symbols in (B) where r_L = 16r_S (highlighted by the red dashed vertical line). (C) 1 − L^ss_iso(ϕ_L) for ε = 5.8kT (red circles) and 5.5kT (blue triangles), with open symbols for r_L = 8r_S and filled symbols for r_L = 16r_S. Schematic cartoon in (D) presents a simplified picture to understand the influence (or lack thereof) of the granular filler on the gel structure, with large grains either fitting into ‘natural’ voids in the gel, leaving the colloidal microstructure unaffected (black arrow), or forcing larger voids, which in turn distorts and compresses the colloidal phase (red arrows).

However, reducing the colloid concentration to ϕ_S = 0.1 gives a significantly wider distribution of void sizes in the unfilled system, with the shoulder in P(r_v) now around r_v = 8r_S and r^max_v ≈ 12r_S (Fig. 3(B)). This indicates there are ‘pre-existing’ voids which can accommodate the larger r_L = 8r_S grains without forcing a significant change in the colloidal microstructure. Indeed, in contrast to the large shift seen for ϕ_S = 0.2, here increasing ϕ_L has only a minor impact on the shape of P(r_v). This suggests a picture where dilute gels with r_v > r_L can effectively form around the immobile granular inclusions, forming a network of colloid–colloid contacts that is essentially indistinguishable from the unfilled case. With no change in this network, L_iso is unaffected by the granular inclusions and there is little shift in the gel phase boundary. We would thus expect that increasing r_L above the characteristic void size would result in a more pronounced filler-effect on L^ss_iso and the gelation point in these more dilute gels.

We find this is indeed the case when r_L is increased from 8r_S to 16r_S. These larger grains now notably shift P(r_v) to higher values (compare open and filled symbols in Fig. 3(B)), and we also now find a clear increase in L^ss_iso(ϕ_L) (Fig. 3(C)), similar to the impact of the r_L = 8r_S grains in the ϕ_S = 0.2 system with smaller voids. This supports a simplified picture of the interplay between the granular inclusions and attractive colloids (Fig. 3(D)); grains with r_L < r_v have little impact on the gel structure or transition point as they easily fit into the gel voids, while grains with r_L > r_v distort and compress colloidal structures, increasing L^ss_iso and reducing the attraction needed to form the gel.

3.4 Phase diagram

Having detailed the influence of granular inclusions at two specific ϕ_S, we now map out the gel phase boundaries over a range of ϕ_S and ϕ_L. Having demonstrated good agreement between the rigidity onset and isostaticity percolation, we use L^ss_iso to classify states as it provides a more direct microstructural measure. Carrying out a series of simulations at varying ε for given ϕ_S and ϕ_L, we define the transition point ε* as the point at which L^ss_iso = L_iso* = 1. The dimensions of our simulation box are such that we cannot reach values of 0.9999 < L^ss_iso < 1, which again places a limitation on the precision with which we can determine ε*. For the range of ϕ_S explored here (up to ϕ_S = 0.4), we find the isostatic percolation boundary ε*(ϕ_S) monotonically decreases with increasing ϕ_S (Fig. 4 inset). For fixed r_L = 8r_S, increasing ϕ_L at fixed ϕ_S generally shifts this boundary to lower attraction strength.

Fig. 4 Isostatic percolation boundaries ε* varying ϕ_S and ϕ_L. Inset: Critical attractive energy ε*(ϕ_S) for varying ϕ_L (indicated in main panel legend) for r_L = 8r_S. Main panel: Open symbols show same data as inset, now plotted against ϕ_eff = ϕ_S/(1 − ϕ_L). Solid symbols show results for larger grains and smaller ϕ_S, with r_L = 16r_S for ϕ_S = 0.1 and r_L = 24r_S for ϕ_S = 0.07 so that r_L > r^max_v in both cases. Error bars on ε* computed using error bars on L^ss_iso to obtain upper and lower bounds for the point the isostatic length reaches the threshold L^ss_iso = 1 and are shown only in the inset for clarity.

Instead plotting these isostatic percolation boundaries as a function of an effective volume fraction ϕ_eff ≡ ϕ_S/(1 − ϕ_L), giving the volume fraction of the small colloids relative to the free volume excluding the large grains (1 − ϕ_L)V, we find reasonable collapse for ϕ_eff ≳ 0.2 (Fig. 4 main panel). This suggests that the filler-induced shifts in the phase boundary can be understood solely through the reduction in free volume available to small colloids, so that adding larger grains is effectively equivalent to shrinking the box volume. However, for ϕ_S ≲ 0.1 we find this collapse breaks down, with points at higher ϕ_L lying clearly above the ϕ_L = 0 boundary. This is consistent with the behavior seen in Fig. 2(D), where the granular inclusions only have a minor effect on L_iso for ϕ_S = 0.1 compared to the significant enhancement seen at a higher ϕ_S = 0.2.

Increasing the size of the large particles to ensure r_L > r^max_v, in this case setting r_L = 16r_S for ϕ_S = 0.1 and r_L = 24r_S for ϕ_S = 0.07, we find that this collapse can be recovered (filled symbols in Fig. 4). We thus see that when the granular inclusions are significantly larger than the typical voids in the unfilled gel, so that they force a notable change in the gel microstructure, the influence of the voids can be captured by the effective free volume available to the small colloids. With smaller grains this effect is diminished, with the phase boundary instead largely independent of the filler concentration.

4 Conclusions

Using Langevin dynamics simulations, we have mapped out the influence of larger granular inclusions on isostaticity percolation and the gel transition in suspensions of smaller attractive colloids. Varying the volume fractions of both species, we demonstrated two distinct regimes: (i) a ‘passive void-filling’ regime, where the granular inclusions can fit into already-present voids within the gel, so that the microstructure is effectively unchanged and the gel transition governed almost solely by ϕ_S and (ii) an ‘active void-enhancing’ regime where the granular inclusions perturb the gel structure by forcing larger voids and the gel transition is governed by an effective volume fraction ϕ_eff = ϕ_S/(1 − ϕ_L). These two limiting regimes are differentiated by the size ratio of the larger grains r_L and the shape of the gel void size distribution P(r_v), so that anticipating the impact of the granular filler requires detailed characterization of the unfilled gel structure.

To obtain these insights it has been necessary to omit more detailed aspects of the physics from our simulation model. Importantly, we are operating under density matched conditions so that gravity may be neglected. Gravity plays a key role in filled gels (indeed in applications the role of the gelled phase is often to stabilise the grains against sedimentation) and in unfilled ones alike,³⁷ and will be an important aspect of future research that builds on the results presented here. We have also omitted full hydrodynamics³⁸ from our model, noting that they likely play an important role under dynamic conditions but are less important in determining the static gel structure.^39,40

There is relatively little experimental work examining the phase behavior of filled colloidal gels, though a recent study using a battery electrode slurry (a carbon black gel with ≈10 μm granular inclusions) found little change with addition of the granular particles.⁷ Given the very low gel point (occurring at ϕ_S ≈ 0.02), it is plausible that the carbon black gel contains sufficiently large voids to place this system in regime (i), though detailed characterisation of the gel structure would be required to confirm this. Our results should be particularly relevant to battery slurry formulation and electrode fabrication, where particle connectivity is key for performance,⁶ providing a road map to match the native gel structure and filler properties to tune the electrode microstructure.

Author contributions

YL, JR, JS and CN planned the research; YL carried out the research; YL, JR and CN wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

YL is funded by the China Scholarship Council (CSC) and by the University of Edinburgh through a School of Engineering studentship. C. N. acknowledges support from the Royal Academy of Engineering under the Research Fellowship scheme. The work was supported by the UK Engineering and Physical Sciences Research Council under grant EP/N025318/1. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission. The data used to generate the figures in this article is available via Edinburgh DataShare at https://doi.org/10.7488/ds/3796.

Notes and references

1. V. Trappe and P. Sandkühler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500.
2. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
3. C. P. Royall, M. A. Faers, S. L. Fussell and J. E. Hallett, J. Phys.: Condens. Matter, 2021, 33, 453002.
4. K. Y. Cho, Y. I. Kwon, J. R. Youn and Y. S. Song, Mater. Res. Bull., 2013, 48, 2922–2926.
5. T.-S. Wei, F. Y. Fan, A. Helal, K. C. Smith, G. H. McKinley, Y.-M. Chiang and J. A. Lewis, Adv. Energy Mater., 2015, 5, 1500535.
6. W. B. Hawley and J. Li, J. Energy Storage, 2019, 25, 100862.
7. S. L. Morelly, M. H. Tang and N. J. Alvarez, Polymers, 2017, 9, 461.
8. V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775.
9. L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16029–16034.
10. G. Wang, A. M. Fiore and J. W. Swan, J. Rheol., 2019, 63, 229–245.
11. J. Rouwhorst, P. Schall, C. Ness, T. Blijdenstein and A. Zaccone, Phys. Rev. E, 2020, 102, 022602.
12. C. Ferreiro-Córdova, G. Foffi, O. Pitois, C. Guidolin, M. Schneider and A. Salonen, Soft Matter, 2022, 18, 2842–2850.
13. C. Ferreiro-Cordova, E. Del Gado, G. Foffi and M. Bouzid, Soft Matter, 2020, 16, 4414–4421.
14. Y. Jiang, S. Makino, J. R. Royer and W. C. Poon, Phys. Rev. Lett., 2022, 128, 248002.
15. Y. Jiang and R. Seto, 2022, preprint, arXiv:2211.12978 DOI:10.48550/arXiv.2211.12978.
16. M. C. Grant and W. B. Russel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 2606–2614.
17. H. Verduin and J. K. Dhont, J. Colloid Interface Sci., 1995, 172, 425–437.
18. W. C. K. Poon, A. D. Pirie and P. N. Pusey, Faraday Discuss., 1995, 101, 65–76.
19. P. N. Segrè, V. Prasad, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2001, 86, 6042–6045.
20. S. A. Shah, Y.-L. Chen, K. S. Schweizer and C. F. Zukoski, J. Chem. Phys., 2003, 119, 8747–8760.
21. H. Sedgwick, K. Kroy, A. Salonen, M. B. Robertson, S. U. Egelhaaf and W. C. K. Poon, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 16, 77–80.
22. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
23. A. P. Eberle, N. J. Wagner and R. Castaneda-Priego, Phys. Rev. Lett., 2011, 106, 105704.
24. M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133.
25. K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Nat. Commun., 2019, 10, 2237.
26. R. Tuinier and H. N. Lekkerkerker, Colloids and the Depletion Interaction, Springer, Netherlands, 2011.
27. S. Zhang, L. Zhang, M. Bouzid, D. Z. Rocklin, E. Del Gado and X. Mao, Phys. Rev. Lett., 2019, 123, 058001.
28. A. Fierro, E. D. Gado, A. de Candia and A. Coniglio, J. Stat. Mech.: Theory Exp., 2008, 2008, L04002.
29. A. Zaccone, H. Wu and E. Del Gado, Phys. Rev. Lett., 2009, 103, 208301.
30. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
31. F. Sciortino, S. Mossa, E. Zaccarelli and P. Tartaglia, Phys. Rev. Lett., 2004, 93, 055701.
32. J. C. Maxwell, London, Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27, 294–299.
33. M. van Hecke, J. Phys.: Condens. Matter, 2009, 22, 033101.
34. G. Wang, A. M. Fiore and J. W. Swan, J. Rheol., 2019, 63, 229–245.
35. H. Tsurusawa, M. Leocmach, J. Russo and H. Tanaka, Sci. Adv., 2019, 5, eaav6090.
36. N. Koumakis, E. Moghimi, R. Besseling, W. C. Poon, J. F. Brady and G. Petekidis, Soft Matter, 2015, 11, 4640–4648.
37. R. Harich, T. Blythe, M. Hermes, E. Zaccarelli, A. Sederman, L. F. Gladden and W. C. Poon, Soft Matter, 2016, 12, 4300–4308.
38. Z. Varga, G. Wang and J. Swan, Soft Matter, 2015, 11, 9009–9019.
39. C. Ness and A. Zaccone, Ind. Eng. Chem. Res., 2017, 56, 3726–3732.
40. J. De Graaf, W. C. Poon, M. J. Haughey and M. Hermes, Soft Matter, 2019, 15, 10–16.

---